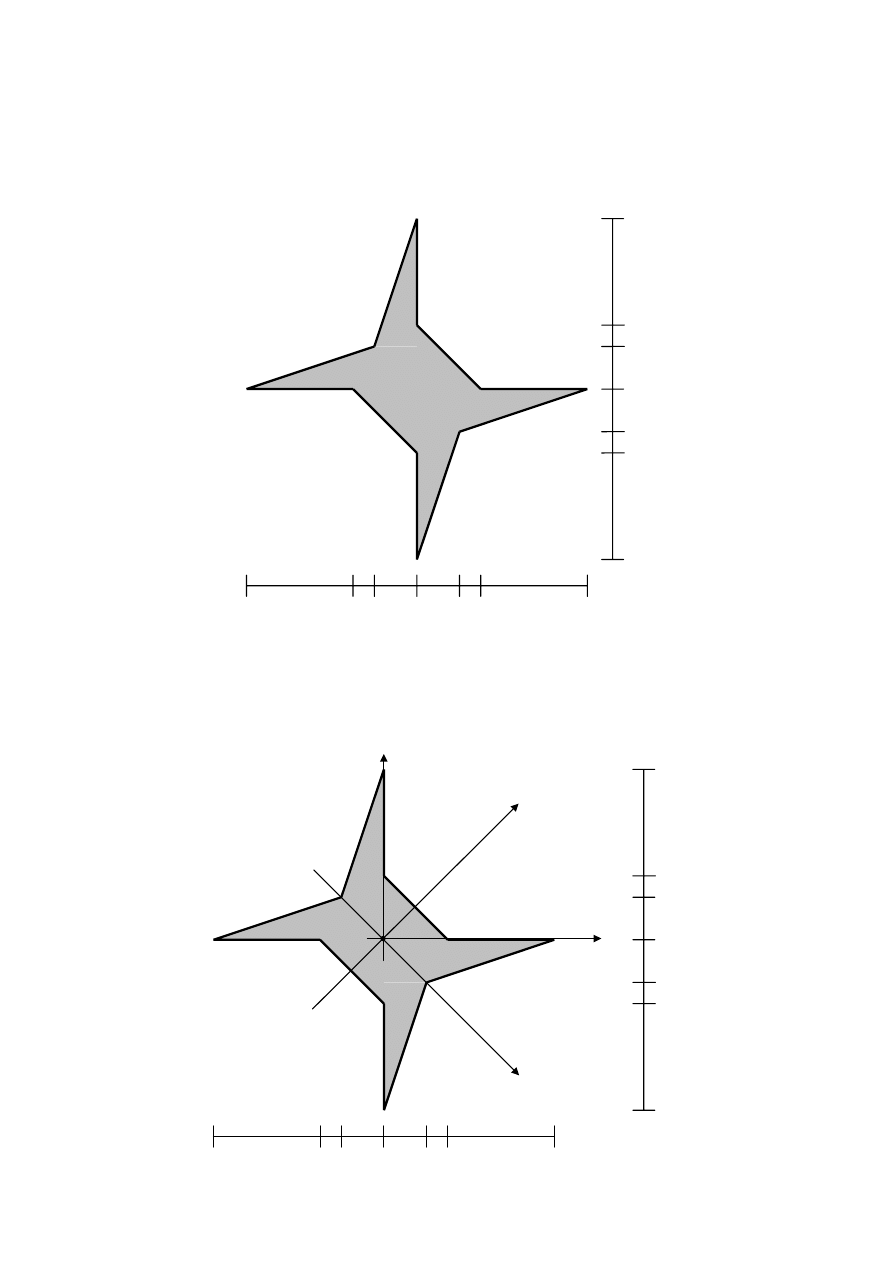
Przykład 2.5. Figura z dwiema osiami symetrii
Polecenie: Wyznaczyć główne centralne momenty bezwładności oraz kierunki główne dla
poniższej figury korzystając z metody analitycznej i graficznej (konstrukcja koła Mohra).
a
a
2a
2a
5a
5a
a
a
2a
2a
5a
5a
Dla rozważanej figury przyjmiemy dwa współśrodkowe układy współrzędnych xy oraz
ξη. Oba układy są układami centralnymi. Układ ξη jest ponadto układem osi głównych
ponieważ osie ξ i η są osiami symetrii figury. Należy oczywiście ustalić, która z osi układu ξη
jest osią maksymalnego momentu bezwładności, a która osią minimalnego momentu
bezwładności.
ξ
η
x
y
C
5a
5a
2a
2a
a
a
5a
5a
2a
2a
a
a
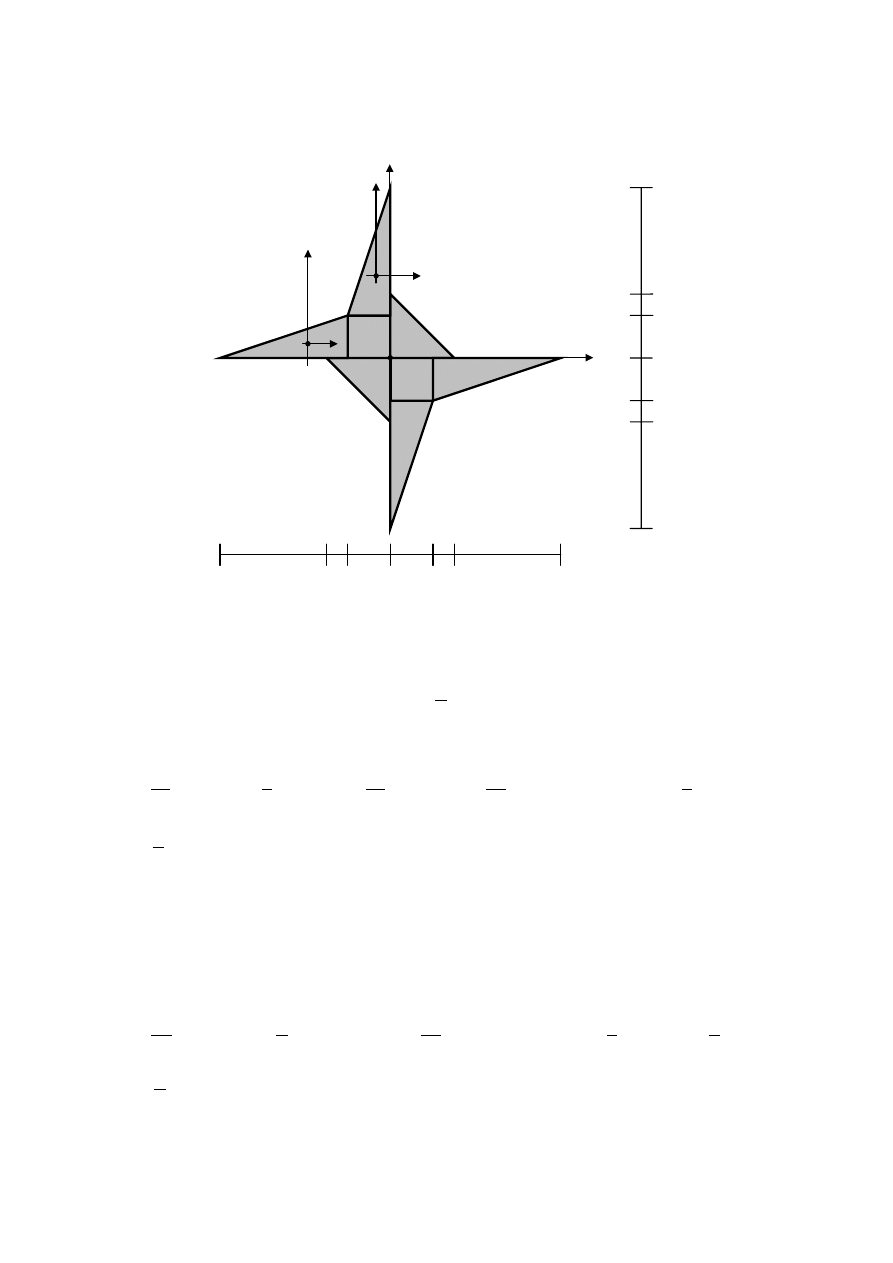
W celu wyznaczenia momentu bezwładności względem osi x dokonamy podziału
rozpatrywanej figury na figury składowe.
a
a
2a
2a
5a
5a
III
3
4
c
x
4
c
y
C
x
y
I
IV
4
C
4
c
x
4
c
y
C
II
5a
5a
2a
2a
a
a
Moment bezwładności rozpatrywanej figury względem osi x policzymy jako
podwojoną sumę momentów bezwładności względem osi x figur składowych (figury I, II, III i
IV). Moment bezwładności figury względem osi y ma taką samą wartość. W przypadku figury
IV należy zastosować twierdzenie Steinera. Pole powierzchni figury III i IV wynosi
2
IV
III
6
6
2
2
1
a
a
a
A
A
=
⋅
⋅
=
=
(
)
( )
( )
( )
( )
4
2
2
3
3
3
3
IV
III
II
I
6
1
248
6
3
1
2
6
6
2
36
1
2
6
12
1
2
2
3
1
3
3
12
1
2
2
a
a
a
a
a
a
a
a
a
a
a
a
I
I
I
I
I
I
x
x
x
x
y
x
=
=
⎪⎭
⎪
⎬
⎫
⎪⎩
⎪
⎨
⎧
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
⋅
+
⋅
+
⋅
⋅
+
⋅
⋅
+
⋅
⋅
+
⋅
⋅
⋅
=
=
+
+
+
⋅
=
=
Dewiacyjny moment rozpatrywanej figury w układzie xy policzymy jako podwojoną
sumę momentów dewiacyjnych figur składowych (figury I, II, III i IV). W przypadku figury
III i IV należy zastosować twierdzenie Steinera. Momenty dewiacyjne tych dwóch figur w
układzie xy mają te same wartości, można więc w obliczeniach uwzględnić to, licząc
podwojoną wartość momentu dewiacyjnego np. dla figury III.
(
) (
)
( ) ( )
( ) ( )
( ) ( )
4
2
2
2
2
2
2
2
III
II
I
IV
III
II
I
4
1
57
6
3
1
2
2
3
1
6
6
2
72
1
2
2
2
4
1
3
3
24
1
2
2
2
2
a
a
a
a
a
a
a
a
a
a
a
I
I
I
I
I
I
I
I
xy
xy
xy
xy
xy
xy
xy
xy
−
=
=
⎭
⎬
⎫
⎩
⎨
⎧
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
⋅
+
⋅
⎟
⎠
⎞
⎜
⎝
⎛
⋅
−
⋅
+
⋅
⋅
+
⋅
−
⋅
⋅
=
=
⋅
+
+
⋅
=
+
+
+
⋅
=
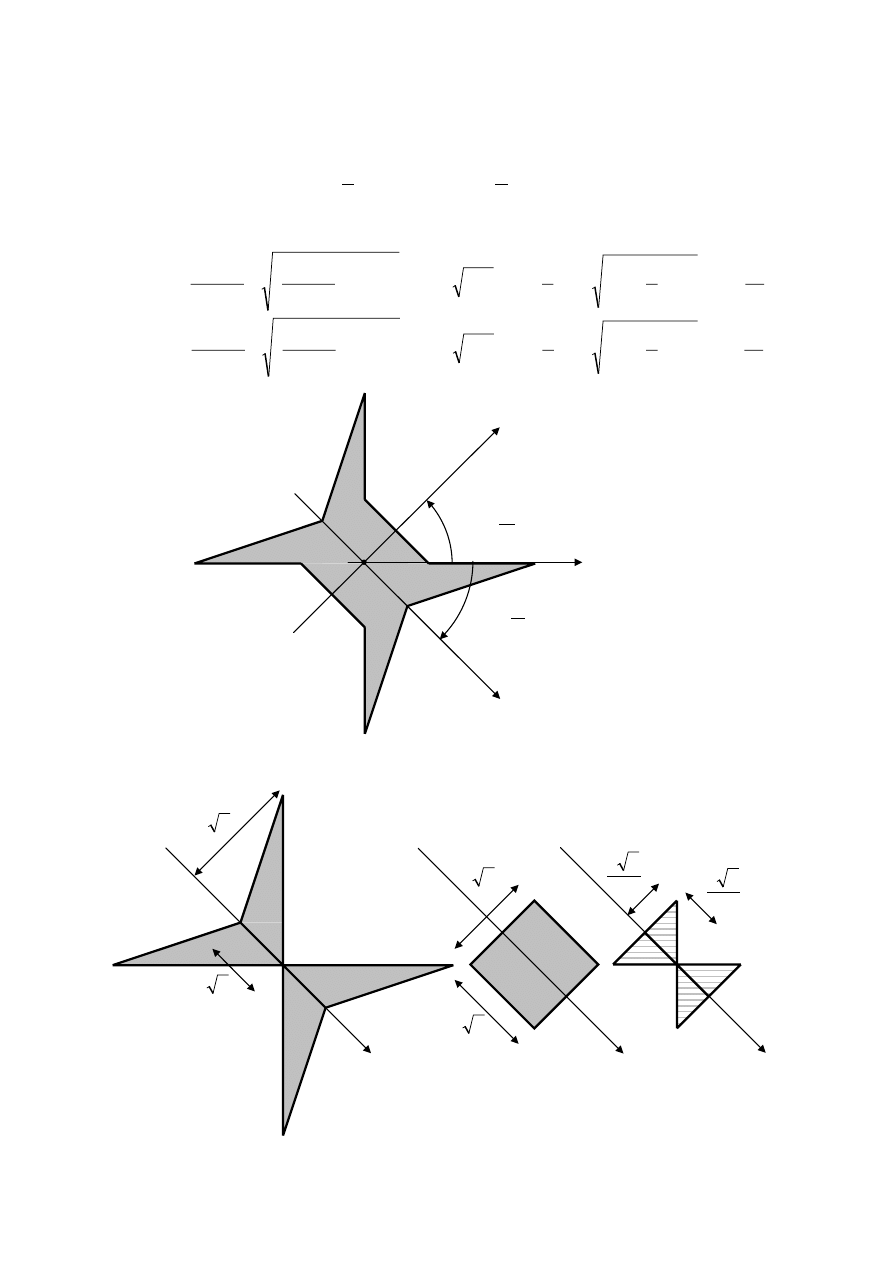
Główna oś bezwładności, względem której moment bezwładności ma wartość
2
max
I
I
=
1
tworzy z osią x kąt
, natomiast główna oś bezwładności, względem której
moment bezwładności ma wartość
1
ϕ
min
I
I
=
2
tworzy z osią x kąt
2
ϕ
.
Ponieważ I
x
= I
y
, I
xy
< 0 to
4
1
π
=
ϕ
, natomiast
4
2
π
−
=
ϕ
.
Momenty bezwładności względem głównych centralnych osi bezwładności osiągają
wartości ekstremalne:
4
2
4
4
2
2
2
1
12
5
305
4
1
57
6
1
248
2
2
a
a
a
I
I
I
I
I
I
I
I
I
xy
x
xy
y
x
y
x
max
=
⎟
⎠
⎞
⎜
⎝
⎛−
+
=
+
=
+
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
+
+
=
=
4
2
4
4
2
2
2
2
12
11
190
4
1
57
6
1
248
2
2
a
a
a
I
I
I
I
I
I
I
I
I
xy
x
xy
y
x
y
x
min
=
⎟
⎠
⎞
⎜
⎝
⎛−
−
=
−
=
+
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
−
+
=
=
ξ - kierunek maksymalnego
momentu bezwładności
η - kierunek minimalnego
momentu bezwładności
x
4
1
π
=
ϕ
4
2
π
=
ϕ
C
Główne centralne momenty bezwładności możemy wyznaczyć w inny sposób.
III
a
2
2
3
a
2
2
3
a
2
3
a
2
3
η
a
2
2
a
2
4
I
II
η
η
3
Obliczymy wartość momentu bezwładności względem osi η, stosując nowy podział na
figury składowe. Figurę III traktujemy jako pole "ujemne". Momenty bezwładności figury I i
III mnożymy przez cztery.
(
)
( )
4
3
4
3
12
11
190
2
2
3
2
2
3
12
1
4
2
3
12
1
2
4
2
2
12
1
4
a
a
a
a
a
a
I
η
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⋅
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⋅
⋅
−
⋅
+
⋅
⋅
⋅
=
W dalszych obliczeniach wykorzystamy to, że suma momentów bezwładności
względem obu osi układów współśrodkowych jest stała.
η
ξ
y
x
I
I
I
I
+
=
+
czyli
4
4
4
12
5
305
12
11
190
6
1
248
2
2
a
a
a
I
I
I
I
I
I
η
x
η
y
x
ξ
=
−
⋅
=
−
⋅
=
−
+
=
Z porównania wartości głównych momentów bezwładności wynika, że oś
ξ jest
kierunkiem maksymalnego momentu bezwładności, a oś
η jest kierunkiem minimalnego
momentu bezwładności.
4
2
12
11
190
a
I
I
I
min
η
=
=
=
,
4
1
12
5
305
a
I
I
I
max
ξ
=
=
=
Główne centralne momenty bezwładności oraz kierunki główne można wyznaczyć metodą
graficzną, stosując konstrukcję koła Mohra. Korzystamy z wyznaczonych wartości
momentów bezwładności w układzie
xy
4
4
167
248
6
1
248
a
.
a
I
I
y
x
=
=
=
oraz wartości momentu dewiacyjnego
4
4
250
57
4
1
57
a
.
a
I
xy
−
=
−
=
.
Kolejność postępowania przy wyznaczaniu głównych momentów bezwładności i kierunków
głównych metodą graficzną jest następująca:
1. Wyznaczenie położenia punktów
A i B
Wartości momentów bezwładności w układzie
xy
stanowią odpowiednio
współrzędne punktów
A
4
167
248
a
.
I
I
y
x
=
=
(
)
0
167
248
4
,
a
.
I
x
=
i B
(
)
0
167
248
4
,
a
.
I
y
=
. W rozpatrywanym
zadaniu położenie punktów A
(
)
0
167
248
4
,
a
.
i B
(
)
0
167
248
4
,
a
.
jest wspólne.
2. Wyznaczenie położenia punktu C
Punkt C
(
)
(
)
0
167
248
5
0
4
,
a
.
I
I
.
y
x
=
+
⋅
, czyli C
(
)
0
167
248
4
,
a
.
, jest środkiem odcinka
AB i
środkiem koła Mohra. W rozpatrywanym zadaniu położenie punktów
C, A i B jest wspólne.
3. Wyznaczenie położenia punktu
D
Po uwzględnieniu wartości
oraz
otrzymamy współrzędne
4
167
248
a
.
I
x
=
4
250
57
a
.
I
xy
−
=
punktu
D
(
)
(
)
4
4
250
57
167
248
a
.
I
,
a
.
I
xy
x
−
−
=
−
=
, czyli
D
(
)
4
4
250
57
167
248
a
.
,
a
.
.
4. Wyznaczenie promienia koła Mohra
Łączymy punkty
C i D odcinkiem
CD
, który stanowi promień
R koła Mohra. Promieniem
tym zataczamy okrąg.
5. Wyznaczenie głównych momentów bezwładności
Koło Mohra przecina oś poziomą w dwu punktach:
E i F. Współrzędne tych punktów są
następujące:
E
(
)
0
917
190
4
,
a
.
,
F
(
)
0
417
305
4
,
a
.
. Długość odcinka
OE
odpowiada
minimalnemu momentowi bezwładności
, natomiast długość odcinka
2
I
F
O
odpowiada
maksymalnemu momentowi bezwładności .
1
I
6. Wyznaczenie kierunków głównych
4
Oś przechodząca przez punkty
E i D jest osią maksymalnego momentu bezwładności, a oś
przechodząca przez punkty
F i D jest osią minimalnego momentu bezwładności.
2
I
O
Momenty bezwładności
Moment
y dewiac
yj
ne
kierunek maksymalnego
momentu bezwładności
kierunek minimalnego
momentu bezwładności
Przyjęta skala: 50
r
4
1
I
E
2
y
x
y
x
I
I
=
=
I
I
+
A=B=C
D
F
R
4
2
π
−
=
ϕ
4
1
π
=
ϕ
(
)
( )
(
)
(
)
( )
0
0
0
2
0
0
1
2
,
I
F
,
I
E
I
,
I
D
,
I
I
C
,
I
B
,
I
A
xy
x
y
x
y
x
−
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
5