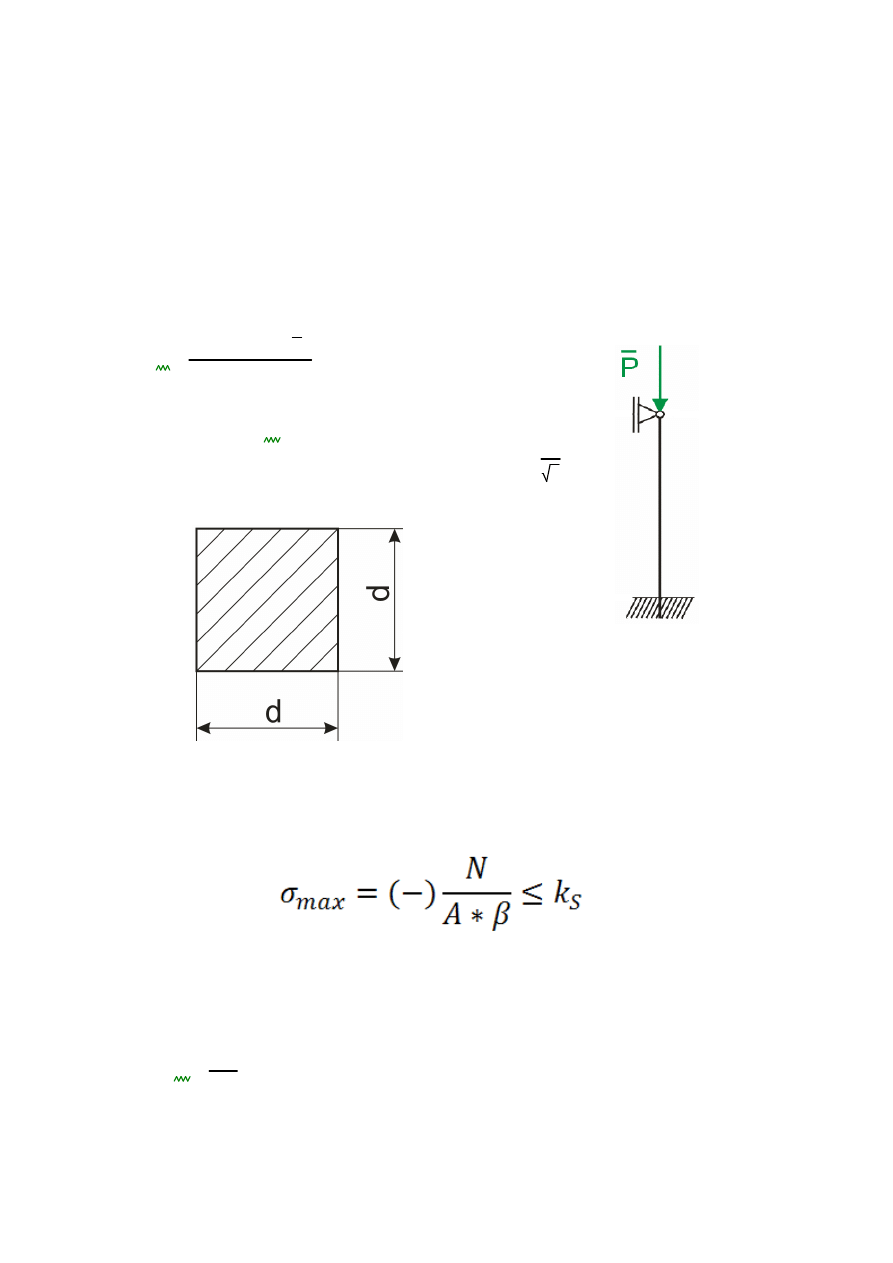
5) Obliczenia wytrzymałościowe

Oblicz jaki przekrój poprzeczny (kwadratowy) powinien mieć pręt aby nie uległ
wyboczeniu. 

DANE:

P

4000 N

⋅

:=

Q

200 N

⋅

:=

a

3 m

⋅

:=

b

2 m

⋅

:=

α

40 deg

⋅

:=

Materiał: Stal St 05

ks

200 MPa

⋅

:=

F

P sin

α

( )

⋅

a

⋅

Q

a

2

⋅

+













b

:=

F

4.007 kN

⋅

=

-Siła ściskająca pręt

Długość pręta:

H

1 m

⋅

:=

Współczynnik zależny od sposobu podparcia pręta:

μ

1

2

:=

SZUKANE:

d

Rys 3. Sposób podparcia pręta

Rys 4. Przekrój poprzeczny pręta

Praktyczny sposób projektowania prętów  ściskanych z uwzględnieniem możliwości
powstania zjawiska wyboczenia.

We wzorze wystąpią  dwie niewiadome A, β. Wstępnie należy jedną z tych wielkości
przyjąć. 

β

0.5

:=

A

F

β ks

⋅

:=

A

40.067 mm

2

⋅

=

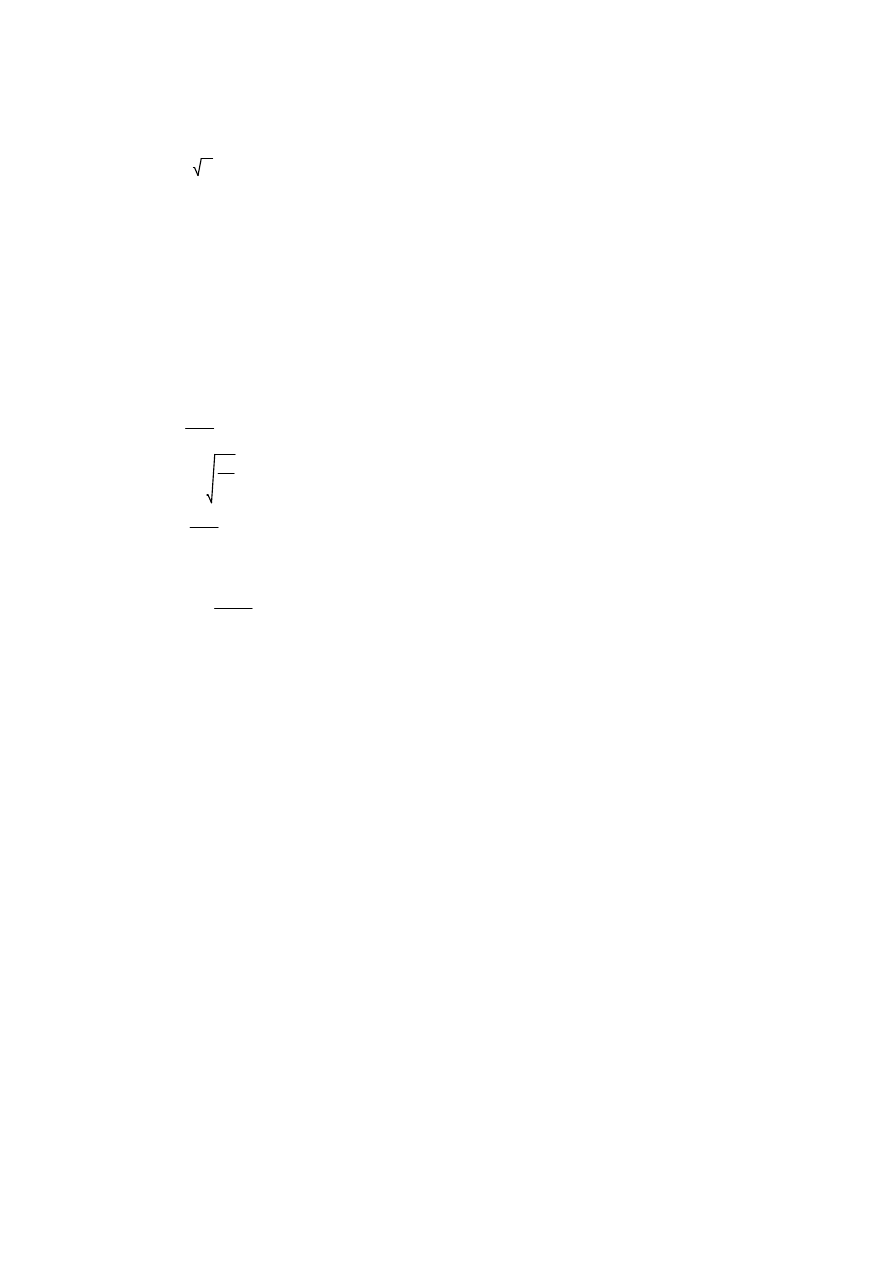
Powierzchnia przekroju:

da

A

:=

da

6.33 mm

⋅

=

Ponieważ pręt ma być wykonany ze stali wymiar a zaokrąglamy do pełnych milimetrów.
(Oraz uwzględnione są poprawki obliczeń)

d

12 mm

⋅

:=

Do sprawdzenia naprężeń potrzebna jest znajomość  faktycznego współczynnika β, który
jest funkcją smukłości λ.Należy obliczyć smukłość pręta:

lw

μ H

⋅

:=

lw

0.707 m

=

I

d d

3

⋅

12

:=

I

0.173 cm

4

⋅

=

imin

I

d

2

:=

imin

3.464 mm

⋅

=

λ

lw

imin

:=

λ

204.124

=

Z tablic odczytano dla otrzymanej λ 

β0

0.158

:=

σmax

F

β0 d

2

⋅

:=

σmax

176.104 MPa

⋅

=

<ks

Naprężenia występujące w przekroju są mniejsze niż naprężenia dpouszczalne