http://www.mbmaster.pl/elektrotechnika-zadania.html

 

 

Strona 1/5 

 

Metoda prądów oczkowych – rozwiązany przykład 

 

Zastosowanie metody prądów oczkowych do wyznaczenia prądów i napięć w gałęziach 
obwodu elektrycznego prądu stałego. Metoda oczkowa opiera się na napięciowym prawie 
Kirchhoffa. Liczba równań dla napięciowego prawa Kirchhoffa i dla metody oczkowej jest 
dana wzorem: 

                    

                             

                             

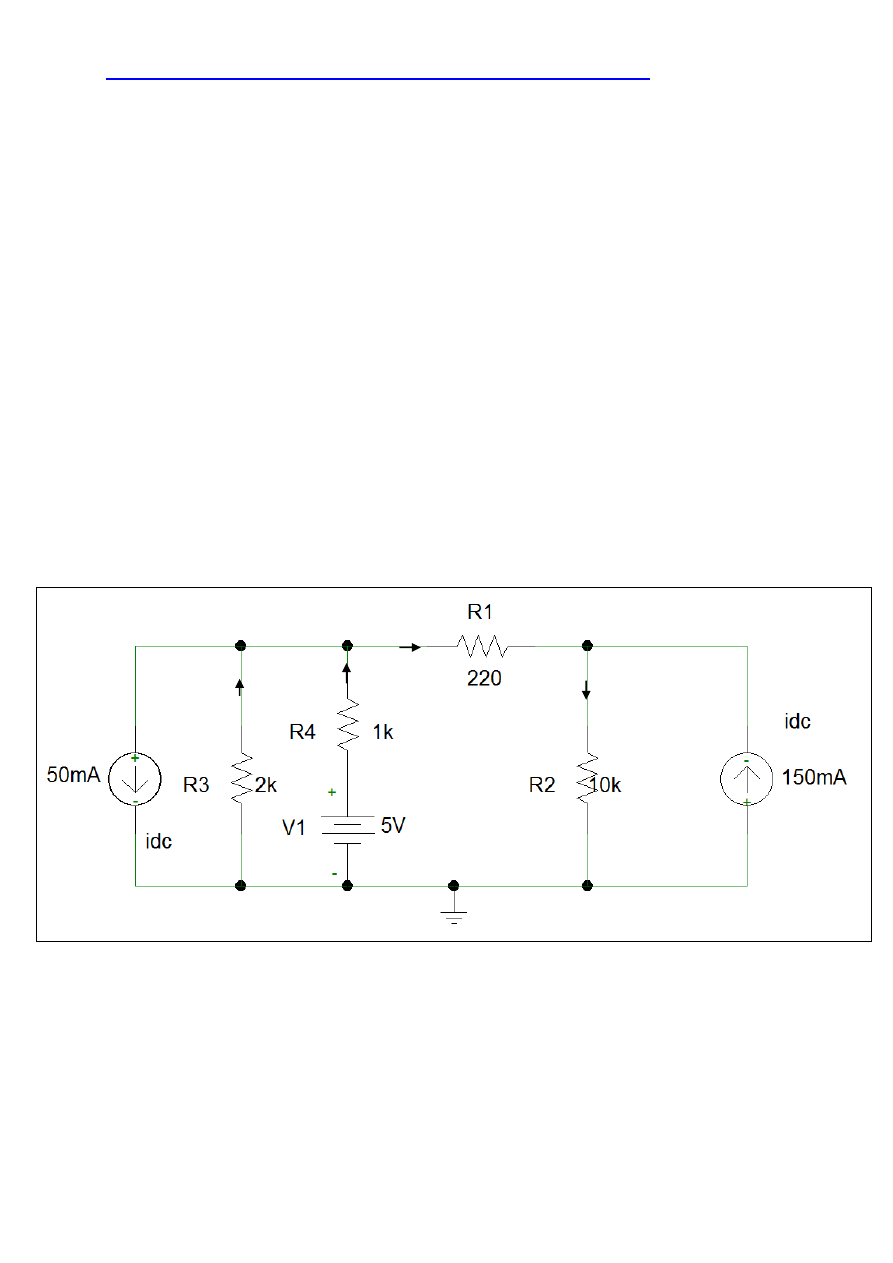
 Obwód elektryczny poniżej ma cztery gałęzie. Należy pamiętać że prąd źródłowy nie jest 
gałęzią. Liczba równań jest więc następująca: 

                        

 

Zasadą metody oczkowej jest to, że „nie widzi” ona fizycznych  źródeł prądu. Wszystkie 
źródła prądowe w obwodzie elektrycznym musimy transformować do postaci „wirtualnych” 
źródeł napięcia. Na następnej stronie schemat obwodu po transformacji. 

Rysunek 1. Obwód elektryczny prądu stałego.

 

 

 

 

 

 

 

 

 

 

 

  

 

 

 

 

 

  

 

http://www.mbmaster.pl/elektrotechnika-zadania.html

 

 

Strona 2/5 

 

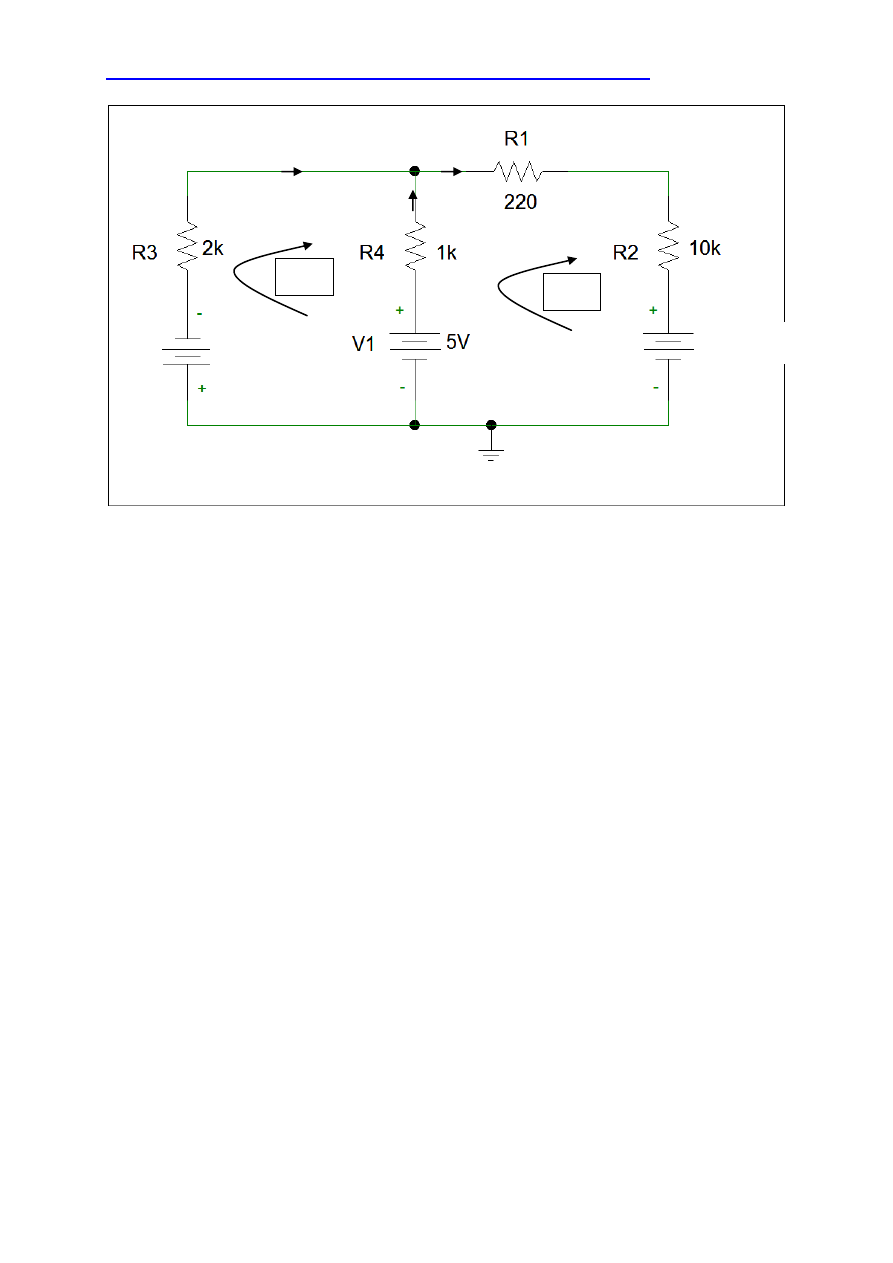
Dla obwodu elektrycznego przedstawionego powyżej zapiszemy równania oczkowe. Jak 
widać jest różnica pomiędzy obwodami z rysunku 1 i rysunku 2. Na rysunku 2 obwód 
elektryczny jest już po transformacji. Źródła prądowe  

  

 i   

  

 zostały transformowane do 

postaci „wirtualnych” źródeł napięcia   

  

 i    

  

. 

Wirtualne źródła napięcia są związane z fizycznymi źródłami prądowymi równaniami: 

  

  

   

  

     

  

  

   

  

     

Równanie oczkowe dla oczka  : 

∑  

 

 

 

        

 

  

   

 

                    

  

     

∑  

 

 

 

        

  

        

 

                    

  

     

Równanie oczkowe dla oczka   : 

∑  

 

 

  

    

 

  

        

  

               

 

     

∑  

 

 

  

    

  

             

  

               

 

     

Z równania na sumę napięć źródłowych w oczku   wyznaczymy prąd oczkowy  

 

. 

Rysunek 2. Obwód elektryczny po transformacji źródeł prądu na wirtualne źródła napięcia.

 

 

 

    

 

 

 

 

 

 

  

 

 

  

  

   

  

     

  

  

   

  

     

 

  

 

 

 

 

  

   

http://www.mbmaster.pl/elektrotechnika-zadania.html

 

 

Strona 3/5 

 

      

  

        

 

                    

  

    

 

 

 

                         

  

        

  

    

 

 

 

 

      

  

        

  

    

            

 

 

Z równania na sumę napięć źródłowych w oczku    wyznaczymy prąd oczkowy  

  

. 

  

  

             

  

               

 

    

 

 

  

                

  

             

 

    

 

 

  

 

  

  

             

 

    

       

 

 

  

   

 

  

    

       

 

  

       

 

 

 

    

       

 

W równaniu na prąd oczkowy  

  

 występuje prąd oczkowy  

 

. Wyeliminujemy teraz prąd  

 

 z 

tego równania. Wykorzystamy w tym celu pierwsze równanie oczkowe. 

 

  

   

 

  

    

       

 

  

       

 

  

       

 

      

  

        

  

    

            

 

 

  

   

 

  

    

       

 

  

       

 

  

         

 

           

  

              

 

  

 

   

  

                          

 

 

  

 

  

 

   

  

                          

   

 

  

    

       

 

  

       

 

  

         

 

           

  

              

 

 

  

  (   

  

 

                          

)    

 

  

    

       

 

  

       

 

  

         

 

           

  

              

 

 

  

 

  

  

    

         

  

         

  

           

           

  

              

(   

  

 

                          )

 

 

  

  (

  

  

    

       

 

  

       

 

  

         

 

           

  

              

)   (   

  

 

                          

)

  

 

 

 

http://www.mbmaster.pl/elektrotechnika-zadania.html

 

 

Strona 4/5 

 

Prąd oczkowy  

  

 jest już wyznaczony. Wykorzystamy teraz wyrażenie na prąd oczkowy  

  

 i 

wstawimy je do równania na prąd oczkowy  

 

. 

 

 

 

 

      

  

        

  

    

            

 

 

 

 

 

      

  

    

            

 

  

            

(

  

  

    

       

 

  

       

 

  

         

 

           

  

              

)   (   

  

 

                          

)

  

 

 

 

 

 

 

      

  

            (

  

  

    

         

  

         

  

           

           

  

              )   (   

  

 

                          )

  

            

 

 

Prądy oczkowe  

 

 oraz   

  

 są już wyznaczone pozostaje wyznaczyć prądy w poszczególnych 

gałęziach. Należy zwrócić uwagę na fakt że w obliczeniach wyznaczających prądy oczkowe 
posługiwaliśmy się schematem z rysunku 2. W schemacie z rysunku dwa  fizyczne źródła 
prądowe były w przedstawione w postaci wirtualnych źródeł napięcia. W schemacie na 
rysunku 2 są prądy

 

  

 

 i   

 

, prądy te są związane równaniami transformacyjnymi z prądami  

 

 i  

 

. 

 

 

 

   

 

 

  

 

   

 

 

  

 

   

  

 

 

 

    

  

   

 

 

 

Prąd  

 

 jest równy różnicy prądów oczkowych oczka    i  , ponieważ gałąź w której płynie ten 

prąd jest częścią i jedno i drugie oczka. Prąd  

 

 ma kierunek zgodny z prądem oczkowym  

 

 i 

przeciwny do prądu oczkowego  

  

. 

Prądy  

 

 i  

 

 są wyznaczone na następnej stronie. 

 

 

 

http://www.mbmaster.pl/elektrotechnika-zadania.html

 

 

Strona 5/5 

 

 

 

 

 

 

 

 

 

 

 

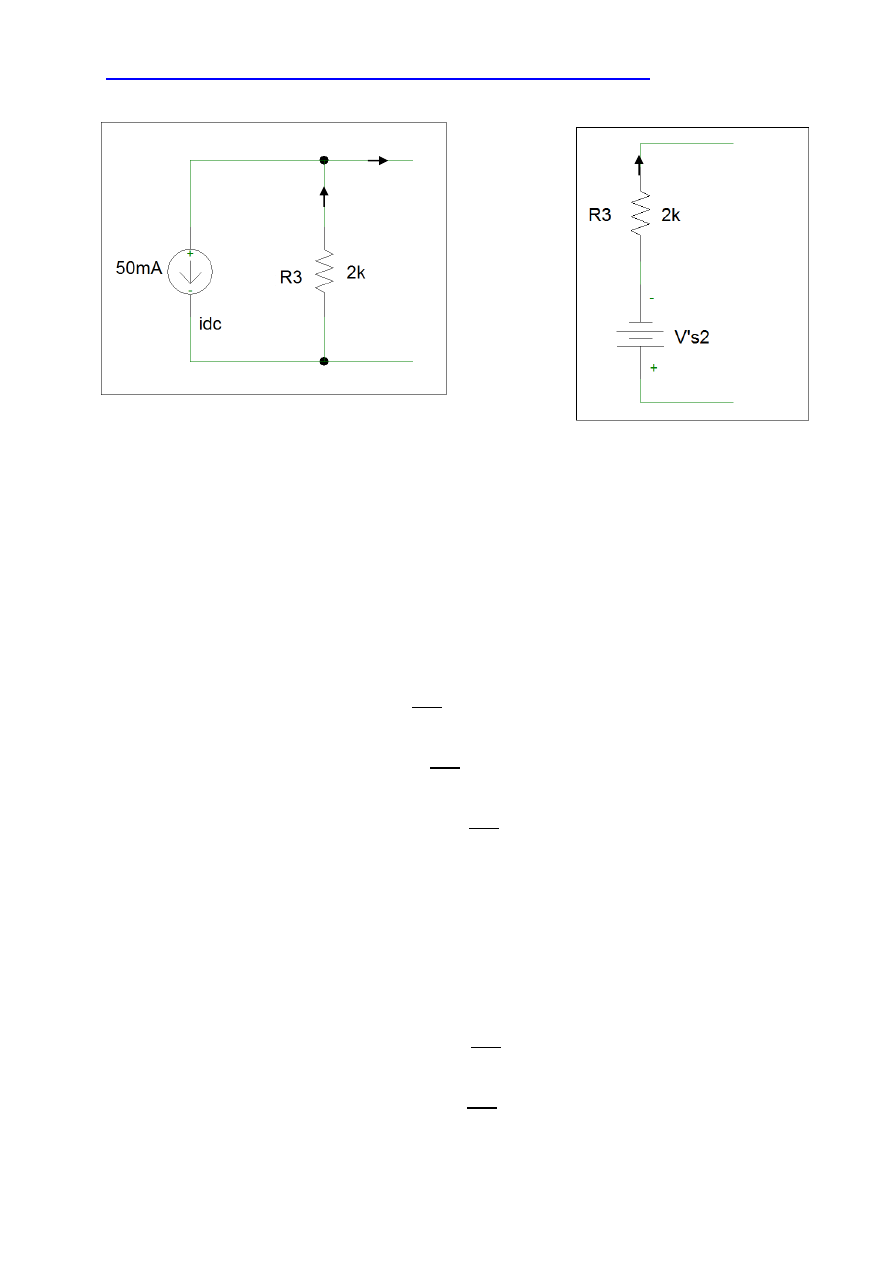
Prąd  

 

 wyznaczymy poprzez porównanie schematu z przed transformacji z schematem po 

transformacji. Zastosujemy do tego celu prądowe prawo Kirchhoffa. 

 

 

   

  

    

 

    

 

 

 

  

  

  

    

 

    

 

 

 

  

  

  

    

 

 

 

 

   

  

 

  

  

  

 

 

W analogiczny sposób wyznaczymy prąd  

 

, ale już bez rysunków pomocniczych. 

  

 

   

  

   

 

    

 

 

    

 

   

  

 

 

 

    

 

 

  

  

  

 

 

 

   

 

 

  

  

  

 

Rysunek 3. Gałąź z rezystorem    i źródłem prądu  

  

 

przed transformacją.

 

Rysunek 4. Gałąź z rezystorem    i 
wirtualnym źródłem napięcia   

  

 po 

transformacji.