Projekt Charakterystyki Momenty Rectan

www.gruparectan.com

Strona :1

Zadanie : Wyznaczyć położenie głównych centralnych osi bezwładności i obliczyć główne centralne momenty
bezwładności

* Rozwiązanie zadania *

Oznaczenia :

A [cm²] - pole powierzchni figury

Xo [cm] - współrzędna X środka ciężkości figury w układzie globalnym

Yo [cm] - współrzędna Y środka ciężkości figury w układzie globalnym

A·x [cm³] - moment statyczny względem osi Y w układzie globalnym

A·y [cm³] - moment statyczny względem osi X w układzie globalnym

Xc [cm] - współrzędna X środka ciężkości układu figur w układzie globalnym

Yc [cm] - współrzędna Y środka ciężkości układu figur w układzie globalnym

xc [cm] - odległość X pomiędzy środkiem ciężkości figury a środkiem ciężkości układu

yc [cm] - odległość Y pomiędzy środkiem ciężkości figury a środkiem ciężkości układu

Jx [cm4] - moment bezwładności figury względem osi X

Jy [cm4] - moment bezwładności figury względem osi Y

Dxy [cm4] - dewiacyjny moment bezwładności figury

A·x·x [cm4] - element do wzoru Steinera

A·y·y [cm4] - element do wzoru Steinera

A·x·y [cm4] - element do wzoru Steinera

...............................................................................................................................................................................................................................

Tabela 1 Środki ciężkości Figur

Fig.

Xo [cm]

Yo [cm]

A [cm²]

A·x [cm³]

A·y [cm³]

5,490

10,000

32,200

176,778

322,000

10,240

17,260

15,500

158,720

267,530

Sumy

47,700

335,498

589,530

/rectanbudownictwo

Strona :2

1. Położenie XcYc głównych centralnych osi bezwładności względem układu XY

Tabela 2 Momenty i Dewiacje

Fig.

xc [cm]

yc [cm]

Jx [cm4]

Jy [cm4]

Dxy [cm4]

A·x·x [cm4]

A·y·y [cm4]

A·x·y [cm4]

-1,544

-2,359

1910,000

148,000

0,000

76,713

179,207

117,250

3,206

4,901

145,000

85,100

159,365

372,289

243,577

Sumy

2055,000

293,000

85,100

236,078

551,496

360,827

1. Momenty bezwładności

1.1.Figura Ceownik 200 U

kąt OX : -180 [stopnie]

1.1.1. Odległości środka ciężkości figury od osi X i Y

1.1.2. Wartości Jxo, Jyo, Dxyo w układzie XoYo pierwsza ćwiartka bez obrotu figury

Strona :3

1.1.3. Obliczenie nowych wartości środka ciężkości figury po obrocie o kąt

dla uproszczenia obliczeń najpierw dokonamy obrotu figury w układzie lokalnym o kąt a potem przemieszczenia o wektor do
punktu docelowego

figura znajduje się teraz w takim położeniu jak wzory podane na obliczanie momentów

układ taki nazywamy układem lokalnym figury

współrzędne X i Y obliczamy ze wzorów na obrót układu :

gdzie X i Y to punkt po transformacji a X' i Y' punkt przed transformacją

gdzie φ to kąt obrotu figury układ X'Y' względem układu XY

i jeżeli jest on zgodny z ruchem wskazówek zegara to jest on ujemny

transformacja figury obróconej do punktu docelowego o wektor dX i dY

Strona :4

Gdzie dX i dY to współrzędne początku figury w nowym położeniu

1.1.4. Momenty i dewiacje dla układu nachylonego względem naszego układu XY

(ponieważ kąt nachylenia analizowanej figury jest różny od zera i wynosi jak poniżej to należy obliczyć układ nachylony )

Momenty wejściowe do obliczenia układu nachylonego

1.1.5. Jx w układzie nachylonym

1.1.6. Jy w układzie nachylonym

Strona :5

1.1.7. Dxy w układzie nachylonym

1.1.8. Ocena czy figura podana została jako ujemna

pole dodatnie : figura została podana jako dodatnia wartości : Jxo, Jyo, Dxyo zostaną przy swoich znakach

1.1.9. Odległości od środka ciężkości figury do środka ciężkości układu

1.2.Figura Kątownik RR 100x100x8

kąt OX : -270 [stopnie]

1.2.1. Odległości środka ciężkości figury od osi X i Y

1.2.2. Wartości Jxo, Jyo, Dxyo w układzie XoYo pierwsza ćwiartka bez obrotu figury

Strona :6

1.2.3. Dewiacja dla kształtownika w układzie XoYo

(Dewiacja jest wyliczana w położeniu bez nachylenia kształtownika względem układu XcYc)

(potrzebny odczyt z tablic Jmin , tanges beta 'n-n' - kąta nachylenia osi głównych)

1.2.4. Obliczenie nowych wartości środka ciężkości figury po obrocie o kąt

dla uproszczenia obliczeń najpierw dokonamy obrotu figury w układzie lokalnym o kąt a potem przemieszczenia o wektor do
punktu docelowego

figura znajduje się teraz w takim położeniu jak wzory podane na obliczanie momentów

układ taki nazywamy układem lokalnym figury

współrzędne X i Y obliczamy ze wzorów na obrót układu :

gdzie X i Y to punkt po transformacji a X' i Y' punkt przed transformacją

gdzie φ to kąt obrotu figury układ X'Y' względem układu XY

i jeżeli jest on zgodny z ruchem wskazówek zegara to jest on ujemny

Strona :7

transformacja figury obróconej do punktu docelowego o wektor dX i dY

Gdzie dX i dY to współrzędne początku figury w nowym położeniu

1.2.5. Momenty i dewiacje dla układu nachylonego względem naszego układu XY

(ponieważ kąt nachylenia analizowanej figury jest różny od zera i wynosi jak poniżej to należy obliczyć układ nachylony )

Momenty wejściowe do obliczenia układu nachylonego

1.2.6. Jx w układzie nachylonym

Strona :8

1.2.7. Jy w układzie nachylonym

1.2.8. Dxy w układzie nachylonym

1.2.9. Ocena czy figura podana została jako ujemna

pole dodatnie : figura została podana jako dodatnia wartości : Jxo, Jyo, Dxyo zostaną przy swoich znakach

1.2.10. Odległości od środka ciężkości figury do środka ciężkości układu

2. Centralne Momenty bezwładności dla układu XcYc względem środka ciężkości Osi
Centralnych

Strona :9

2.1. Sumy częściowe Jxo , Jyo , Dxoyo

3. Jxc , Jyc , Dxyc całego układu zgodnie z twierdzeniem Steinera

3.1. Zestawienie Centralnych Jxc , Jyc , Dxyc do dalszych obliczeń

to są Centralne Momenty Bezwładności układu figur

4. Kąt OXc Głównych Centralnych osi bezwładności

4.1. Kąt alfa

Strona :10

5. Główne Centralne momenty bezwładności

5.1. Jmax

5.2. Jmin

6. Sprawdzenie

6.1. Niezmiennik J1

6.2. Niezmiennik J2

Strona :11

7. Momenty bezwładności dla naszego układu XY w punkcie [0,0]

8. Szkic projektu

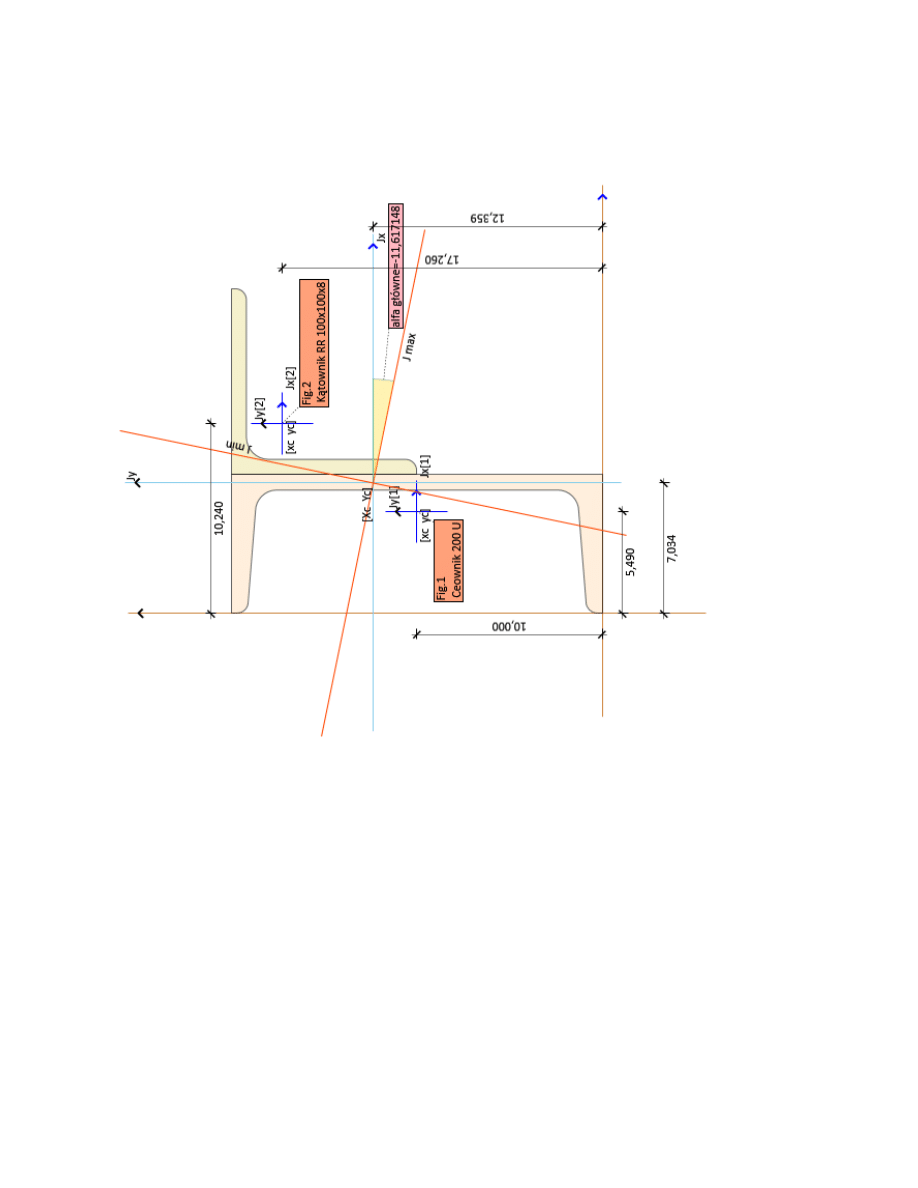
Strona :12

...

Wydruk Rectan

www.gruparectan.com

Wyszukiwarka

Podobne podstrony:

więcej podobnych podstron