
Nierozróżnialność cząstek kwantowo (klasycznie rozróżnialne)
Rozważmy dwie identyczne cząstki nieodziaływujące ze sobą:
∣
r
1,
r
2,
t∣
2
=∣
r
2,
r
1,
t∣
2
Gdyż wszystkie wyniki eksperymentów dają tą samą wartość
w obu sytuacjach.
Możliwe dwa rozwiązania:
r
1,
r
2,
t = r
2,
r
1,
t
r
1,
r
2,
t =−r
2,
r
1,
t
Funkcja symetryczna
Funkcja antysymetryczna
Ze względu na przestawienie cząstek

H r
1,
r
2,
⋯
, r
n
, t =i ℏ ∂
∂
t
r
1,
r
2,
⋯
,r
n
,t
Równanie Schrodingera dla n identycznych cząstek
Operator hamiltona jest symetryczny w/dem przestawienia cząstek
⇒
H r
1,
r
2,
⋯
,r
n
, t
Jest symetryczne bądź
antysymetryczne zależnie od
funkcji falowej
H
Jeżeli
Symetryczne, to
i ℏ ∂
∂
t
Symetryczne
tt = t
∂
∂
t
t
tt
Też symetryczne
Symetria funkcji falowej jest zachowana i jest własnością układu cząstek

Załóżmy, że mamy dwie identyczne cząstki i dwa stany kwantowe
, −stany kwantowe
1, 2−oznaczenia cząstek
Możliwe są sytuacje:
u
1 ,u
2
u
2 ,u
1
u
I
=
u
1⋅u
2
u
II
=
u
2⋅u
1
Oczywiście funkcja może być symetryczna, bądź antysymetryczna –
symetryzujemy funkcję, ponieważ cząstki są nierozróżnialne:
u
s
=
u
I
u
II
=
u
1⋅u
2u
2⋅u
1
u
as
=
u
I
−
u
II
=
u
1⋅u
2−u
2⋅u
1

jeżeli
=−
czyli mamy jeden stan kwantowy
wtedy
u
as
=
u
1⋅u
2−u
2⋅u
1=0
Nie istnieje stan kwantowy opisany funkcją antysymetryczną, który jest
obsadzony przez dwie identyczne cząstki.
Funkcją symetryczną opisane cząstki nazwano bozonami
Funkcją antysymetryczną opisane cząstki nazwano fermionami
Dla fermionów obowiązuje zakaz Pauliego – dwa fermiony nie mogą być w tym
samym stanie kwantowym.
Zasada budowania funkcji falowej dla ncząstek identycznych.
U
s
=
∑
P
P u
1⋅u
,⋯,u
n
U
as
=
det
∣
u
1 , u
2 ,⋯, u
n
u
1 ,u
2 ,⋯, u
n
⋯
,⋯,⋯,⋯
u
1 , u
2 ,⋯, u
n
∣

Jeżeli układ jest opisany funkcją antysymetryczną (fermiony), to każdy stan
układu może być “pusty” nieobsadzony lub zajęty tylko przez jeden fermion.
Jeżeli układ jest opisany funkcją symetryczną (bozony), to każdy stan układu
może być obsadzony przez dowolną liczbę bozonów lub może być pusty.
Statystyki kwantowe
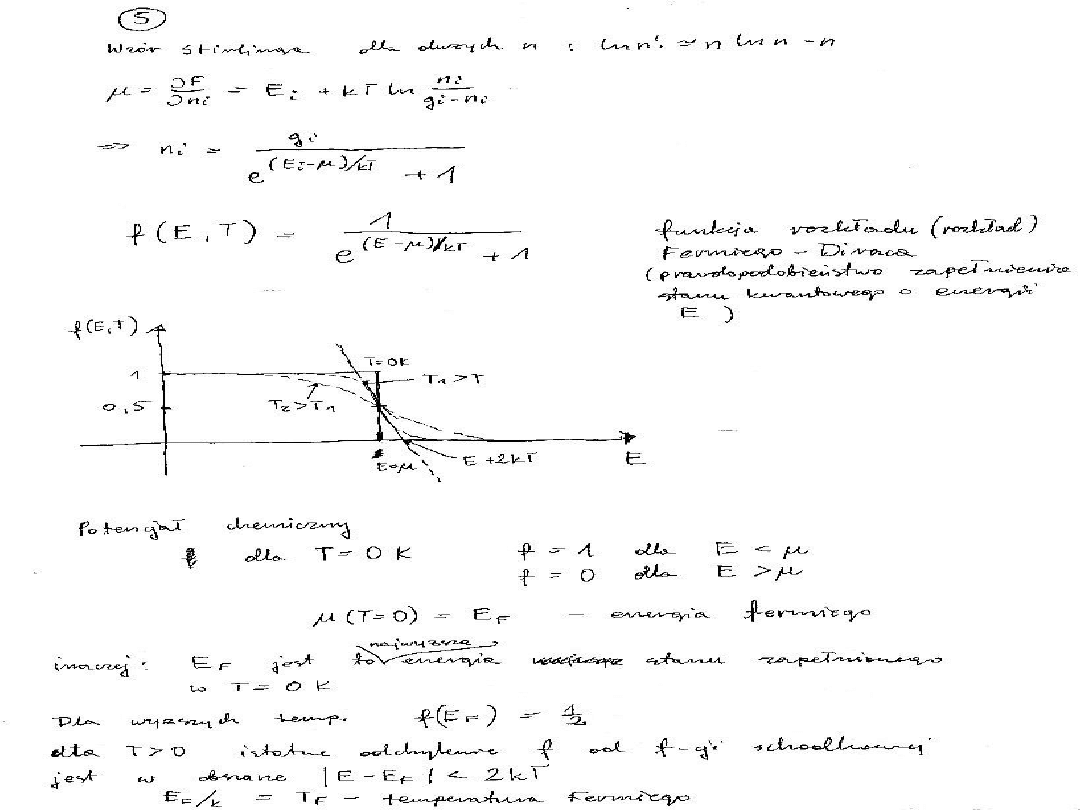
Fermiony – rozkład FermiegoDiraca
Bozony – rozkład BosegoEinsteina
Bozony I fermiony będą miały różne własności statystyczne
To tłumaczy zapełnianie powłok elektronowych w atomach.
Fermiony – cząstki o liczbie spinowej ułamkowej
Bozony –cząstki o liczbie spinowej całkowitej
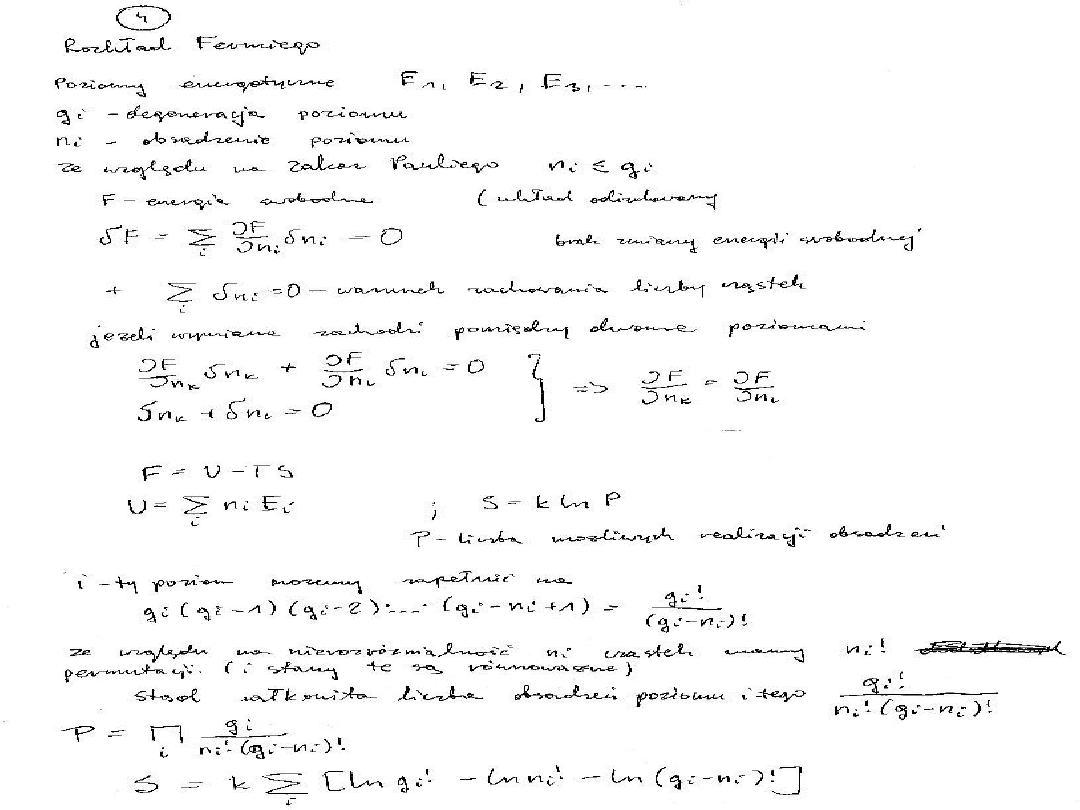
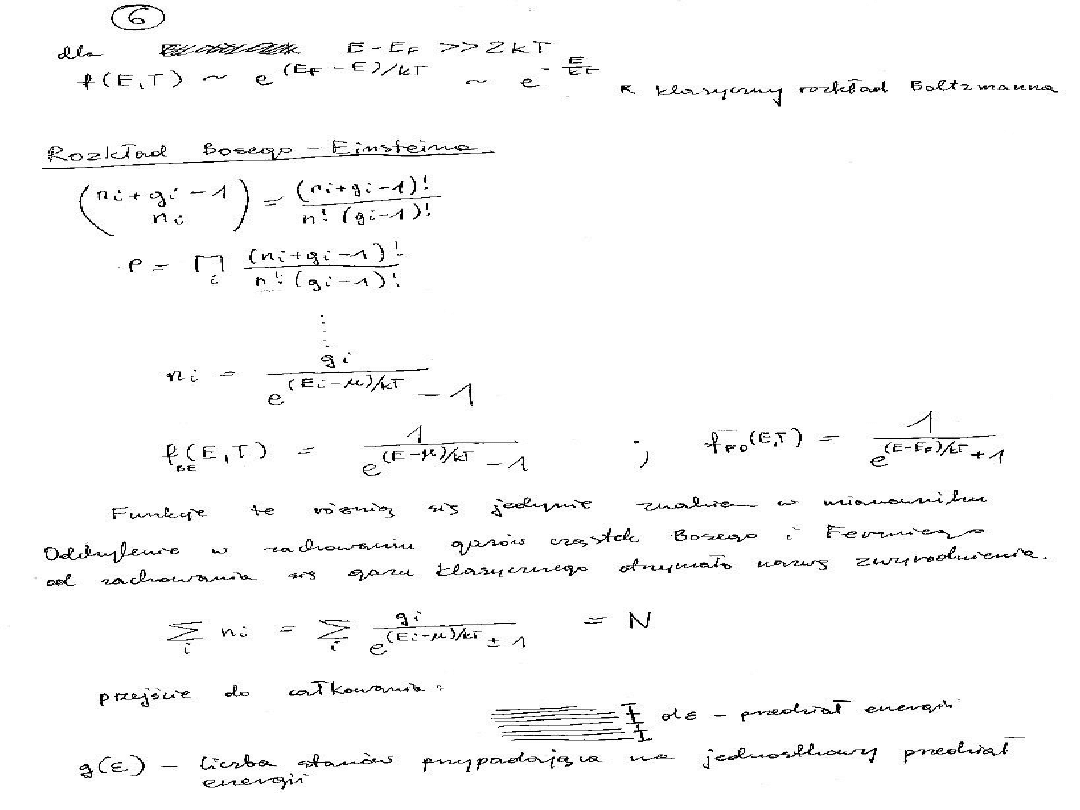

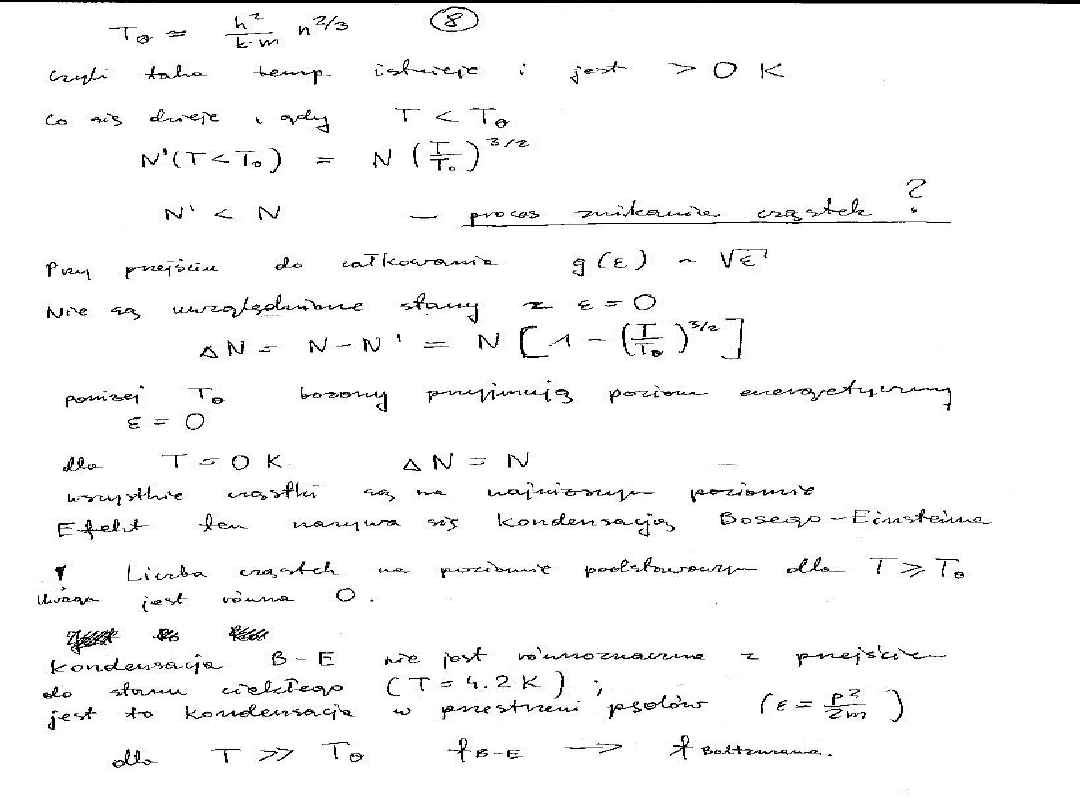
Document Outline
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron