
Obliczanie niepewności
pomiarowej w AAS na podstawie
wybranych przykładów
- przykłady obliczeń niepewności
wielkości wejściowych

Niepewność związana z objętością
kolby miarowej o pojemności 100 ml
Na niepewność kolby miarowej o pojemności
100 ml wpływają trzy składowe:
kalibaracja
powtarzalność
temperatura
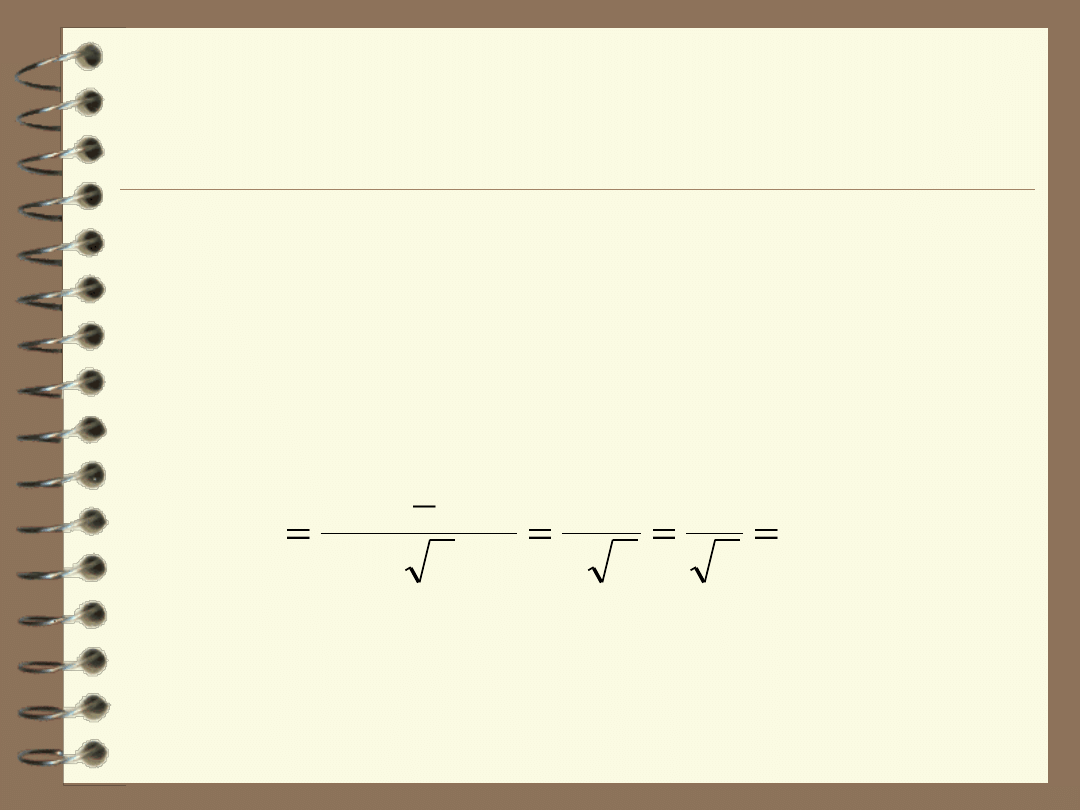
Niepewność związana z objętością
kolby miarowej o pojemności 100 ml
Kalibaracja
Pomiar objętości za pomocą kolby miarowej klasy A o pojemności:
100 ml
charakteryzuje się błędem:
0,1 ml.
Wartość bezwzględnej niepewności standardowej wynosi w tym
przypadku:
Wybrano rozkład tr
ójkątny, gdyż w rzeczywistym procesie
produkcyjnym wartość nominalna jest bardziej prawdopodobna
niż wartości ekstremalne, dlatego rozkład tr
ójkątny znacznie
lepiej oddaje rzeczywistą sytuacje niż rozkład prostokątny
ml
u
v
04
,
0
6
1
,
0
6
2
2
,
0
6
2
9
,
99
1
,
100

Niepewność związana z objętością
kolby miarowej o pojemności 100 ml
powtarzalność
Niepewność wynikającą ze zmienności napełniania można oszacować
po przez badanie powtarzalności z użyciem typowej kolby.
W serii dziesięciu napełnień i ważeń typowej kolby
o pojemności 100 ml.
Obliczenie odchylenia standardowego serii dziesięciu napełnień
i ważeń kolby jest równoważne
z określeniem niepewności standardowej.
Wyznaczone w serii dziesięciu powtórzeń
odchylenie standardowe
napełniania kolby miarowej o pojemności 100 ml
jest równe
0,2 ml

Niepewność związana z objętością
kolby miarowej o pojemności 100 ml
temperatura
Aby uwzględnić niepewność związaną z faktem, iż kolba była kalibrowana w
temperaturze (T=20
0
C) innej niż temperatura jaka panuje w laboratorium
tzw. poprawkę temperaturową. W tym celu należy obliczyć związana z tym
wartość niepewności zakładając maksymalna różnicę temperatur, np..
Temperatura w laboratorium mieści się w granicach: 20 ± 4
o
C.
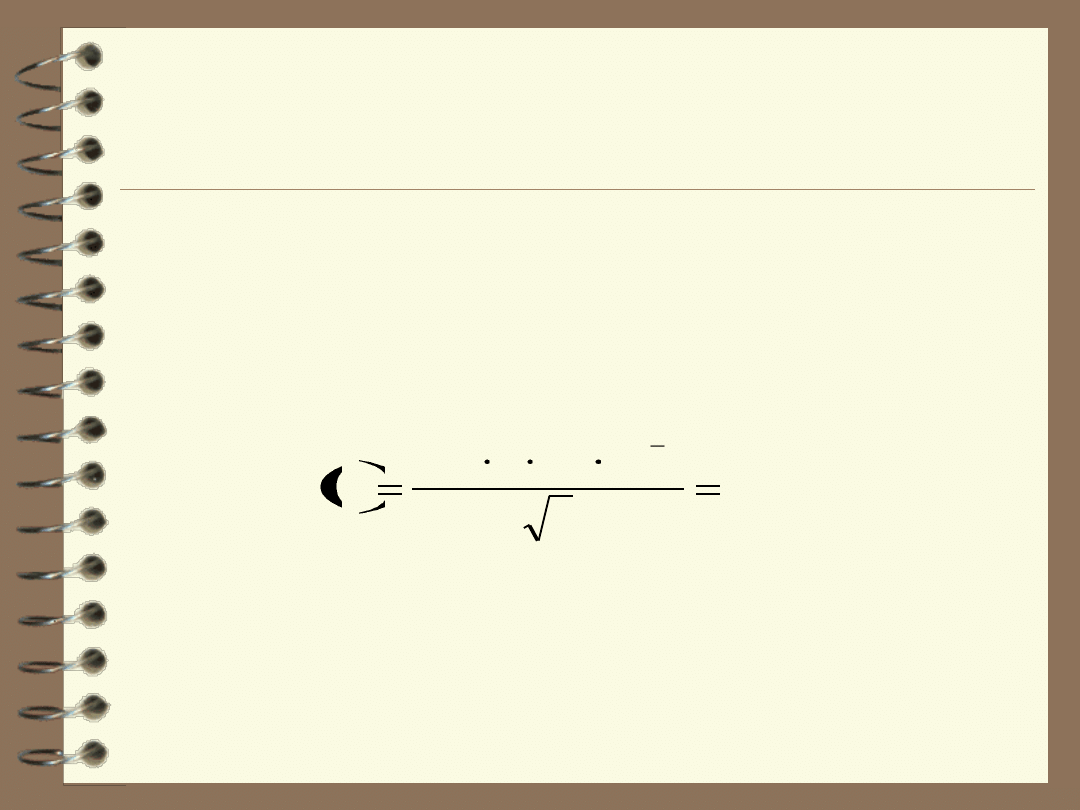
Wartość standardowej niepewności należy obliczyć zgodnie z zależnością:
gdzie:
V – maksymalna objętość roztworu w kolbie (100ml),
ΔT – maksymalna różnica temperatur,
- współczynnik rozszerzalności cieplnej wody (ml/
o
C) równy 2,1 · 10
-4
ml/
o
C.
3
2
O
H
T
V
T
u
O
H
2
Niepewność związana z objętością
kolby miarowej o pojemności 100 ml
temperatura
Po podstawieniu danych otrzymujemy:
ml
T
u
05
,
0
3
10
1
,
2
4
100
4
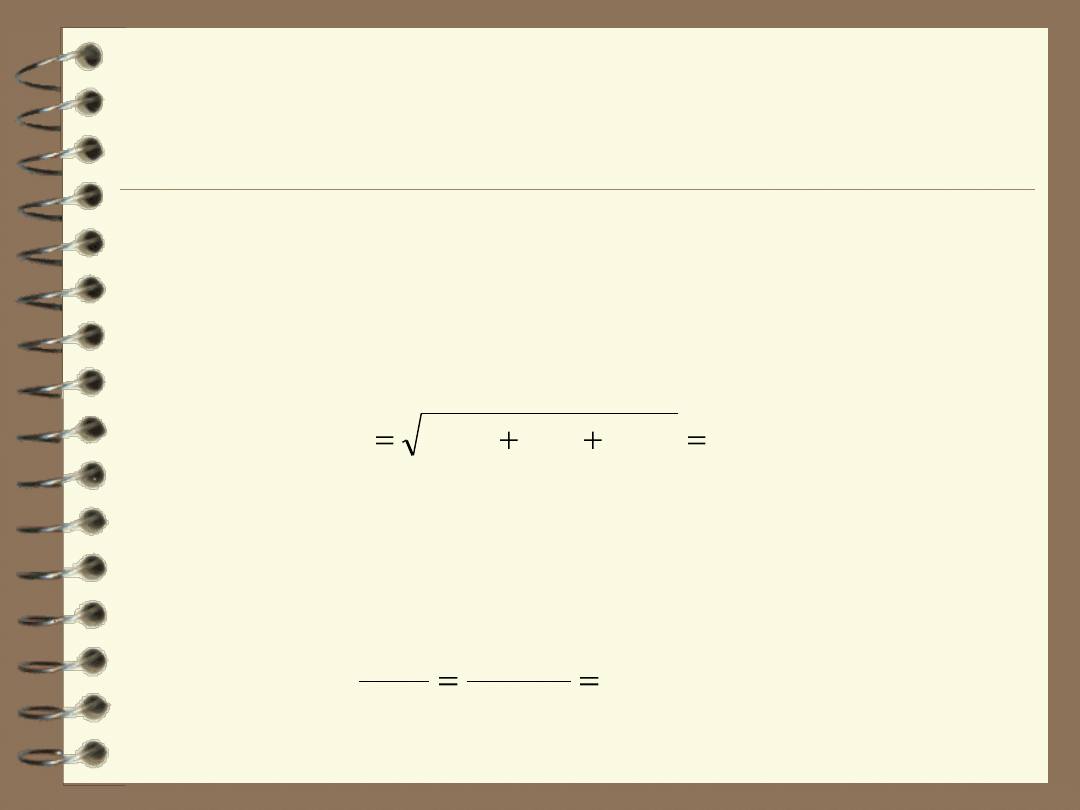
Połączenie trzech składowych, zgodnie z prawem
propagacji błędu, daje niepewność standardową u(V)
objętości V:
Więc względna niepewność standardowa objętości kolby
100 ml wynosi:
ml
V
u
21
,
0
05
,
0
2
,
0
04
,
0
)
(
2
2
2
0021
,
0
100
21
,
0
)
(
ml
ml
V
V
u
Niepewność związana z objętością
kolby miarowej o pojemności 100 ml

Czystość kadmu podana w certyfikacie jako
0,9999
0,0001.
W przypadku braku dodatkowych informacji dotyczących wartości
niepewności, zakłada się zwykle jej rozkład prostokątny.
W celu obliczenia niepewności standardowej korzystamy z zależności:
Po podstawieniu danych otrzymujemy:
Niepewność związana z czystością
np.. metalu używanego do sporządzenia roztworu
wzorcowego
3
)
(
P
u
P
u
st
000058
,
0
3
0001
,
0
)
(P
u
st

Na całkowitą niepewność ważenia wpływają
składowe:
kalibracja
•
liniowość
•
czułość
powtarzalność
Niepewność związana z masą

powtarzalność
Ponieważ powtarzalność ważenia jest zwykle uwzględniana w
powtarzalności całej metody i jest wyznaczona podczas kalibracji
to nie uwzględnia się jej zwykle na etapie obliczania niepewności
ważenia.
W przypadku obliczania niepewności pojedynczego oznaczenia
zachodzi konieczność uwzględnienia niepewności związanej z
powtarzalnością ważenia i wówczas należy wykorzystać wyniki
uzyskane podczas kontroli codziennej wag za pomocą odważników
sprawdzających.
Należy wziąć pod uwagę wyniki uzyskane dla odważnika o masie
najbardziej zbliżonej do masy badanej próbki
Niepewność związana z masą

kalibracja
•
liniowość
•
czułość
Każde systematyczne przesunięcie wagi (czułość) jest
znoszone ponieważ dla każdego odważenia
wykonujemy dwa pomiary: m (brutto) i masa (tara).
Na całkowitą niepewność ważenia wpływa tylko i
wyłącznie niepewność liniowości wagi.
Niepewność związana z masą

kalibracja
•
liniowość
Świadectwo kalibracji wagi podaje w przypadku liniowości wartość:
0,15 mg
, jest to maksymalna r
óżnica pomiędzy rzeczywistą masą
na szalce a odczytem na skali.
Niepewność typu B, rozkład prostokątny:
Więc standardowa niepewność wynosi:
:
Niepewność związana z masą
mg
m
u
st
09
,
0
3
15
,
0
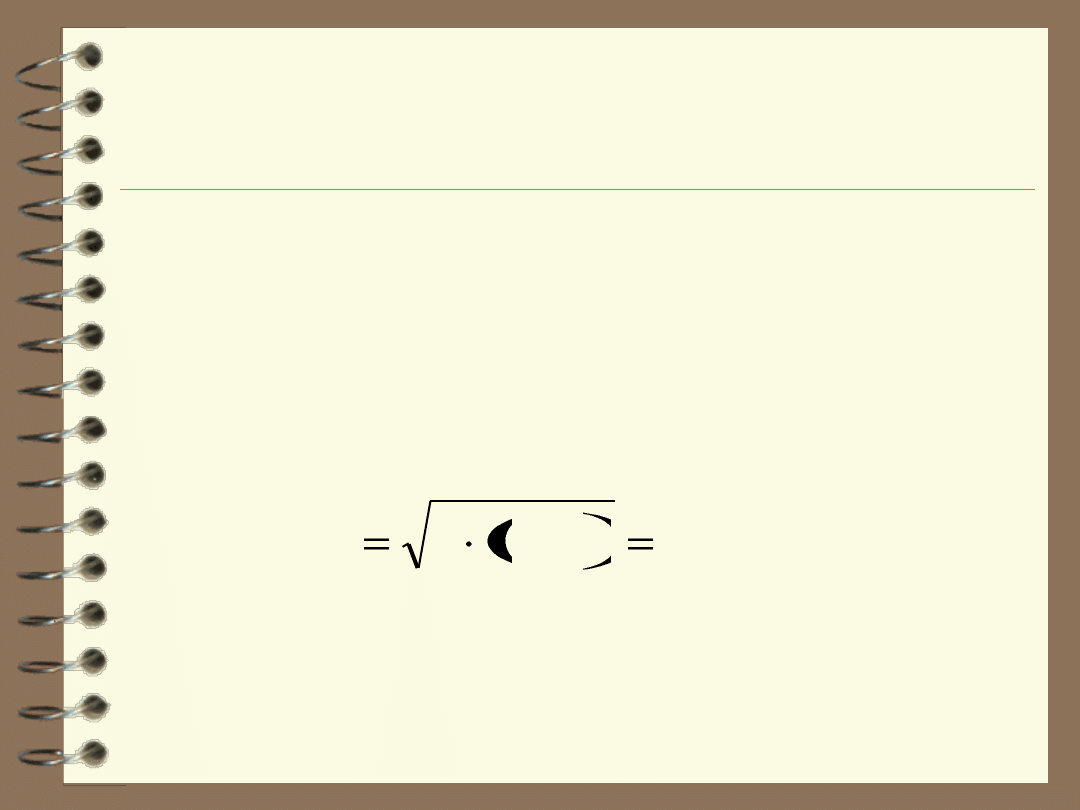
W celu odważenia badanej próby należy wykonać dwa
pomiary (tara i brutto), więc zgodnie z prawem
propagacji
niepewności
wartość
standardowej
niepewności związanej z odważeniem próby wynosi:
Niepewność związana z masą
mg
m
u
st
13
,
0
09
,
0
2
)
(
2

Niepewność związana z masą
molową
Każda masa atomowa została wyznaczona z pewnym
poziomem niepewności.
Niepewność wyznaczenia masy cząsteczkowej oblicza się
zgodnie zgodnie z prawem propagacji błędu,
uwzględniając jako składowe niepewności wyznaczenia
mas atomowych wszystkich pierwiastków wchodzących
w skład cząsteczki
z uwzględnieniem krotności ich atomów.

Niepewność związana z masą
molową
Przykładowe podawane w cyklicznych raportach (IUPAC)
wartości mas atomowych poszczególnych pierwiastków
wraz z ich niepewnościami i obliczone wartości
niepewności standardowych przy założonym rozkładzie
prostokątnym zestawiono w tabeli.
Niepewność standardową każdego pierwiastka oblicza się
przy założeniu, że każda z podanych w tabeli IUPAC
niepewności ma rozkład prostokątny.

Niepewność związana z masą
molową
[264]
Bohrium
Bh
107
208.98038(2)
Bismuth
Bi
83
9.012182(3)
Beryllium
Be
4
[247]
Berkelium
Bk
97
137.327(7)
Barium
Ba
56
[210]
Astatine
At
85
74.92160(2)
Arsenic
As
33
39.948(1)
Argon
Ar
18
121.760(1)
Antimony
Sb
51
[243]
Americium
Am
95
26.981538(2)
Aluminium
Al
13
[227]
Actinium
Ac
89
Atomic Wt
Name
Symbol
At No

Niepewność związana z masą
molową
Wartości niepewności wyznaczenia mas
atomowych można również znaleźć na
stronach internetowych:
http://www.iupac.org/dhtml_home.html
http://www.chem.qmul.ac.uk/iupac/AtWt/index.html
http://www.webelements.com/

Niepewność związana z masą molową
- niepewność masy cząsteczkowej chlorku sodu
Tabela 2. Wartości mas atomowych i niepewności ich
wyznaczenia dla sodu i chloru. (wg IUPAC)
Stosując prawo propagacji niepewności, wartość
standardowej niepewności związanej z masą
cząsteczkową NaCl, obliczono jako:
mol
g
u
NaCl
M
/
0011447
,
0
0011547
,
0
0000012
,
0
2
2

Względna niepewność standardowa związana z masą
cząsteczkową NaCl, wynosi:
000019587
,
0
4429
,
58
0011447
,
0
NaCl
M
M
u
NaCl
Niepewność związana z masą molową
- niepewność masy cząsteczkowej chlorku sodu

Niepewność związana z przygotowaniem
wzorców do krzywej kalibracyjnej metodą
kolejnych rozcieńczeń –
sposób A
W celu przygotowania wzorca Cd do krzywej kalibracyjnej o stężeniu
40 ug/l, stosuje się odpowiednie rozcieńczenia roztworu wzorcowego.
Sporządzano roztwór wzorcowy jonów kadmu Cd
2+
poprzez
rozcieńczenie roztworu podstawowego. Stężenie roztworu
podstawowego było podane przez producenta jako:
1001 ± 2
[mg Cd
2+
/dm
3
].
W celu otrzymania roztworu wzorcowego o stężeniu 40 µg Cd
2+
/dm
3
rozwór podstawowy rozcieńczano najpierw w stosunku 1:100
a następnie 1:250.
Na etapie rozcieńczania wykorzystywano pipety o pojemności 1 ml oraz
kolby miarowe o pojemnościach 100 ml i 250 ml.

Niepewność związana z przygotowaniem
wzorców do krzywej kalibracyjnej metodą
kolejnych rozcieńczeń –
sposób A
Wartość stężenia końcowego analitu w roztworze wzorcowym można
obliczyć wykorzystując następującą zależność:
gdzie:
c
wz
– stężenie roztworu wzorcowego podane przez producenta [µg Cd
2+
/dm
3
];
C
NIST
– certyfikowane stężenie roztworu podstawowego [mg Cd
2+
/dm
3
];
V
p1
, V
p2
– pojemności pipet wykorzystywanych w trakcie rozcieńczania [ml];
V
k1
, V
k2
– pojemności kolb wykorzystywanych w trakcie rozcieńczania [ml];
1000
2
2
1
1
k
p
k
p
NIST
wz
V
V
V
V
C
c

Obliczona zatem stężenie analitu w roztworze wzorcowym wynosi:
c
wz
= 40,04
µg Cd
2+
/dm
3
.
Podane przez producentów wartości poszczególnych parametrów były
następujące:
C
NIST
= 1001 2 [mg Cd
2+
/dm
3
];
V
p1
= V
p2
= 1 0,01 [ml]
V
k1
= 100
0,1 [ml]
V
k2
= 250
0,2 [ml]
Niepewność związana z przygotowaniem
wzorców do krzywej kalibracyjnej metodą
kolejnych rozcieńczeń –
sposób A
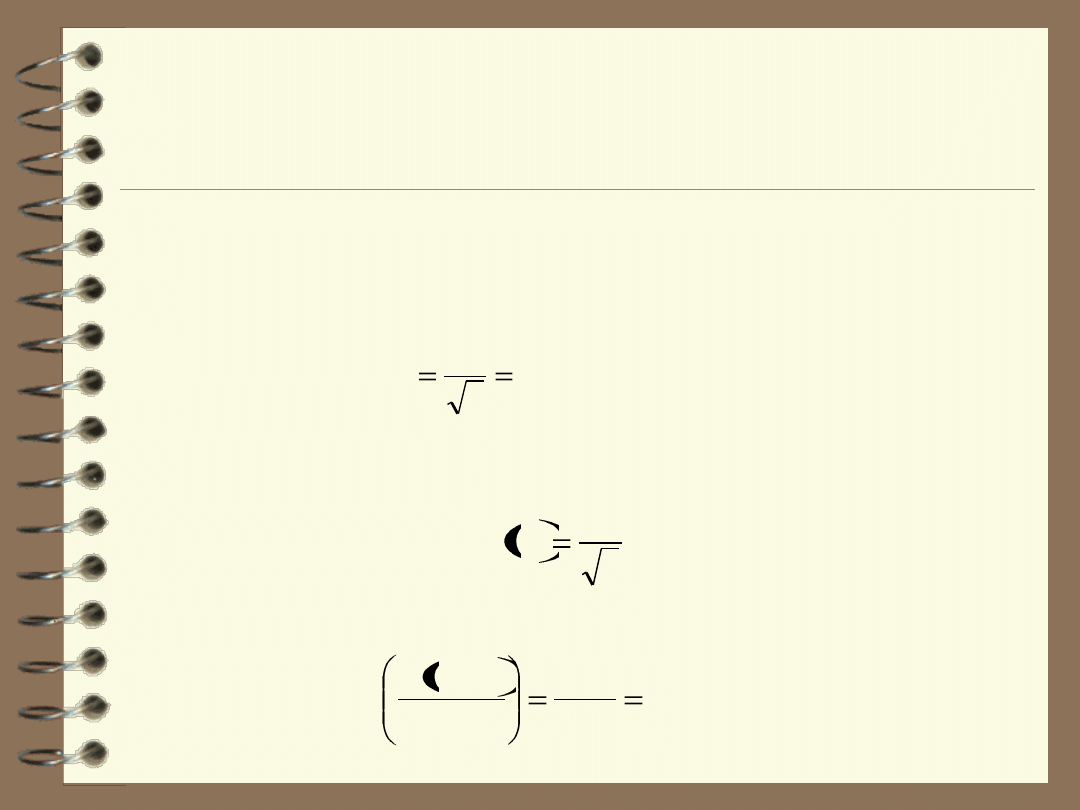
Niepewność związana z przygotowaniem wzorców do krzywej
kalibracyjnej metodą kolejnych rozcieńczeń –
sposób A -
N
iepewność związana ze stężeniem roztworu podstawowego
Stężenie kadmu deklarowane przez producenta charakteryzuje się
błędem:
± 2
[mg Cd
2+
/dm
3
];
Wartość bezwzględnej niepewności standardowej wynosi w tym
przypadku:
Parametr ten charakteryzuje się rozkładem jednostajnym, stąd
wartości poszczególnych niepewności standardowych obliczono
stosując zależność:
Wartość względnej niepewności stężenia Cd
2+
, wynosi:
3
/
15
,
1
3
2
dm
mg
u
c
3
a
x
u
i
00115
,
0
1001
15
,
1
NIST
NIST
C
C
u

kalibracja
Pomiar objętości za pomocą pipety automatycznej o pojemności:
1 ml
charakteryzuje się błędem:
0,01
ml.
Wartość bezwzględnej niepewności standardowej wynosi w tym
przypadku:
Wybrano rozkład trójkątny, gdyż w rzeczywistym procesie produkcyjnym
wartość nominalna jest bardziej prawdopodobna niż wartości
ekstremalne, dlatego rozkład trójkątny znacznie lepiej oddaje
rzeczywista sytuacje niż rozkład prostokątny
Niepewność związana z przygotowaniem wzorców do krzywej
kalibracyjnej metodą kolejnych rozcieńczeń –
sposób A
Niepewność związana z objętością pipety automatycznej
o pojemności 1 ml
ml
u
V
004
,
0
6
01
,
0

powtarzalność
Niepewność wynikającą ze zmienności odmierzania cieczy można
oszacować po przez badanie powtarzalności. W serii dziesięciu
napełnień i ważeń cieczy odmierzanej za pomocą pipety
automatycznej o pojemności 1 ml.
Obliczenie odchylenia standardowego serii dziesięciu napełnień i
ważeń wody jest równoważne z określeniem niepewności
standardowej.
Wyznaczone w serii dziesięciu napełnień pipety i ważeń wody
odchylenie standardowe odmierzanej cieczy o pojemności
1 ml
jest
równe
0,015 ml
Niepewność związana z przygotowaniem wzorców do krzywej
kalibracyjnej metodą kolejnych rozcieńczeń –
sposób A
Niepewność związana z objętością pipety automatycznej
o pojemności 1 ml

Niepewność związana z przygotowaniem wzorców
do krzywej kalibracyjnej metodą kolejnych
rozcieńczeń –
sposób A
Niepewność związana z objętością pipety automatycznej
o pojemności 1 ml
temperatura
Aby uwzględnić niepewność związaną z faktem, iż pipeta była kalibrowana w
temperaturze (T=20
0
C) innej niż temperatura jaka panuje zwykle w
laboratorium tzw. poprawkę temperaturową. W tym celu należy obliczyć
związana z tym wartość niepewności zakładając maksymalna różnicę
temperatur, np. Temperatura w laboratorium mieści się w granicach:
20 ± 4
o
C.
Wartość standardowej niepewności należy obliczyć zgodnie z zależnością:
gdzie:
V – maksymalna objętość pipety (1ml),
ΔT – maksymalna różnica temperatur,
- współczynnik rozszerzalności cieplnej wody (ml/
o
C) równy 2,1 ·10
-4
ml/
o
C.
3
2
O
H
T
V
T
u

Po podstawieniu danych otrzymujemy:
Połączenie trzech składowych, zgodnie z prawem propagacji błędu,
daje niepewność standardową u(V) objętości V:
Więc względna niepewność standardowa objętości pipety
automatycznej 1 ml wynosi:
ml
T
u
0005
,
0
3
10
1
,
2
4
1
4
ml
V
u
015
,
0
0005
,
0
015
,
0
004
,
0
)
(
2
2
2
015
,
0
1
015
,
0
2
2
1
1
ml
ml
V
V
u
V
V
u
p
p
p
p
Niepewność związana z przygotowaniem wzorców do krzywej
kalibracyjnej metodą kolejnych rozcieńczeń –
sposób A
Niepewność związana z objętością pipety automatycznej
o pojemności 1 ml

Niepewność związana z przygotowaniem wzorców do krzywej
kalibracyjnej metodą kolejnych rozcieńczeń –
sposób A
Niepewność związana z objętością kolby miarowej o pojemności 100 ml
Na niepewność kolby miarowej o pojemności 100
ml wpływają trzy składowe:
kalibracja
powtarzalność
temperatura
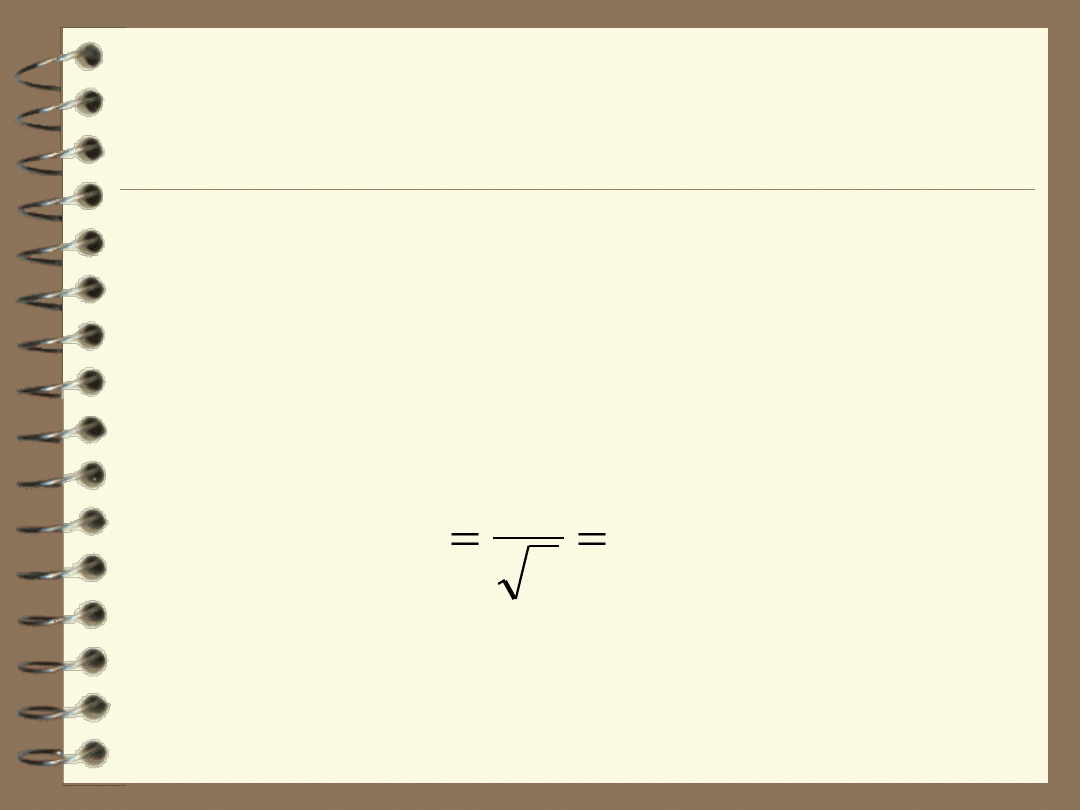
kalibracja
Pomiar objętości za pomocą kolby miarowej klasy A o pojemności:
100 ml
charakteryzuje się błędem:
0,1 ml.
Wartość bezwzględnej niepewności standardowej wynosi w tym
przypadku:
Wybrano rozkład trójkątny, gdyż w rzeczywistym procesie produkcyjnym
wartość nominalna jest bardziej prawdopodobna niż wartości
ekstremalne, dlatego rozkład trójkątny znacznie lepiej oddaje
rzeczywista sytuacje niż rozkład prostokątny
Niepewność związana z przygotowaniem wzorców do krzywej
kalibracyjnej metodą kolejnych rozcieńczeń –
sposób A
Niepewność związana z objętością kolby miarowej o pojemności 100 ml
ml
u
V
04
,
0
6
1
,
0

powtarzalność
Niepewność wynikającą ze zmienności napełniania można oszacować
po przez badanie powtarzalności z użyciem typowej kolby. W serii
dziesięciu napełnień i ważeń typowej kolby o pojemności 100 ml.
Obliczenie odchylenia standardowego serii dziesięciu napełnień i ważeń
kolby jest równoważne z określeniem niepewności standardowej.
Wyznaczone w serii dziesięciu powtórzeń
odchylenie standardowe
napełniania kolby miarowej o pojemności 100 ml jest równe
0,3 ml
Niepewność związana z przygotowaniem wzorców do krzywej
kalibracyjnej metodą kolejnych rozcieńczeń –
sposób A
Niepewność związana z objętością kolby miarowej o pojemności 100 ml

Niepewność związana z przygotowaniem wzorców
do krzywej kalibracyjnej metodą kolejnych
rozcieńczeń –
sposób A
Niepewność związana z objętością kolby miarowej o pojemności 100 ml
temperatura
Aby uwzględnić niepewność związaną z faktem, iż kolba była kalibrowana w
temperaturze (T=20
0
C) innej niż temperatura jaka panuje zwykle w
laboratorium tzw. poprawkę temperaturową. W tym celu należy obliczyć
związana z tym wartość niepewności zakładając maksymalna r
óżnicę
temperatur, np. Temperatura w laboratorium mieści się w granicach:
20 ± 4
o
C.
Wartość standardowej niepewności należy obliczyć zgodnie z zależnością:
gdzie:
V – maksymalna objętość roztworu w kolbie (100ml),
ΔT
– maksymalna różnica temperatur,
- wsp
ółczynnik rozszerzalności cieplnej wody (ml/
o
C) r
ówny 2,1 ·10
-4
ml/
o
C.
3
2
O
H
T
V
T
u

Po podstawieniu danych otrzymujemy:
Połączenie trzech składowych, zgodnie z prawem propagacji błędu, daje
niepewność standardową u(V) objętości V:
Więc względna niepewność standardowa objętości kolby 100 ml wynosi:
ml
T
u
05
,
0
3
10
1
,
2
4
100
4
ml
V
u
31
,
0
05
,
0
3
,
0
04
,
0
)
(
2
2
2
0031
,
0
100
31
,
0
1
1
ml
ml
V
V
u
k
k
Niepewność związana z przygotowaniem wzorców do krzywej
kalibracyjnej metodą kolejnych rozcieńczeń –
sposób A
Niepewność związana z objętością kolby miarowej o pojemności 100 ml

Niepewność związana z przygotowaniem wzorców do krzywej
kalibracyjnej metodą kolejnych rozcieńczeń –
sposób A
Niepewność związana z objętością kolby miarowej o pojemności 250 ml
Na niepewność kolby miarowej o pojemności 250
ml wpływają trzy składowe:
kalibracja
powtarzalność
temperatura

kalibracja
Pomiar objętości za pomocą kolby miarowej klasy A o pojemności:
250 ml
charakteryzuje się błędem:
0,2 ml.
Wartość bezwzględnej niepewności standardowej wynosi w tym
przypadku:
Wybrano rozkład tr
ójkątny, gdyż w rzeczywistym procesie
produkcyjnym wartość nominalna jest bardziej prawdopodobna niż
wartości ekstremalne, dlatego rozkład tr
ójkątny znacznie lepiej
oddaje rzeczywista sytuacje niż rozkład prostokątny
Niepewność związana z przygotowaniem wzorców do krzywej
kalibracyjnej metodą kolejnych rozcieńczeń –
sposób A
Niepewność związana z objętością kolby miarowej o pojemności 250 ml
ml
u
V
08
,
0
6
2
,
0

powtarzalność
Niepewność wynikającą ze zmienności napełniania można oszacować
po przez badanie powtarzalności z użyciem typowej kolby. W serii
dziesięciu napełnień i ważeń cieczy (wody) w typowej kolbie o
pojemności 250 ml.
Obliczenie odchylenia standardowego serii dziesięciu napełnień i
ważeń wody w kolbie jest równoważne z określeniem niepewności
standardowej.
Wyznaczone w serii dziesięciu powtórzeń
odchylenie standardowe
napełniania kolby miarowej o pojemności 250 ml jest równe
0,5 ml
Niepewność związana z przygotowaniem wzorców do krzywej
kalibracyjnej metodą kolejnych rozcieńczeń –
sposób A
Niepewność związana z objętością kolby miarowej o pojemności 250 ml

Niepewność związana z przygotowaniem wzorców do krzywej
kalibracyjnej metodą kolejnych rozcieńczeń –
sposób A
Niepewność związana z objętością kolby miarowej o pojemności 250 ml
temperatura
Aby uwzględnić niepewność związaną z faktem, iż kolba była kalibrowana w
temperaturze (T=20
0
C) innej niż temperatura jaka panuje zwykle w
laboratorium tzw. poprawkę temperaturową. W tym celu należy obliczyć
związana z tym wartość niepewności zakładając maksymalna r
óżnicę
temperatur, np. Temperatura w laboratorium mieści się w granicach:
20 ± 4
o
C.
Wartość standardowej niepewności należy obliczyć zgodnie z zależnością:
gdzie:
V – maksymalna objętość roztworu w kolbie (250ml),
ΔT
– maksymalna różnica temperatur,
- wsp
ółczynnik rozszerzalności cieplnej wody (ml/
o
C) r
ówny 2,1 ·10
-4
ml/
o
C.
3
2
O
H
T
V
T
u

Po podstawieniu danych otrzymujemy:
Połączenie trzech składowych, zgodnie z prawem
propagacji błędu, daje niepewność standardową u(V)
objętości V:
Więc względna niepewność standardowa objętości kolby
250 ml wynosi:
ml
T
u
12
,
0
3
10
1
,
2
4
250
4
ml
V
u
52
,
0
12
,
0
5
,
0
08
,
0
)
(
2
2
2
0021
,
0
250
52
,
0
2
2
ml
ml
V
V
u
k
k
Niepewność związana z przygotowaniem wzorców do krzywej
kalibracyjnej metodą kolejnych rozcieńczeń –
sposób A
Niepewność związana z objętością kolby miarowej o pojemności 250 ml
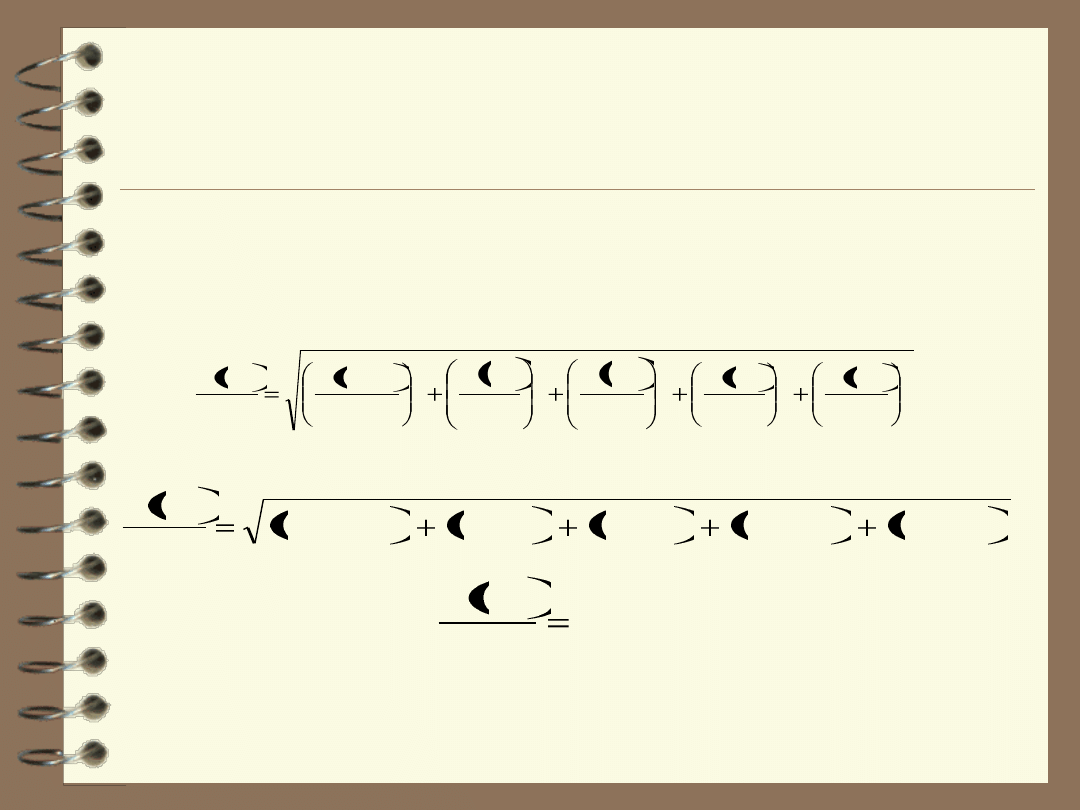
Wartość całkowitej niepewności stężenia otrzymanego roztworu
wzorcowego obliczono stosując prawo propagacji niepewności
zgodnie z poniższą zależnością:
Po podstawieniu danych:
a stąd:
u(c
wz
) = 0,864
µg Cd
2+
/dm
3
2
2
2
2
1
1
2
2
2
2
1
1
2
k
k
k
k
p
p
p
p
NIST
NIST
wz
wz
V
V
u
V
V
u
V
V
u
V
V
u
C
C
u
c
c
u
2
2
2
2
2
0021
,
0
0031
,
0
015
,
0
015
,
0
00115
,
0
wz
wz
c
c
u
0216
,
0
wz
wz
c
c
u
Niepewność związana z przygotowaniem
wzorców do krzywej kalibracyjnej metodą
kolejnych rozcieńczeń –
sposób A

W celu obliczenia całkowitej rozszerzonej niepewności (U) należy wartość
całkowitej niepewności u(c
wz
) pomnożyć przez przyjętą wartość
współczynnika rozszerzenia k. Jeśli k = 2 to U = 1,7 ml.
Poprawnie zapisany wynik stężenia uzyskanego roztworu wzorcowego:
c
wz
U(k=2) = 40,0 1,7 [
µ
g Cd
2+
/dm
3
]
UWAGA!!!
Wartość niepewności zapisuje się z podaniem tylko 2 cyfr znaczących,
a wartość wyniku z taką samą liczbą miejsc dziesiętnych jak
wartość niepewności.
Niepewność związana z przygotowaniem
wzorców do krzywej kalibracyjnej metodą
kolejnych rozcieńczeń –
sposób A
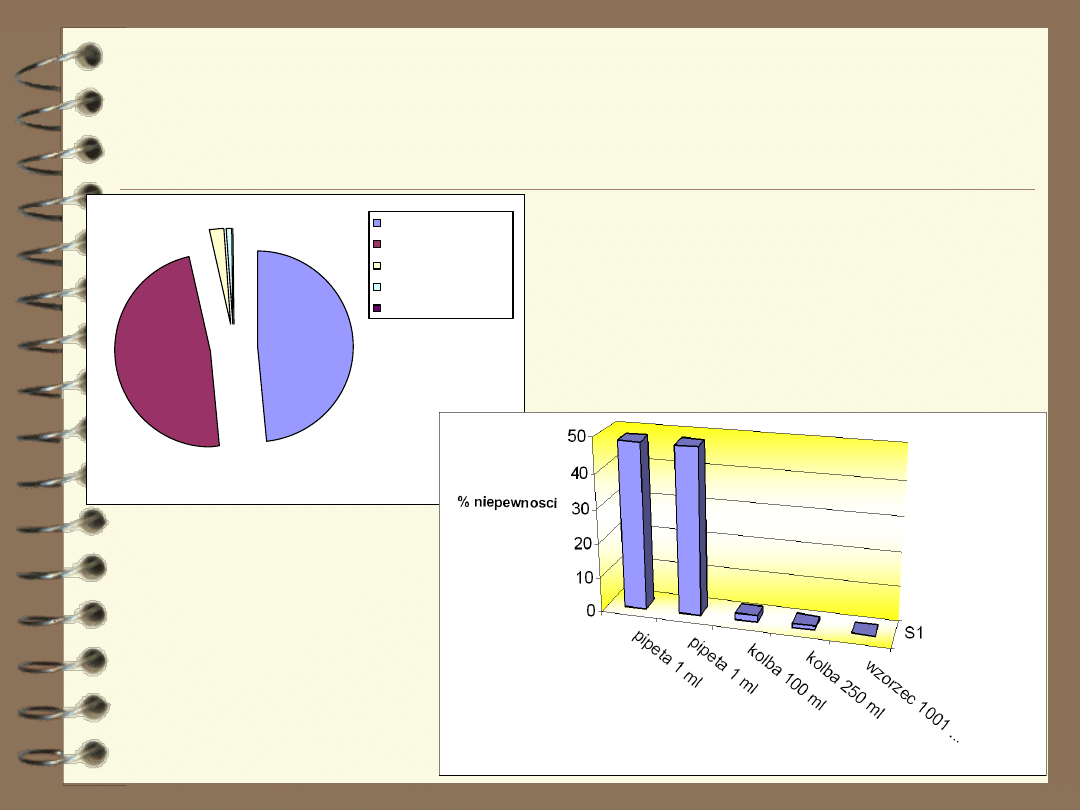
Niepewność związana z przygotowaniem wzorców do krzywej
kalibracyjnej metodą kolejnych rozcieńczeń –
sposób A
% udział poszczególnych składowych niepewności
pipeta 1 ml
pipeta 1 ml
kolba 100 ml
kolba 250 ml
w zorzec 1001 mg/dm3

Niepewność związana z przygotowaniem
wzorców do krzywej kalibracyjnej metodą
kolejnych rozcieńczeń –
sposób B
W celu przygotowania tego samego wzorca Cd do krzywej
kalibracyjnej o stężeniu 40 ug/l, zastosowano inne rozcieńczenia
roztworu wzorcowego.
Stężenie roztworu podstawowego było podane przez producenta jako:
1001 2 [mg Cd
2+
/dm
3
].
W celu otrzymania roztworu wzorcowego o stężeniu 40
µg Cd
2+
/dm
3
rozw
ór podstawowy rozcieńczano kolejno:
10:100
10:100
10:100
10:250.
Na etapie rozcieńczania wykorzystywano pipety szklane klasy A o
pojemności 10 ml oraz kolby miarowe szklane kasy A o
pojemnościach 100 ml i 250 ml.
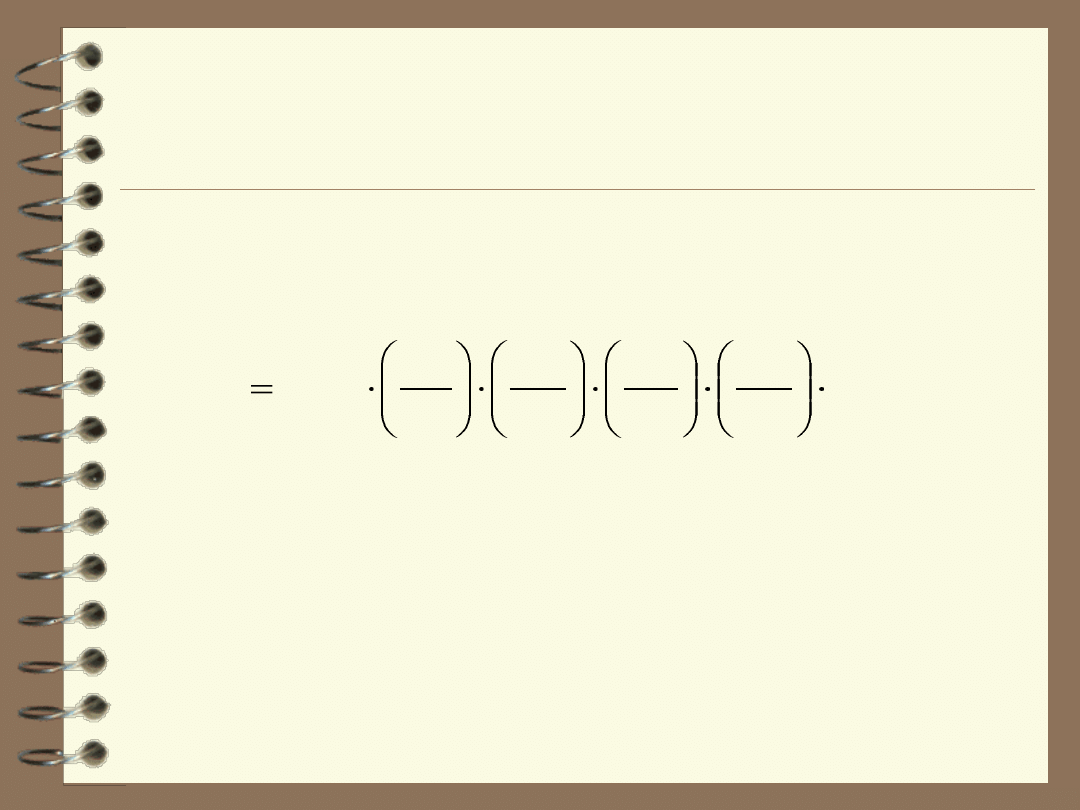
Niepewność związana z przygotowaniem
wzorców do krzywej kalibracyjnej metodą
kolejnych rozcieńczeń –
sposób B
Wartość stężenia końcowego analitu w roztworze wzorcowym można
obliczyć wykorzystując następującą zależność:
gdzie:
c
wz
–
stężenie otrzymanego roztworu wzorcowego
[
µg Cd
2+
/dm
3
];
C
NIST
–
certyfikowane roztworu podstawowego [mg Cd
2+
/dm
3
];
V
p1
, V
p2
,V
p3
, V
p4
–pojemności
pipet wykorzystywanych w trakcie
rozcieńczania [ml];
V
k1
, V
k2
, V
k3
, V
k4
–pojemności
kolb wykorzystywanych w trakcie
rozcieńczania
[ml];
1000
4
4
3
3
2
2
1
1
k
p
k
p
k
p
k
p
NIST
wz
V
V
V
V
V
V
V
V
C
c

Obliczona zatem stężenie analitu w roztworze wzorcowym wynosi:
c
wz
= 40,04
µg Cd
2+
/dm
3
.
Podane przez producentów wartości poszczególnych parametrów były
następujące:
C
NIST
= 1001 2 [mg Cd
2+
/dm
3
];
V
p1
= V
p2
= V
p3
= V
p4
= 10 0,02 [ml]
V
k1
= V
k2
= V
k3
= 100 0,1 [ml]
V
k4
= 250 0,2 [ml]
Niepewność związana z przygotowaniem
wzorców do krzywej kalibracyjnej metodą
kolejnych rozcieńczeń –
sposób B

kalibracja
Pomiar objętości za pomocą pipety o pojemności:
10 ml
charakteryzuje
się błędem:
0,02 ml.
Wartość bezwzględnej niepewności standardowej wynosi w tym
przypadku:
Wybrano rozkład trójkątny, gdyż w rzeczywistym procesie produkcyjnym
wartość nominalna jest bardziej prawdopodobna niż wartości
ekstremalne, dlatego rozkład trójkątny znacznie lepiej oddaje
rzeczywista sytuacje niż rozkład prostokątny
Niepewność związana z przygotowaniem wzorców do krzywej
kalibracyjnej metodą kolejnych rozcieńczeń –
sposób B
Niepewność związana z objętością pipety o pojemności 10 ml
ml
u
V
008
,
0
6
02
,
0

powtarzalność
Niepewność wynikającą ze zmienności napełniania można oszacować
po przez badanie powtarzalności. W serii dziesięciu napełnień i
ważeń cieczy odmierzanej za pomocą pipety o pojemności 10 ml.
Obliczenie odchylenia standardowego serii dziesięciu napełnień i
ważeń wody jest równoważne z określeniem niepewności
standardowej.
Wyznaczone w serii dziesięciu napełnień i ważeń wody
odchylenie
standardowe
odmierzanej cieczy o pojemności 10 ml
jest równe
0,03 ml
Niepewność związana z przygotowaniem wzorców do krzywej
kalibracyjnej metodą kolejnych rozcieńczeń –
sposób B
Niepewność związana z objętością pipety o pojemności 10 ml

Niepewność związana z przygotowaniem wzorców do krzywej
kalibracyjnej metodą kolejnych rozcieńczeń –
sposób B
Niepewność związana z objętością pipety o pojemności 10 ml
temperatura
Aby uwzględnić niepewność związaną z faktem, iż pipeta była kalibrowana
w temperaturze (T=20
0
C) innej niż temperatura jaka panuje zwykle w
laboratorium tzw. poprawkę temperaturową. W tym celu należy obliczyć
związana z tym wartość niepewności zakładając maksymalna r
óżnicę
temperatur, np. Temperatura w laboratorium mieści się
w granicach:
20 ± 4
o
C.
Wartość standardowej niepewności należy obliczyć zgodnie z zależnością:
gdzie:
V – maksymalna objętość pipety (10ml),
ΔT
– maksymalna różnica temperatur,
- wsp
ółczynnik rozszerzalności cieplnej wody (ml/
o
C) r
ówny 2,1·10
-4
ml/
o
C.
3
2
O
H
T
V
T
u
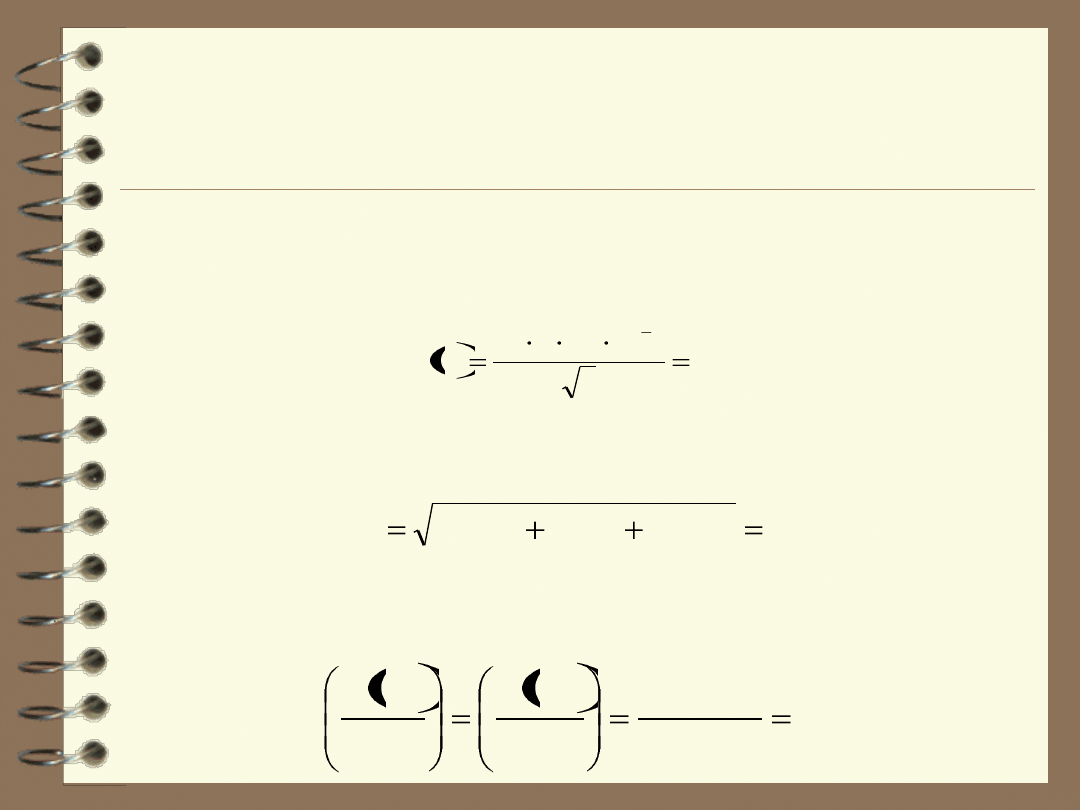
Po podstawieniu danych otrzymujemy:
Połączenie trzech składowych, zgodnie z prawem propagacji błędu,
daje niepewność standardową u(V) objętości V:
Więc względna niepewność standardowa objętości pipety o
pojemności 10 ml wynosi:
ml
T
u
005
,
0
3
10
1
,
2
4
10
4
ml
V
u
036
,
0
005
,
0
03
,
0
008
,
0
)
(
2
2
2
0036
,
0
10
036
,
0
2
2
1
1
ml
ml
V
V
u
V
V
u
p
p
p
p
Niepewność związana z przygotowaniem wzorców
do krzywej kalibracyjnej metodą kolejnych
rozcieńczeń –
sposób B
Niepewność związana z objętością pipety o pojemności 10 ml

Wartość całkowitej niepewności stężenia otrzymanego roztworu
wzorcowego obliczono stosując prawo propagacji niepewności
zgodnie z poniższą zależnością:
Po podstawieniu danych:
a stąd:
u(c
wz
) = 0,372
µg Cd
2+
/dm
3
.
2
4
4
2
3
3
2
2
2
2
1
1
2
4
4
2
3
3
2
2
2
2
1
1
2
k
k
k
k
k
k
k
k
p
p
p
p
p
p
p
p
NIST
NIST
wz
wz
V
V
u
V
V
u
V
V
u
V
V
u
V
V
u
V
V
u
V
V
u
V
V
u
C
C
u
c
c
u
0093
,
0
wz
wz
c
c
u
Niepewność związana z przygotowaniem
wzorców do krzywej kalibracyjnej metodą
kolejnych rozcieńczeń –
sposób B
2
2
2
2
0021
,
0
0031
,
0
3
0036
,
0
4
00115
,
0
wz
wz
c
c
u
2
4
4
2
1
1
2
1
1
2
3
4
k
k
k
k
p
p
NIST
NIST
wz
wz
V
V
u
V
V
u
V
V
u
C
C
u
c
c
u
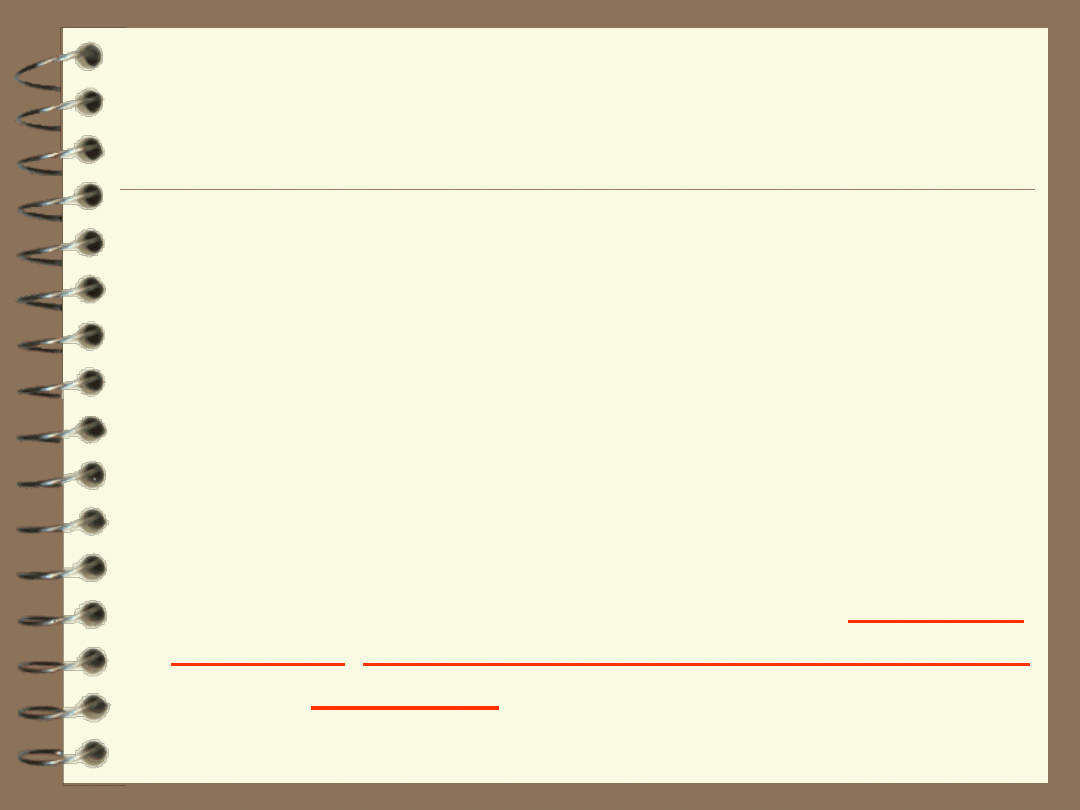
W celu obliczenia całkowitej rozszerzonej niepewności (U) należy
wartość całkowitej niepewności u(
cwz
) pomnożyć przez przyjętą wartość
współczynnika rozszerzenia k. Jeśli k = 2 to U = 0,74 ml.
Poprawnie zapisany wynik stężenia uzyskanego roztworu wzorcowego:
c
wz
U(k=2) = 40,04 0,74 [
µ
g Cd
2+
/dm
3
]
UWAGA!!!
Wartość niepewności zapisuje się z podaniem tylko 2 cyfr
znaczących, a wartość wyniku z taką samą liczbą miejsc
dziesiętnych jak wartość niepewności.
Niepewność związana z przygotowaniem
wzorców do krzywej kalibracyjnej metodą
kolejnych rozcieńczeń –
sposób B
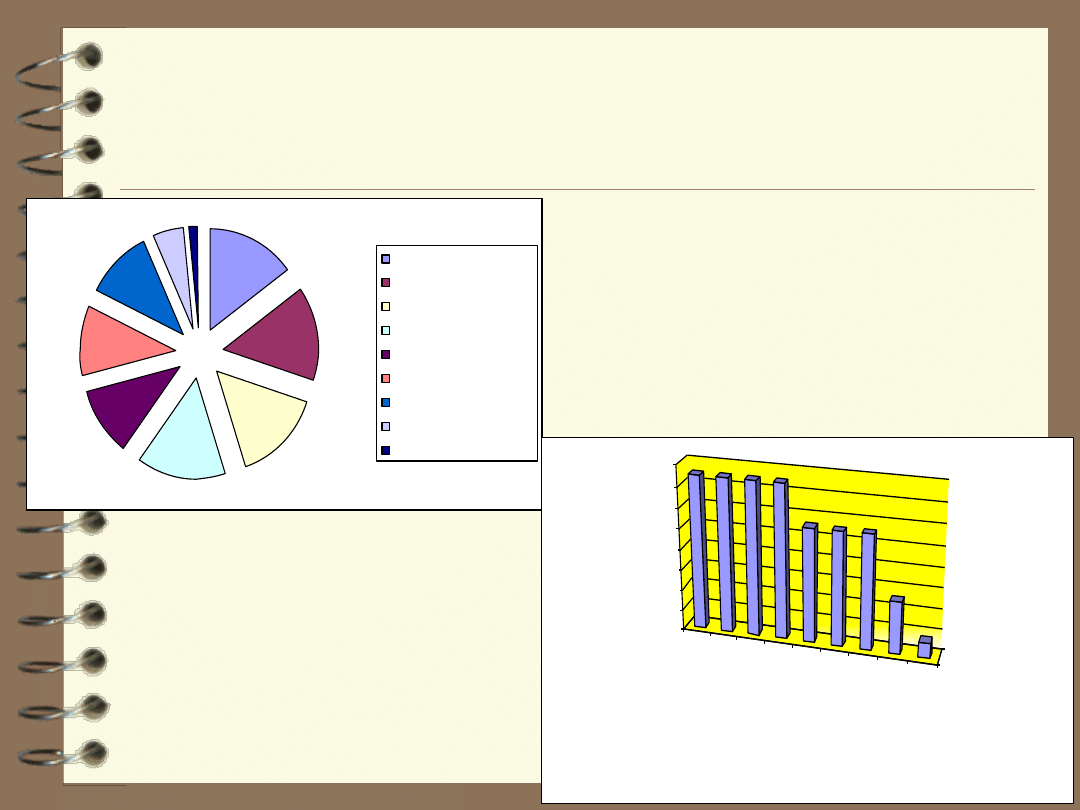
Niepewność związana z przygotowaniem wzorców do
krzywej kalibracyjnej metodą kolejnych rozcieńczeń –
sposób B
% udział poszczególnych składowych niepewności
pipeta 10 ml
pipeta 10 ml
pipeta 10 ml
pipeta 10 ml
kolba 100 ml
kolba 100 ml
kolba 100 ml
kolba 250 ml
wzorzec 1001 mg/dm3
pip
eta
10
m
l
pip
eta
10
m
l
kolb
a 1
00
m
l
kolb
a 1
00
m
l
wz
orz
ec 1
001
...
S1
0
2
4
6
8
10
12
14
16
% niepewnosci
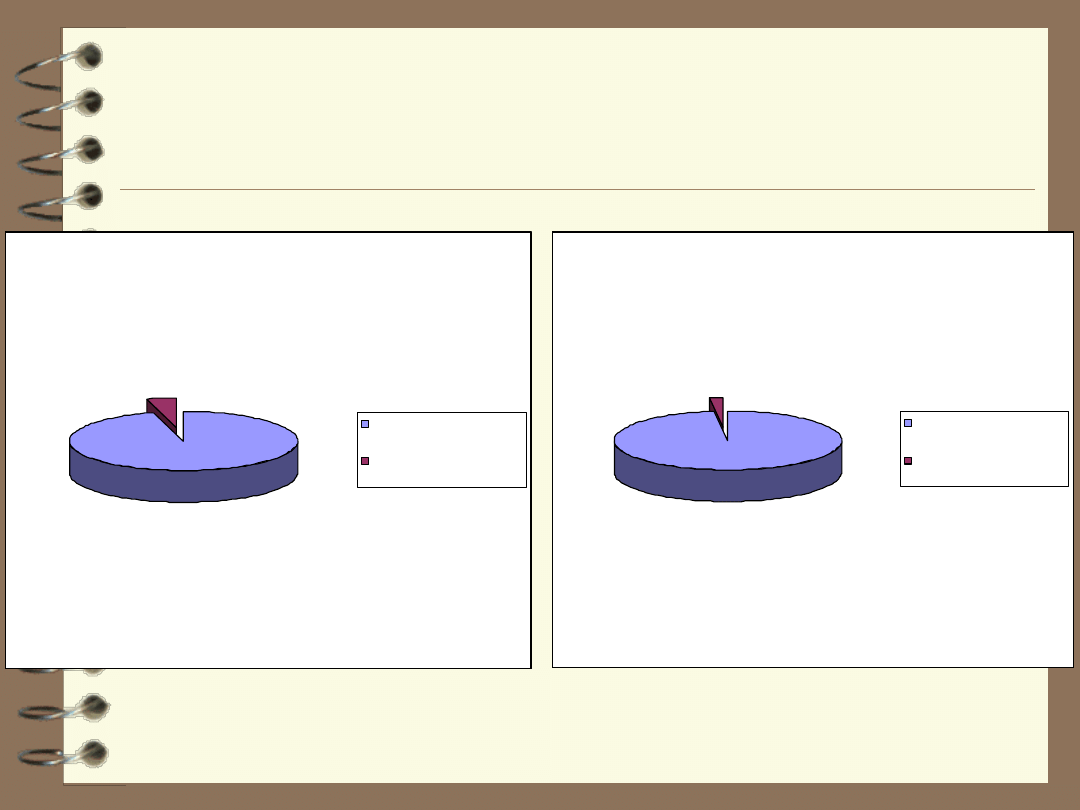
Porównanie niepewności
sposób A; sposób B
w zorzec
niepew ność rozszerzona -
sposób A
w zorzec
niepew ność rozszerzona -
sposób B
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron