Podstawy metrologii – w4

Niniejsza prezentacja zawiera materiały pomocnicze do zagadnień objętych
V jednostką tematyczną wykładu z przedmiotu Podstawy metrologii.

Pomocniczy materiał dydaktyczny – wyłącznie do celów edukacyjnych.

Udostępnianie osobom trzecim zabronione.

Podstawy metrologii – w5/s1

Teoria niepewności

Niepewność

–

parametr związany z wynikiem pomiaru charakteryzujący rozrzut wartości, który można

w uzasadniony sposób przypisać wartości mierzonej

.

Niepewność standardowa

–

dla każdej z wielkości wejściowej x

i

wyrażana przez odchylenie standardowe wyników

pomiarów wykonywanych w niezmiennych warunkach odniesienia

.

S

x

u

i

=

)

(

Niepewność złożona (łączna)

–

złożenie niepewności standardowych wielkości wejściowych

x

i

.

2

1

2

i

n

i

i

C

u

X

f

u

∑

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

∂

∂

=

Niepewność rozszerzona

–

wielkość określająca przedział wartości wokół wyniku pomiaru.

( )

y

u

k

U

C

⋅

=

k

(

k

p

) –

współczynnik rozszerzenia

związany z poziomem ufności

p

( )

y

u

k

U

C

p

p

⋅

=

Niepewność standardowa typu A (metoda A)

–

wyznaczana metodami statystycznymi, odpowiada błędom

spowodowanym efektami przypadkowymi.

Niepewność standardowa typu B (metoda B)

–

wyznaczana metodami innymi, odpowiada m.in. błędom

spowodowanym efektami systematycznymi.

Y

= f (

X

1

, X

2

, X

3

, …, X

n

)

Uogólniony model pomiaru - wynik pomiaru jako funkcja wielu zmiennych

1

∑

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

∂

∂

=

N

i

i

i

c

x

u

x

f

y

u

)

(

)

(

2

2

Prawo propagacji niepewności

kiedy wielkości wejściowe x

i

nie są skorelowane

x

i

wielkości wejściowe mające wpływ na pomiar

Podstawy metrologii – w5/s2

Procedura obliczania niepewno

Procedura obliczania niepewno

ś

ś

ci

ci

Niepewność typu A (metoda A)

–

obliczanie niepewności standardowej, gdy pomiary różnią się na skutek

oddziaływań losowych; przyjmuje się, że mają one rozkład normalny (Gaussa) dla n

≥

30.

(

)

)

1

(

)

(

1

2

−

−

=

=

∑

=

n

n

X

x

x

u

n

i

s

i

s

i

A

σ

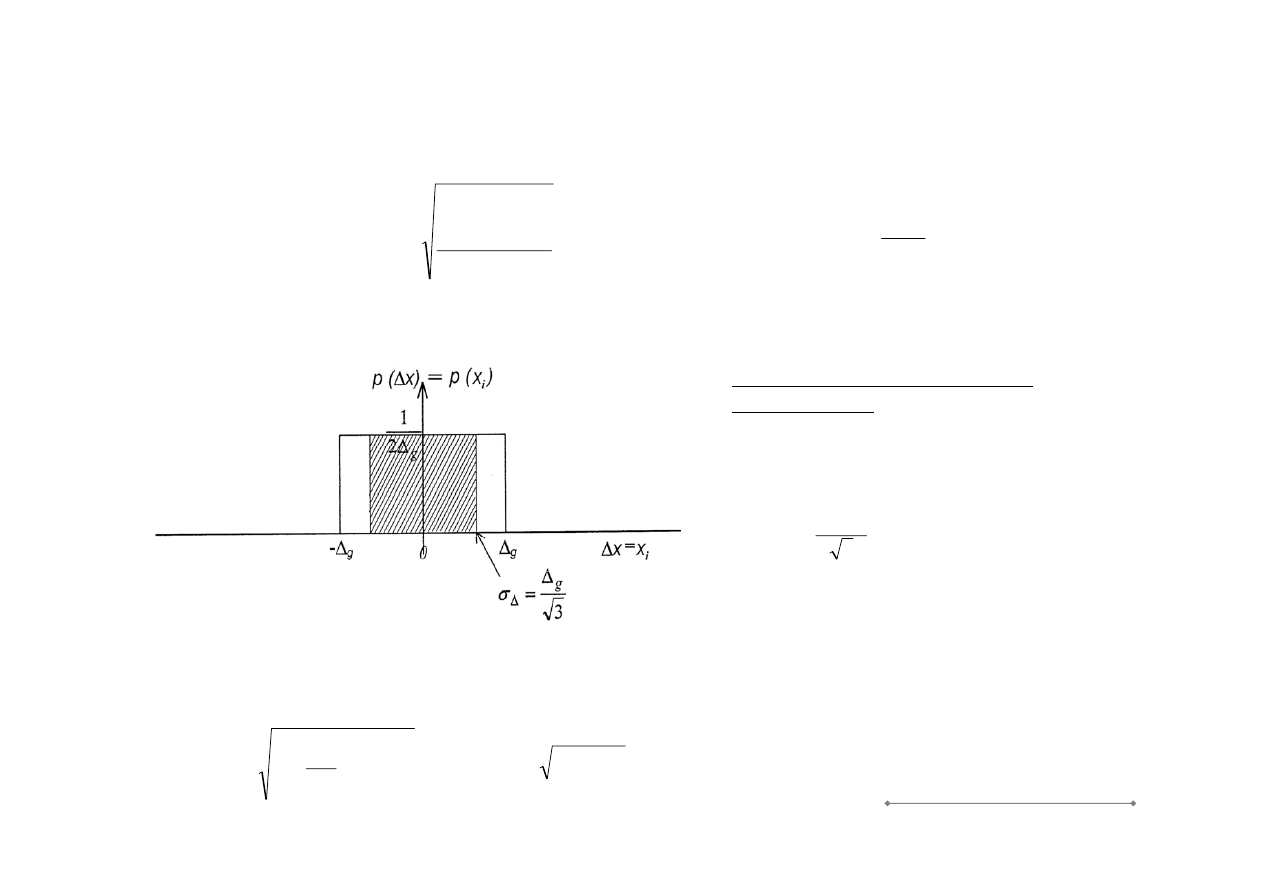
Niepewność typu B (metoda B)

–

obliczanie niepewności standardowej, gdy wartość oczekiwana (estymata)

wielkości wejściowej nie jest wyznaczana z serii pomiarów.

n

x

X

n

i

i

s

∑

=

=

1

wartość oczekiwana

przyjmuje się rozkład równomierny
błędu przyrządu:

każda wartość z wnętrza przedziału
wyznaczonego przez błąd graniczny jest
jednakowo prawdopodobna

3

)

(

i

g

i

B

X

x

u

Δ

=

Δ

g

X

i

– błąd graniczny liczony na

podstawie formuły błędu przyrządu

Niepewność złożona (łączna)

–

na podstawie prawa propagacji niepewności

.

2

2

)

(

B

A

C

u

u

y

u

+

=

)

(

)

(

2

2

1

i

n

i

i

C

x

u

x

f

y

u

∑

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

∂

∂

=

dla 2 addytywnych składowych wejściowych

Podstawy metrologii – w5/s3

Niepewność rozszerzona

( )

y

u

k

U

C

⋅

=

Współczynnik rozszerzenia k

–

ma wartość zależną od przyjętego poziomu ufności p oraz wypadkowego rozkładu

błędów wynikającego ze złożenia rozkładu błędów wielkości wejściowych opisanych przez niepewności
standardowe typu A (Gaussa lub Studenta) i niepewności standardowe typu B (równomiernego)

.

Centralne tw. graniczne:
- splot rozkładów normalnych jest rozkładem normalnym;
- splot kilku rozkładów różnych jest zbieżny do rozkładu normalnego.

Hipoteza :
- splot rozkładów składowych jest zbieżny do rozkładu składowego o większym odchyleniu standardowym
- splot 3 lub więcej rozkładów jednostajnych (równomiernych) jest zbieżny do rozkładu normalnego;
- splot 2 rozkładów jednostajnych jest rozkładem trapezowym.

Pomiar pojedynczy bezpośredni

• nie można wyznaczyć niepewności standardowej typu A
• wyznaczamy niepewność standardową typu B
• niepewność łączna jest równa niepewności standardowej typu B
• rozkład błędów pomiaru ma rozkład błędów wielkości wejściowej opisany niepewnością standardową typu B

Pomiar pojedynczy pośredni

• nie można wyznaczyć niepewności standardowej typu A
• wyznaczamy niepewności standardowe typu B dla każdej wielkości wejściowej x

i

• wyznaczamy niepewność łączną z prawa propagacji niepewności
• rozkład błędów pomiaru jest splotem rozkładów błędów wielkości wejściowych

Podstawy metrologii – w5/s4

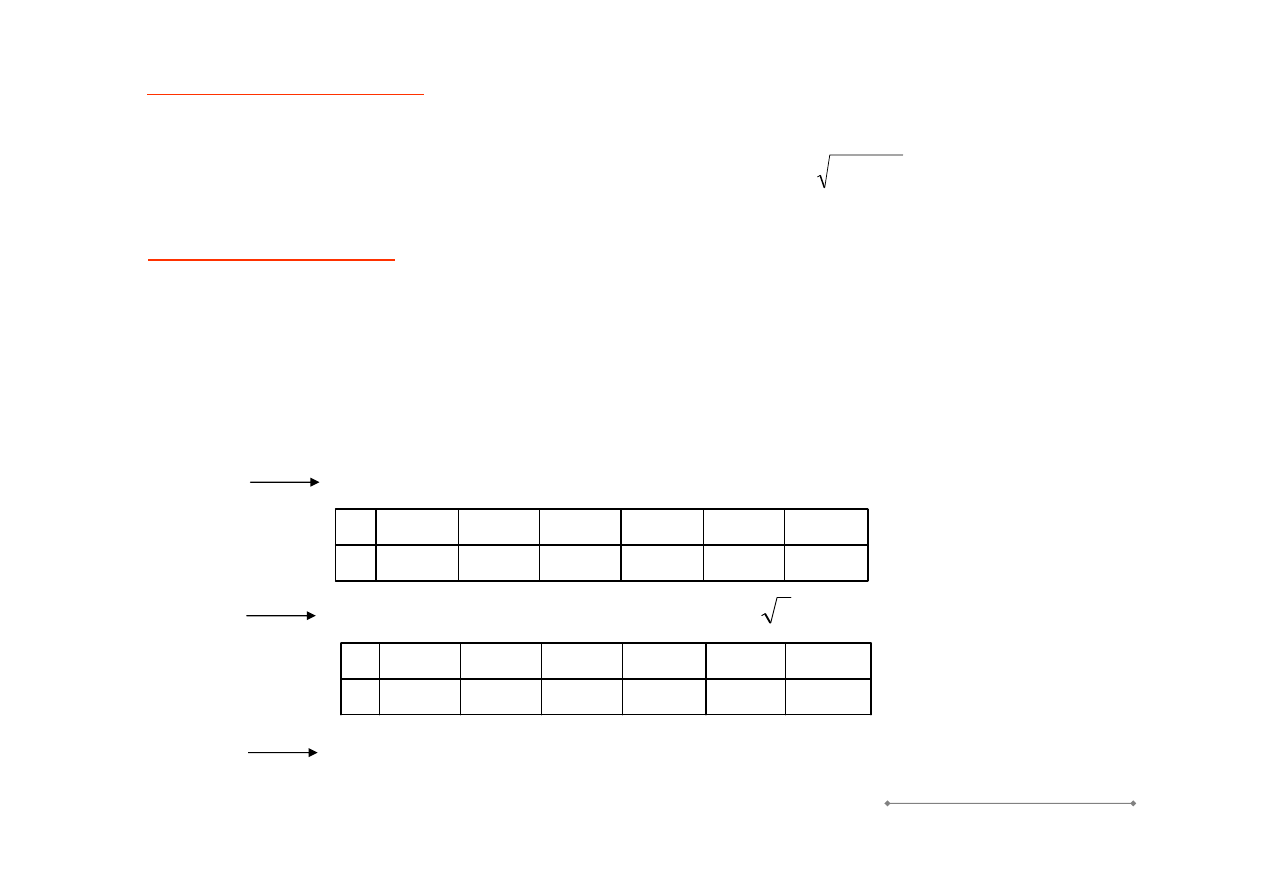
Praktycznie jeśli:

u

A

>> u

B

splot zbieżny do rozkładu normalnego, dla n

≥ 30

3,000

2,576

2,000

1,960

1,645

1,000

k

0,9973

0,9900

0,9545

0,9500

0,9000

0,6827

p

u

A

<< u

B

splot zbieżny do rozkładu równomiernego

1,7273

1,7147

1,6532

1,6454

1,5588

1,1825

k

0,9973

0,9900

0,9545

0,9500

0,9000

0,6827

p

p

k

⋅

= 3

u

A

≈ u

B

ocena niejednoznaczna, zaleca się przyjęcie k jak dla rozkładu normalnego

Pomiar wielokrotny bezpośredni

• wyznaczamy niepewność standardową typu A
• wyznaczamy niepewność standardową typu B
• wyznaczamy niepewność łączną z prawa propagacji niepewności
• rozkład błędów pomiaru jest splotem rozkładów błędów wielkości wejściowych

2

2

)

(

B

A

C

u

u

y

u

+

=

Pomiar wielokrotny pośredni

• wyznaczamy niepewności standardowe typu A dla każdej wielkości wejściowej x

i

• wyznaczamy niepewności standardowe typu B dla każdej wielkości wejściowej x

i

• wyznaczamy niepewność łączną z prawa propagacji niepewności
• rozkład błędów pomiaru jest splotem rozkładów błędów wielkości wejściowych