Część 3

RÓWNOLEG

Ł

Y UK

Ł

AD SI

Ł

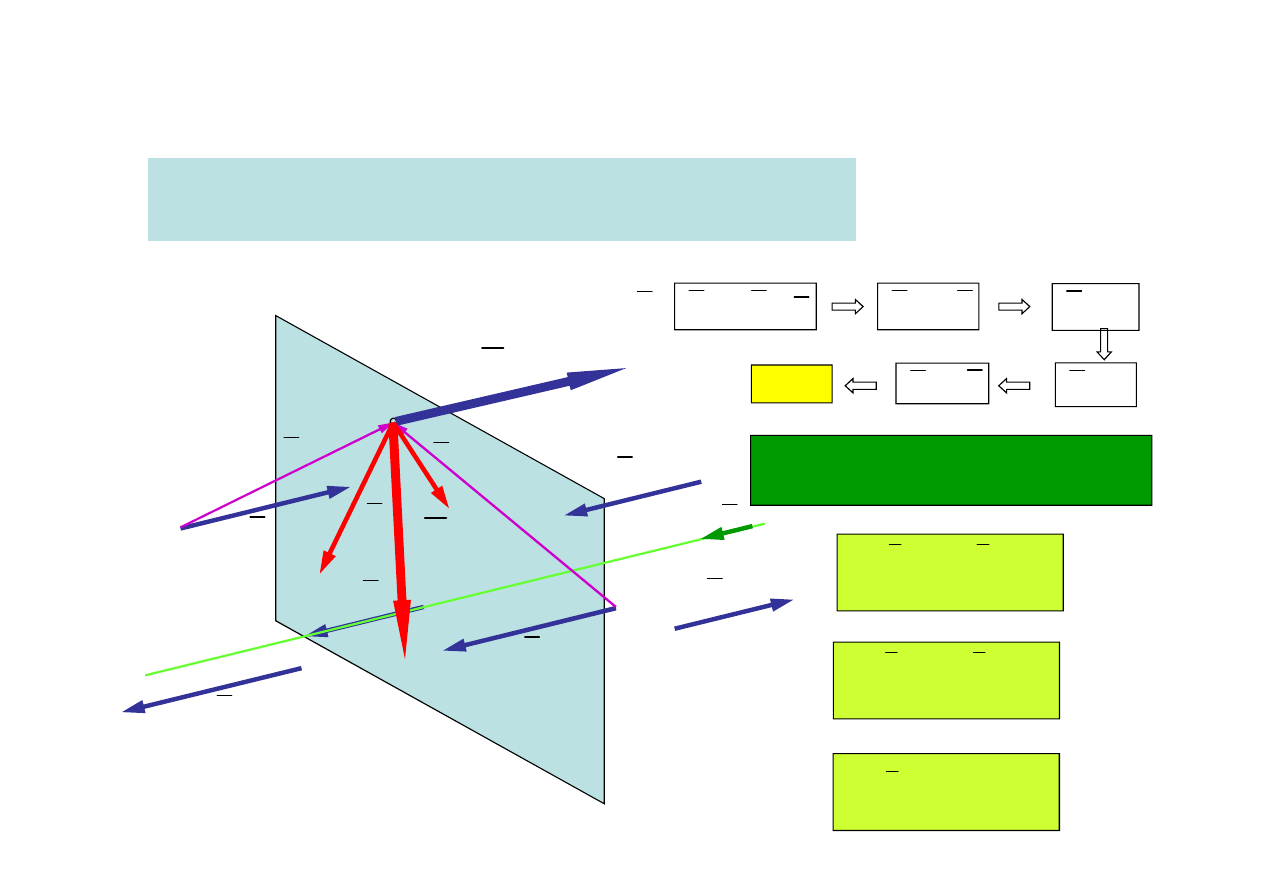
3.1. Definicja równoleg

ł

ego uk

ł

adu si

ł

Równoleg

ł

y uk

ł

ad si

ł

Uk

ł

ad si

ł

, w którym si

ł

y są równoleg

ł

e do sta

ł

ego kierunku

A

r

M

R

S

R

π

π

e

∈ ∩ ⊥

i

i

i

M

F

r

= ×

i

i

M

F

⊥

i

M

π

M

π

M

S

⊥

K

=

0

Trzy przypadki redukcji

2

F

1

F

2

F

3

i

F

F

4

n

F

e

A

1

A

2

A

3

i

A

n

A

A

4

r

1

M

1

i

M

M

π

Trzy przypadki redukcji

do najprostszej postaci

Para si

ł

2. S

M

= ∩

≠

0

0

Wypadkowa

3. S

≠

0

Uk

ł

ad zerowy

1. S

M

= ∩

=

0

0

3.2. Przyk

ł

ady równoleg

ł

ych uk

ł

adów si

ł

Si

ł

a dzia

ł

ająca wzd

ł

uż osi

Uk

ł

ad si

ł

równoleg

ł

ych w nitach

Uk

ł

ad si

ł

w z

ł

ączu nitowanym

3

fotografia własna

Uk

ł

ad si

ł

nacisku kó

ł

na pod

ł

oże

4

Internet

5

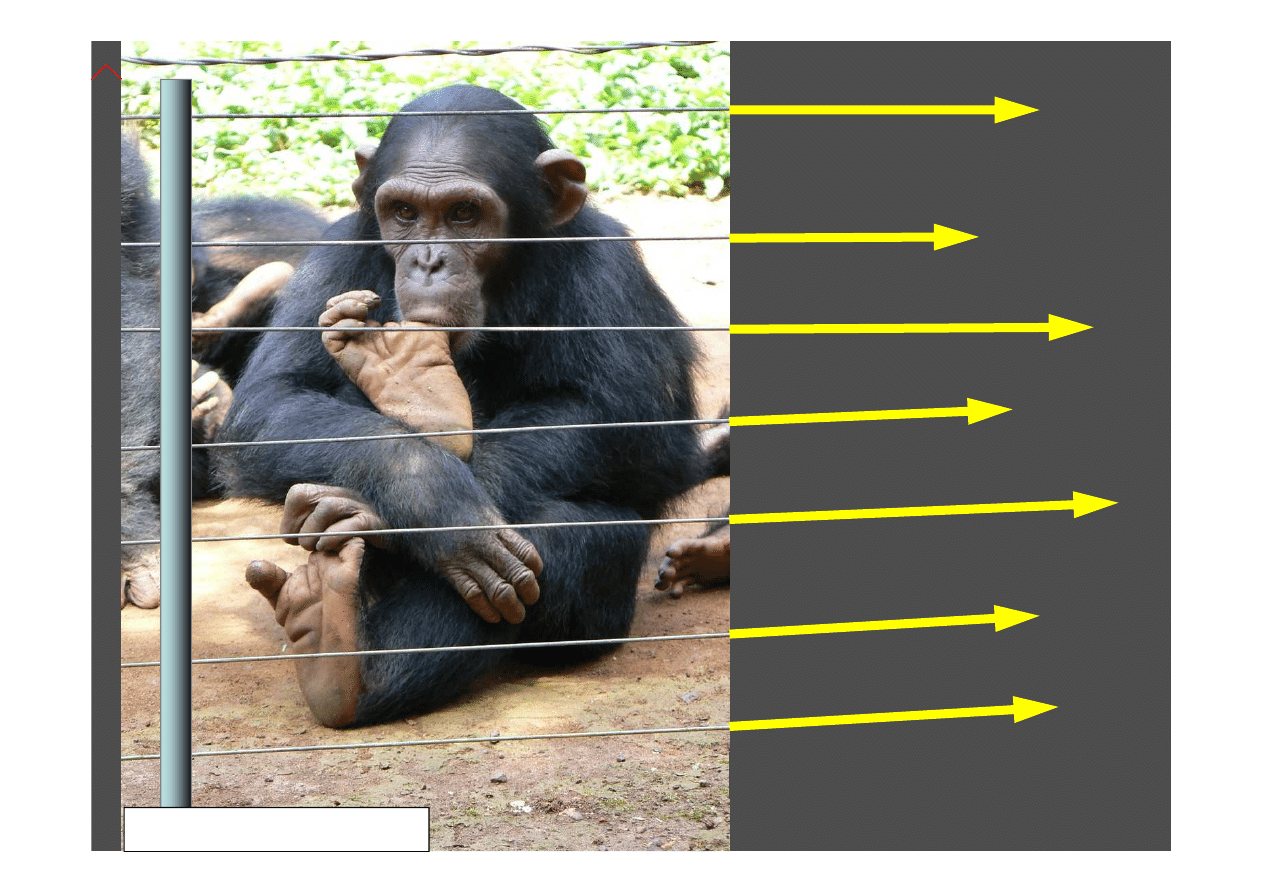
Uk

ł

ad si

ł

w przewodach

Prawie
równoległy

fot. Justyna Laskowska

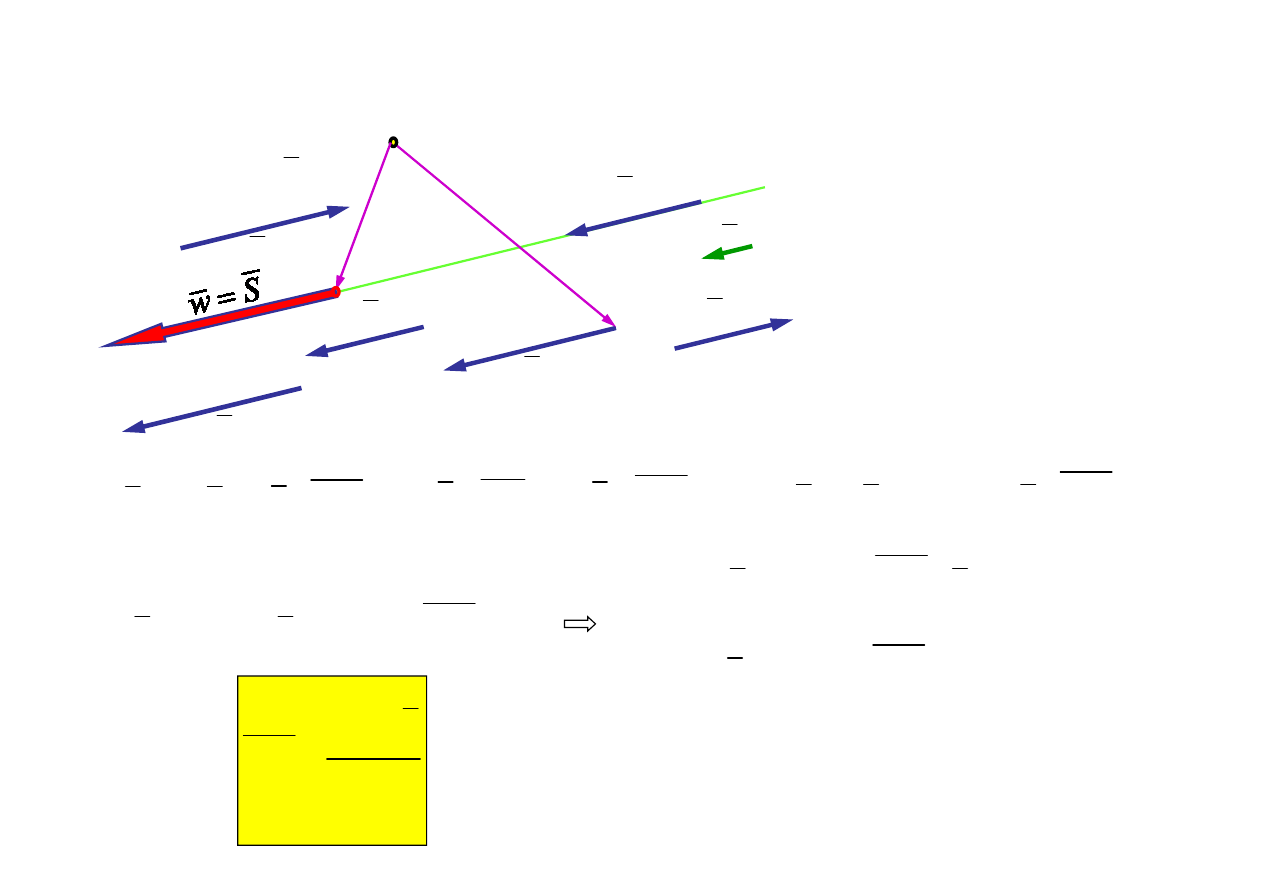
1.3. Środek równoleg

ł

ego uk

ł

adu si

ł

F

1

F

2

F

3

i

F

F

4

n

F

e

A

1

A

2

A

3

i

A

n

A

A

4

r

1

O

*

O

O

– sta

ł

y punkt odniesienia

e

– wersor równoleg

ł

ego

uk

ł

adu si

ł

F

i

– miara si

ł

y

F

i

na

kierunku e

6

F

2

*

O*

O

M

M

S

OO

=

+ ×

n

n

*

i

i

i

i

i

F

A O

F

OO

=

=

=

×

+

×

∑

∑

1

1

( )

n

n

*

i

i

i

i

i

F e

r

F

e OO

=

=





=

⋅ × − +

⋅ ×

=









∑

∑

1

1

0

n

n

*

i

i

i

i

e

F r

F

OO

=

=









× −

⋅ +

⋅

=

















∑

∑

1

1

0

n

n

*

i

i

i

i

n

n

*

i

i

i

i

F r

F

OO

e

F r

F

OO

=

=

=

=







−

⋅ +

⋅





















−

⋅ +

⋅

=













∑

∑

∑

∑

1

1

1

1

0

n

i

*

i

n

i

i

F r

OO

F

=

=

⋅

=













∑

∑

1

1

OO

*

– wektor określający po

ł

ożenie

środka równoleg

ł

ego uk

ł

adu si

ł

W

ł

asności środka równoleg

ł

ego uk

ł

adu si

ł

Uk

ł

ad posiadający środek redukuje się w tym punkcie do wypadkowej

7

Moment uk

ł

adu względem środka jest równy 0

Jeżeli w równoleg

ł

ym uk

ł

adzie si

ł

, posiadającym środek, obrócimy si

ł

y wokó

ł

ich

punktów zaczepienia o ten sam kąt to środek uk

ł

adu nie zmieni swojego po

ł

ożenia