
1
Twierdzenie Taylora
Zało enie
[
]
(
)
(
)
(
)
x
x
D
f
x
x
C
f
n
,
,
0
0
1
∈
∧
∈
−
Teza
(
) ( )
( )( )
( )
c
R
x
x
k
x
f
x
f
x
x
c
n
n
k
k
k
+
−
=
∈
∃
−
=
1
0
0
0
)
(
0
!
:
,
, gdzie
( )
( )(
)
n
n
n
x
x
n
c
f
R
0
!
−
=
n
R
-
n
-ta reszta (w postaci Lagrange’a)
lub inaczej
n
-ty bł d rozwini cia Taylora funkcji
f
umowa:
( )
f
f
=
:
0
( ) ( )
( )(
)
( )(
)
( )
( )
(
) (
)
( )
c
R
x
x
n
x
f
x
x
x
f
x
x
x
f
x
f
x
f
n
n
n
+
−
−
+
+
−
′′
+
−
′
+
=
−
−
1
0
0
1
2
0
0
0
0
0
!
1
!
2
!
1
Uwaga
1. Dla
1
=
n
twierdzenie staje si twierdzeniem Lagrange’a.
2. W ogólnym przypadku twierdzenie pokazuje, e funkcj
f
mo na przybli y wielomianem
stopnia
1
−
n
,
( )
( )(
)
−
=
−
≈
1
0
0
0
)
(
!
n
k
k
k
x
x
k
x
f
x
f
natomiast reszta
n
R
pozwala oszacowa bł d bezwzgl dny
( )
c
R
n
gdy znana jest
najwi ksza warto
( )
( )
x
f
n
.
Dowód
Niech:
( )
( )
( )
( )( )
−
=
−
−
=
1
0
!
:
n
k
k
k
t
x
k
t
f
x
f
t
ϕ
dla
[
]
x
x
t
,
0
∈
( ) ( ) ( )
( )
( )( )
( )
( )
( )
( )
( )
( )
( )( )
( )
( )
(
) (
)
( )
( )
( )( )
( )
( )
(
) (
)
( )
( )
( )( )
( )
( )( )
( )
( )
( )
(
) (
)
( )
( )
( )
(
) (
)
1
1
2
0
1
1
1
1
1
1
1
:
1
1
1
1
1
1
1
1
?
0
1
1
!
1
!
1
!
!
!
1
!
!
1
!
0
!
−
−
−
=
+
−
=
+
−
=
−
=
−
−
=
+
−
=
−
+
−
=
−
−
−
=
′
+
−
−
−
′
−
=
=
−
+
−
−
′
−
=
−
−
+
+
−
−
′
−
=
−
−
−
−
−
′
−
=
′
=
=
−
−
−
=
n
n
n
n
n
j
j
j
n
k
k
k
n
k
k
j
k
k
n
k
k
k
n
k
k
k
k
k
n
n
k
k
k
t
x
n
t
f
t
f
t
x
n
t
f
t
f
t
x
j
t
f
t
x
k
t
f
t
f
t
x
k
t
f
t
x
k
t
f
t
f
t
x
k
t
f
t
x
k
t
f
t
f
t
c
R
x
x
t
x
k
t
f
t
f
x
f
t
ϕ
ϕ
ϕ
ϕ
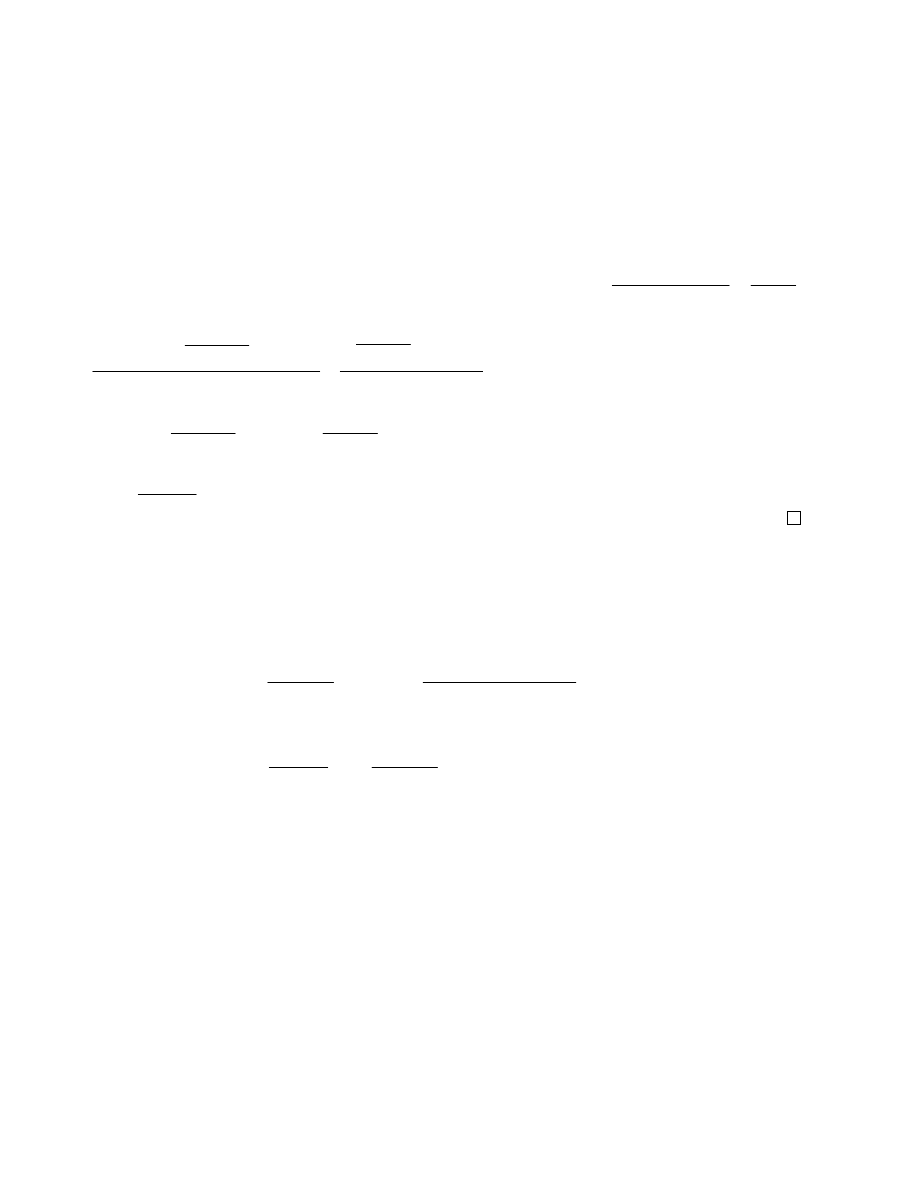
2
Niech
( ) (
)
[ ]
( )
( ) (
)
( )
(
)
1
0
0
0
0
,
:
−
−
−
=
′
−
=
=
∈
∧
−
=
n
n
n
n
n
n
n
t
x
n
t
x
x
x
x
x
x
t
t
x
t
ψ
ψ
ψ
ψ
x
t
≠
∀
0
≠
′
n
ψ
ψ
ϕ
,
- spełniaj zało enia twierdzenia Cauchy’ego
(
)
( ) ( )
( )
( )
( )
( )
c
c
x
x
x
x
x
x
c
n
n
n
ψ
ϕ
ψ
ψ
ϕ
ϕ
′
′
=
−
−
∈
∃
0
0
0
:
,
( )
( )
( )( )
(
)
( )
( )
( ) (
)
(
)
( )
( )
( )( )
( )
( )
( ) (
)
n
n
n
k
k
k
n
n
n
n
n
k
k
k
x
x
n
c
f
x
x
k
x
f
x
f
c
x
n
c
x
n
c
f
x
x
x
x
k
x
f
x
f
0
1
0
0
0
1
1
0
1
0
0
0
!
1
!
!
1
!
−
−
+
−
=
−
−
−
−
−
=
−
−
−
−
−
−
=
−
−
−
=
gdzie
( )
( )
(
) (
)
( )
c
R
x
x
n
c
f
n
n
n
=
−
−
0
!
1
Uwaga. Twierdzenie pozostaje prawdziwe, gdy funkcj
f
rozwa amy w przedziale
[ ]
0
, x
x
.
Tez twierdzenia Taylora mo emy tak e zapisa w sposób nast puj cy:
( )
:
1
,
0
∈
∃
θ
( )
( )( )
( )
(
)
(
)( )
n
n
n
k
k
k
x
x
n
x
x
x
f
x
x
k
x
f
x
f
0
0
0
1
0
0
0
)
(
!
!
−
−
+
+
−
=
−
=
θ
w szczególno ci, gdy
0
0
=
x
, to otrzymujemy wzór MacLaurina:
( )
:
1
,
0
∈
∃
θ
( )
( )
( )
( )
n
n
n
k
k
k
x
n
x
f
x
k
f
x
f
!
!
0
1
0
)
(
θ
+
=
−
=
Twierdzenie (Taylora z reszt Peano)
Zało enie
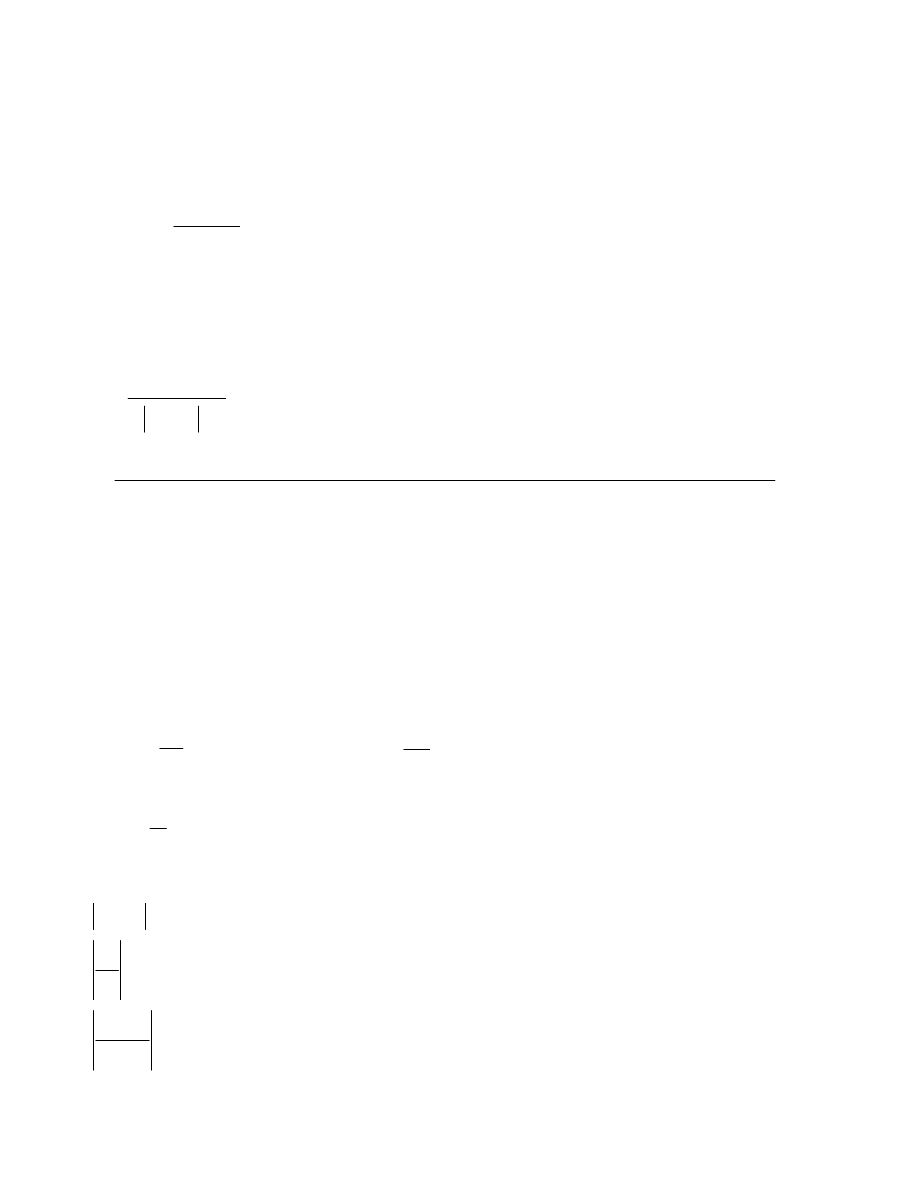
3
[
)
(
)
( )
[
)
b
x
x
x
D
f
b
x
D
f
n
n
,
,
0
0
0
1
∈
∈
∈
−
Teza
( )
( )
( )( ) ( )
(
)
n
n
k
k
k
x
x
o
x
x
k
x
f
x
f
0
0
0
0
!
−
+
−
=
=
,
gdzie funkcj
(
)
(
)
n
x
x
o
0
−
czytamy jako „o małe”, a rozumiemy jako funkcj :
(
)
[
)
(
)
(
)
(
)
R
x
x
o
x
x
x
b
o
n
n
n
∈
−
−
∋
−
0
0
0
,
0
:
Spełniaj c własno własno
(
)
(
)
0
lim
0
0
0
=
−
−
→
n
n
x
x
x
x
x
x
o
Przykład
Wyznaczy warto liczby
e
z dokładno ci do
10
-5
.
Rozwini cie w
0
0
=
x
.
( )
D
f
C
f
e
x
f
x
∈
∧
∈
=
( )
( )
( )
( )
1
0
=
=
n
x
n
f
e
x
f
dla
1
≥
n
( )
x
R
k
x
e
n
n
k
k
x
θ
+
=
−
=
1
0
!
, gdzie
( )
n
x
n
x
n
e
x
R
!
θ
θ
=
Dla
1
=
x
mamy
( )
θ
n
n
k
R
k
e
+
=
−
=
1
0
!
1
( )
( )
5
1
,
0
5
5
10
!
10
!
10
−
∈
−
−
≤
≤
≤
n
e
n
e
R
n
θ
θ
θ
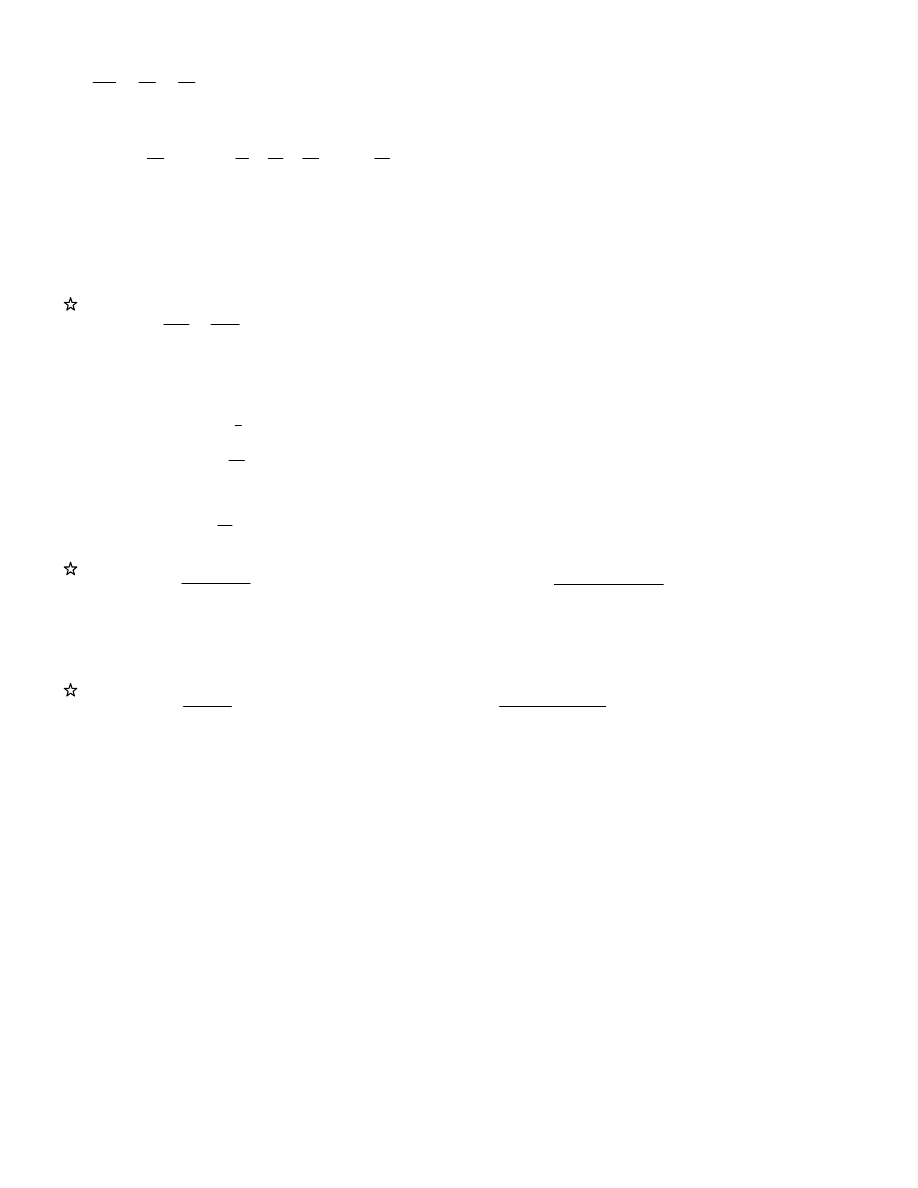
4
9
10
!
3
!
!
5
≥
≤
<
<
−
n
n
n
e
n
e
θ
!
8
1
!
4
1
!
3
1
2
1
1
1
!
1
8
0
+
+
+
+
+
+
=
≈
=
k
k
e
Rozwini cie funkcji
e
x
, sinx, cosx
:
n
x
n
k
k
x
x
n
e
k
x
e
!
!
1
0
θ
+
=
−
=
(na podstawie powy szego przykładu)
( )
( )
( ) ( )
( )
0
,
1
2
,
cos
1
2
,
sin
1
sin
2
1
2
N
k
k
n
x
k
n
x
x
f
x
x
f
n
n
n
∈
+
=
−
=
−
=
=
−
( )
( ) ( )
1
2
2
,
1
,
0
0
2
1
+
=
=
−
=
−
k
n
k
n
f
n
n
( )
(
)
( )
x
R
x
k
x
n
n
k
k
k
θ
1
2
1
0
1
2
!
1
2
1
sin
+
−
=
+
+
+
−
=
, gdzie
( ) ( )
( )
(
)
1
2
1
2
!
1
2
cos
1
+
+
+
−
=
n
n
n
x
n
x
x
R
θ
θ
Bardzo podobnie otrzymujemy rozwini cie funkcji cos:
( )
( )
( )
x
R
x
k
x
n
n
k
k
k
θ
2
1
0
2
!
2
1
cos
+
−
=
−
=
, gdzie
( ) ( )
( )
( )
n
n
n
x
n
x
x
R
2
2
!
2
sin
1
θ
θ
−
=

5
Wyszukiwarka
Podobne podstrony:
12 Twierdzenie Taylora dla funkcji wielu zmiennych (2)
Tales twierdzenie
Twierdzenie Talesa
Analiza Matematyczna Twierdzenia
Czas nie istnieje, to iluzja – twierdzą (niektórzy) fizycy cz 2
10 2009 Twierdzenia mod n
Opis programu komputerowego Twierdzenie Pitagorasa-dowód i z, wrzut na chomika listopad, Informatyka
Twierdzenie sinusów i cosinusów
Algebra Liniowa 2 Definicje Twierdzenia Wzory Jurlewicz Skoczylas
5 Rózniczka, wzór Taylora, tw de L'Hospitala
07 Twierdzenie o istnieniu i jednoznaczno
Fizycy twierdzą, że Wszechświat może przypominać gigantyczny mózg
16 Z Twierdzenia energetyczne
ABY 0027 Linie wroga 2 Twierdza rebelii
Pewne samobójcze twierdzenie Towarzystwa Strażnica
więcej podobnych podstron