4.7. METODA PRZEMIESZCZEŃ. ZAPIS MACIERZOWY
Algorytm rozwiązania dowolnych schematów statycznych za pomocą metody przemieszczeń
można zapisać w postaci macierzowej. Wynika to przede wszystkim z jednolitego układu
podstawowego metody polegającego na blokowaniu obrotów i przemieszczeń wszystkich
węzłów swobodnych. Podejmowano także próby zautomatyzowania obliczeń za pomocą
metody sił, ale brak możliwości unifikacji budowania schematu podstawowego utrudnia, a
nawet uniemożliwia stworzenie podobnego algorytmu. Metoda przemieszczeń stała się więc
metodą powszechnie wykorzystywaną w programach komputerowych. Obliczenia polegają
na zestawieniu z danych problemu kilku macierzy wyjściowych, a następnie wykonaniu na
nich ściśle określonych działań macierzowych prowadzących do końcowego rozwiązania.
Możliwe jest utworzenie różnych wariantów obliczeń. W programach komputerowych
stosowane są algorytmy, w których elementy macierzy wyjściowych wyrażają się wprost
przez dane liczbowe opisujące schemat konstrukcji. W niniejszym rozdziale zostaną jedynie
zasygnalizowane podstawowe pojęcia i wzory umożliwiające zrozumienie zasady
wykorzystania zapisów macierzowych w obliczeniach. Tak jak w przypadku standardowej
metody przemieszczeń rozważania zostaną ograniczone do analizy układów pozbawionych
przegubów wewnętrznych.
Przed omówieniem algorytmu obliczeń zostaną przedstawione wzory umożliwiające
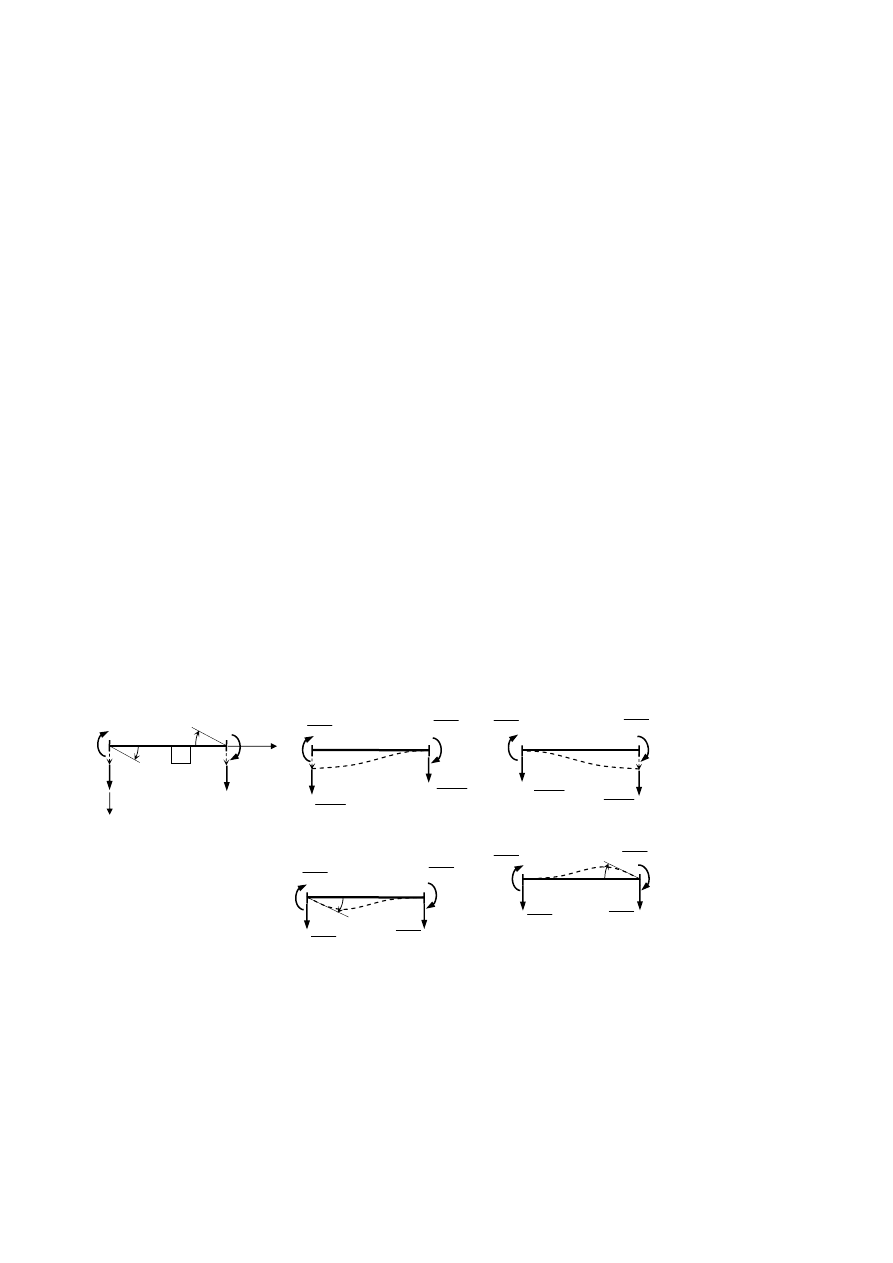
wyznaczenie sił przywęzłowych w przypadku pręta obustronnie utwierdzonego (Rys. 4.1a).
Należy zauważyć, że zwrot momentów podporowych przyjęto identycznie jak w
bezpośrednim ujęciu metody przemieszczeń, natomiast zwroty sił poprzecznych są zgodne
ze zwrotem osi y. Tak jak w przypadku standardowych obliczeń „ręcznych” pominięty będzie
wpływ sił podłużnych, a więc nie zostaną uwzględnione przemieszczenia poziome węzłów i
oraz k. W komputerowej wersji metody przemieszczeń wpływ ten jest brany pod uwagę, gdyż
w efekcie uzyskuje się bardziej zwarty i jednolity algorytm rozwiązania. Dalsza analiza
zostanie ograniczona do rozwiązań najprostszych przypadków, łatwych do porównania z
obliczeniami „ręcznymi”.
Rys. 4.1. Siły węzłowe w pręcie obustronnie utwierdzonym
Obliczenia wszystkich potrzebnych danych wyjściowych zazwyczaj wykonuje się w
identyczny sposób jak w p. 4.6, a więc wykorzystując równanie różniczkowe czwartego
rzędu. Na Rys. 4.1 przedstawiono siły węzłowe od jednostkowego przemieszczenia i obrotu
węzła i (Rys. 4.1b i c) oraz k (Rys. 4.1d i e). Konwencja znaków przemieszczeń i sił
węzłowych wynika z przyjętego lokalnego, związanego z elementem j układu osi xy
(Rys. 4.1a). W wyniku równoczesnego działania wszystkich przemieszczeń węzłów i oraz k,
siły przywęzłowe wyznacza się korzystając z zasady superpozycji:
2
6EJ
l
v
i
=1
3
12EJ
l
−
2
6EJ
l
b)
3
12EJ
l
2
6EJ
l
−
2
6EJ
l
−
v
k
=1
3
12EJ
l
3
12EJ
l
−
d)
a)
M
ik
i
k
V
ik
y
v
k
v
i
φ
k
φ
i
j
EJ
V
ki
x
M
ki
φ
k
=1
2EJ
l
2
6EJ
l
4EJ
l
2
6EJ
l
−
e)
φ
i
=1
2EJ
l
2
6EJ
l
−
4EJ
l
2
6EJ
l
c)
229
3
2
3
2
2
2
3
2
3
2
2
2
12
6
12
6
6
4
6
2
12
6
12
6
6
2
6
4
i
i
i
k
i
i
i
k
k
k
i
i
k
k
i
i
k
k
V
EJ
v
v
l
l
l
l
M
EJ
v
v
l
l
l
l
V
EJ
v
v
l
l
l
l
M
EJ
v
v
l
l
l
l
φ
φ
φ
φ
k
k
φ
φ
φ
φ
⎡
⎤
=
+
−
+
⎢
⎥
⎣
⎦
⎡
⎤
=
+
−
+
⎢
⎥
⎣
⎡
⎤
=
−
−
+
−
⎢
⎥
⎣
⎦
⎡
⎤
=
+
−
+
⎢
⎥
⎣
⎦
⎦
(0.1)
Te same siły przywęzłowe, w zapisie macierzowym, przy uwzględnieniu dodatkowo
zadanego obciążenia czynnego wywołującego reakcje
,
0
i
V
0
i
M
,
i
0
k
V
0
k
M
mają następującą
postać:
3
2
3
2
2
2
3
2
3
2
2
2
12
6
12 6
6
4
6 2
12
6 12
6
6
2
6 4
o
i
i
i
o
i
i
o
k
k
k
o
k
k
k
l
l
l
l
V
v
V
M
M
l
l
l
l
EJ
V
V
l
l
l
l
M
M
l
l
l
l
φ
φ
⎡
⎤
−
⎢
⎥
⎢
⎥
i
v
⎡
⎤
⎡
⎤
⎡ ⎤
⎢
⎥
−
⎢
⎥
⎢
⎥
⎢ ⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢ ⎥
=
⎢
⎥
+ ⎢ ⎥
⎢
⎥
⎢ ⎥
⎢
⎥
−
−
−
⎢
⎥
⎢
⎥
⎢ ⎥
⎢
⎥
⎢
⎥
⎣
⎦
⎣ ⎦ ⎣
⎦
⎢
⎥
⎢
⎥
−
⎣
⎦
(0.2)
Reakcje podporowe z Rys. 4.1b, c, d i e są odpowiednio zapisane w kolejnych kolumnach
macierzy z równania (4.47). W tym miejscu warto przypomnieć, że iloczyn macierzy polega
na mnożeniu kolejnych elementów wierszy pierwszej macierzy przez elementy kolumny
macierzy drugiej. Działanie to można łatwo prześledzić porównując związki (4.46) i (4.47).
Związek (4.47) można zapisać w następujący ogólny sposób:
o
j
j
j
j
=
+
S
K D
S
(0.3)
gdzie pogrubionymi literami oznaczono macierze i wektory: oznacza wektor sił
węzłowych elementu j,
jest tzw. macierzą sztywności elementu j,
wektorem
przemieszczeń węzłów elementu j, a wektorem sił węzłowych od obciążenia
zewnętrznego.
j
S
j
K
j
D
o
j
S
Pierwszy człon związku (4.48) lub (4.47) przedstawia wpływ obrotów i przemieszczeń
węzłów na siły przywęzłowe, a więc są to odpowiednio dostosowane do zapisu
macierzowego wzory transformacyjne z Tabl. 4.6. Drugi człon równań (4.48) lub (4.47)
opisuje reakcje
,
oraz momenty przywęzłowe
o
i
V
o
k
V
o
i
M
,
o
k
M
od sił obciążających pręt.
Odpowiadają one momentom wyjściowym standardowej metody przemieszczeń (Tabl. 4.4 i
4.5).
Dla każdego wyodrębnionego elementu j konstrukcji, na podstawie równania (4.47)
można zdefiniować wektor przemieszczeń
, zapisać macierz sztywności
i obliczyć
wektor .
j
D
j
K
o
j
S
230
Przykład 4.14.
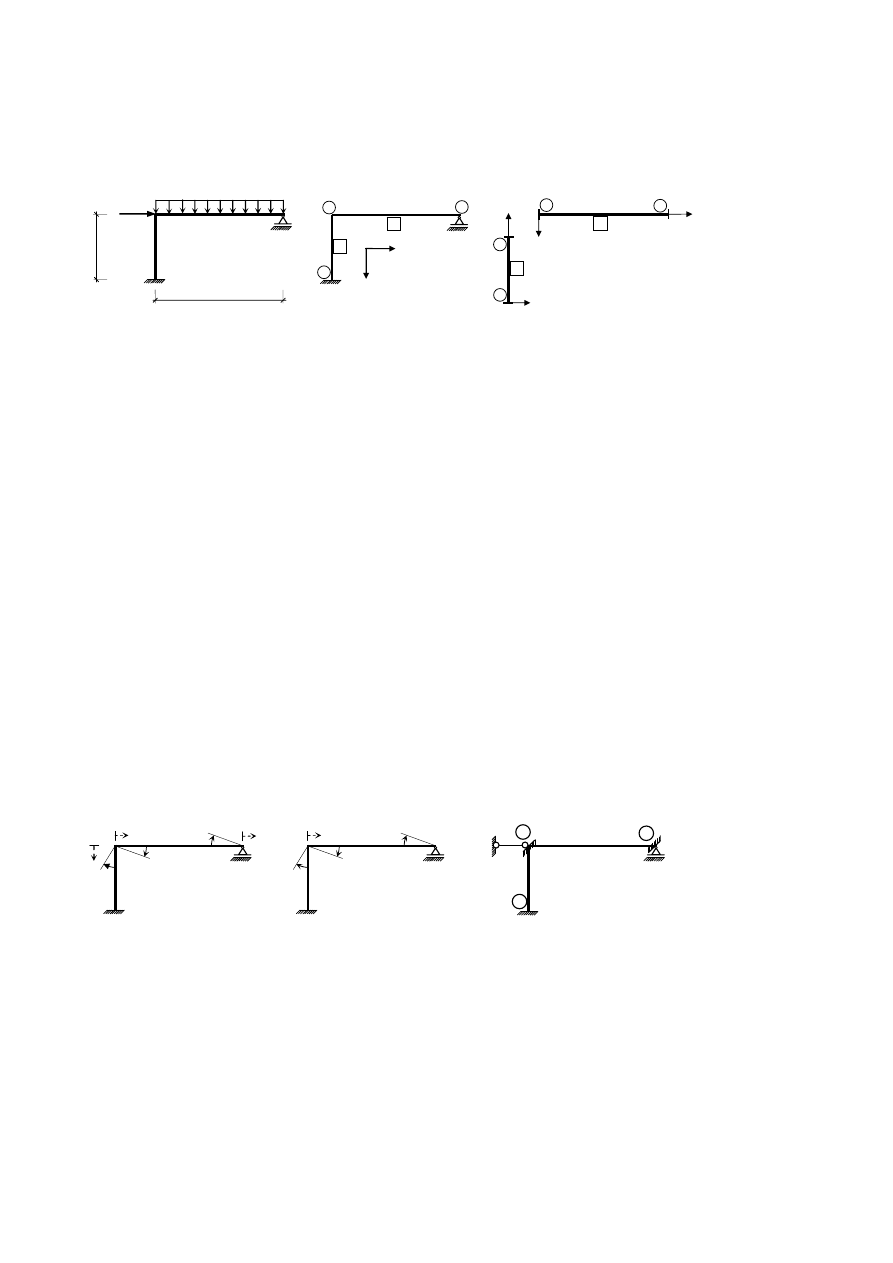
Wyznaczyć siły wewnętrzne w ramie przedstawionej na Rys. 4.2a za pomocą zapisu
macierzowego metody przemieszczeń.
c)
b)
a)
A
B
C
20 kN/m
2 m
40 kN
4 m
EJ
2EJ
Rys. 4.2. Rama geometrycznie niewyznaczalna (opis w tekście)
1
2
3
1
2
y
x
y
2
2
Y
X
1
3
2
1
x
Obliczenia układu przedstawionego na Rys. 4.2a rozpoczynamy od wprowadzenia
numeracji węzłów i elementów (Rys. 4.2b).
Następnie przyjmujemy globalny układ osi, a więc układ związany z całym schematem
konstrukcji, oznaczony dużymi literami XY (Rys. 4.2b). Ponadto dla każdego pręta
wprowadzamy lokalny układ osi, oznaczony małymi literami xy, o początku w dowolnie
wybranym węźle elementu (Rys. 4.2c). Zwróćmy uwagę, że lokalne układy mają taką samą
skrętność (w tym przypadku zgodna z ruchem wskazówek zegara), jak układ globalny XY.
Zgodnie z przyjętymi oznaczeniami, dla prętów 1 i 2 możemy zapisać wektory
przemieszczeń i
, odpowiadające wektorowi
ze związku (4.48):
1
D
2
D
j
D
(0.4)
{
{
}
1
12
12
21
21
2
23
23
32
32
T
T
v
v
v
v
φ
φ
φ
φ
=
=
D
D
}
]
gdzie litera T oznacza transpozycje.
Zwróćmy uwagę, że dla każdego pręta przyjęliśmy komplet przemieszczeń, pomijając
wpływ warunków brzegowych (węzeł 1 i 3) oraz brak przemieszczenia pionowego węzła 2.
Kolejnym krokiem obliczeniowym będzie zapisanie globalnych przemieszczeń węzłów
swobodnych . W ogólnym przypadku jest to wektor, w skład którego wchodzą wszystkie
nieznane przemieszczenia i obroty węzłów. Dla schematu statycznego z Rys. 4.2a wektor
∆
będzie miał następującą postać (Rys. 4.3a):
∆
[
1
1
1
2
2
T
u v
u
φ
φ
=
∆
Rys. 4.3a) Przemieszczenia i obroty węzłów, b) niezależne przemieszczenia, c) układ
podstawowy
b)
c)
u
φ
1
φ
1
φ
2
3
2
1
a)
u
1
φ
1
φ
1
φ
2
v
1
u
2
W rozwiązaniu pomijamy wpływ sił podłużnych (przyjmujemy, że pręty są nieściśliwe),
zatem
oraz
i wektor zredukuje się do trzech niezależnych przemieszczeń
(Rys. 4.3b) wg wzoru
1
2
u
u
u
=
=
1
0
v
=
∆
[
1
2
T
u
]
φ φ
=
∆
(0.5)
Wektor
odpowiada schematowi podstawowemu przedstawionemu na Rys. 4.3c.
Zgodnie z klasyczną wersją metody przemieszczeń, blokada węzła 3 (podpora przegubowo-
∆
231
przesuwna), z uwagi na obrót, nie jest konieczna. Jednak dzięki przyjęciu
2
φ
jako
niewiadomej metody, uzyskuje się bardziej zwarty algorytm rozwiązania.
Wektorowi globalnych przemieszczeń
odpowiada wektor związanych z nimi
obciążeń węzłowych
. Układ jest obciążony jedynie siłą poziomą w węźle 2, zatem
odpowiadającą kierunkowi przemieszczenia (Rys. 4.2a). Wektor będzie miał więc
następująca postać:
∆
R
1
u
R
(0.6)
{
0 0
T
P
=
R
}
W kolejnym kroku obliczeniowym, wykorzystując (4.47), wyznaczymy macierze
sztywności prętów
i
. Podstawiając dane z Rys. 4.2a otrzymamy:
1
K
2
K
1
3
3
3
3
2
2
2
2
3
3
2
1
2
2
3
3
3
3
2
2
2
2
3
3
1
2
2
2
EJ
⎡
⎤
−
⎢
⎥
⎢
⎥
⎢
⎥
−
⎢
⎥
=
⎢
⎥
⎢
⎥
−
−
−
⎢
⎥
⎢
⎥
⎢
⎥
−
⎢
⎥
⎣
⎦
K
,
2
3
3
3
3
8
4
8
4
3
3
2
1
4
4
3
3
3
3
8
4
8
4
3
3
1
2
4
4
EJ
⎡
⎤
−
⎢
⎥
⎢
⎥
⎢
⎥
−
⎢
⎥
=
⎢
⎥
⎢
⎥
−
−
−
⎢
⎥
⎢
⎥
⎢
⎥
−
⎢
⎥
⎣
⎦
K
(0.7)
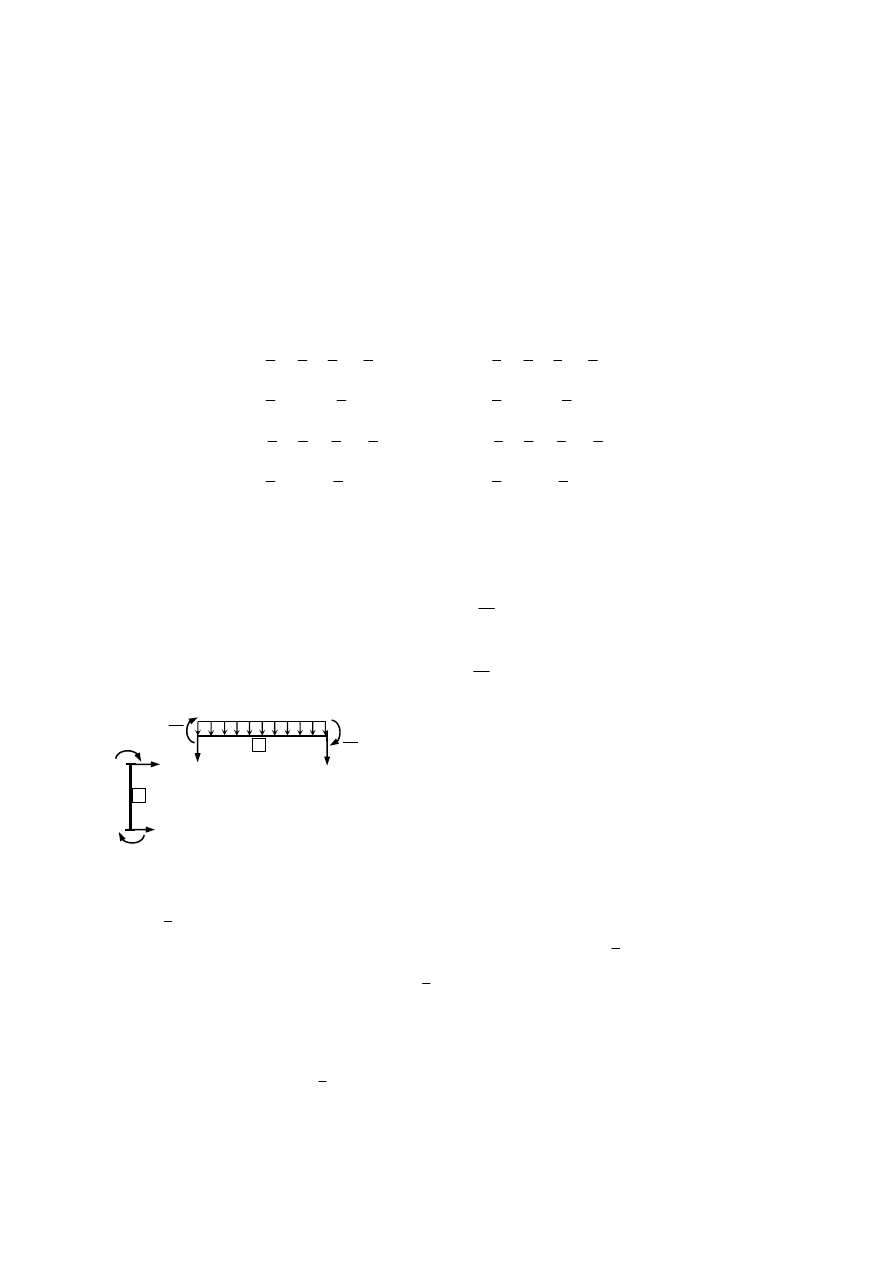
Następnie zapiszemy wektory sił węzłowych
i od obciążenia prętów. Zgodnie z
Tabl. 4.4 oraz Rys. 4.4, siły węzłowe od obciążeń prętów będą miały następujące wartości:
1
o
S
2
o
S
,
1
0
0
0
0
o
⎡ ⎤
⎢ ⎥
⎢ ⎥
=
⎢ ⎥
⎢ ⎥
⎣ ⎦
S
2
40
80
3
40
80
3
o
−
⎡
⎤
⎢
⎥
⎢
⎥
−
⎢
⎥
= ⎢
⎥
−
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
S
(0.8)
1
2
20 kN/m
0
80
3
80
3
−
40
−
0
0
0
40
−
Rys. 4.4. Siły węzłowe w elementach ramy
Dla każdego elementu j (j = 1, 2) utworzymy ponadto podwektor przemieszczeń
węzłowych
j
D
odpowiadający globalnemu przemieszczeniu układu
. Należy także
zbudować macierz transformacji
wiążącą odpowiednio wektory
z
∆
j
A
j
D
j
D
:
j
j
=
D
A D
j
(0.9)
Dla prętów z Rys. 4.2b wyznaczymy następujące zależności:
12
12
1
1
1
21
1
21
1
0
0 0
0
0 0
1 0
0 1
v
u
v
u
φ
φ
φ
φ
⎡ ⎤ ⎡ ⎤ ⎡ ⎤
⎢ ⎥ ⎢ ⎥ ⎢
⎥ ⎡ ⎤
⎢ ⎥ ⎢ ⎥ ⎢ ⎥
=
⇒
=
=
⎢ ⎥
⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦
⎢ ⎥ ⎢ ⎥ ⎢
⎥
⎢
⎥
⎢ ⎥ ⎢ ⎥ ⎣ ⎦
⎣ ⎦ ⎣ ⎦
D
A D
(0.10)
232
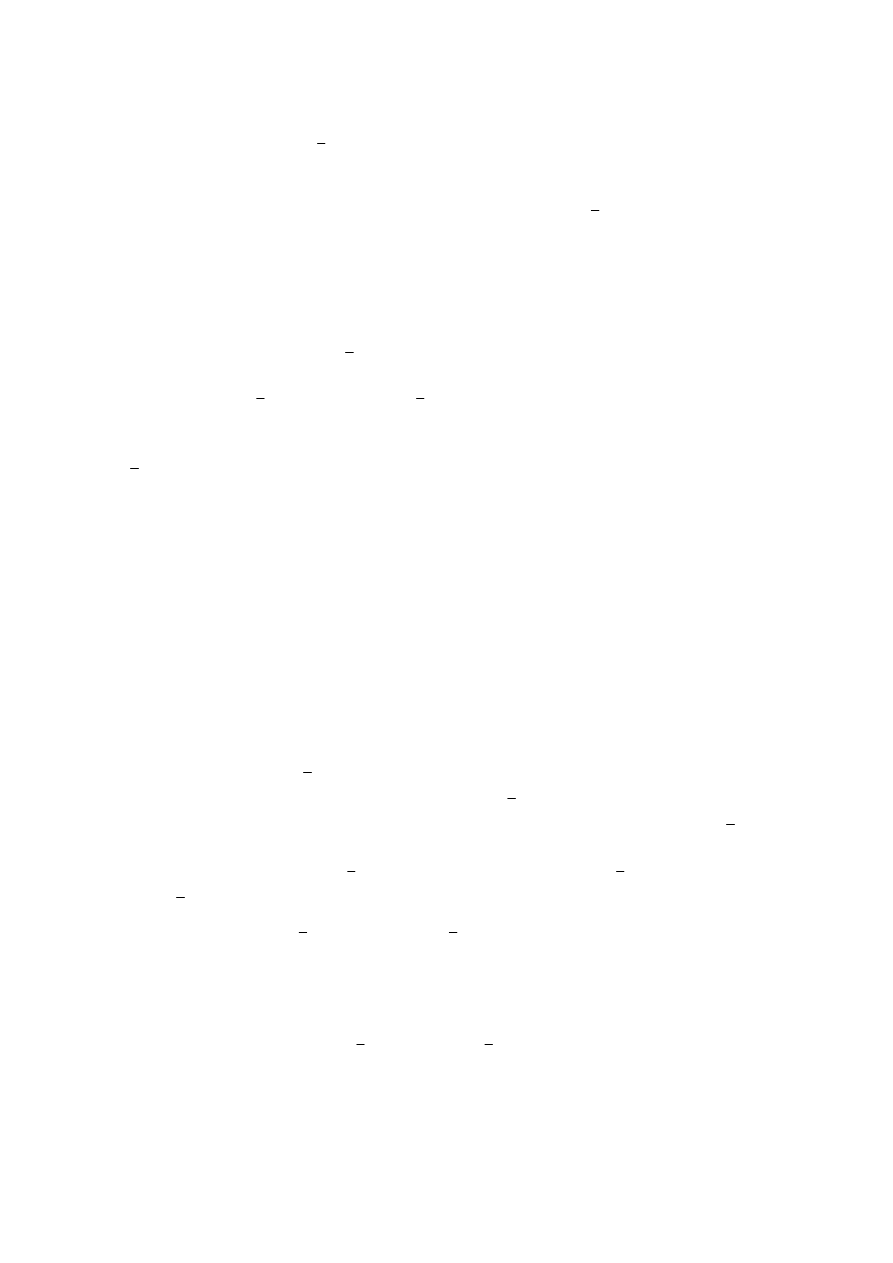
23
23
1
2
2
2
32
2
32
2
0
0 0
1 0
0
0 0
0 1
v
v
φ
1
φ
φ
φ
φ
φ
⎡
⎤ ⎡ ⎤ ⎡ ⎤
⎢
⎥ ⎢ ⎥ ⎢ ⎥ ⎡ ⎤
⎢
⎥ ⎢ ⎥ ⎢ ⎥
=
⇒
=
=
⎢ ⎥
⎢
⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦
⎢
⎥ ⎢ ⎥ ⎢ ⎥
⎢
⎥
⎢ ⎥
⎢
⎥
⎣
⎦
⎣ ⎦
⎣
⎦
D
A D
(0.11)
Z analizy powyższych związków wynika, że za pomocą wektorów
j
D
oraz macierzy
definiuje się przemieszczenia poszczególnych węzłów elementów. Tak więc, dla elementu 1
można zapisać następujące warunki brzegowe:
j
A
12
0
v
=
,
12
0
φ =
,
21
v
u
=
,
21
1
φ
φ
=
, a dla
elementu 2:
,
23
0
v
=
23
1
φ
φ
=
,
,
32
0
v
=
32
2
φ
φ
=
.
Ostatnim działaniem przygotowującym obliczenia macierzowe jest utworzenie tzw.
wektorów alokacji
, które identyfikują numery wierszy w globalnym wektorze
przemieszczeń układu z wektorami
j
t
∆
j
D
:
1
1
1
2
2
1
2
1
,
2
3
u
φ
φ
φ
⎡ ⎤
⎡ ⎤
⎡ ⎤
⎡ ⎤
=
⇒
=
=
⇒
=
⎢ ⎥
⎢ ⎥
⎢ ⎥
⎢ ⎥
⎣ ⎦
⎣ ⎦
⎣ ⎦
⎣ ⎦
D
t
D
t
2
(0.12)
Przykładowo pierwszy element wektora oznacza, że kąt obrotu
2
t
1
φ
(pierwsza składowa
wektora
2
D
) występuje na drugiej pozycji w wektorze .
∆
Dalsze obliczenia będą polegały na standardowych działaniach na utworzonych
macierzach. Nim je wykonamy, podsumujmy przedstawione powyżej działania w formie
ogólnego algorytmu obliczeń. Do wyznaczania sił wewnętrznych w dowolnym układzie
prętowym niezbędne są następujące działania:
1. Dyskretyzacja schematu konstrukcji: numeracja węzłów i prętów.
2. Wprowadzenie globalnego układu współrzędnych XY oraz lokalnych układów xy
związanych z każdym elementem j.
3. Przyjęcie niewiadomych geometrycznych definiujących wektor
∆
.
4. Określenie wektora obciążeń węzłowych bezpośrednio związanego z wektorem .
R
∆
5. Dla
każdego elementu j kolejno:
5a) obliczenie i zapisanie lokalnej macierzy sztywności
związanej z wektorami
i
(4.47),
j
K
j
D
j
S
5b) obliczenie wektora sił węzłowych wywołanych obciążeniem pręta,
o
j
S
5c) zdefiniowanie podwektora
j
D
w globalnym wektorze niewiadomych
∆
oraz budowa
macierzy
transformującej wektor
do podwektora
j
A
j
D
j
D
,
5d) zapisanie macierzy alokacji
przyporządkowującej elementy podwektora
j
t
j
D
odpowiednim pozycjom w wektorze przemieszczeń układu
∆
.
5e) obliczenie macierzy sztywności
j
K
oraz wektorów sił węzłowych
o
j
S
związanych z
wektorem
j
D
:
T
j
j
j
=
K
A K A
j
,
o
T
j
j
=
S
A S
o
j
(0.13)
6. Budowa globalnej macierzy sztywności
oraz globalnego wektora sił węzłowych od
obciążeń prętów
. Wymiary tych macierzy odpowiadają wymiarowi wektora . W
obliczeniach stosujemy zasadę agregacji sterowanej wektorami alokacji :
K
o
R
∆
j
t
j
j
=
∑
K
K
,
o
j
j
=
∑
R
S
(0.14)
7. Obliczenie wektora prawej strony układu równań:
o
= −
P R R
(0.15)
233
8. Rozwiązanie układu równań:
(0.16)
1
−
=
⇒
=
K∆
P
∆ K P
9. W celu wyznaczenia sił wewnętrznych dla każdego elementu j:
9a) wybranie z wektora
∆
podwektora
j
D
wg wektorów alokacji ,
j
t
9b) obliczenie wektora przemieszczeń
w układzie lokalnym elementu j:
j
D
j
j
=
D
A D
j
j
(0.17)
9c) obliczenie sił przywęzłowych:
o
j
j
j
=
+
S
K D
S
(0.18)
10. Narysowanie wykresu sił wewnętrznych.
Pominiemy wyprowadzenie wzorów występujących w powyższym algorytmie. Czytelnik
z łatwością znajdzie odpowiedni materiał w obszernej literaturze dotyczącej metod
komputerowych w mechanice budowli, np. [Chmielewski, 1996].
Pierwsze kilka kroków algorytmu, od punktu 1) do punkty 5d) już wykonaliśmy. Punkty
te wymagały szczegółowej analizy układu i obliczeń „ręcznych”. Pozostałe kroki rozwiązania
polegają na wykonaniu „mechanicznych” działań na macierzach, które można przeprowadzić
za pomocą wielu dostępnych programów komputerowych lub dla prostych schematów nawet
za pomocą kalkulatora z działaniami macierzowymi. Wzory (4.58) oraz (4.60)
÷ (4.63) są
standardowymi działaniami na macierzach. Jedynie agregacja globalnych wektorów i
(wzór 4.59) wymagają wyjaśnienia. Wykonajmy kolejne kroki algorytmu, od punktu 5e do 10.
K
o
R
Macierze sztywności prętów
1
K
i
2
K
otrzymamy przeprowadzając następujące mnożenie
macierzowe:
1
1
1
1
3
3
3
3
2
2
2
2
0 0
3
3
3
2
1
0 0 1 0
0 0
2
2
2
0 0 0 1
3
3
3
3 1 0
3
2
2
2
2
2
0 1
3
3
1
2
2
2
T
EJ
EJ
⎡
⎤
−
⎢
⎥
⎢
⎥ ⎡ ⎤
3
2
2
⎡
⎤
⎢
⎥
−
−
⎢
⎥
⎢
⎥
⎢
⎥
⎡
⎤
⎢
⎥
=
=
=
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
⎢
⎥
⎢
⎥
−
−
−
−
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
⎢
⎥
⎣
⎦
⎢
⎥
⎢
⎥
−
⎢
⎥
⎣
⎦
K
A K A
(0.19)
2
2
2
2
3
3
3
3
8
4
8
4
0 0
3
3
2
1
0 1 0 0
1 0
2 1
4
4
0 0 0 1
3
3
3
3 0 0
1 2
8
4
8
4 0 1
3
3
1
2
4
4
T
EJ
EJ
⎡
⎤
−
⎢
⎥
⎢
⎥ ⎡ ⎤
⎢
⎥
−
⎢
⎥
⎢
⎥
⎡
⎤
⎡
⎢
⎥
=
=
=
⎢
⎥
⎢
⎥
⎢
⎢
⎥
⎣
⎦
⎣
⎢
⎥
−
−
−
⎢
⎥
⎢
⎥ ⎢ ⎥
⎣
⎦
⎢
⎥
⎢
⎥
−
⎢
⎥
⎣
⎦
K
A K A
⎤
⎥
⎦
(0.20)
W podobny sposób obliczymy wektory :
o
j
S
1
1
1
0
0 0 1 0 0
0
0 0 0 1 0
0
0
o
T
o
⎡ ⎤
⎢ ⎥
⎡
⎤
⎡
⎢ ⎥
=
=
=
⎢
⎥
⎢
⎢ ⎥
⎣
⎦
⎣
⎢ ⎥
⎣ ⎦
S
A S
⎤
⎥
⎦
,
2
2
2
40
80
80
0 1 0 0
3
0 0 0 1
40
80
3
80
3
o
T
o
−
⎡
⎤
⎢
⎥
3
⎡
⎤
⎢
⎥
−
−
⎢
⎥
⎡
⎤ ⎢
⎥
=
=
= ⎢
⎥
⎢
⎥ ⎢
⎥
−
⎢
⎥
⎣
⎦ ⎢
⎥ ⎢
⎥
⎣
⎦
⎢
⎥
⎢
⎥
⎣
⎦
S
A S
(0.21)
234
Następnie budujemy globalną macierz sztywności wykonując agregację macierzy
K
1
K
(4.64) i
2
K
(4.65) według wektorów alokacji i (4.57). Numery wektorów alokacji
przypisujemy odpowiednim wierszom i kolumnom lokalnych macierzy sztywności
1
t
2
t
j
K
:
2
1
1
1
11
12
1
1
1
21
22
3
3
2
2
3
2
2
k
k
EJ
EJ
k
k
⎡
⎤
−
⎢
⎥
⎢
⎥
⎢
⎥
−
⎢
⎥
⎣
⎦
⎡
⎤
=
=
⎢
⎥
⎢
⎥
⎣
⎦
K
,
2
2
11
12
2
2
2
21
22
2 1
1 2
k
k
EJ
EJ
k
k
⎡
⎤
⎡
⎤
=
=
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
⎣
⎦
K
(0.22)
2
3
1
2
3
2
Zgodnie z tą numeracją kolejno dodajemy odpowiednie elementy lokalnych macierzy
sztywności
1
K
i
2
K
do globalnej macierzy sztywności . Wymiar macierzy
K
odpowiada
wymiarowi wektora zdefiniowanego w (4.50) i wynosi
3
K
∆
3
×
:
1
1
11
12
1
1
2
2
1
2
21
22
11
12
2
2
21
22
3
3
3
3
0
0
2
2
2
2
0
3
3
2 2 1
4 1
2
2
0
0
1
2
0
1 2
k
k
EJ k
k
k
k
EJ
EJ
k
k
⎡
⎤
⎡
−
−
⎤
⎢
⎥
⎢
⎡
⎤
⎥
⎢
⎥
⎢
⎢
⎥
⎥
⎢
⎥
⎢
=
+
=
+
=
−
+
=
−
⎢
⎥
⎥
⎢
⎥
⎢
⎢
⎥
⎥
⎢
⎥
⎢
⎣
⎦
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
⎣
K K
K
⎦
(0.23)
W powyższym wzorze przez oznaczono element z macierzy sztywności
j
ik
k
ik
k
j
K
elementu j.
Specyficzne sumowanie macierzy wykonane w równaniu (4.68) nazywamy agregacją.
W podobny sposób, wykorzystując wektory alokacji
t
i
t
, wykonujemy agregację
wektora
:
1
2
o
R
1
11
1
2
1
2
22
11
2
22
0
0
80
80
0
3
80
80
3
3
o
o
o
s
s
s
s
3
⎡
⎤ ⎡
⎤
⎢
⎥ ⎢
⎥
⎡
⎤ ⎢
⎥ ⎢
⎥
⎢
⎥ ⎢
⎥ ⎢
⎥
=
+
=
+
=
−
= −
⎢
⎥ ⎢
⎥ ⎢
⎥
⎢
⎥ ⎢
⎥ ⎢
⎥
⎣
⎦
⎢
⎥ ⎢
⎥
⎢
⎥ ⎢
⎥
⎣
⎦ ⎣
⎦
R
S
S
(0.24)
Następnie obliczamy wektor prawych stron :
P
0
40
40
80
80
0
3
3
0
80
80
3
3
o
⎡
⎤ ⎡
⎤
⎢
⎥ ⎢
⎥
⎡ ⎤ ⎢
⎥ ⎢
⎥
⎢ ⎥ ⎢
⎥ ⎢
⎥
= −
=
− −
=
⎢ ⎥ ⎢
⎥ ⎢
⎥
⎢ ⎥ ⎢
⎥ ⎢
⎥
⎣ ⎦
⎢
⎥ ⎢
⎥
−
⎢
⎥ ⎢
⎥
⎣
⎦ ⎣
⎦
P R R
(0.25)
W ten sposób zbudowaliśmy wszystkie potrzebne macierze pozwalające na rozwiązanie
układu równań:
-1
7
1
1
200
40
6
2
4
3
1
1
1
1
80
1
40
2
2
4
3
100
1
1 5
80
3
4
4 8
3
EJ
EJ
⎡
⎤ ⎡
⎤
−
⎡
⎤
⎢
⎥ ⎢
⎥
⎢
⎥
⎢
⎥ ⎢
⎥
⎢
⎥
⎢
⎥ ⎢
⎥
⇒
=
−
=
⎢
⎥
⎢
⎥ ⎢
⎥
⎢
⎥
⎢
⎥ ⎢
⎥
⎢
⎥
−
⎢
⎥ ⎢
⎥
−
−
−
⎢
⎥
⎣
⎦
⎢
⎥
⎢
⎥ ⎣
⎦
⎣
⎦
K∆ = P
∆ = K P
(0.26)
gdzie macierz
jest odwrotna do macierzy .
1
−
K
K
235
Zgodnie z przedstawionym algorytmem, w celu wyznaczenia sił wewnętrznych dla
elementów 1 i 2 należy wykonać kilka działań. Najpierw wybieramy z wektora (4.71)
podwektory
∆
1
D
i
2
D
wg wektorów alokacji i (4.57):
1
t
2
t
1
2
200
40
1
1
,
3
100
40
3
EJ
EJ
⎡
⎤
⎡
⎢
⎥
⎢
=
=
⎢
⎥
⎢−
⎢
⎥
⎢
⎣
⎦
⎣
D
D
⎤
⎥
⎥
⎥⎦
(0.27)
Następnie obliczamy wektory przemieszczeń
1
D
i
2
D
elementów w układach lokalnych,
wykorzystując następujące zależności:
1
1
1
2
2
2
0
0
0 0
0 0
200
0
40
40
0 0
1 0
1
1
1
1
,
3
200
100
0
1 0
0 0
40
3
3
100
0 1
0 1
40
3
EJ
EJ
EJ
EJ
⎡
⎤
⎡
⎡
⎤
⎡
⎤
⎢
⎥
⎢
⎡
⎤
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
=
=
=
=
=
=
⎢
⎥
⎢
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
−
⎢
⎥
⎢
⎢
⎥
⎢
⎥
⎣
⎦
⎣
⎦
⎢
⎥
⎢
⎥
⎢
⎥
⎢−
⎢
⎥
⎢
⎥
⎣
⎦
⎣
⎦
⎢
⎥
⎢
⎣
⎦
⎣
D
A D
D
A D
⎤
⎥
⎥
⎥
⎥
⎥
⎥⎦
(0.28)
Wyznaczenie wektorów sił przywęzłowych i
S
wykonujemy na podstawie równania
(4.63):
1
S
2
1
1
1
1
3
3
3
3
2
2
2
2
0
0
40
3
3
0
2
1
0
60
1
2
2
200
3
3
3
3
0
40
3
2
2
2
2
0
20
40
3
3
1
2
2
2
o
EJ
EJ
⎡
⎤
−
⎢
⎥
⎡
⎤
⎢
⎥
−
⎡ ⎤ ⎡
⎤
⎢
⎥
⎢
⎥
−
⎢ ⎥ ⎢
⎥
⎢
⎥
⎢
⎥
−
⎢ ⎥ ⎢
⎥
=
+
=
+
=
⎢
⎥
⎢
⎥
⎢ ⎥ ⎢
⎥
⎢
⎥
⎢
⎥
−
−
−
⎢ ⎥ ⎢
⎥
⎢
⎥
⎢
⎥
−
⎢ ⎥ ⎢
⎥
⎣ ⎦ ⎣
⎦
⎢
⎥
⎢
⎥
⎣
⎦
⎢
⎥
−
⎢
⎥
⎣
⎦
S
K D
S
(0.29)
2
2
2
2
3
3
3
3
40
8
4
8
4
0
35
80
3
3
40
2
1
20
1
3
4
4
0
3
3
3
3
40
45
100
8
4
8
4
80
0
3
3
3
3
1
2
4
4
o
EJ
EJ
⎡
⎤
−
⎢
⎥
−
⎡
⎤
⎡
⎤
⎢
⎥
⎢
⎥
−
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
−
−
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥ ⎢
⎥
=
+
=
+
=
⎢
⎥
⎢
⎥
⎢
⎥ ⎢
⎥
−
−
⎢
⎥
⎢
⎥
⎢
⎥
−
−
−
⎢
⎥
⎢
⎥
⎢
⎥
−
⎢
⎥
⎢
⎥ ⎣
⎦
⎢
⎥
⎢
⎥
⎣
⎦ ⎢
⎥
⎣
⎦
⎢
⎥
−
⎢
⎥
⎣
⎦
S
K D
S
(0.30)
Wykresy sił wewnętrznych rysujemy podobnie jak w przypadku standardowych obliczeń
„ręcznych”. Przywęzłowe siły poprzeczne uzyskaliśmy bezpośrednio z rozwiązania – ich
wartości można odczytać z wektorów
S
(4.74) i
S
(4.75). Gdybyśmy w algorytmie
rozwiązania uwzględnili siły podłużne, ich wartości także uzyskalibyśmy w sposób
automatyczny, czyli wykonując standardowe działania macierzowe. Jednakże z powodu
zastosowania uproszczonego algorytmu obliczeń, siły podłużne należy wyznaczyć tak jak w
przypadku obliczeń „ręcznych” analizując równowagę sił w węźle 2. Nie opisując szczegółów
tych obliczeń, na Rys. 4.5 przedstawiono ostateczne wykresy sił wewnętrznych.
1
2
M
[kN]
N
V
[kN]
[kN
⋅m]
35
35
45
40
20
50,6
20
60
Rys. 4.5. Wykresy sił wewnętrznych
236
Document Outline