AS

1

Przewodność

T przewodnośd warstwy, współczynnik przewodności

Miara przepuszczalności(przewodnictwa) wyrażająca jednostkowe natężenie

(wydatek) strumienia wody na jednostkę szerokości, przy jednostkowym spadku
hydraulicznym, odniesiona do przekroju prostopadłego do kierunku strumienia. Jest więc
liczbowo równa iloczynowi współczynnika filtracji i miąższości warstwy wodonośnej(w
nasyconej warstwie jednorodnej i izotropowej) T = km.
Wymiar: [L

2

T

–1

].

Jednostki: m

2

/h, m

2

/d, cm

2

/s.

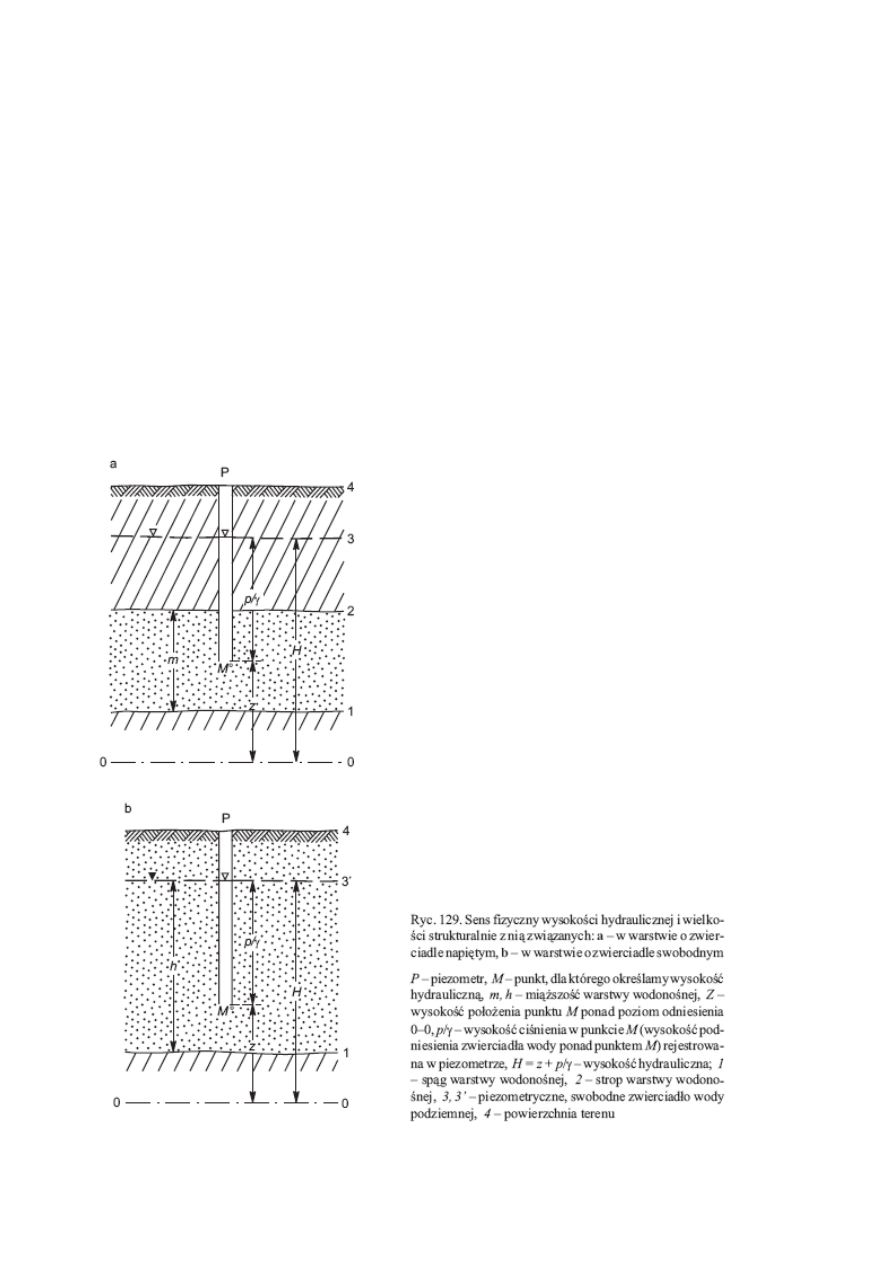
Wysokość hydrauliczna

H, napór

W.h. w określonym punkcie w polu filtracji wyraża sumę wysokości położenia tego

punktu ponad poziom odniesienia (zwykle poziom morza) i wysokości ciśnienia
piezometrycznego p/γ w tym punkcie (ryc. 129):
H = z + p/γ.

Dla niezmineralizowanych wód podziemnych w.h.
jest równoznaczna z rzędną zwierciadła wody,
jeżeli poziomem odniesienia jest poziom morza.
W.h. wyraża energię strumienia wody podziemnej
przypadającą na jednostkę masy. Zwraca się uwagę
na fakt, że w przypadku wód o zmiennej gęstości
wyznaczenie w.h. komplikuje się i wymaga
określenia

tzw.

zredukowanej

w.h.

przez

uwzględnienie zmienności gęstości cieczy ρ,
uwzględnienie i znormalizowanie warunków
pomiaru zarówno ze względu na płyn wypełniający
piezometr(rurę), jak i rozmieszczenie w warstwie
punktów pomiarowych. W warunkach filtracji
płynów niejednorodnych przepływ zależy od
rozkładu „zredukowanych w.h.”, a nie od rozkładu
w.h., może nawet odbywad się w kierunku
odwrotnym do nachylenia zwierciadła wody
podziemnej.
Wymiar: [L].
Jednostka: m.

AS

2

Prędkość filtracji

v, prędkośd przesączania

Fikcyjna makroskopowa prędkośd przepływu wody podziemnej w ośrodku

nasyconym. Wyraża natężenie strumienia filtracji przypadające na jednostkowy przekrój
poprzeczny (ortogonalny do linii prądu) ośrodka porowatego(skały), a nie względem
przekroju efektywnej przestrzeni porowej, którą płynie woda:
v = Q/A

sk

gdzie:
v – prędkośd filtracji *LT

–1

],

Q – wydatek strumienia filtracji [L

3

T

–1

],

A

sk

– pole powierzchni przekroju poprzecznego skały *L

2

].

Wymiar: [LT

–1

].

Jednostki: m/s, m/h, m/a.

Przepływ wód podziemnych

Ruch wody (proces płynięcia) przez określony przekrój poziomu wodonośnego,

strumienia wód podziemnych, w którym na określonych odcinkach następuje dopływ i
odpływ wód podziemnych. Natężenie przepływu.

Współczynnik filtracji

k, współczynnik wodoprzepuszczalności

Parametr wyrażający przepuszczalnośd ośrodka izotropowego dla płynu

jednorodnego(ρ = const, ν = const), za jaki przyjmowana jest zwykła woda podziemna. Dla
zwykłych wód podziemnych fizycznie wyraża prędkośd filtracji przy spadku hydraulicznym
równym jedności, pod warunkiem że filtracja (przepływ wody podziemnej) podlega
liniowemu prawu Darcy’ego. Uogólnieniem współczynnika filtracji na warstwy anizotropowe
jest tensor przepuszczalności. Współczynnik przepuszczalności.
Uwaga: w większości krajów omawiana wielkośd jest nazywana bardzo różnie, znanych jest
nawet po kilkadziesiąt określeo.
Wymiar: [LT

–1

].

Jednostki: m/s, m/h, m/d.

Współczynnik przepuszczalności

k

p

, przepuszczalnośd, p. wewnętrzna

Parametr wyrażający przepuszczalnośd samego ośrodka porowatego niezależnie od

właściwości płynu. Fizycznie wyraża objętośd płynu o jednostkowej lepkości dynamicznej,
który w jednostce czasu, pod wpływem jednostkowego gradientu potencjału ciśnienia
przepływa przez jednostkowy przekrój ortogonalny do kierunku przepływu. Jednostką w.p.
jest darcy. Parametr stosowany w dynamice płynów niejednorodnych: ropy naftowej, gazów
i wód mineralnych.
Wymiar: [L

2

].

Jednostki: D, mD, de, cm

2

, m

2

.

Infiltracja

Wsiąkanie wody pochodzącej z opadów atmosferycznych, z cieków i zbiorników

powierzchniowych oraz z kondensacji pary wodnej z powierzchni terenu do strefy aeracji, a
następnie (po oddaniu części tych wód do atmosfery - ewapotranspiracja) przesączanie do
strefy saturacji ( infiltracja efektywna). Infiltracja może byd również wywołana sztucznie.
Wielkośd infiltracji jest wyrażana w dm

3

/km

2

lub w mm/rok.

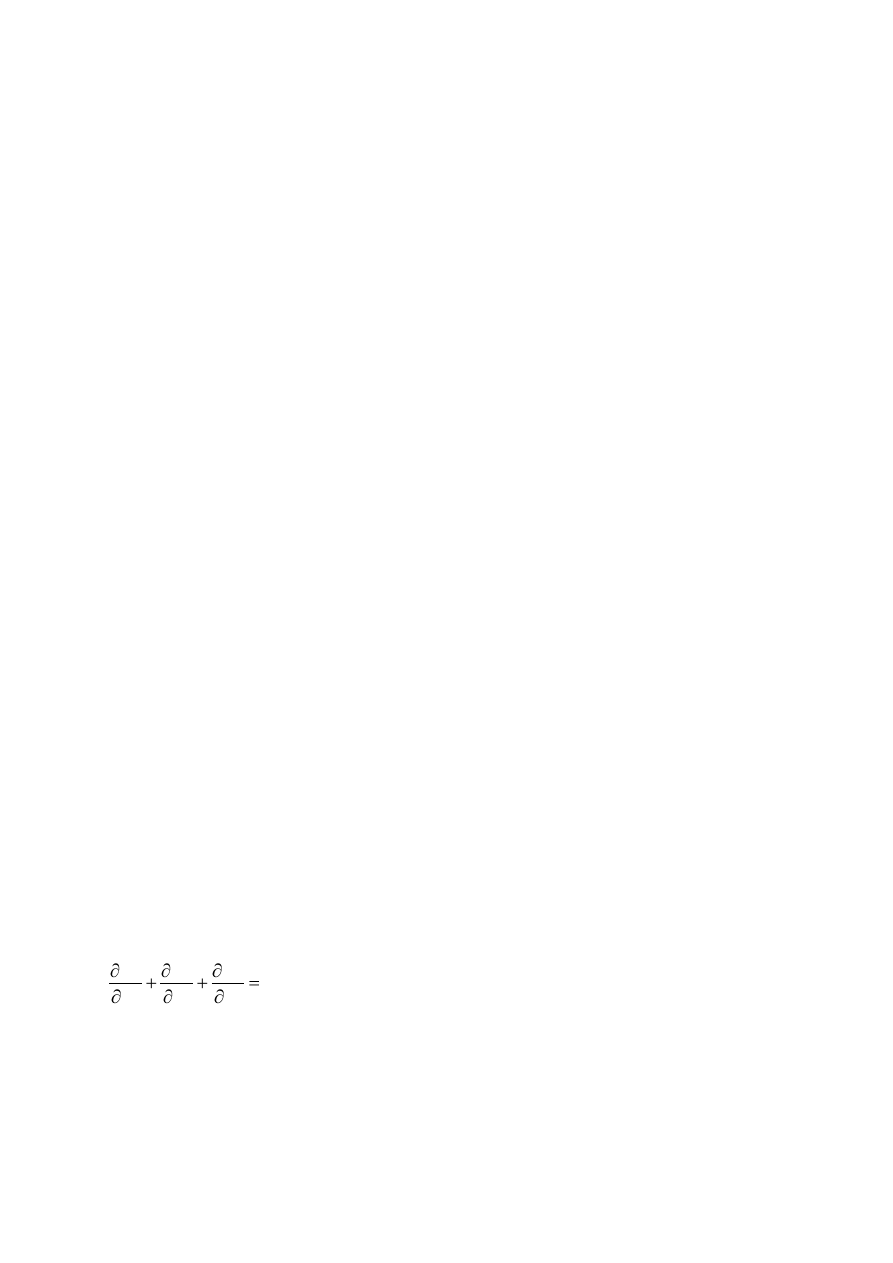
AS

3

Zasilanie wód podziemnych

, alimentacja

Dopływ wody do strefy saturacji określonego poziomu wodonośnego na drodze

infiltracji wód opadowych (infiltracja efektywna), przesiąkania z innych _ poziomów
wodonośnych(wyżej lub niżej ległych) przez utwory półprzepuszczalne lub z sąsiednich
zbiorników(zasilanie lateralne), a także w wyniku sztucznego doprowadzenia wody z
powierzchni terenu. Wzbogacanie zasobów(sztuczne zasilanie) wód podziemnych.

Gradient hydrauliczny,

grad H,

spadek hydrauliczny I

G.h. określa wartośd i kierunek największego spadku wysokości hydraulicznej w

danym punkcie pola prędkości filtracji. Bez hipotezy continuum byłby więc pojęciem
fikcyjnym. W hydrogeologii częściej używa się pojęcia średniego spadku hydraulicznego,
który wyznacza różnica wysokości hydraulicznej w warstwie wodonośnej między dwoma
punktami położonymi na jednej linii prądu (na kierunku maksymalnego spadku),
przypadającą na jednostkową odległośd między tymi punktami:
grad H = -∂H/∂L ≈ –(H

2

– H

1

)/∆L = I

Wymiar: [1].

Darcy’ego prawo

Liniowe doświadczalne prawo filtracji wyrażające proporcjonalnośd prędkości filtracji

do spadku hydraulicznego. D.p. wyraża się wzorem:
v = kI
gdzie:
v – prędkośd filtracji [LT

-1

],

k – współczynnik filtracji [LT

-1

],

I – spadek hydrauliczny *1+ wyrażający się wzorem:
I = ∆H/s
gdzie:
H – wysokośd hydrauliczna [L],
s – droga filtracji [L].
W zapisie różniczkowym D.p. ma postad:
v = -k(∂H/∂s)
Znak minus oznacza, że dodatniemu przyrostowi drogi filtracji odpowiada ujemny przyrost
wysokości hydraulicznej.

Laplace’a równanie

Równanie różniczkowe cząstkowe drugiego rzędu, eliptyczne, postaci:

0

z

H

y

H

x

H

2

2

2

2

2

2

gdzie:
H – wysokośd hydrauliczna [L].
W hydrogeologii L.r. opisuje pole filtracji ustalonej bez zasilania.

AS

4

Bernoulliego równanie

Równanie ruchu cieczy doskonałej (nieściśliwej,
nielepkiej) równoważne prawu zachowania
energii cieczy. Jeśli ruch jest ustalony i
bezwirowy, B.r. ma postad:
z + p/ρg + v

2

/2g = const

gdzie:
z – wysokośd nad poziomem odniesienia[L],
p – ciśnienie [ML

–1

T

–2

],

ρ – gęstośd cieczy [ML

–3

],

γ = ρg – ciężar właściwy cieczy [ML

–3

],

g – przyspieszenie ziemskie [LT

–2

],

v – prędkośd cieczy [LT

–1

].

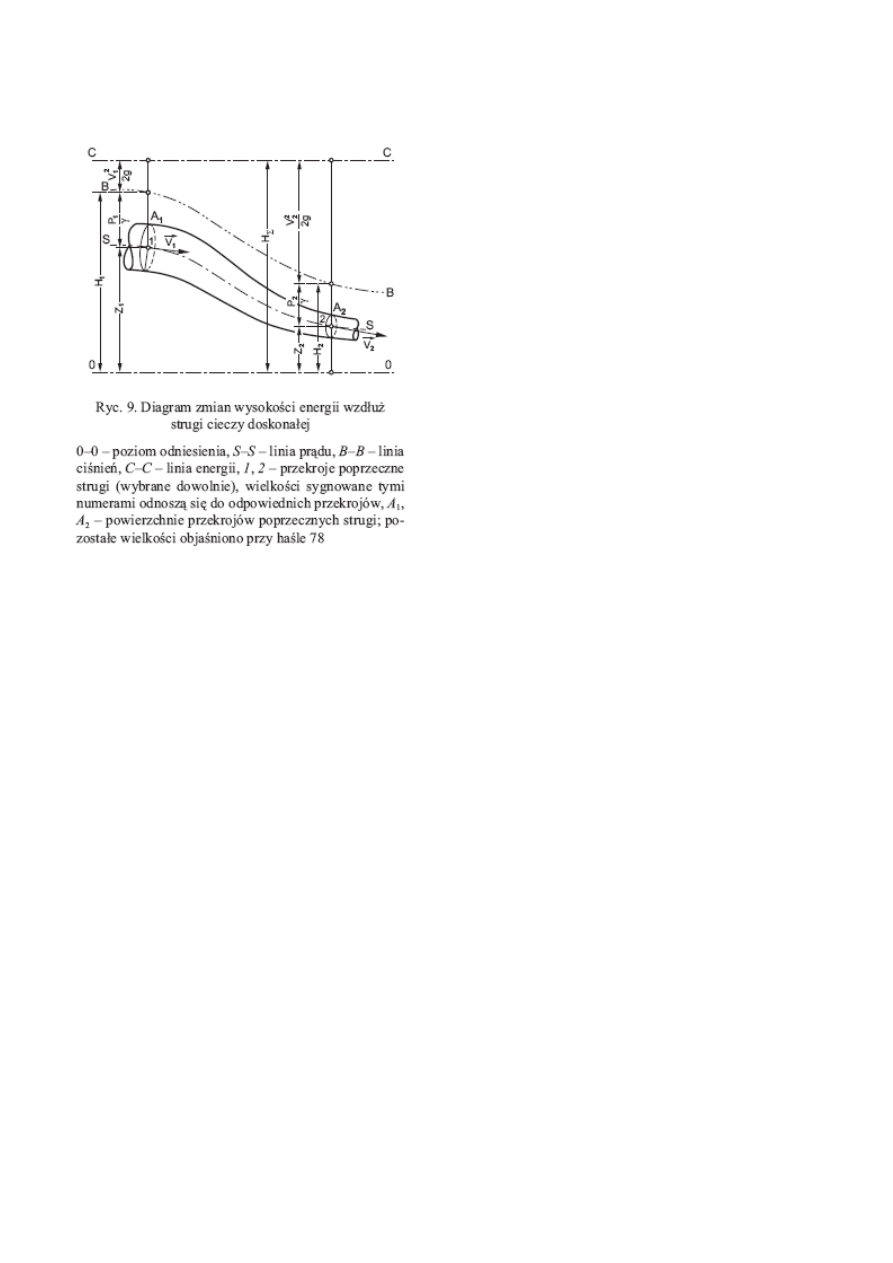
B.r. jest słuszne dla każdej linii prądu lub środka
elementarnej strugi cieczy i wyraża stałośd
wysokości energii całkowitej H

Σ

jednostki masy

strumienia, będącej sumą energii położenia i
energii ciśnienia (ich suma to energia potencjalna
zwana Ù wysokością hydrauliczną: H = z + p/γ)
oraz energii prędkości (energia kinetyczna:
v2/2g) (ryc. 9).

Wskaźnik infiltracji efektywnej

, moduł (wskaźnik) zasilania

Stosunek ilości infiltrującej wody docierającej do strefy saturacji ( infiltracja

efektywna) do wysokości średnich rocznych opadów atmosferycznych na określonym
obszarze.