
COSMOSFFE Static
1-1
1
Introduction
Introduction
COSMOSFFE Static is a fast, robust, and accurate finite element program for the
analysis of linear static structural problems. The program exploits a new technology
developed at Structural Research for the solution of large systems of simultaneous
equations using sparse matrix technology along with iterative methods combined
with novel database management techniques to substantially reduce solution time,
disk space, and memory requirements.
COSMOSFFE Static has been written from scratch using state of the art techniques
in FEA with two goals in mind: 1) to address basic design needs, and 2) to use the
most efficient possible solution algorithms without sacrificing accuracy. The
program is particularly suitable to solve large basic models subjected to a variety of
loading and boundary conditions environments.
COSMOSFFE Static is not meant to be a replacement for STAR, the COSMOSM
conventional linear static structural analysis module. The capabilities of FFE Static
are a subset of the capabilities of STAR. Problems that can be solved by FFE Static
can also be solved by STAR. The advantage is that FFE Static for the class of
problems it supports is far superior in terms of robustness, speed, and use of
computer resources. Clear messages of unsupported capabilities and options are
given whenever encountered. Appendix A gives a list of these messages along with
suggestions for fixing the problem.
In
de
x
In
de
x

Chapter 1 Introduction
1-2
COSMOSFFE Static
Theoretical Background
Linear Static Analysis
Static analysis deals with the computation of displacements strains, and stresses
due to static loading. The term static loads refers to loading that does not cause
inertial or damping effects to be significant for consideration in the analysis. Static
analysis is linear if nonlinearities due to plasticity, large deflection, large strain, in-
plane effects, contact surfaces, creep and relaxation effects, and other sources can
be either linearized or completely ignored.
Dynamic loads with frequencies less than one-third of the fundamental frequency
of the structure may be approximated as static loads. If you are in doubt about
whether a loading environment is static or dynamic, it is recommended to calculate
the fundamental frequency of the structure.
The stress-strain relationship for linear analysis is linear, and so is the relation
between the load and deflection. Doubling the load vector for a problem will result
in doubling all the results associated with it. This property of linear analysis is
exploited in the creation of secondary load cases as will be described below.
The formulation of a linear static problem for solution by the displacement method
is fully described by the matrix equation:
[K]{U} = {F} = {F
a
} + {F
c
}
(1-1)
where [K] is the structural (assembled) stiffness matrix, {U} is the vector of
unknown nodal displacements, and {F} is the load vector. The load vector {F} has
components from mechanical, thermal, and gravitational loads. The load vector {F}
can be expressed as a combination of applied nodal forces {F
a
} and reaction (or
single point constraint) forces {F
c
}. For linear static problems, each of these load
vectors are the superposition of mechanical, thermal, and gravitational loads as
shown below:
{F
a
} = {F
m
} + {F
th
} + {F
gr
}
(1-2)
The mechanical load vector {F
m
} is computed as the sum of applied nodal forces
and moments, and element pressures as shown below:
In
de
x
In
de
x

COSMOSFFE Static
1-3
Chapter 1 Introduction
(1-3)
where {F
nd
} is the applied nodal force vector, and {F
e
pr
} is the element pressure
load vector. The thermal, and gravitational load vectors are computed as follows:
(1-4)
where {F
nt
} is the load vector of nodal temperatures, {F
e
th
} is the element thermal
load vector, [M
e
] is the element mass matrix, and {a} is the acceleration vector.
Multiple Load Cases
Multiple loading is an important feature in linear analyses that is supported by both
STAR and FFE Static. The utility is very popular due to time saving, convenience,
and ease of book keeping of “what-if” load combination scenarios. The user may
define loading conditions for up to 50 primary load cases and the program will
calculate the displacements, strains and stresses in a single run. All results will be
available simultaneously for all primary load cases. Secondary load cases may then
be defined using the results of primary load cases. Refer to Chapter 4 for more
details on multiple load cases.
Consistent Systems of Units
In COSMOSM modules including FFE Static, you are free to adopt standard or
non-standard systems of units, but you are responsible for consistency and the
interpretation of the units of results. The table below shows consistent standard
systems of units for the physical quantities used in the FFE Static module.
In
de
x
In
de
x

Chapter 1 Introduction
1-4
COSMOSFFE Static
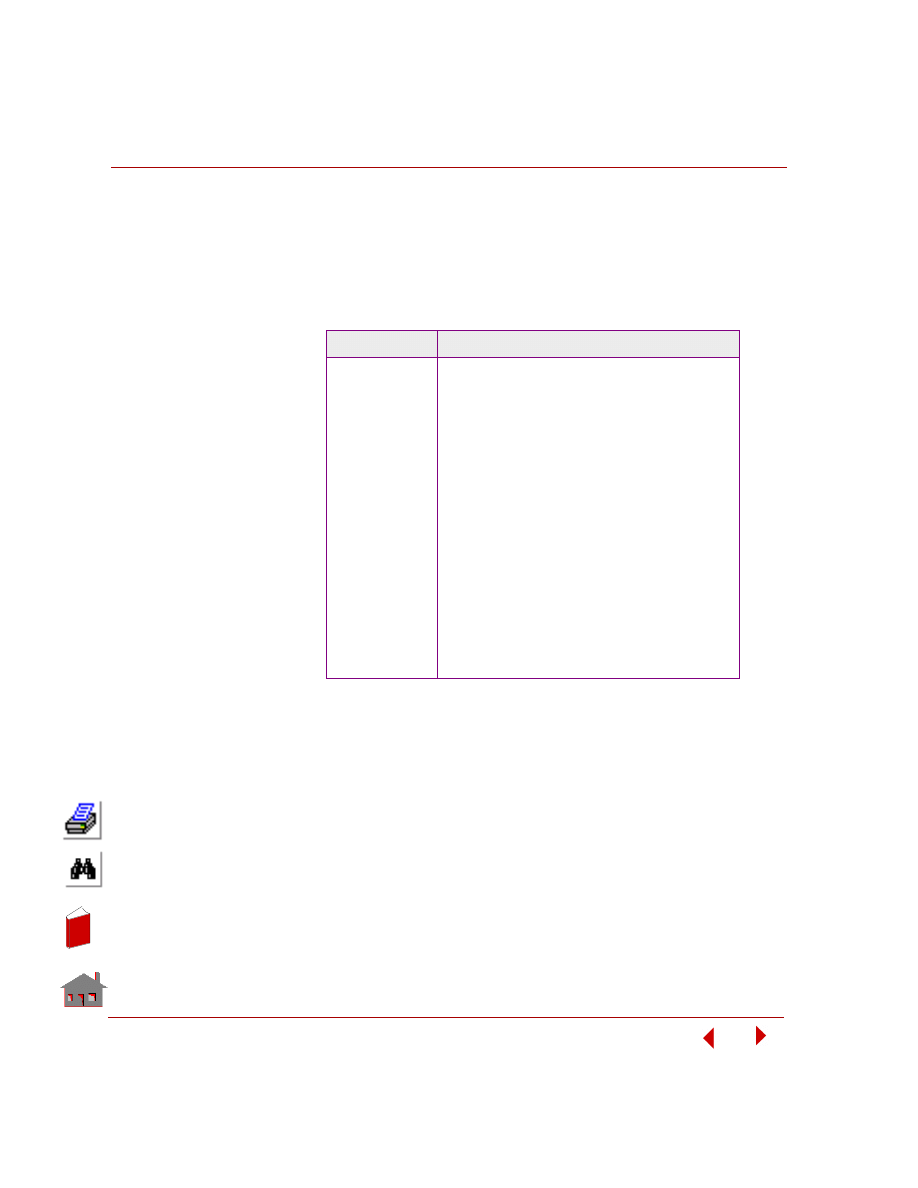
Table 1-1. Table of Consistent Units for COSMOSFFE Static
Description
COSMOS Name
*
FPS
1
(gravitational)
*
SI
2
(absolute)
*
MKS
3
(gravitational)
CGS
4
(absolute)
Measure
Length
X, Y, Z
in
m
cm
cm
Material Properties
Elastic Modulus
EX, EY, EZ
lbs/in
2
Newton/m
2
or Pascal
kg/cm
2
dyne/cm
2
Shear Modulus
GXY, GYZ, GXZ
lbs/in
2
N/m
2
or Pa
kg/cm
2
dyne/cm
2
Poisson's Ratio
NUXY, NUYZ, NUXZ
in/in
(no units)
m/m
(no units)
cm/cm
(no units)
cm/cm
Mass Density
DENS
lbs sec
2
/in
4
kg/m
3
kg
sec
2
/cm
4
g/cm
3
Coeff. of Thermal
Expansion
ALPX, ALPY, ALPZ
in/(in
°
F)
m/(m
°
K)
cm/(cm
°
C)
cm/(cm
°
K)
Loads and Boundary Conditions
Temperature
TEMP
°
F
°
K
°
C
°
K
Translational
Displacements
UX, UY, UZ
in
m
cm
cm
Rotational Displacements RX, RY, RZ
radians
radians
radians
radians
Forces (nodal)
FX, FY, FZ
lbs
Newton
kg
dyne
Moments (nodal)
MX, MY, MZ
in lbs
m N
cm kg
cm dyne
Pressure
P
lbs/in
2
N/m
2
or Pa
kg/cm
2
dyne/cm
2
Distributed Beam Load
PB
lbs/in
N/m
kg/cm
dyne/cm
Linear Acceleration
ACEL
in/sec
2
m/sec
2
cm/sec
2
cm/sec
2
Angular Velocity
OMEGA, CGOMEGA
rad/sec
rad/sec
rad/sec
rad/sec
Angular Acceleration
DOMEGA, DCGOMEGA
rad/sec
2
rad/sec
2
rad/sec
2
rad/sec
2
Results
Displacements
UX, UY, UZ, RES
in
m
cm
cm
Stresses
SX, SY, SZ, TXY, TYZ, TXZ,
P1, P2, P3, VON, INT
lbs/in
2
N/m
2
or Pa
kg/cm
2
dyne/cm
2
Strains
EPSX, EPSY, EPSZ, GMXY,
GMYZ, GMXZ, ESTRN
in/in
(no units)
m/m
(no units)
cm/cm
(no units)
cm/cm
(no units)
*
Units are consistent with the COSMOSM material library.
1 FPS refers to the U.S. customary system of units.
2 SI refers to the International system of units.
3 MKS refers to the Metric system of units.
4 CGS refers to the French system of units.
In
de
x
In
de
x

COSMOSFFE Static
2-1
2
Brief Overview
Introduction
COSMOSFFE Static currently addresses basic classes of structural problems
encountered in practical engineering applications. The program is being constantly
updated to include more capabilities and support more options. This chapter lists
the current capabilities of the program.
Element Library
•
Two and three dimensional trusses (TRUSS2D and TRUSS3D)
•
Three dimensional beam elements (BEAM3D)
•
First order triangular plane stress, plane strain and axisymmetric elements
(TRIANG)
•
Second order triangular plane stress, plane strain and axisymmetric elements
(TRIANG)
•
First order quad plane stress, plane strain and axisymmetric elements
(PLANE2D)
•
Second order quad plane stress, plane strain and axisymmetric elements
(PLANE2D)
In
de
x
In
de
x

Chapter 2 Brief Overview
2-2
COSMOSFFE Static
•
First order triangular (3-node) shell elements (SHELL3)
•
First order quad (4-node) shell elements (SHELL4)
•
First and second order hexahedral elements (SOLID)
•
First and second order prism-shaped elements (SOLID with a face collapsed to
an edge)
•
First order tetrahedral elements (TETRA4)
•
Second order tetrahedral elements (TETRA10)
Refer to Chapter 3 for details on elements.
Loads
Loads may be applied to nodes or elements directly or through association with
geometric entities. Up to 50 primary load cases may be created.
The applied load may be:
•
Pressure on element faces in any Cartesian coordinate system
•
Nodal concentrated forces in any coordinate system
•
Nodal concentrated moments for shell elements
•
Edge pressure for plane and shell elements
•
Acceleration of gravity for gravity loading
•
Angular velocity and/or acceleration for centrifugal loading
•
Thermal loading through temperatures defined by the user
•
Thermal loading obtained from steady state thermal analysis
•
Thermal loading obtained from transient thermal analysis
•
Prescribed displacement in the desired coordinate system
✍
Thermal, gravity, and centrifugal loadings are referred to as special loading in
COSMOSM literature. Special loading is considered on top of other mechanical
loads defined for a load case. The consideration of special loading effects must
be activated before running the analysis using the
A_FFESTATIC
(Analysis >
STATIC >
FFE Static Options
) command.
In
de
x
In
de
x
COSMOSFFE Static
2-3
Chapter 2 Brief Overview
Displacement Constraints
•
Displacement constraints in the global Cartesian coordinate system
•
Displacement constraints in the global Cylindrical coordinate system
•
Displacement constraints in the global Spherical coordinate system
•
Displacement constraints in the any local coordinate system defined by the user
Material Properties
In this release only isotropic materials are supported. Use STAR for orthotropic or
anisotropic materials.
Analysis Capabilities
Analysis options are specified through the
A_FEESTATIC
(Analysis > STATIC >
FFE Static Options
) command. The following choices are available:
1. Element order in analysis
•
Use first order elements with first order elements in GEOSTAR
•
Use second order elements with first order elements in GEOSTAR
•
Use first order elements with second order elements in GEOSTAR
•
Use second order elements with second order elements in GEOSTAR
2. Special loading to be considered on top of mechanical loading
•
Thermal loading
•
Gravity loading
•
Centrifugal loading
In
de
x
In
de
x

Chapter 2 Brief Overview
2-4
COSMOSFFE Static
Results
Results will be available for all primary load cases.
•
Displacement lists, plots, and extremes
•
Stresses lists, plots, and extremes
•
Strains lists, plots, and extremes
•
Output file contains displacement results and useful information on resources
used during analysis
•
Define secondary load cases through the
LCCOMB
(Results >
Combine Load
Case
) command
In
de
x
In
de
x
COSMOSFFE Static
3-1
3
Element Library
Introduction
This chapter lists the elements currently supported by COSMOSFFE Static. Most
of 2D and 3D continuum elements are programmed on the first and second order
hierarchical basis. The elements may be modeled in GEOSTAR as linear or
parabolic, but still the order used in the analysis is controlled by the flag in the
A_FFESTATIC
(Analysis > STATIC >
FFE Static Options
) command rather than
the name of the element group. As an example, you may define TETRA10 elements
in GEOSTAR but specify first order in the
A_FFESTATIC
command. In this case
the middle node information for elements on the boundary will still be used for the
geometry. Similarly, you may define TETRA4 elements in GEOSTAR but specify
second order in the
A_FFESTATIC
command.
Plane 2D Continuum Elements
•
First order (3-node) triangular plane stress elements (TRIANG)
•
Second order (6-node) triangular plane stress elements (TRIANG)
•
First order (3-node) triangular plane strain elements (TRIANG)
•
Second order (6-node) triangular plane strain elements (TRIANG)
•
First order (3-node) triangular axisymmetric elements (TRIANG)
•
Second order (6-node) triangular axisymmetric elements (TRIANG)
•
First order (4-node) quadratic plane stress elements (PLANE2D)
In
de
x
In
de
x

Chapter 3 Element Library
3-2
COSMOSFFE Static
•
Second order (8-node) quadratic plane stress elements (PLANE2D)
•
First order (4-node) quadratic plane strain elements (PLANE2D)
•
Second order (8-node) quadratic plane strain elements (PLANE2D)
•
First order (4-node) quadratic axisymmetric elements (PLANE2D)
•
Second order (8-node) quadratic axisymmetric elements (PLANE2D)
Continuum 3D Solid Elements
•
First order (8-node) hexahedral elements (SOLID)
•
Second order (20-node) hexahedral elements (SOLID)
•
First order (8-node) pentahedral elements (SOLID with a face collapsed to an
edge)
•
Second order (20-node) pentahedral prism-shaped elements (SOLID with a face
collapsed to an edge)
•
First order tetrahedral elements (TETRA4)
•
Second order tetrahedral elements (TETRA10)
Structural Elements
•
Two and three dimensional truss elements (TRUSS2D and TRUSS3D)
•
Three dimensional beam elements (BEAM3D)
•
First order triangular (3-node) shell elements (SHELL3)
•
First order quad (4-node) shell elements (SHELL4)
The elements given above are to be defined using the
EGROUP
(Propsets >
Element Group
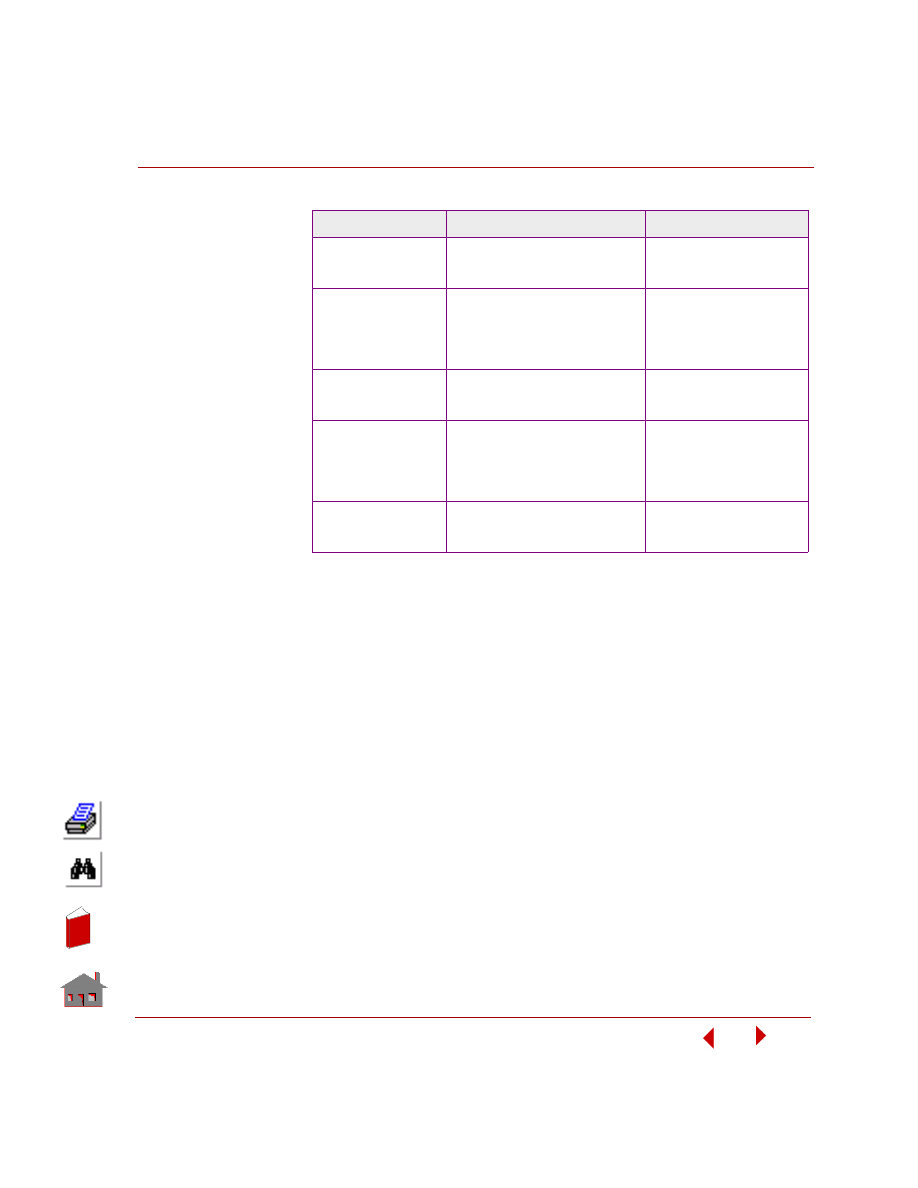
) command shown in the table below. Table 3-1 also lists other
commands for the manipulation of the associated element properties. These
commands can be issued by following the menu path given in Table 3-1 between
parenthesis.
In
de
x
In
de
x
COSMOSFFE Static
3-3
Chapter 3 Element Library
Table 3-1. Commands for Element Group Definition, Modification, and Listing
Every element has different analysis and modeling options (maximum of eight
entries), designated as OP1, …, OP8. When you execute the
EGROUP
command,
you are prompted for their input with sufficient physical interpretation for the
selected element.
✍
You can choose to perform the analysis with either first order or second order
elements in spite of the actual elements generated.
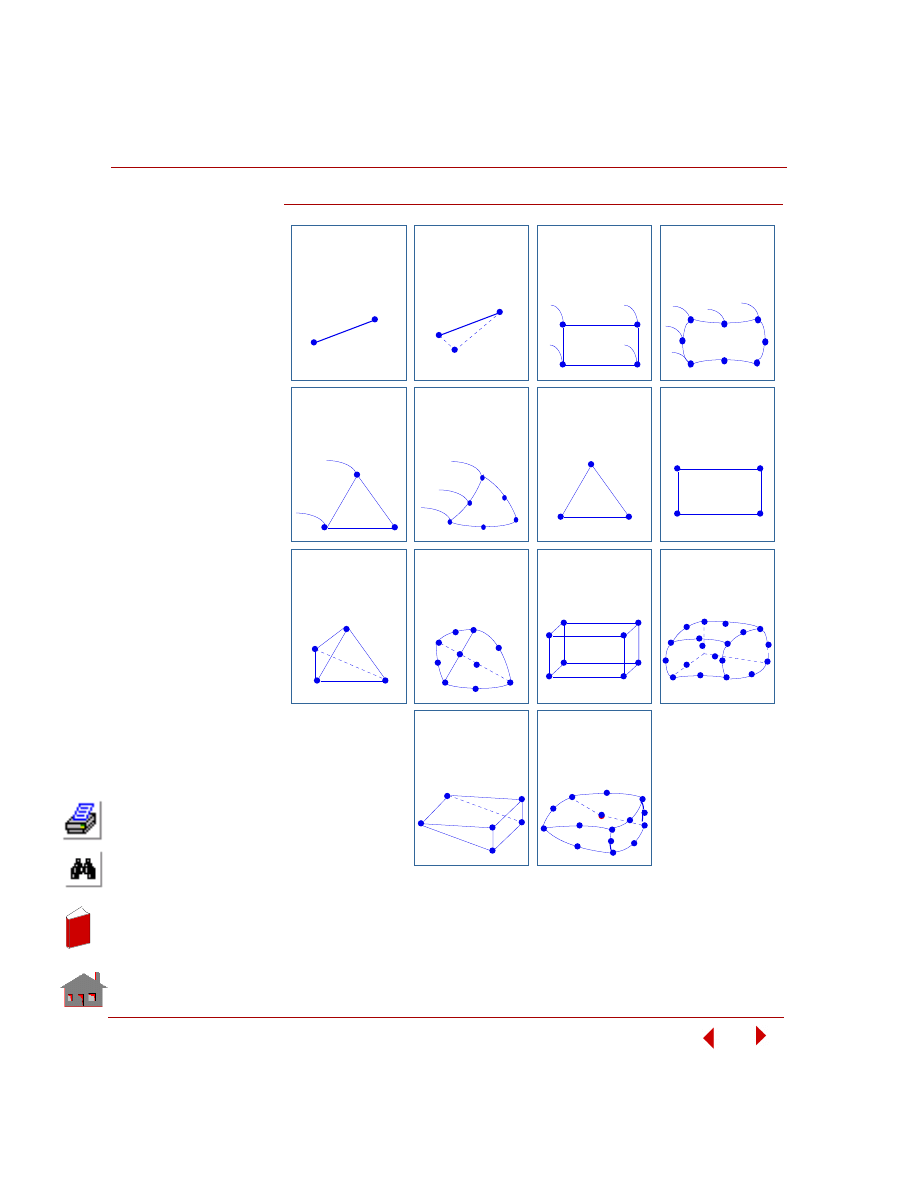
The following figure shows pictorial representations of all elements available in the
COSMOSFFE Static module. COSMOSM User Guide (Volume 1) presents a
detailed description of all elements in Chapter 4, Element Library.
The
RCONST
(Propsets >
Real Constant
) command should be used to specify the
cross-sectional dimensions of the element such as the thickness of SHELL3
element. Material properties may be specified using
MPROP
,
PICK_MAT
, or
R_MATLIB
(if the InfoDex Mil 5 material library options is available to you) found
in the Propsets menu.
Command
Function
Comments
EGROUP (Propsets >
Element Group)
Defines element groups and the
associated element analysis
options.
The maximum number of
element groups permitted in
a model is 20.
EPROPSET (Propsets
> New Property Set)
Assigns the existing element
group, material property, and real
constant groups as well as element
coordinate system to newly created
elements.
EPROPCHANGE
(Propsets > Change
El-Prop)
Changes the association between
element groups, real constants
sets, and material property sets.
EGLIST (Edit > LIST >
Element Groups)
Lists specified element groups and
the associated element analysis
options.
The on-screen listing can be
piped to a text file if desired,
using the LISTLOG (Control
> MISCELLANEOUS > List
Log) command.
EGDEL (Edit >
DELETE > Element
Groups)
Deletes specified element groups
and the associated element
analysis options.
In
de
x
In
de
x
Chapter 3 Element Library
3-4
COSMOSFFE Static
Figure 3-1. Supported Elements
4 - Node P la ne or
Ax is y mme t ric
Q ua drila t e ra l
Element: PLANE2D
Nodes: 4
8 - Node P la ne or
Ax is y mme t ric
Q ua drila t e ra l
Element: PLANE2D
Nodes: 8
3 - Node P la ne or
Ax is y mme t ric
Tria ngle
Element: TRIANG
Nodes: 3
6 - Node P la ne or
Ax is y mme t ric
Tria ngle
Element: TRIANG
Nodes: 6
3 - Node Thin
S he ll
Element: SHELL3
Nodes: 3
4 - Node S he ll
Element: SHELL4
Nodes: 4
4 - Node
Te t ra he dra l S olid
Element: TETRA4
Nodes: 4
1 0 - Node
Te t ra he dra l S olid
Element: TETRA10
Nodes: 10
8 - Node S olid
Element: SOLID
Nodes: 8
2 0 - Node S olid
Element: SOLID
Nodes: 20
Firs t O rde r
P ris m- S ha pe d S olid
Element: SOLID
Nodes: 8 with a face
collasping to
an edge
S e c ond O rde r
P ris m- S ha pe d S olid
Element: SOLID
Nodes: 20 with a face
collasping to
an edge
Trus s / S pa r
Element: TRUSS2D or
TRUSS3D
Nodes: 2
Be a m
Element: BEAM2D or
BEAM3D
Nodes: 2 or 3
In
de
x
In
de
x

COSMOSFFE Static
3-5
Chapter 3 Element Library
Top and Bottom Faces of Shell Elements
Only the mid surface of a shell element is shown in GEOSTAR. Each shell element
has a top and a bottom face determined by the order of the connectivity in the
element definition. Use the
ELIST
(Edit > LIST >
Elements
) command to list the
connectivity of elements. The direction of the thumb when using the right-hand rule
points to the direction of the top face.
Figure 3-2. Top and Bottom Faces of Shell Elements
Elements generated by meshing a surface will have their top face in the direction of
the outside normal of the surface determined by the right-hand rule. The direction
of the outer contour of a region is used to determine the top face of elements
generated by meshing regions. The
ACTMARK
(Control > ACTIVATE >
Entity
Mark
) command may be used to show the parametric directions of surfaces.
ACTMARK
may also be activated from the
STATUS1
table.
✍
Full integration is always used for the TRIANG, PLANE2D, SOLID, TETRA4,
and TETRA10 elements. The corresponding option in the element group
definition is ignored. Results from FFE Static should compare with results from
STAR when the full integration option is used.
S HE LL5
S HE LL4
S HE LL3
S HE LL3
1
3
2
Top face (Face 5) is
directed towards you.
Bottom face (Face 5) is
directed towards you.
Bottom face (Face 5) is
directed towards you.
Top face (Face 5) is
directed towards you.
1
2
3
3
4
2
1
3
2
4
1
In
de
x
In
de
x

3-6
COSMOSFFE Static
In
de
x
In
de
x
COSMOSFFE Static
4-1
4
Input Data
Introduction
Proper modeling and analysis specifications are crucial to the success of any finite
element analysis. Irrespective of the type of analysis, numerical solution using
finite element analysis requires complete information of the model under
consideration. The finite element model you submit for analysis must contain all
the necessary data for each step of numerical simulation - geometry, elements,
loads, boundary conditions, solution of system of equations, visualization and
output of results, etc. This chapter attempts to conceptually illustrate the procedure
for building a model for analysis in the COSMOSFFE Static module.
The COSMOSM User Guide (Volume 1) presents in-depth information on the pre-
and postprocessing procedures in GEOSTAR. This chapter therefore will not repeat
the information here but will offer a brief overview of those commands which are
relevant to the COSMOSM FFE Static module.
For a detailed description of all commands, refer to the on-line help, accessed by
pressing the left button of the mouse on the Help icon shown in the command
dialog box, or refer to the COSMOSM Command Reference Manual (Volume 2).
In
de
x
In
de
x

Chapter 4 Input Data
4-2
COSMOSFFE Static
Modeling and Analysis Cycle in the
COSMOSFFE Static Module
The basic steps involved in a finite element analysis are:
1. Create the problem geometry.
2. Define the appropriate element group.
3. Define material properties.
4. Define real constants for truss, beam, plane stress and shell elements.
5. Mesh the desired part of geometry with appropriate type of elements.
6. Repeat steps 2 through 5 as desired if needed.
7. Merge coinciding nodes along the common boundaries of different geometric
entities using the
NMERGE
(Meshing > NODES >
Merge
) command.
8. Apply constraints on the finite element model.
9. Define the loads on the model.
10. If multiple load cases are desired, use the
ACTSET, LC
(Control > ACTIVATE >
Set Entity
) command and define load cases as desired.
11. Use the
A_FFESTATIC
(Analysis > STATIC >
FFE Static Options
) command
to specify desired options including special loading and element order.
12. Submit the completed finite element model for analysis using the
R_STATIC
(Analysis > STATIC >
Run Static Analysis
) command.
13. Use the Results menu to postprocess the results. Results may be displayed in
text or graphical formats. Use the
LISTLOG
(Control > MISCELLANEOUS >
List Log
) command to pipe list screens to a file.
In
de
x
In
de
x
COSMOSFFE Static
4-3
Chapter 4 Input Data
✍
R_STATIC
runs either STAR or FFE Static. The following two factors determine
which one will run: 1) If you have not issued the
A_STATIC
nor the
A_FFESTATIC
commands,
R_STATIC
will run STAR. 2) If both of the two commands have been
issued, the later one will determine which code to run. STAR will run if
A_STATIC
has been issued later, and
FFE Static if
A_FFESTATIC
has been issued
later. 3) If only one of the two commands has been issued, then STAR will run if
A_STATIC
has been issued, or FFE Static if
A_FFESTATIC
has been issued later.
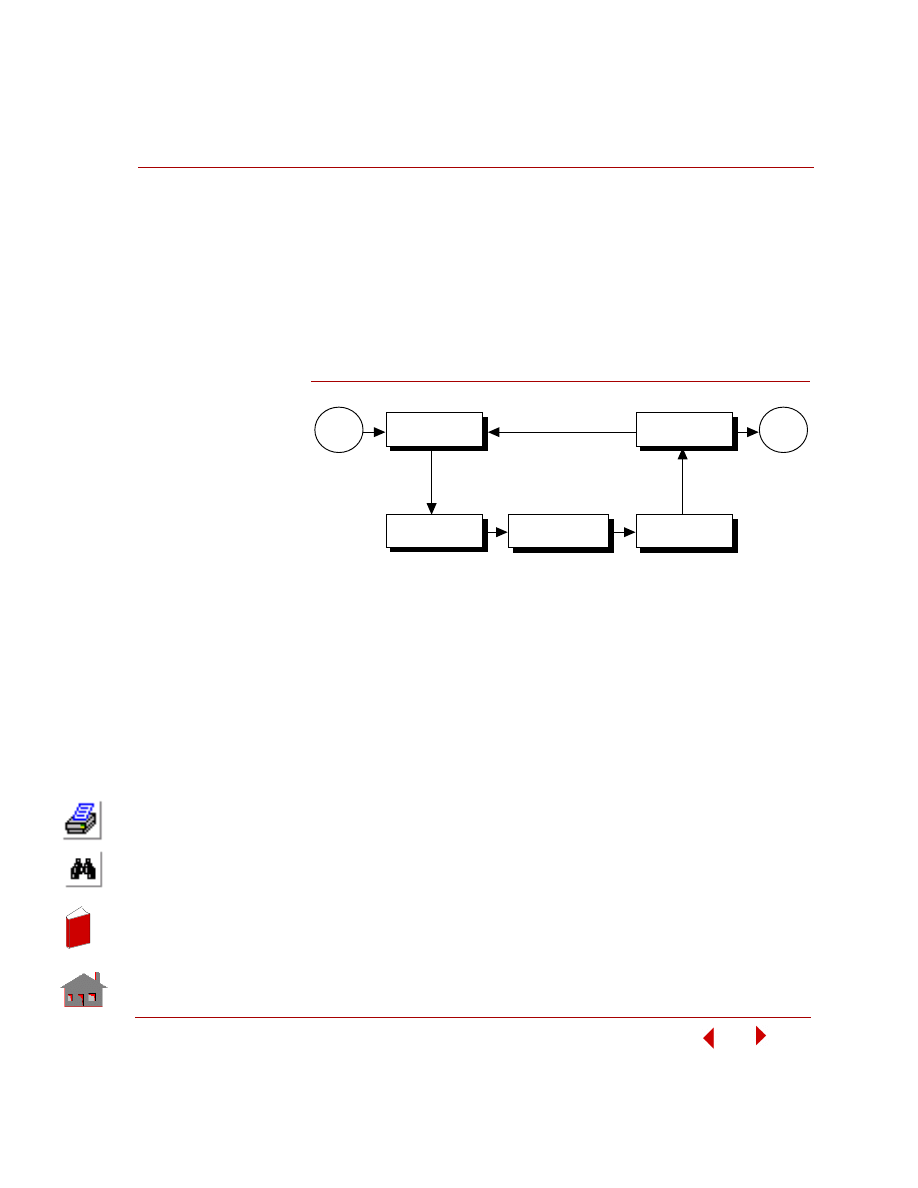
These steps can be schematically represented as shown in the figure below.
Figure 4-1. Finite Element Modeling and Analysis Steps
Preprocessing refers to the operations you perform prior to submitting the model
for analysis. Such operations include defining the model geometry, mesh
generation, applying loads and boundary conditions, and other information needed.
The term analysis in the above figure refers to the phase of specifying the analysis
options and executing the actual analysis. Postprocessing refers to the manipulation
of the analysis results for easy understanding and interpretation in a graphical
environment.
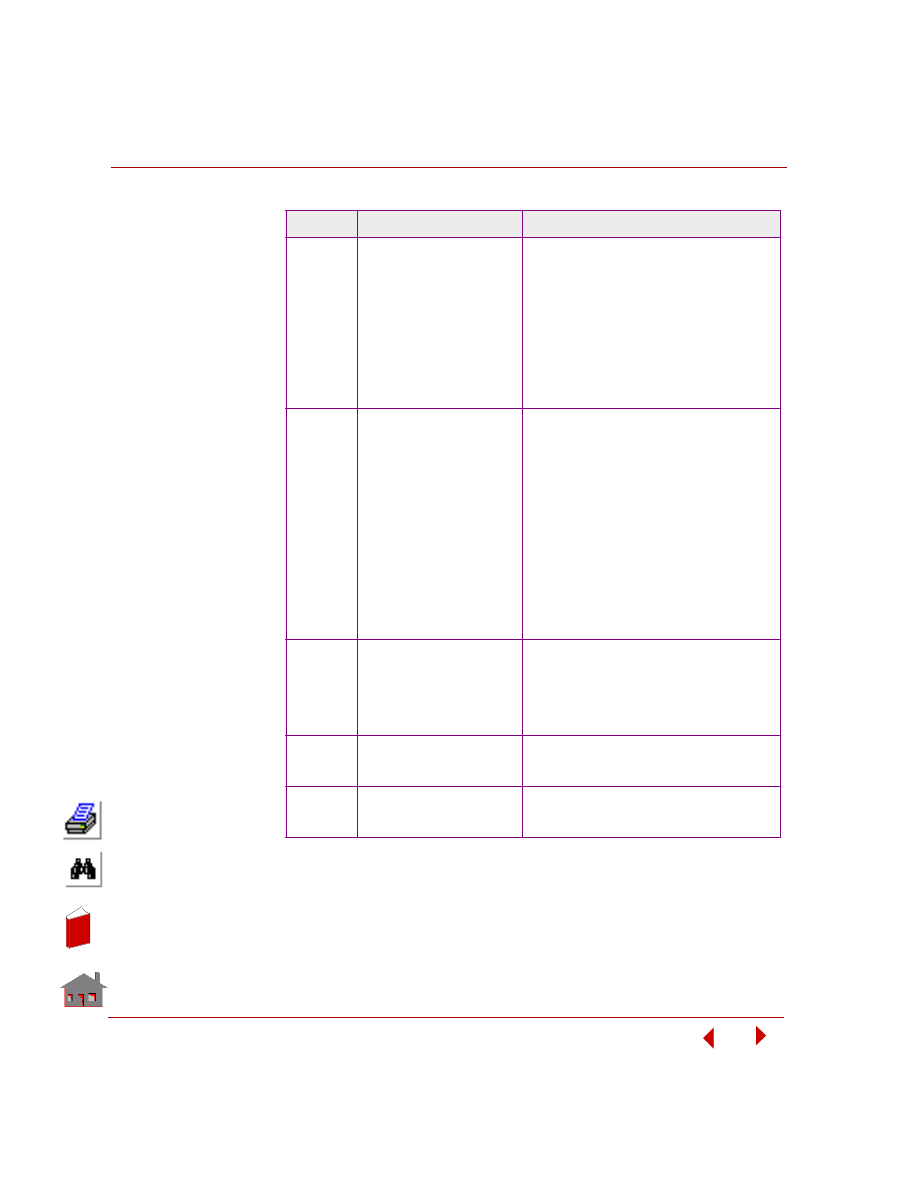
The commands summarized in the table below provide you with information on the
input of element groups, material properties, loads and boundary conditions,
analysis options, and out-put specifications.
START
PREPROCESSING
POSTPROCESSING
STOP
Analysis and
Design Decisions
Problem Definition
ANALYSIS
In
de
x
In
de
x
Chapter 4 Input Data
4-4
COSMOSFFE Static
Table 4-1. Commands for FFE Static Analysis
Function
Using COSMOSM Menu
Typing the Command
Property
Definition
Propsets
> Element Group
> Material Property
> Real Constant
> Pick Material Lib
> User Material Lib
> Material Browser
> AISC Sect Table
> Change El-Prop
> New Property Set
> Beam Section
. . .
EGROUP
MPROP
RCONST
PICK_MAT
USER_MAT
R_MATLIB
PICK_SEC
EPROPCHANGE
EPROPSET
BMSECDEF
Loads and
Boundary
Conditions
LoadsBC
> STRUCTURAL
> DISPLACEMENT
> FORCE
> PRESSURE
> GRAVITY
> THERMAL
> TEMPERATURE
> LOAD OPTIONS
> Read Temp as Load
. . .
. . .
D_ commands for prescribed displacements
*
F_ commands for nodal forces
*
P_ commands for element pressure
*
Commands for gravity and centrifugal forces:
ACEL, OMEGA, DOMEGA, CGOMEGA,
DCGOMEGA, CGLOC, GRVLIST
. . .
NT_ commands for nodal temperatures
*
(thermal loading)
. . .
TEMPREAD command to read temperatures
for thermal loading from subsequent transient
thermal analysis
Model
Verification
Meshing
> ELEMENTS
> Check Element
Analysis
> Data Check
> Run Check
. . .
. . .
E_CHECK
. . .
DATA_CHECK
R_CHECK
Specifying
Analysis
Options
Analysis
> STATIC
> FFE Static Options
. . .
. . .
A_FFESTATIC
Executing
Static
Analysis
Analysis
> STATIC
> Run Static Analysis
. . .
. . .
R_STATIC
In
de
x
In
de
x
COSMOSFFE Static
4-5
Chapter 4 Input Data
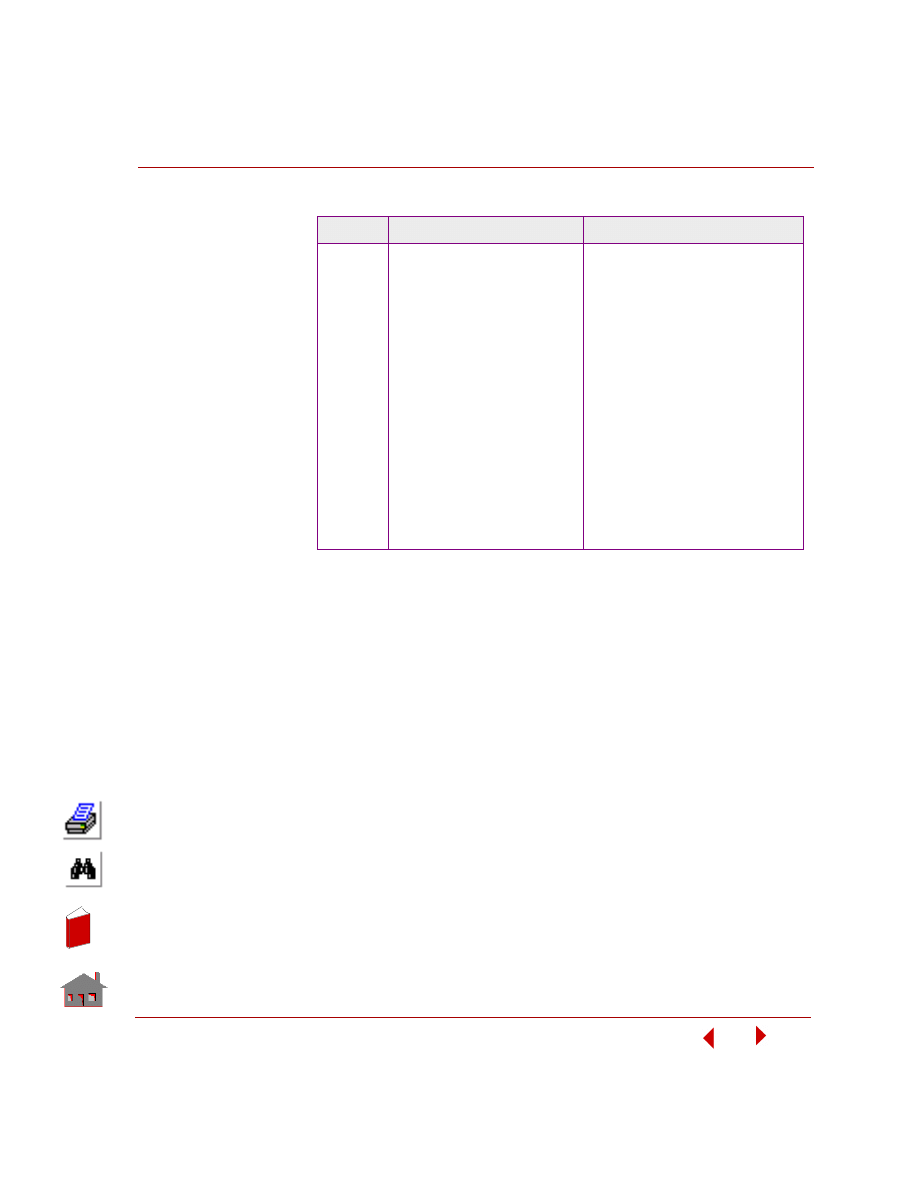
Table 4-1. Commands for FFE Static Analysis (Concluded
Special Loading
Thermal, gravitational, and centrifugal loading are referred to as special loading in
COSMOSM literature. Consideration of special loading must be specified by the
A_FFESTATIC
(Analysis > STATIC >
FFE Static Options
) command before
running the analysis. Gravity and centrifugal loading may be specified for all load
cases.
For gravity loading, a value for the acceleration of gravity must be specified for
every load case (while the load case is active) whenever gravity loading is to be
considered. The mass density of the material(s) must also be specified so that it can
be used to calculate the gravity forces.
Function
Using COSMOSM Menu
Typing the Command
Post-
processing
Results
> Combine Load Case
> PLOT
> Deformed Shape
> Stress
> Strain
> Displacement
> Shear Diagram
> LIST
> Displacement
> Stress Component
> Strain Component
> Shear/Moment Value
> Beam End Force
> EXTREMES
> Min/Max Displacement
> Min/Max Stress
> Min/Max Strain
> Shear/Moment
> Beam End Force
. . .
LCCOMB
. . .
DEFPLOT
ACTSTRS + STRPLOT
ACTSTN + STNPLOT
ACTDIS + DISPLOT
SMPLOT
. . .
DISLIST
STRLIST
STNLIST
SMLIST
BEAMRESLIST
. . .
DISMAX
STRMAX
STNMAX
SMMAX
BEAMRESMAX
*
See Command Reference Manual or the on-line help
for more details about the command
In
de
x
In
de
x

Chapter 4 Input Data
4-6
COSMOSFFE Static
For centrifugal loading, values for angular velocity and/or accelerations should be
specified for every load case (while the load case is active) whenever centrifugal
loading is to be considered. The mass density of the material(s) must also be
specified so that it can be used to calculate the centrifugal forces.
Thermal Stress Analysis
Thermal stress analysis may be performed by directly specifying the nodal
temperatures, or by reading the temperature profile from a preceded thermal
analysis.
Thermal Stress Analysis by Specifying Temperatures
To specify the nodal temperatures, use commands like
NTND
,
NTPT
,
NTCR
,
NTSF
, ... etc., in the LoadsBC > THERMAL menu to define the temperatures
directly. Activate the thermal loading flag in the
A_FFESTATIC
(Analysis >
STATIC >
FFE
Static Options
) command and run the analysis. Do not forget to
specify the coefficient of thermal expansion(s) for the material(s) used in the
model. In COSMOSM, different set of temperatures may be specified for different
load cases and thermal loading may be considered in all load cases.
Thermal Stress Analysis Using Results from Thermal Analysis
Once a thermal analysis is completed, resulting temperature distribution can be
used to calculate thermal stresses in the material. The following steps can be used to
calculate thermal stresses.
•
Complete the thermal analysis
•
Activate the thermal loading using the
A_FFESTATIC
(Analysis > STATIC >
FFE Static Options
) command
•
If you have performed transient analysis, use the
TEMPREAD
(LoadsBC >
LOAD OPTIONS >
Read Temp as Load
) command to specify the time step at
which thermal stress analysis is to be done
•
Run the static analysis using the
R_STATIC
(Analysis > STATIC >
Run Static
Analysis
) command
•
The change of temperature is calculated at each node by subtracting the offset
temperature, defined by the
TREF
(LoadsBC > LOAD OPTIONS >
Reference
Temp
) command, from the temperature profile obtained from the thermal
analysis.
In
de
x
In
de
x

COSMOSFFE Static
4-7
Chapter 4 Input Data
•
If temperatures were defined as boundary conditions for a heat transfer analysis,
then these temperatures are ignored if the “problem-name.HTO” file for the
current problem exists in the database. If no HTO file exists however, then the
specified temperatures are used as thermal loading to calculate the
corresponding static analysis results. The HTO file is the file in which
temperature results from thermal analysis are stored.
Static Analysis Options
The
A_FFESTATIC
command is used to specify several static analysis options to be
used for subsequent analysis using the
A_FFESTATIC
command. The syntax and
help for the
A_FFESTATIC
and
R_STATIC
commands are given below.
The A_FFESTATIC Command
Geo Panel: Analysis > STATIC > FFE Static Options
The
A_FFESTATIC
command specifies analysis options for linear static analysis
using the FFE Static module. Note that the
A_STATIC
command specifies analysis
options for linear static analysis using the STAR module. The most recently issued
command out of the two commands (
A_STATIC
and
A_FFESTATIC
) determines
whether the
R_STATIC
command will run STAR or FFE Static. The default is to
run STAR.
Entry & Option Description
element-order
Order of the element to be used. In spite of the element group name in the data-
base, you may specify through this option whether first (linear) or second (para-
bolic) elements will be used. As an example, if you define TETRA4 elements
and use second order, middle nodes on straight edges will be considered during
analysis. On the other hand you may define TETRA10 elements and specify to
use first order. SOLID elements are treated similarly except that for these ele-
ments the same element group names are used for both first and second orders.
0
use first order for continuum elements.
1
use second order for continuum elements.
(default is 1)
special-loading
Special loading flag. Any one character can be assigned. Two or three characters
can be assigned in any combination of C, G and T.
In
de
x
In
de
x

Chapter 4 Input Data
4-8
COSMOSFFE Static
N
do not include special loading.
include
centrifugal
loading.
G
include gravity loading.
T
include thermal loading.
(default is N)
rigid connections flag
This flag controls the continuity between solid and shell or beam elements
connected to each other. Solid elements like TETRA4, TETRA10), and SOLID
do not have explicit rotational degrees of freedom (DOF). Rotations of solid
elements can be expressed in terms of the translational DOF. Beam and shell
elements on the other hand have explicit rotational DOF.
Traditionally, you need to introduce some coupling constraints when connecting
such incompatible elements to ensure continuity. This flag, when active, takes
care of this condition automatically and rigid connections between all such
incompatible elements in the model are assumed.
When you want to specify hinge connections or you need to compare
COSMOSFFE results to results from traditional finite element systems which
assume hinge connections between solid and shell or beam elements, you must
turn this flag off before running the analysis.
YES; activate
rigid
connections.
NO;
deactivate rigid connections.
(default is YES)
The R_STATIC Command
Geo Panel: Analysis > STATIC > Run Static Analysis
The
R_STATIC
command performs linear static analysis. The command runs FFE
Static if the
A_FFESTATIC
command has been issued and was not followed by the
A_STATIC
command. On the other hand, the command runs STAR module if the
A_FFESTATIC
command has not been issued or was issued but followed by the
A_STATIC
command. Upon a successful run, the command automatically
calculates strains and stresses in addition to displacements unless the STAR module
was used and the
STRESS
(Analysis > STATIC >
Stress Analysis Options
)
command has been used to turn off stress calculations in which case the
R_STRESS
(Analysis > STATIC >
Run Stress Analysis
) command may be used
later to calculate stresses.
In
de
x
In
de
x

COSMOSFFE Static
4-9
Chapter 4 Input Data
Notes:
1. Use flags specified by the
A_STATIC
command or the
A_FFESTATIC
command.
2. Recommended steps for performing analysis:
a. Create the model.
b. Plot, list and examine the model.
c. Execute the
R_CHECK
(Analysis >
Run Check
) command to check input
data.
d. Issue the
A_FFESTATIC
(Analysis > STATIC >
FFE Static Options
)
command to specify the element order and specify special loading flags or the
A_STATIC
(Analysis > STATIC >
Static Analysis Options
) command to
specify STAR options. Use equivalent commands for other types of analyses.
e. Issue the
R_STATIC
(Analysis > STATIC >
Run Static Analysis
) command
to perform linear static analysis. Use the equivalent command for other types
of analyses.
f. If the run is not successful, a clear message will be given. For FFE messages,
refer to Appendix A of this manual for explaining and fixing the problem. The
message is also written to the output file (extension OUT).
3. The command will calculate displacements and stresses for all load cases set to
run. Use the
LCCOMB
(Results >
Combine Load Case
) command to define
secondary load cases.
4. The command will calculate displacements and stresses for all load cases set to
run.
5. If H_method adaptive meshing is specified, the
R_STATIC
command will
progressively repeat the analysis as instructed by the
ADAPTIVE
(Analysis >
STATIC >
Adaptive Method
) command if STAR is used.
✍
FFE Static always calculates stresses and ignores the flag controlled by the
STRESS
command for the option to calculate or not calculate stresses when
STAR is used.
✍
All stresses are calculated in the global directions. The
STRLIST
(Results > LIST
>
Stress Component
) and
ACTSTR
(Results > PLOT >
Stress
) commands will
prompt you for a coordinate system to be used for listing and plotting during
postprocessing.
✍
Stresses are not written to the output file. Use the
LISTLOG
(Control >
MISCELLANEOUS >
List Log
) and
STRLIST
commands to redirect stress
results to a file.
In
de
x
In
de
x
Chapter 4 Input Data
4-10
COSMOSFFE Static
Postprocessing
An output file problem-name.OUT is generated by FFE Static. The file is an ASCII
file that can be viewed and edited as desired. The results in the database can be
viewed in both text and graphical formats in GEOSTAR. The following table gives
a brief description of the postprocessing commands related to FFE Static.
Table 4-2. Postprocessing Commands Related to FFE Static
Verification of Model Input Data
One of the difficulties you may come across in the solution is avoiding errors in the
model input data. Some of the errors can be detected by plotting the model in
various views, listing the elements, nodes, element groups, material properties and
real constant sets. Plotting or listing loads and constraints, and many other on-line
tools. For small problems, it is often easier to perform these checks to see if all
required input data have been properly generated and defined. However, you may
still miss some errors that are not easily identifiable. For these types of situations
and also for larger problems, it is plausible to perform model checks in an
automated environment.
Command
*
Description
DEFPLOT
DISLIST
DISMAX
STRLIST
STRMAX
STNLIST
STNMAX
SMLIST
SMMAX
BEAMRESLIST
BEAMRESMAX
ACTDIS
DISPLOT
ACTSTN
STNPLOT
ACTSTR
STRPLOT
SMPLOT
SETPLOT
LCCOMB
LISTLOG
Plots the deformed shape
Lists displacements
Searches for extreme displacement values
Lists stresses
Searches for extreme stress values
Lists strains
Searches for extreme strain values
Lists shear and moment for beam element
Searches for extreme shear and moment values
Lists beam element forces
Searches for extreme beam element results
Activates a displacement component for plotting
Plots the activated displacement component
Activates a strain component for plotting
Plots the activated strain component
Activates a stress component for plotting
Plots the activated stress component
Plots shear and moment diagrams for beam elements
Sets color set, range, and scale values for all plots
Creates secondary load cases
Can be used to pipe the list screens to a file
*
See Table 4-1 for the menu path
In
de
x
In
de
x

COSMOSFFE Static
4-11
Chapter 4 Input Data
The
R_CHECK
(Analysis >
Run Check
) command performs rigorous checks on
the validity, compatibility, and completeness of the input data and gives messages
for any warnings and errors encountered. The
ECHECK
(Meshing > ELEMENTS >
Check Element
) performs a quick check on the elements in the model and deletes
any degenerate elements.
You are strongly recommended to run the checking program using the
R_CHECK
command and fix all errors before performing submitting the model to analysis.
Note that the
R_CHECK
command is a general model verification tool. You may
still find some errors that are not trapped by the use of this command. In most cases,
the diagnostic messages either printed on the screen or written to an ASCII file
(problem_name.CHK) provide further information as to the nature of errors and
their remedies. In addition, the FFE Static module will give you clear messages if
any problems are encountered during the analysis process. Refer to Appendix A for
more information about error messages.
In
de
x
In
de
x

4-12
COSMOSFFE Static
In
de
x
In
de
x
COSMOSFFE Static
5-1
5
Examples
Introduction
This chapter presents step-by-step examples for performing linear static analysis
using the FFE Static module. The examples discussed in this chapter are large size
practical problems that demonstrate the savings in time and resources when using
FFE Static compared to using the conventional solvers. Chapter 6 includes a
number of small size problems that demonstrate most of the capabilities of FFE
Static and that are suitable for verification purposes and academic studies.
The input files for the examples in this chapter and the verification problems in
Chapter 6 are available in PROBS subdirectory of your COSMOSM directory. The
names of the input files are FFESX1.GEO, FFESX2.GEO, and FFESX3.GEO for
examples 1, 2, and 3 respectively.
In order to run an example, follow the following steps:
•
Create a new working directory,
•
Copy the input file to the new working directory,
•
Launch GEOSTAR,
•
Choose a new problem name while you are inside GEOSTAR,
•
Read the input file using the
FILE
(File >
Load...
) command,
•
Follow the instructions given in the following sections.
In
de
x
In
de
x
Chapter 5 Examples
5-2
COSMOSFFE Static
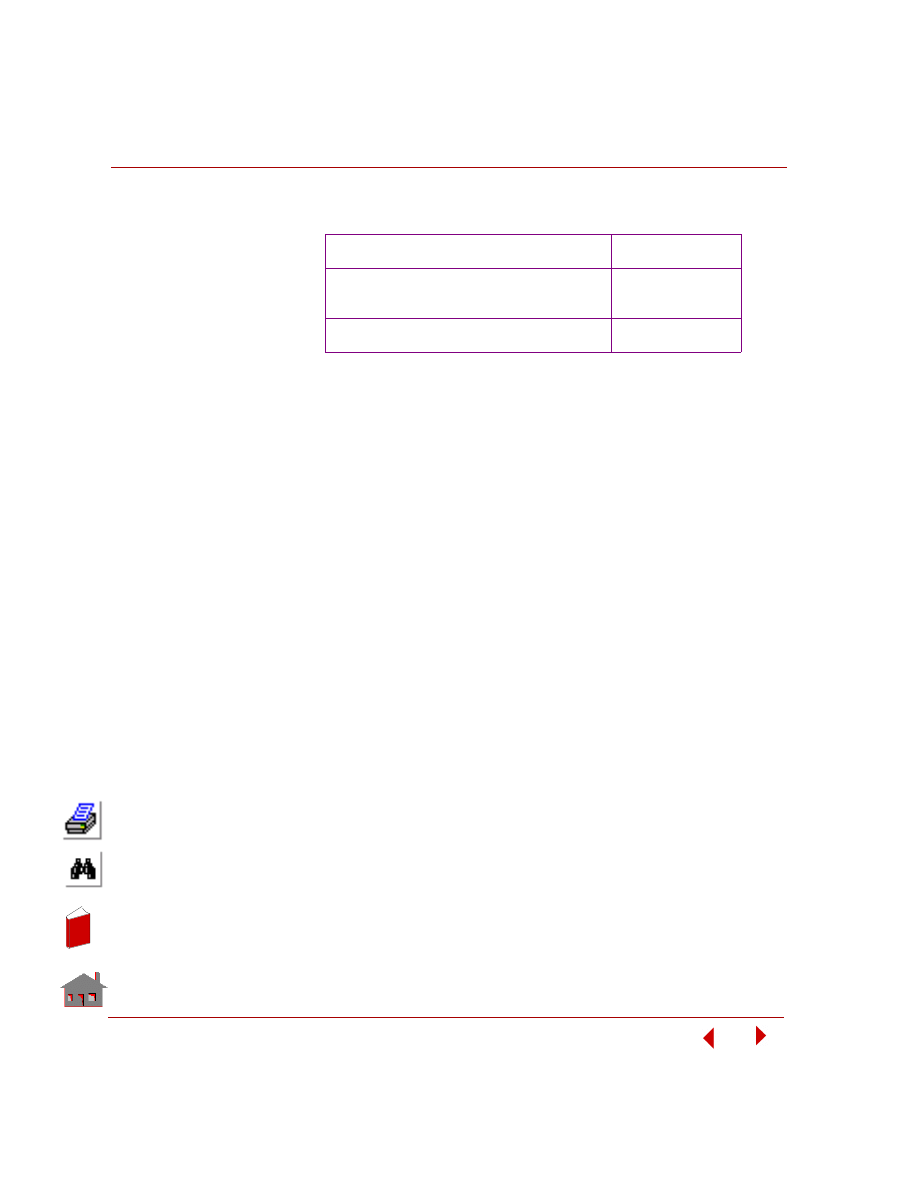
Table 5-1. List of Static Examples
1 - Analysis of an Engine Bearing Cap
2 - Analysis of a Column Connection Bracket
Using Shell Elements
3 - A Model Fan
In
de
x
In
de
x
COSMOSFFE Static
5-3
Chapter 5 Examples
Model Information
Length Units:
Millimeters (mm)
Force Units:
Newtons (N)
Pressure Units:
N/mm
2
Element Type:
Tetrahedral
Element Order:
Second
Number of Elements:
2700
Number of Corner Nodes:
853
Number of Degrees of Freedom:
15,393
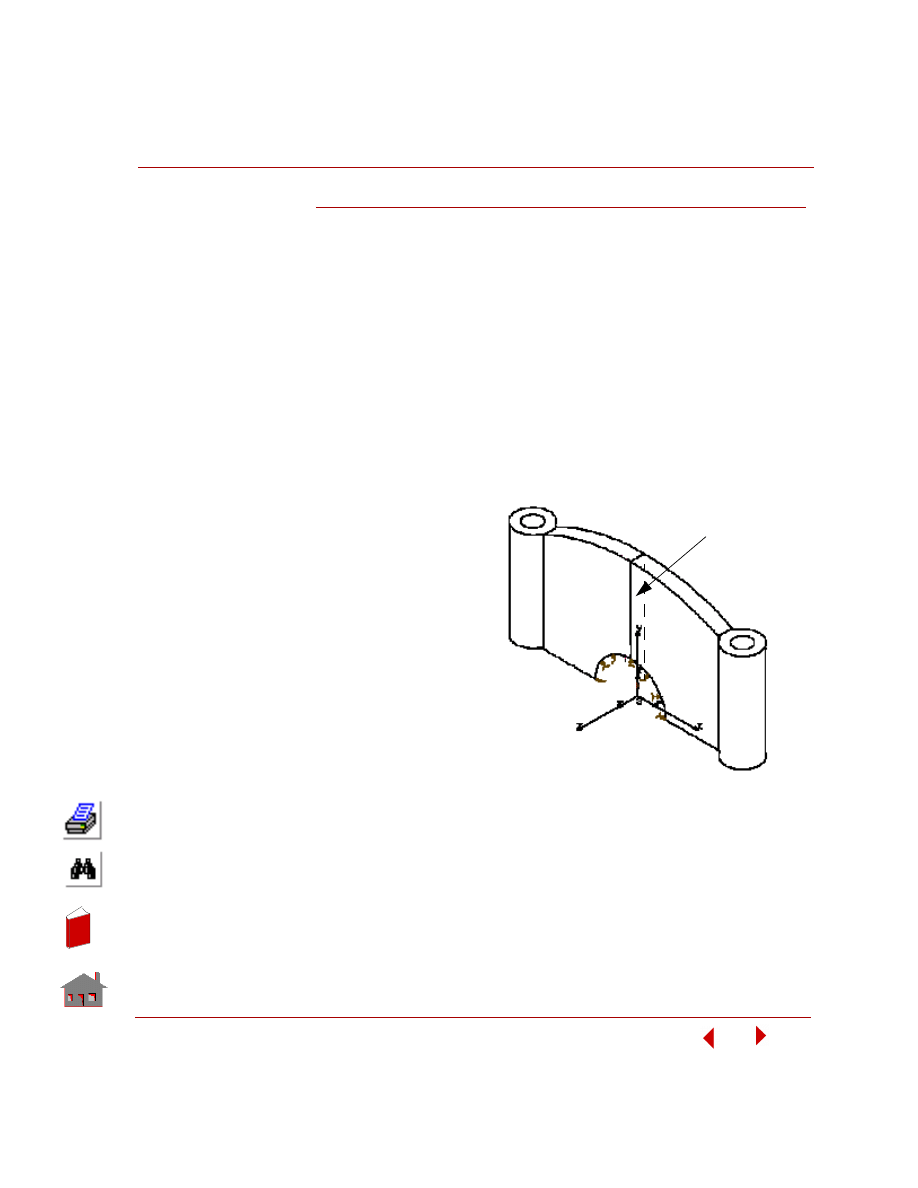
The bearing cap shown in
the figure below is
subjected to loads and
boundary conditions as
shown. Due to symmetry,
only one half of the
model need to be
modeled. It is very
important when modeling
only a portion of the
actual model due to
symmetry, to specify the
proper boundary
conditions for the
modeled portion along its
interface with the other
symmetrical portions. It is
obvious in this case that
the Y-Z plane of
symmetry should not
move in the global X-direction. GEOSTAR provides you with convenient options to
specify symmetrical and asymmetrical boundary conditions (refer to the on-line
help for the
DND
(LoadsBC > STRUCTURAL > DISPLACEMENT >
Define
Nodes
) command). Note, however, that rotational degrees of freedom are not
considered by tetrahedral elements and the preprocessor will fix them
automatically.
Example 1 – Analysis of an Engine Bearing Cap
Figure 5-1. Full Model of Engine Bearing Cap
Plane of Symmetry
Radially
constrained
pressure
pressure
In
de
x
In
de
x

Chapter 5 Examples
5-4
COSMOSFFE Static
The file needed to create the geometry is called FFESX1.GEO and may be retrieved
from the PROBS subdirectory in your COSMOSM directory. The file is also listed
below for convenience. Use the
FILE
(File >
Load...
) command to read in the
FFESX1.GEO file, or you may choose to follow the commands and construct the
database step-by-step by following the commands below. In case of constructing
the model step-by-step, the user is referred to the Command Reference Manual or
the On-line help for information about the menu path required to issue the given
command. Note that the model maybe alternatively be created by extruding the
circular ring in the Y-direction and extruding a face of the web in the Z-direction.
List of the FFESX1.GEO File
TITLE, ENGINE BEARING CAP
PLANE,Y,0,1,
PT,1,75,0,0,
PT,2,0,0,0,
CRPCIRCLE,1,1,2,6,360,4,
CRPCIRCLE,5,1,2,12,360,6,
PT,13,25,0,5,
PT,14,25,0,-5,
CREXTR,13,14,1,X,44,
CRINTCC,11,5,5,1,2,0.00005,
CRDEL,5,14,9,
CRINTCC,12,10,10,1,2,0.00005,
CRDEL,14,15,1,
CRFILLET,14,13,11,2.696,1,0,1E-006,
CRFILLET,15,10,12,2.696,1,0,1E-006,
CRLINE,16,21,24,
CT,1,0,5,1,4,0,
CT,2,0,5,9,16,14,13,6,7,8,9,10,15,0,
RG,1,2,2,1,0,
SFEXTR,1,10,1,Y,70,
SFEXTR,13,16,1,Y,70,
RGGEN,1,1,1,1,0,0,70,0,
PT,38,0,0,5,
PLANE,Z,5,1,
CRPCIRCLE,43,38,13,25,90,1,
PT,40,62.4803,70,5,
PT,41,0,85,5,
PT,42,0,-52.62607,5,
CRARCCPT,44,36,41,42,
CRLINE,45,39,41,
CRDEL,12,12,1,
SCALE,0,
SFDEL,13,13,1,
SFEXTR,11,11,1,Z,-10,
SFEXTR,43,45,1,Z,-10,
CT,5,0,6,5,11,43,45,44,39,0,
RG,3,1,5,0,
RGGEN,1,3,3,1,0,0,0,-10,
RGSF,1,16,1,6,
UNSELINP,SF,1,16,1,1,
PH,1,RG,1,6,0.0001,1,
PART,1,1,
RGDENS,2,18,16,3,0,0001,1,
EGROUP,1,TETRA4,0,1,0,0,0,0,0,
MPROP,1,EX,200000,NUXY,0.3,
MA_PART,1,1,1,1,0,4,
CSANGLE,3,1,0,0,0,0,0,0,0,
DRG,18,UX,0,18,1,UZ
ACTSET,CS,0,
DRG,20,UX,0,20,1,UZ,
PRG,6,5,6,1,5,1,
PRG,2,50,2,1,50,4
HIDDEN;
EPLOT;
In
de
x
In
de
x

COSMOSFFE Static
5-5
Chapter 5 Examples
Running Analysis
Now the model has been created, we are ready to specify analysis options and run
the analysis, choose:
Geo Panel: Analysis > STATIC >
FFE Static Options (A_FFESTATIC)
Element Order 1=First 2=Second [2] >
Loading Flag [N] >
Accept entries
✍
It is always recommended to use the
second order option for more accurate
solutions.
The default flag for special loading is
accepted. If special loading effects are to be
considered, then the proper combination of T
(thermal loading), G (gravitational loading),
and C (centrifugal loading) should be
specified.
Next, run the analysis, choose:
Geo Panel: Analysis > STATIC >
Run Static Analysis (R_STATIC)
GEOSTAR screen will disappear and the
FFE Static screen will show up after the
message “Writing Static Analysis File!”. The
FFE Static screen shows the version and date
at the top, model name and size information in the middle, the current stage of
solution and a bar representing its progress at the bottom. Elapsed time since the
process has been started is shown at the lower right corner. If multiple load cases
exist, the current load case that FFE Static is solving for, will be also shown. After
loading the database, the solution for each load case will go through building the
stiffness matrix, calculating displacements by solving the resulting equations, and
finally calculating strains and stresses. After finishing the analysis, FFE Static gives
control to GEOSTAR to continue with postprocessing.
Figure 5-2. Meshed Model of
Engine Bearing Cap
In
de
x
In
de
x

Chapter 5 Examples
5-6
COSMOSFFE Static
Postprocessing
All postprocessing commands are included in the Results menu. In many cases, you
will get nicer plots if you suppress plotting element edges which may be done
through the
BOUNDARY
(Display > DISPLAY OPTION >
Set Bound Plot
)
command. Better plots can be obtained by evaluating the edges of the model. Edge
evaluation may be used even in cases where geometric entities are not present in the
model. To activate edge evaluation, choose:
Geo Panel: Display > DISPLAY OPTION >
Eval Element Bound
(EVAL_BOUND)
Boundary face evaluation flag [No] >
Boundary edge evaluation flag [No] >
Yes
Tolerance angle to ignore curvature [20] >
60
Accept entries
Generate four windows for postprocessing using
WCREATE
(Geo Panel:
New Win
)
command. You may need to adjust or relocate the newly created windows for your
convenience. To activate one of these windows, click on the window using the left
button of the mouse.
Animation of Deformed Shape
Activate the element shading using the
SHADE
(Display > DISPLAY OPTION >
Shaded Element Plot
) command and accept all default entries.
Animate the deformed shaded shape in window 1, choose:
Geo Panel: Display > DISPLAY OPTION >
Animate (ANIMATE)
Load Case [1] >
1
Animation type 0=one-way 1=two-way [1] >
Delay number [0] >
Accept entries
✍
You may delay the animation speed using a large delay factor and/or larger
window. Use default value for the delay factor and a smaller window to animate
faster. An instance in the animation is shown in the figure below.
In
de
x
In
de
x
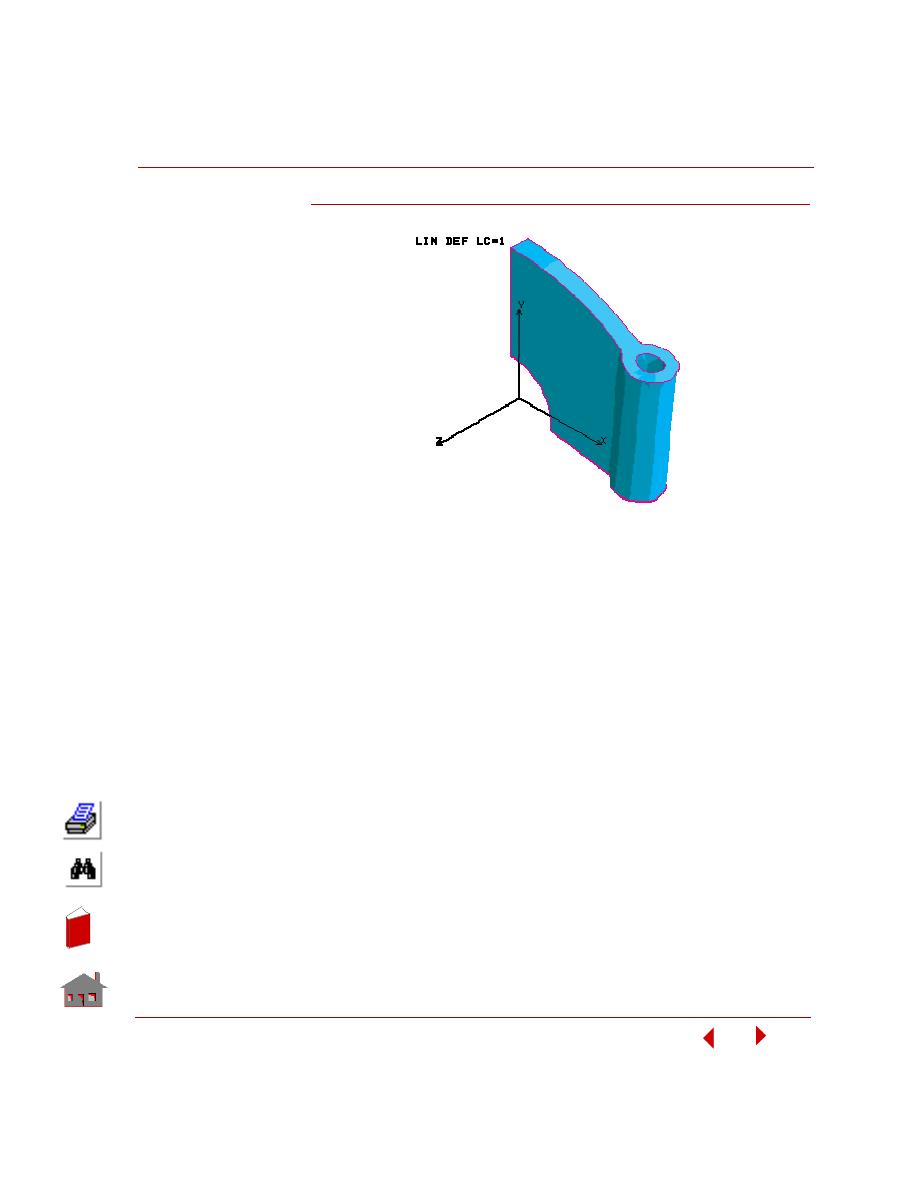
COSMOSFFE Static
5-7
Chapter 5 Examples
Figure 5-3. Deflected Shape
Displacement Contours
Displacement contours may be generated on undeformed or deformed geometry.
Activate window 2 and plot the resultant displacement contour by choosing:
Geo Panel: Results > PLOT >
Displacement (DISPLOT)
Load case number [1] >
Component [URES] >
Coordinate system [0] >
Click on Contour icon
Plot type 0=Fill 1=Line 2=Vect [0] >
Beginning element [1] >
Ending Element [2700] >
Increment [1] >
Shape flag >
Deformed shape
Scale Factor [277.346] >
Accept entries
The generated displacement contour is plotted in the figure below. Use the
ANIMATE
command again to animate the displacement contour on the deformed
shape. You may need to resize the window to see the color code bar.
In
de
x
In
de
x

Chapter 5 Examples
5-8
COSMOSFFE Static
Figure 5-4. Displacement Contour Plot
Element Strain
Activate window 3 and plot the element strain contour, choose
Geo Panel: Results > PLOT >
Strain (STNPLOT)
Load case number [1] >
1
Component [ESTRN] >
Layer number [1] >
(used only for composite elements)
Face flag 0=Top [0] >
Coordinate system [0] >
Click on Contour icon
Plot Type >
Color_filled contour
Beginning element [1] >
Ending [2700] >
Increment [1] >
Shape flag >
Undeformed shape
In
de
x
In
de
x
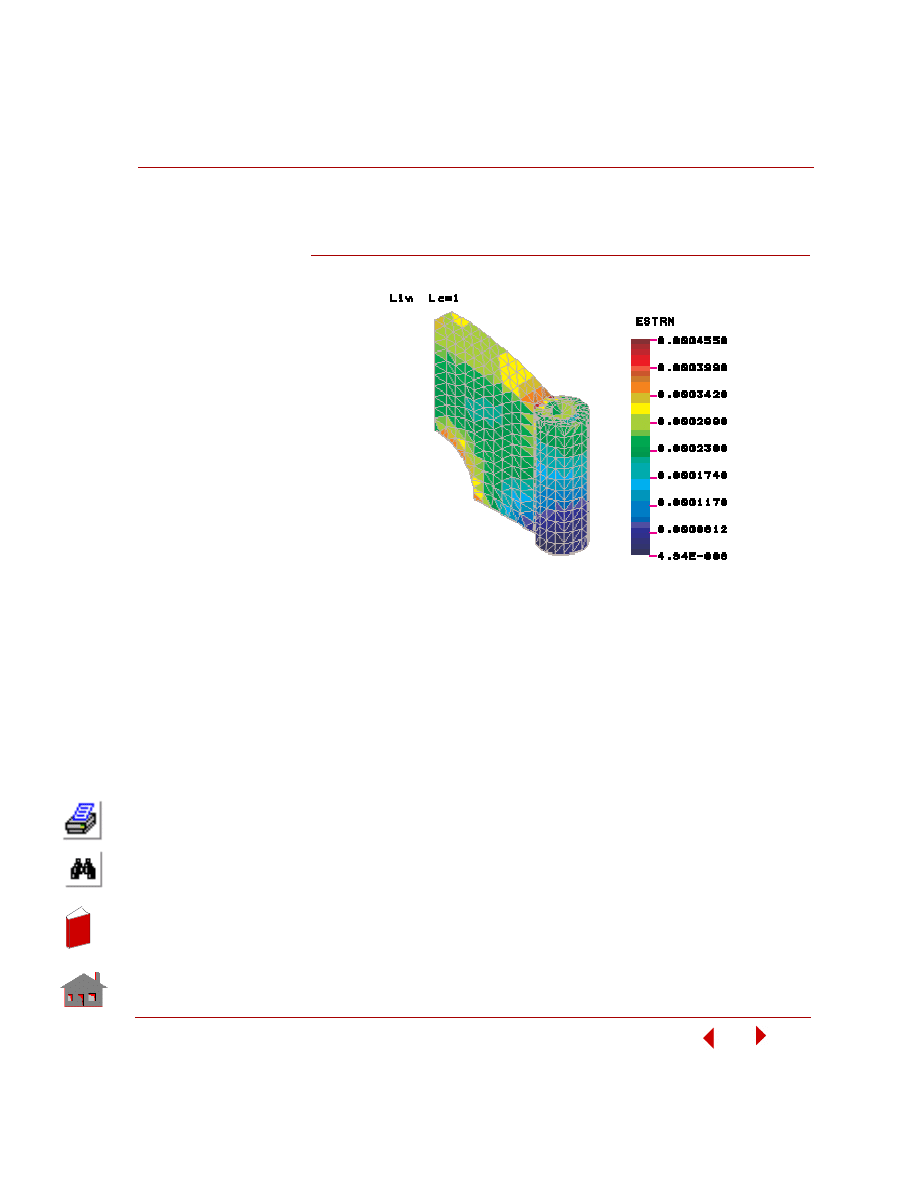
COSMOSFFE Static
5-9
Chapter 5 Examples
The generated plot is shown in the figure below. Note that strains are element-based
quantities and, therefore, each element is shown in one color.
Figure 5-5. Element Strain Plot
Note:
The equivalent strain (ESTRN) is calculated from:
ESTRN = 2[(
ε
1
+
ε
2
)/3]
(1/2)
where:
ε
1
= 0.5[(EPSX -
ε
a
)
2
+ (EPSY -
ε
a
)
2
+ (EPSZ -
ε
a
)
2
]
ε
2
= [(GMXY)
2
+ (GMXZ)
2
+ (GMYZ)
2
]/4
ε
a
= (EPSX + EPSY + EPSZ)/3
Where:
Strain EPSX:
Average element strain in the X-direction.
Strain EPSY:
Average element strain in the Y-direction.
Strain EPSZ:
Average element strain in the Z-direction.
In
de
x
In
de
x

Chapter 5 Examples
5-10
COSMOSFFE Static
Strain GMXY:
Element shear strain in the X-Y plane (change in angle
between lines initially parallel to the X- and Y-axes).
Strain GMYZ:
Element shear strain in the Y-Z plane (change in angle
between lines initially parallel to the Y- and Z-axes).
Strain GMZX:
Element shear strain in the Z-X plane (change in angle
between lines initially parallel to the Z- and X-axes).
Strain ESTRN:
Equivalent strain.
Nodal Stresses
Activate window 4 and plot von Mises stresses as follows:
Geo Panel: Results > PLOT >
Stress (STRPLOT)
Load case number [1] >
1
Component [VON] >
Layer number [1] >
Coordinate system [0] >
Stress flag >
Nodal stress
Face-flag (shell) 0=Top 1=Bot 2=Memb 3=Bend [0] >
Click on Contour icon
Plot Type 0 =Fill 1=Line 2=Vect [0] >
Beginning Element [1] >
Ending Element [2700] >
Increment [1] >
Shape flag 0=Undsef 1=Def [0] >
Scale factor [277.346]
The von Mises stress component is calculated from the stress components as shown
below:
VON=
{
(
1
/
2
)
[
(SX - SY)
2
+ (SX - SZ)
2
+ (SY - SZ)
2
]
+ 3 (TXY
2
+ TXZ
2
+ TYZ
2
)
}
(1/2)
Where:
VON
= von Mises stress component
SX
= normal stress in the x-direction
SY
= normal stress in the y-direction
SZ
= normal stress in the z-direction
In
de
x
In
de
x
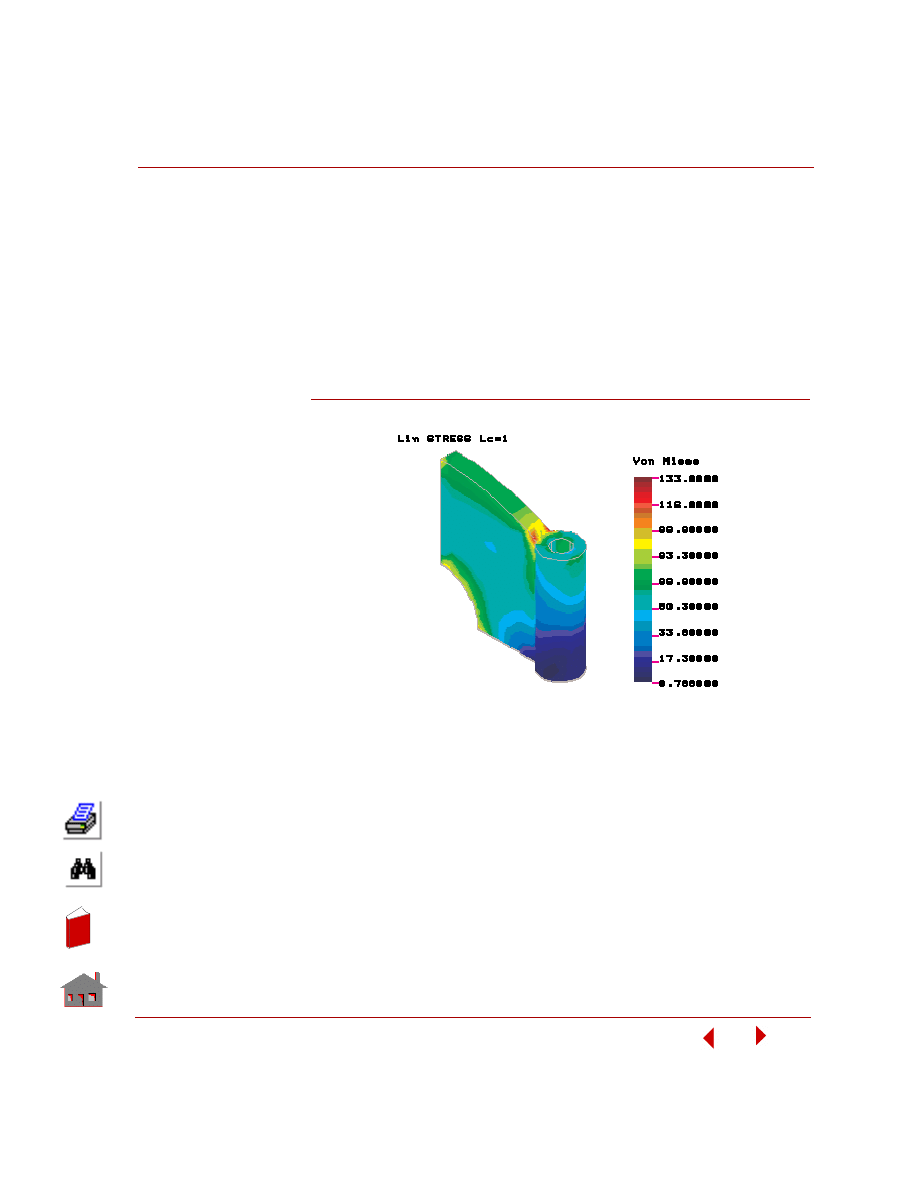
COSMOSFFE Static
5-11
Chapter 5 Examples
TXY
= shear stress in the x-y plane
TXZ
= shear stress in the x-z plane
TYZ
= shear stress in the y-z plane
VON may also be expressed in terms of principal stresses P1, P2, and P3 as given
below:
VON =
{
(
1
/
2
)
[
(P1 - P2)
2
+ (P1 - P3)
2
+ (P2 - P3)
2
]}
(1/2)
The generated von Mises stress plot is shown below.
Figure 5-6. von Mises Stress Plot
The generated plots as shown in the 4-window screen are shown below. Note that
the
METAFILE
(Control > Devices > Device_File >
Save Meta File
) command
may be used to store images in files that may be viewed later using the
VIEW_META
(File >
View Metafile
) command, or plotted using commands like
PLOT_META
(Control > Devices > Device_File >
Plot Meta File
). PostScript and
HPGL files may be also generated (refer to the File > Printer SetUp submenu). The
PAPER_SETUP
(Control > Devices >
Paper Set Up
) command may be used to
setup the hardcopy including whether single or multiple windows will be stored in
the meta file.
In
de
x
In
de
x
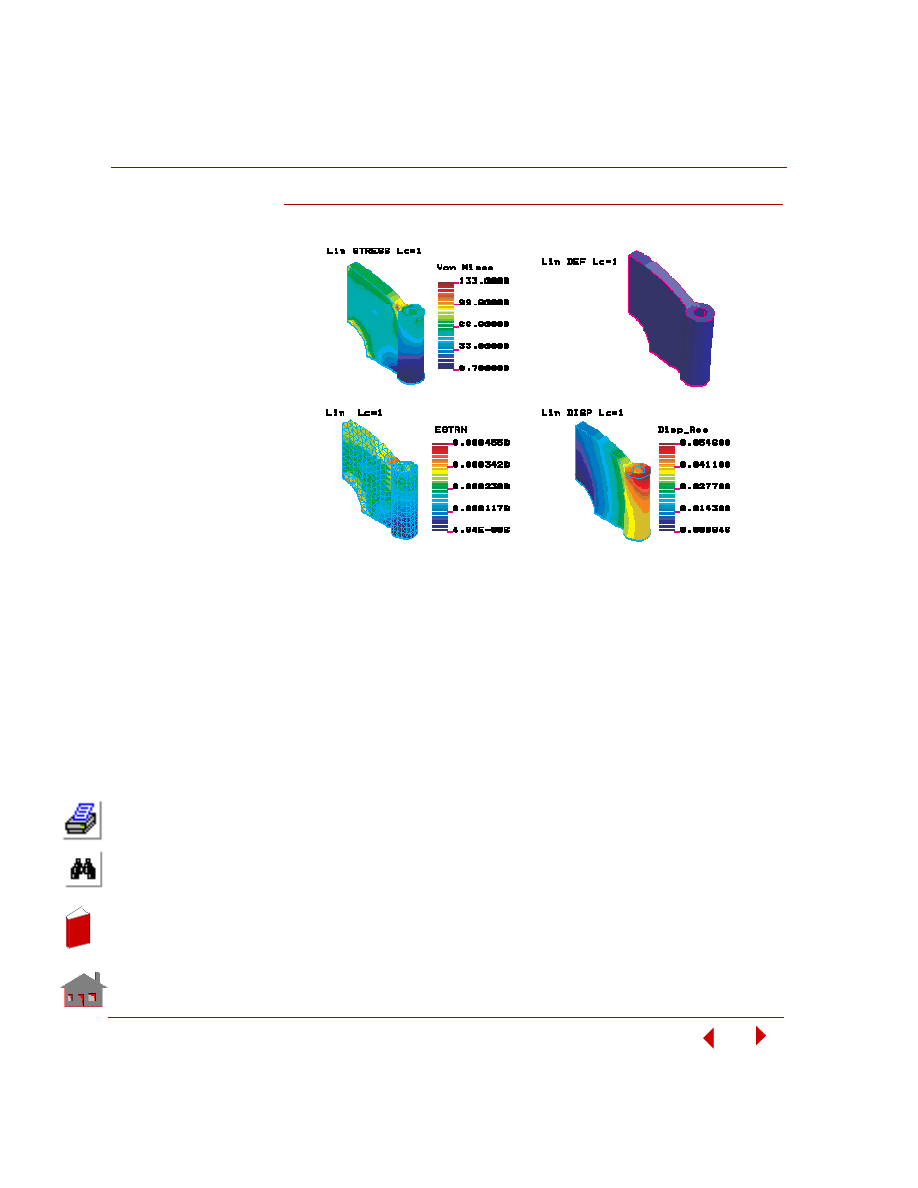
Chapter 5 Examples
5-12
COSMOSFFE Static
Figure 5-7. Multiple-Window Plots
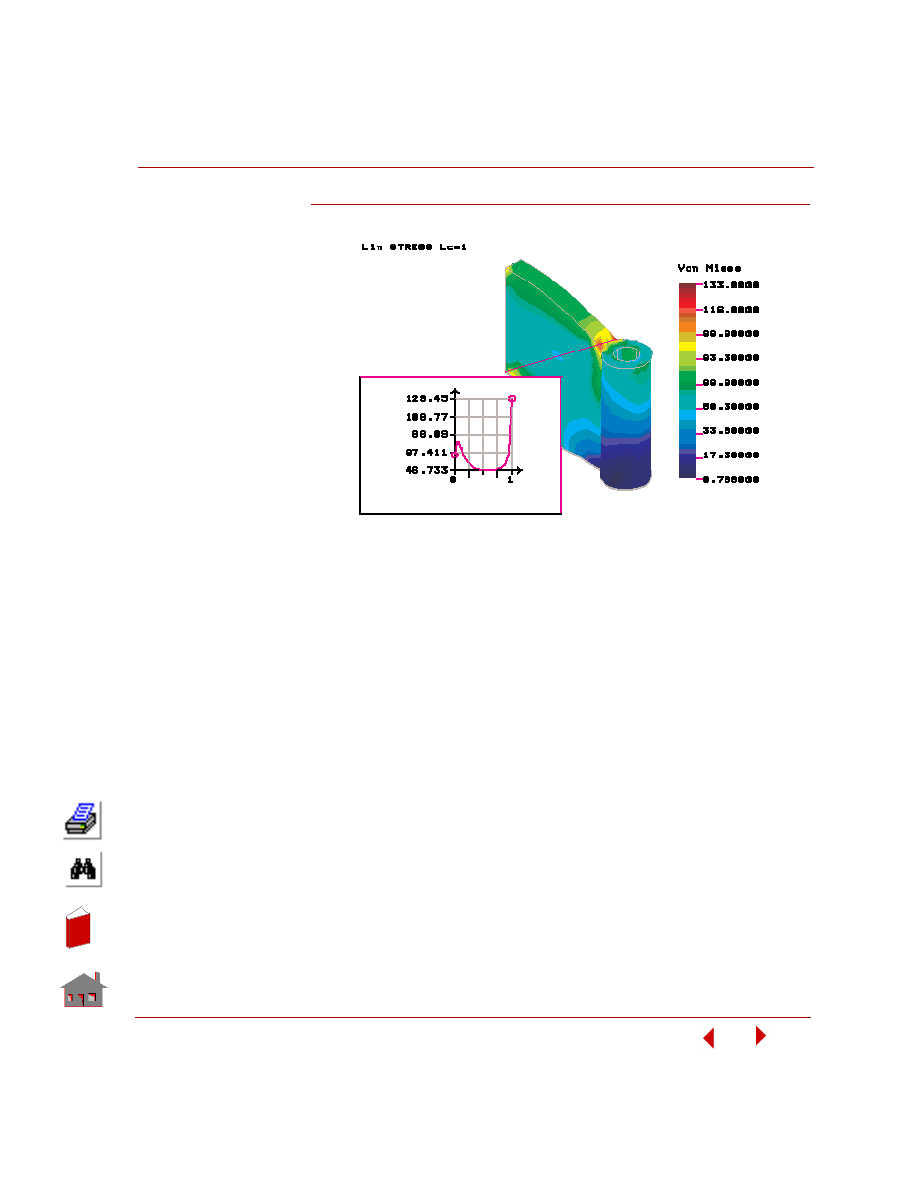
Graphing Results Along a Defined Path
You can trace the variation of the results plotted on the screen along an arbitrary
path defined by up to 20 nodes. The variation along the path will be automatically
graphed. The horizontal axis represents normalized distance starting from the path's
first node and the vertical axis represents the value of the plotted quantity. We will
graph the stress variation plotted in window 4 along the path defined by the nodes
shown below, choose:
Geo Panel: Results > PLOT >
Path Graph (LSECPLOT)
Pick/Input Node >
81
Pick/Input Node >
262
Pick/Input Node >
262
Resize the window to get a better view.
✍
Boundary evaluation is window-dependent.
In
de
x
In
de
x
COSMOSFFE Static
5-13
Chapter 5 Examples
Figure 5-8. Graph of von Mises Stresses Along a Path
Use the
ANIMATE
command as before to animate the von Mises stresses on the
deformed shape and corresponding graph.
Other plotting, listing, and searching for extreme values options are also available
including vector plots which are particularly useful for principal stresses. Refer to
the User Guide (Volume 1) and the Results menu for more information.
In
de
x
In
de
x
Chapter 5 Examples
5-14
COSMOSFFE Static
Model Information
Length Units:
Inches (in)
Force Units:
Pounds Weight (lb)
Pressure Units:
Lbs/in
2
Element Type:
Shells
Element Order:
First
Number of Elements:
3622
Number of Corner Nodes:
1968
Number of Degrees of Freedom:
11,808
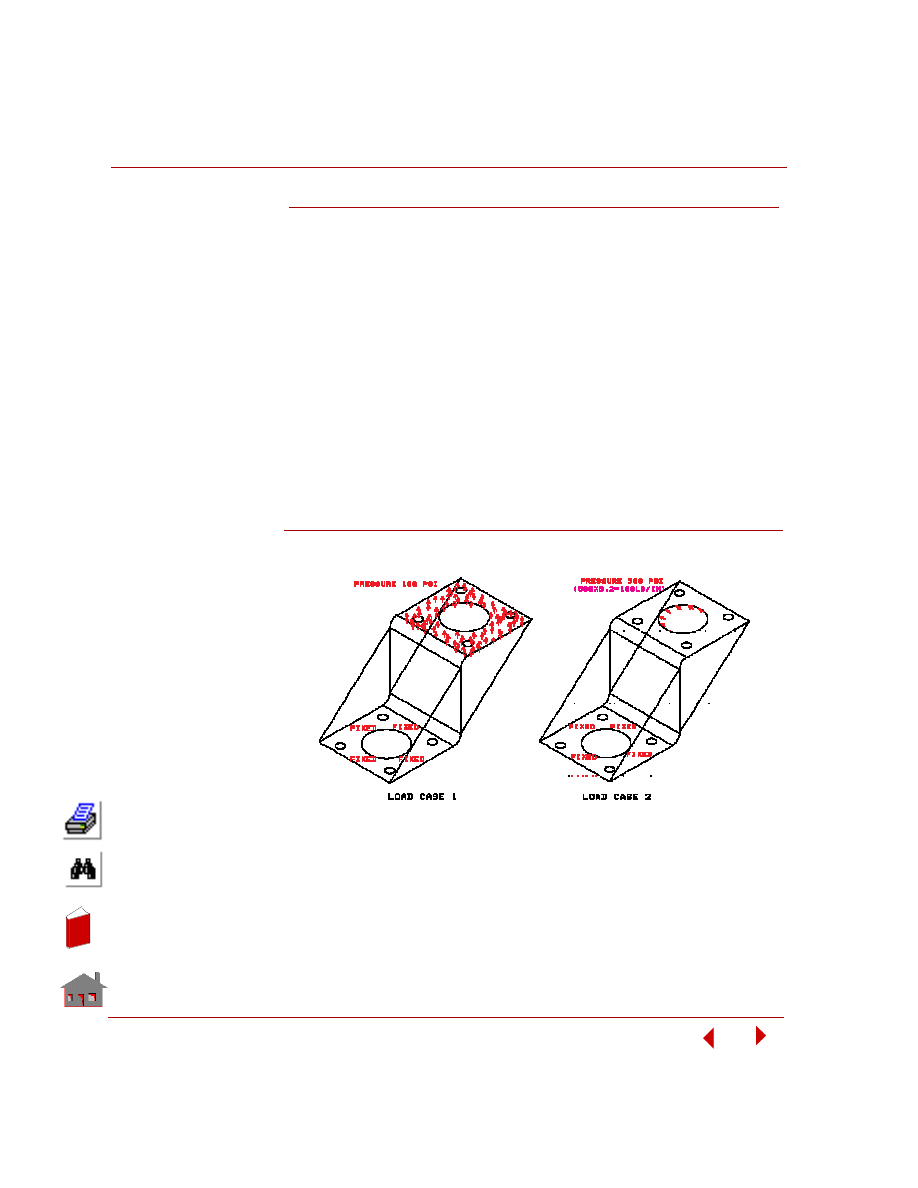
It is desired to calculate the stresses for the column connection bracket shown in the
figure below.
Figure 5-9. Column Connection Bracket
Example 2 – Analysis of a Column Connection
Bracket Using Shell Elements
In
de
x
In
de
x

COSMOSFFE Static
5-15
Chapter 5 Examples
The model shown above is made up of thin plates convenient to be modeled using
shell elements. This release of FFE Static supports triangular (SHELL3) and quad
(SHELL4) elements. A shell element has 6 degrees of freedom per node. The
example will be used to demonstrate multiple load case scenarios. It should be
noted, in using multiple load cases, that the displacement boundary conditions are
common across all load cases but the load vector may vary from one load case to
another. The 4 small holes at the bottom region will be completely fixed at all
degrees of freedom representing a rigidly bolted connection.
The file needed to create the geometry is called FFESX1.GEO and may be retrieved
from the PROBS subdirectory in your COSMOSM directory. The file is also listed
below for convenience. Use the
FILE
(File >
Load...
) command to read in the
FFESX2.GEO file, or you may choose to follow the commands and construct the
database step-by-step by following the commands below. In case of constructing
the model step-by-step, the user is referred to the Command Reference Manual or
the On-line help for information about the menu path required to issue the given
command.
List of the FFESX2.GEO File
C*
C*
Define element attributes
C*
EGROUP,1,SHELL3,0,0,0,0,0,0,0,
RCONST,1,1,1,6,0.20,0,0,0,0,0,
PICK_MAT,1,A_STEEL,FPS,
C*
C*
Create geometry
C*
PT,1,0,0,0,
CREXTR,1,1,1,Z,5,
CREXTR,1,1,1,Y,5,
CREXTR,3,3,1,Z,-5,
SCALE,0,
CRFILLET,4,2,1,.5,1,0,1E-006,
CRFILLET,5,3,2,.5,1,0,1E-006,
CRCOMPRESS,1,5,
SFEXTR,1,5,1,X,5,
SCALE,0,
PT,17,2.5,0,2.75,
PLANE,Y,0,1,
CRPCIRC,17,17,7,1.25,360,6,
PT,24,.75,0,1.25,
CRPCIRCLE,23,24,7,.25,360,6,
CSANGLE,3,0,2.5,0,2.75,0,0,0,0,
CRGEN,3,23,28,1,1,0,-90,0,
CT,1,0,.25,3,6,8,1,0,
CT,2,0,.25,1,22,0,
CT,3,0,.125,1,26,0,
CT,4,0,.125,1,32,0,
CT,5,0,.125,1,36,0,
CT,6,0,.125,1,42,0,
RG,1,6,1,2,3,4,5,6,0,
SCALE,0,
ACTDMESH,RG,1,
RGGEN,1,1,1,1,0,0,5,-5.5,
RGSF,2,4,2,.25,
RGSF,5,5,1,.25,
CRLINE,79,15,13,
CRLINE,80,14,11,
CRLINE,81,10,2,
CRLINE,82,4,6,
CT,16,0,.25,4,47,16,9,79,0,1,
CT,17,0,.25,4,80,6,15,9,0,1,
CT,18,0,.25,4,3,5,2,82,0,1,
CT,19,0,.25,4,81,1,4,2,0,1,
RG,6,1,16,0,
RG,7,1,17,0,
RG,8,1,18,0,
RG,9,1,19,0,
C*
C*
Mesh and merge coincident nodes
C*
MA_RG,1,9,1,0,0,
NMERGE,1,2208,1,0.0001,0,0,0,
C*
C*
Activate shade plotting and plot elements
C*
to check orientation of adjacent elements
C*
SHADE,1;
EPLOT;
C*
C*
Reorient elements on regions 1, 2, 3, and 7
C*
RGREORNT,1,3,1,
RGREORNT,7,7,1,
C*
C*
Fix region 1
C*
DRG,1,ALL,0,1,1,
In
de
x
In
de
x
Chapter 5 Examples
5-16
COSMOSFFE Static
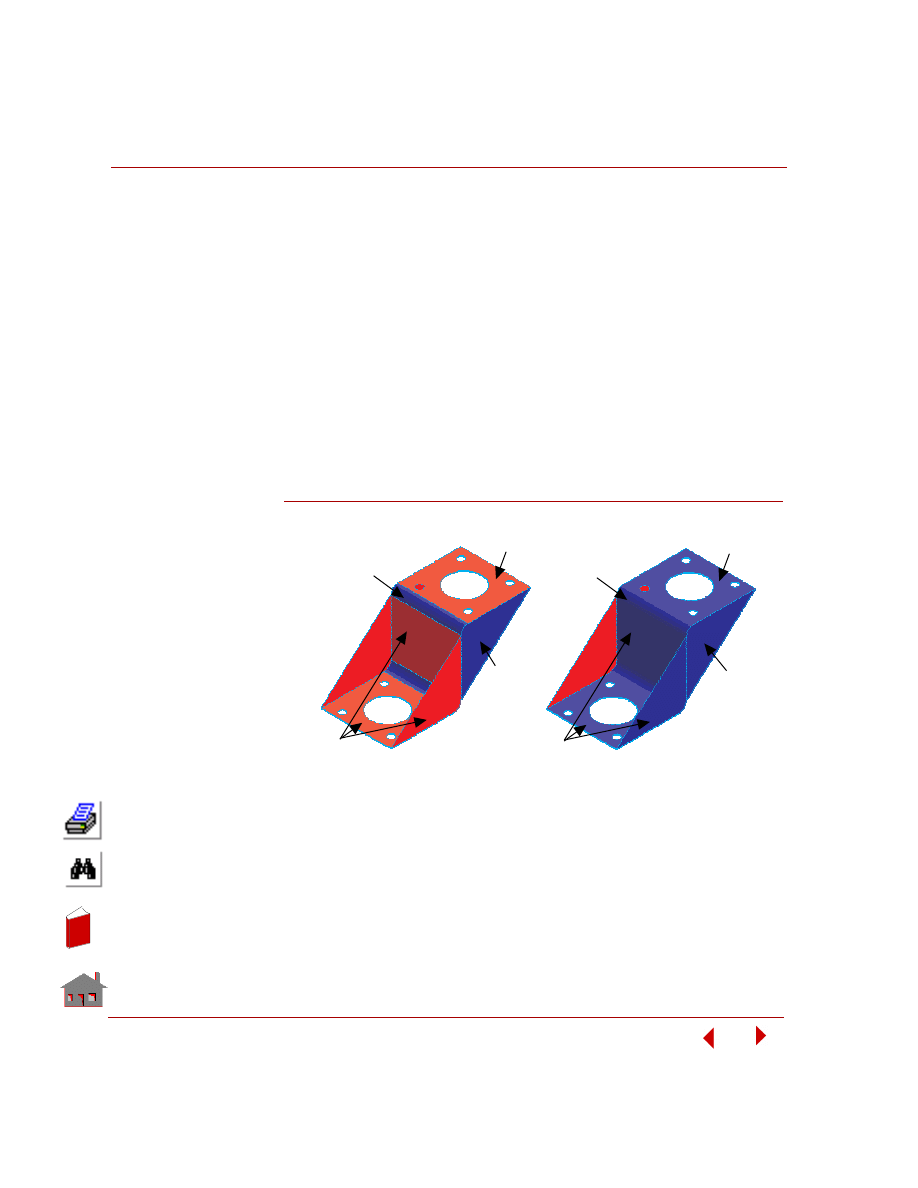
Shell elements have top and bottom faces which are determined by the order of the
nodal connectivity of the element. The top face is determined by the direction of the
thumb using the right-hand rule and the nodal connectivity. Adjacent shell
elements, that are not in orthogonal planes, should be oriented properly so that
stress averaging during postprocessing will be meaningful. If adjacent shell
elements are not properly oriented, stress results at the top fiber of an element will
be averaged with stress results at the bottom of an adjacent one leading to
inaccurate results. Shaded element plots are very useful since the top is shown in
blue and the bottom is shown in red. The
ACTDMESH
(Control > Activate >
Default
Meshing
) and
RGREORNT
(Geometry > REGIONS >
Re-orient
)
commands have been used to reorient elements on regions 1, 2, 3, and 7. Selection
sets may be used however, for plotting the stresses on the selected elements without
averaging across boundaries (refer to the
AVERAGE
(Results >
Average Nodal
Stress
) command for more information). The figure below shows a shaded plot
before and after reorientation.
Figure 5-10. Shaded Element Plot Before and After Reorientation
(edge plotting suppressed)
Defining Primary Load Cases
The FFESX2.GEO file does not include the definition of load cases. Note that we
do not need to activate the first load case since it is active by default. To define the
first load case, choose:
TOP FA CE
TOP FA CE
TOP FA CE
TOP FA CE
TOP FA CE
TOP FA CE
BOTTOM FA CE
BOTTOM FA CE
In
de
x
In
de
x

COSMOSFFE Static
5-17
Chapter 5 Examples
Geo Panel: LoadsBC > STRUCTURAL > PRESSURE >
Define Regions
(PRG)
Beginning region >
2
Pressure magnitude >
100
Ending region [2] >
Increment [1] >
Unused option >
Pressure Direction [Normal Direction] >
Accept entries
Define the Second Load Case
Loads are associated with the load case that is active during their definition. To
activate and define the second load case, choose:
Geo Panel: Control > ACTIVATE >
Set Entity (ACTSET)
Set label >
LC
Click on Continue icon
Load Case set number [1] >
2
Now that load case 2 is active, any defined loading will be associated with it. It
should be noted, however, that prescribed displacements are considered across all
load cases. To define the pressure associated with load case 2, choose:
Geo Panel: LoadsBC > STRUCTURAL > PRESSURE >
Define Curve (PCR)
Beginning curve >
49
Pressure magnitude >
-500
Ending curve [49] >
51
Increment [1] >
Pressure at the end of direction 1 [-500]>
Pressure Direction [Normal Direction] >
Accept entries
Use the
RGLIST
,
MPLIST
, and
RCLIST
commands from the Edit > LIST submenu
to list element groups, material properties, and real constants. Use
PLIST
(LoadsBC
> STRUCTURAL > PRESSURE >
List
) to list pressure for the active load case.
You may also use the
R_CHECK
(Analysis >
Run Check
) command.
In
de
x
In
de
x

Chapter 5 Examples
5-18
COSMOSFFE Static
Running Analysis
Now the model has been created, we are ready to specify analysis options and run
the analysis, choose:
Geo Panel: Analysis > STATIC >
FFE Static Options (A_FFESTATIC)
Element Order [Second] >
First
Loading Flag [N] >
Note that only the first order is currently supported for shells. The default flag for
special loading is accepted. If special loading effects are to be considered, then the
proper combination of T, G, and C should be specified.
Next, run the analysis, choose:
Geo Panel: Analysis > STATIC >
Run Static Analysis (R_STATIC)
Control will transfer to FFE Static which will inform you about the progress of the
analysis. When the analysis is completed, GEOSTAR will get control again any you
may start postprocessing the results as shown below.
Postprocessing
All postprocessing commands are available in the Results menu. You may list, plot,
and search for extreme values. List screens may be piped to files using the
LISTLOG
(Control > MISCELLANEOUS >
List Log
) command.
Deformed Shape
To plot the deformed shape, choose:
Geo Panel: Results > PLOT >
Deformed Shape (DEFPLOT)
Load Case [2] >
1
Beginning element [1] >
Ending element [3622] >
Increment [1] >
Scale factor [38.037] >
Accept entries
In
de
x
In
de
x

COSMOSFFE Static
5-19
Chapter 5 Examples
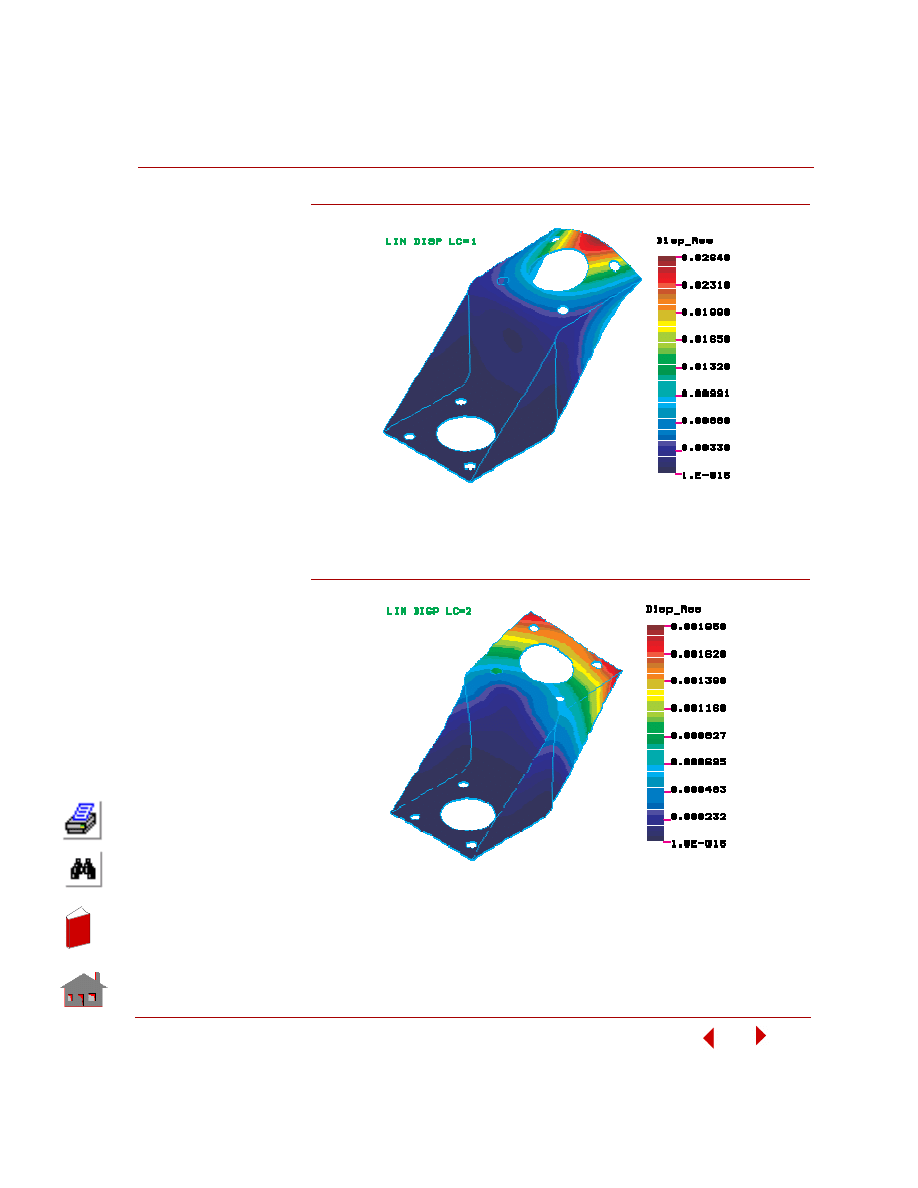
The generated plot is shown below. Note that the default scale factor exaggerates
deflections to 10% of the model size. Input a scale factor of 1.0 to plot the true
deformed shape.
Figure 5-11. Deformed Shape Plot for Load Case 1
A similar plot for load case 2 is shown below.
Figure 5-12. Deformed Shape Plot for Load Case 2
In
de
x
In
de
x

Chapter 5 Examples
5-20
COSMOSFFE Static
Displacement Contours
Displacement contours may be generated on undeformed or deformed geometry.
Activate boundary edge evaluation, choose:
Geo Panel: Display > DISPLAY OPTION >
Eval Element Bound
(EVAL_BOUND)
Boundary face evaluation flag [No]>
Boundary edge evaluation flag [No]>
Yes
Click on Continue icon
Tolerance angle to ignore curvature [20]>
60
To plot the resultant displacement contour, choose:
Geo Panel: Results > PLOT >
Displacement (DISPLOT)
Load case number [1] >
Component [URES] >
Coordinate system [0] >
Click on Contour icon
Plot Type >
Color_filled contour
Beginning element [1] >
Ending Element [3622] >
Increment [1] >
Shape flag >
Deformed shape
Scale Factor [38.037] >
Accept entries
The generated displacement contour is shown in the figure below. Use the
ANIMATE
(Results > PLOT >
Animate
) command to animate the displacement
contour on the deformed shape.
In
de
x
In
de
x
COSMOSFFE Static
5-21
Chapter 5 Examples
Figure 5-13. Displacement Contour Plot for Load Case 1
A similar plot for load case 2 is shown below.
Figure 5-14. Displacement Contour Plot for Load Case 2
In
de
x
In
de
x
Chapter 5 Examples
5-22
COSMOSFFE Static
Element Strain
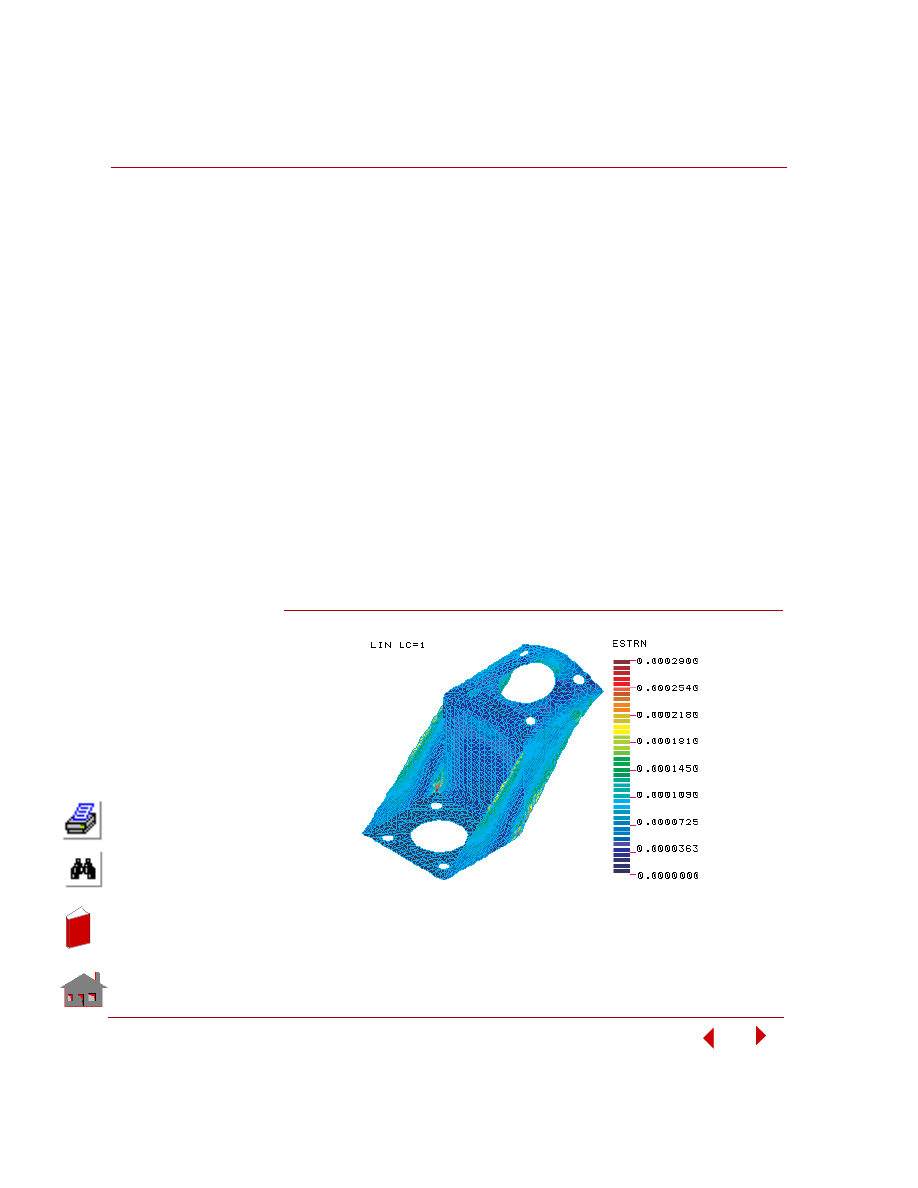
Strains are calculated for each element. To plot element strains, choose:
Geo Panel: Results > PLOT >
Strain (STNPLOT)
Load case number [2] >
1
Component [ESTRN] >
Layer number [1] >
(used only for layered elements)
Face-flag [Top] >
Coordinate system [0] >
Click on Contour icon
Plot Type >
Color_filled contour
Beginning element [1] >
Ending element [3622] >
Increment [1] >
Shape flag >
Undeformed shape
Scale factor [38.037] >
Accept entries
The generated plot is shown in the figure below. Note that strains are element-based
quantities and, therefore, each element is shown in one color.
Figure 5-15. Element Strain Plot for Load Case 1
In
de
x
In
de
x

COSMOSFFE Static
5-23
Chapter 5 Examples
A similar plot for load case 2 is shown below.
Figure 5-16. Element Strain Plot for Load Case 2
Stress Plots
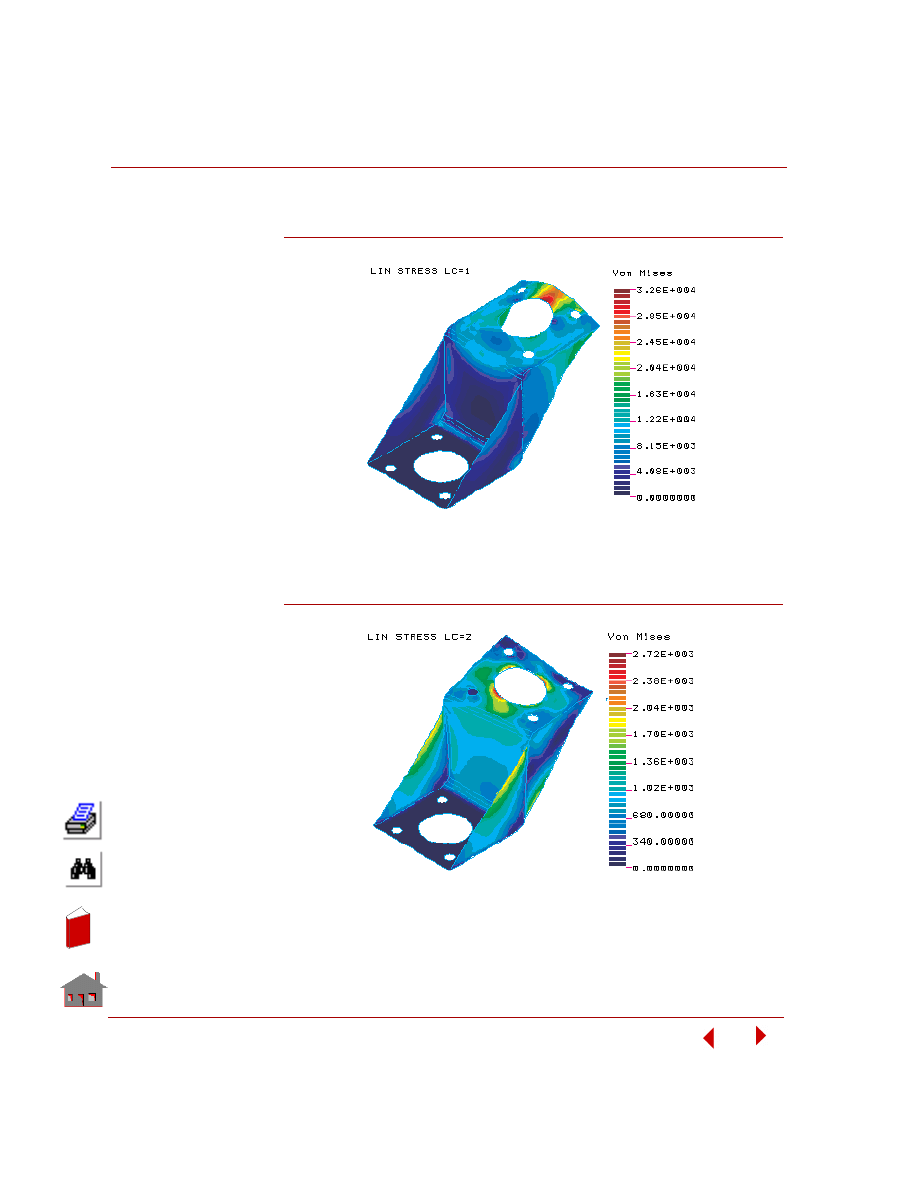
To plot von Mises stresses, choose:
Geo Panel: Results > PLOT >
Stress (STRPLOT)
Load case number [2] >
1
Component [VON] >
Stress flag >
Nodal stress
Layer number [1] >
(used only for layered elements)
Face-flag [Top] >
Coordinate system [0] >
Click on Contour icon
Plot Type >
Color_filled contour
Beginning element [1] >
Ending element [3622] >
Increment [1] >
Shape flag >
Deformed shape
Scale factor [38.037] >
Accept entries
In
de
x
In
de
x
Chapter 5 Examples
5-24
COSMOSFFE Static
The generated von Mises stress plot is shown below.
Figure 5-17. von Mises Stress Plot for Load Case 1
A similar plot for load case 2 is shown below.
Figure 5-18. von Mises Stress Plot for Load Case 2
In
de
x
In
de
x
COSMOSFFE Static
5-25
Chapter 5 Examples
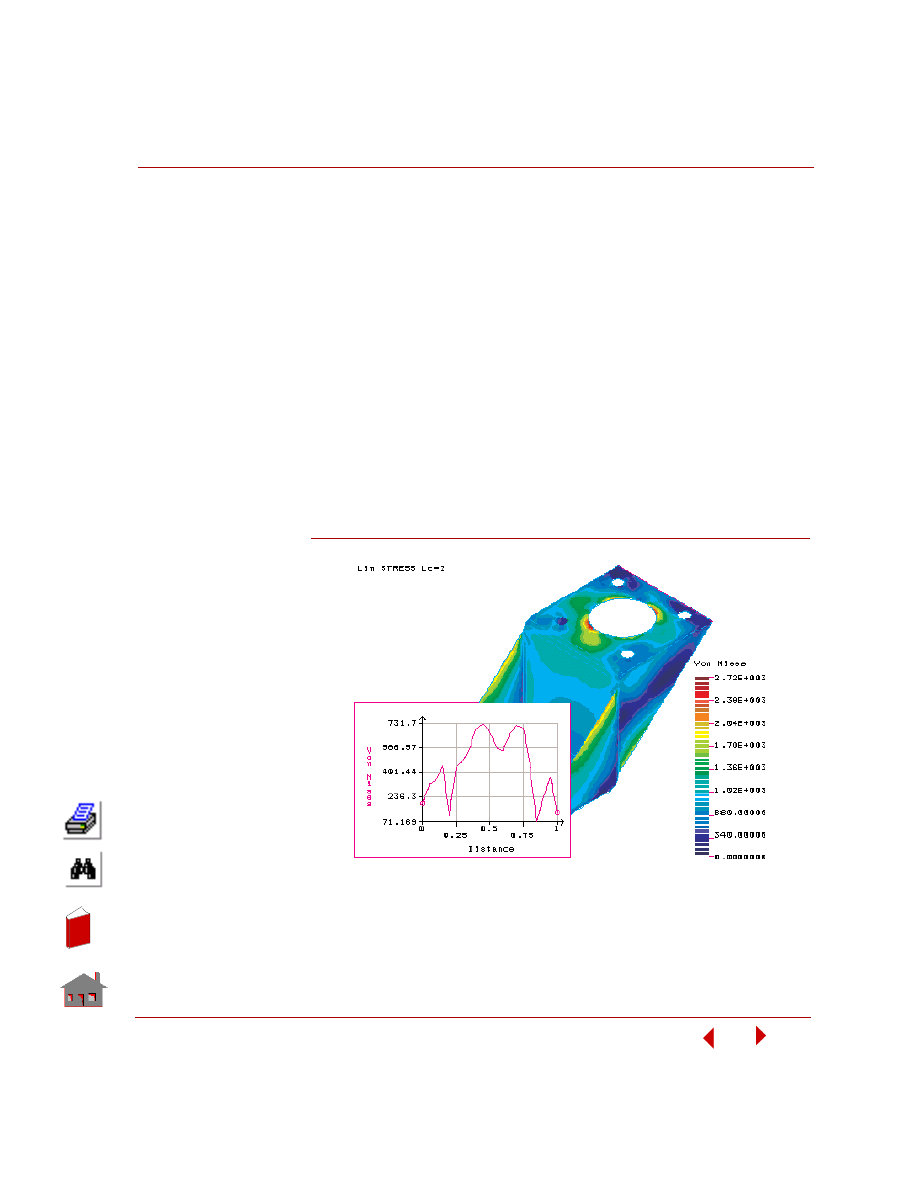
Graphing Results Along a Defined Path
You can trace the variation of the results plotted on the screen along an arbitrary
path defined by up to 20 nodes. The variation along the path will be automatically
graphed. The horizontal axis represents normalized distance starting from the path's
first node and the vertical axis represents the value of the plotted quantity. We will
graph the stress variation along the path defined by the nodes shown below, choose:
Geo Panel: Results > PLOT >
Path Graph (LSECPLOT)
Pick/Input Node >
409
Pick/Input Node >
429
Pick/Input Node >
429
✍
Nodes to determine the path for the
LSECPLOT
command are picked from
their undeformed locations on the screen. It is suggested, therefore, to use
contour plots on undeformed shape for this purpose.
The generated plot is shown below.
Figure 5-19. Graph of von Mises Stresses Along a Path for Load Case 2
In
de
x
In
de
x
Chapter 5 Examples
5-26
COSMOSFFE Static
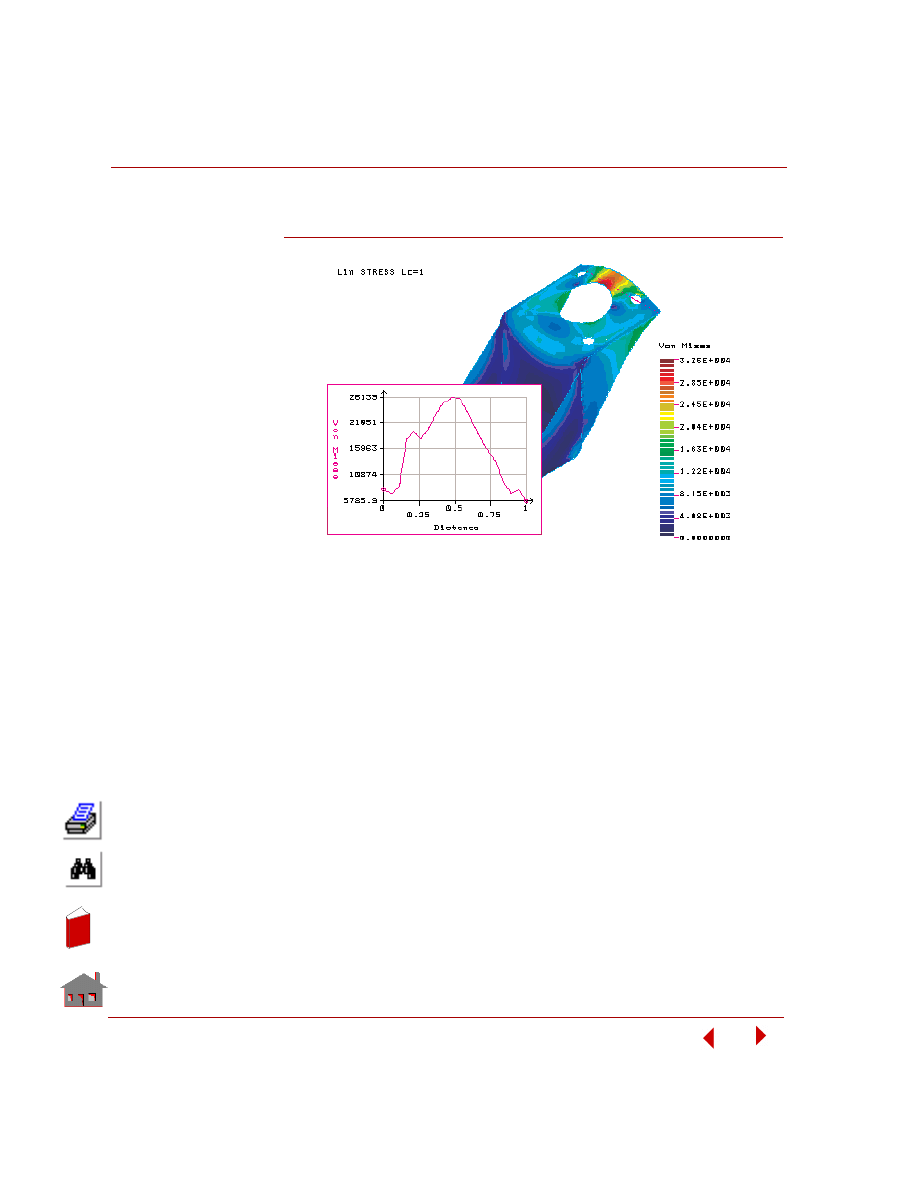
A similar plot for load case 1 is shown below.
Figure 5-20. Graph of von Mises Stresses Along a Path for Load Case 1
Use the
ANIMATE
(Results > PLOT >
Animate
) command to animate the von
Mises stresses on the deformed shape and corresponding graph simultaneously.
Secondary Load Cases
Now that results in the database are available for primary load cases, we may define
secondary load cases as desired. We will create secondary load case 51 defined by
superimposing 1.5 times load case 1 and 3 times load case 2, choose:
Geo Panel: Results >
Combine Load Case (LCCOMB)
New load case number >
51
Load case number for term 1 >
1
Load case factor for term 1 [1] >
1.5
Load case number for term 2 >
2
Load case factor for term 1 [1] >
3
Load case number for term 3 >
In
de
x
In
de
x
COSMOSFFE Static
5-27
Chapter 5 Examples
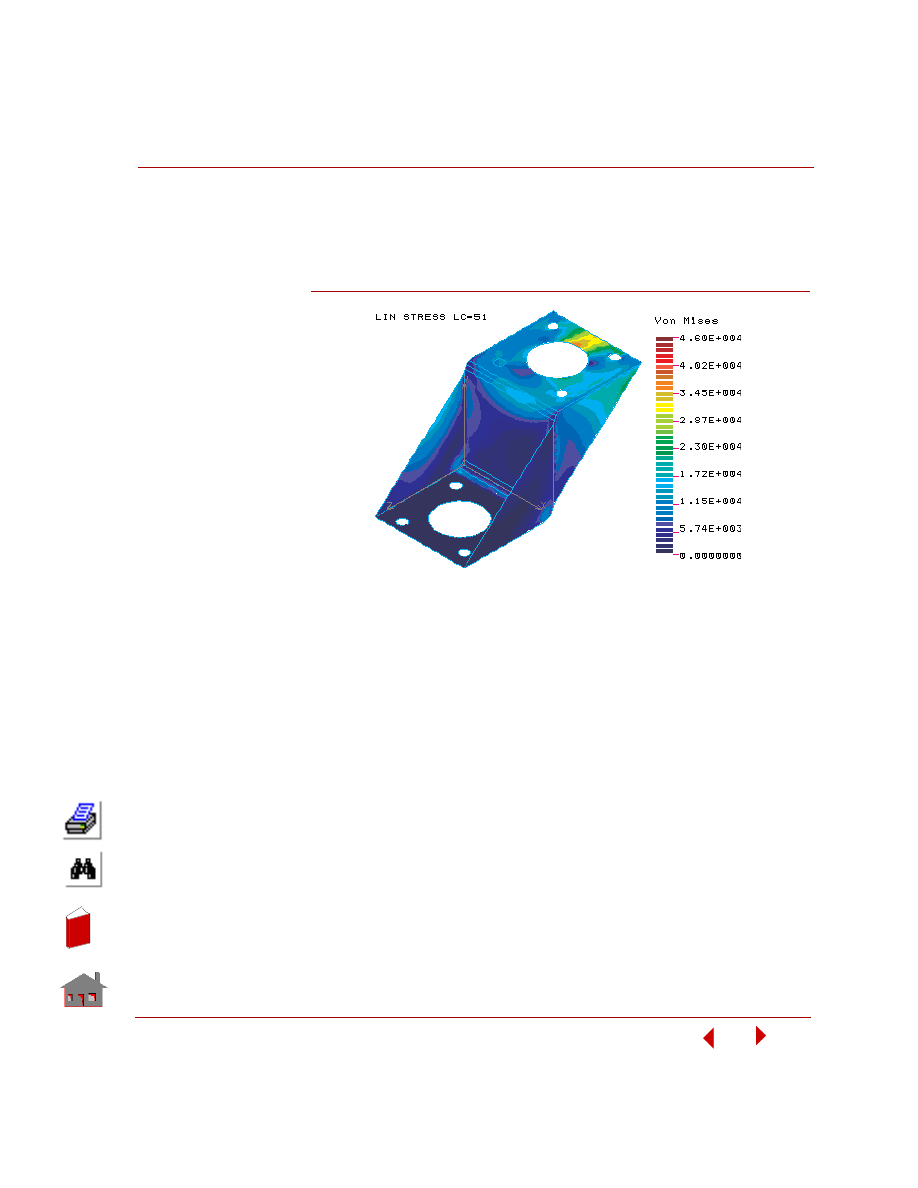
The results for load case 51 will be calculated by adding the corresponding results
of load case 1 multiplied by 1.5 and the results of load case 2 multiplied by 3.
Postprocessing may proceed as explained for load cases 1 and 2. A von Mises stress
plot for load case 51 is shown below.
Figure 5-21. von Mises Stress Plot for Load Case 51
In
de
x
In
de
x

Chapter 5 Examples
5-28
COSMOSFFE Static
The file for this model is called FFESX3.GEO and may be retrieved from the
PROBS subdirectory in COSMOSM directory as explained earlier. Create a new
GEOSTAR problem and use the
FILE
(File >
Load...
) command to construct the
database. Once the model has been generated, you may continue with running the
analysis and postprocessing as explained earlier. The following information
describes the size of the model.
Model Information
Element Type:
Tetrahedral
Element Order:
Second
Number of Elements:
21,430
Number of Corner Nodes:
5,103
Number of Degrees of Freedom:
104,175
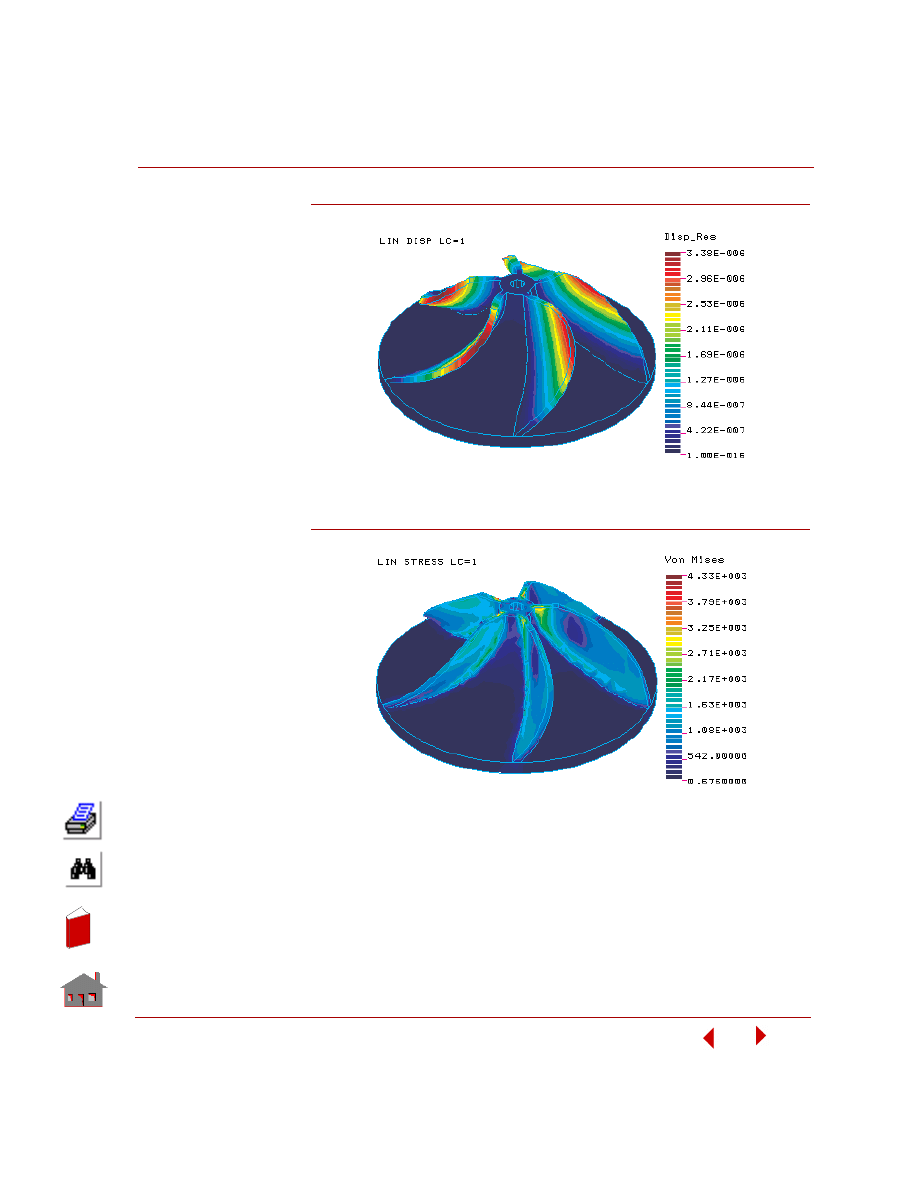
Some results of the analysis are shown below.
Figure 5-22. Meshed Fan Model
Example 3 – A Model of a Fan
In
de
x
In
de
x
COSMOSFFE Static
5-29
Chapter 5 Examples
Figure 5-23. Displacement Contour Plot
Figure 5-24. von Mises Stress Contour Plot
In
de
x
In
de
x

5-30
COSMOSFFE Static
In
de
x
In
de
x
COSMOSFFE Static
6-1
6
Verification Problems
Introduction
This chapter includes a set of verification problems that check various elements and
features of the FFE Static module. The problems are carefully selected to check the
numerical answers versus theoretical results.
The input files for theses verification problems are available in the
“,,,\Vprobs\FFE” subdirectory in your COSMOSM directory.
To extract the input files for the verification problems, it is suggested to create a
new working directory and then copy the desired input file to that directory. To run
a verification problem, create a new GEOSTAR database and use the
FILE
(File >
Load...
) command to reconstruct the database and run the problem
The table below lists the verification problems in this chapter.
In
de
x
In
de
x
Chapter 6 Verification Problems
6-2
COSMOSFFE Static
Table 6-1. List of Verification Problems
Problem
Element
Order
Title
FFES1
PLANE2D
First
Long Thick-Walled Cylinder
FFES2A
SHELL3
First
Simply Supported Rectangular Plate
FFES2B
SHELL3
First
Simply Supported Rectangular Plate
FFES3
PLANE2D
Second
Thermal Stress Analysis of a 2D Structure
FFES4
PLANE2D
Second
Deflection of a Cantilever Beam
FFES5
SHELL3
First
Tip Displacements of a Circular Beam
FFES6A
SOLID
Second
Bending of a Solid Beam
FFES6B
SOLID
Second
Bending of a Solid Beam
FFES7
SOLID
Second
Thermal Stress Analysis of a 3D Structure
FFES8
PLANE2D
Second
Rectangular Plate Under Triangular Thermal Loading
FFES9
PLANE2D
Second
Hollow Thick-Walled Cylinder Subj to Temp & Pressure
FFES10
SHELL4
First
Cylindrical Shell Roof
FFES11
SHELL4
First
Torsion of a Square Box Beam
FFES12
SOLID
Second
Spherical Cap Under Uniform Pressure (Solid)
FFES13
PLANE2D
Second
Rotating Solid Disk
FFES14
SHELL4
First
Reactions and Deflections of a Cantilever Beam
FFES15A
PLANE2D
First
Deflection of a Curved Beam
FFES15B
PLANE2D
Second
Deflection of a Curved Beam
FFES15C
TRIANG
Second
Deflection of a Curved Beam
FFES15D
TETRA10
Second
Deflection of a Curved Beam
FFES15E
SOLID
First
Deflection of a Curved Beam
FFES15F
SOLID
Second
Deflection of a Curved Beam
In
de
x
In
de
x

COSMOSFFE Static
6-3
Chapter 6 Verification Problems
Table 6-1. List of Verification Problems (Concluded)
Problem
Element
Order
Title
FFES16
TRIANG
First
Analysis of an Elliptic Membrane Under Pressure
FFES17
PLANE2D
Second
Thermal Stress Analysis of a Flat Plate
FFES18
TRUSS3D
--
Pin Jointed Truss
FFES19
TRUSS2D
--
Thermal Stress Analysis of a Truss Structure
FFES20
BEAM3D
--
Beam Stresses and Deflections
FFES21A
BEAM3D
--
Clamped Beam Subject to Imposed Displacement
FFES21B
BEAM3D
--
Clamped Beam Subject to Imposed Rotation
FFES22
TRUSS3D
--
Deflection of a Hinged Support
FFES23
TRUSS3D
--
Statically Indeterminate Reaction Force Analysis
FFES24A
TRUSS3D
--
Space Truss with Vertical Load
FFES24B
TRUSS3D
--
Space Truss with Vertical Load
FFES25
BEAM3D
--
Thermal Stress Analysis of a Frame
FFES26
BEAM3D
--
Thermal Stress Analysis of a Simple Frame
FFES27
BEAM3D
--
Frame Analysis with Combined Loads
FFES28
TRUSS2D
--
Truss Structure Subject to a Concentrated Load
In
de
x
In
de
x

Chapter 6 Verification Problems
6-4
COSMOSFFE Static
TYPE:
Static analysis, 2-D axisymmetric elements (PLANE2D).
REFERENCE:
Timoshenko, S. P. and Goodier, J., “Theory of Elasticity,” McGraw-Hill, New York,
1951, pp. 58-60.
PROBLEM:
Calculate the radial stresses for an infinitely long, thick walled cylinder subjected to
an internal pressure p.
GIVEN:
a
= 100 in
b =
115
in
p
= 1000 psi
E
= 30 x 10
6
psi
ν =
0.3
MODELING HINTS:
The model is composed of three elements through the thickness and three along the
length.
COMPARISON OF RESULTS:
FFES1: Long Thick-Walled Cylinder
r (Radial Distance)
(in)
Radial Stress
σ
r
(psi)
Theory
COSMOSM
102.5 (Element 1)
- 802.40
- 802.50
107.5 (Element 2)
- 447.75
- 447.80
112.5 (Element 3)
- 139.34
- 139.40
In
de
x
In
de
x
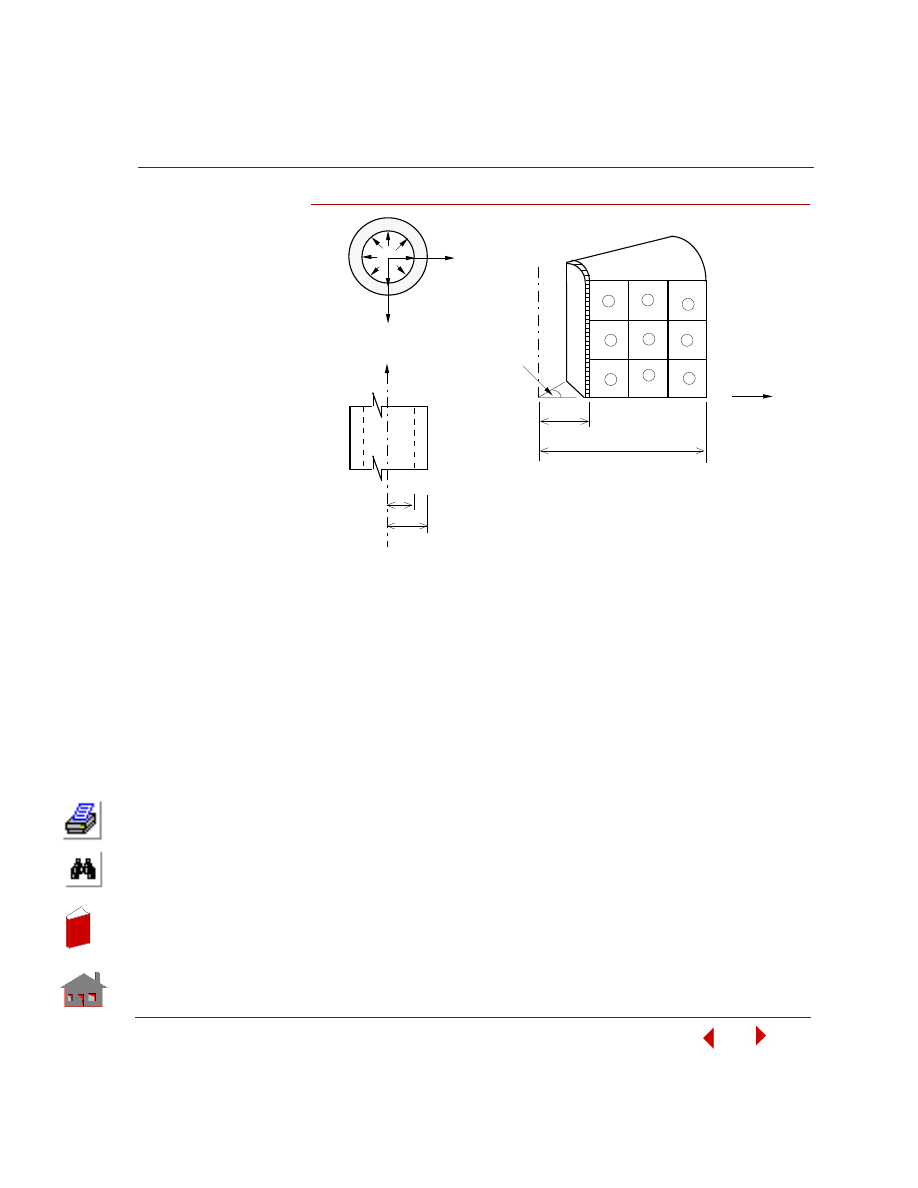
COSMOSFFE Static
6-5
Chapter 6 Verification Problems
Figure FFES1-1
a
b
x
σ
r
4
5
6
7
8
9
1
2
3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
a
b
p
y
1 rad
Finite Element Model
Problem Sketch
x
z
y
p
In
de
x
In
de
x
Chapter 6 Verification Problems
6-6
COSMOSFFE Static
TYPE:
Static analysis, 3-node thin plate element (SHELL3).
REFERENCE:
Timoshenko, S. P. and Woinowsky-Krieger, “Theory of Plates and Shells,”
McGraw-Hill Book Co., 2nd edition. pp. 143-120, 1962.
PROBLEM:
Calculate the deflection
and stresses at the
center of a simply
supported isotropic
plate subjected to (A)
concentrated load F, (B)
uniform pressure (P).
GIVEN:
E
= 30,000,000 psi
ν
= 0.3
h
= 1 in
a
= b = 40 in
F
= 400 lb
p
= 1 psi
MODELING HINTS:
Due to double symmetry in geometry and loads, a quarter of the plate is taken for
modeling.
COMPARISON OF RESULTS:
FFES2A, FFES2B: Simply Supported Rectangular
Plate
Case
X (in)
Y (in)
W
max
at Node 25 (in)
Theory
COSMOSM
A
20
20
0.0270230
0.027123
B
20
20
3.78327 x 10
-3
3.7915 x 10
-3
Z
Y
X
h
1
b
a
Problem Sketch and Finite Element Model
5
21
25
F
Figure FFES2-1
In
de
x
In
de
x
COSMOSFFE Static
6-7
Chapter 6 Verification Problems
TYPE:
Linear thermal stress analysis, 2-D elements (plane strain, PLANE2D).
PROBLEM:
Determine the displacements and stresses of the plane strain problem indicated in
figure below due to a uniform temperature rise.
Figure FFES3-1
FFES3: Thermal Stress Analysis of a 2-D
Structure
GIVEN:
E
= 30 x 10
6
psi
α = 0.65 x 10
-5
/
°F
ν
= 0.25
T
= 100
° F
L
= 1 in
COMPARISON OF RESULTS:
Displacements at Nodes (2, 4, and 6)
Y-
Displacement
(in)
XX-
Stress
(psi)
Theory
0.001083
- 26000.0
COSMOSM
0.001083
- 26000.1
1
2
L
y
x
1
2
3
4
5
6
L
L
Problem Sketch and Finite Element Model
In
de
x
In
de
x

Chapter 6 Verification Problems
6-8
COSMOSFFE Static
TYPE:
Static analysis, plane stress element PLANE2D and SHELL6.
PROBLEM:
A cantilever beam is subjected to a concentrated load at the free end. Determine the
deflections at the free end and the uniform shear stress.
Figure FFES4-1
FFES4: Deflection of a Cantilever Beam
GIVEN:
COMPARISON OF RESULTS:
E
= 30 x 10
6
psi
L
= 10 in
h
= 1 in
A
= 0.1 in
2
ν
= 0
P
= 1 lb
Max.
Deflection
(inch)
Shear
Stress
(psi)
Theory
- 0.001333
- 10.0
COSMOSM
PLANE2D
- 0.001341
- 10.0
SHELL6
- 0.00139
- 10.0
1
10
2
y
2
4
6
l
3
5
22
21
x
P
h
Finite Element Model
L
t
Problem Sketch
h
P
In
de
x
In
de
x
COSMOSFFE Static
6-9
Chapter 6 Verification Problems
TYPE:
Static analysis, thin or thick shell element (SHELL3).
REFERENCE
Warren C. Young, “Roark's Formulas for Stress and Strain,” Sixth Edition, McGraw
Hill Book Company, New York, 1989.
PROBLEM:
Determine the deflections in X, Y direction of a circular beam fixed at one end and
free at the other end, when subjected to a force along X direction at force end.
Figure FFES5-1
FFES5: Tip Displacements of a Circular Beam
GIVEN:
E
= 30E6 psi
ν
= 0
b
= 4 in
h
= 1 in
R
= 10 in
F
= 200 lb
COMPARISON OF RESULTS:
The loaded end.
Displacement (inch)
X
Y
Theory
0.712E-2
0.99E-2
COSMOSM
0.718E-2
0.99E-2
F/2
F/2
y
z
x
h
b
R
Problem Sketch and Finite Element Model
In
de
x
In
de
x

Chapter 6 Verification Problems
6-10
COSMOSFFE Static
TYPE:
Static analysis, SOLID element.
REFERENCE:
Roark, R. J., “Formulas for Stress and Strain,” 4th Edition, McGraw-Hill Book Co.,
New York, 1965, pp. 104-106.
PROBLEM:
A beam of length L and height h is built-in at one end and loaded at free end: (A)
with a shear force F, and (B) a moment M. Determine the deflection at the free end.
GIVEN:
L
= 10 in
h
= 2 in
E
= 30 x 10
6
psi
ν
= 0
F
= 300 lb
M
= 2000 in-lb
MODELING HINTS:
Two load cases have been used (FFES6A, FFES6B).
1.
Four forces equal to F/4 have been applied at nodes 6, 12, 18, and 24 in xz
direction (FFES6A), and,
2.
Two couples equal M/2 have been applied at nodes 6, 12, 18 and 24 (FFES6B).
COMPARISON OF RESULTS:
Displacement in Z-direction (in) (node 21-24):
FFES6A, FFES6B: Bending of a Solid Beam
FFES6A
FFES16B
Theory
0.00500
– 0.00500
COSMOSM
0.00507
– 0.00495
In
de
x
In
de
x
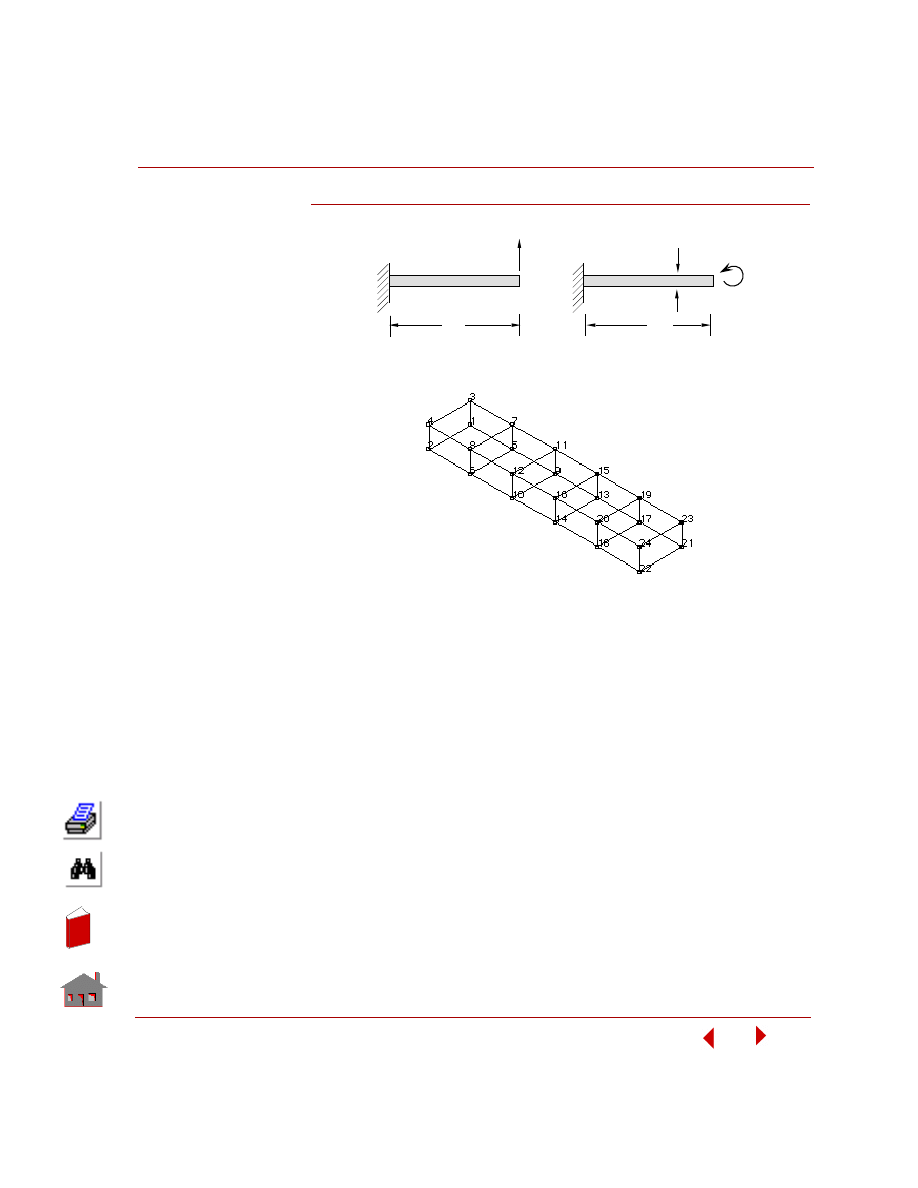
COSMOSFFE Static
6-11
Chapter 6 Verification Problems
Figure FFE6-1
F
L
h
M
L
Case 1
Case 2
Problem Sketch
Finite Element Model
In
de
x
In
de
x
Chapter 6 Verification Problems
6-12
COSMOSFFE Static
TYPE:
Linear thermal stress analysis, 3-D SOLID element.
PROBLEM:
Determine the displacements of the three-dimensional structure shown below due to
a uniform temperature rise.
Figure FFES7-1
FFES7: Thermal Stress Analysis of a 3-D
Structure
GIVEN:
COMPARISON OF RESULTS:
E
= 3 x 10
7
psi
α = 0.65 x 10
-5
/
°F
ν
= 0.25
T =
100
° F
L
= 1 in
X-Displacement (Nodes)
5, 6, 7, 8
9, 10, 11, 12
Theory
0.000650
0.001300
COSMOSM
0.000650
0.001300
5
8
9
2
1
L
L
L
L
1
2
3
4
6
7
10
11
12
x,r
z,t
y,s
Problem Sketch and Finite Element Model
In
de
x
In
de
x
COSMOSFFE Static
6-13
Chapter 6 Verification Problems
TYPE:
Linear thermal stress analysis, 2-D elements (plane stress analysis, PLANE2D).
REFERENCE:
Johns, D. J., “Thermal Stress Analysis,” Pergamon Press, Inc., 1965, pp. 40-47.
PROBLEM:
A finite rectangular plate is subjected to a temperature distribution in only one
direction as shown in figure. Determine the normal stress at point A.
GIVEN:
a
= 15 in
b
= 10 in
T
o
= -100
°F
t
= 1 in
E
= 30 x 10
6
psi
α
c
= 0.65 x 10
-5
in/in/
°F
MODELING HINTS:
Due to the double
symmetry in geometry and
loading, only one quarter
of the plate was analyzed.
COMPARISON OF RESULTS:
FFES8: Rectangular Plate Under Triangular
Thermal Loading
σ
xx
/ (E
α
T
o
) (Node 45)
Reference
Method 1
0.42
Method 2
0.40
COSMOSM
0.43
Same Boundary Condition
S
a
m
e
B
ounda
ry
C
ondi
ti
on
x
A
y
Figure FES8-1
In
de
x
In
de
x
Chapter 6 Verification Problems
6-14
COSMOSFFE Static
TYPE:
Static analysis, 2-D axisymmetric element (PLANE2D).
REFERENCE:
Timoshenko, S. P. and Goodier, “Theory of Elasticity,” McGraw-Hill Book Co.,
New York, 1961, pp. 448-449.
PROBLEM:
The hollow cylinder in plane strain is subjected to two independent load conditions.
1.
An internal pressure.
2.
A steady state axisymmetric temperature distribution given by the equation:
T(r) = (Ta/ln(b/a)) · ln(b/r)
where Ta is the temperature of the inner surface
and T(r) is the temperature at any radius.
FFES9: Hollow Thick-Walled Cylinder Subject to
Temperature and Pressure
GIVEN:
E
= 30 x 10
6
psi
a
= 1 in
b
= 2 in
ν =
0.3
α = 1 x 10
-6
1/deg
Pa = 100 psi
Ta = 100 leg
COMPARISON OF RESULTS:
At r = 1.2875 in (elements 13, 15)
σ
r
, psi
σ
θ
, psi
Theory)
- 398.34
- 592.47
COSMOSM
- 398.20
- 596.50
Figure FFES9-1
T(r)
Pa
x
y
b
a
0.1
Problem Sketch
Finite Element Model
a
b
Ta
In
de
x
In
de
x
COSMOSFFE Static
6-15
Chapter 6 Verification Problems
TYPE:
Static analysis, shell element (SHELL4, SHELL6).
REFERENCE:
Pawsley, S. F., “The Analysis of Moderately Thick to Thin Shells by the Finite
Element Method,” Report No. USCEM 70-l2, Dept. of Civil Engineering,
University of California, l970.
PROBLEM:
Determine the vertical deflections across the midspan of a shell roof under its own
weight. Dimensions and boundary conditions are shown in the figure below.
GIVEN:
r
= 25 ft
E
= 3 x 10
6
psi
ν =
0
Shell Weight = 90 lbs/sq ft
MODELING HINTS:
Due to symmetry, a quarter of the shell is considered for modeling. The distributed
force (self weight) is lumped at the nodes.
COMPARISON OF RESULTS:
Vertical Deflection at Midspan of free edge (Node 25):
FFES10: Cylindrical Shell Roof
δ
x
, (inch)
Theory
0.3024
COSMOSM
SHELL4
0.3036
In
de
x
In
de
x
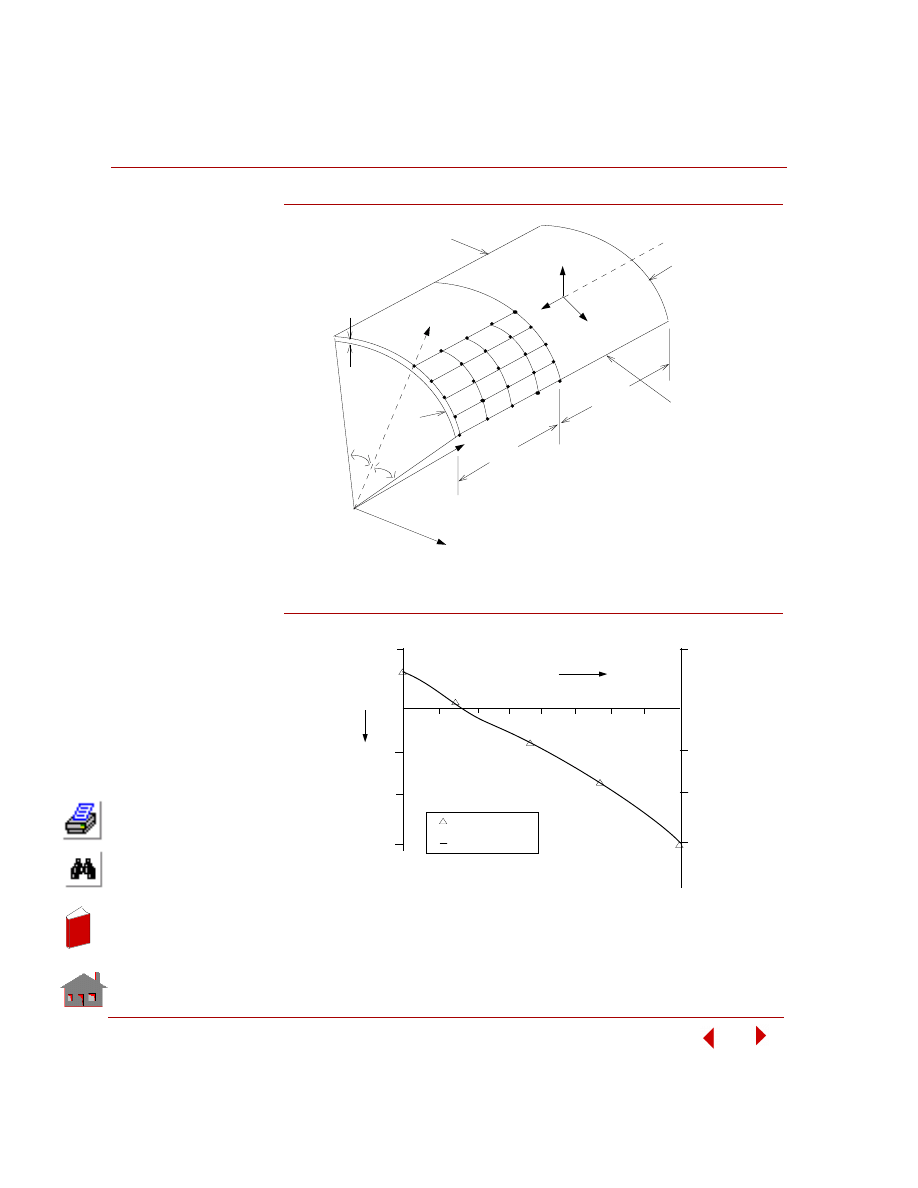
Chapter 6 Verification Problems
6-16
COSMOSFFE Static
Figure FFES10-1
Figure FFES10-2
25 ft
25 ft
Free Edge
Free Edge
v =
w = 0
t = 0.25 ft
v = w = 0
40
°
40
°
Y
Z
U
V
W
1
5
21
25
X
Problem Sketch and Finite
Element Model
r
0.18961
0.30365
-.2
0.07423
0.01335
0.004676
-.1
-.3
.1
.1
-.1
-.2
-.3
W
θ
COSMOS/M
EXACT
0
5
10 15
20
25
30
35
40
In
de
x
In
de
x
COSMOSFFE Static
6-17
Chapter 6 Verification Problems
TYPE:
Static analysis, shell elements (SHELL4).
REFERENCE:
Timoshenko, S. P., and Goodier, J. N., “Theory of Elasticity,” McGraw-Hill, New
York, 1951, p. 299.
PROBLEM:
Find the shear stress and the angle of twist for the square box beam subjected to a
torsional moment T.
GIVEN:
E
= 7.5 psi
ν
= 0.3
t
= 3 in
a
= 150 in
L
= 1500 in
T
= 300 lb in
COMPARISON OF RESULTS: :
FFES11: Torsion of a Square Box Beam
Shear Stress
τ,
lb/in
Rotation
θ
, rad
Theory
0.00222
0.0154074
COSMOSM
0.00222 (avg)
0.01503
In
de
x
In
de
x
Chapter 6 Verification Problems
6-18
COSMOSFFE Static
Figure FFES11-1
a
t
Y
Z
X
L
Z
Problem Sketch
Section
I-I
I
I
y
z
x
150
1500
.25
.5
.25
150
Finite Element Model
T
In
de
x
In
de
x

COSMOSFFE Static
6-19
Chapter 6 Verification Problems
TYPE:
Static analysis, solid and composite solid elements (SOLID).
REFERENCE:
Reddy, N. J. “Exact Solutions of Moderately Thick Laminated Shells,” J. Eng.
Mech. Div. ASCE, Vol. 110, (1984), pp. 794-809.
PROBLEM:
Calculate the center deflection of a simply supported spherical cap under uniform
pressure (q = 1) in the direction normal to the cap surface. To impose simply-
supported boundary conditions by solid elements, 2 layers of elements through the
thickness are required.
To capture the geometry of a curved surface by a bi-linear shape function accurately,
at least 8 elements per side have to be used. The model used below is an 8x8x2 mesh.
GIVEN:
MODELING HINTS:
FFES12: Spherical Cap Under Uniform Pressure
(Solid)
Geometry:
R
= 96
h
= 0.32 in
Length of side a = b = c = d = 32 in
Material Properties:
E
= 1E7 psi
ν = 0.3
Boundary Conditions
Due to symmetry:
1. All nodes on plane A, Uy = 0
2. All nodes on plane B, Ux = 0
Simply supported:
1. All nodes on side c, radial displacement
= 0, Disp. on plane C = 0
2. All nodes on side d, radial displacement
= 0, Disp. on plane D = 0
In
de
x
In
de
x
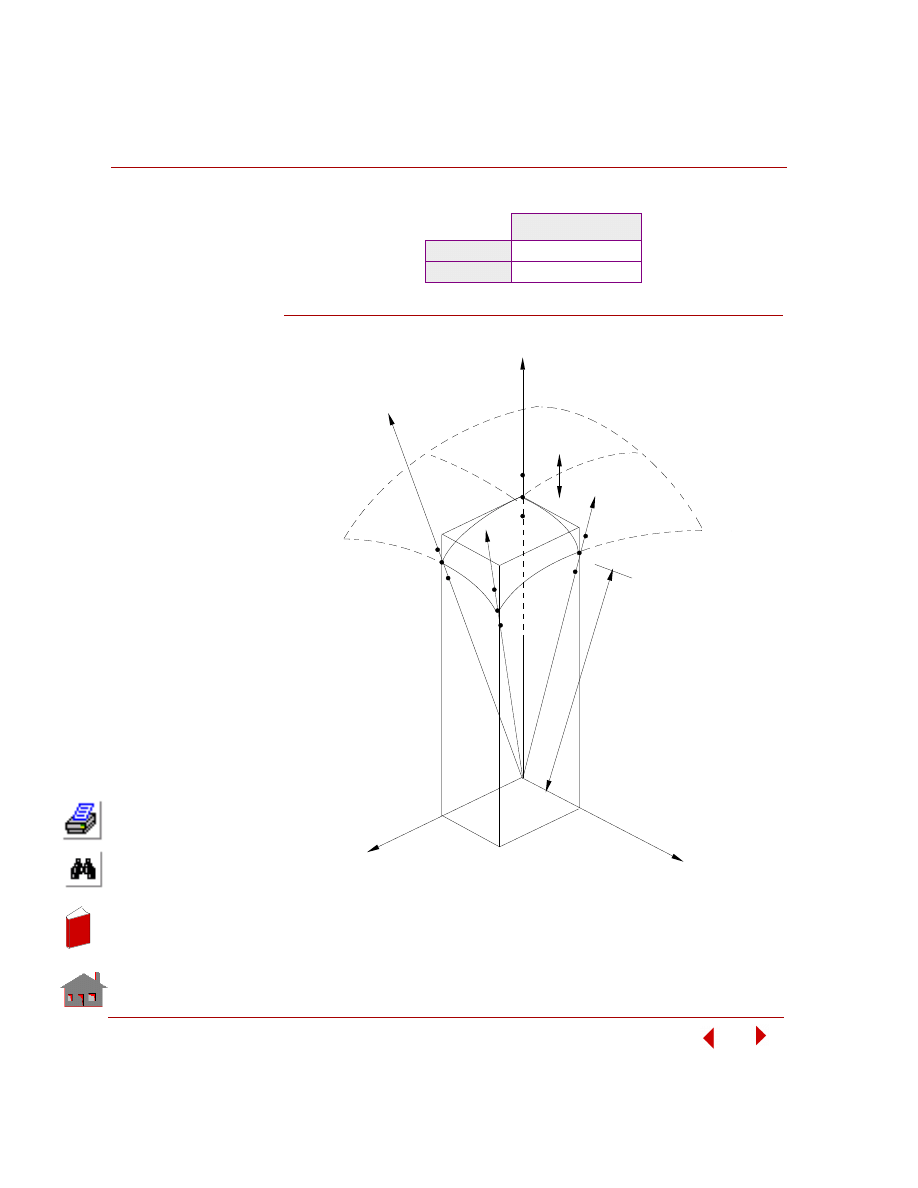
Chapter 6 Verification Problems
6-20
COSMOSFFE Static
COMPARISON OF RESULTS:
Figure FFES12-1
W
max
(inch)
Theory
0.3139E-2
COSMOSM
0.3232E-2
243
a
c
d
1
sym.
9
162
81
R
PLAN
E C
PLAN
E D
PLAN
E A
X
Y
Z
b
PLAN
E D
PLAN
E C
Problem Sketch and Finite Element Model
PLAN
E B
163
82
h
90
171
sym
.
154
73
235
In
de
x
In
de
x
COSMOSFFE Static
6-21
Chapter 6 Verification Problems
TYPE:
Static analysis, axisymmetric (PLANE2D) elements, centrifugal loading
;
.
REFERENCE:
S. P. Timoshenko and J. N. Goodier, “Theory of Elasticity,” McGraw-Hill, New
York, l970, p. 80.
PROBLEM:
A solid disk rotates about center 0 with angular velocity
ω. Determine the stress
distribution in the disk.
GIVEN:
COMPARISON OF RESULTS:
Figure FFES13-1
FFES13: Rotating Solid Disk
E
= 30 x l0
6
psi
DENS = 0.02 lb sec
2
/in
4
ν
= 0.3
h
= l in
ω = 25 rad/sec
R
= 9 in
Location
Element 1 (r = 0.5 inch)
Location
Element 9 (r = 8.5 inch)
Stress
σ
r
psi
σ
θ
psi
σ
r
psi
σ
θ
psi
Theory
416.37
416.91
45.12
203.16
COSMOSM
416.82
416.82
46.18
202.03
1
X
R
h
20
Y
2
Y
19
1
9
2R
Problem Sketch and Finite Element Model
ω
In
de
x
In
de
x

Chapter 6 Verification Problems
6-22
COSMOSFFE Static
TYPE:
Static analysis, shell elements (SHELL4).
PROBLEM:
Calculate reactions and deflections of a cantilever beam subject to a concentrated
load at tip.
Figure FFES14-1
FFES14: Reactions and Deflections of a
Cantilever Beam
GIVEN:
COMPARISON OF RESULTS:
E
= 30E6 psi
h
= 1 in
L
= 10 in
W = 4 in
P
= 8 lb
Theory
COSMOSM
SHELL4
Tip Deflection (Node 33)
2.667 x 10
-4
2.667 x 10
-4
Total Force Reaction
8 lb
8 lb
Total Moment Reaction
80 lb-in
80 lb-in
L
P
1
31
40
10
45
55
33
11
1
W
Problem Sketch
Finite Element Model
Y
X
h
In
de
x
In
de
x
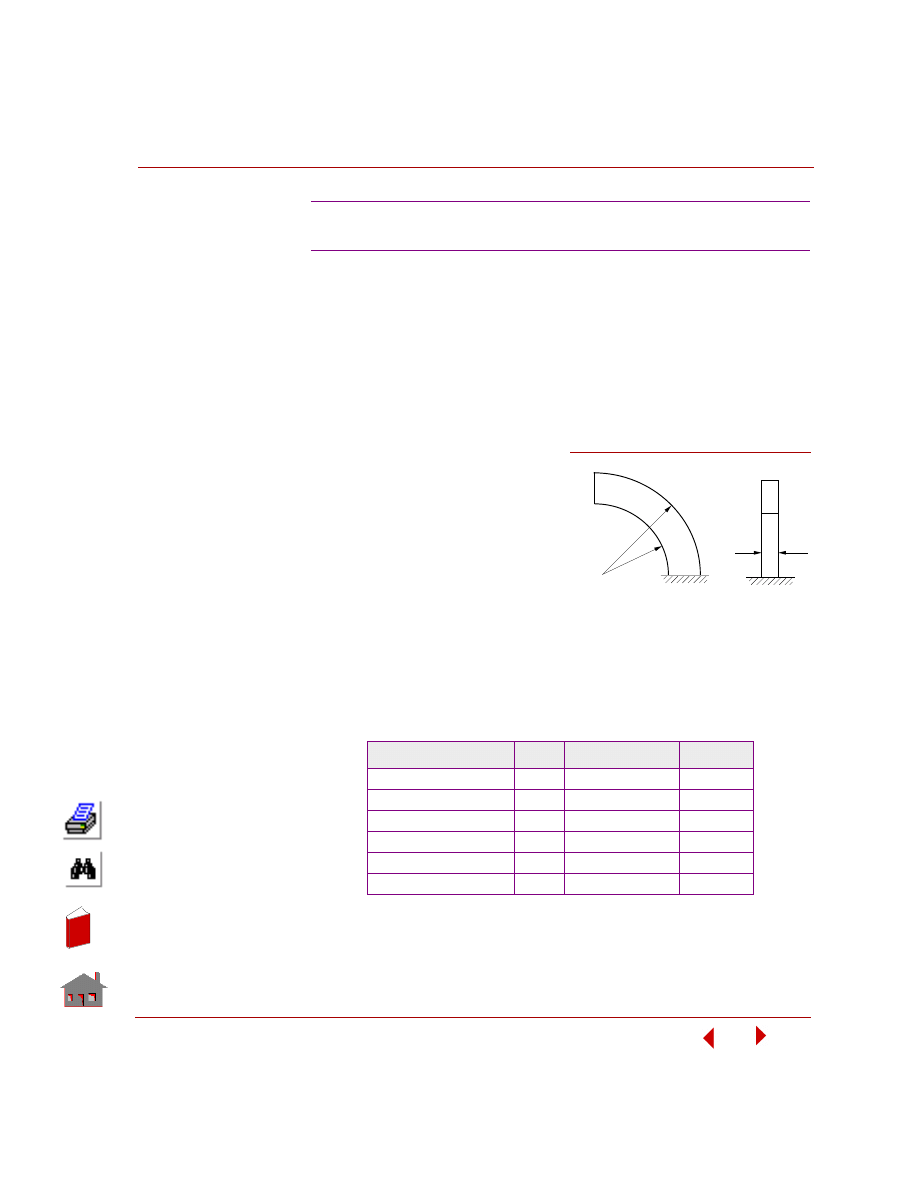
COSMOSFFE Static
6-23
Chapter 6 Verification Problems
TYPE:
Static analysis, multi-field elements (4-node PLANE2D, 8-node PLANE2D,
SHELL4T, 6-node TRIANG, 8-node SOLID, 10-node TETRA4R10 and 20-node
SOLID).
REFERENCE:
Roark, R. J., “Formulas for Stress and Strain,” 4th Edition, McGraw-Hill Book Co.,
New York, l965, pp. 166.
PROBLEM:
A curved beam is clamped at one
end and subjected to a shear pressure
P at the other end. Determine the
deflection at the free end.
GIVEN:
COMPARISON OF RESULTS:
Deflections at free end by theoretical solution is equal to 0.08854 in
FFES15A, 15B, 15C, 15D, 15E, 15F: Deflection of a
Curved Beam
E
= 10E6 psi
ν
= 0.25
R
l
= 4.12 in
R
2
= 4.32 in
t
= 0.1 in
p
= 50 lb/in
2
(total force
is 1 lb)
Element
Order
COSMOSM
δ
y
in
2
Error (%)
PLANE2D (4-Node) (15A) First
0.07919
10.56
PLANE2D (8-Node) (15B) Second
0.08843
0.12
TRIANG (6-Node) (15C)
Second
0.08842
0.14
TETRA10 (15D)
Second
0.08839
0.17
SOLID (8-Node) (15E)
First
0.07852
11.32
SOLID (20-Node) (15F)
Second
0.08847
0.08
Figure FFES15-1
P
R
R
2
1
t
Problem Sketch
In
de
x
In
de
x
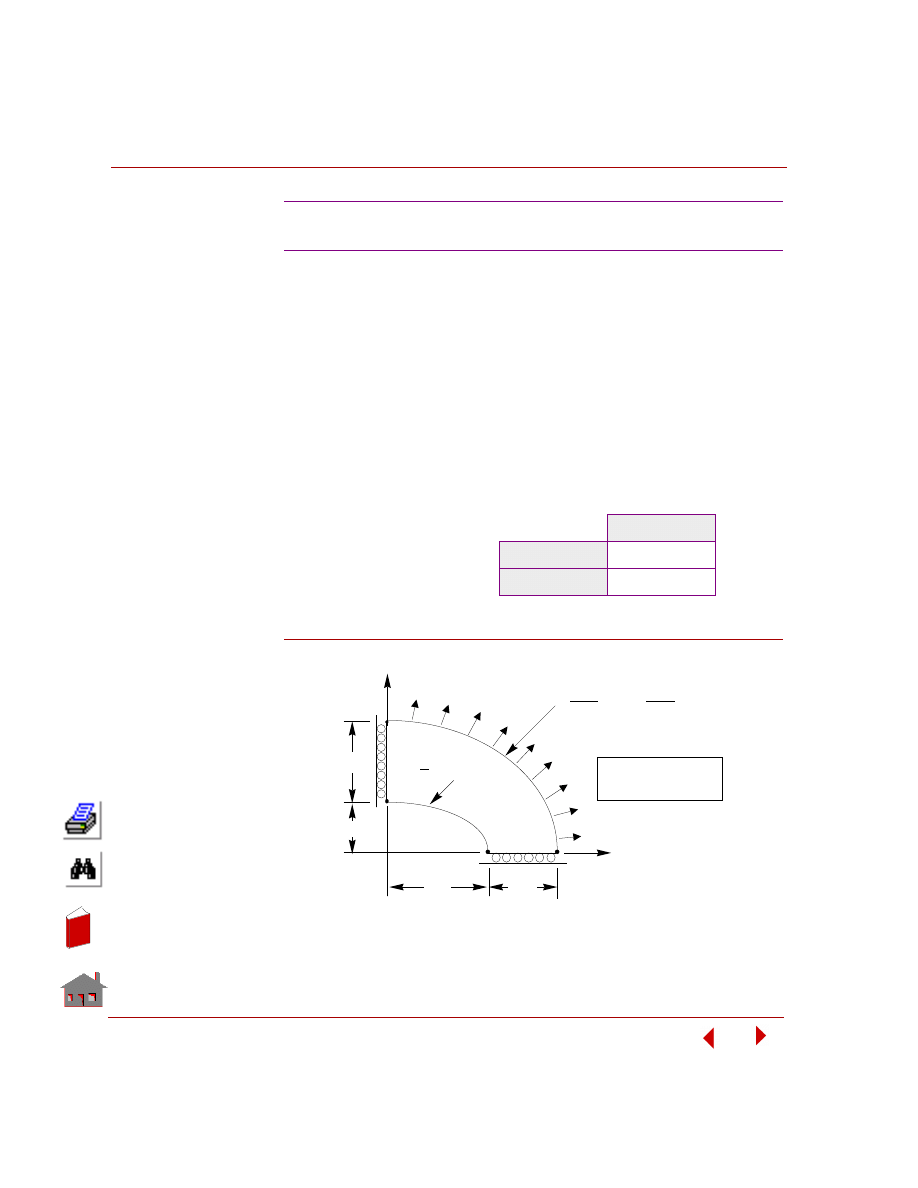
Chapter 6 Verification Problems
6-24
COSMOSFFE Static
TYPE:
Static analysis, plane stress triangular p-element (6-node TRIANG).
REFERENCE:
Barlow, J., and Davis, G. A. O., “Selected FE Benchmarks in Structural and Thermal
Analysis,” NAFEMS Rept. FEBSTA, Rev. 1, October, 1986, Test No. LG1.
PROBLEM:
Calculate the stresses at point D of an elliptic membrane under a uniform outward
pressure.
Figure FFES16-1
FFES16: P-Method Analysis of an Elliptic
Membrane Under Pressure
GIVEN:
COMPARISON OF RESULTS
E = 210 x 10
3
MPa
ν = 0.3
t = 0.1
p = 10 MPa
σ
y
, at Point D
Theory
92.7
COSMOSM
92.6
x
y
2.0
1.25
D
2
y
2
x
2
All dimensions in meters
Thickness = 0.1
1.0
1.75
A
B
x
3.25
2
2
Y
2.75
= 1
C
+ = 1
(
(
(
(
(
)
)
)
)
)
+
+
+
+
+
(
(
(
(
(
)
)
)
)
)
(
(
(
(
(
)
)
)
)
)
In
de
x
In
de
x
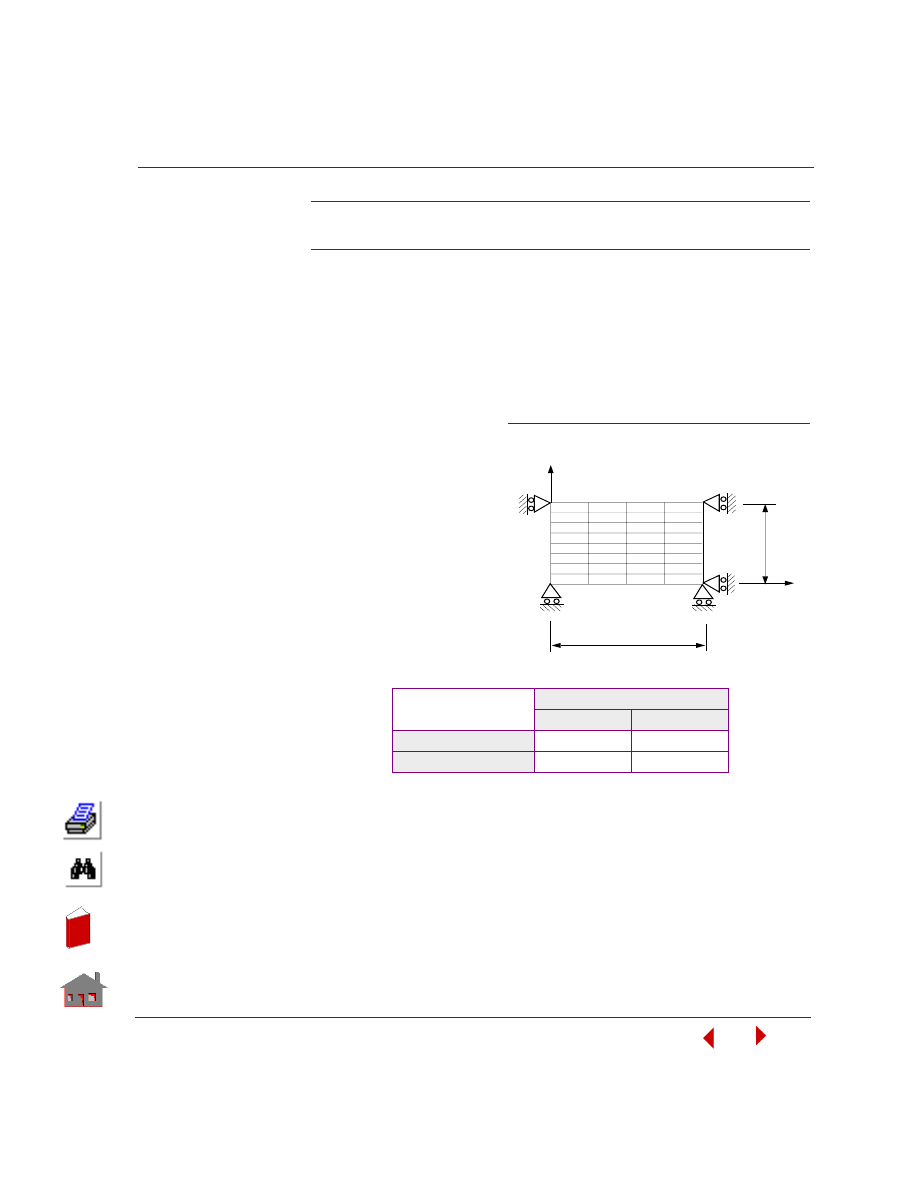
COSMOSFFE Static
6-25
Chapter 6 Verification Problems
TYPE:
Linear thermal stress analysis, plane continuum element (PLANE2D).
PROBLEM:
Determine the deflections and thermal stresses in the plate due to uniform changes
of temperature equal to 100
° F and 200° F.
GIVEN:
t
= 0.1 in
x
= 0.00001 in/in/
°F
ν
= 0
E
= 30,000 ksi
GIVEN:
t
= 0.1 in
x
= 0.00001 in/in/
°F
ν
= 0
E
= 30,000 ksi
COMPARISON OF RESULTS:
FFES17: Thermal Stress Analysis of a Flat Plate
σ
x
for all elements
T = 100
°
F *
T = 200
°
F
Theory
- 30 ksi
- 60 ksi
COSMOSM
- 30 ksi
- 60 ksi
* The temperature in the input file corresponds to T = 200
°
F. You need to delete the applied temperature using the
NTNDEL command and apply tempera-ture of 100
°
F
using the NTND command.
Figure FFES17-1
Same Boundary Condition
S
am
e
B
ounda
ry
C
ondi
tion
x
A
y
In
de
x
In
de
x
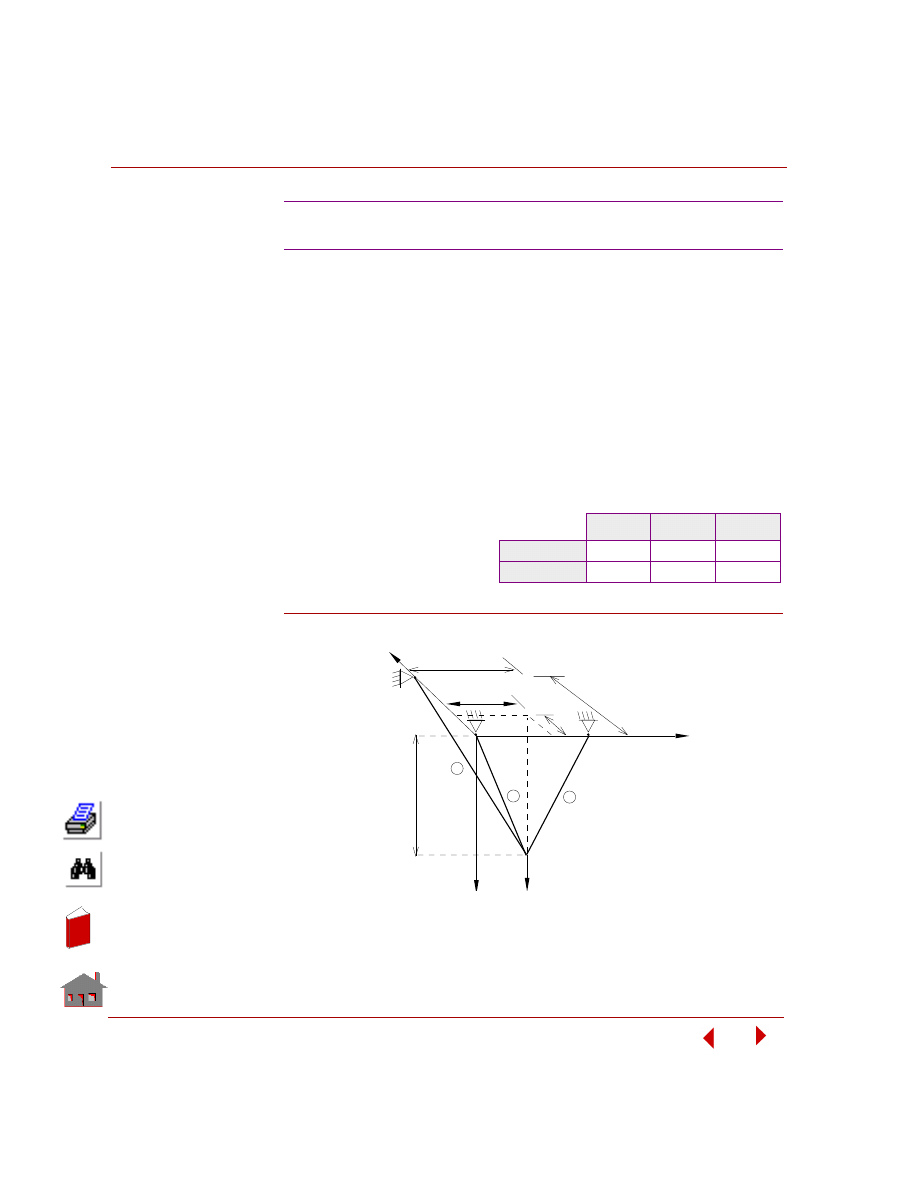
Chapter 6 Verification Problems
6-26
COSMOSFFE Static
TYPE:
Static analysis, truss element (TRUSS3D).
REFERENCE:
Beer, F. P., and Johnston, E. R., Jr., “Vector Mechanics for Engineers: Statics and
Dynamics,” McGraw-Hill Book Co., Inc. New York, 1962, p. 47.
PROBLEM:
A 50 lb load is supported by three bars which are attached to a ceiling as shown.
Determine the stress in each bar.
Figure FFES18-1
FFES18: Pin Jointed Truss
GIVEN:
COMPARISON OF RESULTS
Area of each bar = 1 in
2
E = 30 x 10
6
psi
σ
1-4
, psi
σ
2-4
, psi
σ
3-4
, psi
Theory
10.40
31.20
22.90
COSMOSM
10.39
31.18
22.91
x
2
2
6 ft
2 ft
6 ft
8 ft
4 ft
4
1
y
1
3
3
In
de
x
In
de
x
COSMOSFFE Static
6-27
Chapter 6 Verification Problems
TYPE:
Linear thermal stress analysis, truss elements (TRUSS2D).
REFERENCE:
Hsieh, Y. Y. “Elementary Theory of Structures,” Prentice-Hall, Inc., 1970, pp. 200-
202.
PROBLEM:
Determine the member forces of truss shown below subject to the rise of 50
° F at the
top chords, elements 13 and 14.
GIVEN:
E = 30 x 10
6
psi
Expansion coefficient =
α = 0.65 x 10
-5
/
°F
L(ft) / A(in
2
) = 1 (for all members)
COMPARISON OF RESULTS:
FFES19: Thermal Stress Analysis of a Truss
Structure
Member Forces (kips)
Members
Theory
COSMOSM
Members
Theory
COSMOSM
1
0
0
8
35.1
35.1
1
0
0
8
35.1
35.1
2
0
0
9
0
0
3
- 21.1
- 21.1
10
0
0
4
0
0
11
+ 35.1
+ 35.1
5
0
0
12
0
0
6
- 28.1
- 28.1
13
0
0
7
- 28.1
- 28.1
14
- 21.1
- 21.1
In
de
x
In
de
x
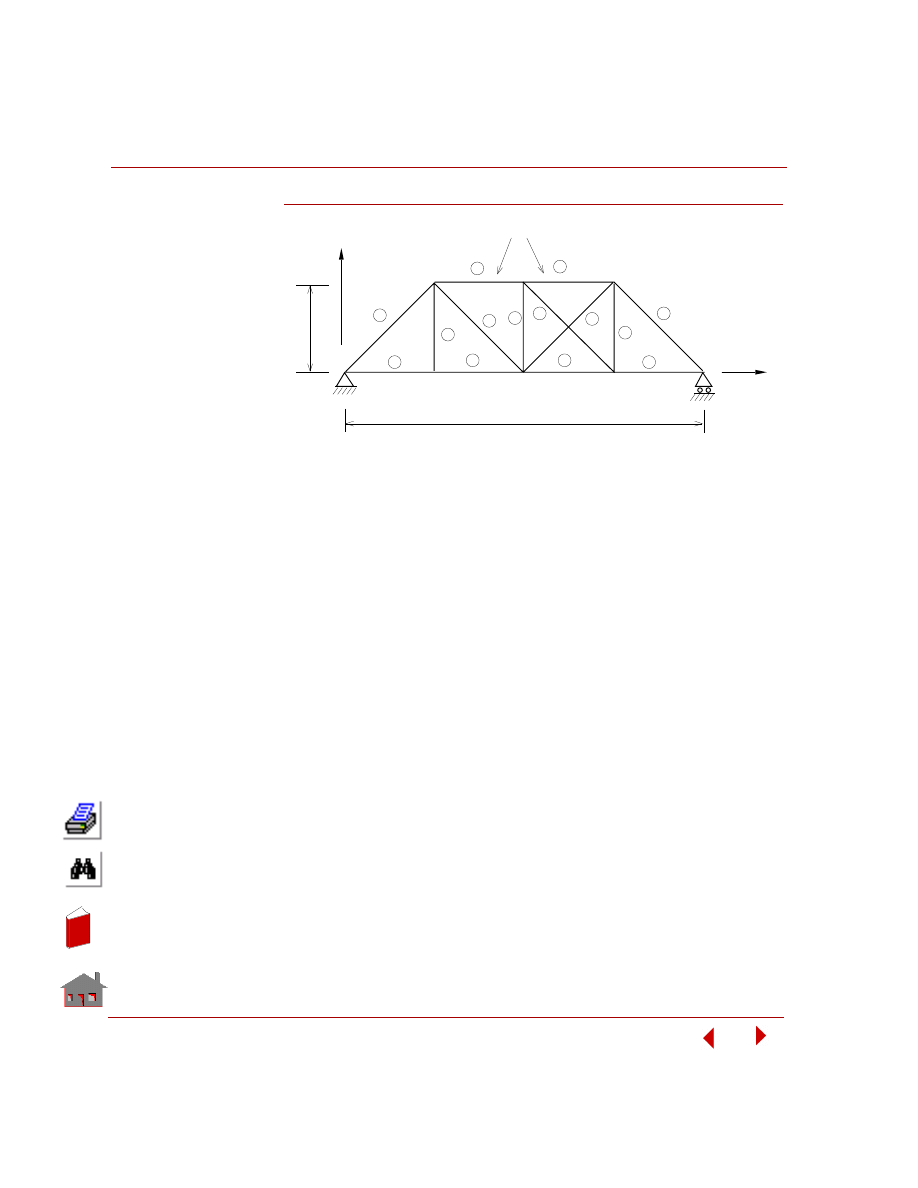
Chapter 6 Verification Problems
6-28
COSMOSFFE Static
Figure FFES19-1
14
50
°
F
x
8
6
4
2
7
5
3
1
13
8
11
12
10
1
9
5
3
2
4
7
6
4 x @ 24 ft = 96 ft
32 ft
Y
Problem Sketch and Finite Element Model
In
de
x
In
de
x
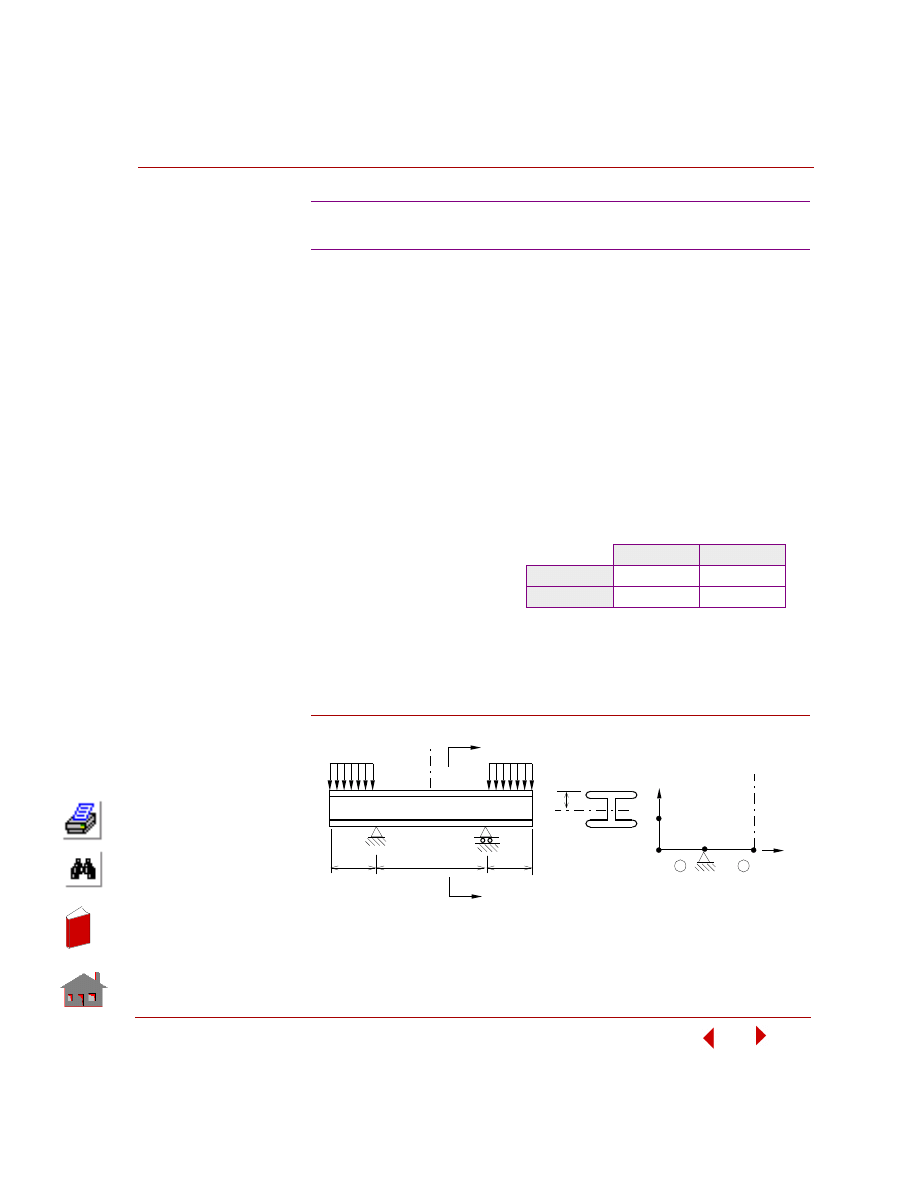
COSMOSFFE Static
6-29
Chapter 6 Verification Problems
TYPE:
Static analysis, beam elements (BEAM3D).
REFERENCE:
Timoshenko, S. P., “Strength of Materials, Part 1, Elementary Theory and
Problems,” 3rd Ed., D. Van Nostrand Co., Inc., New York, 1965, p. 98.
PROBLEM:
A standard 30" Wide Flange beam is supported as shown below and loaded on the
overhangs by a uniformly distributed load of 10,000 lb per ft. Determine the
maximum stress in the middle portion of the beam and the deflection at the center of
the beam.
MODELING HINTS:
Use consistent length units. A half-model has been used because of symmetry.
Resultant force and moment have been applied at node 2 instead of distributed load.
Figure FFES20-1
FFES20: Beam Stresses and Deflections
GIVEN:
Area = 50.65 in
2
E
= 30 x 10
6
psi
p
= 10,000 lb/ft
COMPARISON OF RESULTS:
At the middle of the span (node 3):
σ
max
, psi
δ,
inch
Theory
11400.0
0.182
COSMOSM
11400.0
0.182
Finite Element Model
z
15"
Section a-a
10'
10'
20'
CL
a
Problem Sketch
a
P
P
C
2
1
x
3
2
L
4
y
1
In
de
x
In
de
x

Chapter 6 Verification Problems
6-30
COSMOSFFE Static
TYPE:
Static analysis, beam elements (BEAM3D).
REFERENCE
Gere, J. M. and Weaver, W. Jr., “Analysis of Framed Structures,” D. Van Nostrand
Co., 1965.
PROBLEM:
Determine the end forces of a clamped beam due to a 1 inch settlement at the right
end.
GIVEN:
E
= 30 x 10
6
psi
l
= 80 in
A
= 4 in
2
I
= 1.33 in
4
h
= 2 in
ANALYTICAL SOLUTION:
Reaction: R = -12EI / L
3
Moment: M = 6EI / L
2
COMPARISON OF RESULTS:
FFES21A: Clamped Beam Subject to Imposed
Displacement
Theory
COSMOSM
Imposed Displacement (in)
- 1.0
- 1.0
End Shear (lb)
- 937.5
- 937.5
End Moment (lb-in)
37,500.0
37,500.0
In
de
x
In
de
x
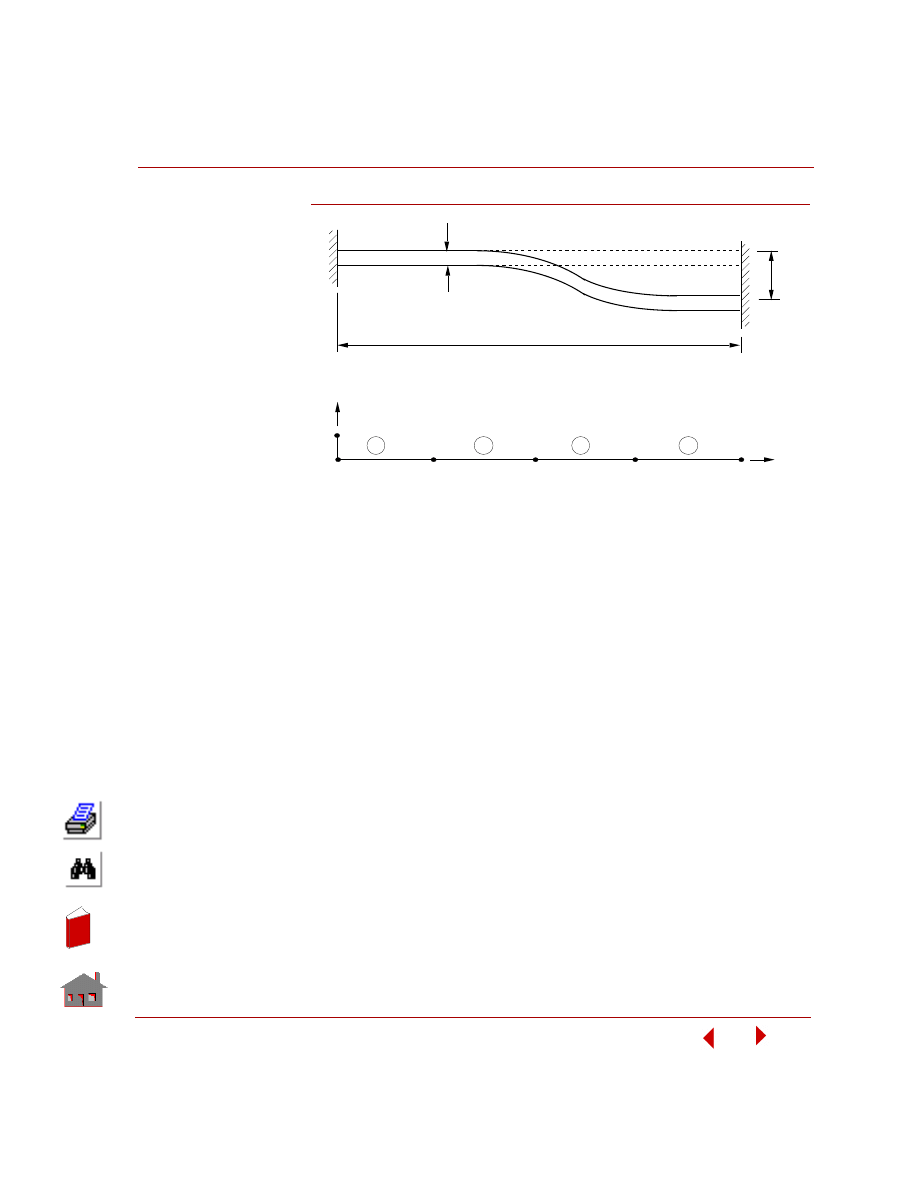
COSMOSFFE Static
6-31
Chapter 6 Verification Problems
Figure FFES21A-1
1
2
3
4
5
1.0 in
h
6
x
y
4
3
2
1
Problem Sketch
Finite Element Model
L
In
de
x
In
de
x
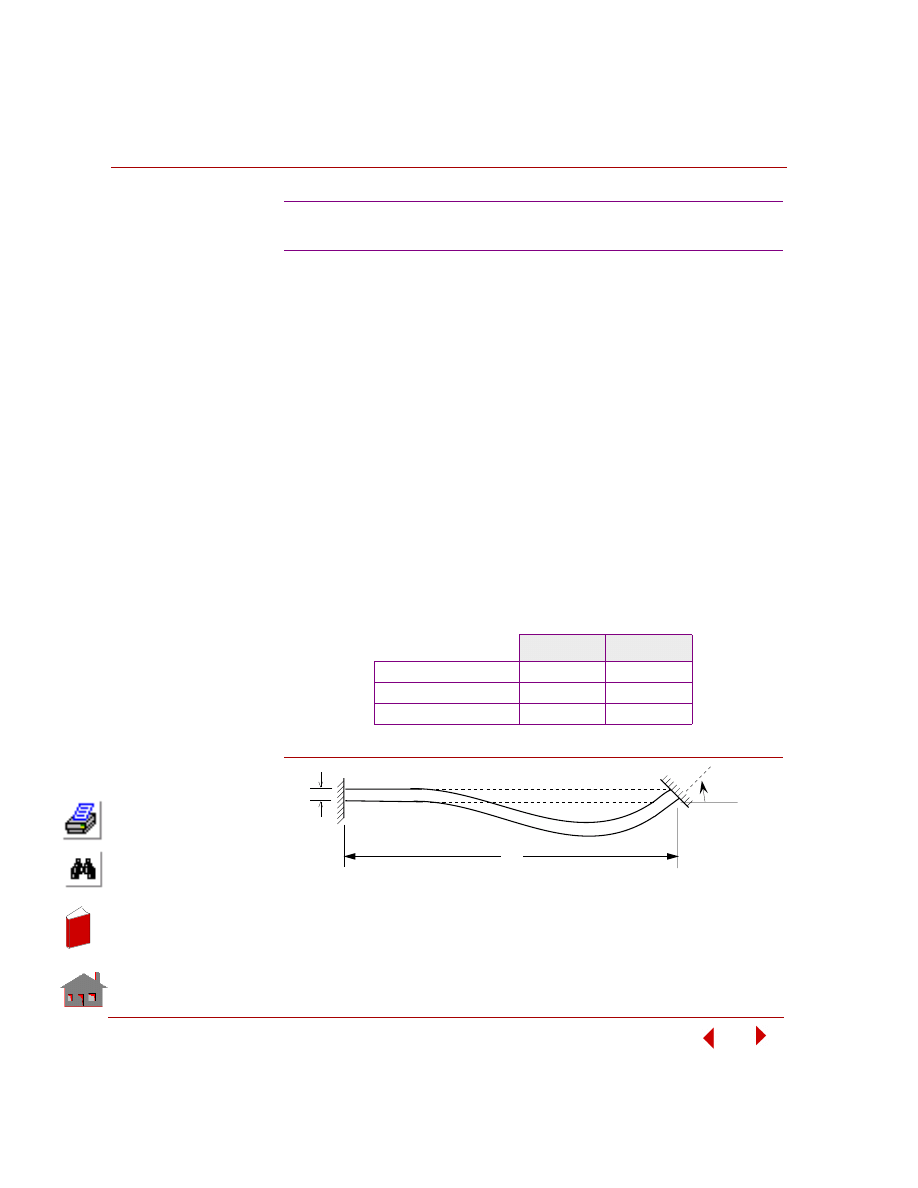
Chapter 6 Verification Problems
6-32
COSMOSFFE Static
TYPE:
Static analysis, beam elements (BEAM3D).
REFERENCE:
Gere, J. M. N. and Weaver, W. Jr., “Analysis of Framed Structures,” D. Van Nostrand
Co., 1965.
PROBLEM:
Determine the end forces of a clamped-clamped beam due to a 1 radian imposed
rotation at the right end.
COMPARISON OF RESULTS:
Figure FFES21B-1
FFES21B: Clamped Beam Subject to Imposed
Rotation
GIVEN:
E
= 30 x 10
6
psi
L
= 80 in
A
= 4 in
2
I
= 1.3333 in
4
h
= 2 in
ANALYTICAL SOLUTION:
Reaction: R = -6EI / L
2
Moment: M = 4EI / L
Theory
COSMOSM
Imposed Rotation (1 rad)
1
1
End Shear
- 37,500
- 37,500
End Moment
- 2,000,000
- 2,000,000
φ
= 1 rad
2
L
h
Problem Sketch
In
de
x
In
de
x
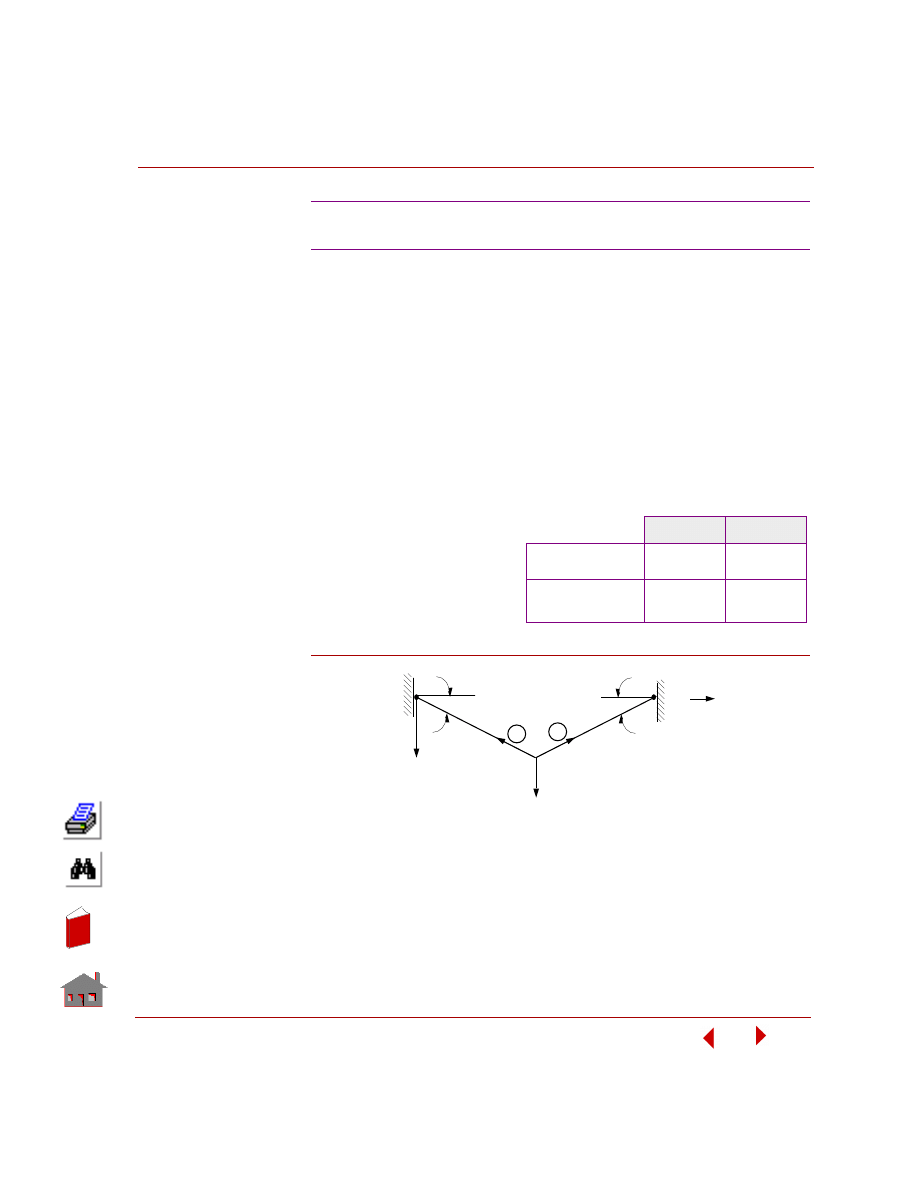
COSMOSFFE Static
6-33
Chapter 6 Verification Problems
TYPE:
Static analysis, truss element (TRUSS3D).
REFERENCE:
Timoshenko, S. P., and MacCullough, Glesson, H., “Elements of Strength of
Materials,” D. Van Nostrand Co., Inc., 3rd edition, June 1949, p. 13.
PROBLEM:
A structure consisting of two equal steel bars, 15 feet long and with hinged ends, is
submitted to the action of a vertical load P. Determine the forces in the members AB
and BC along with the vertical deflection at B.
Figure FFES22-1
FFES22: Deflection of a Hinged Support
GIVEN:
P
= 5000 lbs
θ = 30°
AB = BC = 15 ft
E
= 30 x 10
6
psi
Cross-sectional area
= 0.5 in
2
COMPARISON OF RESULTS:
Theory
COSMOSM
Vertical Deflection at
B in inches
0.12
0.12
Forces in Members
AB and BC in lbs
5000
5000
Y
3
C
2
1
B
P
2
Z
1
θ
θ
A
Problem Sketch and Finite Element Model
In
de
x
In
de
x
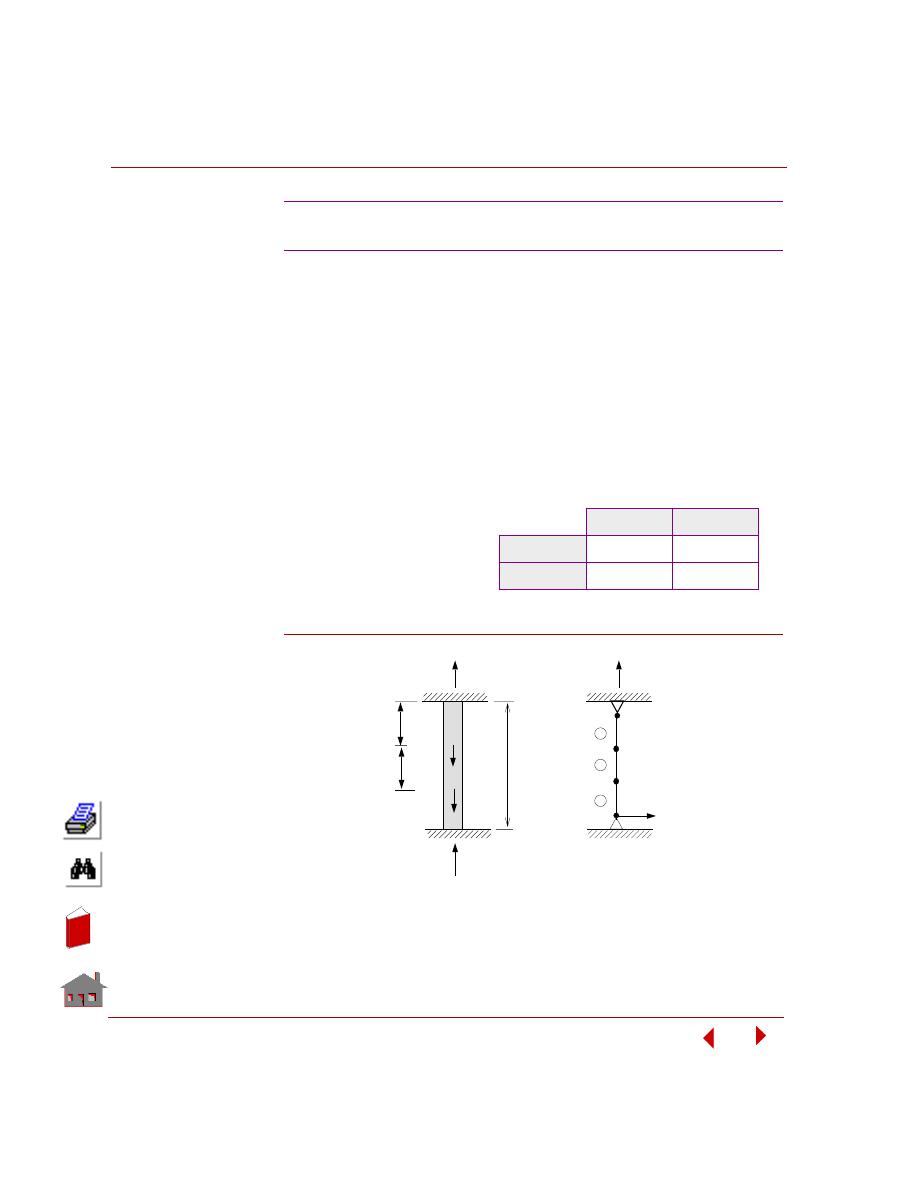
Chapter 6 Verification Problems
6-34
COSMOSFFE Static
TYPE:
Static analysis, truss elements (TRUSS3D).
REFERENCE:
Timoshenko, S. P., “Strength of Materials, Part 1, Elementary Theory and
Problems,” 3rd edition, D. Van Nostrand Co., Inc., 1956, p. 26.
PROBLEM:
A prismatic bar with built-in ends is loaded axially at two intermediate cross-
sections by forces F1 and F2. Determine the reaction forces R1 and R2.
Figure FFES23-1
FFES23: Statically Indeterminate Reaction Force
Analysis
GIVEN:
COMPARISON OF RESULTS:
a
= b = 0.3 L
L =
10
in
F
1
=
2F
2
= 1000 lb
E
= 30 x 10
6
psi
R
1
lbs
R
2
lbs
Theory
900
600
COSMOSM
900
600
Y
X
1
2
3
4
3
2
1
Finite Element Model
F
F
a
b
R
L
1
1
2
Problem Sketch
R2
In
de
x
In
de
x

COSMOSFFE Static
6-35
Chapter 6 Verification Problems
TYPE:
Static analysis, truss elements (TRUSS3D).
REFERENCE:
Timoshenko, S. P. and Young, D. H. “Theory of Structures,” end Ed., McGraw-Hill,
New York, 1965, pp. 330-331.
PROBLEM:
The simple space truss shown in the figure below consists of two panels ABCD and
ABEF, attached to a vertical wall at points C, D, E, F, the panel ABCD being in a
horizontal plane. All bars have the same cross-sectional area, A, and the same
modulus of elasticity, E.
Calculate:
1.
The axial force produced in the
redundant bar AD by the vertical
load P = 1 kip at joint A
(FFES24A).
2.
The thermal force induced in the
bar AD if there is a uniform rise
in temperature of 50
° F
(FFES24B).
GIVEN:
E
= 30 x 10
6
psi
α
= 6.5 x 10
-6
/
°F
A =
1in
2
L
= 4 ft
COMPARISON OF RESULTS:
For Element 2:
FFES24A, FFES24B: Space Truss with Vertical
Load
S14A
S14B
Theory
56.0 lb
-1259.0 lb
COSMOSM
55.92 lb
-1292.4 lb
Figure FFES24-1
E
6
x
y
z
4
L
1
A
5
4
1
2
3
6
5
7
P
Problem Sketch and Finite
Element Model
2
F
D
C
3
L
L
In
de
x
In
de
x
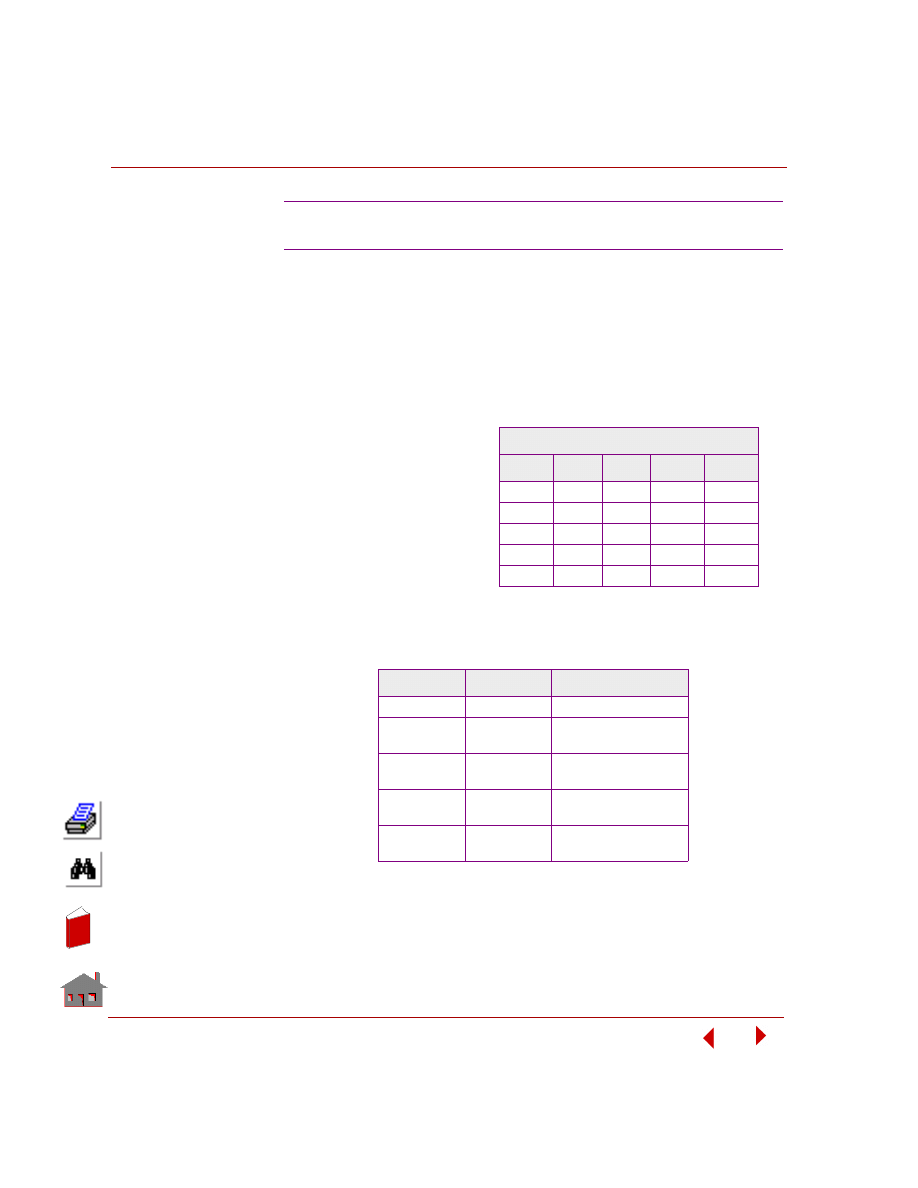
Chapter 6 Verification Problems
6-36
COSMOSFFE Static
TYPE:
Linear thermal stress analysis, beam elements (BEAM3D).
REFERENCE:
Rygol, J., “Structural Analysis by Direct Moment Distribution,” Gordon and Breach
Science Publishers, New York, l968, pp. 292-294.
PROBLEM:
COMPARISON OF RESULTS:
Moments (lb-in):
FFESS25: Thermal Stress Analysis of a Frame
An irregular frame
subjected to differential
temperature. Find
member end moments.
GIVEN:
E
= 192,857 tons/ft
2
α = 0.0000l ft/ft °C
Member Specifications
Member
d (ft)
b (ft)
Ar-r (ft)
lt-t (ft)
1
1.5
1.5
2.25
0.422
2
2.25
1.25
2.8125
1.187
3
2.0
1.5
3.0
1.0
4
2.5
1.25
3.125
1.628
5
2.0
1.5
3.0
1.0
Member No.
COSMOSM
Reference Solution
1
- 17.96
- 17.96
2
+ 17.96
- 42.87
+ 17.96
- 42.96
3
+ 38.73
- 41.92
+ 38.64
- 41.96
4
+ 84.79
- 82.61
+ 84.92
- 82.61
5
- 57.50
+ 82.61
- 57.40
+ 82.61
In
de
x
In
de
x
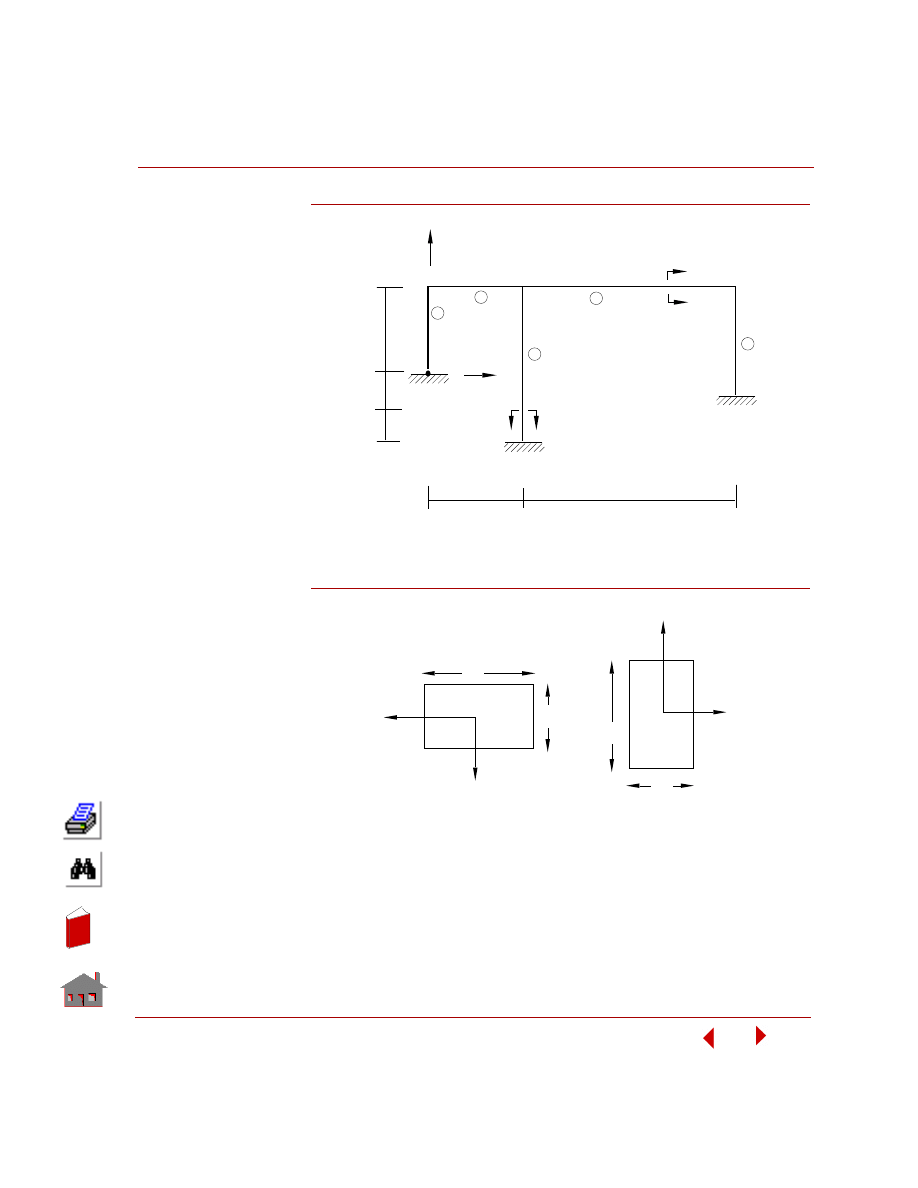
COSMOSFFE Static
6-37
Chapter 6 Verification Problems
Figure FFES25-1
Figure FFES25-2
4
2
1
3
5
1
2
3
4
5
6
18'
27'
3'
3'
12'
A
A
B
B
Y
X
40 C
o
80 C
o
10 C
10 C
o
o
Problem Sketch and Finite Element Model
d
b
s
b
t
s
d
Section A-A
Section B-B
t
In
de
x
In
de
x

Chapter 6 Verification Problems
6-38
COSMOSFFE Static
TYPE:
Linear thermal stress analysis, beam elements (BEAM2D).
PROBLEM:
Determine displacements and end forces of the frame shown in the figure below due
to temperature rise at the nodes and thermal gradients of members as specified
below.
COMPARISON OF RESULTS:
Displacements at node 2 (in):
Figure FFES26-2
FFES26: Thermal Stress Analysis of a Simple
Frame
GIVEN:
E
= 30,000 kips/in
2
α
= 0.65 x l0 in/in/°F
Element No.
Difference in Temperature
S-dir
T-dir
1
72
°
F
0
2
0
13.5
°
F
δ
x
δ
y
Theory
- 0.0583
0.1157
COSMOSM
- 0.0583
+ 0.1168
2
50
°
F
100
°
F
50
°
F
A
B
B
A
240"
1
2
x
120"
1
y
Problem Sketch and Finite Element Model
3
width
= 5"
t
depth
s(y)
(z)
t (z)
s(y)
width
= 3"
depth
= 6"
In
de
x
In
de
x

COSMOSFFE Static
6-39
Chapter 6 Verification Problems
TYPE:
Static analysis, beam elements (BEAM3D).
REFERENCE:
Laursen, Harold I., “Structural Analysis,” McGraw-Hill Book Co., Inc., New York,
1969, pp. 310-312.
PROBLEM:
Determine the forces in the beam members under the loads shown in the figure.
Consider two separate load cases represented by the uniform pressure and the
concentrated force. Set up the input to solve each one individually and then combine
them together to obtain the final result.
GIVEN:
I
y
y
= I
zz
= 0.3215 ft
4
I
= 0.6430 ft
4
A
1
= 3.50 ft
2
A
2,3
= 4.40 ft
3
A
4
= 2.79 ft
2
E
= 432 x 10
4
K/ft
2
Areas of members were made to be larger than the actual area in order to neglect
axial deformation.
COMPARISON OF RESULTS:
The results are shown in the figure below with COSMOSM results shown in
parentheses.
FFES27: Frame Analysis with Combined Loads
In
de
x
In
de
x
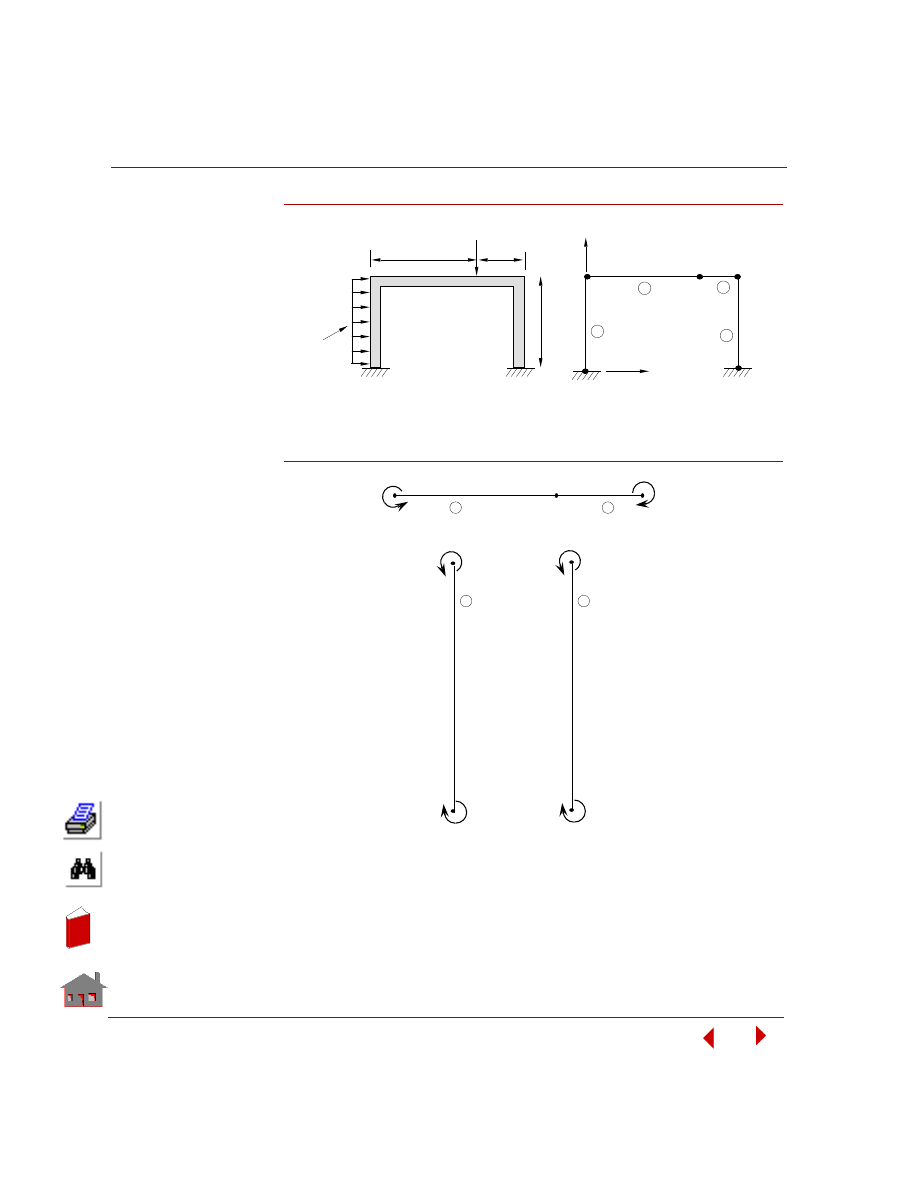
Chapter 6 Verification Problems
6-40
COSMOSFFE Static
Figure FFES27-1
Figure FFES27-2
5
4
3
2
1
Y
X
2k
5'
15'
15'
0.5 K/ft
E, I
1
2
3
4
Problem Sketch
Finite Element Model
4
2
3
1
1
2
3
4
5
2
10.547 K ft
(10.51)
6.766K ft
(6.76)
28.256K ft
(28.32)
10.682 K ft
(10.67)
In
de
x
In
de
x
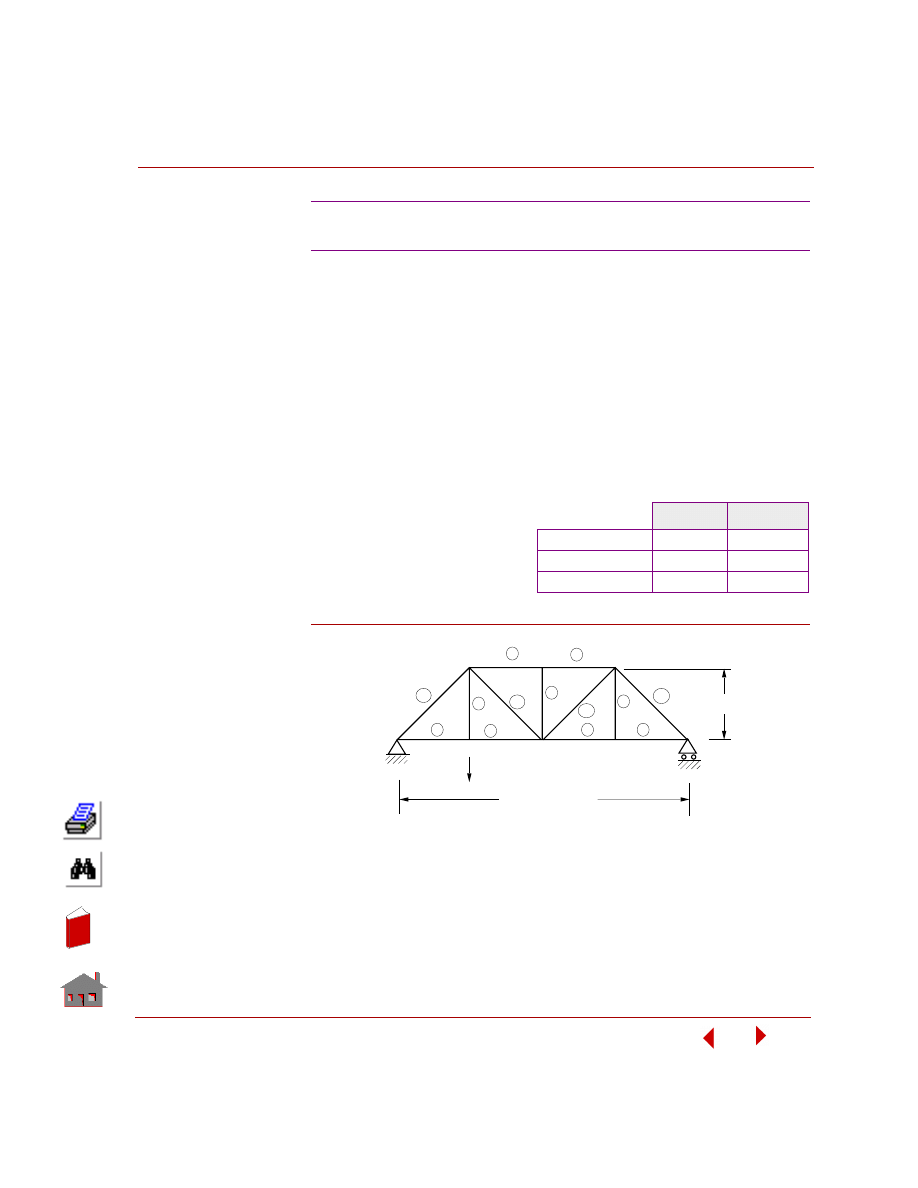
COSMOSFFE Static
6-41
Chapter 6 Verification Problems
TYPE:
Static analysis, truss elements (TRUSS2D).
REFERENCE:
Hsieh, Y. Y., “Elementary Theory of Structures,” Prentice-Hall Inc., l970, pp. l62-
l63.
PROBLEM:
Calculate the reactions and the vertical deflection of joint 2 of the loaded truss
shown below subject to a concentrated load.
Figure FFES28-1
FFES28: Truss Structure Subject to a
Concentrated Load
GIVEN:
COMPARISON OF RESULTS:
E
= 30,000 kips/in
2
P
= 64 kips
L (ft)/A(in) = 1 for all members
Theory
COSMOSM
Deflection of Joint 2
0.006733 in
0.006733 in
Reaction at Node 1
48 K
48 K
Reaction at Node 5
16 K
16 K
12
13
11
10
6
5
2
7
3
8
4
9
1
2
3
4
5
6
7
8
P
32 ft
4 at 24 ft = 96 ft
Problem Sketch and Finite Element Model
1
In
de
x
In
de
x

Chapter 6 Verification Problems
6-42
COSMOSFFE Static
In
de
x
In
de
x
COSMOSFFE Static
A-1
A
Troubleshooting
Introduction
This appendix lists the error messages produced by the COSMOSFFE Static in
alphabetic order. Explanation of the diagnostics and the needed corrective measures
are provided.
PROBLEM:
Bonding is not supported
You have defined bonding of two or more bodies in your model. Bonding is not
supported in this release by FFE Static. Use the conventional solver STAR or
remesh your model so that the mesh is compatible between the parts to be
bonded.
PROBLEM:
Coordinate system <number> is referenced but not defined
Define the missing coordinate system and try again or modify your input such
that the named coordinate system is not referred to.
PROBLEM:
Coupling is not supported
You have defined coupling using the
CPDOF
,
CPCNS
, or
CPEQN
commands.
Coupling is not supported in this release by FFE Static. Use the conventional
solver STAR or delete the defined coupling.
In
de
x
In
de
x

Appendix A Troubleshooting
A-2
COSMOSFFE Static
PROBLEM:
Crack elements are not supported
You have defined CRACK elements in your model. CRACK elements are not
supported in this release of FFE Static. Use the conventional solver STAR or
delete the defined CRACK elements.
PROBLEM:
Degenerate
element
<number>
Degenerate elements were detected in your model. Degenerate elements are bar
elements with 0-length, area elements with 0-area, or solid elements with 0-
volume. Use the
ECHECK
(Meshing > ELEMENTS >
Check Element
)
command to correct the problem and automatically delete bar elements whose
length is less than
PTTOL
, area elements whose area is less than
PTTOL
square,
and solid elements whose volume is less than
PTTOL
cubed. The point tolerance
is defined by the
PTTOL
(Geometry > POINTS >
Merge Tolerance
) command.
PROBLEM:
Element <number> has unsupported type
The given element is associated with an element group that is not supported in
this release of FFE Static. Use the conventional solver, or redefine the element
group if possible.
PROBLEM:
Element <number> is pyramid shaped, which is not supported
The named element belongs to a SOLID element group. The nodes defining a
face of the solid have collapsed to a single location. This type of collapsed
element is not currently supported by FFE Static. This element may have been
defined manually or resulted from the parametric meshing of a volume with a
collapsed face. Delete the mesh, define a TETRA4, or TETRA10 element group,
and use automatic meshing instead of parametric meshing. Prism-shaped
elements are automatically supported by FFE Static.
PROBLEM:
Error while closing a temporary file
An I/O error occurred while closing a temporary file
PROBLEM:
Error while positioning a temporary file
An I/O error has occurred while reading information from a temporary working
file.
In
de
x
In
de
x

COSMOSFFE Static
A-3
Appendix A Troubleshooting
PROBLEM:
Error while reading file <filename>
An I/O error has occurred while reading from the named file which is part of the
COSMOSM database. The file may have been corrupted. Check the integrity of
your hard disk, reconstruct the model by creating a new problem and using the
FILE
(File >
Load...
) command, and try again.
PROBLEM:
An I/O error has occurred while reading information from a
temporary working file.
PROBLEM:
Error while writing to a temporary file
An error occurred while writing data to the temporary file. Check the available
disk space, and the integrity of your system, especially the hard disk. Reconstruct
the database and try again.
PROBLEM:
Error while writing to file <filename>
An error occurred while writing data to the named file. Check the integrity of
your system, especially the hard disk. Reconstruct the database and try again.
PROBLEM:
Excessive warping in element <number>
Warping in the specified quad shell element is too high and will lead to erroneous
results. Delete the existing mesh and generate a finer quad mesh or use triangular
shell elements instead. If you want to use triangular elements, redefine the
corresponding element group to be SHELL3 instead of SHELL4.
PROBLEM:
File <filename> does not contain necessary data
The specified file name does not contain the expected data in the expected
format. Either the file is corrupted, overwritten, or created by a different
COSMOSM version.
PROBLEM:
File <filename> has invalid format
The format of the data in the named file is not as expected. Either the file is
corrupted, overwritten, or created by a different COSMOSM version.
PROBLEM:
Fluid option is not supported (element <number>)
The specified element belongs to an element group where the fluid option has
been specified. This option is not supported in this release. Redefine the element
group, or use the conventional STAR module.
In
de
x
In
de
x

Appendix A Troubleshooting
A-4
COSMOSFFE Static
PROBLEM:
Improper
axisymmetric
model
The defined axisymmetric model is improper. Axisymmetric elements must be
defined in the global X-Y plane with the Y-axis as the axis of symmetry.
PROBLEM:
Improper mesh near element <number>
The mesh elements are not compatible in the neighborhood of the named
element. This can be the result of improper node merging, invalid parametric
tetrahedral mesh, or invalid manually created elements.
PROBLEM:
Improper mesh, properties, or boundary conditions
Either the mesh, material properties, or boundary conditions of the model have
been improperly defined. Use the
R_CHECK
(Analysis >
Run Check
) command
to check the elements. Also list and examine the material properties and
boundary conditions.
PROBLEM:
Incompatible element groups
The generated mesh connects elements with incompatible element groups to
each other. Try to use other alternatives such that connected elements have
compatible degrees of freedom.
PROBLEM:
Internal error # <number>
An internal error has occurred. Record the error number and report to S.R.A.C.
PROBLEM:
Invalid combination of first and second order elements
First order (linear) and second order (parabolic) elements are connected to each
other resulting in incompatible common edges. An example is connecting
TETRA4 elements to TETRA10 elements. Use the
ECHANGE
(Meshing >
Element Order
) command to fix the problem by raising the order of first order
elements or lowering the order of second order elements. It is recommended,
though not necessary to change the element group(s).
PROBLEM:
Invalid order of nodes for element <number>, try ECHECK
command to fix
The order in which the nodes of the specified element are defined is invalid. Plot
the element with active node numbering, and use the
ELIST
(Edit > LIST >
Elements
) command to examine the order. This error may only occur if the
element is manually defined through the (Meshing > ELEMENTS >
Define
In
de
x
In
de
x

COSMOSFFE Static
A-5
Appendix A Troubleshooting
Element
) command. Use the
ECHECK
(Meshing > ELEMENTS >
Check
Element
) command if the element is degenerate.
PROBLEM:
Invalid Poisson's ratio (<wrong_value>) in material set <number>
The value given to the Poisson's ratio for the specified element group is wrong.
Redefine Poisson's ratio such that its value is greater than zero, and less than 0.5.
If you have a hyper-elastic material, you may need to use the nonlinear structural
module NSTAR where such material modules are supported.
PROBLEM:
No temperature data found for the time step number <number>
Thermal loading has been activated for FFE Static with temperatures to be read
from previous steady-state or transient thermal analysis. The
TEMPREAD
(LoadsBC > LOAD OPTIONS >
Read Temp as Load
) command must have
been used to specify the time step in the case of transient thermal analysis. Verify
your input and if needed rerun the thermal analysis.
PROBLEM:
Not enough boundary conditions
The boundary conditions defined are not adequate to support the model which
results in infinite displacements or rotations in one or more directions. Add or
modify the displacement boundary conditions to stabilize the model and rerun
the analysis.
PROBLEM:
Orthotropic material properties are not supported
A material set has been defined to include orthotropic material. Only isotropic
materials are supported in this release. Modify the properties and rerun, or use
the conventional STAR module using the
R_STATIC
(Analysis > STATIC >
Run
Static Analysis
) command.
PROBLEM:
Out of memory or swap space
Available virtual memory is not sufficient to run this problem.
On UNIX systems contact your system administrator to increase size of the swap
space.
PROBLEM:
Pure membrane or shear panel analysis is not supported
A shell element group has been defined such that pure membrane or shear panel
analysis specified. Only the default option of considering both membrane and
In
de
x
In
de
x

Appendix A Troubleshooting
A-6
COSMOSFFE Static
bending effects is supported. Redefine the shell element group and use the
default analysis type option.
PROBLEM:
Second order shell elements are not supported
Second order shell elements like SHELL6 and SHELL9 are not supported. Use
SHELL3 instead.
PROBLEM:
Stress output in the local coordinate systems is not supported
You have requested the calculation of stresses in a local coordinate system. This
option is not currently supported. All stresses are calculated in the global
Cartesian coordinate system. Stresses in other coordinate systems are however
available in the postprocessing phase using the
ACTSTR
(Results > PLOT >
Stress
) command.
PROBLEM:
There is no active load case to solve
No load case is active for analysis. Either you do not have any forces defined, or
you defined load cases but deactivate them using the
LCSET
(Analysis > STATIC
>
Activate Load Case
) command. Define loads, or use the
LCSET
command to
activate load cases for running analysis.
PROBLEM:
Thermal analysis results don't correspond to the current model
You have activated thermal loading such that temperatures will be read from a
previous thermal analysis but FFE Static has determined that the temperature file
does not correspond to the current model. This could happen if changes in the
model (like adding or deleting elements) were made after running the thermal
analysis, or the file problem-name.HTO was not generated by the correct
COSMOSM thermal analysis version. Check the model and try running FFE
Static again.
PROBLEM:
Unable to create a temporary file
FFE Static could not create a temporary file. Check the integrity of your system
and verify that adequate disk space is available.
PROBLEM:
Unable to create file <filename>
FFE Static could not create the named file. Check the integrity of your system
and verify that adequate disk space is available.
In
de
x
In
de
x

COSMOSFFE Static
A-7
Appendix A Troubleshooting
PROBLEM:
Unable to open file <filename>
FFE Static could not open the named file which is part of the COSMOSM
database. The file may have been deleted. Check the integrity of your hard disk,
reconstruct the model by creating a new problem and using the
FILE
(File >
Load...
) command.
PROBLEM:
Unable to open problem database
FFE Static could not open the database for this problem. Verify that the database
files for this problem exist in the proper path and directory specified and that the
correct version is being used. Also check the integrity of your system and verify
that adequate disk space is available.
PROBLEM:
Unexpected end of file while reading <filename>
An end-file mark was found before reading all needed data from the named file.
Check related input, fix the problem if any, and try again. Regenerate the file if
possible, check the integrity of your system and reconstruct the database through
the
FILE
(File >
Load...
) command if the problem could not be fixed otherwise.
PROBLEM:
Unsupported
element
type
You have defined an element group that is not yet supported. Try to use an
equivalent element group if possible, or use the conventional STAR module.
PROBLEM:
You are not authorized to use this type of analysis
You are not authorized to use this type of analysis. Use the
PRODUCT_INFO
(Control > MISCELLANEOUS >
Product Info
) command to get a list of the
modules you are authorized to use. Contact S.R.A.C.
PROBLEM:
Zero or negative thickness for element <number>
The thickness of the specified the element is either negative or zero. Use the
ELIST
(Edit > LIST >
Elements
) command to list the element group and real
constant sets associated with this element and then use the
RCONST
(Propsets >
Real Constant
) command to define the thickness.
PROBLEM:
Zero or negative Young modulus in material set <number>
The young's modulus in the specified material property set has been given a
negative value or zero. Use the
MPROP
(Propsets >
Material Property
)
command to define a new positive value for EX.
In
de
x
In
de
x

A-8
COSMOSFFE Static
In
de
x
In
de
x
COSMOSFFE Static
I-1
Index
A
Acceleration of gravity 2-2, 4-5
activate load case A-6
analysis options 2-3, 3-3, 4-3, 4-
Animate 5-6, 5-7, 5-13, 5-20, 5-
anisotropic 2-3
axisymmetric 2-1, 3-1, 3-2, 6-4,
axisymmetric elements 2-1, 3-1,
B
beam 1-4, 2-1, 3-2, 4-2, 4-4, 4-5,
4-10, 6-2, 6-3, 6-8, 6-9, 6-10, 6-
17, 6-22, 6-23, 6-29, 6-30, 6-32,
6-36, 6-38, 6-39
beam elements 2-1, 3-2, 4-10, 6-
29, 6-30, 6-32, 6-36, 6-38, 6-39
BEAM2D 6-38
BEAM3D 2-1, 3-2, 6-3, 6-29, 6-
bottom face 3-5
boundary conditions 1-1, 1-4, 4-
1, 4-3, 4-4, 4-7, 5-3, 5-15, 6-15,
6-19, A-4, A-5
boundary edge evaluation 5-6, 5-
C
Cartesian coordinate system 2-2,
centrifugal 2-2, 2-3, 4-4, 4-5, 4-6,
centrifugal loading 2-2, 2-3, 4-5,
coefficient of thermal
expansion 4-6
Commands for FFE Static
constraints 2-3, 4-2, 4-10
coordinate system 2-2, 2-3, 3-3,
4-9, 5-7, 5-8, 5-10, 5-20, 5-22, 5-
23, A-1, A-6
coupling A-1
CRACK elements A-2
Cylindrical coordinate system 2-
D
damping effects 1-2
database management 1-1
Define element 5-15, A-4
deformed shape 4-5, 4-10, 5-6, 5-
7, 5-13, 5-18, 5-19, 5-20, 5-23, 5-
26
disk space 1-1, A-3, A-6, A-7
Displacement constraints 2-3
Displacement contours 5-7, 5-20
Displacements 1-2, 1-3, 1-4, 4-4,
4-8, 4-9, 4-10, 5-5, 5-17, 6-2, 6-7,
6-9, 6-12, 6-38, A-5
Dynamic loads 1-2
E
Edge evaluation 5-6, 5-20
Edge pressure 2-2
Element group 3-1, 3-2, 3-3, 3-5,
4-2, 4-4, 4-7, A-2, A-3, A-4, A-5,
A-6, A-7
Element Library 2-1, 3-1, 3-3
element pressures 1-2
element strain contour 5-8
element strains 5-22
equivalent strain 5-9, 5-10
error messages 4-11, A-1
Extreme strain 4-10
Extreme stress 4-10
In
de
x
In
de
x

Index
I-2
COSMOSFFE Static
F
Finite Element Modeling and
Analysis Steps 4-3
First order 2-1, 2-2, 2-3, 3-1, 3-2,
first order elements 2-3, A-4
forces 1-2, 1-4, 2-2, 4-4, 4-5, 4-6,
4-10, 6-10, 6-27, 6-30, 6-32, 6-33,
6-34, 6-38, 6-39, A-6
Full integration 3-5
fundamental frequency 1-2
G
GEOSTAR 2-3, 3-1, 3-5, 4-1, 4-
10, 5-1, 5-3, 5-5, 5-18, 5-28, 6-1
gravitational loading 5-5
H
hexahedral elements 2-2, 3-2
hierarchical basis 3-1
I
internal error A-4
iterative methods 1-1
L
linear 1-1, 1-2, 1-3, 1-4, 3-1, 4-7,
4-8, 4-9, 5-1, 6-7, 6-12, 6-13, 6-
19, 6-25, 6-27, 6-36, 6-38, A-4
load cases 1-2, 1-3, 2-2, 2-4, 4-2,
4-5, 4-6, 4-9, 4-10, 5-5, 5-15, 5-
16, 5-17, 5-26, 5-27, 6-10, 6-39,
A-6
load vector 1-2, 1-3, 5-15
loads and boundary conditions 1-
local coordinate system 2-3, A-6
M
manually created elements A-4
material properties 1-4, 2-3, 3-3,
4-2, 4-3, 4-10, 5-17, 6-19, A-4, A-
5
mechanical load vector 1-2
memory requirements 1-1
mesh generation 4-3
meta file 5-11
mid surface 3-5
model geometry 4-3
moments 1-2, 1-4, 2-2, 6-36
N
nodal displacements 1-2
nodal forces 1-2, 4-4
node merging A-4
nonlinearities 1-2
O
orthotropic 2-3, A-5
orthotropic material A-5
P
parabolic 3-1, 4-7, A-4
pentahedral elements 3-2
plane strain 2-1, 3-1, 3-2, 6-7, 6-
PLANE2D 2-1, 3-1, 3-2, 3-5, 6-2,
6-3, 6-4, 6-7, 6-8, 6-13, 6-14, 6-
21, 6-23, 6-25
Plot meta 5-11
Poisson's ratio 1-4, A-5
Postprocessing 4-1, 4-3, 4-9, 4-10,
5-5, 5-6, 5-16, 5-18, 5-27, 5-28,
A-6
Prescribed displacement 2-2
Pressure 1-3, 1-4, 2-2, 4-4, 5-3, 5-
14, 5-17, 6-2, 6-3, 6-4, 6-6, 6-14,
6-19, 6-23, 6-24, 6-39
primary load cases 1-3, 2-2, 2-4,
prism-shaped elements 2-2, 3-2,
Product Info A-7
R
real constants 3-3, 4-2, 5-17
resultant displacement 5-7, 5-20
Results menu 4-2, 5-6, 5-13, 5-18
rigid connections flag 4-8
rotational degrees of freedom 5-3
Run check 4-4, 4-9, 4-11, 5-17, A-
Run static analysis 4-2, 4-4, 4-6,
S
Second order 2-1, 2-2, 2-3, 3-1, 3-
secondary load cases 1-2, 1-3, 2-
Shade 5-6, 5-15
shear and moment diagrams 4-10
shear stress 5-11, 6-8, 6-17
shell 2-2, 3-2, 3-5, 4-2, 5-2, 5-10,
5-14, 5-15, 5-16, 6-2, 6-9, 6-15,
6-17, 6-22, A-3, A-5, A-6
shell elements 2-2, 3-2, 3-5, 4-2,
5-2, 5-14, 5-15, 5-16, 6-17, 6-22,
A-3, A-6
SHELL3 2-2, 3-2, 3-3, 5-15, 6-2,
SHELL4 2-2, 3-2, 5-15, 6-2, 6-15,
SHELL6 6-8, 6-15, A-6
SHELL9 A-6
SOLID 2-2, 3-2, 3-5, 4-7, 6-2, 6-
10, 6-12, 6-19, 6-21, 6-23, A-2
solid elements 3-2, 4-7, 6-19, A-2
solution time 1-1
special loading 2-2, 2-3, 4-2, 4-5,
Spherical coordinate system 2-3
STAR 1-1, 1-3, 2-3, 3-5, 4-3, 4-7,
4-8, 4-9, A-1, A-2, A-3, A-5, A-7
Static analysis 1-2, 4-2, 4-4, 4-5,
4-6, 4-7, 4-8, 4-9, 5-1, 5-5, 5-18,
6-4, 6-6, 6-8, 6-9, 6-10, 6-14, 6-
15, 6-17, 6-19, 6-21, 6-22, 6-23,
6-24, 6-26, 6-29, 6-30, 6-32, 6-33,
6-34, 6-35, 6-39, 6-41, A-5
Static analysis options 4-7, 4-9
static loading 1-2
steady state thermal analysis 2-2
stress averaging 5-16
stress variation 5-12, 5-25
In
de
x
In
de
x

COSMOSFFE Static
I-3
Index
stress-strain 1-2
symmetry 5-3, 6-6, 6-13, 6-15, 6-
T
TETRA10 2-2, 3-1, 3-2, 3-5, 4-7,
TETRA4 2-2, 3-1, 3-2, 3-5, 4-7,
tetrahedral elements 2-2, 3-2, 5-3
tetrahedral mesh A-4
Thermal 1-2, 1-3, 1-4, 2-2, 2-3, 4-
4, 4-5, 4-6, 4-7, 4-8, 5-5, 6-2, 6-3,
6-7, 6-12, 6-13, 6-24, 6-25, 6-27,
6-35, 6-36, 6-38, A-5, A-6
Thermal loading 2-2, 2-3, 4-4, 4-
6, 4-7, 4-8, 5-5, 6-2, 6-13, A-5,
A-6
Thermal stress analysis 4-6, 6-2,
6-3, 6-7, 6-12, 6-13, 6-25, 6-27,
6-36, 6-38
thick shell 6-9
thin plate 6-6
tolerance 5-6, 5-20, A-2
transient thermal analysis 2-2, 4-
TRIANG 2-1, 3-1, 3-5, 6-2, 6-3,
truss 3-2, 4-2, 6-3, 6-26, 6-27, 6-
truss elements 3-2, 6-27, 6-34, 6-
TRUSS2D 2-1, 3-2, 6-3, 6-27, 6-
TRUSS3D 2-1, 3-2, 6-3, 6-26, 6-
V
verification problems 5-1, 6-1, 6-
virtual memory A-5
von Mises stress 5-10, 5-11, 5-24,
W
warping A-3
In
de
x
In
de
x

Index
I-4
COSMOSFFE Static
In
de
x
In
de
x
Document Outline
- COSMOSFFE Static Analysis Module
Wyszukiwarka
Podobne podstrony:
Module 10
Module 8
Food ćwiczenia angielski Starland 1 module 8
Instrukcja montażu sufitów podwieszanych w module 600x600mm System standardowy 600x600 1 AMF REINRAU
AT Commands for Bluetooth Module
Module 07
CISCO CCNA Certifications CCNA 2 Module 10
CISCO CCNA Certifications CCNA 2 Module 9
Module 12
CISCO CCNA Certifications CCNA 2 Module 1
delta module1 sample test01 1
06 BS Module 1 Section 6
CISCO CCNA Certifications CCNA 3 Module 3
Module 11
CISCO CCNA Certifications CCNA 2 Module 8
CISCO CCNA Certifications CCNA 2 Module 11
module 8, studia, remedial, testy
static
więcej podobnych podstron