Understanding Volatility

Sheldon Natenberg

Chicago Trading Co.

440 S. LaSalle St.

Chicago, IL 60605

[phone]

[e-mail]

Options Trading Forum

October 2

nd

, 2002

theoretical

value

theoretical

value

pricing

model

exercise price

time to expiration

underlying price

interest rate

volatility

(dividends)

pricing

model

exercise price

time to expiration

underlying price

interest rate

volatility

(dividends)

exercise price

time to expiration

underlying price

interest rate

volatility

(dividends)

-1

-

long an underlying contract

10%*90 + ……. + 10%*110

long a 100 call

20%*5 + 10%*10 = 2.00

= 100

90

95

105

110

100

20%

20%

20%

20%

20%

10% 20%

40%

20%

10%

90

95

105

110

100

20%

20%

20%

20%

20%

90

95

105

110

100

90

95

105

110

90

95

105

110

100

20%

20%

20%

20%

20%

20%

20%

20%

20%

20%

10% 20%

40%

20%

10%

Expected Return

-2

-

If the expected return of the 100 call
is 2.00, what is its theoretical value?

The theoretical value is the price
you would be willing to pay today
in order to just break even.

interest rates = 12%
2 months to expiration

2.00 - (2.00 x 2%) = 1.96

-3

-

underlying prices

probabilities

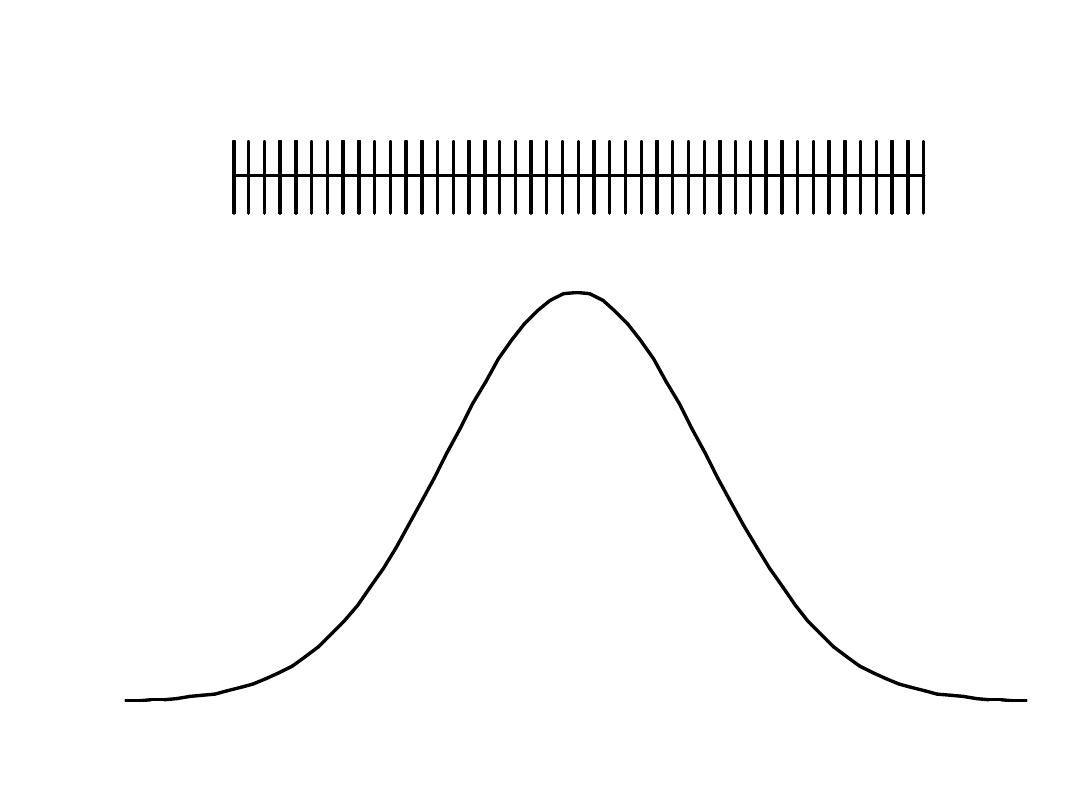
normal

distribution

normal

distribution

-4

-

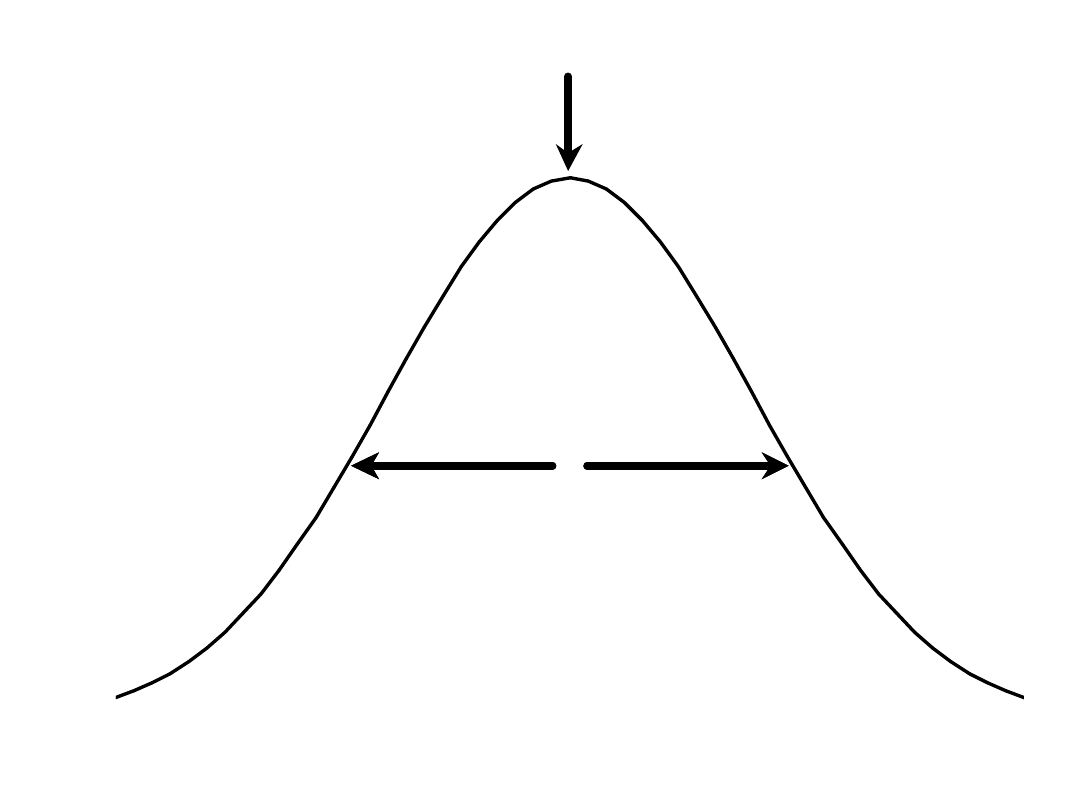
All normal distributions

are defined by their mean

and their standard deviation.

Mean – where the
peak of the curve
is located

Standard deviation –
how fast the curve
spreads out.

-5

-

100

100

120 call

120 call

90 days to

expiration

.25 each day

+

–.25 each day

+

–.25 each day

+

–

+

–

2.00 each day

+

–2.00 each day

+

–2.00 each day

+

–

+

–

10.00 each day

+

–10.00 each day

+

–10.00 each day

+

–

+

–

value =.05

value =.75

value = 8.00

80 put

80 put

option value

option value

-6

-

+1 S.D.

+1 S.D.

+1 S.D. ˜ 34%

-1 S.D.

-1 S.D.

-1 S.D. ˜ 34%

+2 S.D.

+2 S.D.

-2 S.D.

-2 S.D.

+2 S.D. ˜ 47.5%

-2 S.D. ˜ 47.5%

±1 S.D. ˜

68% (2/3)

±1 S.D. ˜

68% (2/3)

±2 S.D. ˜

95% (19/20)

±2 S.D. ˜

95% (19/20)

mean

mean

-7

-

Mean

Standard deviation

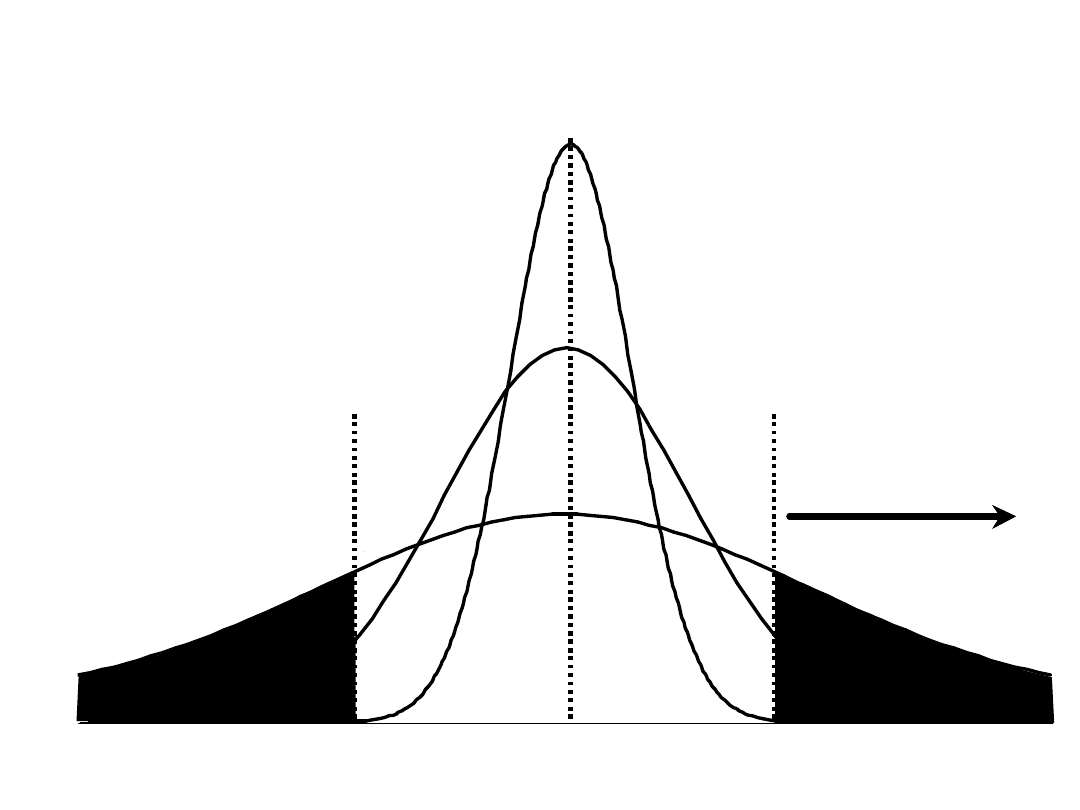
Volatility: one standard deviation,

in percent, over a one year period.

– the break even price at

expiration for a trade made at
today’s price (forward price)

– volatility

-8

-

1-year forward price = 100.00
volatility = 20%
One year from now:

• 2/3 chance the contract will be

between 80 and 120 (100 ± 20%)

• 19/20 chance the contract will be

between 60 to 140 (100 ± 2 x 20%)

• 1/20 chance the contract will be

less than 60 or more than 140

-9

-

-10
-

What does an annual volatility tell
us about movement over some other
time period?

monthly price movement?

weeky price movement?
daily price movement?

volatility

t

= volatility

annual

x t

v

volatility

annual

x t

v t

v

-11
-

Daily volatility (standard deviation)

Trading days in a year? 250 – 260

Assume 256 trading days

volatility

daily

˜ volatility

annual

/ 16

t = 1/256

=

t

v

v1/256

=

t

v t

v

v1/256 = 1/16

-12
-

volatility

daily

= 20% / 16 = 1¼%

One trading day from now:

• 2/3 chance the contract will be

between 98.75 and 101.25

(100 ± 1¼%)

• 19/20 chance the contract will be

between 97.50 and 102.50

(100 ± 2 x 1¼%)

16

2/3

19/20

-13
-

Weekly volatility:

volatility

weekly

= volatility

annual

/ 7.2

t = 1/52

=

t

v

v1/52

=

t

v t

v

v1/52 ˜ 1/7.2

volatility

monthly

= volatility

annual

/ 3.5

t = 1/12

=

t

v

v1/12

=

t

v t

v

v1/12 ˜ 1/3.5

Monthly volatility:

-14
-

daily standard deviation?

stock = 68.50; volatility = 42.0%

˜ 68.50 x 42% / 16

= 68.50 x 2.625% ˜ 1.80

weekly standard deviation?

˜ 68.50 x 42% / 7.2

= 68.50 x 5.83% ˜ 4.00

-15
-

daily standard deviation = 1.80

stock = 68.50; volatility = 42.0%

+1.25 -.95

+.35

+.70

-1.60

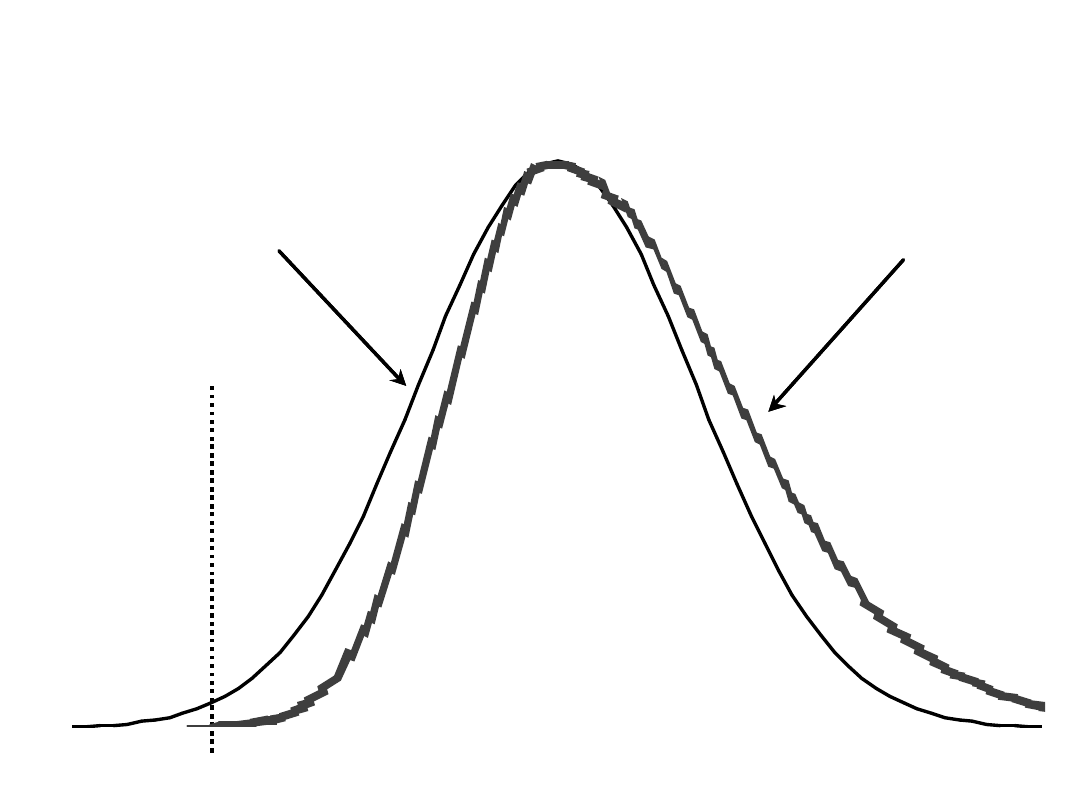
Is 42% a reasonable volatility
estimate?

How often do you expect to see
an occurrence greater than one
standard deviation?

-16
-

8

+

8

+

8

–

8

–

0

0

normal

distribution

normal

distribution

lognormal

distribution

lognormal

distribution

-17
-

normal

distribution

110 call

lognormal

distribution

underlying price = 100

3.00

90 put

3.00

3.00

2.50

110 call = 2.75

90 put = 3.00

Are the options mispriced?
Could there is something wrong
with the model?

-18
-

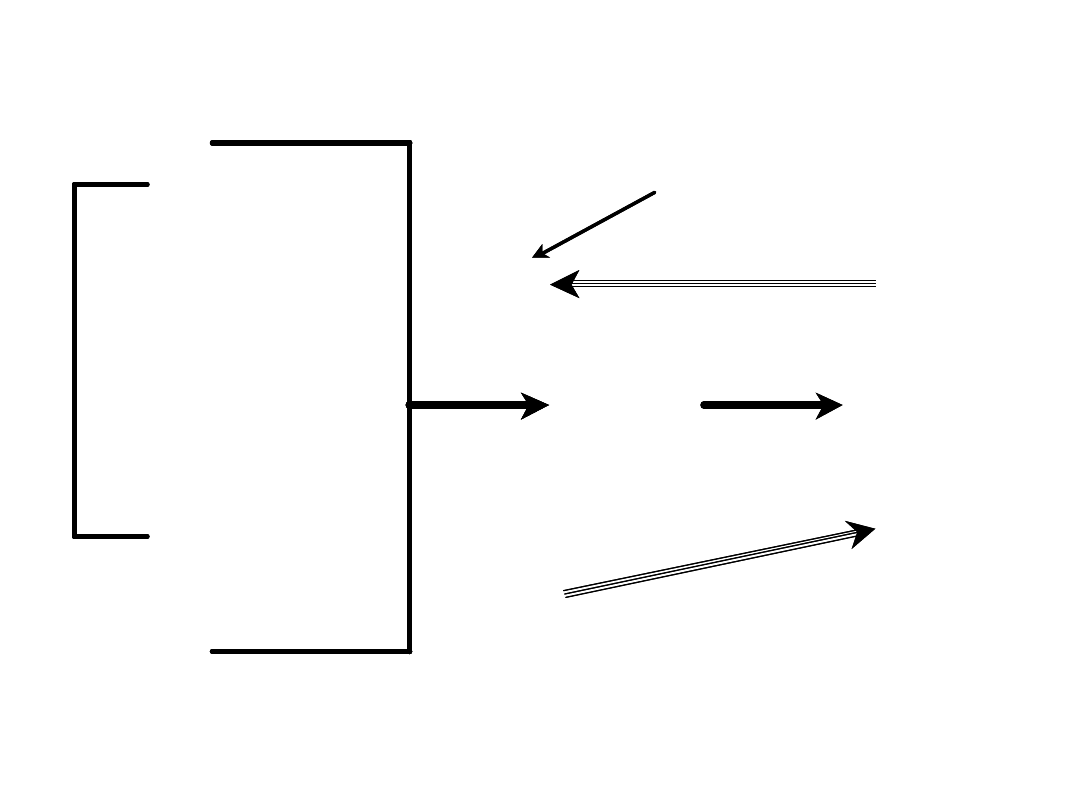
The volatility of

the underlying contract over some
period in the future

future volatility:

historical volatility:

forecast volatility:

The volatility

of the underlying contract over
some period in the past

Someone’s

estimate of future volatility

-19
-

derived from the prices of options
in the marketplace

implied volatility:

the marketplace’s forecast of
future volatility

-20
-

exercise price

time to expiration

underlying price

interest rate

volatility

exercise price

time to expiration

underlying price

interest rate

volatility

pricing

model

pricing

model

theoretical

value

theoretical

value

2.50

3.25

volatility

27%

27%

???

???

31%

implied volatility

implied volatility

-21
-

future volatility

implied volatility

= value

= price

historical volatility

forecast volatility

historical volatility

forecast volatility

Option trading decisions often
begin by comparing

to

-22
-

Volatility Trading

Initially buy underpriced options or strategies, or sell
overpriced options or strategies

Offset the option position by taking an opposing market
position, delta neutral, in the underlying contract

Periodically buy or sell an appropriate amount of the
underlying contract to remain delta neutral over the life
of the strategy (dynamic hedging)

At expiration liquidate the entire position

In theory, when the position is closed out the total
profit (or loss) should be approximately equal to the
amount by which the options were originally mispriced.

-23
-

Volatility Trading Risks

You may have incorrectly
estimated the future volatility

The model may be wrong

-24
-

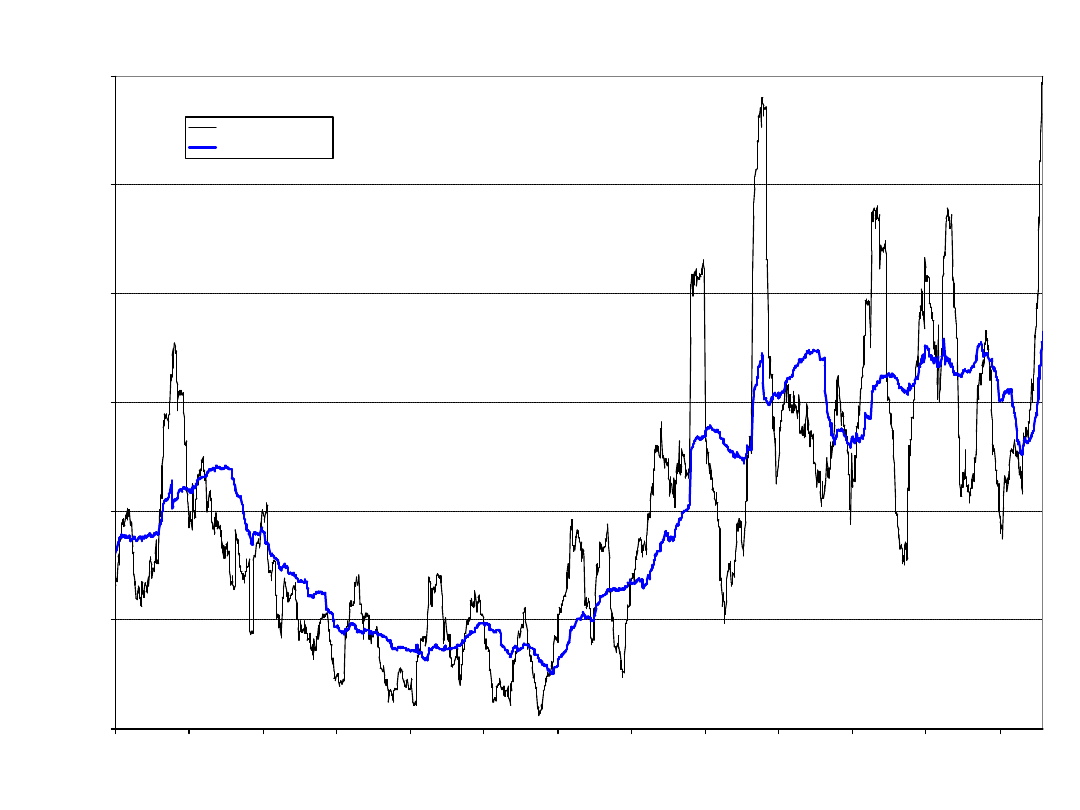
SPX Historical Volatility

January 1990 - August 2002

5%

10%

15%

20%

25%

30%

35%

Jan-90

Jan-91

Jan-92

Jan-93

Jan-94

Jan-95

Jan-96

Jan-97

Jan-98

Jan-99

Jan-00

Jan-01

Jan-02

50-day volatility

250-day volatility

-25
-

Volatility characteristics

mean reversion – volatility tends to
return to its historical average

serial correlation – in the absence of
other data, the best volatility guess over
the next time period is the volatility which
occurred over the previous time period.

momentum – a trend in volatility is
likely to continue

-26
-

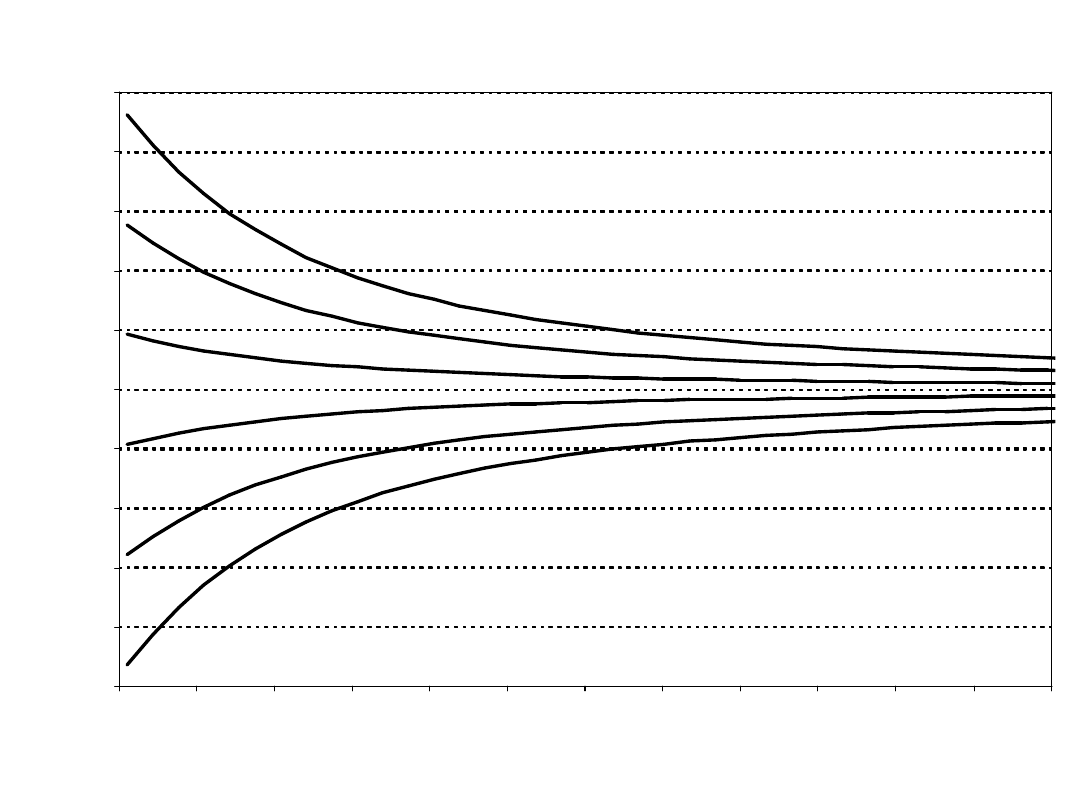
Volatility Cones

20

22

24

26

28

30

32

34

36

38

40

0

3

6

9

12

15

18

21

24

27

30

33

36

time to expiration (months)

implied volatility (%)

-27
-

(G)ARCH

Volatility Forecasting Methods

– (generalized) auto-

regressive conditional
heteroscedasticity

(V)ARIMA – (vector) auto-

regressive integrated
moving average

-28
-

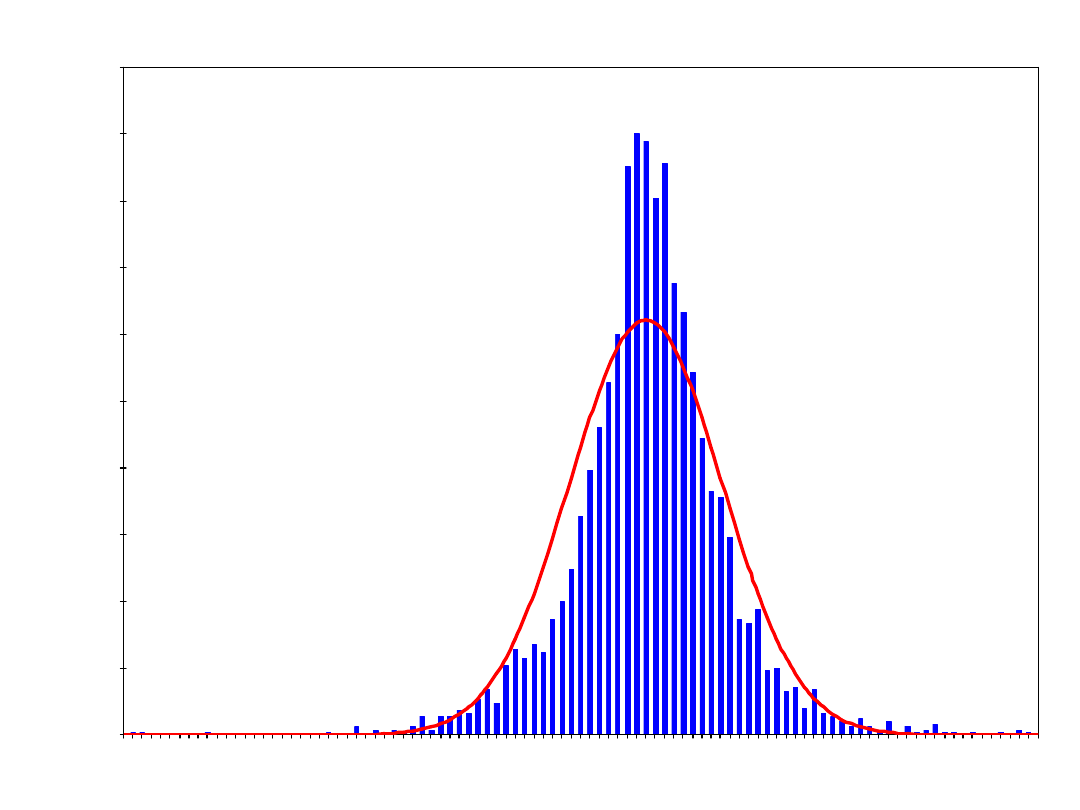
SPX Daily Price Changes: January 1990 - August 2002

0

25

50

75

100

125

150

175

200

225

250

-7%

-6%

-5%

-4%

-3%

-2%

-1%

0%

1%

2%

3%

4%

5%

daily price change (nearest 1/8 percent)

number of occurrences

number of days: 3186
biggest up move: +5.73% (24 July 2002)
biggest down move: -6.87% (27 October 1997)
mean: +.0364%
standard deviation: 1.0217%
volatility: 16.24%
skewness: -.0263
kurtosis: +3.9072

-29
-

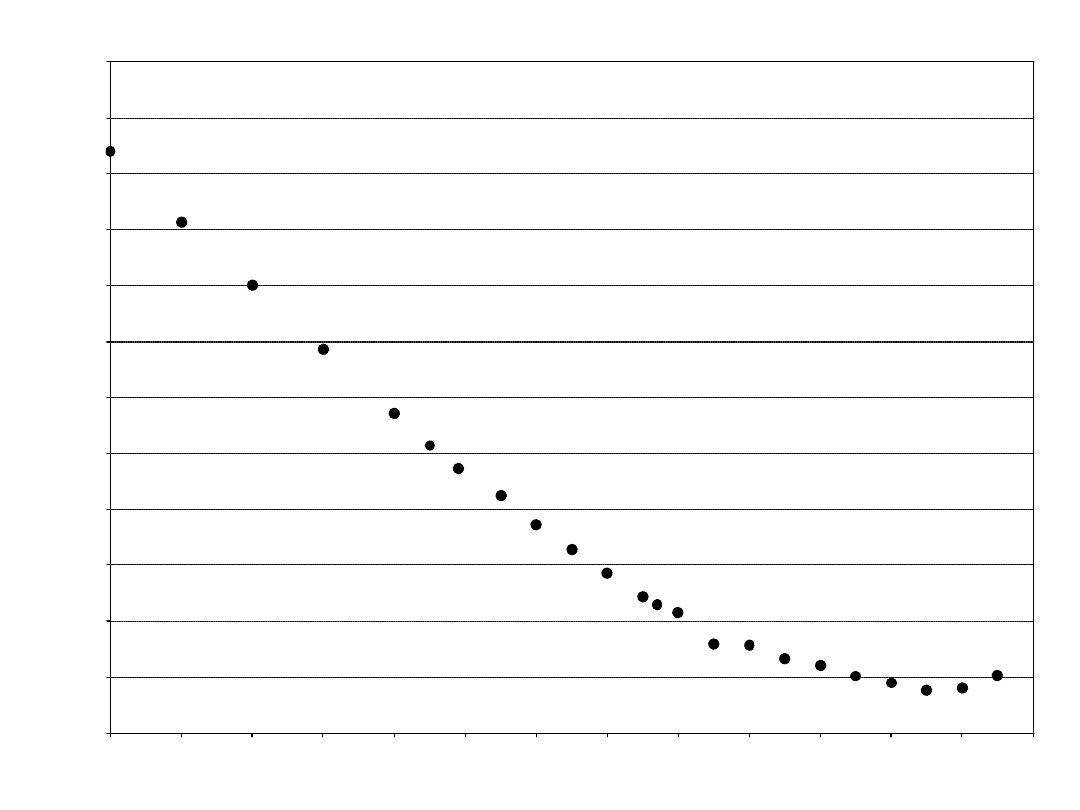
Volatility Skew:

The tendency of options at
different exercise prices to trade
at different implied volatilities

A consequence of

how people use options

weaknesses in the pricing model

-30
-

SPX June Implied Volatilities - 22 February 2002

14

16

18

20

22

24

26

28

30

32

34

36

38

750

800

850

900

950

1000

1050

1100

1150

1200

1250

1300

1350

1400