WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

1

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

1 Charakterystyki geometryczne przekroju w układzie YZ

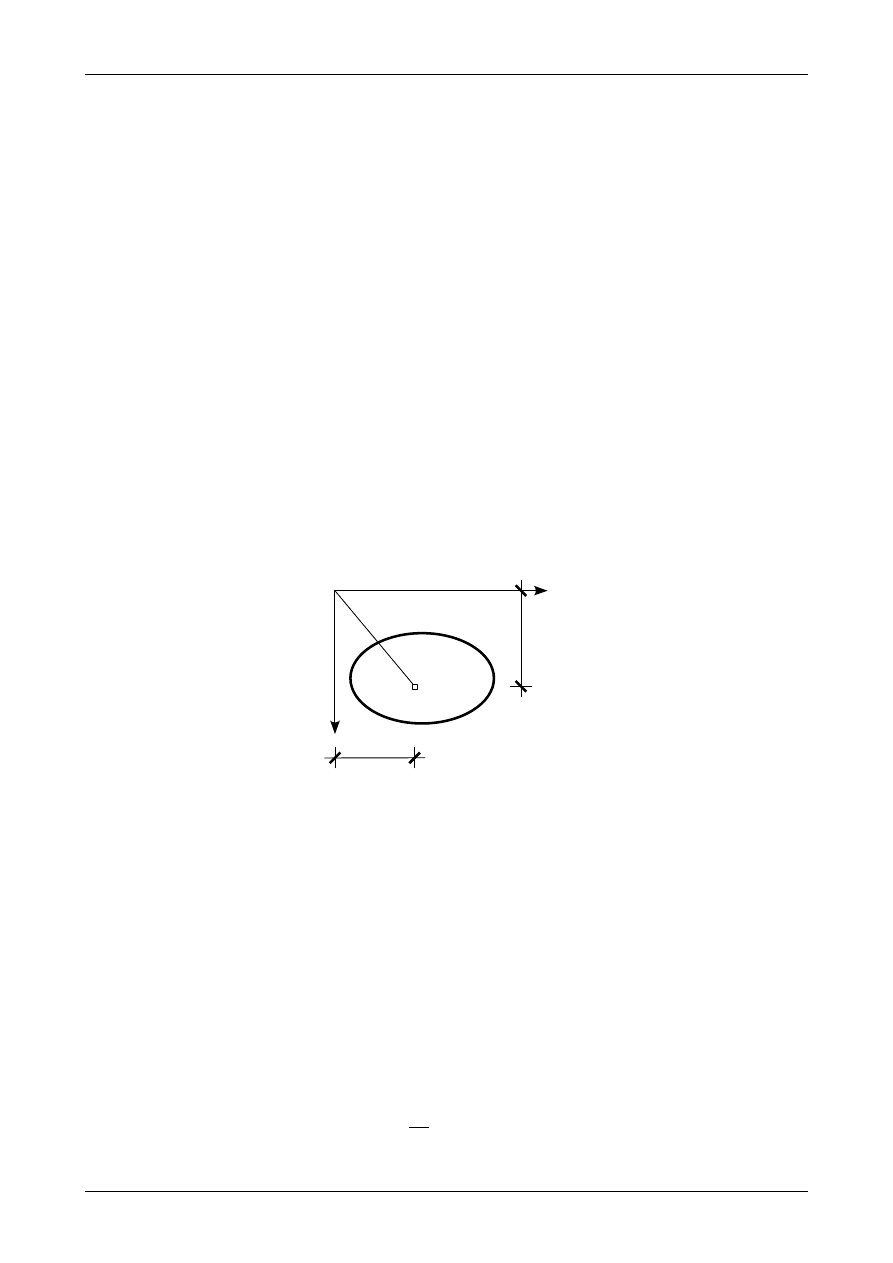
Rysunek 1 przedstawia przekrój pręta w dowolnym układzie osi YZ. Elementarne pole powierzchni dA

posiada współrzędne y oraz z.

Z

Y

dA

z

y

Rys. 1. Przekrój pręta.

Pole powierzchni przekroju wynosi

A

=

∫

A

dA

.

(1)

Jednostką pola powierzchni w układzie SI jest m

2

. W budownictwie najczęściej będziemy używać cm

2

. Pole

powierzchni przekroju jest wielkością zawsze większą od zera.

Moment statyczny względem osi Y wynosi

S

Y

=

∫

A

z

⋅dA

.

(2)

Moment statyczny względem osi Z wynosi

S

Z

=

∫

A

y

⋅dA

.

(3)

Jednostką momentu statycznego w układzie SI jest m

3

. W budownictwie najczęściej będziemy używać cm

3

.

Moment statyczny może przyjmować dowolne wartości.

Osiowy moment bezwładności względem osi Y wynosi

I

Y

=

∫

A

z

2

⋅dA

.

(4)

Dr inż. Janusz Dębiński

BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

2

Osiowy moment bezwładności względem osi Z wynosi

I

Z

=

∫

A

y

2

⋅dA

.

(5)

Dewiacyjny moment bezwładności w układzie YZ wynosi

I

YZ

=

∫

A

y

⋅z⋅dA

.

(6)

Biegunowy moment bezwładności w układzie YZ wynosi

I

0

=

∫

A

r

2

⋅dA=

∫

A

z

2

⋅dA

∫

A

y

2

⋅dA=I

Y

I

Z

,

(7)

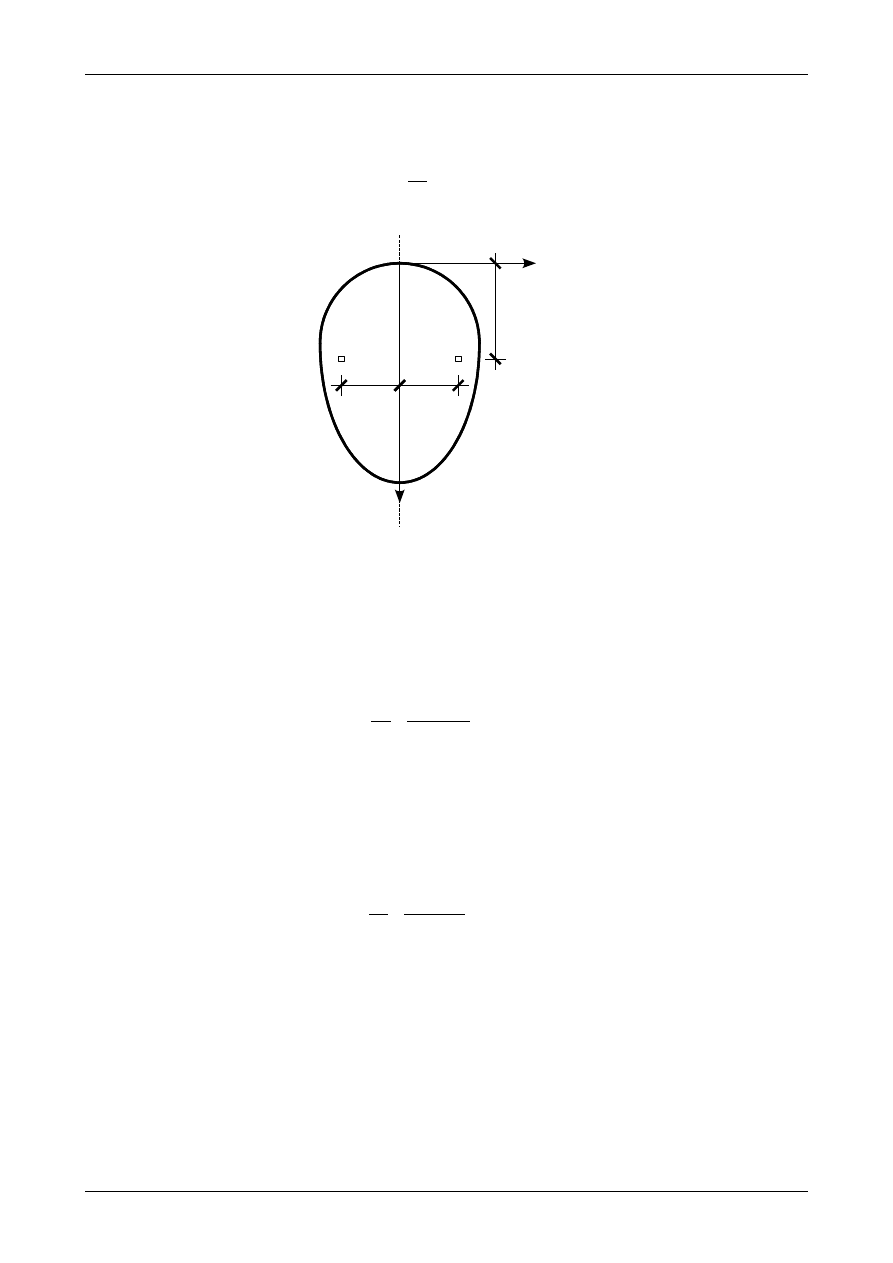
w którym r oznacza odległość elementarnego pola powierzchni dA od początku układu współrzędnych YZ
zgodnie z rysunkiem 2.

Z

Y

dA

z

y

r

Rys. 2. Położenie bieguna elementarnego pola powierzchni dA.

Jednostką wszystkich momentów bezwładności w układzie SI jest m

4

. W budownictwie najczęściej będziemy

używać cm

4

. Osiowe momenty bezwładności są zawsze większe od zera i stanowią pewną miarę rozproszenia

przekroju pręta względem osi. Im to rozproszenie większe tym wartość osiowego momentu bezwładności jest
większa.

Dewiacyjny moment bezwładności może przyjmować dowolne wartości i jest on pewną miarą asymetrii
przekroju pręta w przyjętym układzie współrzędnych. Ponadto moment dewiacyjny w układzie współrzędnych,
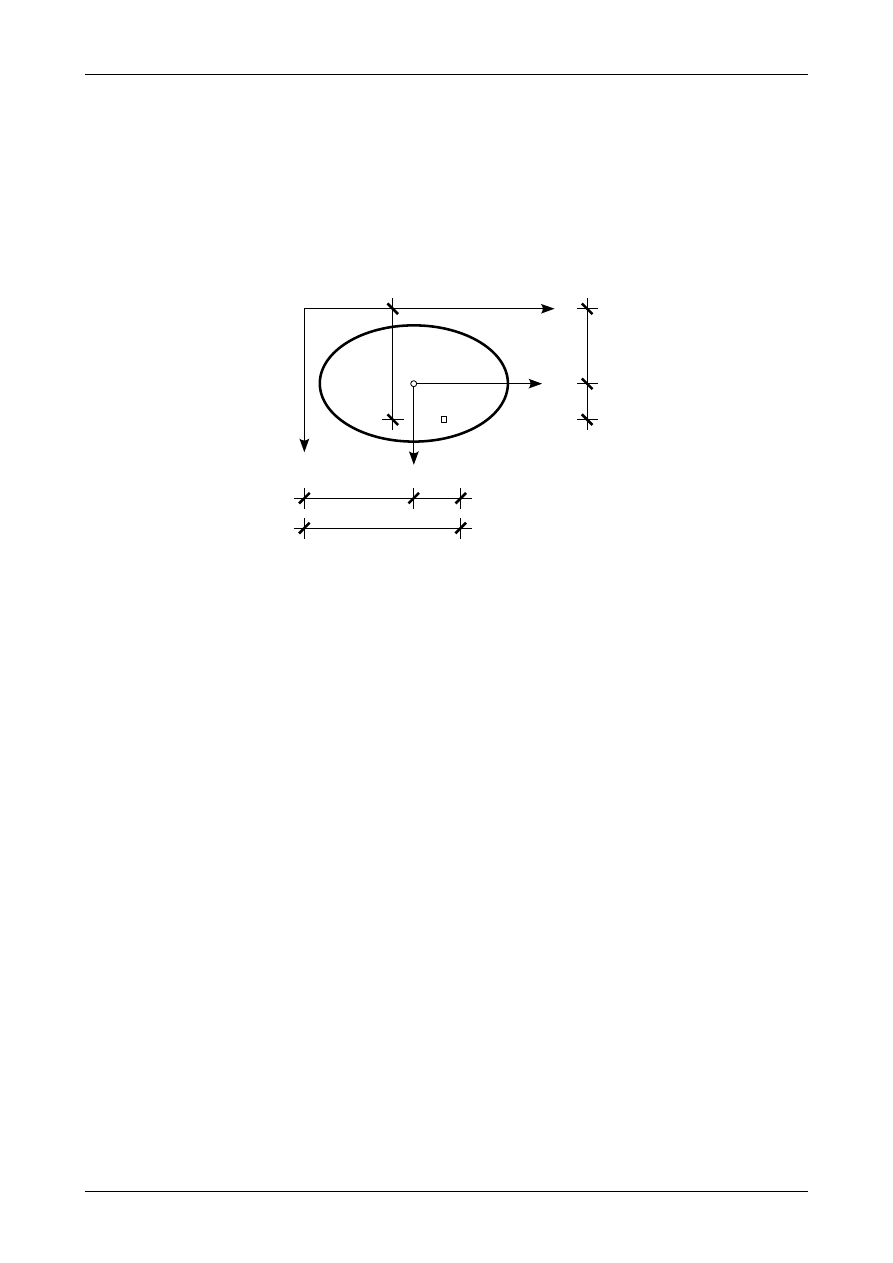
w którym jedna z osi jest osią symetrii przekroju pręta, wynosi zero. Sytuację taką przedstawia rysunek 3.

Osią środkową nazywamy taką oś względem, której odpowiedni moment statyczny wynosi zero.

Środkiem ciężkości nazywamy punkt przecięcia się dwóch osi środkowych.

Współrzędna y

C

środka ciężkości przekroju pręta będzie miała postać

y

C

=

S

Z

A

.

(8)

Dr inż. Janusz Dębiński

BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

3

Współrzędna z

C

środka ciężkości przekroju pręta będzie miała postać

z

C

=

S

Y

A

.

(9)

Z

Y

dA

z

y

dA

-z

I

YZ

=0

Rys. 3. Przekrój pręta z jedną osią symetrii.

Złożony przekrój najlepiej podzielić na figury, dla których znamy położenie środka ciężkości i pole
powierzchni. Wzory na położenie środka ciężkości będą miały postać

y

C

=

S

Z

A

=

∑

i

=1

i

=n

A

i

⋅y

i

∑

i

=1

i

=n

A

i

(10)

oraz

z

C

=

S

Y

A

=

∑

i

=1

i

=n

A

i

⋅z

i

∑

i

=1

i

=n

A

i

.

(11)

w których to y

i

i z

i

oznaczają współrzędne środka ciężkości i-tej figury w układzie YZ natomiast A

i

oznacza

pole powierzchni i-tej figury.

Środek ciężkości posiada następujące właściwości:

1. Środek ciężkości może znajdować się w punkcie poza przekrojem pręta.

2. Jeżeli przekrój posiada jedną oś symetrii to środek ciężkości znajduje się na niej.

3. Jeżeli przekrój posiada dwie osie symetrii to środek ciężkości znajduje się w punkcie ich przecięcia.

Dr inż. Janusz Dębiński

BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

4

4. Jeżeli przekrój posiada więcej niż dwie osie symetrii to wszystkie osie przecinają się w środku

ciężkości.

5. Jeżeli przekrój składa się z dwóch figur, które dodajemy do siebie to środek ciężkości znajduje się na

linii łączącej środki ciężkości poszczególnych figur składowych.

6. Jeżeli przekrój składa się z trzech lub więcej figur składowych, które dodajemy do siebie, to środek

ciężkości znajduje się wewnątrz wieloboku, którego wierzchołkami są środki ciężkości
poszczególnych figur składowych.

Z

Y

dA

z

y

Y

0

Z

0

z

C

z

0

sc

y

C

y

0

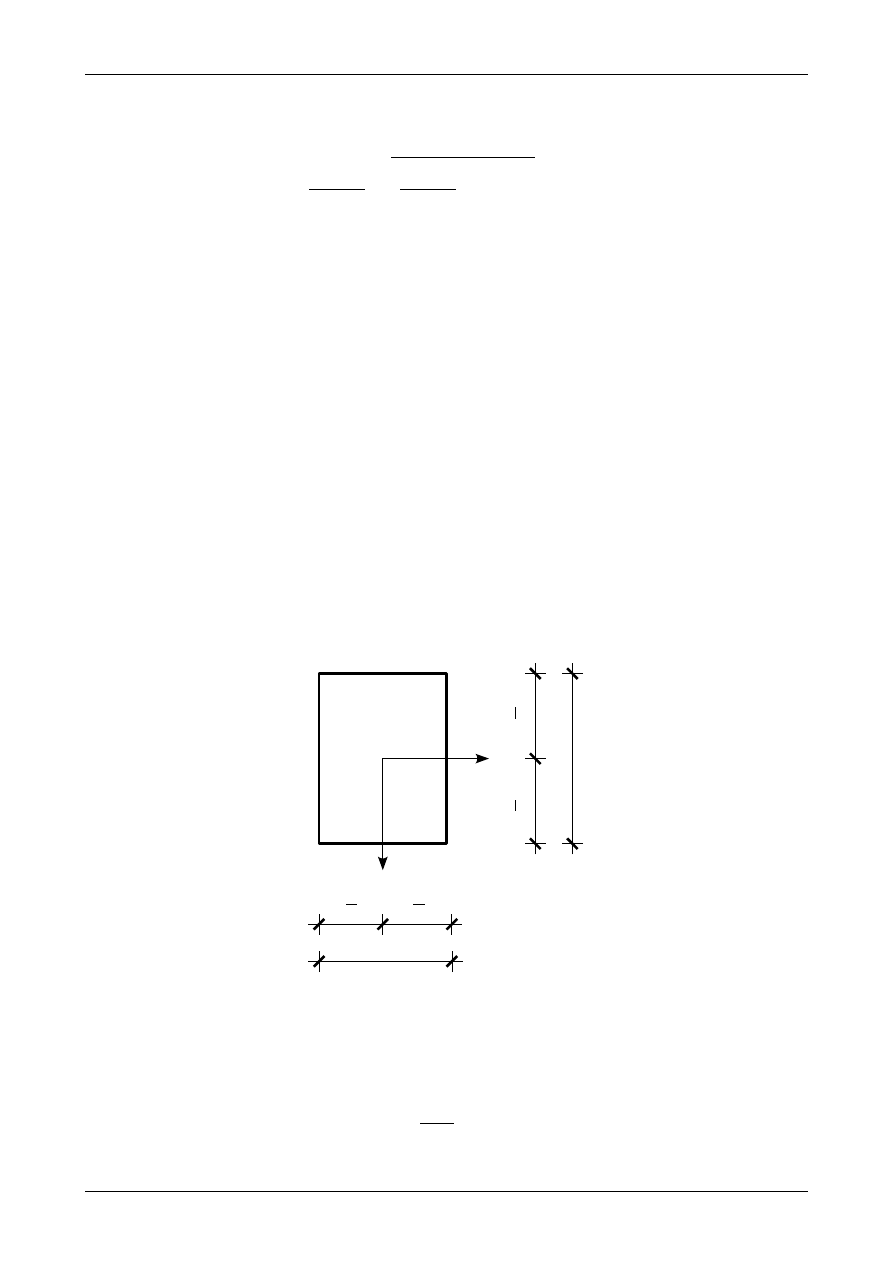
Rys. 4. Przekrój pręta oraz układy współrzędnych Y

0

Z

0

oraz YZ.

Załóżmy, że znane są momenty bezwładności przekroju pręta w dowolnym układzie osi środkowych Y

0

Z

0

czyli

I

Y0

, I

Z0

oraz I

Y0Z0

. Moment bezwładności względem osi Y wynosi

I

Y

=I

Y0

z

C

2

⋅A

.

(12)

Moment bezwładności względem osi Z wynosi

I

Z

=I

Z0

 y

C

2

⋅A

.

(13)

Dewiacyjny moment bezwładności w układzie YZ wynosi

I

YZ

=I

Y0Z0

 y

C

⋅z

C

⋅A

.

(14)

Wzory (12), (13) i (14) nazywamy wzorami Steinera. Najczęściej chcemy wyznaczyć momenty bezwładności
w układzie osi środkowych całego przekroju pręta Y

0

Z

0

.Wzory Steinera będą miały wtedy postać

I

Y0

=

∑

i

=1

i

=n



I

Y0i

z

0i

2

⋅A

i



,

(15)

Dr inż. Janusz Dębiński

BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

5

I

Z0

=

∑

i

=1

i

=n



I

Z0i

y

0i

2

⋅A

i



(16)

oraz

I

Y0Z0

=

∑

i

=1

i

=n



I

Y0iZ0i

 y

0i

⋅z

0i

⋅A

i



.

(17)

We wzorach (15), (16) oraz (17) I

Y0i

, I

Z0i

oznaczają osiowe momenty bezwładności względem osi środkowych

i-tej figury. I

Y0iZ0i

oznacza dewiacyjny moment bezwładności w układzie osi środkowych i-tej figury. A

i

oznacza

pole powierzchni i-tej figury natomiast y

0i

, z

0i

oznaczają współrzędne środka ciężkości i-tej figury w układzie

osi środkowych całego przekroju pręta Y

0

Z

0

.

Transformacja układu współrzędnych polega na obrocie tego układu względem jego początku o pewien kąt.
Dodatni kąt obrotu będzie kręcił osią Y

0

w kierunku osi Z

0

. Momenty bezwładności w układzie osi

transformowanych Y

0'

Z

0'

oblicza się ze wzorów

I

Y0'

=

I

Y0

I

Z0

2



I

Y0

−I

Z0

2

⋅cos



2

⋅



−I

Y0Z0

⋅sin



2

⋅



,

(18)

I

Z0 '

=

I

Y0

I

Z0

2

−

I

Y0

−I

Z0

2

⋅cos



2

⋅



I

Y0Z0

⋅sin



2

⋅



,

(19)

I

Y0'Z0 '

=

I

Y0

−I

Z0

2

⋅sin



2

⋅



I

Y0Z0

⋅cos



2

⋅



.

(20)

Istnieje taki układ osi środkowych, w którym osiowe momenty bezwładności I

Y0'

i I

Z0'

osiągają wartości

ekstremalne. Taki układ osi środkowych nazywa się układem osi głównych. Ponadto okazuje się, że w
układzie osi głównych dewiacyjny moment bezwładności równa się zero. Kąt nachylenia osi głównych
wyznacza się ze wzoru

tg



2

⋅

gl



=

−2⋅I

Y0Z0

I

Y0

−I

Z0

.

(21)

Główne momenty bezwładności wyznaczymy ze wzorów

I

Ygl

=

I

Y0

I

Z0

2



I

Y0

−I

Z0

2

⋅cos



2

⋅

gl



−I

Y0Z0

⋅sin



2

⋅

gl



,

(22)

I

Zgl

=

I

Y0

I

Z0

2

−

I

Y0

−I

Z0

2

⋅cos



2

⋅

gl



I

Y0Z0

⋅sin



2

⋅

gl



.

(23)

Dr inż. Janusz Dębiński

BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

6

Wartości głównych momentów bezwładności możemy sprawdzić za pomocą zależności

I

1

/2

=

I

Y0

I

Z0

2

±





I

Y0

−I

Z0

2



2





I

Y0Z0



2

,

(24)

w którym I

1

oznacza największy osiowy moment bezwładności natomiast I

2

najmniejszy osiowy moment

bezwładności.

Niezmiennikiem nazywamy wielkość fizyczną, która nie zmienia wartości przy obrocie (transformacji) układu
współrzędnych. W przypadku momentów bezwładności będziemy mieli dwa niezmienniki. Pierwszy z nich ma
postać

J

1

=I

Y0

I

Z0

=I

Y0'

I

Z0'

=I

Ygl

I

Zgl

.

(25)

Drugi z niezmienników ma postać

J

2

=I

Y0

⋅I

Z0

−I

Y0Z0

2

=I

Y0'

⋅I

Z0'

−I

Y0' Z0'

2

=I

Ygl

⋅I

Zgl

.

(26)

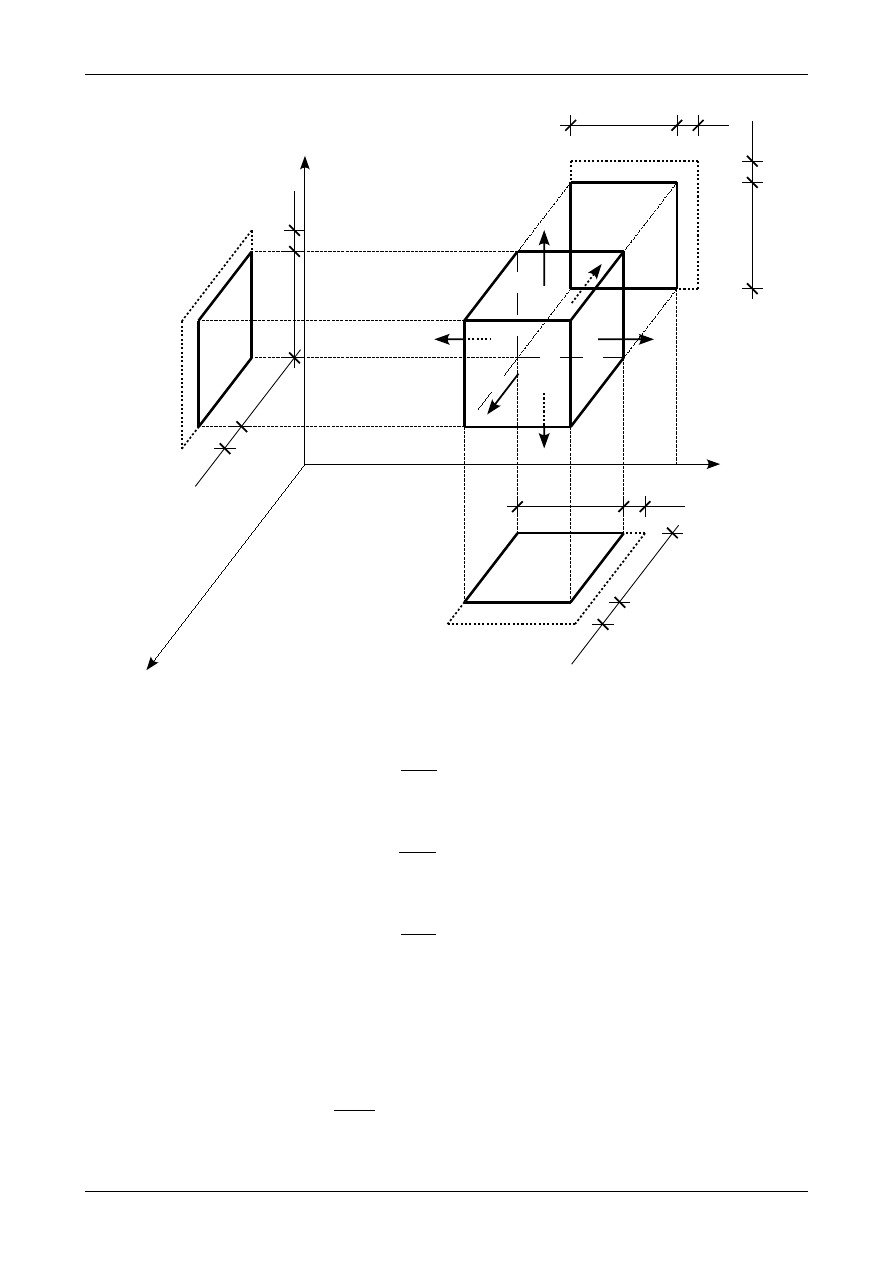
Rysunek 5 przedstawia prostokąt o wymiarach b na h. Na rysunku tym zaznaczone jest położenie osi
środkowych, które są także osiami symetrii. Możemy więc stwierdzić, że osie te będą także osiami głównymi
bezwładności dla prostokąta.

Z

0

=Z

gl

Y

0

=Y

gl

b

h

b
2

b
2

h

2

h

2

Rys. 5. Położenie osi środkowych i głównych w przekroju prostokątnym.

Osiowe (główne) momenty bezwładności wynoszą

I

Y0

=I

Ygl

=

h

⋅b

3

12

,

(27)

Dr inż. Janusz Dębiński

BZZ

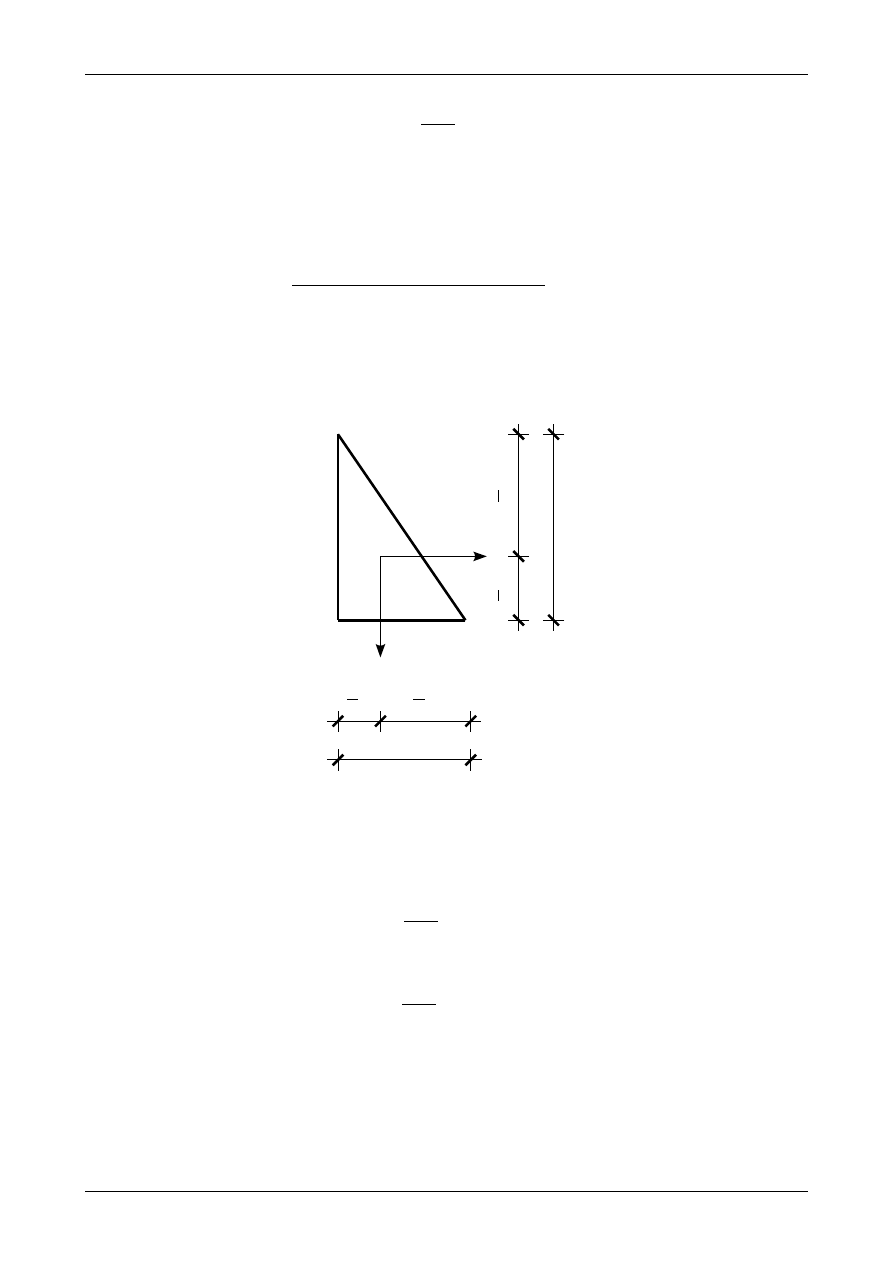
WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

7

I

Z0

=I

Zgl

=

b

⋅h

3

12

.

(28)

Wzory (27) i (28) mogą być kłopotliwe w użyciu, ponieważ można pomylić wymiar b i h. Ogólnie wzór na
moment bezwładności dla prostokąta w układzie jego osi głównych można zapisać jako

I

oś

=



wymiar

∥do osi



⋅



wymiar

⊥do osi



3

12

.

(29)

Dewiacyjny moment bezwładności dla prostokąta wynosi oczywiście zero.

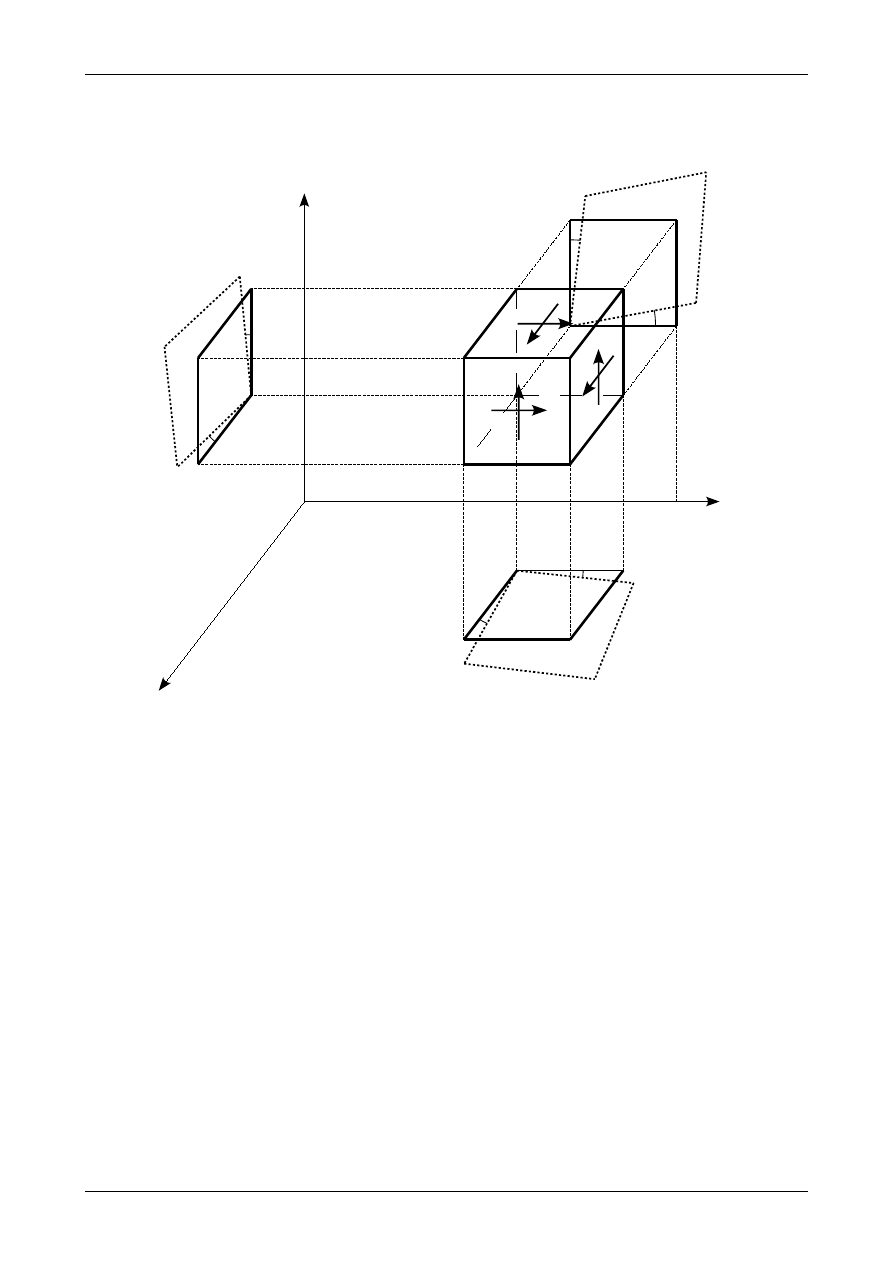
Rysunek 6 przedstawia położenie osi środkowych w trójkącie prostokątnym o wymiarach b na h.

Z

0

Y

0

b

h

2
3

⋅b

1
3

⋅b

1

3

⋅h

2

3

⋅h

Rys. 6. Położenie osi środkowych w przekroju będącym trójkątem prostokątnym.

Osiowe (główne) momenty bezwładności wynoszą

I

Y0

=

h

⋅b

3

36

(30)

I

Z0

=

b

⋅h

3

36

.

(31)

Wzory (30) i (31) mogą być kłopotliwe w użyciu, ponieważ można pomylić wymiar b i h. Ogólnie wzór na
moment bezwładności dla trójkąta prostokątnego w układzie jego osi środkowych można zapisać jako

Dr inż. Janusz Dębiński

BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

8

I

oś

=



wymiar

∥do osi



⋅



wymiar

⊥do osi



3

36

.

(32)

Osie przedstawione na rysunku 6 nie są osiami głównymi dla trójkąta prostokątnego więc w tym układzie osi
będzie niezerowy dewiacyjny moment bezwładności. Jego wartość bezwzględną wyznacza się ze wzoru

∣

I

Y0Z0

∣

=

b

2

⋅h

2

72

.

(33)

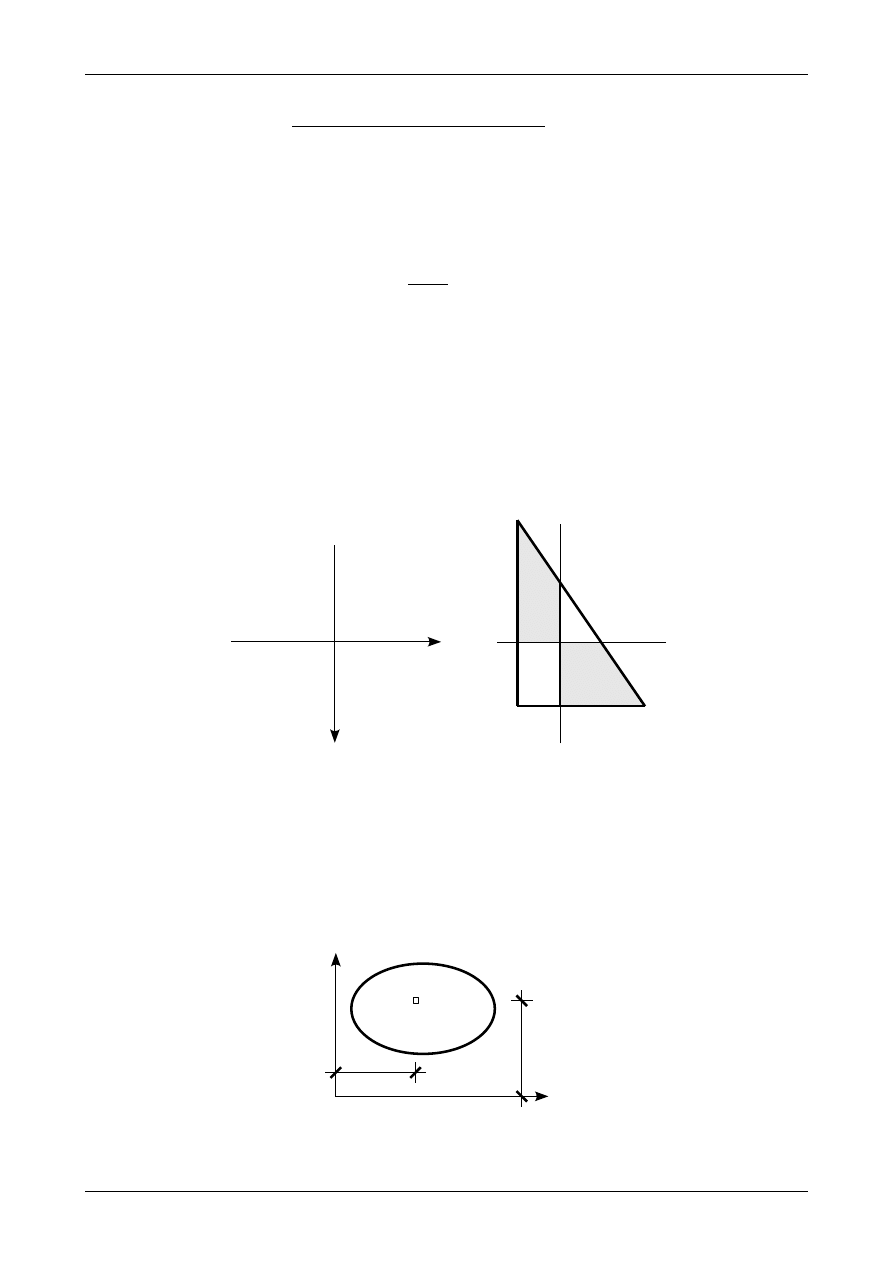
W celu ustalenia znaku dewiacyjnego momentu bezwładności dla trójkąta prostokątnego podzielmy ćwiartki
układu osi środkowych na dodatnie, w których iloczyn

y

0

⋅z

0

⋅dA

jest dodatni i ćwiartki ujemne, w których

iloczyn

y

0

⋅z

0

⋅dA

jest ujemny. Rysunek 7 przedstawia taki podział. Jeżeli większa część trójkąta

prostokątnego znajduje się w ćwiartkach dodatnich to dewiacyjny moment bezwładności jest dodatni. Jeżeli
większa część trójkąta prostokątnego znajduje się w ćwiartkach ujemnych to dewiacyjny moment
bezwładności jest ujemny. Rysunek 7 przedstawia także większą część przekroju pręta, który jest trójkątem
prostokątnym.

Z

0

Y

0

dodatnia

dodatnia

ujemna

ujemna

Rys. 7. Ćwiartki dodatnie i ujemne oraz większa część trójkąta prostokątnego.

2 Charakterystyki geometryczne przekroju w układzie XY

Rysunek 8 przedstawia przekrój pręta w dowolnym układzie osi XY. Elementarne pole powierzchni dA

posiada współrzędne x oraz y.

X

Y

dA

x

y

Rys. 8. Przekrój pręta.

Dr inż. Janusz Dębiński

BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

9

Pole powierzchni przekroju wynosi

A

=

∫

A

dA

.

(34)

Jednostką pola powierzchni w układzie SI jest m

2

. W budownictwie najczęściej będziemy używać cm

2

. Pole

powierzchni przekroju jest wielkością zawsze większą od zera.

Moment statyczny względem osi X wynosi

S

X

=

∫

A

y

⋅dA

.

(35)

Moment statyczny względem osi Y wynosi

S

Y

=

∫

A

x

⋅dA

.

(36)

Jednostką momentu statycznego w układzie SI jest m

3

. W budownictwie najczęściej będziemy używać cm

3

.

Moment statyczny może przyjmować dowolne wartości.

Osiowy moment bezwładności względem osi X wynosi

I

X

=

∫

A

y

2

⋅dA

.

(37)

Osiowy moment bezwładności względem osi Y wynosi

I

Y

=

∫

A

x

2

⋅dA

.

(38)

Dewiacyjny moment bezwładności w układzie XY wynosi

I

XY

=

∫

A

x

⋅y⋅dA

.

(39)

Biegunowy moment bezwładności w układzie XY wynosi

I

0

=

∫

A

r

2

⋅dA=

∫

A

y

2

⋅dA

∫

A

x

2

⋅dA=I

X

I

Y

,

(40)

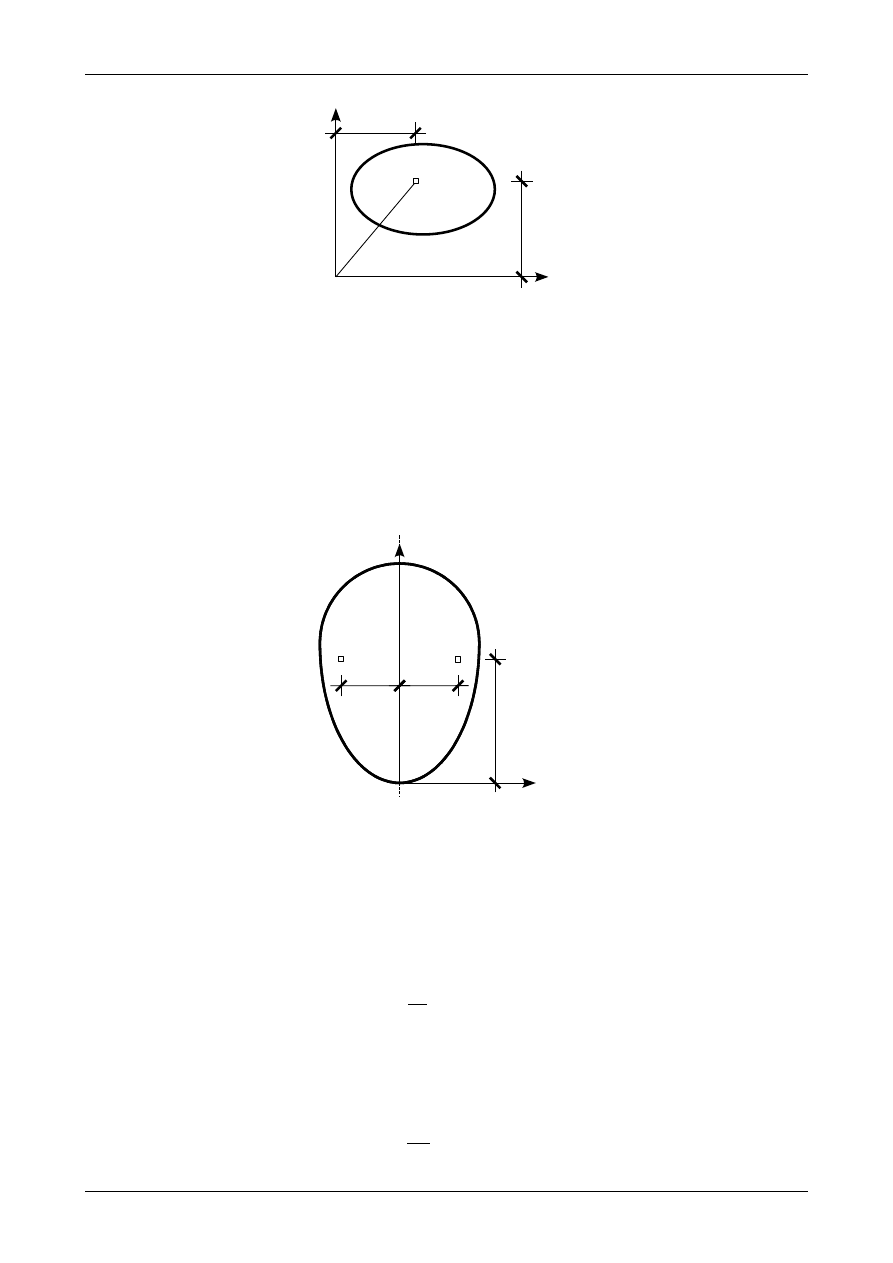
w którym r oznacza odległość elementarnego pola powierzchni dA od początku układu współrzędnych XY
zgodnie z rysunkiem 9.

Dr inż. Janusz Dębiński

BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

10

r

X

Y

dA

x

y

Rys. 9. Położenie bieguna elementarnego pola powierzchni dA.

Jednostką wszystkich momentów bezwładności w układzie SI jest m

4

. W budownictwie najczęściej będziemy

używać cm

4

. Osiowe momenty bezwładności są zawsze większe od zera i stanowią pewną miarę rozproszenia

przekroju pręta względem osi. Im to rozproszenie większe tym wartość osiowego momentu bezwładności jest
większa.

Dewiacyjny moment bezwładności może przyjmować dowolne wartości i jest on pewną miarą asymetrii
przekroju pręta w przyjętym układzie współrzędnych. Ponadto moment dewiacyjny w układzie współrzędnych,
w którym jedna z osi jest osią symetrii przekroju pręta, wynosi zero. Sytuację taką przedstawia rysunek 10.

X

Y

dA

x

y

dA

-x

I

XY

=0

Rys. 10. Przekrój pręta z jedną osią symetrii.

Osią środkową nazywamy taką oś względem, której odpowiedni moment statyczny wynosi zero.

Środkiem ciężkości nazywamy punkt przecięcia się dwóch osi środkowych.

Współrzędna x

C

środka ciężkości przekroju pręta będzie miała postać

x

C

=

S

Y

A

.

(41)

Współrzędna y

C

środka ciężkości przekroju pręta będzie miała postać

y

C

=

S

X

A

.

(42)

Dr inż. Janusz Dębiński

BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

11

Złożony przekrój najlepiej podzielić na figury, dla których znamy położenie środka ciężkości i pole
powierzchni. Wzory na położenie środka ciężkości będą miały postać

x

C

=

S

Y

A

=

∑

i

=1

i

=n

A

i

⋅x

i

∑

i

=1

i

=n

A

i

(43)

oraz

y

C

=

S

X

A

=

∑

i

=1

i

=n

A

i

⋅y

i

∑

i

=1

i

=n

A

i

.

(44)

w których to x

i

i y

i

oznaczają współrzędne środka ciężkości i-tej figury w układzie XY natomiast A

i

oznacza

pole powierzchni i-tej figury.

Środek ciężkości posiada następujące właściwości:

1. Środek ciężkości może znajdować się w punkcie poza przekrojem pręta.

2. Jeżeli przekrój posiada jedną oś symetrii to środek ciężkości znajduje się na niej.

3. Jeżeli przekrój posiada dwie osie symetrii to środek ciężkości znajduje się w punkcie ich przecięcia.

4. Jeżeli przekrój posiada więcej niż dwie osie symetrii to wszystkie osie przecinają się w środku

ciężkości.

5. Jeżeli przekrój składa się z dwóch figur, które dodajemy do siebie to środek ciężkości znajduje się na

linii łączącej środki ciężkości poszczególnych figur składowych.

6. Jeżeli przekrój składa się z trzech lub więcej figur składowych, które dodajemy do siebie, to środek

ciężkości znajduje się wewnątrz wieloboku, którego wierzchołkami są środki ciężkości
poszczególnych figur składowych.

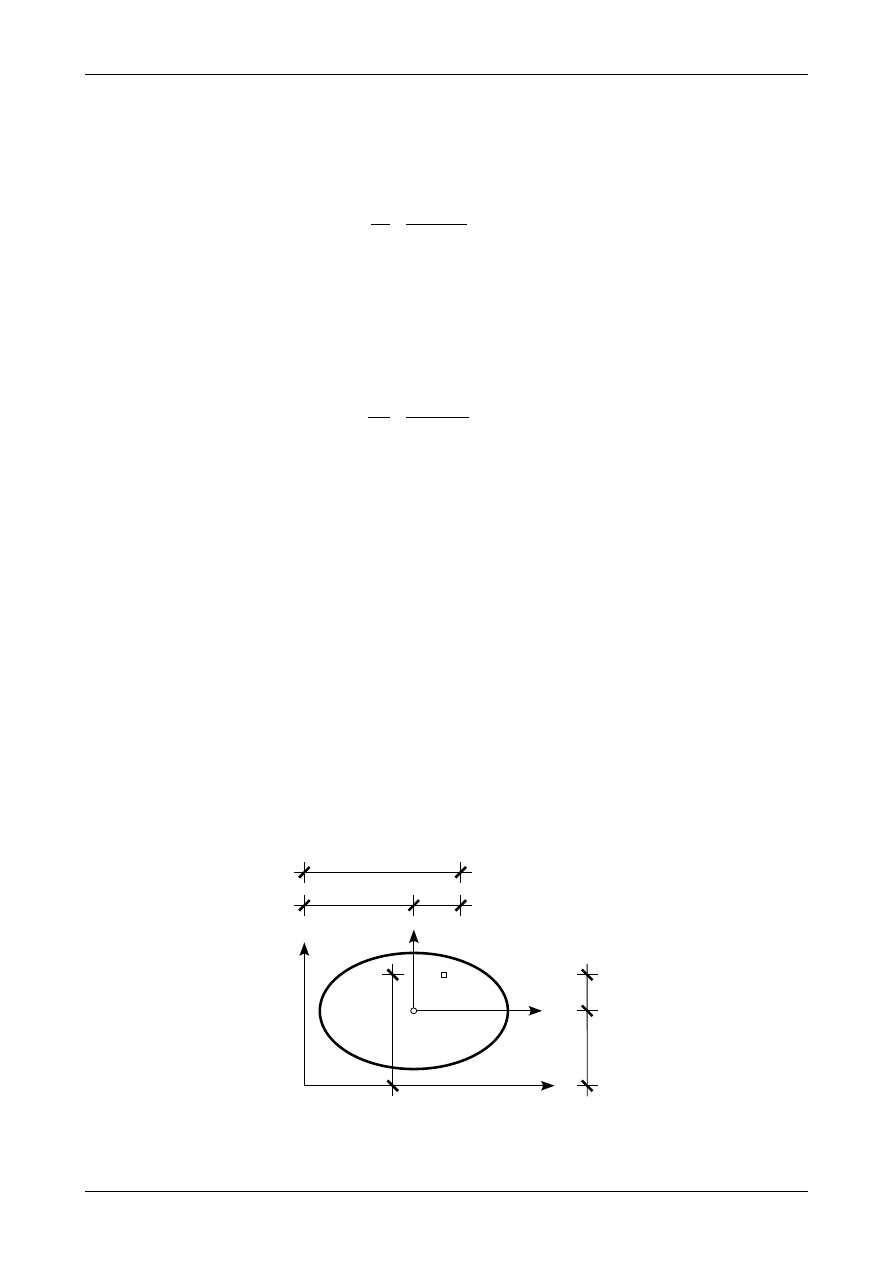
X

Y

dA

x

y

Y

0

X

0

x

C

x

0

sc

y

C

y

0

Rys. 11. Przekrój pręta oraz układy współrzędnych X

0

Y

0

oraz XY.

Dr inż. Janusz Dębiński

BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

12

Załóżmy, że znane są momenty bezwładności przekroju pręta w dowolnym układzie osi środkowych X

0

Y

0

czyli I

X0

, I

Y0

oraz I

X0Y0

. Moment bezwładności względem osi X wynosi

I

X

=I

X0

 y

C

2

⋅A

.

(45)

Moment bezwładności względem osi Y wynosi

I

Y

=I

Y0

x

C

2

⋅A

.

(46)

Dewiacyjny moment bezwładności w układzie XY wynosi

I

XY

=I

X0Y0

x

C

⋅y

C

⋅A

.

(47)

Wzory (45), (46) i (47) nazywamy wzorami Steinera. Najczęściej chcemy wyznaczyć momenty bezwładności
w układzie osi środkowych całego przekroju pręta X

0

Y

0

.Wzory Steinera będą miały wtedy postać

I

X0

=

∑

i

=1

i

=n



I

X0i

 y

0i

2

⋅A

i



,

(48)

I

Y0

=

∑

i

=1

i

=n



I

Y0i

x

0i

2

⋅A

i



(49)

I

X0Y0

=

∑

i

=1

i

=n



I

X0iY0i

x

0i

⋅y

0i

⋅A

i



.

(50)

We wzorach (48), (49) oraz (50) I

X0i

, I

Y0i

oznaczają osiowe momenty bezwładności względem osi środkowych

i-tej figury. I

X0iY0i

oznacza dewiacyjny moment bezwładności w układzie osi środkowych i-tej figury. A

i

oznacza pole powierzchni i-tej figury natomiast x

0i

, y

0i

oznaczają współrzędne środka ciężkości i-tej figury w

układzie osi środkowych całego przekroju pręta X

0

Y

0

.

Transformacja układu współrzędnych polega na obrocie tego układu względem jego początku o pewien kąt.
Dodatni kąt obrotu będzie kręcił osią X

0

w kierunku osi Y

0

. Momenty bezwładności w układzie osi

transformowanych X

0'

Y

0'

oblicza się ze wzorów

I

X0 '

=

I

X0

I

Y0

2



I

X0

−I

Y0

2

⋅cos



2

⋅



−I

X0Y0

⋅sin



2

⋅



,

(51)

I

Y0'

=

I

X0

I

Y0

2

−

I

X0

−I

Y0

2

⋅cos



2

⋅



I

X0Y0

⋅sin



2

⋅



,

(52)

Dr inż. Janusz Dębiński

BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

13

I

X0 'Y0'

=

I

X0

−I

Y0

2

⋅sin



2

⋅



I

X0Y0

⋅cos



2

⋅



.

(53)

Istnieje taki układ osi środkowych, w którym osiowe momenty bezwładności I

X0'

i I

Y0'

osiągają wartości

ekstremalne. Taki układ osi środkowych nazywa się układem osi głównych. Ponadto okazuje się, że w
układzie osi głównych dewiacyjny moment bezwładności równa się zero. Kąt nachylenia osi głównych
wyznacza się ze wzoru

tg



2

⋅

gl



=

−2⋅I

X0Y0

I

X0

−I

Y0

.

(54)

Główne momenty bezwładności wyznaczymy ze wzorów

I

Xgl

=

I

X0

I

Y0

2



I

X0

−I

Y0

2

⋅cos



2

⋅

gl



−I

X0Y0

⋅sin



2

⋅

gl



,

(55)

I

Ygl

=

I

X0

I

Y0

2

−

I

X0

−I

Y0

2

⋅cos



2

⋅

gl



I

X0Y0

⋅sin



2

⋅

gl



.

(56)

Wartości głównych momentów bezwładności możemy sprawdzić za pomocą zależności

I

1

/2

=

I

X0

I

Y0

2

±





I

X0

−I

Y0

2



2





I

X0Y0



2

,

(57)

w którym I

1

oznacza największy osiowy moment bezwładności natomiast I

2

najmniejszy osiowy moment

bezwładności.

Niezmiennikiem nazywamy wielkość fizyczną, która nie zmienia wartości przy obrocie (transformacji) układu
współrzędnych. W przypadku momentów bezwładności będziemy mieli dwa niezmienniki. Pierwszy z nich ma
postać

J

1

=I

X0

I

Y0

=I

X0 '

I

Y0'

=I

Xgl

I

Ygl

.

(58)

Drugi z niezmienników ma postać

J

2

=I

X0

⋅I

Y0

−I

X0Y0

2

=I

X0 '

⋅I

Y0'

−I

X0 'Y0'

2

=I

Xgl

⋅I

Ygl

.

(59)

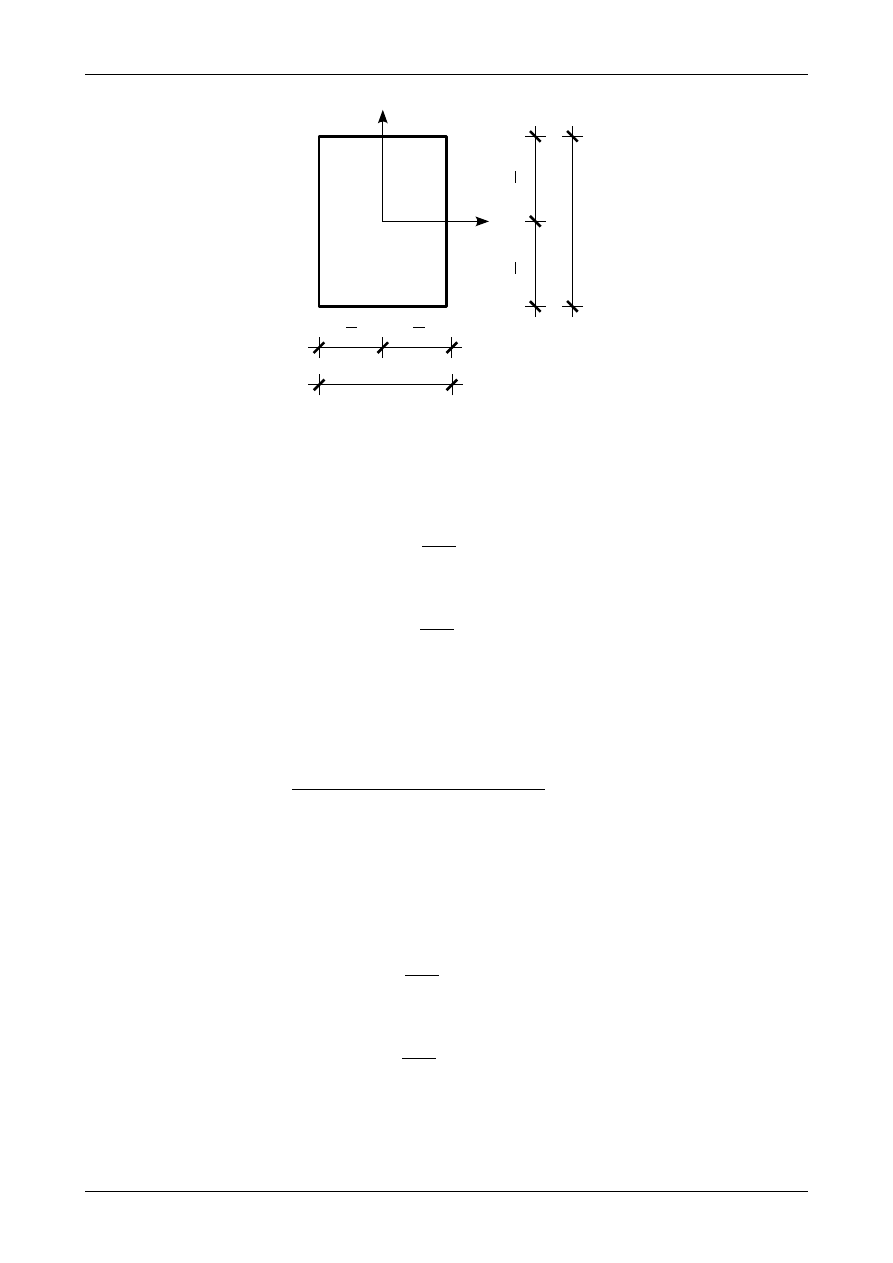
Rysunek 12 przedstawia prostokąt o wymiarach b na h. Na rysunku tym zaznaczone jest położenie osi
środkowych, które są także osiami symetrii. Możemy więc stwierdzić, że osie te będą także osiami głównymi
bezwładności dla prostokąta.

Dr inż. Janusz Dębiński

BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

14

X

0

=X

gl

Y

0

=Y

gl

b

h

b
2

b
2

h

2

h

2

Rys. 12. Położenie osi środkowych i głównych w przekroju prostokątnym.

Osiowe (główne) momenty bezwładności wynoszą

I

X0

=I

Xgl

=

b

⋅h

3

12

,

(60)

I

Y0

=I

Ygl

=

h

⋅b

3

12

.

(61)

Wzory (60) i (61) mogą być kłopotliwe w użyciu, ponieważ można pomylić wymiar b i h. Ogólnie wzór na
moment bezwładności dla prostokąta w układzie jego osi głównych można zapisać jako

I

oś

=



wymiar

∥do osi



⋅



wymiar

⊥do osi



3

12

.

(62)

Dewiacyjny moment bezwładności dla prostokąta wynosi oczywiście zero.

Rysunek 13 przedstawia położenie osi środkowych w trójkącie prostokątnym o wymiarach b na h. Osiowe
(główne) momenty bezwładności wynoszą

I

X0

=

b

⋅h

3

36

(63)

I

Y0

=

h

⋅b

3

36

.

(64)

Wzory (63) i (64) mogą być kłopotliwe w użyciu, ponieważ można pomylić wymiar b i h. Ogólnie wzór na
moment bezwładności dla trójkąta prostokątnego w układzie jego osi środkowych można zapisać jako

Dr inż. Janusz Dębiński

BZZ

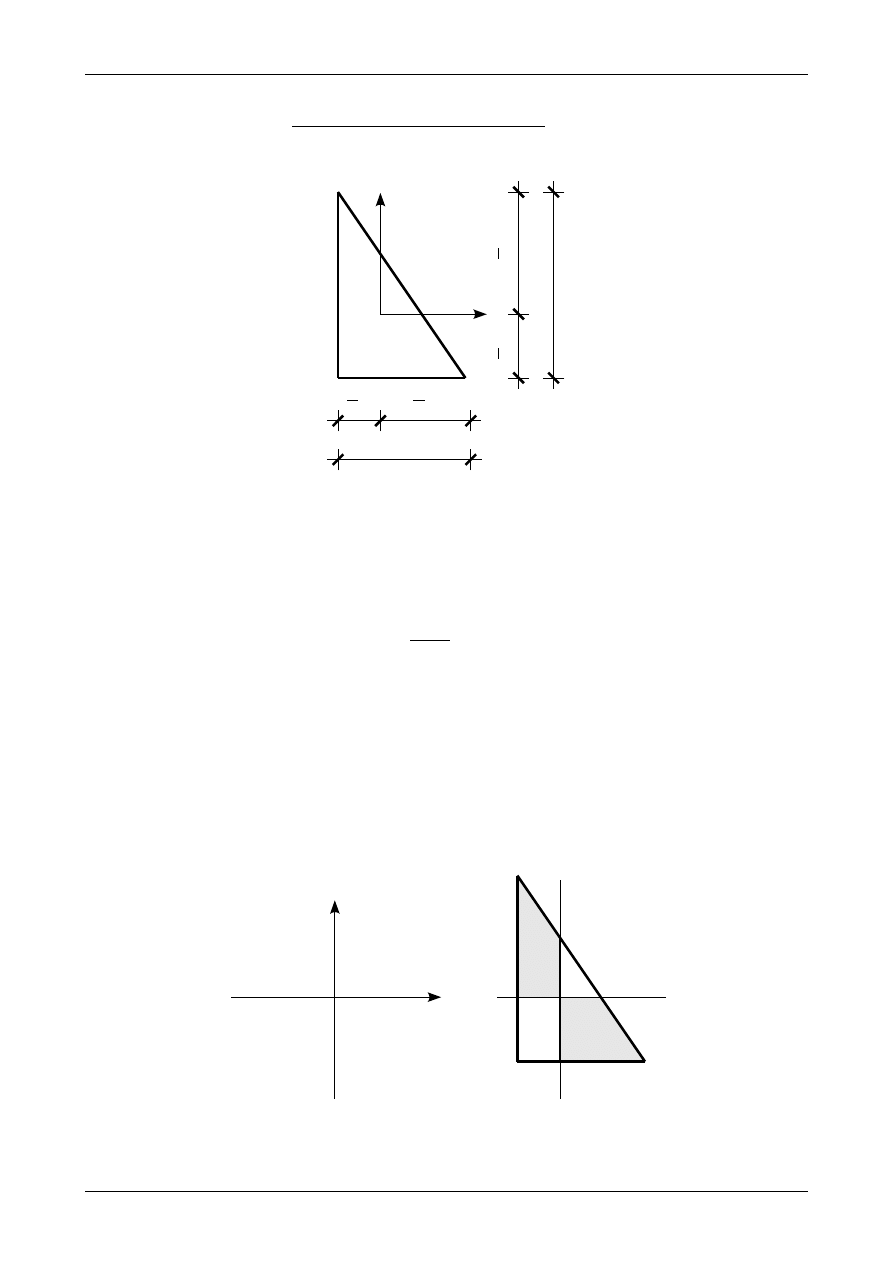
WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

15

I

oś

=



wymiar

∥do osi



⋅



wymiar

⊥do osi



3

36

.

(65)

X

0

Y

0

b

h

2
3

⋅b

1
3

⋅b

1

3

⋅h

2

3

⋅h

Rys. 13. Położenie osi środkowych w przekroju będącym trójkątem prostokątnym.

Osie przedstawione na rysunku 13 nie są osiami głównymi dla trójkąta prostokątnego więc w tym układzie osi
będzie niezerowy dewiacyjny moment bezwładności. Jego wartość bezwzględną wyznacza się ze wzoru

∣

I

X0Y0

∣

=

b

2

⋅h

2

72

.

(66)

W celu ustalenia znaku dewiacyjnego momentu bezwładności dla trójkąta prostokątnego podzielmy ćwiartki
układu osi środkowych na dodatnie, w których iloczyn

x

0

⋅y

0

⋅dA

jest dodatni i ćwiartki ujemne, w których

iloczyn

x

0

⋅y

0

⋅dA

jest ujemny. Rysunek 14 przedstawia taki podział. Jeżeli większa część trójkąta

prostokątnego znajduje się w ćwiartkach dodatnich to dewiacyjny moment bezwładności jest dodatni. Jeżeli
większa część trójkąta prostokątnego znajduje się w ćwiartkach ujemnych to dewiacyjny moment
bezwładności jest ujemny. Rysunek 7 przedstawia także większą część przekroju pręta, który jest trójkątem
prostokątnym.

X

0

Y

0

dodatnia

dodatnia

ujemna

ujemna

Rys. 14. Ćwiartki dodatnie i ujemne oraz większa część trójkąta prostokątnego.

Dr inż. Janusz Dębiński

BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

16

3 Przestrzenny stan naprężenia

Podstawowym założeniem w analizie stanu naprężenia jest założenie ciągłości ośrodka. Założenie

ciągłości ośrodka pozwala na wprowadzenie pojęcia gęstości, które definiuje się jako

= lim

 V 0

m
V

=

dm
dV

,

(67)

w którym

∆

m oznacza masę zawartą w objętości

∆

V. Najczęściej zakłada się, że gęstość jest stała w całym

ciele.

Opisane dalej zależności są słuszne tylko dla materiałów izotropowych, które to materiały mają takie same
właściwości we wszystkich kierunkach. Opisane poniżej zależności są także słuszne w zakresie sprężystym
pracy materiału. Oznacza to, że po przyłożeniu obciążenia ciało ulegnie deformacjom. Jednak po odciążeniu
ciało to powróci do swej pierwotnej postaci czyli nie ulegnie deformacjom trwałym.

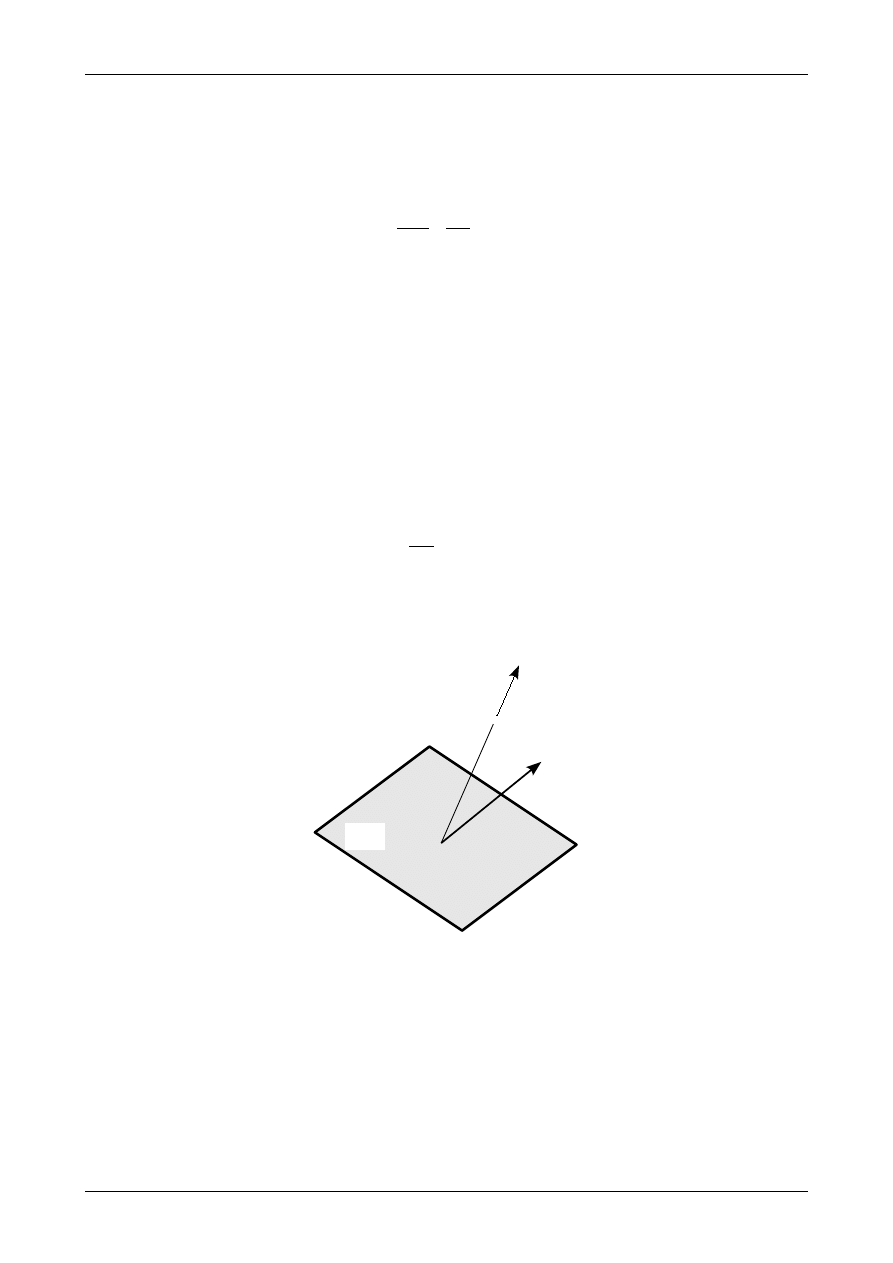
Wielkością, która służy do opisu stanu naprężenia jest wektor naprężenia. Na płaszczyźnie o normalnej

n

wyodrębiniamy elementarne pole powierzchni dS Na elementarnym polu powierzchni działa siła

d F

.

Wektor naprężenia definiuje się jako

f

n 

=

d F

dS

.

(68)

Rysunek 15 przedstawia wektor naprężenia na płaszczyźnie o normalnej

n

.

dS

n

f

n 

Rys. 15. Wektor naprężenia.

Wektor naprężenia możemy rozłożyć na dwie składowe: normalną



n

i styczną



n

. Rozkład wektora

naprężenia na dwie składowe przedstawia rysunek 16. Składowe wektora naprężenia nazywają się
naprężeniem normalnym

σ

i naprężeniem stycznym

τ

. Jednostką naprężenia w układzie SI jest Pa (Pascal). W

budownictwie będziemy używać wielokrotności MPa.

Aby jednoznacznie określić stan naprężenia w dowolnym punkcie należy znać wektory naprężenia na
trzech wzajemnie prostopadłych płaszczyznach.

Dr inż. Janusz Dębiński

BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

17

dS

n

f

n 



n



n

Rys. 16. Rozkład wektora naprężenie na składową normalną i styczną.

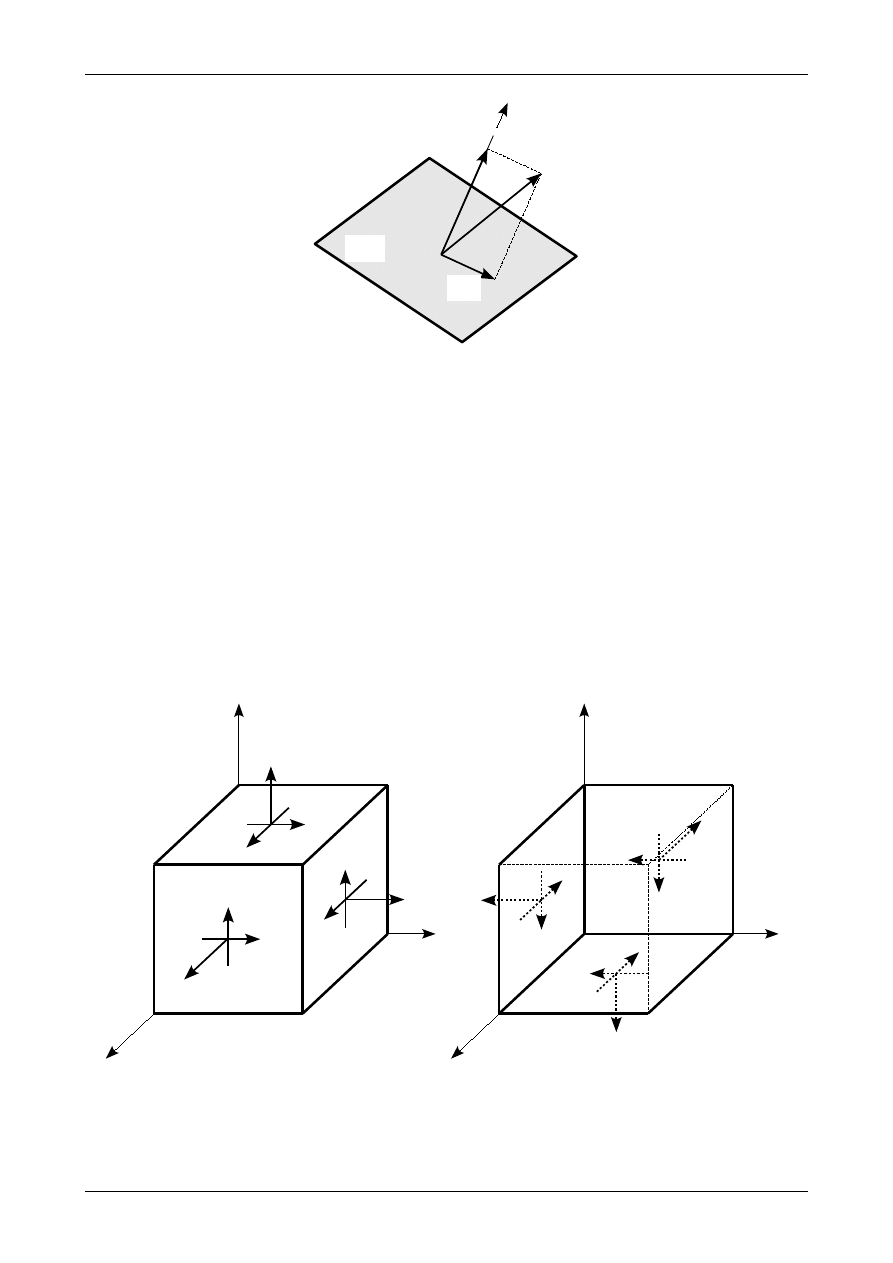
Na każdej z tych trzech płaszczyzn określa się naprężenie normalne oraz dwie składowe naprężenia stycznego.
Graficznie stan naprężenia przedstawia się na ściankach elementarnego sześcianu w kartezjańskim układzie
współrzędnych XYZ. Naprężenia normalne zapisuje się jako

σ

X

,

σ

Y

, oraz

σ

Z

. Indeks dolny określa nam oś,

która jest normalna (prostopadła) do płaszczyzny, na której działa dane naprężenie normalne. Naprężenia
styczne określa się jako

τ

XY

,

τ

YX

,

τ

XZ

,

τ

ZX

,

τ

YZ

oraz

τ

ZY

. Pierwszy z tych indeksów określa normalną do

płaszczyzny, na której działa dane naprężenie styczne natomiast drugi indeks określa nam kierunek danego
naprężenia stycznego. Naprężenie jest dodatnie jeżeli na ściankach dodatnich na zwrot zgodny ze zwrotem
osi układu współrzędnych XYZ. Ścianki dodatnie są to ścianki, które są widoczne, jeżeli patrzymy na
elementarny sześcian z punktu, który ma wszystkie współrzędne dodatnie. Rysunek 17 a) przedstawia
naprężenia dodatnie na ściankach dodatnich. Natomiast rysunek 17 b) przedstawia dodatnie naprężenia na
ściankach ujemnych. Dodatnie naprężenia na ściankach ujemnych będą miały zwroty przeciwne do zwrotów
osi układu współrzędnych XYZ.

X

Y

Z

X

Y

Z



X



Y



Z



XY



YX



YZ



ZY



XZ



ZX



X



Y



Z



XY



YX



YZ



ZY



ZX



XZ

a)

b)

Rys. 17. Stan naprężenia w punkcie: a) na ściankach dodatnich, b) na ściankach ujemnych.

Dr inż. Janusz Dębiński

BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

18

Wszystkie dziewięć składowych stanu naprężenia zapisuje się w tablicy nazywanej tensorem naprężenia.
Tensor ma więc postać

=

[



X



XY



XZ



YX



Y



YZ



ZX



ZY



Z

]

.

(69)

Pierwszą kolumnę tensora (69) stanowią składowe wektora naprężenia na płaszczyźnie o normalnej X, drugą
składowe wektora naprężenia na płaszczyźnie o normalnej Y trzecią natomiast składowe wektora naprężenia
na płaszczyźnie o normalnej Z.

Tensor naprężenia posiada ponadto właściwość, że jest symetryczny względem przekątnej, na której
znajdują się naprężenia normalne. Zachodzą więc zależności



XY

=

YX

,

(70)



XZ

=

ZX

(71)



YZ

=

ZY

.

(72)

Dowolna płaszczyzna jest definiowana poprzez swój wektor normalny

n

, który można opisać trzema

kosinusami kątów pomiędzy kierunkiem wektora normalnego a poszczególnymi osiami układu współrzędnych
XYZ. Kosinusy te tworzą macierz kolumnową w postaci

[

cos



n , x



cos



n , y



cos



n , z



]

.

(73)

Wektor naprężenia

f

n 

na płaszczyźnie o normalnej

n

będzie miał trzy składowe, które można

wyznaczyć korzystając ze wzoru

[

f

X

n 

f

Y

n 

f

X

n 

]

=

[



X



YX



ZX



XY



Y



ZY



XZ



YZ



Z

]

⋅

[

cos



n , x



cos



n , y



cos



n , z



]

.

(74)

Układ współrzędnych XYZ możemy transformować (obrócić) względem początku układu. Transformacja ta
jest opisana za pomocą macierzy transformacji, która ma postać

Dr inż. Janusz Dębiński

BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

19

B

=

[

cos



x ' , x



cos



x ' , y



cos



x ' , z



cos



y ' , x



cos



y ' , y



cos



y ' , z



cos



z' , x



cos



z' , y



cos



z' , z



]

.

(75)

Wyrazy tej macierzy nie mogą być dowolne. Muszą one spełniać warunki ortogonalności (prostopadłości).
Warunków tych jest sześć. Pierwsze trzy z nich to suma kwadratów kosinusów w poszczególnych wierszach
macierzy (75), która musi się równać jeden.

cos

2



x ' , x



cos

2



x ' , y



cos

2



x ' , z



=1

,

(76)

cos

2



y ' , x



cos

2



y ' , y



cos

2



y ' , z



=1

,

(77)

cos

2



z ' , x



cos

2



z ' , y



cos

2



z ' , z



=1

.

(78)

Pozostałe trzy równania to poszczególne wiersze macierzy (75) przemnożone przez siebie, które są równe zero

cos



x ' , x



⋅cos



y ' , x



cos



x' , y



⋅cos



y' , y



cos



x ' , z



⋅cos



y ' , z



=0

,

(79)

cos



x ' , x



⋅cos



z ' , x



cos



x' , y



⋅cos



z' , y



cos



x ' , z



⋅cos



z ' , z



=0

,

(80)

cos



y ' , x



⋅cos



z ' , x



cos



y' , y



⋅cos



z' , y



cos



y ' , z



⋅cos



z ' , z



=0

.

(81)

Współrzędne tensora naprężenia (69) w układzie transformowanym wyznaczymy korzystając ze wzoru

 '=B⋅⋅B

T

,

(82)

w którym B

T

jest transponowaną macierzą transformacji. Tensor naprężenia w układzie transponowanym

będzie miał postać

 '=

[



X '



X 'Y '



X ' Z '



Y ' X '



Y'



Y 'Z '



Z ' X '



Z 'Y '



Z '

]

.

(83)

Istnieje taki układ transponowany, w którym naprężenia normalne osiągają wartości ekstremalne natomiast
naprężenia styczne wynoszą zero. Układ taki nazywa się układem głównym. Ekstremalne naprężenia
normalne nazywają się naprężeniami głównymi. Naprężenia główne wyznacza się jako pierwiastki równania
trzeciego stopnia nazywanego równaniem charakterystycznym w postaci

Dr inż. Janusz Dębiński

BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

20



3

−I

1

⋅

2

I

2

⋅−I

3

=0

,

(84)

w którym współczynnik I

1

równa się sumie naprężeń normalnych

I

1

=

X



Y



Z

.

(85)

I

2

równa się sumie podwyznaczników tensora (69)

I

2

=

∣



X



XY



YX



Y

∣



∣



Y



YZ



ZY



Z

∣



∣



X



XZ



ZX



Z

∣

.

(86)

I

3

równa się wyznacznikowi z macierzy opisującej tensor (69)

I

3

=

∣



X



XY



XZ



YX



Y



YZ



ZX



ZY



Z

∣

.

(87)

Tensor naprężenia w układzie osi głównych ma postać



gl

=

[



1

0

0

0



2

0

0

0



3

]

.

(88)

Chcąc wyznaczyć kierunki główne należy wykorzystać poniższy układ równań

{





X

−



⋅n

1



YX

⋅n

2



ZX

⋅n

3

=0



XY

⋅n

1







Y

−



⋅n

2



ZY

⋅n

3

=0



XZ

⋅n

1



YZ

⋅n

2







Z

−



⋅n

3

=0

,

(89)

w którym

σ

oznacza jedno z naprężeń głównych natomiast n

1

, n

2

oraz n

3

oznaczają trzy kosinusy kierunkowe

pomiędzy kierunkiem głównym i osiami układu współrzędnych XYZ. Układ równań (89) jest układem
jednorodnym, którego wyznacznik główny wynosi zero. Chcąc wyznaczyć kierunki główne zamiast

σ

należy

postawić poszczególne naprężenia główne oraz jedno z równań zamienić na warunek ortogonalności w postaci

n

1

2

n

2

2

n

3

2

=1

.

(90)

Dr inż. Janusz Dębiński

BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

21

Układy równań do wyznaczenia kierunków głównych dla naprężeń głównych

σ

1

,

σ

2

oraz

σ

3

będą miały postać

{





X

−

1



⋅n

1

1 



YX

⋅n

2

1 



ZX

⋅n

3

1

=0



XY

⋅n

1

1 







Y

−

1



⋅n

2

1



ZY

⋅n

3

1 

=0

[

n

1

1 

]

2



[

n

2

1 

]

2



[

n

3

1 

]

2

=1

,

(91)

{





X

−

2



⋅n

1

2



YX

⋅n

2

2 



ZX

⋅n

3

2 

=0



XY

⋅n

1

2 







Y

−

2



⋅n

2

2 



ZY

⋅n

3

2

=0

[

n

1

2 

]

2



[

n

2

2 

]

2



[

n

3

2 

]

2

=1

,

(92)

{





X

−

3



⋅n

1

3



YX

⋅n

2

3 



ZX

⋅n

3

3 

=0



XY

⋅n

1

3 







Y

−

3



⋅n

2

3 



ZY

⋅n

3

3

=0

[

n

1

3 

]

2



[

n

2

3 

]

2



[

n

3

3 

]

2

=1

.

(93)

Macierz transformacji dla kierunków głównych będzie miała postać

B

gl

=

[

n

1

1 

n

2

1 

n

3

1 

n

1

2 

n

2

2 

n

3

2

n

1

3 

n

2

3 

n

3

3

]

.

(94)

Możemy ją zapisać także jako

B

gl

=

[

cos



1 , x



cos



1 , y



cos



1 , z



cos



2 , x



cos



2 , y



cos



2 , z



cos



3 , x



cos



3 , y



cos



3 , z



]

.

(95)

Wartości współczynników I

1

, I

2

oraz I

3

nie mogą zależeć od położenia układu współrzędnych są więc one

niezmiennikami stanu naprężenia. W przypadku tensora (83) mają one postać

I

1

=

X '



Y '



Z '

,

(96)

I

2

=

∣



X '



X 'Y '



Y' X '



Y'

∣



∣



Y'



Y' Z '



Z 'Y '



Z'

∣



∣



X '



X 'Z '



Z ' X '



Z '

∣

.

(97)

Dr inż. Janusz Dębiński

BZZ

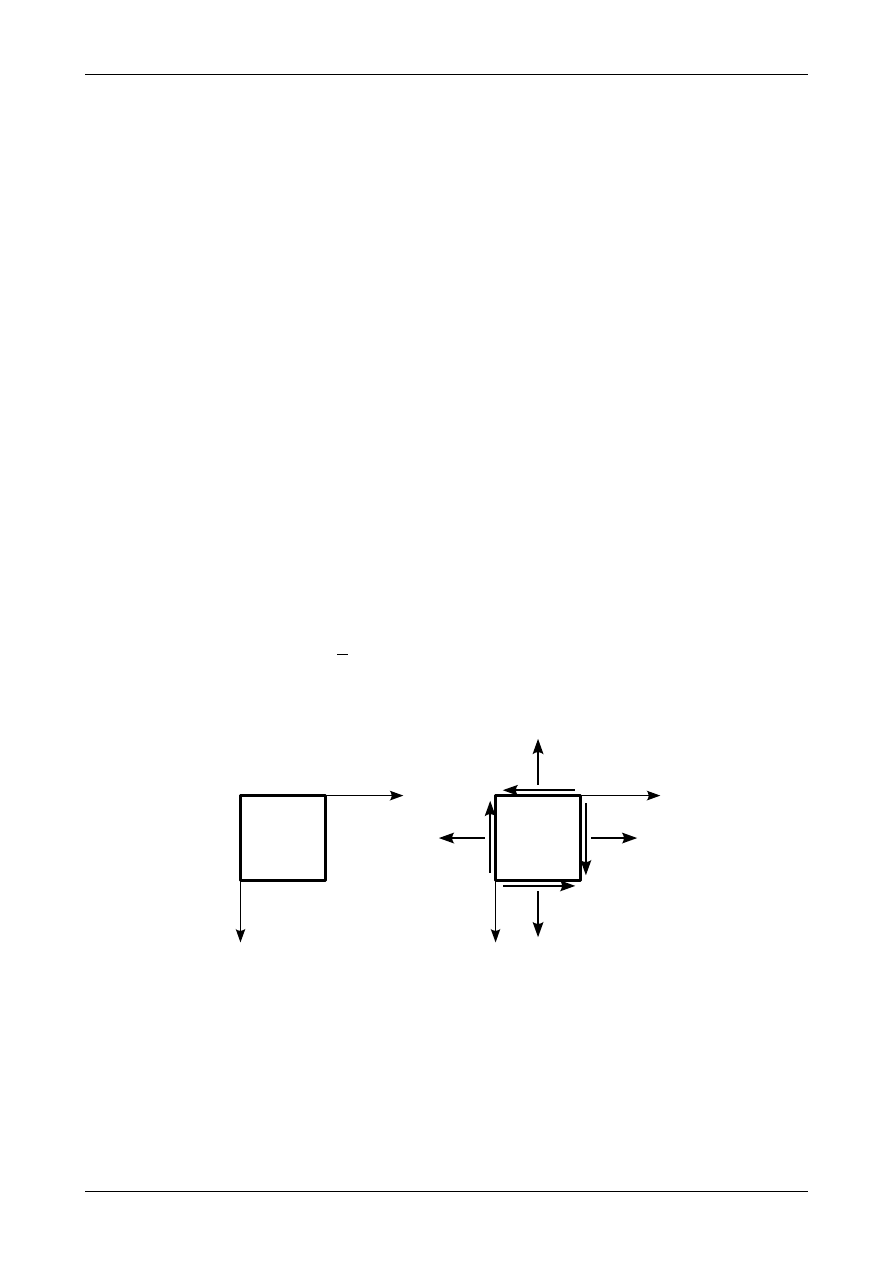
WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

22

I

3

=

∣



X '



X 'Y '



X ' Z '



Y ' X '



Y'



Y 'Z '



Z ' X '



Z 'Y '



Z '

∣

.

(98)

W przypadku tensora (88) mają one postać

I

1

=

1



2



3

,

(99)

I

2

=

1

⋅

2



2

⋅

3



3

⋅

1

,

(100)

I

3

=

1

⋅

2

⋅

3

,

(101)

4 Płaski stan naprężenia

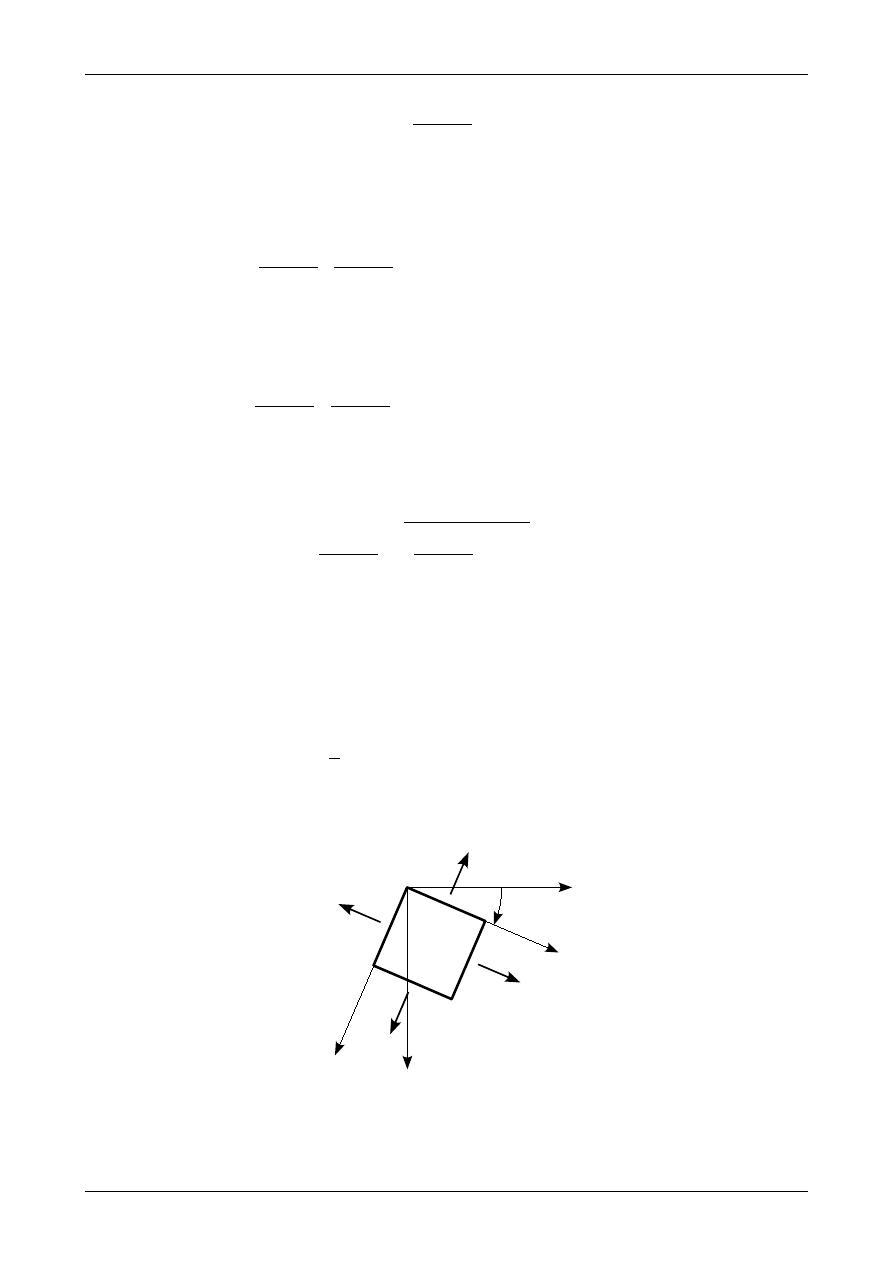
Jeżeli jeden z trzech wektorów naprężenia, które opisują stan naprężenia w punkcie, jest równy zero to

stan taki nazywamy płaskim stanem naprężenia. Przyjmijmy, że zerowy jest wektor na płaszczyźnie o
normalnej Z. Dla uproszczenia będziemy przedstawiać płaski stan naprężenia na elementarnym kwadracie,
który przedstawiony jest na rysunku 18. Tensor naprężenia będzie miał w płaskim stanie naprężenia postać

=

[



X



XY

0



YX



Y

0

0

0

0

]

(102)

bok dodatni

b

ok

d

od

at

n

i

bok ujemny

b

ok

u

je

m

n

y

X

Y

X

Y



X



Y



XY



YX



Y



X



YX



XY

Rys. 18. Płaski stan naprężenia.

Wiadomo, że przy obrocie układu współrzędnych XY składowe stanu naprężenia zmieniają swoje wartości.
Istnieje taki układ współrzędnych, w którym naprężenia normalne przyjmują wartości ekstremalne (największą
i najmniejszą z możliwych) natomiast naprężenie styczne przyjmuje wartość zero. Taki układ współrzędnych
nazywa się układem osi głównych. Natomiast ekstremalne naprężenia normalne nazywają się naprężeniami
głównymi. Wzór na kąt obrotu układu osi głównych ma postać (kąt dodatni kręci od osi X do osi Y)

Dr inż. Janusz Dębiński

BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

23

tg

2⋅

gl

=

2

⋅

XY



X

−

Y

.

(103)

Naprężenia główne będziemy wyznaczać ze wzorów



Xgl

=



X



Y

2





X

−

Y

2

⋅cos2⋅

gl



XY

⋅sin2⋅

gl



(104)

oraz



Ygl

=



X



Y

2

−



X

−

Y

2

⋅cos2⋅

gl

−

XY

⋅sin2⋅

gl



.

(105)

W celu sprawdzenia obliczeń naprężeń głównych będziemy stosować następujący wzór



1

/2

=



X



Y

2

±







X

−

Y

2



2



XY

2

,

(106)

w którym

σ

1

oznacza maksymalne naprężenie główne natomiast

σ

2

oznacza minimalne naprężenie główne.

Rysunek 19 przedstawia elementarny kwadrat z zaznaczonymi naprężeniami głównymi. Tensor naprężenia w
przypadku naprężeń głównych będzie miał postać



gl

=

[



Xgl

0

0

0



Ygl

0

0

0

0

]

(107)

X

Y

X

gl

Y

gl



gl



Xgl



Xgl



Ygl



Ygl

Rys. 19. Naprężenia główne w płaskim stanie naprężenia.

Dr inż. Janusz Dębiński

BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

24

Kąt nachylenia układu współrzędnych, w którym naprężenia styczne osiągają wartości ekstremalne wynosi

tg

2⋅



=−



X

−

Y

2

⋅

XY

.

(108)

Ekstremalne naprężenie normalne wyznacza się ze wzoru



MAX

=−



X

−

Y

2

⋅sin2⋅





XY

⋅cos2⋅





.

(109)

Jako sprawdzenie można wykorzystać zależność

∣

MAX

∣=







X

−

Y

2



2



XY

2

.

(110)

Naprężenia normalne stowarzyszone z ekstremalnymi naprężeniami stycznymi wyznacza się ze wzorów



X



=



X



Y

2





X

−

Y

2

⋅cos2⋅





XY

⋅sin2⋅





,

(111)



Y



=



X



Y

2

−



X

−

Y

2

⋅cos2⋅



−

XY

⋅sin2⋅





.

(112)

Naprężenia normalne stowarzyszone z ekstremalnymi naprężeniami stycznymi mają te same wartości i mogą
być także wyznaczone z zależności



X



=

Y



=



X



Y

2

.

(113)

Tensor naprężenia będzie w przypadku ekstremalnych naprężeń stycznych miał postać





=

[



X





MAX

0



MAX



Y



0

0

0

0

]

.

(114)

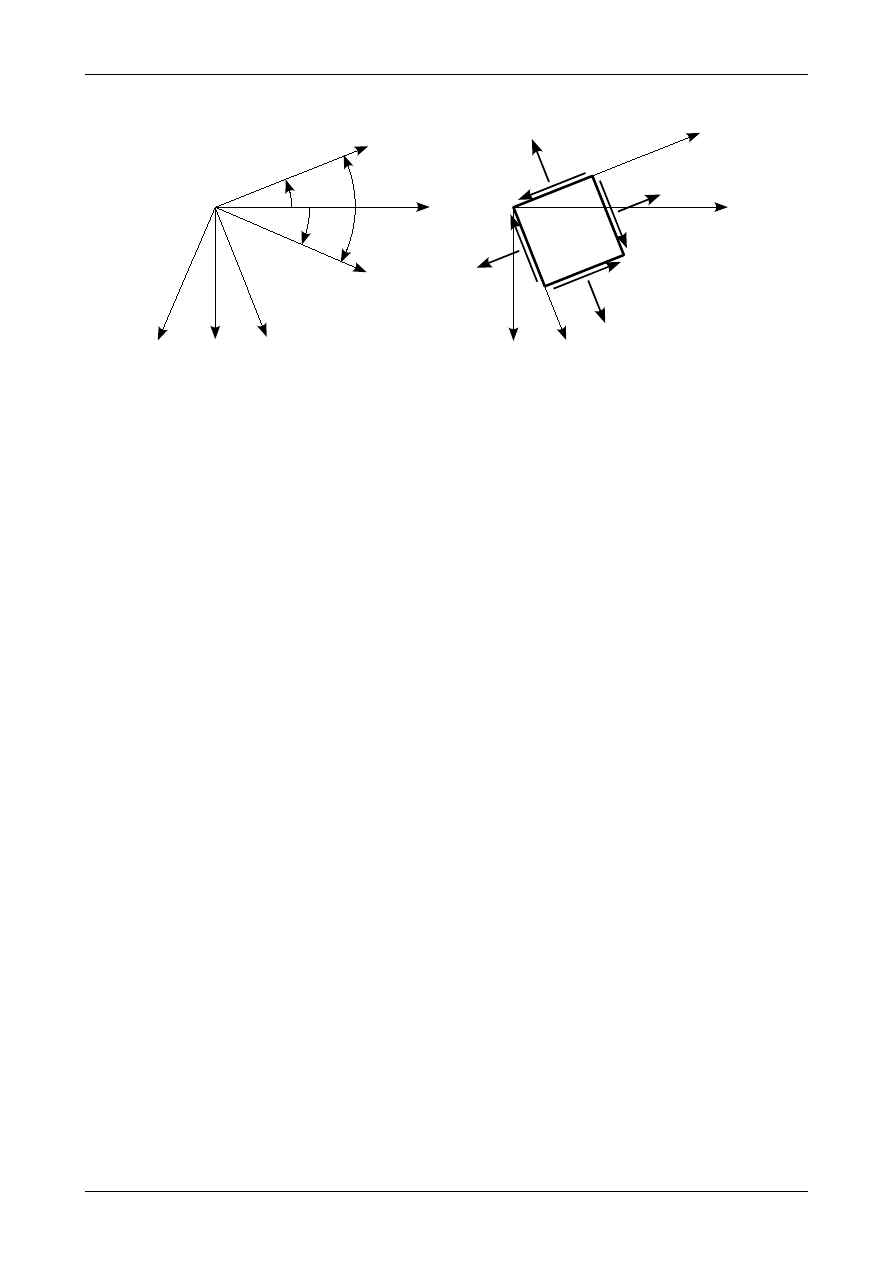
Osie naprężeń głównych i ekstremalnych naprężeń stycznych są wzajemnie obrócone o kąt 45

o

. Rysunek

20 przedstawia stan naprężenia w układzie ekstremalnych naprężeń stycznych.

Dr inż. Janusz Dębiński

BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

25

X

Y

X

gl

Y

gl



gl

X

τ

Y

τ





45

o

X

Y

X

τ

Y

τ







X 



X 



Y 



Y 



MAX



MAX



MAX



MAX

Rys. 20. Ekstremalne naprężenia styczne.

W płaskim stanie naprężenia trzeci niezmiennik zawsze jest równy zero niezależnie od układu
współrzędnych. Pierwszy niezmiennik tensora (102) wynosi

I

1

=

X



Y

.

(115)

Drugi niezmiennik tensora (102) wynosi

I

2

=

X

⋅

Y

−

XY

2

.

(116)

Pierwszy niezmiennik tensora (107) wynosi

I

1

=

Xgl



Ygl

.

(117)

Drugi niezmiennik tensora (107) wynosi

I

2

=

Xgl

⋅

Ygl

.

(118)

Pierwszy niezmiennik tensora (114) wynosi

I

1

=

X





Y



.

(119)

Drugi niezmiennik tensora (114) wynosi

I

2

=

X



⋅

Y



−

MAX

2

.

(120)

Dr inż. Janusz Dębiński

BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

26

5 Geometria stanu odkształcenia

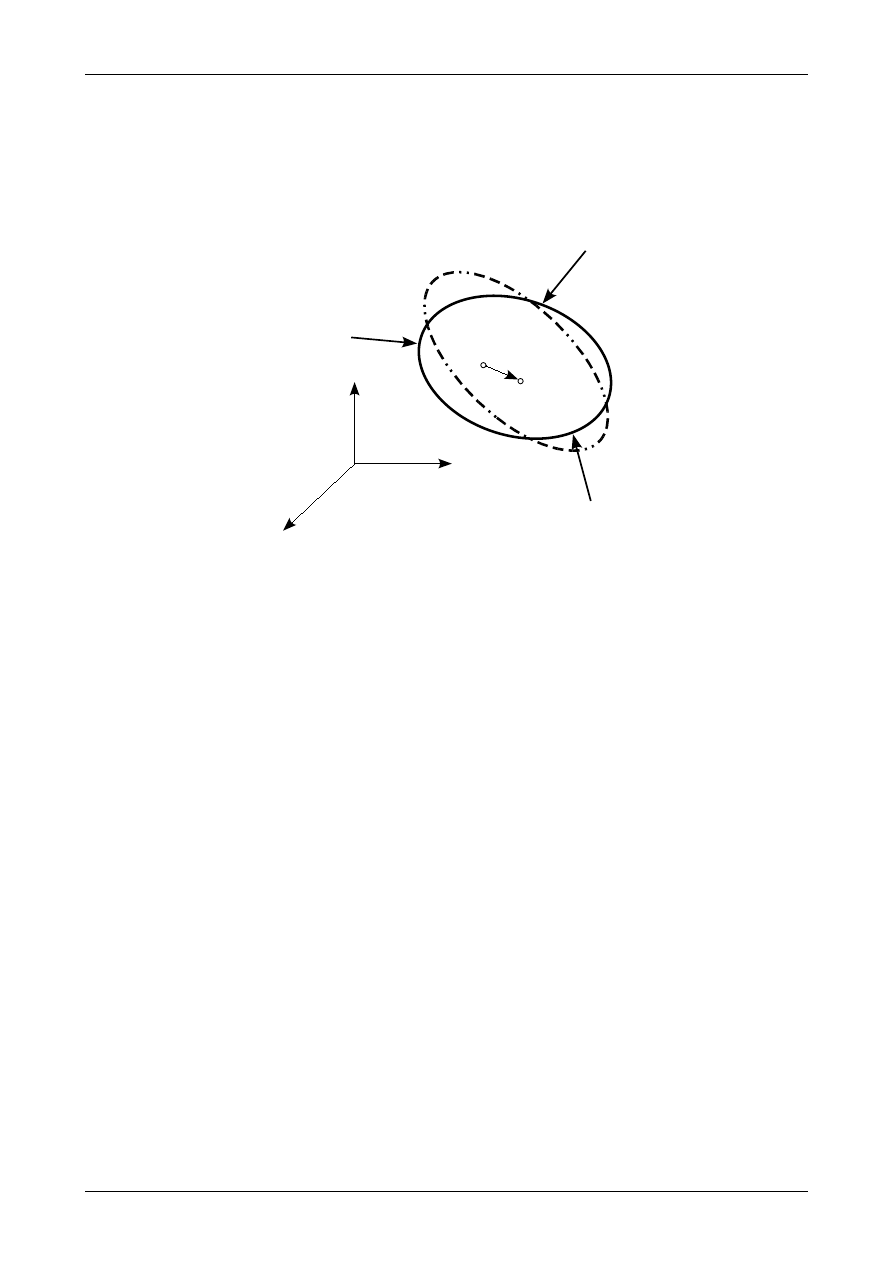
Konstrukcje poddane działaniu sił czynnych i biernych (reakcji) doznają odkształcenia, które jest

widoczne jako zmiana wymiarów i kształtów ciała. Najbardziej widocznym efektem odkształcenia jest
przemieszczanie się punktów ciała. Rysunek 21 przedstawia ciało przed odkształceniem i po podkształceniu.
Punkt A przemieścił się do punktu A' o wektor

u

 A

. Wektor ten nazywa się wektorem przemieszczenia.

X

Y

Z

P

1

R

1

R

2

A

A'

u

 A

Rys. 21. Przemieszczenia ciała wywołane siłami czynnymi i biernymi.

Wektor przemieszczenia można wyrazić jako

u

 A

=u

A

⋅iv

A 

⋅jw

A

⋅k

,

(121)

w którym u

(A)

, v

(A)

i w

(A)

są składowymi wektora przemieszczenia punktu A natomiast i, j i k są wersorami

układu współrzędnych XYZ.

Możemy wyróżnić dwa rodzaje odkształceń:

1. Odkształcenia objętościowe, które powodują zmianę objętości bez zmiany postaci.

2. Odkształcenia postaciowe, które powodują zmianę kształtu (postaci).

Aby określić stan odkształcenia w punkcie należy rozpatrzyć równowagę elementarnego prostopadłościanu o
wymiarach dx, dy i dz, który będzie obciążony tensorem naprężenia (69). Zależność między naprężeniami a
odkształceniami jest liniowa, czyli jeżeli naprężenia wzrosną dwa razy to i odkształcenia wzrosną dwa razy.
Jeżeli skutek (odkształcenia) są liniową funkcją przyczyny (naprężenia) to można zastosować zasadę
superpozycji, czyli rozpatrywać osobno działanie naprężeń normalnych

σ

X

,

σ

Y

,

σ

Z

i naprężeń stycznych

τ

XY

,

τ

YZ

,

τ

XZ

. Na koniec należy tylko zsumować skutki.

Zakładając, że naprężenia normalne są dodatnie (rozciągające) będą one powodowały zwiększenie długości
krawędzi prostopadłościanu. Na rysunku 22 przedstawiono elementarny prostopadłościan pod wpływem
działania naprężeń normalnych. Zmiany długości krawędzi zostały pokazane na rzutach prostopadłościanu na
trzy płaszczyzny.

Jak widać na rysunku 22 zmiany długości krawędzi wynoszą

∆

dx,

∆

dy i

∆

dz. Taki stan odkształcenia można

jednoznacznie opisać za pomocą trzech wielkości

Dr inż. Janusz Dębiński

BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

27

X

Y

Z

P

d

z

∆

dz

dy

∆

dy

dx

∆

dx

dx

∆

dx

dy

∆

dy

d

z

∆

dz



X



Y



Z



X



Z



Y

Rys. 22. Odkształcenia liniowe.



X

=

 dx

dx

.

(122)



Y

=

 dy

dy

,

(123)



Z

=

 dz

dz

.

(124)

Wielkości (122), (123) i (124) nazywamy odkształceniami liniowymi. Odkształcenia liniowe mogą
przyjmować wartości dodatnie, ujemne oraz zero. Zmianie długości krawędzi towarzyszy zmiana objętości.
Zmianę tą nazywa się względnym odkszta ceniem obj to ciowym albo dylatacj

ł

ę ś

ą. Wynosi ona

 dV

dV

=

X



Y



Z

.

(125)

Dr inż. Janusz Dębiński

BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

28

Odkształcenie prostopadłościanu wynikające z działania naprężeń stycznych wiąże się ze zmianą kształtu lub
inaczej zmianą postaci. Zmianie ulegają kąty nachylenia krawędzi prostopadłościanu bez zmiany ich długości.

P

X

Y

Z



XY



YX



YZ



ZY



XZ



ZX



XY



YZ



XY



YZ



XZ



XZ

Rys. 23. Odkształcenia postaciowe.

Miarą zmiany postaci prostopadłościanu są trzy kąty. Pierwszy z nich w płaszczyźnie XY wynosi



XY

=

XY



XY

.

(126)

Drugi z nich w płaszczyźnie YZ wynosi



YZ

=

YZ



YZ

.

(127)

Trzeci z nich w płaszczyźnie XZ wynosi



XZ

=

XZ



XZ

.

(128)

Dr inż. Janusz Dębiński

BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

29

Odkształceniami postaciowymi nazywamy wielkości



XY

=



XY

2

=



XY



XY

2

,

(129)



YZ

=



YZ

2

=



YZ



YZ

2

,

(130)



XZ

=



XZ

2

=



XZ



XZ

2

.

(131)

Odkształcenia liniowe i postaciowe tworzą tensor odkształcenia w postaci

=

[



X



XY



XZ



YX



Y



YZ



ZX



ZY



Z

]

.

(132)

Stan odkształcenia w punkcie opisują trzy składowe odkształcenia liniowego

ε

X

,

ε

Y

,

ε

Z

oraz trzy składowe

odkształcenia postaciowego

ε

XY

,

ε

YZ

,

ε

XZ

. Jak widać odkształcenia są wielkościami bezwymiarowymi.

Składowe wektora przemieszczenia są w ogólnym przypadku funkcjami zmiennych x, y oraz z. Równaniami,
które wiążą składowe wektora przemieszczenia oraz składowe tensora odkształcenia są równania Cauchy'ego.
Mają one postać



X

=

∂u
∂x



Y

=

∂v

∂ y



Z

= ∂

w

∂ z



XY

=

YX

=

1
2

⋅



∂u
∂ y



∂v
∂x





YZ

=

ZY

=

1
2

⋅



∂v
∂ z

∂

w

∂ y





XZ

=

ZX

=

1
2

⋅



∂w

∂x



∂u
∂ z



.

(133)

Jak widać ze wzoru (133) tensor odkształcenia jest tensorem symetrycznym. Tensor odkształcenia możemy
transformować. Wielkością opisującą nam transformację jest macierz transformacji (75). Współrzędne tensora
odkształcenia w układzie transformowanym wyznacza się ze wzoru.

'=B⋅⋅B

T

,

(134)

Dr inż. Janusz Dębiński

BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

30

w którym B

T

jest transponowaną macierzą transformacji. Tensor odkształcenia w układzie transponowanym

będzie miał postać

'=

[



X '



X 'Y '



X ' Z '



Y' X '



Y'



Y ' Z'



Z ' X '



Z 'Y '



Z '

]

.

(135)

Istnieje taki układ transponowany, w którym odkształcenia liniowe osiągają wartości ekstremalne natomiast
odkształcenia postaciowe wynoszą zero. Układ taki nazywa się układem głównym. Ekstremalne odkształcenia
liniowe nazywają się odkształceniami głównymi. Odkształcenia główne wyznacza się jako pierwiastki
równania trzeciego stopnia nazywanego równaniem charakterystycznym w postaci



3

−I

1

⋅

2

I

2

⋅−I

3

=0

,

(136)

w którym współczynnik I

1

równa się sumie odkształceń liniowych

I

1

=

X



Y



Z

.

(137)

I

2

równa się sumie podwyznaczników tensora (132)

I

2

=

∣



X



XY



YX



Y

∣



∣



Y



YZ



ZY



Z

∣



∣



X



XZ



ZX



Z

∣

.

(138)

I

3

równa się wyznacznikowi z macierzy opisującej tensor (132)

I

3

=

∣



X



XY



XZ



YX



Y



YZ



ZX



ZY



Z

∣

.

(139)

Tensor odkształcenia w układzie osi głównych ma postać



gl

=

[



1

0

0

0



2

0

0

0



3

]

.

(140)

Chcąc wyznaczyć kierunki główne należy wykorzystać poniższy układ równań

Dr inż. Janusz Dębiński

BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

31

{





X

−



⋅n

1



YX

⋅n

2



ZX

⋅n

3

=0



XY

⋅n

1







Y

−



⋅n

2



ZY

⋅n

3

=0



XZ

⋅n

1



YZ

⋅n

2







Z

−



⋅n

3

=0

,

(141)

w którym

ε

oznacza jedno z odkształceń głównych natomiast n

1

, n

2

oraz n

3

oznaczają trzy kosinusy

kierunkowe pomiędzy kierunkiem głównym i osiami układu współrzędnych XYZ. Układ równań (141) jest
układem jednorodnym, którego wyznacznik główny wynosi zero. Chcąc wyznaczyć kierunki główne zamiast

ε

należy postawić poszczególne odkształcenia główne oraz jedno z równań zamienić na warunek ortogonalności
w postaci

n

1

2

n

2

2

n

3

2

=1

.

(142)

Układy równań do wyznaczenia kierunków głównych dla naprężeń głównych

ε

1

,

ε

2

oraz

ε

3

będą miały postać

{





X

−

1



⋅n

1

1



YX

⋅n

2

1



ZX

⋅n

3

1 

=0



XY

⋅n

1

1 







Y

−

1



⋅n

2

1 



ZY

⋅n

3

1 

=0

[

n

1

1

]

2



[

n

2

1

]

2



[

n

3

1

]

2

=1

,

(143)

{





X

−

2



⋅n

1

2 



YX

⋅n

2

2 



ZX

⋅n

3

2 

=0



XY

⋅n

1

2







Y

−

2



⋅n

2

2



ZY

⋅n

3

2 

=0

[

n

1

2 

]

2



[

n

2

2 

]

2



[

n

3

2 

]

2

=1

,

(144)

{





X

−

3



⋅n

1

3 



YX

⋅n

2

3 



ZX

⋅n

3

3 

=0



XY

⋅n

1

3







Y

−

3



⋅n

2

3



ZY

⋅n

3

3 

=0

[

n

1

3 

]

2



[

n

2

3 

]

2



[

n

3

3 

]

2

=1

.

(145)

Macierz transformacji dla kierunków głównych będzie miała postać

B

gl

=

[

n

1

1 

n

2

1 

n

3

1 

n

1

2 

n

2

2 

n

3

2

n

1

3 

n

2

3 

n

3

3

]

.

(146)

Możemy ją zapisać także jako

Dr inż. Janusz Dębiński

BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

32

B

gl

=

[

cos



1 , x



cos



1 , y



cos



1 , z



cos



2 , x



cos



2 , y



cos



2 , z



cos



3 , x



cos



3 , y



cos



3 , z



]

.

(147)

Wartości współczynników I

1

, I

2

oraz I

3

nie mogą zależeć od położenia układu współrzędnych są więc one

niezmiennikami stanu odkształcenia. W przypadku tensora (135) mają one postać

I

1

=

X '



Y'



Z '

,

(148)

I

2

=

∣



X '



X 'Y '



Y ' X '



Y'

∣



∣



Y '



Y 'Z '



Z 'Y '



Z '

∣



∣



X '



X ' Z '



Z ' X '



Z '

∣

.

(149)

I

3

=

∣



X '



X 'Y'



X ' Z '



Y ' X '



Y'



Y 'Z '



Z' X '



Z 'Y'



Z '

∣

.

(150)

W przypadku tensora (140) mają one postać

I

1

=

1



2



3

,

(151)

I

2

=

1

⋅

2



2

⋅

3



3

⋅

1

,

(152)

I

3

=

1

⋅

2

⋅

3

,

(153)

6 Płaski stan odkształcenia

Do czynienia z płaskim stanem odkształcenia mamy wtedy, gdy tensor odkształcenia (132) będzie miał

postać

=

[



X



XY

0



YX



Y

0

0

0

0

]

.

(154)

Taki stan odkształcenia występuje w bardzo długich ścianach (murach oporowych), które są obciążone
prostopadle do największego swojego wymiaru (długości). W takim właśnie przypadku wszystkie
odkształcenia po kierunku długości mają wartość zero.

W przypadku płaskiego stanu odkształcenia wektor przemieszczenia będzie miał tylko dwie składowe czyli u i
v. Obie składowe będą funkcjami zmiennych x i y,

Dr inż. Janusz Dębiński

BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

33

u

=u



x , y



v

=v



x , y



(155)

natomiast składowa w będzie wynosiła zero. Pochodne cząstkowe składowych u i v po zmiennej z będą
pochodnymi stałych czyli wynoszą

∂u



x , y



∂ z

=0

∂v



x , y



∂ z

=0

.

(156)

Natomiast pochodne składowej w po zmiennych x, y, z wynoszą

∂w

∂x

=0

∂w
∂ y

=0

∂w

∂ z

=0

.

(157)

Ostatecznie równania Cauchy'ego będą miały w płaskim stanie odkształcenia postać



X

=

∂u
∂x



Y

=

∂v

∂ y



Z

=0



XY

=

YX

=

1
2

⋅



∂u
∂ y

 ∂

v

∂x





YZ

=

ZY

=0



XZ

=

ZX

=0

.

(158)

Wiadomo, że przy obrocie układu współrzędnych XY składowe stanu odkształcenia zmieniają swoje wartości.
Istnieje taki układ współrzędnych, w którym odkształcenia liniowe osiągają wartości ekstremalne (największą i
najmniejszą z możliwych) natomiast odkształcenie postaciowe przyjmuje wartość zero. Taki układ
współrzędnych nazywa się układem osi głównych. Natomiast ekstremalne odkształcenia liniowe nazywają się
odkształceniami głównymi. Wzór na kąt obrotu układu osi głównych ma postać (kąt dodatni kręci od osi X
do osi Y)

tg

2⋅

gl

=

2

⋅

XY



X

−

Y

.

(159)

Dr inż. Janusz Dębiński

BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

34

Odkształcenia główne będziemy wyznaczać ze wzorów



Xgl

=



X



Y

2





X

−

Y

2

⋅cos2⋅

gl



XY

⋅sin2⋅

gl



,

(160)



Ygl

=



X



Y

2

−



X

−

Y

2

⋅cos2⋅

gl

−

XY

⋅sin2⋅

gl



.

(161)

W celu sprawdzenia obliczeń naprężeń głównych będziemy stosować następujący wzór



1

/2

=



X



Y

2

±







X

−

Y

2



2



XY

2

,

(162)

w którym

ε

1

oznacza maksymalne odkształcenie główne natomiast

ε

2

oznacza minimalne odkształcenie główne.

Tensor odkształcenia w przypadku odkształceń głównych będzie miał postać



gl

=

[



Xgl

0

0

0



Ygl

0

0

0

0

]

.

(163)

Kąt nachylenia układu współrzędnych, w którym odkształcenia postaciowe osiągają wartości ekstremalne
wynosi

tg

2⋅



=−



X

−

Y

2

⋅

XY

.

(164)

Ekstremalne odkształcenia postaciowe wyznacza się ze wzoru



MAX

=−



X

−

Y

2

⋅sin2⋅





XY

⋅cos2⋅





.

(165)

Jako sprawdzenie można wykorzystać zależność

∣

MAX

∣=







X

−

Y

2



2



XY

2

.

(166)

Odkształcenia liniowe stowarzyszone z ekstremalnymi odkształceniami postaciowymi wyznacza się ze wzorów

Dr inż. Janusz Dębiński

BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

35



XP

=



X



Y

2





X

−

Y

2

⋅cos2⋅





XY

⋅sin2⋅





,

(167)



YP

=



X



Y

2

−



X

−

Y

2

⋅cos2⋅



−

XY

⋅sin2⋅





.

(168)

Odkształcenia liniowe stowarzyszone z ekstremalnymi odkształceniami postaciowymi mają te same wartości i
mogą być także wyznaczone z zależności



XP

=

YP

=



X



Y

2

.

(169)

Tensor odkształcenia będzie w przypadku ekstremalnych odkształceń postaciowych miał postać





=

[



XP



MAX

0



MAX



YP

0

0

0

0

]

.

(170)

Osie odkształceń głównych i ekstremalnych odkształceń postaciowych są wzajemnie obrócone o kąt 45

o

.

Pierwszy niezmiennik tensora (154) wynosi

I

1

=

X



Y

.

(171)

Drugi niezmiennik tensora (154) wynosi

I

2

=

X

⋅

Y

−

XY

2

.

(172)

Pierwszy niezmiennik tensora (163) wynosi

I

1

=

Xgl



Ygl

.

(173)

Drugi niezmiennik tensora (163) wynosi

I

2

=

Xgl

⋅

Ygl

.

(174)

Pierwszy niezmiennik tensora (170) wynosi

Dr inż. Janusz Dębiński

BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

36

I

1

=

XP



YP

.

(175)

Drugi niezmiennik tensora (170) wynosi

I

2

=

XP

⋅

YP

−

MAX

2

.

(176)

Trzeci niezmiennik we wszystkich opisanych powyżej przypadkach jest zawsze równy zero.

7 Rozciąganie osiowe

Podstawowym testem laboratoryjnym służącym do wyznaczenia zależności pomiędzy naprężeniami i

odkształceniami jest statyczna próba rozciągania. Próba ta polega na osiowym rozciąganiu próbki wykonanej
z materiału w maszynie wytrzymałościowej. Słowo statyczna oznacza, że badanie wykonywane jest przy
powoli rosnącej sile rozciągającej. Próbka jest umocowana w szczękach maszyny wytrzymałościowej. Siła
rozciągająca P jest wymuszana za pomocą szczęk.

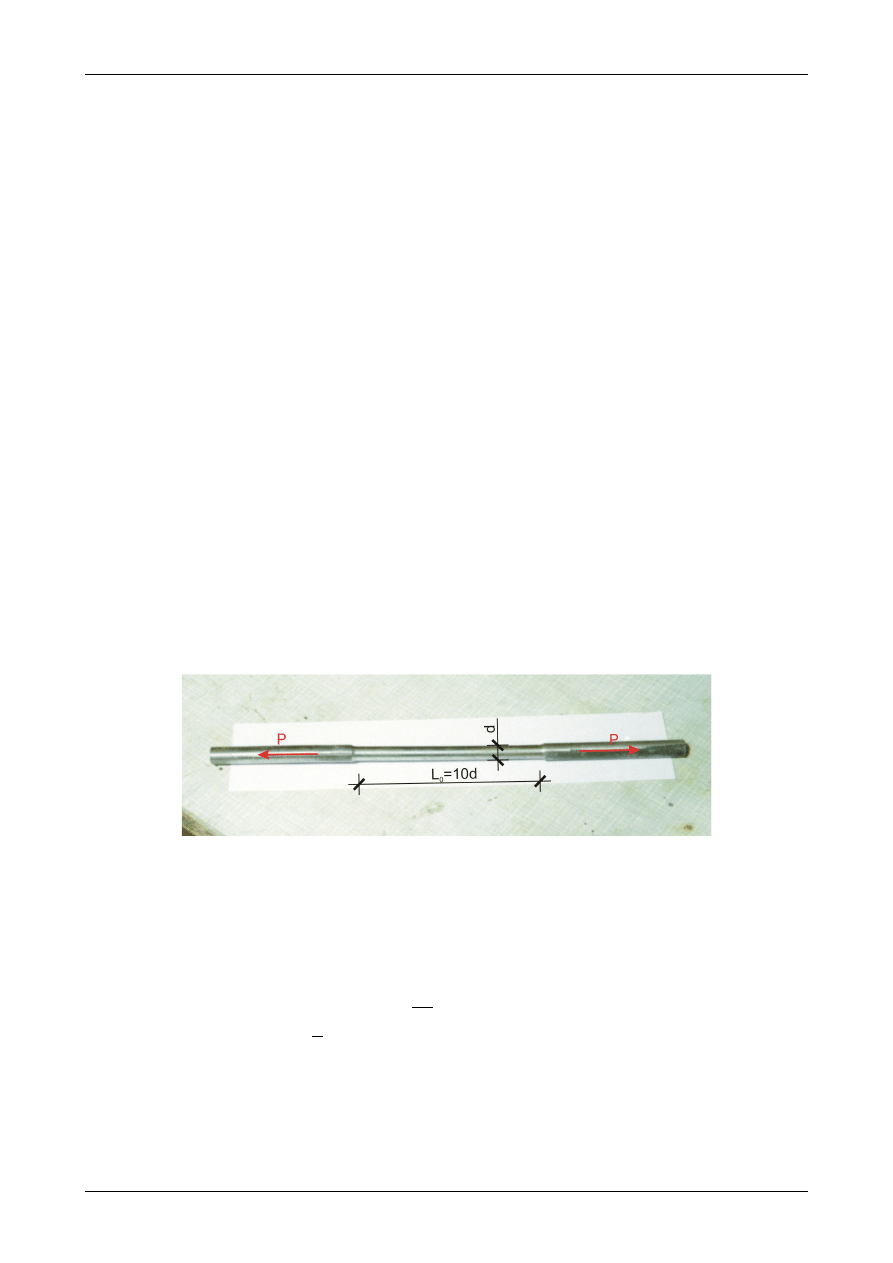
Rysunek 24 przedstawia próbkę wykonaną ze stali niskowęglowej (na przykład St3S). Jest to najczęściej
wykorzystywana stal w budownictwie. Próbka ma przekrój kołowy o średnicy d. Długość części pomiarowej
próbki jest dziesięciokrotnie większa od średnicy (próbka dziesięciokrotna). Obok próbek dziesięciokrotnych
są także próbki pięciokrotne (długość pomiarowa jest pięciokrotnie większa niż średnica takiej próbki).
Pogrubione elementy służą do ułożenia próbki w szczękach maszyny wytrzymałościowej. Wadą takiego
zamocowania jest w początkowym etapie obciążania próbki brak osiowego przyłożenia siły rozciągającej P.
Taka próbka musi się “ułożyć” w szczękach maszyny.

Rys. 24. Próbka dzieięciokrotna do statycznej próby rozciągania.

Pod wpływem działania siły rozciągającej P w przekroju próbki powstanie stan naprężenia opisany tensorem
naprężenia

=

[



X

= =

P

A

0

0 0

0

0 0

0

0 0

]

,

(177)

w którym P jest osiową siłą rozciągającą, A

0

jest początkowym polem powierzchni przekroju próbki. Przekrój

ten jest w naszym przypadku kołem o średnicy 10 mm. Tensor naprężenia (177) jest oczywiście tensorem w

Dr inż. Janusz Dębiński

BZZ

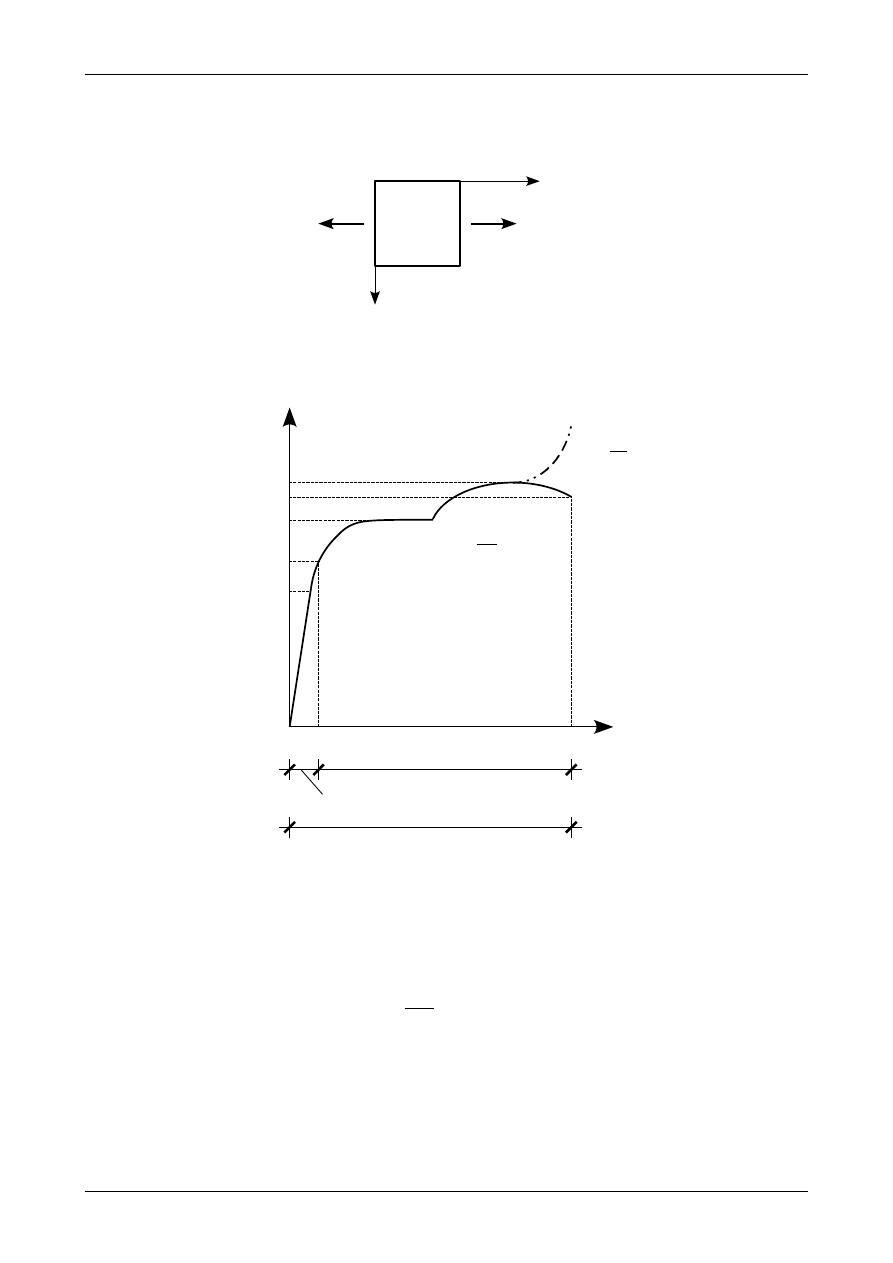
WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

37

układzie osi głównych, ponieważ wszystkie naprężenia styczne są równe zero. Rysunek 25 przedstawia
elementarny kwadrat opisujący osiowe rozciąganie.

X=X

gl

Y=Y

gl





Rys. 25. Stan naprężenia przy osiowym rozciąganiu.



X



X



S



P



H



W



Z

zakres sprężysty

odkształcenia sprężysto-plastyczne



X

=

N

A

0



X

rz

=

N

A

odkształcenie graniczne

≈0,2

Rys. 26. Wykres zależności pomiędzy naprężeniem i odkształceniem dla stali niskowęglowej.

Próbka pod wpływem siły rozciągającej będzie się wydłużać. Miarą tego wydłużenia jest odkształcenie liniowe
po kierunku osi pręta

ε

X

, które wynosi



X

=

 L

L

0

.

(178)

We wzorze (178)

∆

L jest wydłużeniem próbki pod wpływem działania osiowej siły rozciągającej P, L

0

jest

początkową długością części pomiarowej próbki, która w przypadku naszej próbki dziesięciokrotnej będzie
wynosiła 10,0 cm.

W wyniku statycznej próby rozciągania uzyskuje się wykres zależności pomiędzy naprężeniami normalnymi

Dr inż. Janusz Dębiński

BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

38

σ

X

i odkształceniami liniowymi

ε

X

. Przykładowy wykres dla stali niskowęglowej przedstawia rysunek 26.

Na wykresie 26 znajdują się następujące punkty charakterystyczne:

1. Granica proporcjonalności

σ

H

– jest największą wartością naprężenia normalnego, przy której zależność

naprężenie-odkształcenie jest jeszcze liniowa.

2. Granica sprężystości

σ

S

– jest największą wartością naprężenia normalnego, dla której krzywa odciążania

pokrywa się z krzywą obciążania. Jeżeli próbka zostanie najpierw obciążona poniżej granicy sprężystości a
potem obciążenie zmaleje do zera to próbka wróci do swojej pierwotnej długości.

3. Granica plastyczności

σ

P

– jest to wartość naprężenia, przy którym występują znaczne odkształcenia trwałe

nazywane odkształceniami plastycznymi. bez wzrostu siły rozciągającej. Materiał płynie. Jeżeli
powierzchnia boczna próbki byłaby wypolerowana to po przekroczeniu granicy plastyczności powierzchnia
ta by zmatowiała i pojawiłyby się linie Lüdersa. Przyczyną tego zjawiska są ekstremalne naprężenia
styczne występujące na płaszczyznach nachylonych pod kątem 45 stopni do osi pręta (naprężeń głównych).
Ekstremalne naprężenia styczne będą w stali niskowęglowej powodowały poślizg warstw materiału
względem siebie i w konsekwencji zmatowienie wypolerowanej powierzchni. Granica plastyczności może
mieć dwie wartości dolną i górną, ponieważ siła normalna może w małym zakresie zmieniać swoją
wartość oscylując wokół granicy plastyczności.

4. Wytrzymałość doraźna

σ

W

– jest równa maksymalnej wartości naprężenia normalnego na całym wykresie.

Od tego miejsca próbka przestaje się równomiernie odkształcać. Tworzy się wyraźne przewężenie
nazywane szyjką. Z chwilą pojawienia się szyjki dalsze odkształcenia próbki będą występowały przy
malejącej sile rozciągającej P ale przy rosnących naprężeniach normalnych, ponieważ pole przekroju
próbki zmalało wskutek pojawienia się szyjki.

Wykres narysowany na rysunku 26 liną ciągłą odnosi się do naprężeń nominalnych (obliczonych dla
początkowego pola powierzchni). Wykres narysowany na rysunku 26 linią przerywaną odnosi się do naprężeń
rzeczywistych (obliczonych dla aktualnego pola powierzchni). Zmniejszanie się pola powierzchni próbki
następuje już od początku procesu rozciągania. Zmniejszenie to jest jednak bardzo małe i znika po usunięciu
obciążenia. Widoczne zmniejszenie pola powierzchni następuje dopiero z chwilą pojawienia się szyjki.
Zaznaczone na rysunku 26 odkształcenie graniczne odpowiada sile zrywającej próbkę. Odkształcenie
graniczne wynosi około 0,2 czyli 20%. Próbka ulega zerwaniu w miejscu pojawienia się szyjki.



X



X



S



P



W



X

=

N

A

0

odkształcenie graniczne



S



P

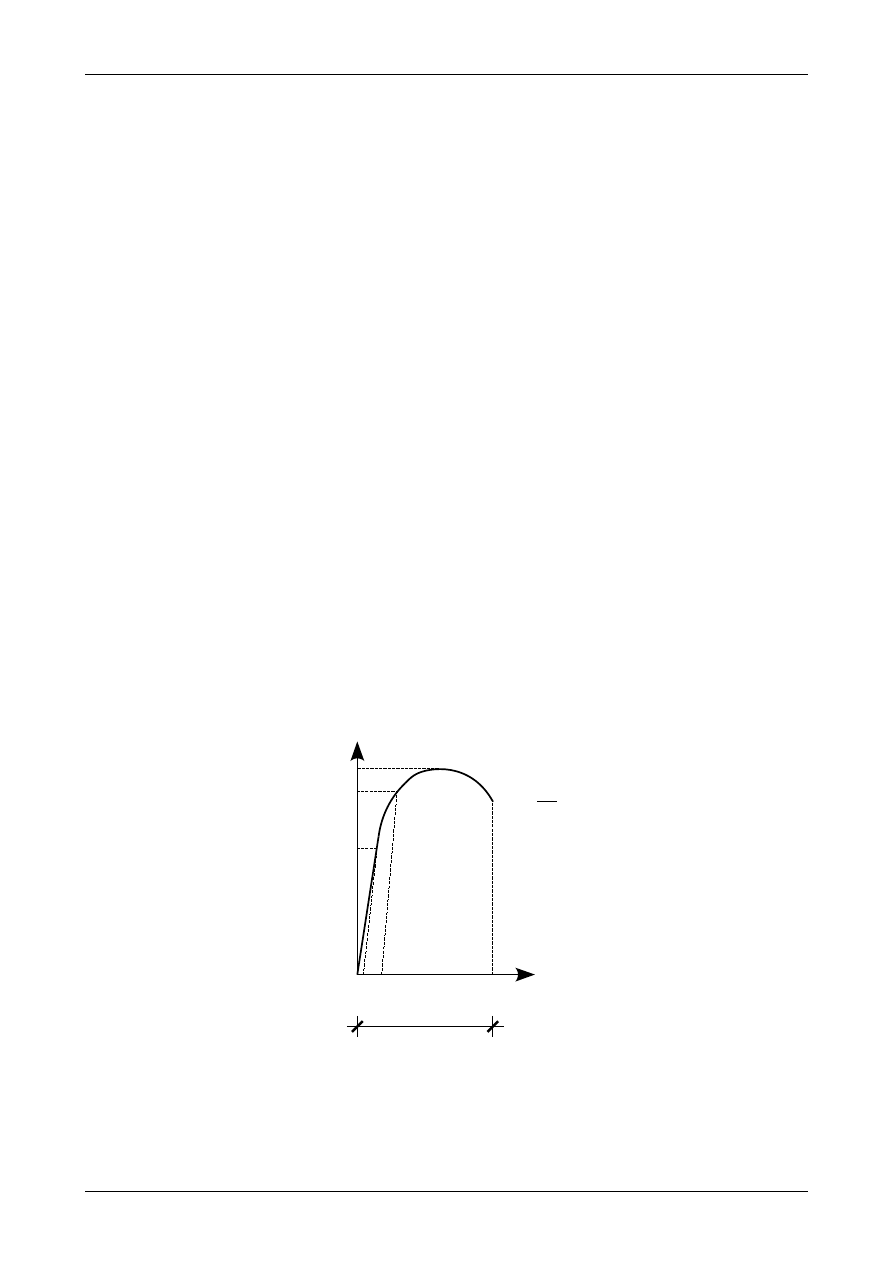
Rys. 27. Wykres zależności pomiędzy naprężeniem i odkształceniem dla stali wysokowęglowej.

W przypadku stali wysokowęglowej lub stopów aluminium wykres zależności pomiędzy naprężeniami i
odkształceniami ma postać przedstawioną na rysunku 27. W odróżnieniu od wykresu na rysunku 26 na
wykresie tym nie ma wyraźnej granicy plastyczności. Jako granicę plastyczności przyjmuje się takie

Dr inż. Janusz Dębiński

BZZ

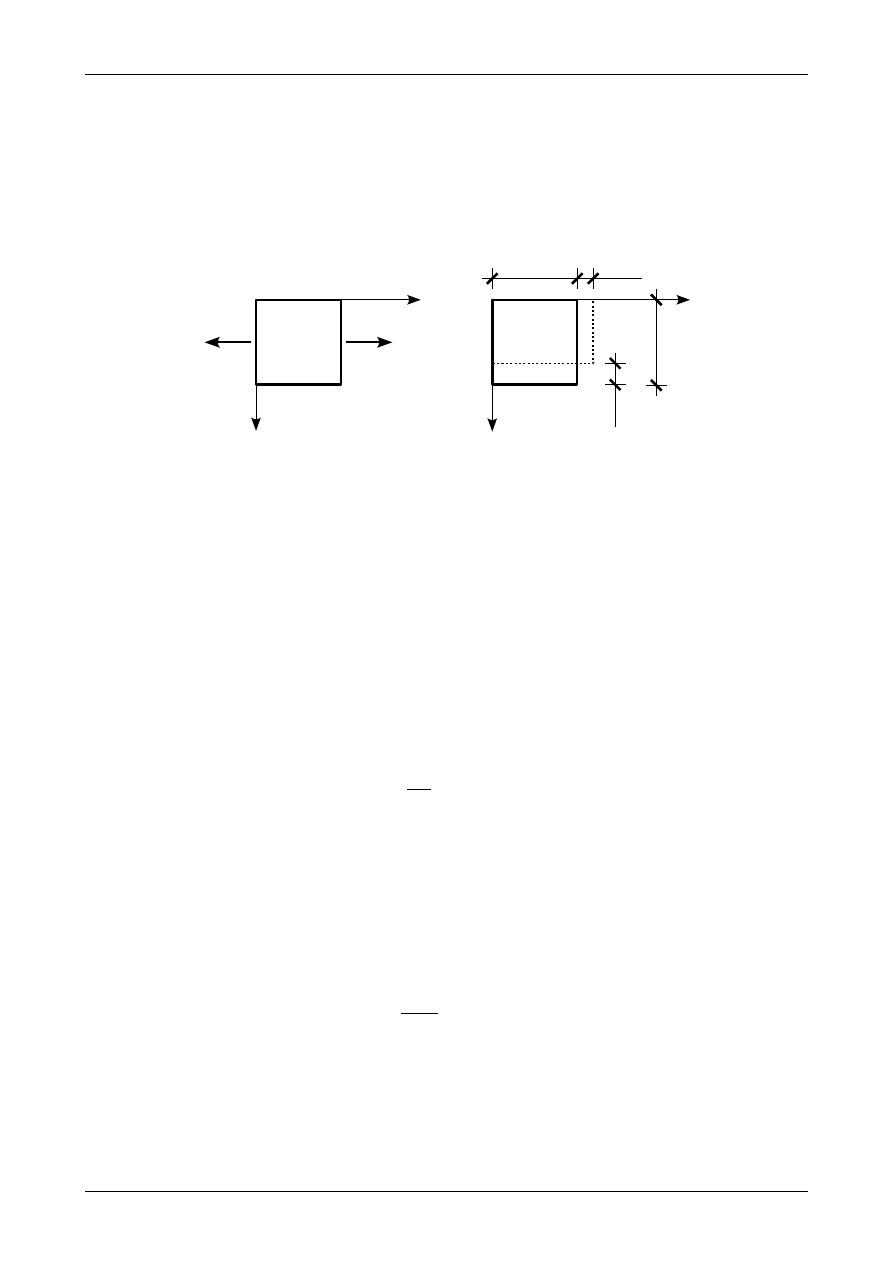
WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

39

naprężenie normalne, które odpowiada odkształceniom plastycznym wynoszącym 0,002. Jako granicę
sprężystości przyjmuje się takie naprężenie normalne, które odpowiada odkształceniom plastycznym 0,0005.

Cechą wspólną materiałów takich jak stal niskowęglowa lub aluminium jest ich ciągliwość. Wynika ona z
faktu, że zerwanie próbki poprzedzone jest pojawieniem się dużych odkształceń trwałych (plastycznych)
wynoszących 15% do 30% początkowej długości próbki. Materiały takie nazywamy materiałami ciągliwymi.
Materiały takie jak beton, cegła, skała lub stal wysokowęglowa nazywamy materiałami kruchymi.

X

Y



X

X

Y

dx

dx



dy

dy



X

Rys. 28. Odkształcenia spowodowane działaniem naprężenia normalnego

σ

X

.

Rysunek 28 przedstawia elementarny kwadrat po odkształceniu spowodowanym działaniem naprężenia
normalnego

σ

X

. Zostało doświadczalnie dowiedzione, że pomiędzy naprężeniem rozciągającym

σ

X

a

odkształceniem liniowym

ε

X

w zakresie sprężystej pracy materiału istnieje zależność liniowa.

Możemy więc napisać, że



X

=E⋅

X

.

(179)

Odkształcenie liniowe będzie więc wynosiło



X

=



X

E

.

(180)

Współczynnikiem proporcjonalności E jest moduł Younga. Jest to pierwsza z wielkości nazywanych stałymi
materiałowymi. Stałe materiałowe są charakterystyczne dla danego materiału i są określane na podstawie
badań laboratoryjnych. Jednostką modułu Younga jest w układzie SI Pascal (Pa). Jednak w materiałach
stosowanych w budownictwie używa się wielokrotności GPa.

Odkształcenie



Y

=

 dy

dy

(181)

jest jest ujemne (elementarny kwadrat w kierunku osi Y uległ skróceniu). Zostało doświadczalnie dowiedzione,
że pomiędzy odkształceniem liniowym

ε

X

a odkształceniem liniowym

ε

Y

w zakresie sprężystej pracy materiału

istnieje zależność liniowa. Możemy więc napisać, że

Dr inż. Janusz Dębiński

BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

40



Y

=−⋅

X

.

(182)

Współczynnikiem proporcjonalności

ν

jest współczynnik Poissona. Minus we wzorze (182) wynika z faktu,

że współczynnik Poissona jest wartością dodatnią a odkształcenia liniowe są różnego znaku. Należy
podkreślić, że współczynnik Poissona jest wielkością bezwymiarową. Otrzymywany jest także na drodze
badań laboratoryjnych. Dla materiałów sprężystych współczynnik Poissona nie może być większy niż
0,5.Uwzględniając zależność (180) otrzymany



Y

=−⋅



X

E

.

(183)

Analogicznie możemy napisać, że



Z

=−⋅

X

=−⋅



X

E

.

(184)

Tensor odkształcenia dla osiowego rozciągania będzie miał postać

=

[



X

E

0

0

0

−⋅



X

E

0

0

0

−⋅



X

E

]

.

(185)

Moduł Younga oraz współczynnik Poissona stanowią dwie stałe materiałowe dla materiału izotropowego.

8 Związki fizyczne w przestrzennym stanie naprężenia

W przypadku tensora naprężenia (69) dla naprężeń normalnych możemy wykorzystać analogię do

związków przedstawionych w poprzednim punkcie. Skutki działania wszystkich naprężeń normalnych
przedstawia Tabela 1. Sumując wiersze Tabeli 1 możemy otrzymać zależności pomiędzy naprężeniami
normalnymi i odkształceniami liniowymi w postaci



X

=

1

E

⋅

[



X

−⋅





Y



Z



]

,

(186)



Y

=

1

E

⋅

[



Y

−⋅





X



Z



]

,

(187)

Dr inż. Janusz Dębiński

BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

41



Z

=

1

E

⋅

[



Z

−⋅





X



Y



]

.

(188)

Tabela 1. Skutki działania naprężeń normalnych.



X



Y



Z



X



X

E

−⋅



Y

E

−⋅



Z

E



Y

−⋅



X

E



Y

E

−⋅



Z

E



Z

−⋅



X

E

−⋅



Y

E



Z

E

X

Y



XY



YX

X

Y



1



2

X

Y



XY



XY



YX

Rys. 29. Deformacja przy działaniu naprężenia stycznego.

W przypadku działania naprężenia stycznego deformację elementarnego kwadratu przedstawia rysunek 29.
Teoretycznie zostało udowodnione, że pomiędzy naprężeniem stycznym

τ

XY

w całkowitym kątem odkształcenia

γ

XY

istnieje także zależność liniowa. Możemy więc napisać, że



XY

=G⋅

XY

.

(189)

Współczynnikiem proporcjonalności jest moduł Kirchhoffa. Wielkość ta nie jest jednak stałą materiałową,
ponieważ pomiędzy modułem Kirchhoffa a modułem Younga i współczynnikiem Poissona istnieje zależność

G

=

E

2

⋅



1





.

(190)

Wzór (189) możemy napisać w postaci



XY

=



XY

G

.

(191)

Dr inż. Janusz Dębiński

BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

42

Odkształcenie postaciowe na płaszczyźnie XY będzie miało postać



XY

=



XY

2

⋅G

.

(192)

Analogicznie odkształcenia postaciowe na pozostałych płaszczyznach można zapisać



YZ

=



YZ

2

⋅G

,

(193)



XZ

=



XZ

2

⋅G

.

(194)

Komplet sześciu równań fizycznych dla materiału izotropowego w zakresie sprężystej pracy materiału ma
postać

{



X

=

1
E

⋅

[



X

−⋅





Y



Z



]



Y

=

1

E

⋅

[



Y

−⋅





X



Z



]



Z

=

1

E

⋅

[



Z

−⋅





X



Y



]



XY

=



XY

2

⋅G



YZ

=



YZ

2

⋅G



XZ

=



XZ

2

⋅G

.

(195)

Zależność pomiędzy tensorem naprężenia (83) a tensorem odkształcenia (135) będzie miała postać

{



X '

=

1
E

⋅

[



X '

−⋅





Y'



Z '



]



Y '

=

1

E

⋅

[



Y '

−⋅





X '



Z '



]



Z '

=

1
E

⋅

[



Z '

−⋅





X '



Y'



]

,

(196)

Dr inż. Janusz Dębiński

BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

43

{



X 'Y'

=



X 'Y '

2

⋅G



Y 'Z '

=



Y 'Z '

2

⋅G



X 'Z '

=



X 'Z '

2

⋅G

.

(197)

W przypadku tensora naprężenia (88) i tensora odkształcenia (140) związki fizyczne mają postać

{



1

=

1

E

⋅

[



1

−⋅





2



3



]



2

=

1

E

⋅

[



2

−⋅





1



3



]



3

=

1

E

⋅

[



3

−⋅





1



2



]

.

(198)

W przypadku płaskiego stanu naprężenia (102) związki fizyczne mają postać

{



X

=

1
E

⋅





X

−⋅

Y





Y

=

1

E

⋅





Y

−⋅

X





Z

=

−

E

⋅





X



Y





XY

=



XY

2

⋅G

.

(199)

Względna zmiana objętości (dylatacja) wynosi

 dV

dV

=

X



Y



Z

.

(200)

Uwzględniając związki fizyczne (195) możemy ją zapisać jako

dV

dV

=

1
E

⋅

[



X

−⋅





Y



Z



]



1

E

⋅

[



Y

−⋅





X



Z



]



1

E

⋅

[



Z

−⋅





X



Y



]

.

(201)

Dr inż. Janusz Dębiński

BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

44

Wzór (201) możemy zapisać

 dV

dV

=

1

E

⋅





X



Y



Z



−

2

⋅

E

⋅





X



Y



Z



.

(202)

Czyli ostatecznie otrzymamy

 dV

dV

=

1

−2⋅

E

⋅





X



Y



Z



.

(203)

Współczynnik

K

=

1

−2⋅

E

(204)

nazywamy modułem ściśliwości. Ze wzoru (204) wynika, że wartość współczynnika Poissona musi być
mniejsza niż 0,5, ponieważ gdyby była większa niż 0,5 to przy wszechstronnym ściskaniu elementarna kostka
powiększałaby się, co przeczyłoby wynikom badań laboratoryjnych.

9 Twierdzenie Clapeyrona

Pojęcie układów Clapeyrona zostanie pokazane na przykładzie sprężyny rozciąganej siłą P, zależną od

wydłużenia sprężyny u. Sprężynę przedstawia rysunek 30.

u

P(u)

P=0

Rys. 30. Sprężyna.

Pracę siły P(u), która powoduje rozciągnięcie sprężyny możemy wyznaczyć ze wzoru

L

=

∫

0

u

k

P

 u ⋅du

.

(205)

Dr inż. Janusz Dębiński

BZZ

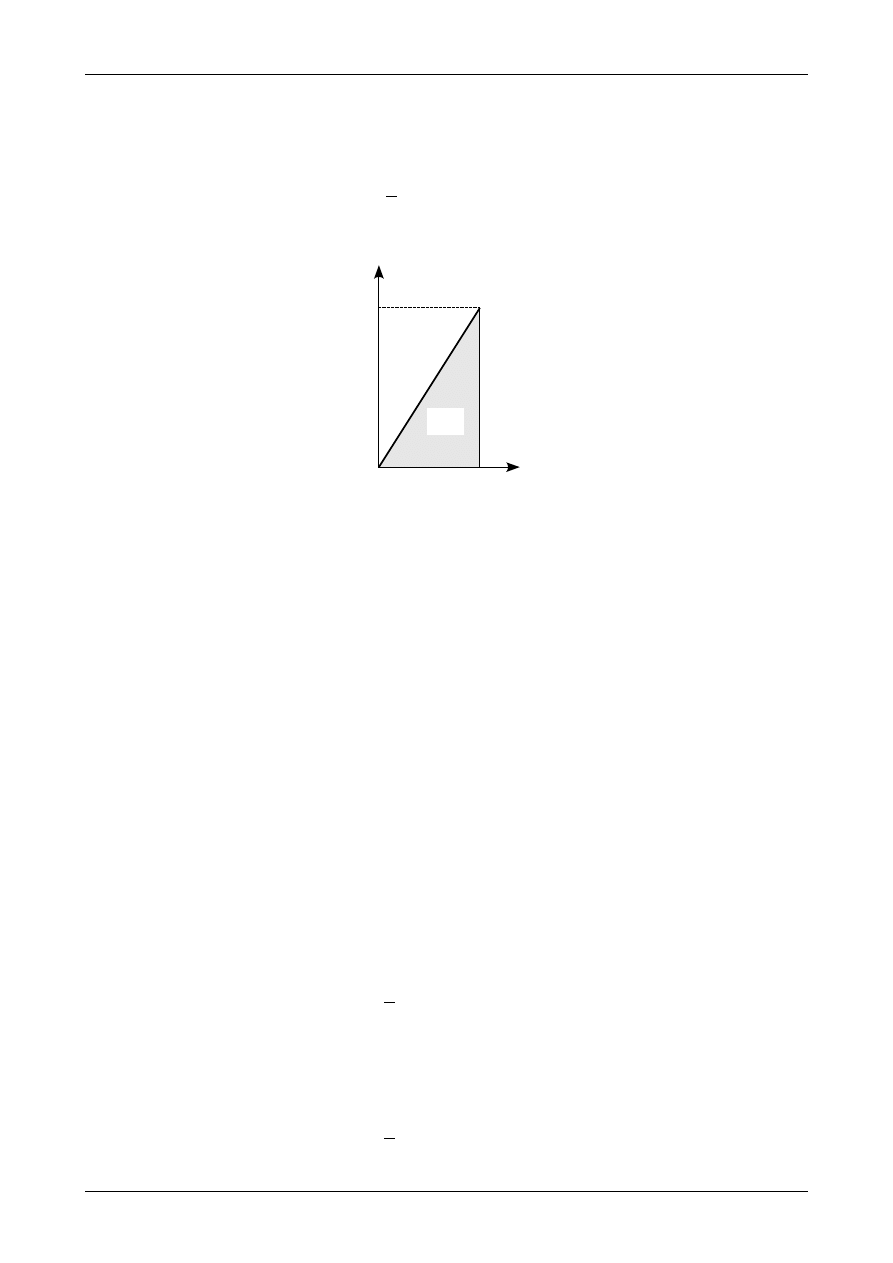
WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

45

Jeżeli zależność pomiędzy siłą P a wydłużeniem sprężyny u jest liniowa, tak jak to przedstawia rysunek 31 to
praca siły P równa się polu powierzchni trójkąta prostokątnego czyli

L

=

1
2

⋅P

k

⋅u

k

.

(206)

P

u

P

k

u

k

L

Rys. 31. Liniowa zależność pomiędzy siłą a wydłużeniem sprężyny.

Przedstawiony powyżej przykład sprężyny z liniową charakterystyką stanowi układ Clapeyrona. Układ taki
charakteryzuje się następującymi właściwościami:

1. materiał jest liniowo sprężysty,

2. w trakcie odkształcenia nie występują nowe punkty podparcia,

3. w układzie nie ma naprężeń i odkształceń wstępnych

4. w układzie nie występują zmiany temperatury.

Twierdzenie Clapeyrona głosi, że praca obciążeń równa się energii sprężystej zgromadzonej wewnątrz układu
czyli

L

=U

,

(207)

w którym L oznacza pracę obciążeń (sił zewnętrznych) natomiast U oznacza energię sprężystą
zmagazynowaną wewnątrz układu. Praca sił zewnętrznych wzrastających liniowo nieskończenie powoli od
zera do ostatecznych ich wartości wyraża się dla układów Clapeyrona

L

=

1
2

⋅ P⋅u

.

(208)

Wzór (208) możemy zapisać ogólnie jako

L

=

1
2

⋅ F⋅f

,

(209)

Dr inż. Janusz Dębiński

BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

46

w którym F oznacza siłę uogólnioną natomiast f oznacza przemieszczeni uogólnione. Jeżeli F oznaczać będzie
moment pary sił zaczepiony w pewnym przekroju to f będzie kątem obrotu tego przekroju.

10 Energia sprężysta

Jednostkową energią sprężystą nazywamy ilość energii sprężystej nagromadzonej w jednostce objętości

ciała. Dla układów Clapeyrona wynosi ona

W

=

1
2

⋅





X

⋅

X



Y

⋅

Y



Z

⋅

Z



XY

⋅

XY



YX

⋅

YX



YZ

⋅

YZ



ZY

⋅

ZY



XZ

⋅

XZ



ZX

⋅

ZX



.

(210)

Uwzględniając symetrię tensorów naprężenia i odkształcenia jednostkowa energia sprężysta będzie wynosiła

W

=

1
2

⋅





X

⋅

X



Y

⋅

Y



Z

⋅

Z

2⋅

XY

⋅

XY

2⋅

YZ

⋅

YZ

2⋅

XZ

⋅

XZ



.

(211)

Jednostkową energię sprężystą możemy rozłożyć na dwa składniki: energię sprężystą odkształcenia
objętościowego oraz energię sprężystą odkształcenia postaciowego.

Energia sprężysta odkształcenia objętościowego wynosi

W

o

=

1

−2⋅

6

⋅E

⋅





X



Y



Z



2

.

(212)

Energia sprężysta odkształcenia postaciowego wynosi

W

p 

=

1

12

⋅G

⋅

[





X

−

Y



2







Y

−

Z



2







Z

−

X



2

6⋅





XY

2



YZ

2



XZ

2



]

.

(213)

W układzie osi naprężeń głównych energia sprężysta odkształcenia objętościowego wynosi

W

o

=

1

−2⋅

6

⋅E

⋅





1



2



3



2

.

(214)

W układzie osi naprężeń głównych energia sprężysta odkształcenia postaciowego wynosi

W

 p

=

1

12

⋅G

⋅

[





1

−

2



2







2

−

3



2







3

−

1



2

]

.

(215)

Dr inż. Janusz Dębiński

BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

47

11 Wytężenie materiału i naprężenie zredukowane

Analizując wykresy zależności pomiędzy naprężeniem rozciągającym a odkształceniem liniowym

przedstawione na rysunkach 26 i 27 możemy stwierdzić, że w przypadku materiału ciągliwego (rysunek 26) za
stan niebezpieczny uznaje się osiągnięcie granicy plastyczności

σ

P

. Natomiast dla materiału kruchego (rysunek

27) za stan niebezpieczny przyjmuje się doraźną granicę wytrzymałości

σ

W

.

Podstawowym problemem jest wyznaczenie współczynnika bezpieczeństwa, który określa nam ile razy
aktualne naprężenie

σ

jest mniejsze od naprężenia niebezpiecznego

σ

n

.

n

=





n

.

(216)

Obliczenie współczynnika bezpieczeństwa dla osiowego rozciągania jest bardzo proste, trudniej sprawa
przedstawia się w trójosiowym stanie naprężenia opisanym tensorem naprężenia (69). Problem ten rozwiązują
hipotezy wytrzymałościowe (wytężeniowe), które sprowadzają stan naprężenia opisany tensorem (69) do
przypadku osiowego rozciągania. W tym celu hipotezy te wprowadzają pojęcie naprężenia zredukowanego,
które to jest właśnie naprężeniem rozciągającym w sprowadzonym przypadku osiowego rozciągania.

Naprężenie zredukowane musi być funkcją niezmienników stanu naprężenia czyli



red

=

red



I

1

, I

2

, I

3



.

(217)

Naprężenie zredukowane musi być funkcją składowych stanu naprężenia czyli



red

=

red





X

,



Y

,



Z

,



XY

,



YZ

,



XZ



.

(218)

Naprężenie zredukowane dla osiowego rozciągania musi się równać naprężeniu rozciągającemu



red



 , 0 , 0 , 0 , 0 , 0



=

.

(219)

Naprężenie zredukowane dla zerowego tensora naprężenia musi się równać zero



red



0 , 0 , 0 ,0 , 0 , 0



=0

.

(220)

12 Hipoteza Hubera-Misesa-Hencky'ego (H-M-H)

Jest to hipoteza dla materiałów ciągliwych. Jako naprężenie niebezpieczne przyjmuje się granicę

plastyczności

σ

P

. Możemy więc zapisać



red

=

P

.

(221)

Dr inż. Janusz Dębiński

BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

48

Według tej hipotezy materiał przechodzi w stan niebezpieczny wtedy, gdy jednostkowa energia
odkształcenia postaciowego osiągnie pewną wartość graniczną, charakterystyczną dla tego materiału.
Matematyczne sformułowanie tego warunku ma postać

W

 p

=C

,

(222)

w którym C jest pewną stałą materiałową. Dla osiowego rozciągania jednostkowa energia odkształcenia
postaciowego wynosi

W

 p

=

1

12

⋅G

⋅





X

2



X

2



=



X

2

6

⋅G

=



P

2

6

⋅G

.

(223)

Czyli stała C wynosi

C

=



P

2

6

⋅G

.

(224)

Warunek H-M-H możemy więc zapisać jako

1

12

⋅G

⋅

[





X

−

Y



2







Y

−

Z



2







Z

−

X



2

6⋅





XY

2



YZ

2



XZ

2



]

=



P

2

6

⋅G

.

(225)

Czyli naprężenie zredukowane, zgodnie z (221), wynosi

1

12

⋅G

⋅

[





X

−

Y



2







Y

−

Z



2







Z

−

X



2

6⋅





XY

2



YZ

2



XZ

2



]

=



red

2

6

⋅G

.

(226)

Ostatecznie naprężenie zredukowane wynosi



red

=

1



2

⋅







X

−

Y



2







Y

−

Z



2







Z

−

X



2

6⋅





XY

2



YZ

2



XZ

2



.

(227)

Stan sprężysty mamy, wtedy gdy



red



P

.

(228)

Dr inż. Janusz Dębiński

BZZ

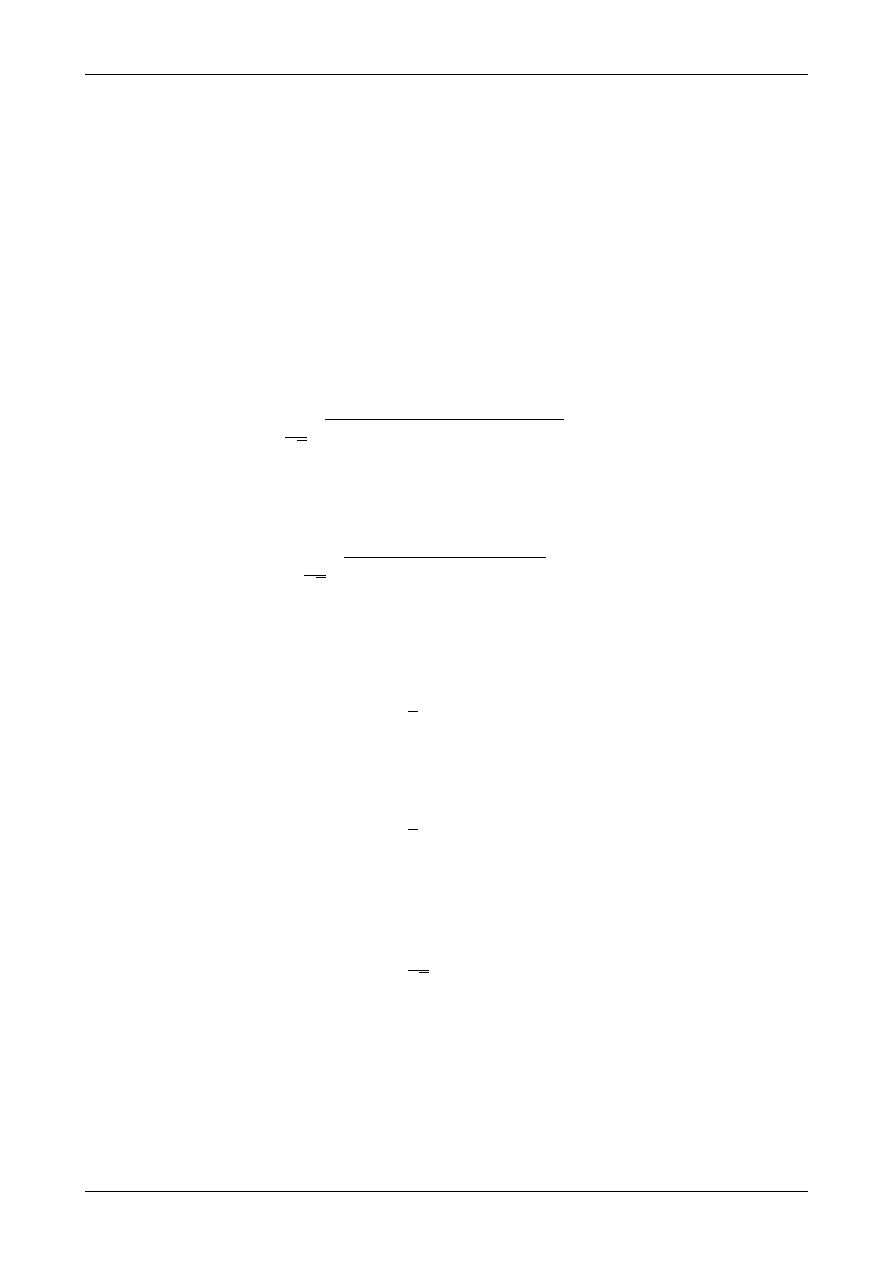
WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

49

Uplastycznienie materiału nastąpi wtedy gdy



red

=

P

.

(229)

Stan, w którym



red



P

(230)

jest nierealny.

W układzie osi głównych naprężenie zredukowane wynosi



red

=

1



2

⋅







1

−

2



2







2

−

3



2







3

−

1



2

.

(231)

W płaskim stanie naprężenia naprężenie zredukowane wyznacza się ze wzoru



red

=

1



2

⋅







X

−

Y



2



X

2



Y

2

6⋅

XY

2

.

(232)

W przypadku działania tylko naprężenia stycznego czyli tak zwanego czystego ścinania naprężenie
zredukowane oblicza się ze wzoru



red

=



3

⋅

XY

.

(233)

Czyli wytrzymałość materiału na ścianie wyznacza się ze wzoru



P

=



3

⋅

P

,

(234)

który ostatecznie ma postać



P

=



P



3

,

(235)

W płaskim stanie naprężenia stan niebezpieczny jest reprezentowany przez elipsę przedstawioną na rysunku
32. Elipsę tą nazywa się elipsą Hubera. Punkt A reprezentuje stan sprężysty, punkt B reprezentuje stan
niebezpieczny natomiast punkt C reprezentuje stan, który nie może się dla danego materiału zrealizować.

W przypadku płaskiego stanu naprężenia, który występuje w belkach i ramach płaskich (naprężenie normalne

σ

Y

wynosi zero) naprężenie zredukowane oblicza się ze wzoru

Dr inż. Janusz Dębiński

BZZ

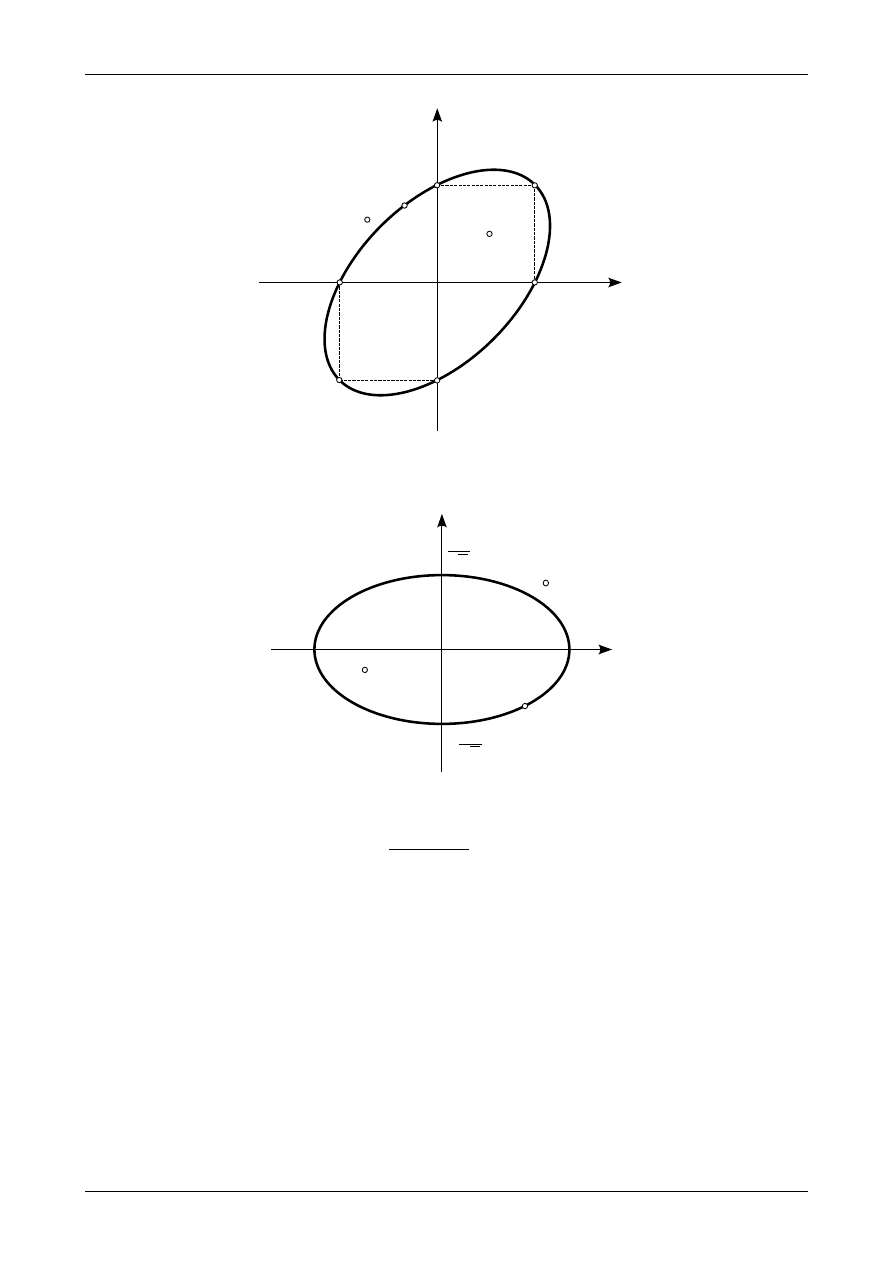
WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

50



1



2



P



P

A

B

C

−

P

−

P

Rys. 32. Elipsa Hubera dla płaskiego stanu naprężenia.



X



P

−

P



P



3

−



P



3



XY

A

B

C

Rys. 33. Elipsa Hubera dla stanu naprężenia występującego w belkach.



red

=





X

2

3⋅

XY

2

.

(236)

Rysunek 33 przedstawia elipsę dla stanu naprężenia występującego w belkach. Punkt A reprezentuje stan
sprężysty, punkt B reprezentuje stan niebezpieczny natomiast punkt C reprezentuje stan, który nie może się dla
danego materiału zrealizować.

13 Hipoteza Treski

Jest to hipoteza dla materiałów ciągliwych. Jako naprężenie niebezpieczne przyjmuje się granicę

plastyczności

σ

P

. Prawdziwa jest zatem zależność (221).

Według tej hipotezy materiał przechodzi w stan niebezpieczny wtedy, gdy maksymalne naprężenie
styczne osiągnie pewną wartość graniczną, charakterystyczną dla tego materiału.

Dr inż. Janusz Dębiński

BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

51

Maksymalne naprężenie styczne wyznacza się ze wzoru



MAX

=



I

−

III

2

,

(237)

w którym

σ

I

jest największym naprężeniem głównym czyli



I

=max

{



1



2



3

.

(238)

Natomiast

σ

III

jest najmniejszym naprężeniem głównym czyli



III

=min

{



1



2



3

.

(239)

Matematyczny zapis tego warunku ma postać



I

−

III

2

=C

1

,

(240)

w którym C

1

oznacza stałą materiałową. Dla osiowego rozciągania największe i najmniejsze naprężenia

główne wynoszą



I

=

P



III

=0

.

(241)

Czyli stała materiałowa wynosi

C

1

=



P

2

.

(242)

Warunek Treski możemy więc zapisać jako



I

−

III

=

P

.

(243)

Dr inż. Janusz Dębiński

BZZ

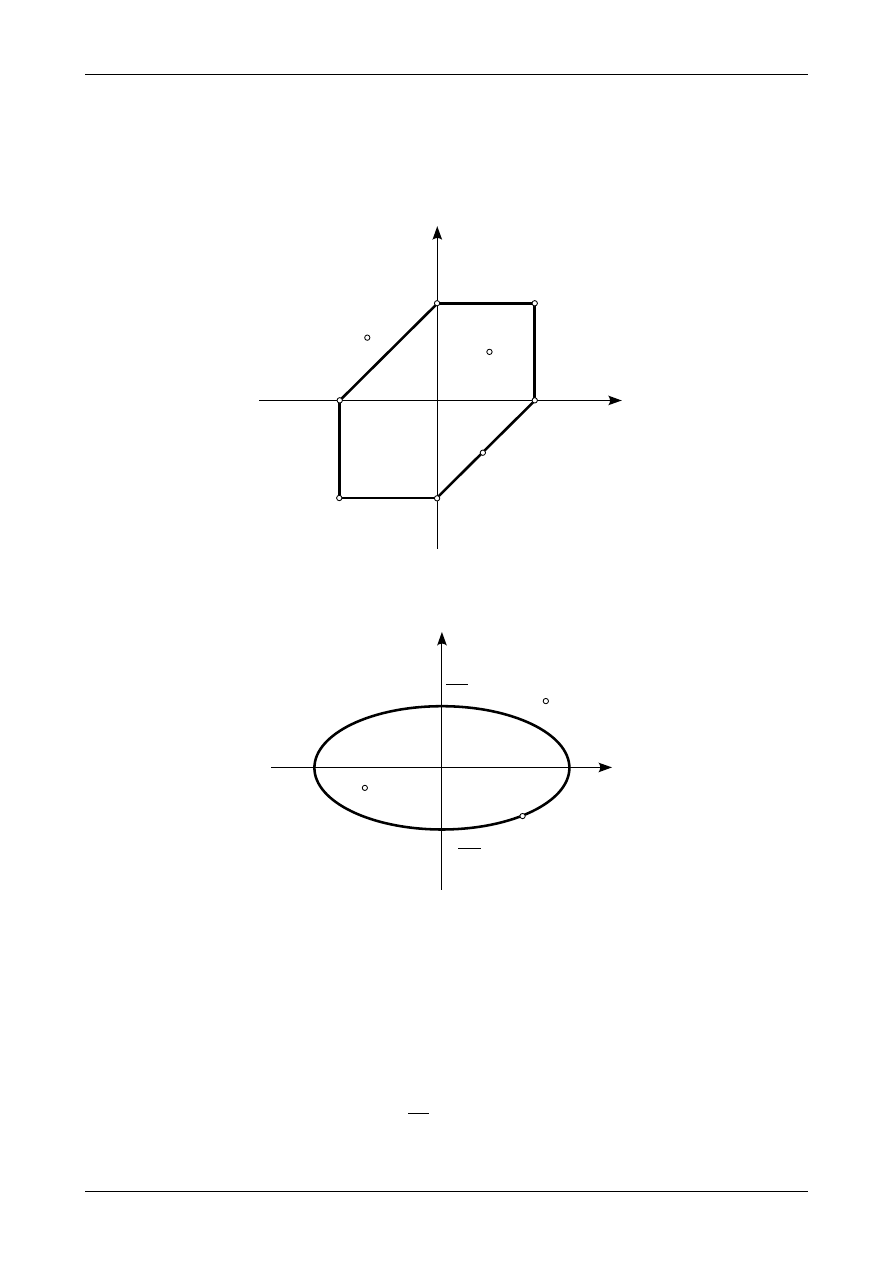
WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

52

Ostatecznie naprężenie zredukowane według hipotezy Treski wynosi



red

=

I

−

III

.

(244)



1



2



P



P

A

B

C

−

P

−

P

Rys. 34. Warunek Treski dla płaskiego stanu naprężenia.



X



P

−

P



XY

A

B

C



P

2

−



P

2

Rys. 35. Warunek Treski dla płaskiego stanu naprężenia występującego w belkach.

Rysunek 34 przedstawia warunek Treski dla płaskiego stanu naprężenia. Punkt A reprezentuje stan sprężysty,
punkt B reprezentuje stan niebezpieczny natomiast punkt C reprezentuje stan, który nie może się dla danego
materiału zrealizować.

Wytrzymałość materiału na ścianie według hipotezy Treski wynosi



P

=



P

2

.

(245)

Dr inż. Janusz Dębiński

BZZ

WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

53

W przypadku płaskiego stanu naprężenia, który występuje w belkach i ramach płaskich (naprężenie normalne

σ

Y

wynosi zero) naprężenie zredukowane oblicza się ze wzoru



red

=





X

2

4⋅

XY

2

.

(246)

Rysunek 35 przedstawia elipsę dla stanu naprężenia występującego w belkach. Punkt A reprezentuje stan
sprężysty, punkt B reprezentuje stan niebezpieczny natomiast punkt C reprezentuje stan, który nie może się dla
danego materiału zrealizować.

14 Porównanie hipotez H-M-H i Treski

Rysunki 36 i 37 przedstawiają porównanie hipotez Hubera-Misesa-Hencky'ego w płaskim stanie

naprężenia oraz w płaskim stanie naprężenia występującym w belkach. Jak widać hipoteza H-M-H pozwala
na większe wytężenie materiału niż hipoteza Treski.



1



2



P



P

H-M-H

−

P

−

P

Treska

Rys. 36. Porównanie hipotez H-M-H i Treski dla płaskiego stanu naprężenia.



X



P

−

P



P



3

−



P



3



XY



P

2

−



P

2

H-M-H

Treska

Rys. 37. Porównanie hipotez H-M-H i Treski dla płaskiego stanu naprężenia występującego w belkach.

Dr inż. Janusz Dębiński

BZZ

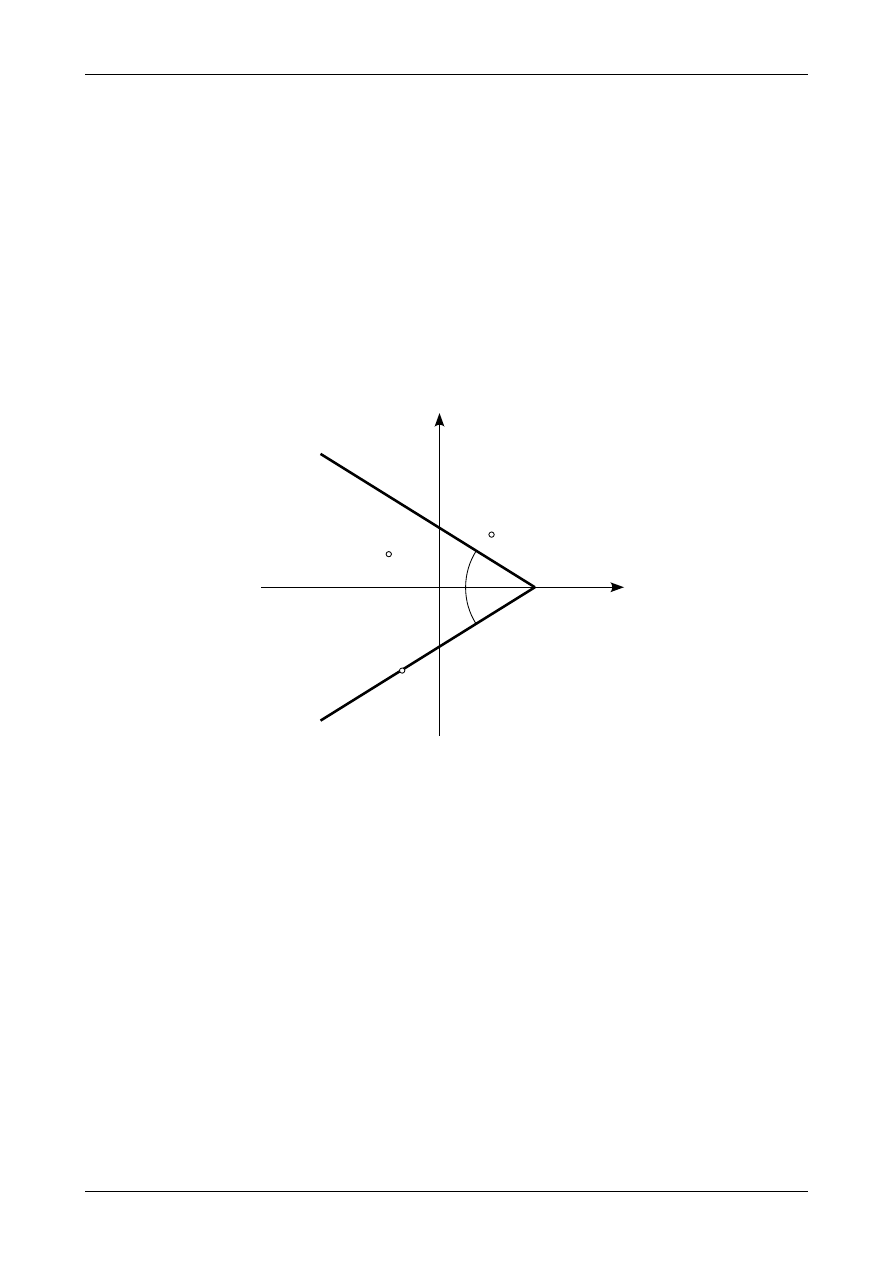
WYTRZYMAŁOŚĆ MATERIAŁÓW – PODSTAWY TEORII – CZĘŚĆ 1

54

15 Hipoteza Coulomba-Mohra

Jest to hipoteza. która ma zastosowanie w materiałach kruchych i plastyczno-kruchych. Materiałem

kruchym jest na przykład beton lub podłoże gruntowe. Materiałem plastyczno-kruchym jest żeliwo.

Najprostsza postać warunku Coulomba-Mohra składa się z dwóch prostych

∣



∣

=c−⋅tg







,

(247)

w którym c oznacza spójność, to znaczy wytrzymałość na ścinanie bez nacisku, natomiast

φ

jest kątem tarcia

wewnętrznego. Hipotezę Coulomba-Mohra przedstawia rysunek 38. Punkt A reprezentuje stan sprężysty,
punkt B reprezentuje stan niebezpieczny natomiast punkt C reprezentuje stan, który nie może się dla danego
materiału zrealizować.





c

-c




A

B

C

Rys. 38. Hipoteza Coulomba-Mohra.

Dr inż. Janusz Dębiński

BZZ