1
WIADOMOŚCI TEORETYCZNE
Otwór mały w hydromechanice charakteryzuje się tym, że rozkład prędkości w strumieniu
wypływającej cieczy w przekroju tego otworu jest w przybliżeniu stały. Założenie powyższe
obowiązuje w przypadku gdy wysokość ciśnienia w środku geometrycznym otworu jest co najmniej
dziesięciokrotnie wyższa od wysokości otworu. Gdy różnica prędkości w przekroju otworu jest
znacząca nie można stosować zależności dla małych otworów niezatopionych. Wypadek ten wymaga
zastosowania równań opisujących wypływ z dużego otworu niezatopionego. Otwór w praktyce
traktujemy jako mały, jeśli jego wysokość nie przekracza 10-25% zagłębienia środka ciężkości otworu
pod zwierciadłem cieczy. Otwory duże mogą występować w zależności od wpływu na ich wydatek
położenia zwierciadła cieczy w stanowisku dolnym:
- jako niezatopione – położenie zwierciadła wody w stanowisku dolnym nie wpływa na wydatek
otoworu (rys.1),
- jako częściowo zatopione – położenie zwierciadła wody w stanowisku dolnym wpływa na jego
wydatek. Wraz ze wzrostem poziomu zwierciadła wody wydatek otworu ulega obniżeniu (rys.1a).
- jako zatopione – wpływu poziomu wody dolnej w odpływie jest efektem wyrównania profilu
prędkości w jego świetle (rys.1b). Wartość wydatku otworu zależy od różnicy położenia poziomów
zwierciadeł cieczy przed i za otworem.
Ze względu na grubość ścianki otwory można podzielić na:
- otwór w cienkiej ściance, tj. strumień nie przylega do wewnętrznych krawędzi otworu, grubość
ścianki tj. L<(3,4-4,0d), rys.1c,
- przystawki, strumień przylega do wewnętrznych krawędzi otworu powodując zwiększenie wydatku,
Wydatek otworu małego niezatopionego
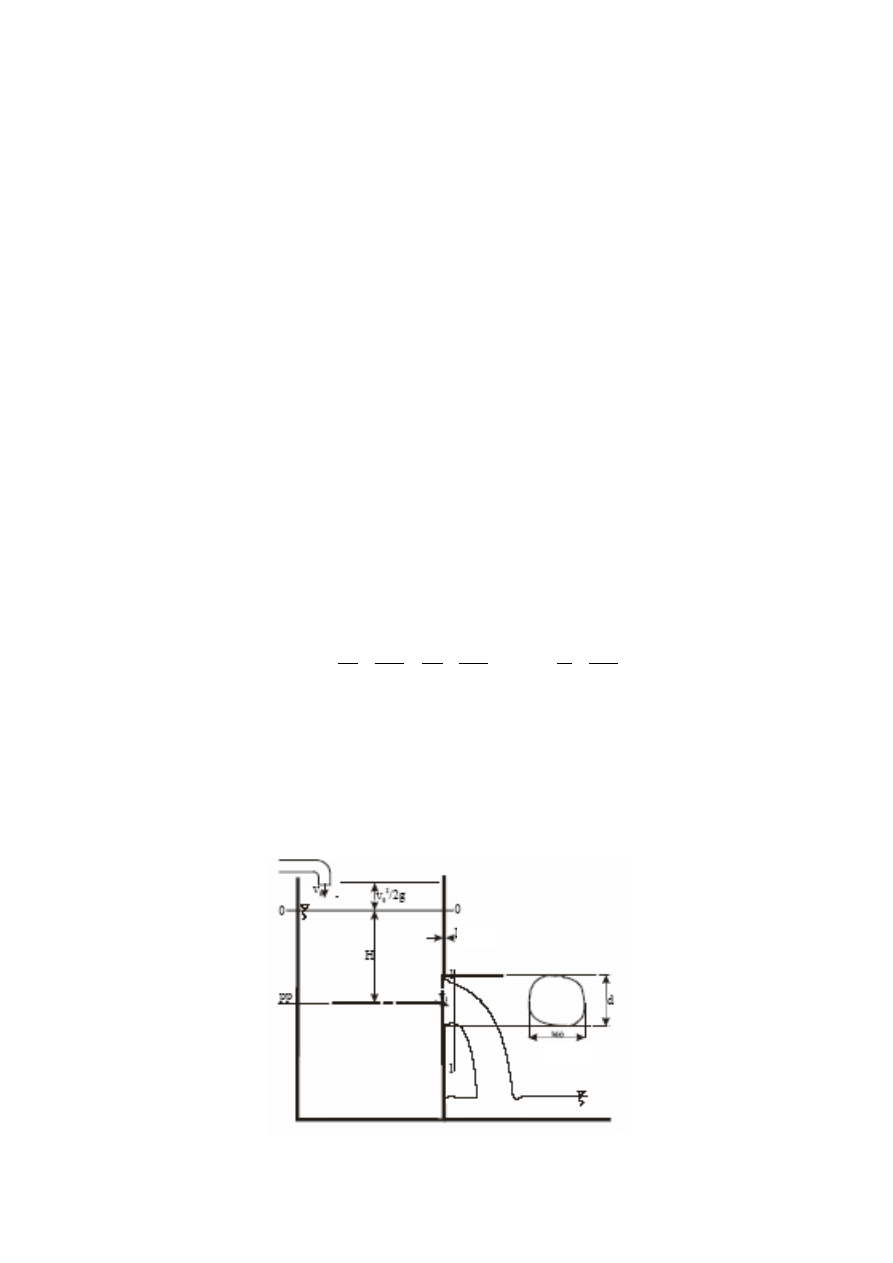
Rozkład prędkości na wysokości otworu jest stały dlatego jego wydatek można określić
zapisując równanie Bernoulliego dla przekrojów 0-0, 1-1 (rys.2):
g
D
L
g
p
g
p
H
a
a
2
2
2
2
1
2
1
2
0
(1)
gdzie:
H – poziom zwierciadła wody w stanowisku górnym, m
p
a
– ciśnienie atmosferyczne, Pa
γ – ciężar objętościowy wody, N/m
3
υ
0
– prędkość dopływającej wody, m/s
υ
1
– prędkość wody wypływającej z otworu, m/s
g – przyspieszenie ziemskie, m/s
2
h
str
– wysokość strat ciśnienia
ξ – współczynnik oporów miejscowych
Rys. 2. Schemat obliczeniowy małego otworu niezatopionego.
b(z)
L
2
Uwzględniając równanie ciągłości strumienia powyższe równanie przekształca się do postaci:
4
2
2
4
2
2
2
0
8
8
2
d
g
Q
D
L
d
g
Q
g
H
(2)
Dokonując odpowiednich przekształceń, pomijając straty ciśnienia na długości otworu oraz
wprowadzając oznaczenie
50
,
0
1
wydatek otworu małego nie zatopionego obliczyć można ze
wzoru:
g
H
g
d
Q
2
2
4
2
0
2
(3)
Wydatek dużego otworu niezatopionego
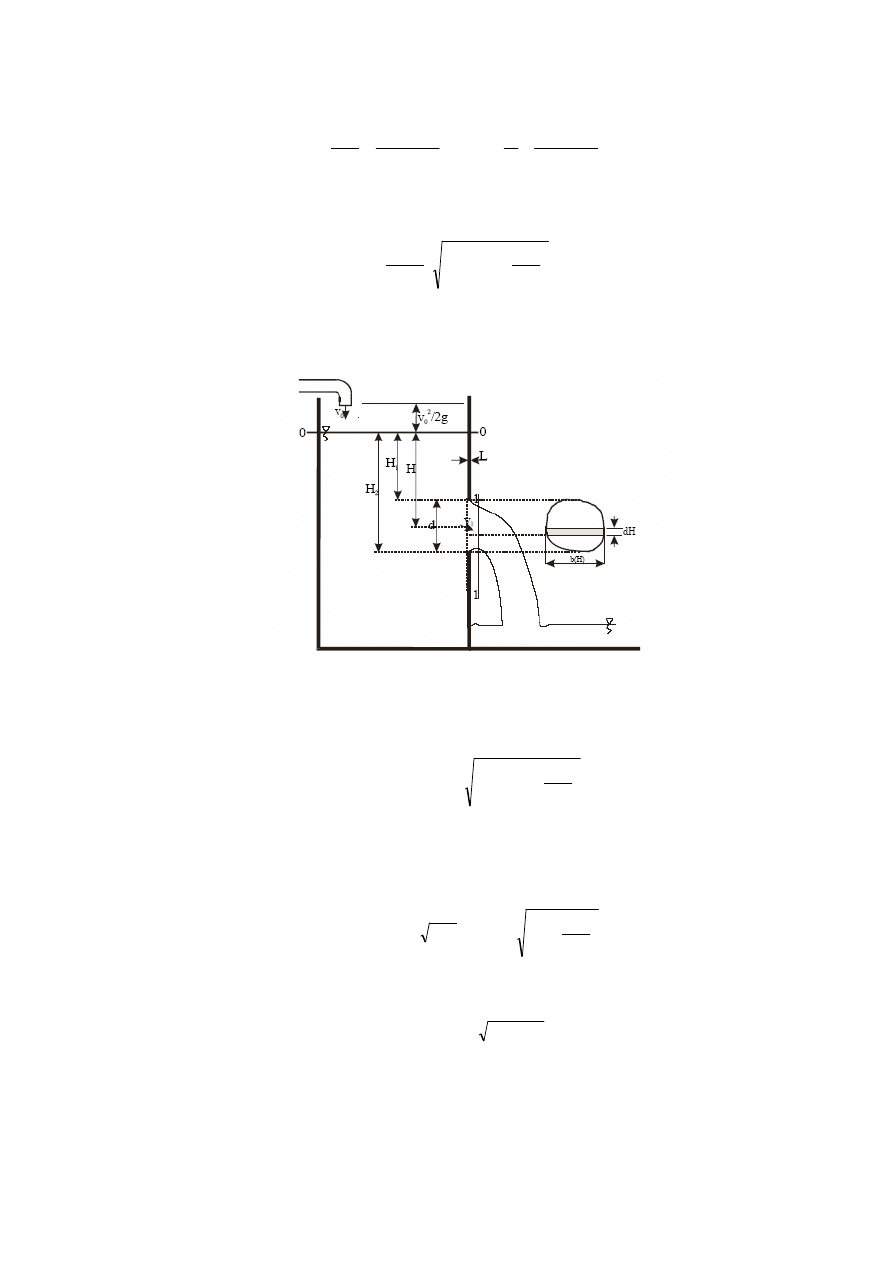
W tym przypadku ze względu na rozmiary otworu odpływowego, rozkład prędkości na jego
wysokości ulega zmianie (rys. 3).
Rys. 3. Schemat obliczeniowy duże otworu niezatopionego.
Dlatego też aby określić jego wydatek konieczne jest rozdzielnie przekroju wypływającego
strumienia na elementarne paski, w których prędkość przepływu jest w przybliżeniu stała. Wydatek
pojedynczego paska po zapisaniu równania Bernoulliego dla przekroju 0-0, 1-1 jest następujący:
g
H
g
dH
h
b
dQ
2
2
)
(
2
0
(4)
gdzie:
b(H) – szerokość elementarnego paska, m
dH – wysokość elementarnego paska, m
Całkowity wydatek otworu można wyznaczyć z następującej zależności poprzez całkowanie w
zakresie H
2
do H
1
(górna, dolna krawędź otworu):
dH
g
H
H
b
g
dH
h
b
Q
H
H
2
)
(
2
)
(
2
0
2
1
(5)
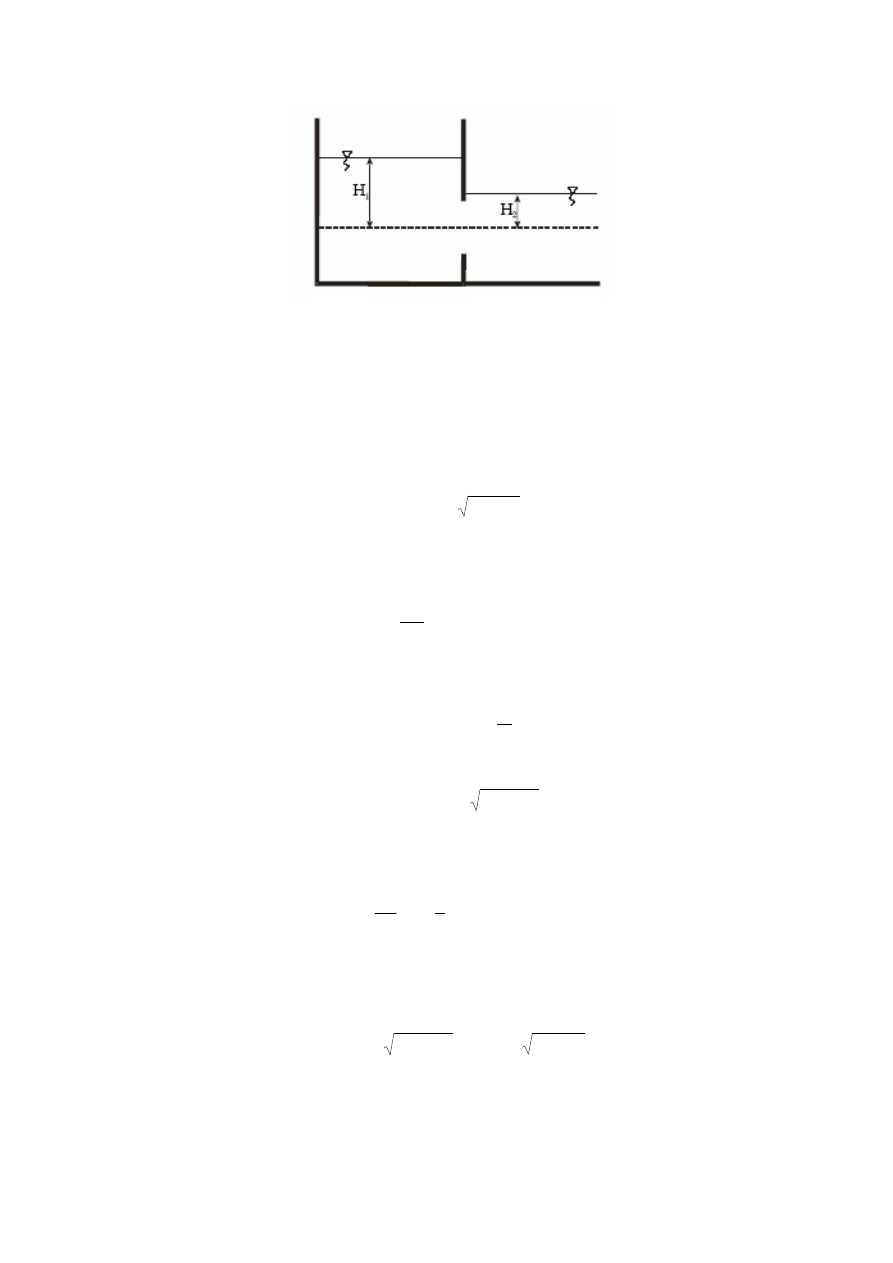
Wydatek otworu zatopionego
W tym przypadku na wydatek otworu wpływa wyłącznie różnica poziomów zwierciadła wody
(rys.4) oraz współczynnik jego wydatku. Wydatek otworu zatopionego wyznaczany jest ze wzoru:
H
g
F
Q
2
(6)
gdzie:
F – pole powierzchni otworu, m
2
ΔH – różnica poziomów zwierciadeł wody;ΔH=H
2
-H
1
, m
3
Rys. 4. Schemat obliczeniowy otworu zatopionego.
Wydatek otworu częściowo zatopionego
Na wydatek rozważanego otworu wpływa poziom zwierciadła wody dolnej i górnej (rys.5).
Całkowity wydatek stanowi sumę części zatopionej i niezatopionej, dlatego tez obliczany jest ze
wzoru:
nzat
zat
Q
Q
Q
(7)
gdzie:
Q – wydatek całkowity otworu, m
3
/s
Q
zat
– wydatek części zatopionej, m
3
/s
H
g
F
Q
z
z
zat
2
(8)
μ
z
- współczynnik wydatku części zatopionej,
H – różnica wysokości poziomów zwierciadła wody dolnej i górnej, m
F
z
– pole powierzchni części zatopionej otworu, m
2
2
sin
2
8
2
D
F
z
(9)
β – kąt środkowy odpowiadający poziomowi zwierciadła wody h nad krawędzią dolną otworu
kołowego,
D – średnica otworu kołowego, m
D
h
2
1
arccos
(10)
Q
nzat
– wydatek części nie zatopionej, m
3
/s
o
nzat
nzat
H
g
F
Q
2
(11)
μ – współczynnik wydatku części nie zatopionej otworu
F
nzat
– pole powierzchni nie zatopionej części otworu, m
2
2
sin
2
2
1
4
2
D
F
nzat
(12)
H
o
– różnica wysokości pomiędzy poziomem zwierciadła wody górnej a środkiem ciężkości
powierzchni F
nzat
, m
Ostatecznie wydatek otworu można określić ze wzoru:
H
g
F
H
g
F
Q
z
z
o
nzat
2
2
(13)
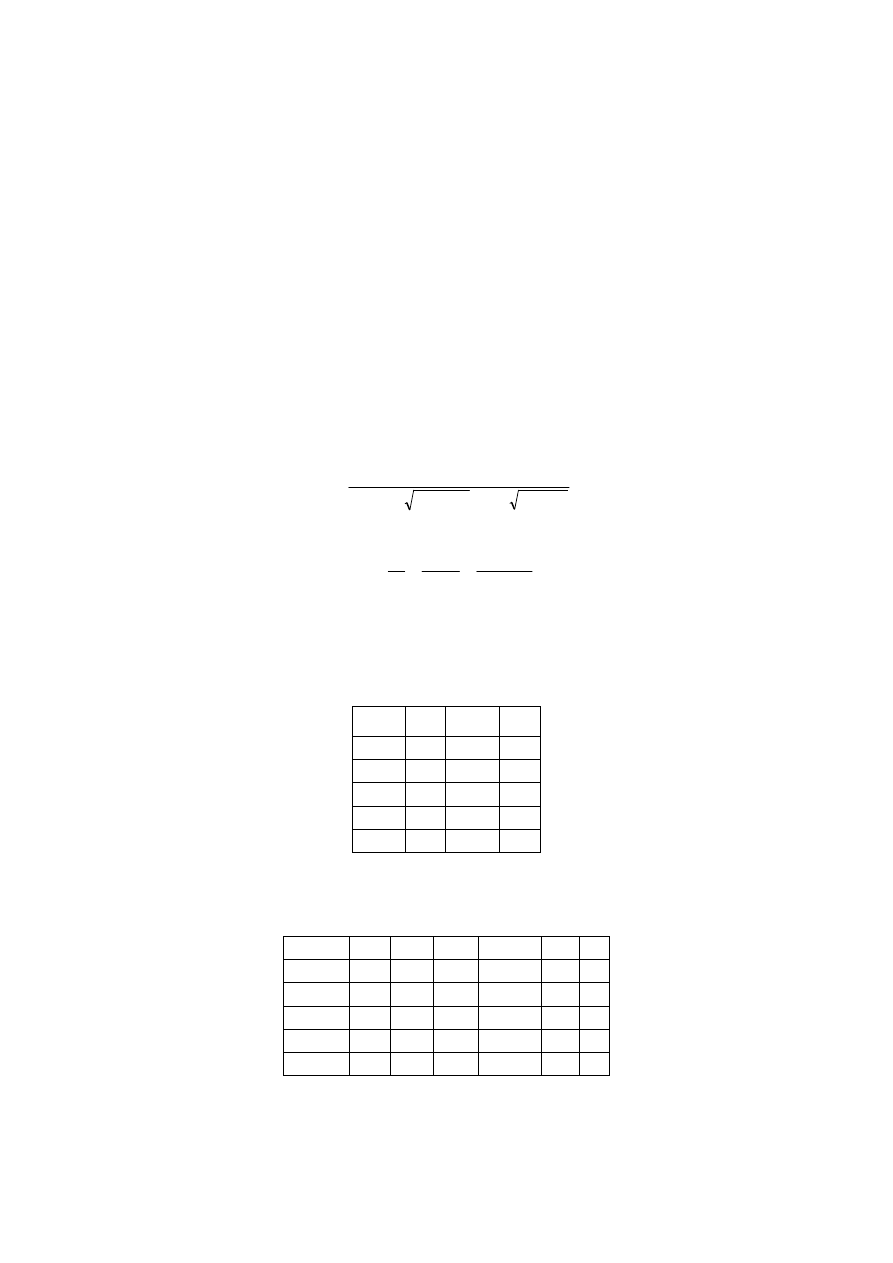
STANOWISKO BADAWCZE.
Schemat stanowiska badawczego przedstawiono na Rys. 6. W celu podtopienia otworu
kołowego ustalony jest minimalny spadek koryta.
4
WYKONANIE ĆWICZENIA.
W celu wyznaczenia współczynnika wydatku otworu kołowego koryto jest napełniane do
wysokości krawędzi przelewowej. Równocześnie odczytać należy za pomocą wodowskazu
szpilkowego poziom dna koryta przy krawędzi przelewowej oraz rzędną dna krawędzi otworu
kołowego (h
k
). Koryto powyżej zainstalowanej przegrody jest napełniane wodą dopóki poziom
zwierciadła wody nie przekroczy górnej krawędzi. W tym momencie należy wyłączyć pompę, oraz
odciąć dopływ wody do koryta zamykając zasuwę. Od tego momentu poziom zwierciadła wody w
korycie powyżej zamontowanej przegrody obniża się, co jest spowodowane odpływem otworem
kołowym w zmiennych warunkach (zatopiony, podtopiony). Gdy poziom zwierciadła wody osiągnie
krawędź instalowanej przegrody uruchamiany jest stoper i równocześnie mierzona jest rzędna
zwierciadła wody, następnie w niemalże tej samej chwili określany jest poziom zwierciadła wody w
stanowisku dolnym. W dalszej kolejności mierzone są poziomy zwierciadła wody w obu stanowiskach
oraz czas jaki jest potrzebny na obniżenie się wody z poziomu h do h
i+1
w stanowisku górnym.
Pomiary są kontynuowane dopóki poziom zwierciadła wody nie osiągnie górnej krawędzi otworu
kołowego. Na rys.5 przedstawiono schemat obliczeniowy otworu kołowego podtopionego. Wyniki
pomiarów zestawić należy w tab.1 podanej w instrukcji opracowania ćwiczenia. Wyniki obliczeń
przedstawić zestawić w tab. 2. Współczynnik wydatku określić należy ze wzoru:
H
g
F
H
g
F
Q
z
o
nzat
z
2
2
(14)
Natężenie przepływu wyznaczyć z zależności:
t
h
L
B
t
h
A
t
V
Q
(15)
gdzie:
A – pole powierzchni koryta w rzucie, m
2
Δt – odstępy czasu pomiędzy kolejnymi pomiarami poziomu zwierciadła wody w stanowisku górnym,
s
Tabela 1
L. p
Hg
Hd
t
m
m
s
1
2
3
…
Tabela 2
L.p
β
F
nzat
F
zat
S
c
(F
zat
)
μ
z
μ
rad
m
2
m
2
m
1
2
3
…
Literatura:
1. Kisiel A., Mrowiec M., Malmur R., Kisiel J., Bielecka D.: Poradnik hydromechanika i
hydrotechnika, Wydawnictwo Politechniki Częstochowskiej, Częstochowa 2001.
5