SPRAWOZDANIE Z BADAŃ LABORATORYJNYCH
Wydział Inżynierii Środowiska i Biotechnologii, Instytut Inżynierii Środowiska
Laboratorium
Hydrologia oraz nauki o Ziemi
Temat ćwiczenia:
Analiza granulometryczna gruntu w celu wyznaczenia
własności hydrogeologicznych
Imię i Nazwisko
Marta Wachowicz
Grupa: I, III semestr studiów
niestacjonarnych, Inżynieria
Środowiska
Ocena Data
1. Cel ćwiczenia
a. Wykreślenie krzywych sumarycznych uziarnienia dla pobranych próbek.
b. Określenie rodzaju gruntu.
c. Wyznaczenie średnic miarodajnych.
d. Wyznaczenie współczynników filtracji metodą wzorów empirycznych dla pobranych
próbek.
2. Stosowana metodyka
Do określenia współczynników filtracji pobranych próbek przeprowadzono analizę
granulometryczną metodą mechaniczną – sitową.
Skorzystano ze wzorów empirycznych Hazena, Terzaghi’ego i USBSC.
Ponieważ zastosowano wzory empiryczne które zawierają pewne przybliżenia,
współczynnik k należy traktować jako orientacyjny.
3. Uzyskane wyniki
Z wysuszonego materiału badawczego pobrano i odważono z dokładnością do 0,01 g
dwie próbki. Próbki zostały przesiane w kolumnie sit o oczkach od 0,063 mm
do 10,00 mm. Sita umieszczono na wstrząsarce. Wstrząsanie dla każdej z próbek trwało
7 min. Z sit zebrano i zważono klasę górną z dokładnością do 0,01 g.
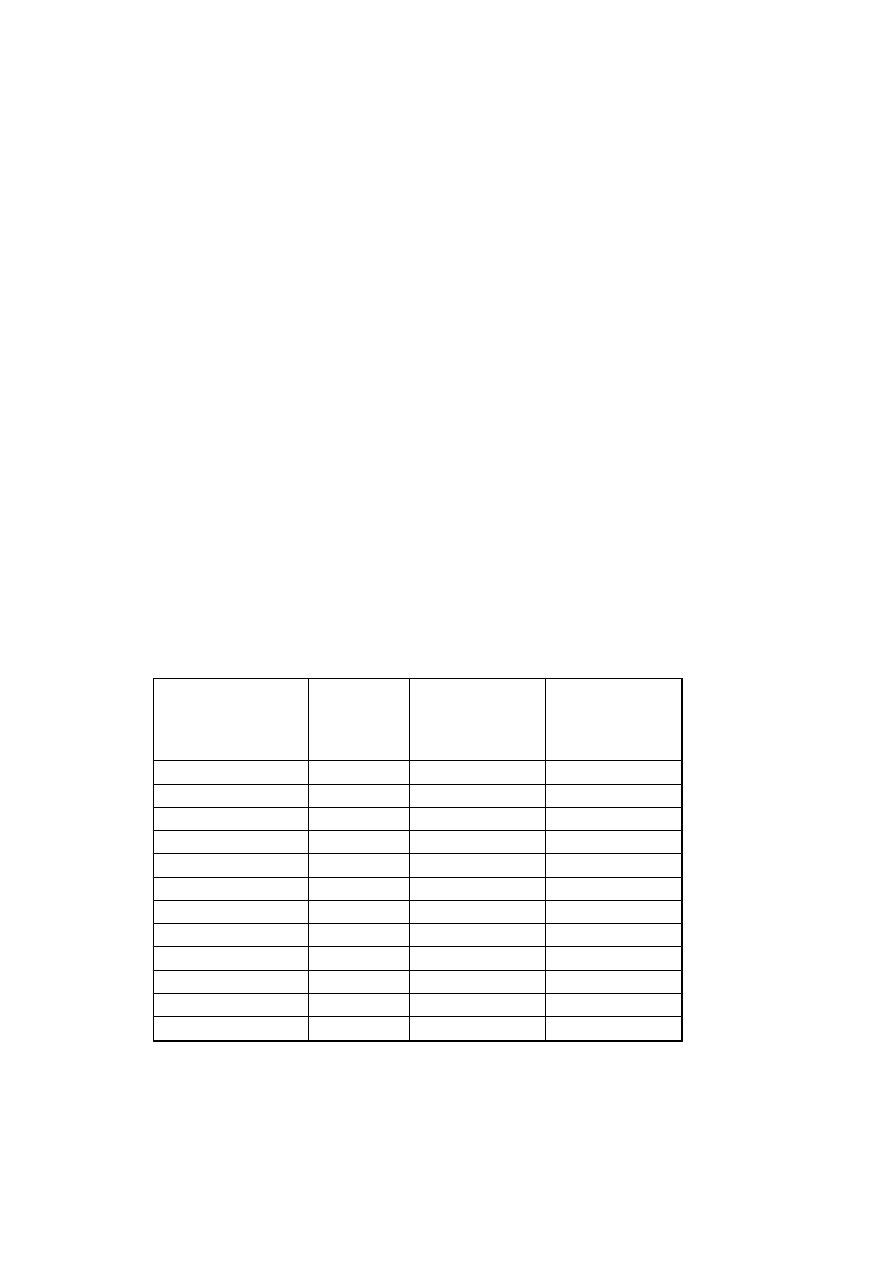
Skład ziarnowy przedstawiono poniżej.
Skład ziarnowy wyznaczony metodą analizy sitowej. Próbka nr 1
Wymiar oczek sita
[mm]
Masa
pozostałości
na sicie
[g]
Obliczona
zawartość frakcji
[%]
Suma zawartości
kolejnych frakcji
[%]
d > 10,00
45,91
11,42
11,42
10,00 ≥ d > 5,00
54,43
13,54
24,95
5,00 ≥ d > 4,00
15,12
3,76
28,71
4,00 ≥ d > 2,00
61,72
15,35
44,06
2,00 ≥ d > 1,00
82,3
20,47
64,53
1,00 ≥ d > 0,50
53,32
13,26
77,79
0,50 ≥ d > 0,30
44,11
10,97
88,76
0,30 ≥ d > 0,20
32,37
8,05
96,81
0,20 ≥ d > 0,10
10,11
2,51
99,33
0,10 ≥ d > 0,063
1,09
0,27
99,60
0,063 ≥ d
1,61
0,40
100,00
Suma
402,09
100,00
100,00
Masa próbki pobranej do badań m
c
= 402,26g
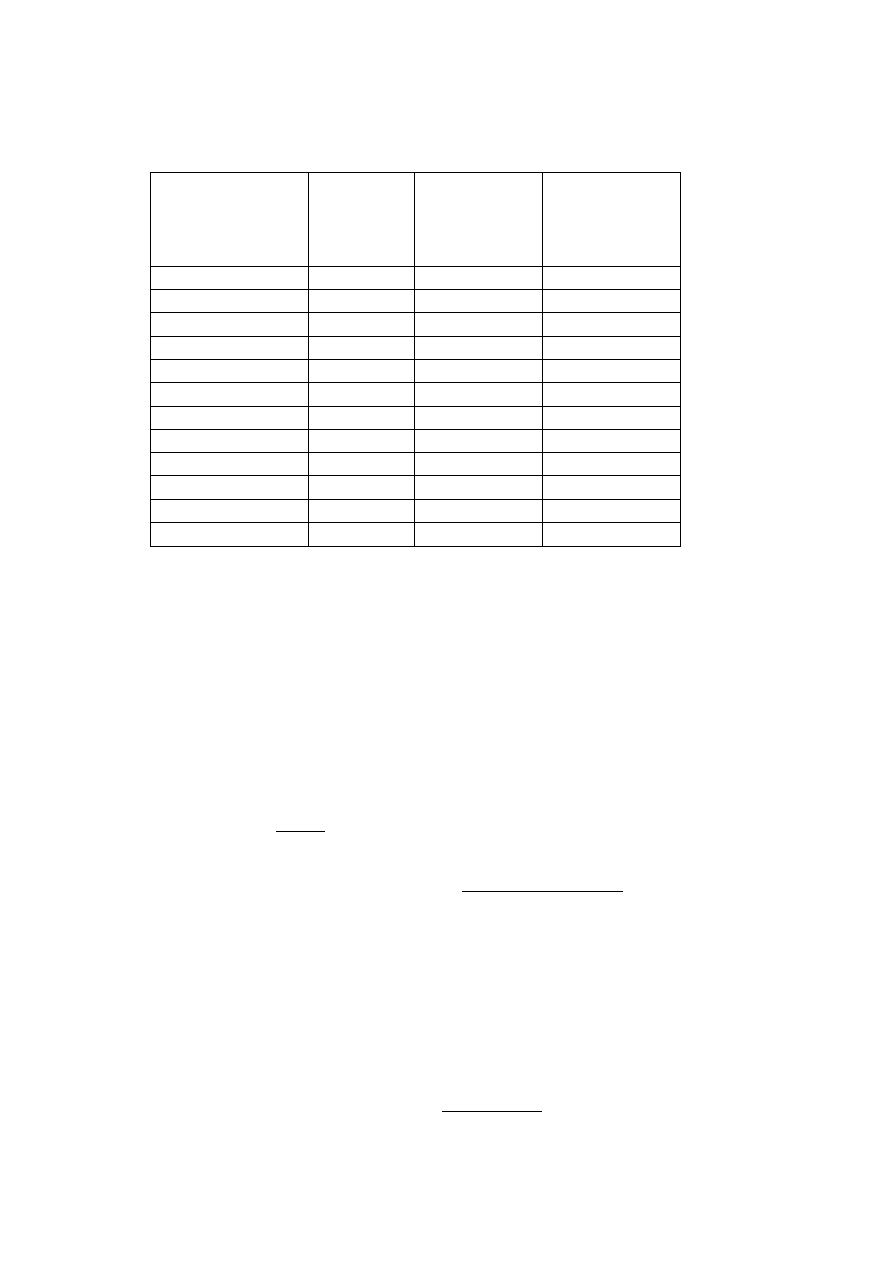
Skład ziarnowy wyznaczony metodą analizy sitowej. Próbka nr 2
Wymiar oczek sita
[mm]
Masa
pozostałości
na sicie
[g]
Obliczona
zawartość frakcji
[%]
Suma zawartości
kolejnych frakcji
[%]
d > 10,00
11,61
2,43
2,43
10,00 ≥ d > 5,00
91,89
19,26
21,69
5,00 ≥ d > 4,00
10,77
2,26
23,95
4,00 ≥ d > 2,00
30,76
6,45
30,40
2,00 ≥ d > 1,00
104,92
21,99
52,39
1,00 ≥ d > 0,50
93,05
19,50
71,90
0,50 ≥ d > 0,30
67,03
14,05
85,95
0,30 ≥ d > 0,20
42,72
8,95
94,90
0,20 ≥ d > 0,10
18,51
3,88
98,78
0,10 ≥ d > 0,063
3,74
0,78
99,56
0,063 ≥ d
2,08
0,44
100,00
Suma
477,08
100,00
100,00
Masa próbki pobranej do badań m
c
= 477,12g
4. Analiza wyników
4.1. Próbka nr 1
4.1.1. Sprawdzenie poprawności przesiewu
Masa próbki pobranej do badań m
c
= 402,26g
Suma mas wszystkich rozdzielonych frakcji ∑m
i
=402,09g
1
402,09
402,26
∗ 100%
0,042%
D < 0,5% ‐ próbkę należy uznać za prawidłowo przesianą.
Niewielka ilość ziaren o średnicy d ≤ 0,06 mm, rzędu 0,44% w pełni uzasadnia
zastosowanie analizy sitowej.
4.1.2. Klasyfikacja gruntu wg PN‐86/B‐02480.
D
50
≤ 40 mm oraz D
90
> 2 mm ‐ próbka gruntu gruboziarnistego
Biorąc pod uwagę powyższe oraz:
f
k
+f
z
= 0%+44% =44%
f
i
≤ 2% oraz 50% ≥ f
k
+f
z
> 10% ‐ pospółka (Po)
4.1.3. Wybór metody (wzoru empirycznego) i wyliczenie współczynnika filtracji
Analiza sitowa, którą rozdzielono próbkę na frakcje, wykazuje, że średnica
miarodajna d
e
= d
10
= 0,28 mm, zatem spełnia warunek 0,1 mm ≤ d
e
≤ 3 mm
dla metody oznaczania Hazena.
Jednak próbka zawiera ziarna o wielkości d < 0,1 mm. W związku z tym, jako
średnicę miarodajną użyto d
20
która wynosi:
d
e
= d
20
= 0,47 mm,
oraz do wyliczeń współczynnika nierównomierności użyto wzoru
Terzaghi’ego:
3,80
0,47
8,08
Współczynnik U zawierający się w przedziale 5 ≤ U ≤ 15 określa grunt jako
nierównomiernie uziarniony, jednocześnie wyklucza zastosowanie wzoru
Hazena w związku z ograniczeniem stosowalności dla 1 ≤ U ≤ 5.
Do wyznaczenia współczynnika filtracji użyto wzoru amerykańskiego (USBSC)
którego stosowalność określa przedział w jakim zawiera się średnica ziaren d
20
Dla próbki nr 1: 0,01 < d
20
< 2,00 mm, gdzie d
20
= 0,47 mm.
0,36 ∗
,
⁄
,
∗ ,
,
,
⁄
Zatem współczynnik filtracji k dla próbki nr 1 wynosi 0,063 m/s.
4.2. Próbka nr 2
4.2.1. Sprawdzenie poprawności przesiewu
Masa próbki pobranej do badań m
c
= 477,12g
Suma mas wszystkich rozdzielonych frakcji ∑m
i
=477,08g
1
477,08
477,12
∗ 100%
0,008%
D < 0,5% ‐ próbkę należy uznać za prawidłowo przesianą.
Niewielka ilość ziaren o średnicy d ≤ 0,06 mm, rzędu 0,44% w pełni uzasadnia
zastosowanie analizy sitowej.
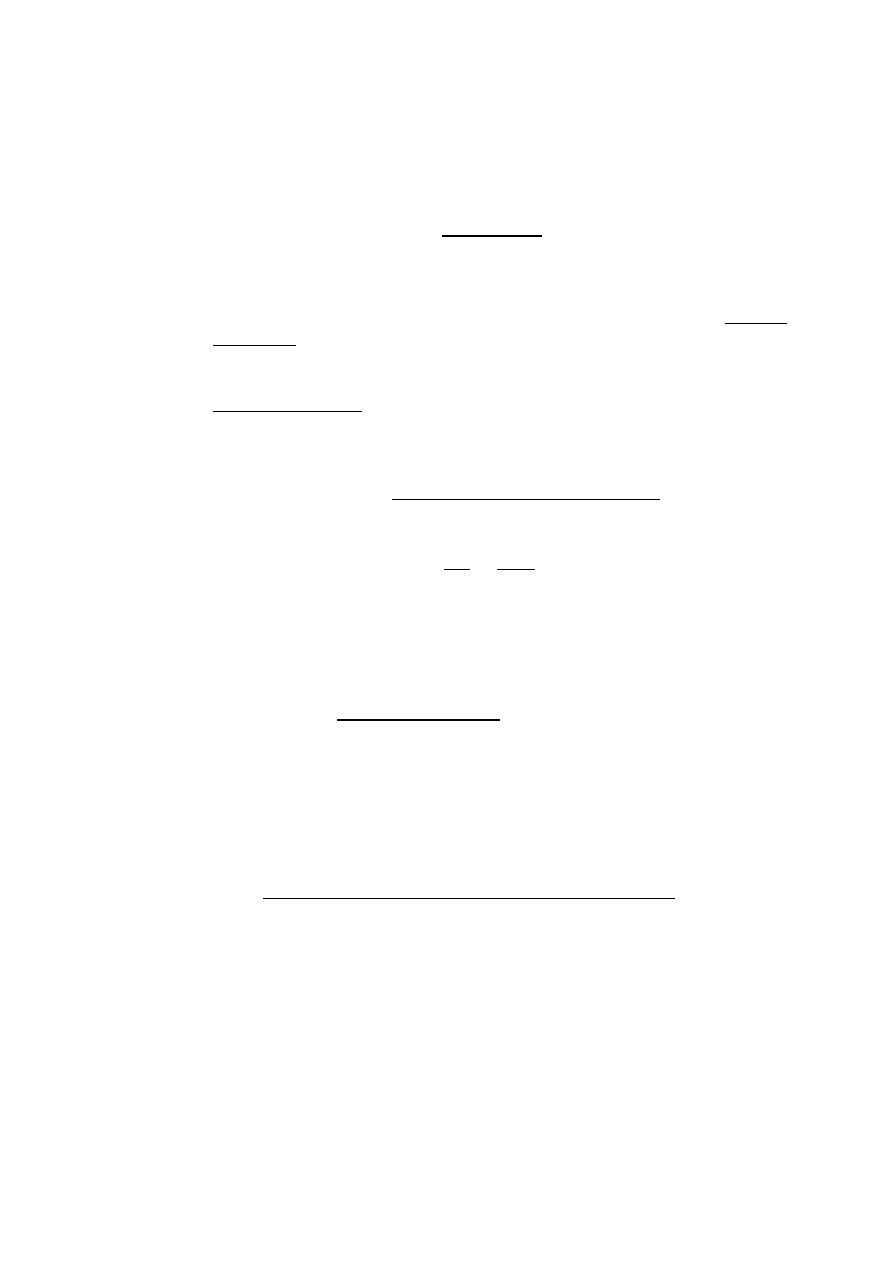
4.2.2. Klasyfikacja gruntu wg PN‐86/B‐02480.
D
50
≤ 40 mm oraz D
90
> 2 mm ‐ próbka gruntu gruboziarnistego
Biorąc pod uwagę powyższe oraz:
f
k
+f
z
= 0%+35%=35%
f
i
≤ 2% oraz 50% ≥ f
k
+f
z
> 10% ‐ pospółka (Po)
4.2.3. Wybór metody (wzoru empirycznego) i wyliczenie współczynnika filtracji
Analiza sitowa, którą rozdzielono próbkę na frakcje, wykazuje, że średnica
miarodajna d
e
= d
10
= 0,25 mm, zatem spełnia warunek 0,1 mm ≤ d
e
≤ 3 mm
dla metody oznaczania Hazena.
Jednak próbka zawiera ziarna o wielkości d < 0,1 mm. W związku z tym, jako
średnicę miarodajną użyto d
20
która wynosi:
d
e
= d
20
= 0,38 mm,
oraz do wyliczeń współczynnika nierównomierności użyto wzoru
Terzaghi’ego:
2,45
0,38
6,44
Współczynnik U zawierający się w przedziale 5 ≤ U ≤ 15 określa grunt jako
nierównomiernie uziarniony, jednocześnie wyklucza zastosowanie wzoru
Hazena w związku z ograniczeniem stosowalności dla 1 ≤ U ≤ 5.
Do wyznaczenia współczynnika filtracji użyto wzoru amerykańskiego (USBSC)
którego stosowalność określa przedział w jakim zawiera się średnica ziaren d
20
Dla próbki nr 2: 0,01 < d
20
< 2,00 mm, gdzie d
20
= 0,38 mm.
0,36 ∗
,
⁄
,
∗ ,
,
,
⁄
Zatem współczynnik filtracji k dla próbki nr 1 wynosi 0,039 m/s.
5. Wnioski
Po przeprowadzeniu analizy można stwierdzić, że pomimo zbliżonego składu
granulometrycznego i tej samej klasyfikacji gruntu (zgodnie z PN‐86/B‐02480), próbki
charakteryzują się bardzo różnym współczynnikiem filtracji.
W tym przypadku, próbka o większej różnoziarnistości U (próbka nr 1) wykazuje wyższy
współczynnik k. Wynika z tego, że współczynnik U ma mniejszy wpływ na współczynnik
filtracji niż zawartość ziaren wyższych frakcji. Ze wzoru USBSC wynika wprost, że im
wyższa frakcja d
20
mieszcząca się w zakresie stosowalności, tym większy współczynnik
filtracji.
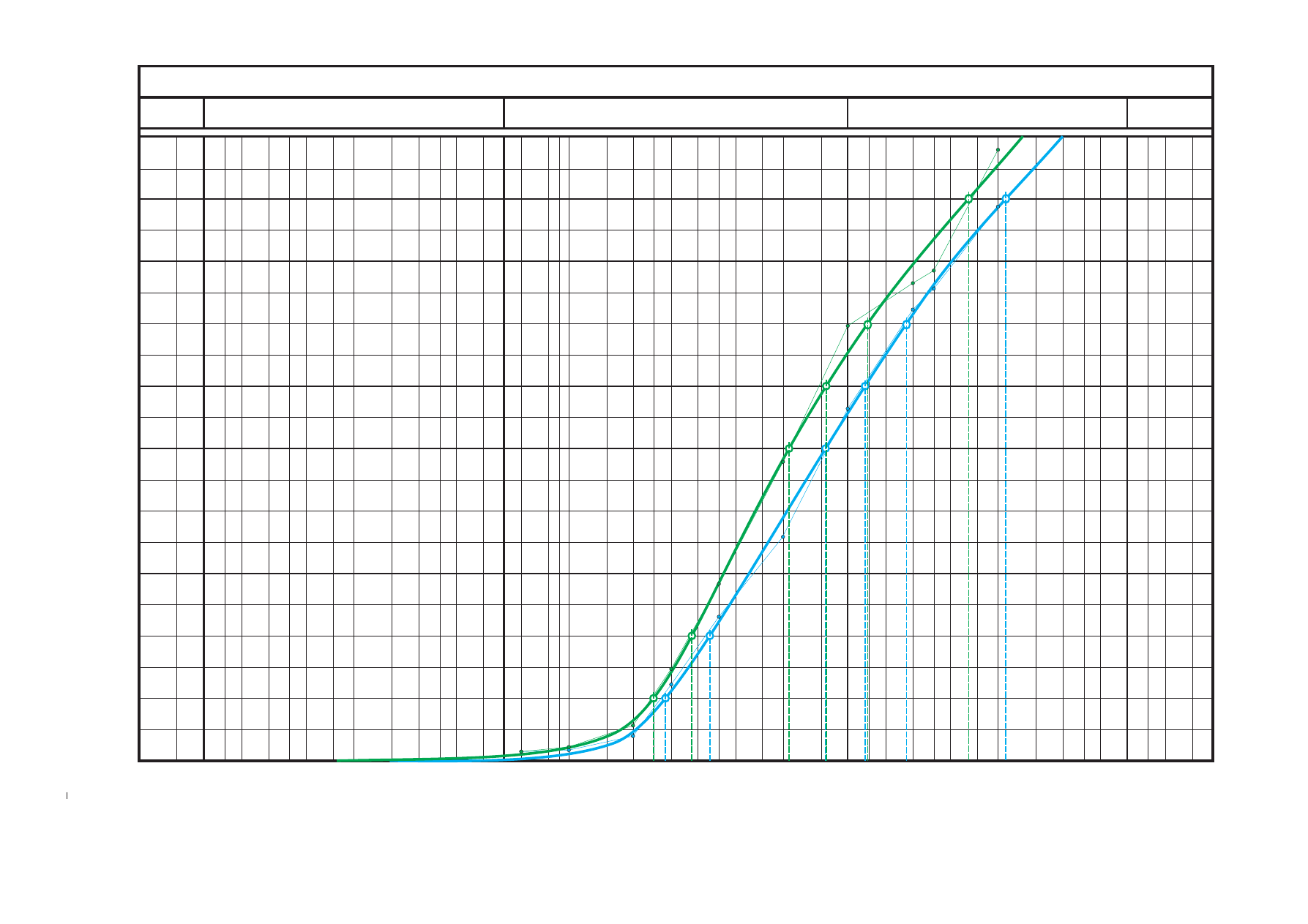
W Y K R E S U Z I A R N I E N I A
Iłowa
Pyłowa
Piaskowa
Żwirowa
Kam.
0,0010
0,0015
0,0020
0,0025
0,003
0,004
0,005
0,006
0,008
0,010
0,015
0,020
0,025
0,03
0,04
0,05
0,06
0,08
0,10
0,15
0,20
0,3
0,4
0,5
0,6
0,8
1,0
1,5
2,0
2,5
3
4
5
6
8
10
15
20
25
30
40
50
60
80
100
0,09
0,25
Zawartość
cząstek o
średnicy mniejszej niż
[%]
d
Zawartość
cząstek o
średnicy mniejszej niż
[%]
d
100
90
80
70
60
50
40
30
20
10
0
100
90
80
70
60
50
40
30
20
10
0
Zawartość
cząstek o
średnicy większej niż
[%]
d
Zawartość
cząstek o
średnicy większej niż
[%]
d
Średnica zastępcza ziarna (frakcja) [mm]
d
(d ) = 0,25
10
e
d
(d ) = 0,25
10
e
próbka
nr 1
d
(d ) = 0,28
10
e
d
(d ) = 0,28
10
e
d
= 0,47
20
d
= 0,47
20
d
= 0,
20
38
d
= 0,
20
38
d
= 1,55
50
d
= 1,55
50
d
= 1,05
50
d
= 1,05
50
d
= 2,40
60
d
= 2,40
60
d
= 1,56
60
d
= 1,56
60
d
= 3,80
70
d
= 3,80
70
d
= 2,45
70
d
= 2,45
70
d
= 11,00
90
d
= 11,00
90
d
= 6,80
90
d
= 6,80
90
próbka
nr 2