Niwelacja
trygonometryczna

wykłady z przedmiotu
„Geodezja i kartografia”

Dr hab. inż. Andrzej Kobryń

Najważniejsze metody pomiarów
wysokościowych



niwelacja geometryczna



niwelacja trygonometryczna

Ogólna charakterystyka niwelacji
trygonometrycznej

Mankamenty (do niedawna):



niewystarczająca dokładność (na poziomie centymetrów i decymetrów)



wpływ refrakcji pionowej



niedokładny pomiar kątów pionowych

Zalety:



przydatność przy trudnych warunkach pomiaru



duże różnice wysokości mierzonymi punktami



przeszkody terenowe lub trudna dostępność mierzonych punktów

Przesłanki wzrostu znaczenia:



poznanie natury zjawiska refrakcji i ograniczenie jej wpływu na dokładność pomiaru



rozwój techniki komputerowej



postęp w konstrukcji elektronicznego sprzętu pomiarowego



zwiększenie dokładności sprzętu



automatyzacja procesu pomiaru i automatyczna rejestracja wyników



efektywne przetwarzanie wyników



nowe pola zastosowań (pomiary inżynierskie)

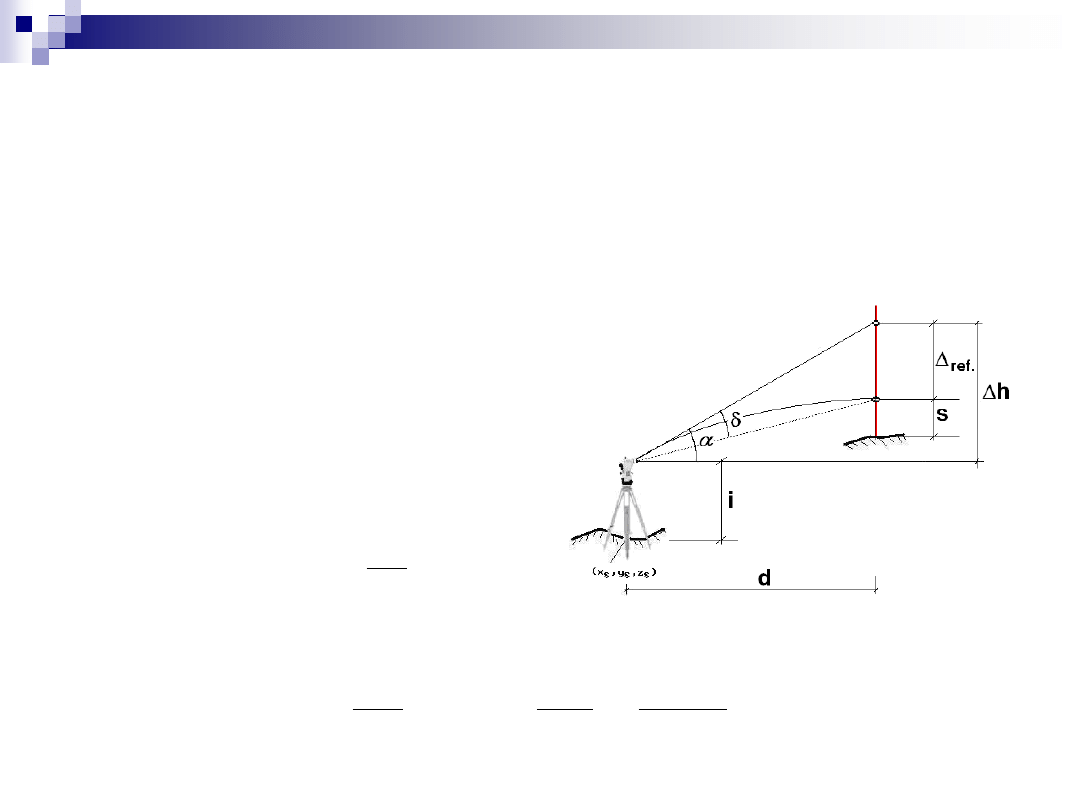
Różnica wysokości pomierzona metodą
niwelacji trygonometrycznej



wzór przybliżony

(przy krótszych odległościach,
mniejszych wysokościach
punktów ponad poziom
odniesienia oraz mniejszych
kątach nachylenia celowej)



wzór ścisły





s

R

d

k

d

i

H

H

h

st

pkt

pkt

st





















2

1

tan

2

.

.



s

d

R

k

d

R

H

i

h

st

pkt

st

















 













2

2

.

.

cos

1

2

1

tan

1

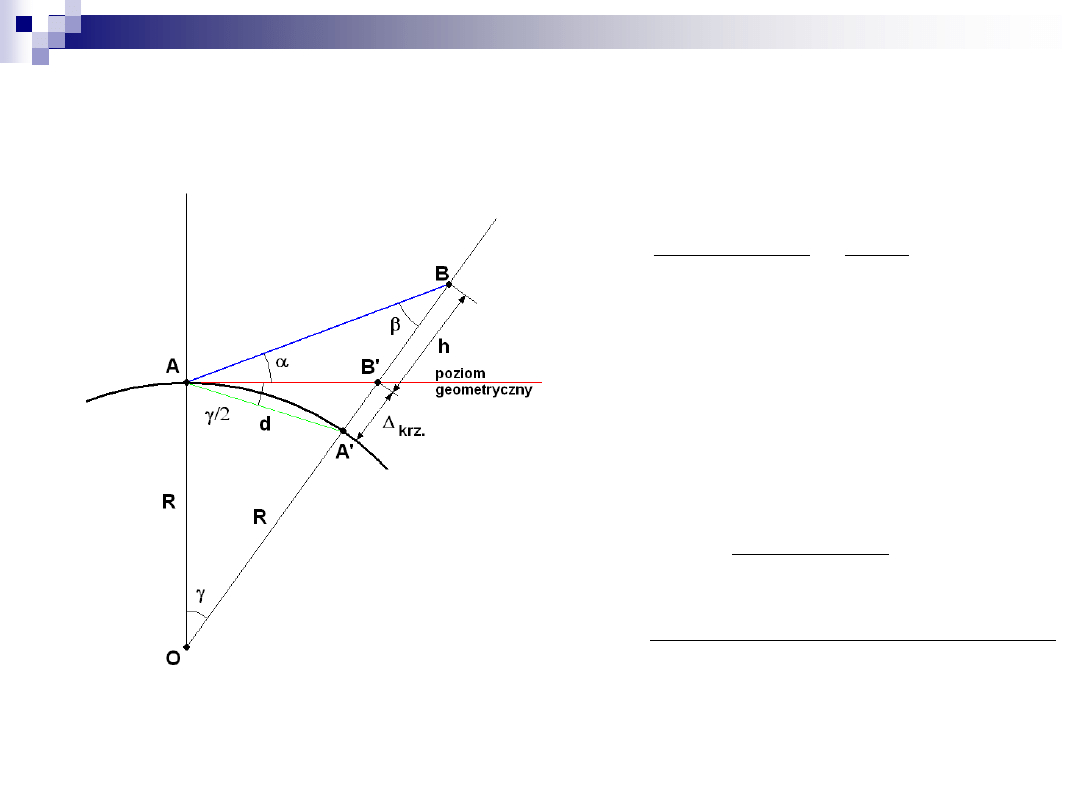
Wpływ krzywizny



z tw.sinusów w trójkącie ABA’



z sumy kątów trójkąta ABO



stąd

















g

100











sin

2

/

sin

'

d

h

B

A



























































cos

cos

)

2

/

sin(

2

/

cos

sin

cos

2

/

sin

'

d

d

h

B

A

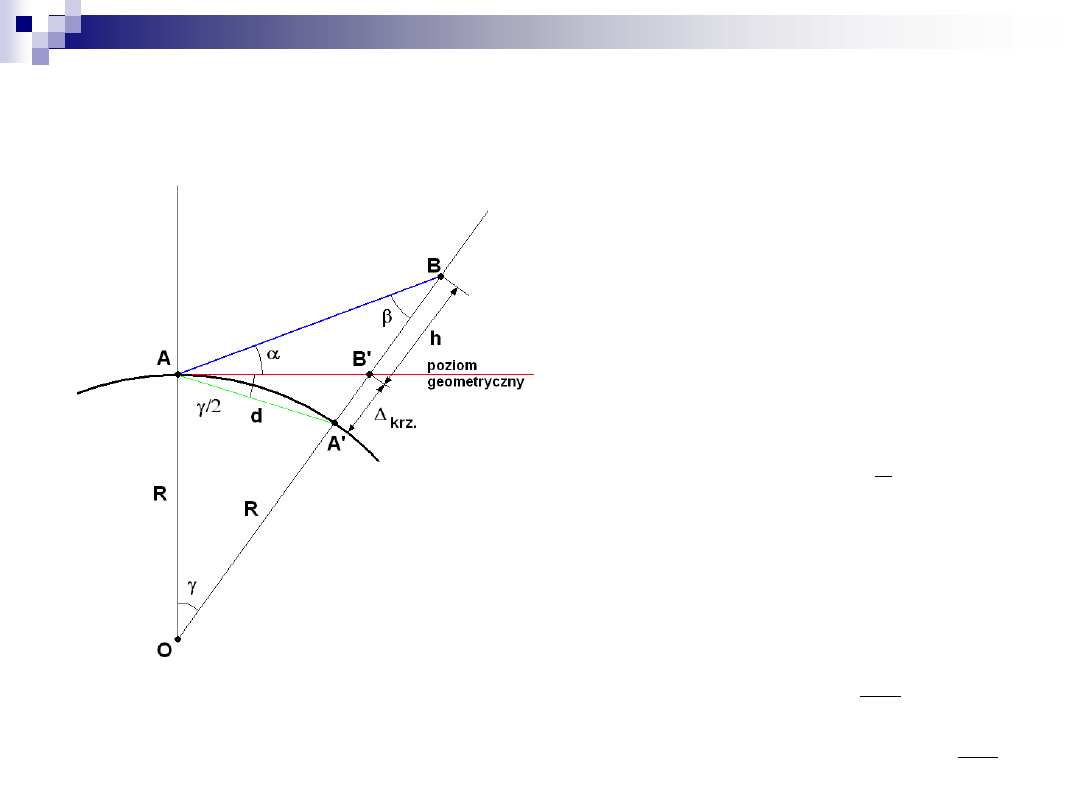
Wpływ krzywizny (c.d.)



ponieważ kąt



jest bardzo

mały w stosunku do kąta



,

więc:



uwzględniając powyższe,
otrzymamy:



ponieważ można przyjąć:



więc ostatecznie (*)



wpływ krzywizny











cos

cos





1

2

/

cos





2

/

2

/

sin







R

d /





R

d

krz

2

2

.





2

tan

'





d

d

h

B

A







R

d

d

h

B

A

2

tan

2

'









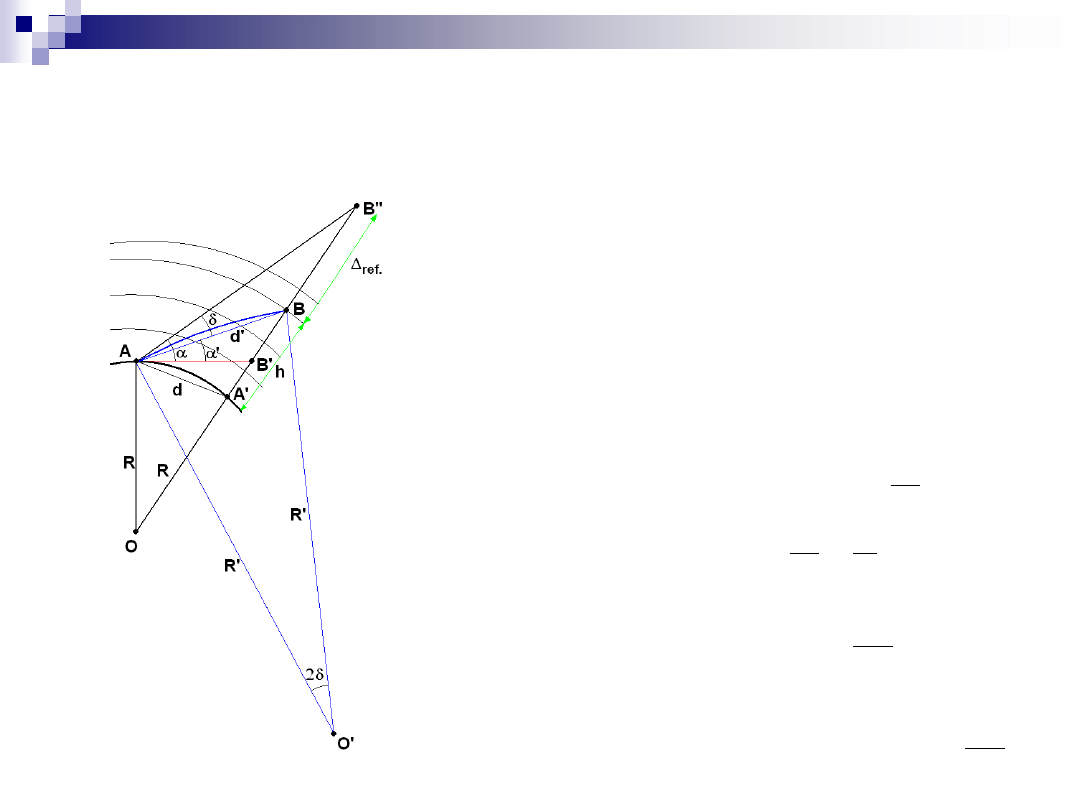
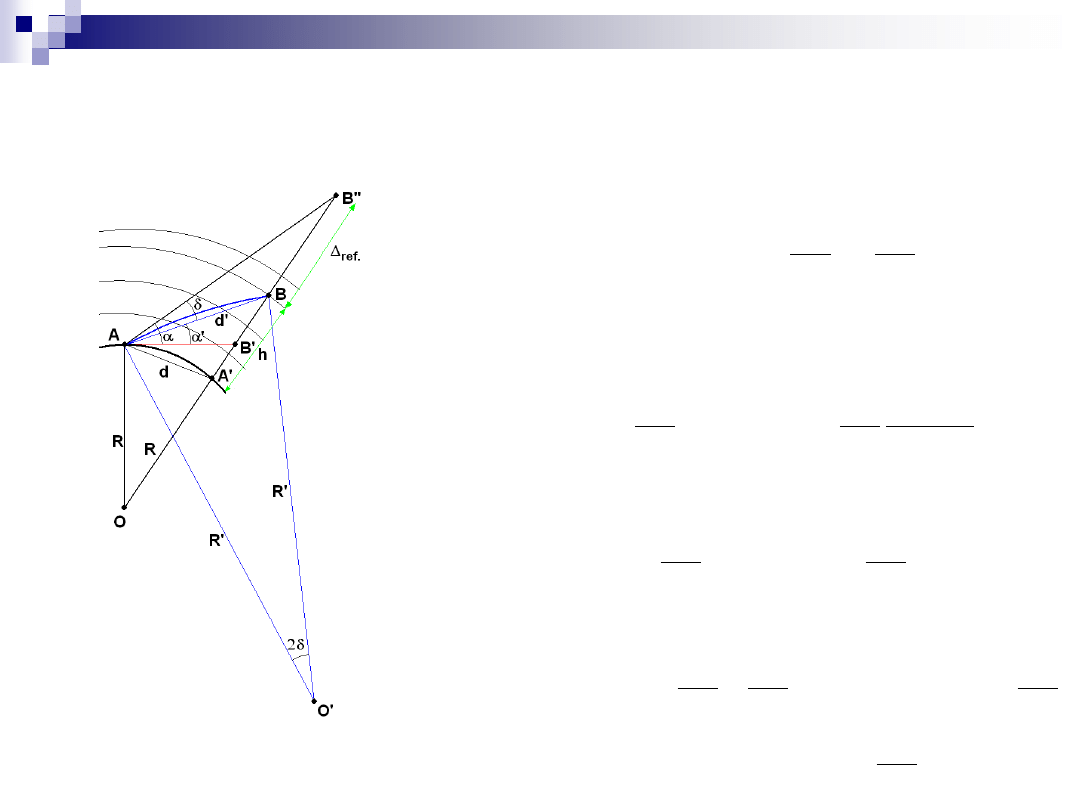
Wpływ refrakcji



w rzeczywistości gęstość atmosfery
zmienia się w sposób ciągły, a
promień świetlny ma kształt krzywej
(tzw. krzywej refrakcyjnej) zbliżonej
do łuku kołowego, skierowanego
wypukłością ku górze



współczynnik refrakcji:



kąt refrakcji:



z rysunku wynika:



ponieważ:



więc:



właściwy kąt pionowy:

'

/ R

R

k



'











'

'

2

R

d





R

k

R



'

1

R

d

k

2





R

d

k

2

'









Wpływ refrakcji (c.d.)



wzór na przewyższenie (*) z
uwzględnieniem powyższego:



po rozwinięciu funkcji tangens w szereg
Taylora



przy założeniu małej wartości kąta





stąd ostatecznie:



wpływ refrakcji

...

cos

1

2

tan

2

tan

2

















 







R

d

k

R

d

k

R

d

k

R

d

k

2

tan

2

tan















 





R

d

k

ref

2

2

.







R

d

R

d

k

d

h

B

A

2

2

tan

2

'













 











R

d

k

d

R

d

R

d

k

d

h

B

A

2

1

tan

2

2

tan

2

2

2

'



















Charakterystyka refrakcji pionowej



zależność refrakcji od nieraz bardzo zmiennych parametrów
atmosferycznych



trudna uchwytność

(większe długości celowych, urozmaicona rzeźba terenu, zmienne

zacienienie wzdłuż przebiegu celowej)



zmienność wartości współczynnika refrakcji

(specyfika obiektu, zmienność war. atmosferycznych)



przykładowo (sąsiedztwo zapory wodnej) dla temperatur od 0 do
22

o

C, odległości od 151 do 280 m)



współczynnik refrakcji od -1.08 do +0.69



skrócenie długości celowych

(warunki typowe, tj. K=0.13 i celowe do 380 m)



błąd z tytułu pominięcia refrakcji i krzywizny Ziemi nie większy

niż 1 cm

Charakterystyka refrakcji pionowej (c.d.)



dopuszczalność pominięcia wpływu refrakcji pionowej i
kulistości Ziemi



maksymalne długości celowych (dla różnych wartości
współczynnika refrakcji, kątów pionowych i odległości)

m



h

0.3 mm

1 mm

3 mm

5 mm

k



=0

g



=30

g



=0

g



=30

g



=0

g



=30

g

=0

g

=30

g

0.5

87.4

83.1

159.7

151.8

276.5

262.5

357.0

339.5

0.0

61.8

55.1

112.9

100.6

195.5

174.2

252.4

224.9

-0.5

50.4

44.1

92.2

80.5

159.6

139.4

206.1

180.0

-1.0

43.7

37.8

79.8

56.9

138.2

119.6

178.5

154.4



sposoby wyznaczania współczynnika refrakcji



pomiar parametrów atmosferycznych



synchroniczne pomiary dwustronne



pomiar znanej różnicy wysokości

Wyznaczanie współczynnika refrakcji
na podstawie parametrów
atmosferycznych



tzw. całkowity współczynnik refrakcji (wzór
Brocksa)

n -

ilość równych odcinków, na jakie

zostaje podzielona cała celowa

i - numer odcinka liczony od punktu
obserwacyjnego

-

tzw. cząstkowe współczynniki refrakcji

określone na podstawie pomiaru

parametrów atmosferycznych (ciśnienie,
temperatura, pionowy gradient
temperatury)

i



i

n

i

i

i

n

n

K













1

2

)

1

2

2

(

1

Współczynnik refrakcji na podstawie
parametrów atmosferycznych



wzory na cząstkowe współczynniki refrakcji



Izotow-Pellinen



Jordan



Brocks



Angus-Leppan



efekty realizacji poszczególnych wzorów



warunki: T=20

o

C=293.2

o

K=68

o

F

, P=760 mm Hg =1013.25 mbar

dT/dh=-0.1

o

C/m



Izotow-Pellinen:

-0.389



Jordan:

-0.391



Brocks:

-0.390



Angus-Leppan:

-0.387





cos

d

d

0342

.

0

8

.

668

2

















h

T

T

P

)

d

d

39

.

29

1

(

)

1

(

1

760

2325

.

0

2

h

T

T

P





















 



h

T

T

P

d

d

2925

.

0

1

19

.

17

2

























h

T

T

P

R

d

d

0187

.

0

)

460

(

141

2



Współczynnik refrakcji na podstawie
parametrów atmosferycznych (c.d.)

Uwagi ogólne



profil terenu a całkowity współczynnik refrakcji



dominujący wpływ wartości współczynników cząstkowych z odcinków
położonych najbliżej stanowiska



praktyczne aspekty określania współczynnika refrakcji:



niemożliwe ścisłe wyznaczenie cząstkowych współczynników refrakcji
wzdłuż celowej



wykorzystanie parametrów atmosferycznych pomierzonych na stanowisku
pomiarowym



praktyczne aspekty określania gradientu temperatury:



niemożliwość pomiaru bezpośredniego



wykorzystanie różnicy temperatur pomierzonych na odpowiednich
wysokościach względem podłoża



dobór odpowiedniej funkcji do obliczenia temperatury jako funkcji
odległości od podłoża gruntowego)

Wyznaczanie współczynnika refrakcji
na podstawie synchronicznych
obserwacji dwustronnych



nie zawsze możliwe wykonanie
pomiaru (

gdy tylko jeden z końców

określonej celowej można brać

pod uwagę jako stanowisko
pomiarowe

)



wysokie koszty odpowiedniego

oprzyrządowania (

praktycznie

niemożliwe uniknięcie czasowego

przesunięcia między pomiarami
dwustronnymi

)



tzw. pomiary quasi-synchroniczne

(niecałkowita eliminacja wpływ
refrakcji)



większy wpływ refrakcji w

porównaniu z synchronicznym
pomiarem dwustronnym

(recepta to skrócenie długości
celowych)

Pomiar synchroniczny



współczynnik refrakcji

































)

(

180

1

B

A

d

R

k



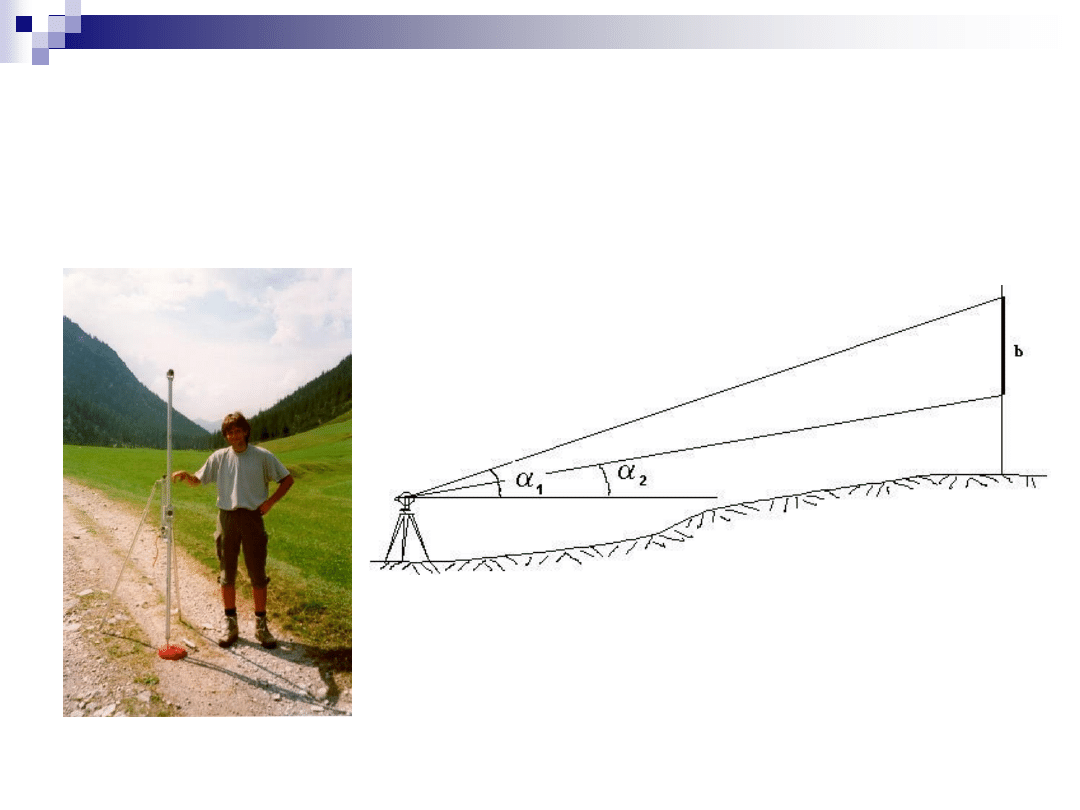
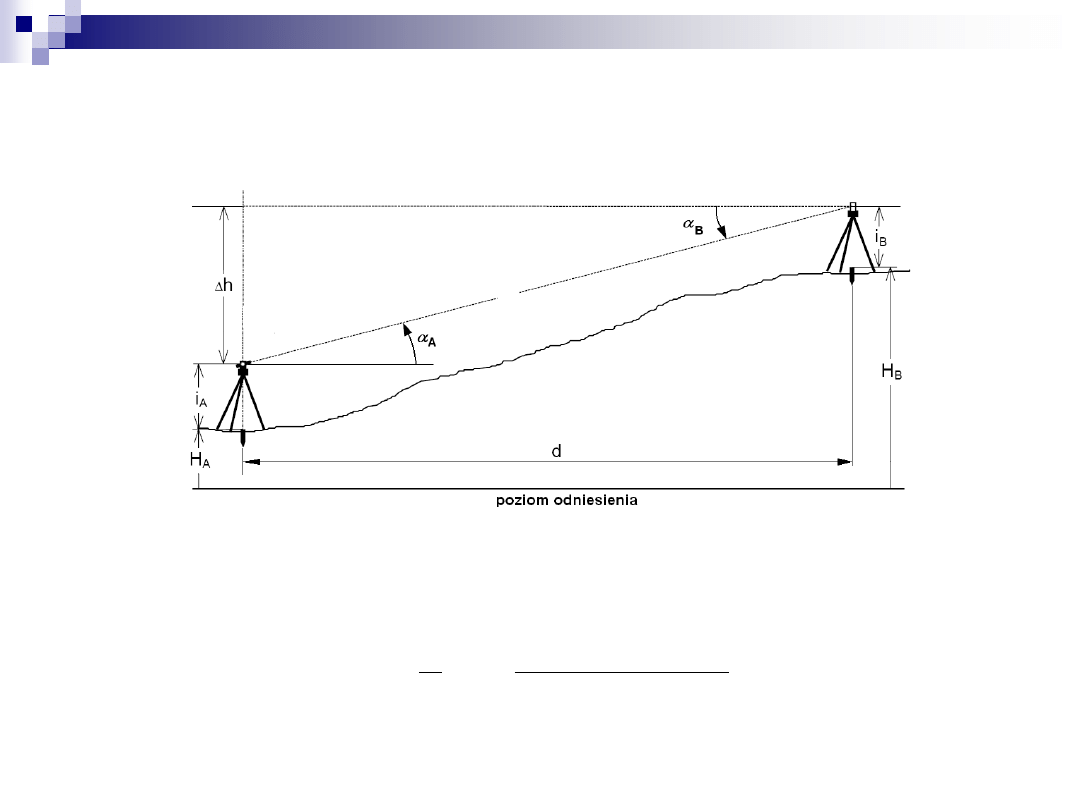
Wyznaczanie współczynnika
refrakcji na podstawie znanej
różnicy wysokości

Wyznaczanie współczynnika refrakcji
na podstawie znanej różnicy
wysokości



przydatność w pomiarach trudno dostępnych punktów



wykorzystanie wartości kąta pionowego skorygowanej o wartość

poprawki z tytułu refrakcji pionowej



poprawka z tytułu refrakcji

lub

przy czym

gdzie:



d

par.

-

odległość mierzonego punktu od stanowiska (określona

paralaktycznie na podstawie kątów



1

i



2

pomierzonych do końców

bazy pionowej b)



d -

odległość j.w. pomierzona bezpośrednio lub pośrednio

























)

cos

(cos

)

(

cos

cos

2

4

1

4

2

2

4

1

2

1







p

p

d

d

d

b













)

cos

(cos

)

(

cos

cos

2

4

1

4

2

2

2

1

4

2







p

p

d

d

d

b

)

sin(

cos

cos

2

1

2

1













b

d

p

Sprzęt pomiarowy



tachimetry elektroniczne



automatyzacja pomiaru



koncentracja wszystkich funkcji związanych z pomiarem i rejestracją
danych



kontrola wyników i lokalizowanie błędów



zbędność redukcji jak dla nasadek dalmierczych



uproszczona konstrukcja znaków pomiarowych

(w porównaniu z systemami dwuosiowymi)



sprzęt pomiarowy najwyższej klasy

(wysoka dokładność pomiaru kątów pionowych)



dokładność wybranych teodolitów, dalmierzy i tachimetrów elektronicznych

Sprzęt

Błąd kierunku/ kąta pionowego

Błąd odległości

Leica T2002

1.5

cc

/0.5”

-

Leica T3000

1.5

cc

/0.5”

Leica DI 2002

-

1 mm + 1ppm

Leica DI 3000S

-

3 mm + 1ppm

Leica DI 1600

-

3 mm + 2ppm

Leica TC 2002

1.5

cc

/0.5”

1 mm + 1ppm

Zeiss Elta 2

2

cc

/0.6”

2 mm + 2 ppm

Sprzęt pomiarowy (c.d.)



specjalne znaki pomiarowe



kilka tarcz pionowo jedna nad drugą

Aspekty praktyczne



doskonalenie konstrukcji tachimetrów



odpowiednie kształtowanie łat i znaków pomiarowych



5 znaczków i ta sama liczba pryzmatów na łacie pomiarowej



4 znaczki i pryzmat umieszczone na pionowej bazie



3 znaczki na pionowej bazie połączonej z przyrządem

Aspekty praktyczne (c.d.)



wnioski z pomiarów doświadczalnych



niemożliwe osiągnięcie dokładności precyzyjnej



niwelacji geometrycznej



(ograniczona dokładność celowania - powyżej 0.9

cc

)



niekontrolowane zmiany stałych dodawania dalmierza



porównanie dokładności niwelacji trygonometrycznej i
precyzyjnej niwelacji geometrycznej

Odcinek

Długość [km]

Różnica wysokości

[m]

Tachimetr

m

geom.

[mm]

m

tryg.

[mm]

I

4.3

720

TC 2000

1.5

2.5

II

21.9

230

TC 2000

0.5

1.4

III

6.2

130

TC 2000

0.5

3.0

IV

6.2

130

TC 1600

0.5

2.8

V

5.1

580

TC 2000

2.0

2.1

Aspekty praktyczne (c.d.)



możliwości zwiększenia dokładności



użycie automatycznych tachimetrów



motoryczne sterowanie



automatyczne celowanie do tarcz i pomiar



zwiększenie dokładności określenia współczynnika refrakcji



dyspersometr (użycie przy celowych do 250 m)



dwubarwne źródło światła (podczerwień i błękit, długości fali 864 nm
i 432 nm)



specjalny system detekcyjny



zintegrowana z lunetą optyka z włókien szklanych



podstawa wyznaczenia całkowitego współczynnika refrakcji to kąt

dyspersji (różnica kątów refrakcji dla fal o różnych długościach)



całkowity współczynnik refrakcji z błędem poniżej 0.1

(w warunkach stabilnej refrakcji)



wymuszone ustawienie wysokościowe

(gwarancja stałej wysokości osi obrotu)

Możliwe obszary zastosowań
niwelacji trygonometrycznej

Możliwe obszary zastosowań
niwelacji trygonometrycznej



badania przemieszczeń i odkształceń oraz pomiary
inwentaryzacyjne i kontrolne trudno dostępnych budowli i obiektów
inżynierskich (

np. pokazanych na poprzednim slajdzie

)



badania przemieszczeń i odkształceń na terenach osuwisk



zakładanie osnów geodezyjnych na terenach górzystych

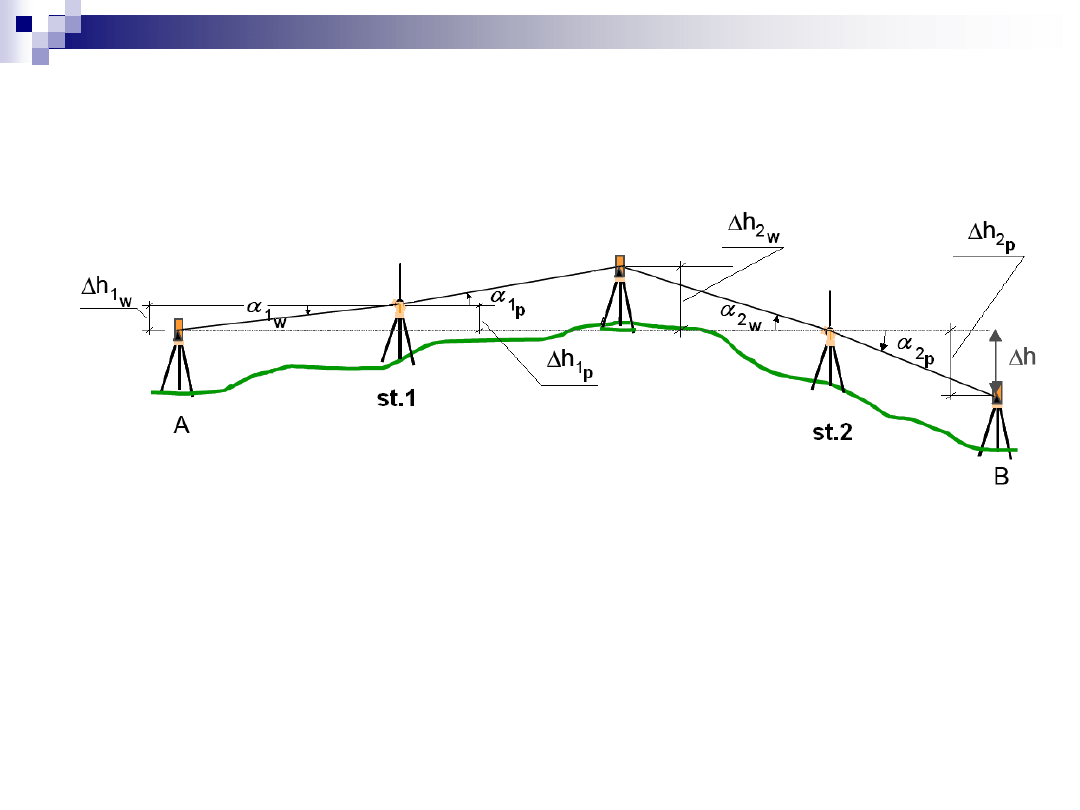
Ciąg niwelacji trygonometrycznej



różnica wysokości między punktami A i B

p

n

w

n

p

w

p

w

AB

h





























...

2

2

1

1

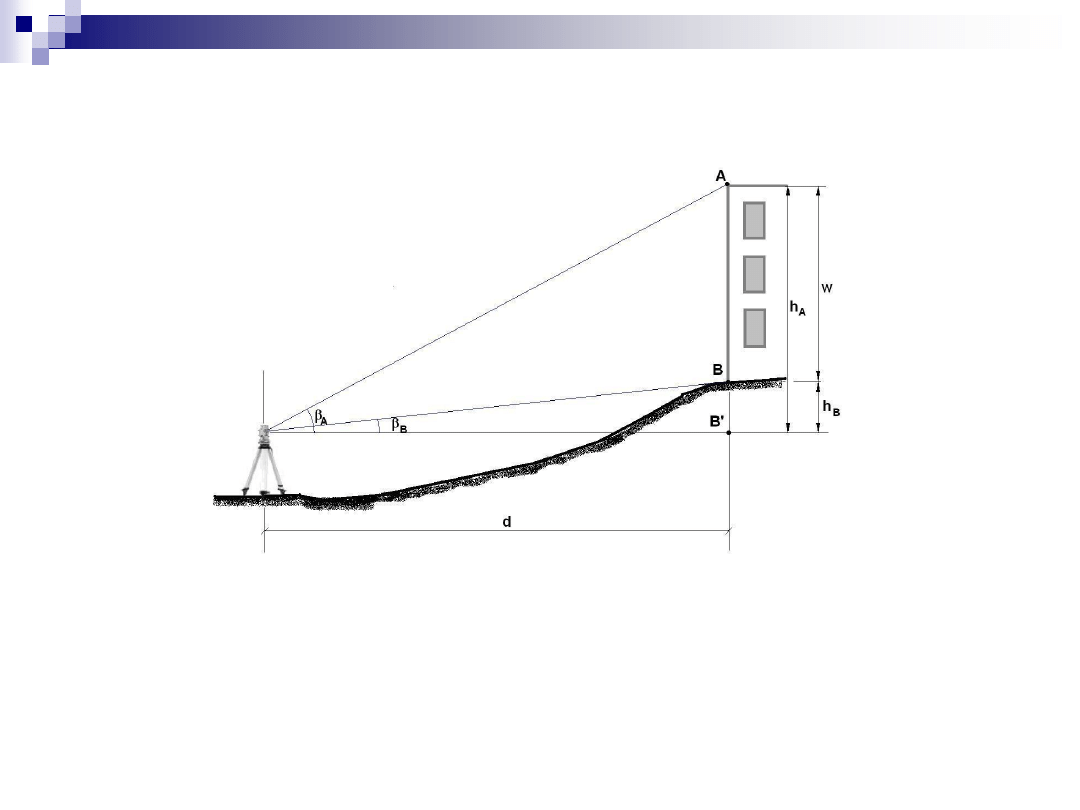
Pomiar punktu niedostępnego (I)



obiekt jest dostępny do pomiaru odległości



wysokość obiektu to różnica przewyższeń





B

A

B

A

B

A

d

d

d

h

h

w









tan

tan

tan

tan















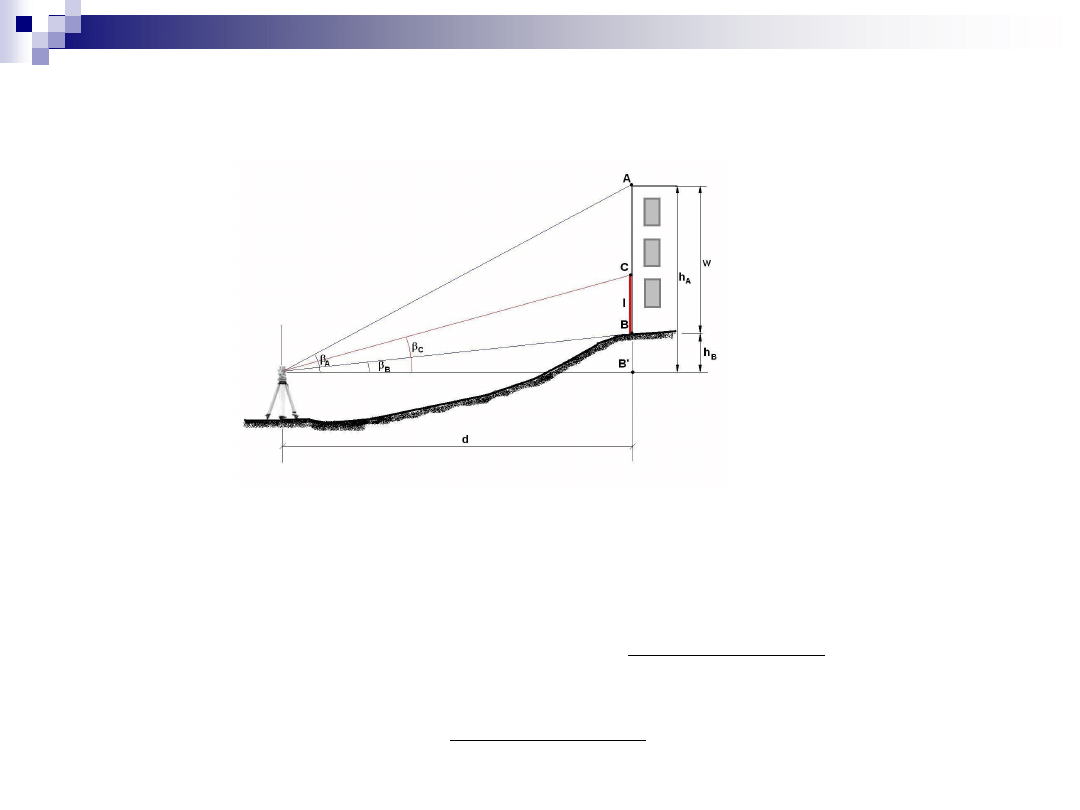
Pomiar punktu niedostępnego (II)



obiekt jest dostępny, lecz nie ma warunków do zmierzenia
odległości d



odległość obiektu od stanowiska



wysokość obiektu





B

C

d

l





tan

tan





B

C

l

d





tan

tan





B

C

B

A

l

w









tan

tan

tan

tan







Pomiar punktu niedostępnego (III)



obiekt jest niedostępny



na stanowisku I



na stanowisku II



stąd:



ostatecznie



oraz wysokość obiektu:





B

A

d

w

'

tan

'

tan















B

A

a

d

w

'

'

tan

'

'

tan













 





B

A

B

A

a

d

d

'

'

tan

'

'

tan

'

tan

'

tan



















 



B

A

B

A

B

A

a

d

'

tan

'

tan

'

'

tan

'

'

tan

'

'

tan

'

'

tan































 



B

A

B

A

B

A

B

A

a

w

'

tan

'

tan

'

'

tan

'

'

tan

'

'

tan

'

'

tan

'

tan

'

tan





























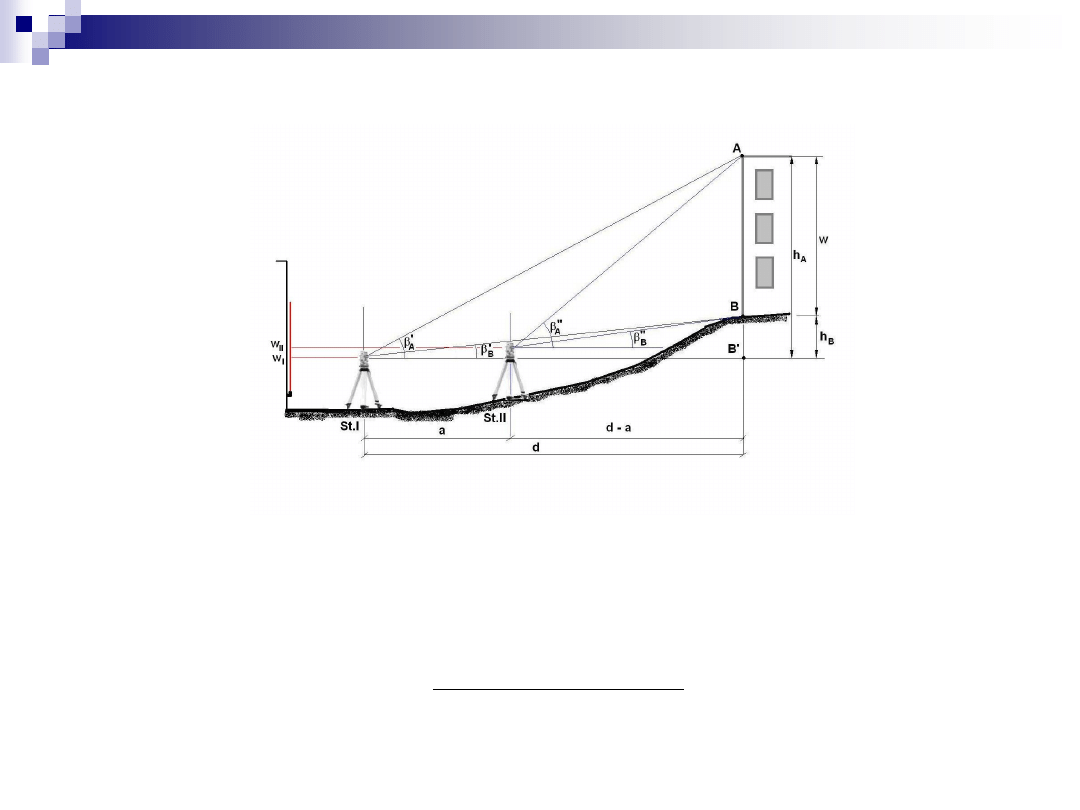
Pomiar punktu niedostępnego (IV)



celem jest wyznaczenie bezwzględnych wysokości punktów



z pomiaru na dwóch różnych wysokościach horyzontu



stąd odległość d



w rezultacie

– możliwość dwukrotnego wyznaczenia wysokości

A

I

rp

A

d

w

H

H

'

tan

.













A

II

rp

A

a

d

w

H

H

'

'

tan

.











A

A

A

I

II

a

w

w

d

'

'

tan

'

tan

'

'

tan















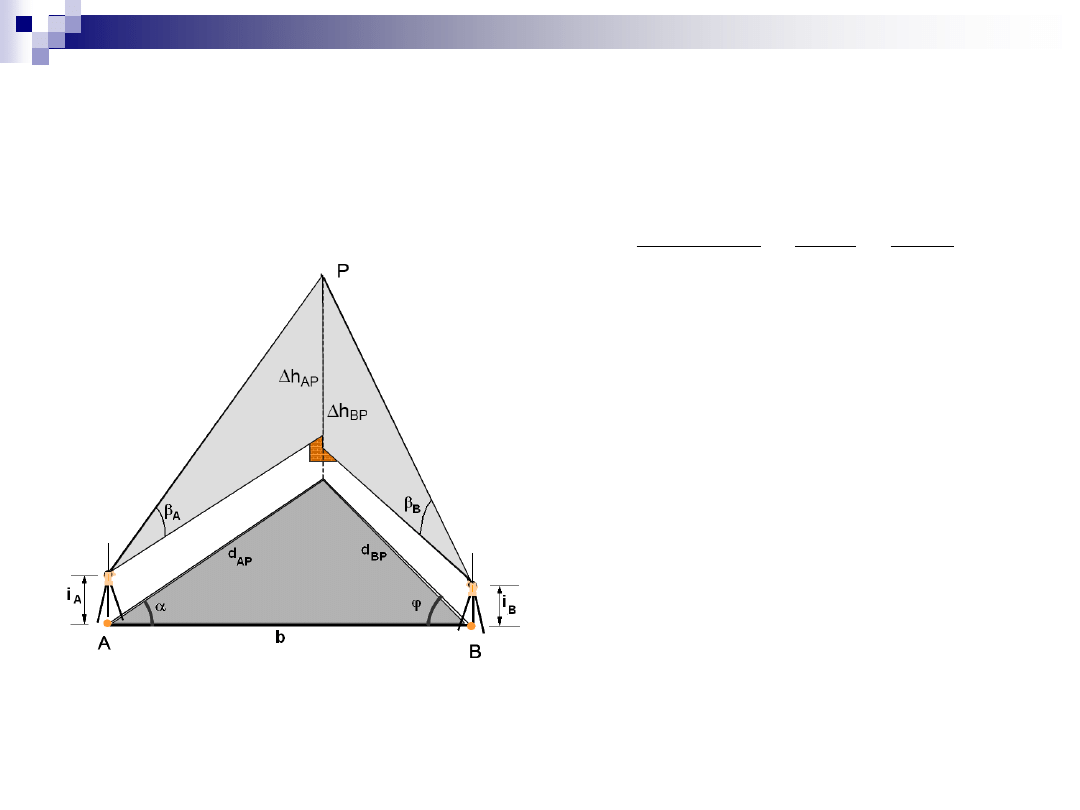
Pomiar punktu niedostępnego (V)



na podstawie tw. Sinusów



wysokość punktu P

lub













sin

sin

sin

BP

AP

d

d

b







A

AP

A

A

P

d

i

H

H



tan







B

BP

B

B

P

d

i

H

H



tan







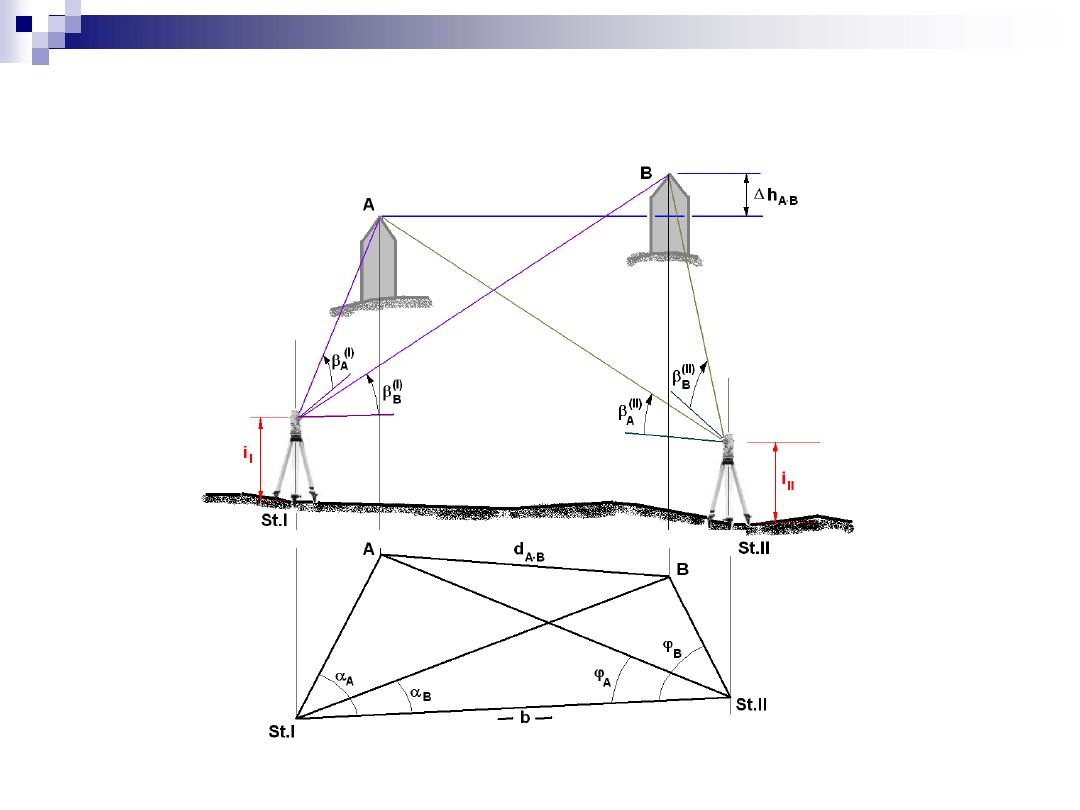
Pomiar punktów niedostępnych

Pomiar punktów nieodstępnych (c.d.)



długość bazy b z pomiaru lub ze współrzędnych



odległości punktów A i B (z tw. sinusów) od stanowisk I i II

oraz:



wysokości punktów nieodstępnych

2

2

II

I

II

I

y

x

b

















A

A

A

b

A

I













sin

sin





B

B

B

b

B

I













sin

sin





A

A

A

b

A

II













sin

sin





B

B

B

b

B

II













sin

sin

A

I

I

St

A

A

I

i

H

H

'

tan

'

.











B

I

I

St

B

B

I

i

H

H

'

tan

'

.











A

II

II

St

A

A

II

i

H

H

'

'

tan

'

'

.











B

II

II

St

B

B

II

i

H

H

'

'

tan

'

'

.











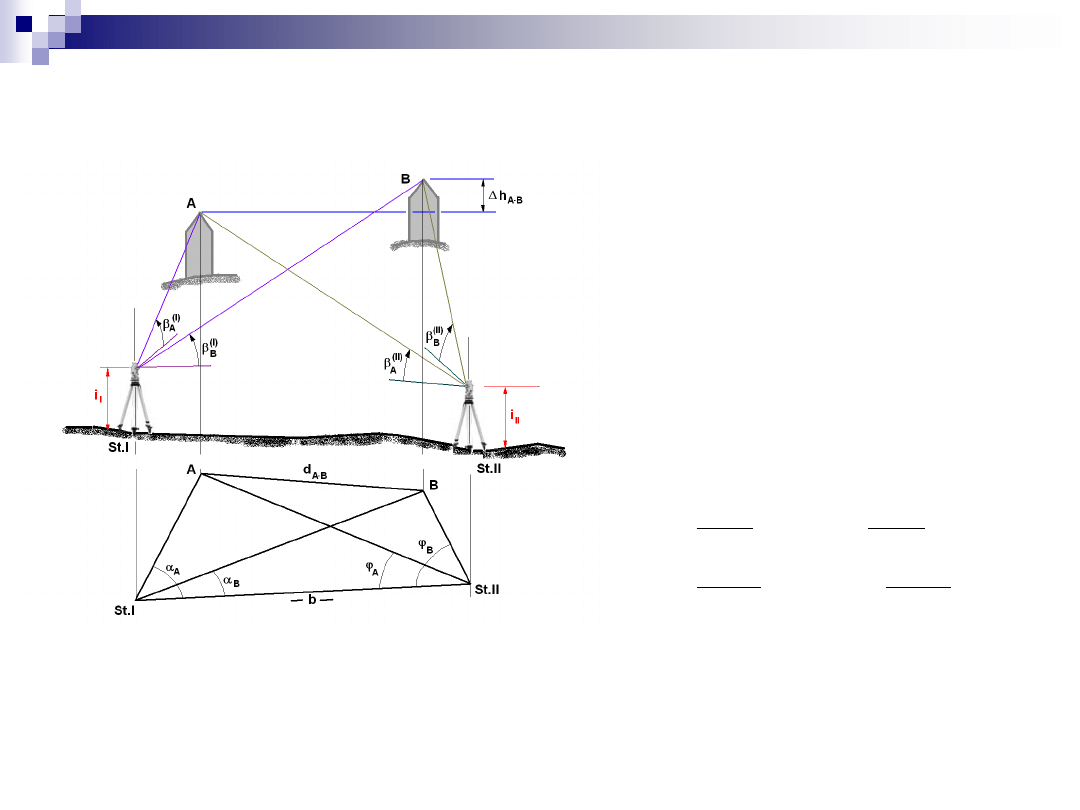
Pomiar punktów nieodstępnych (c.d.)



możliwość dwukrotnego
wyznaczenia różnicy
wysokości punktów
niedostępnych (kontrola)

A

B

B

A

A

I

B

I

h

'

tan

'

tan

'

















A

B

B

A

A

II

B

II

h

'

'

tan

'

'

tan

'

'















