Rozdział

2

BŁ

Ę

DY OBLICZE

Ń

KOMPUTEROWYCH

2.1.

Podstawowe

ź

ródła bł

ę

dów w obliczeniach

komputerowych

Większość problemów obliczeniowych występujących w praktyce wymaga

zastosowania przybliżonych metod ich rozwiązania. Stosowanie analitycznych
metod dokładnych jest często trudne, jeśli nie wręcz niemożliwe w praktyce.
Przykładem niech będzie wyznaczanie prawdopodobieństwa zdarzenia

[

[

2

1

, x

x

x

∈

opisanego rozkładem normalnym

N(0,1):

(

)

( ) ( )

1

2

2

2

1

2

1

2

2

1

x

x

dt

e

x

x

x

P

p

x

x

t

Φ

Φ

π

−

=

=

<

≤

=

∫

−

.

Ponieważ funkcja

Φ

należy do tzw. funkcji specjalnych

*)

, której nie można

przedstawić w postaci skończonej przez funkcje elementarne, obliczenie jej można
przeprowadzić tylko w sposób przybliżony.
Obliczenie wartości prawdopodobieństwa można przeprowadzić przez rozwinięcie
funkcji

Φ

w szereg Maclaurin’a bądź też obliczenie całki. W przypadku pierwszym

obliczanie (rozwinięcie nieskończone) z konieczności należy przerwać po
wyznaczeniu skończonej liczby wyrazów szeregu, w przypadku drugim całka
zastąpiona zostanie sumą skończoną. Zarówno w pierwszym jak i drugim
przypadku otrzymana wartość będzie przybliżona.

Jednym z ważniejszych problemów w metodach numerycznych jest

zagadnienie badania błędów obliczeń. Szacowanie wielkości błędów jest
nieodłącznym ich elementem. Podobnie, bardzo ważne jest określanie jak mocno
błędy danych wejściowych przenoszą się na dokładność rozwiązania. Analiza
przenoszenia błędu, dokładności i zbieżności stosowanych metod czy wpływ
przybliżeń (aproksymacji) stosowanych modeli matematycznych ma zasadnicze
znaczenie dla wiarygodności otrzymywanych rozwiązań.

Rozróżnić można podstawowe typy błędów:

– błędy opisu problemu,
– błędy zaokrągleń,
– błędy danych wejściowych,
– błędy obcięcia

*)

Dystrybuanta rozkładu normalnego (całka Laplace’a) - patrz zadanie 1.7.

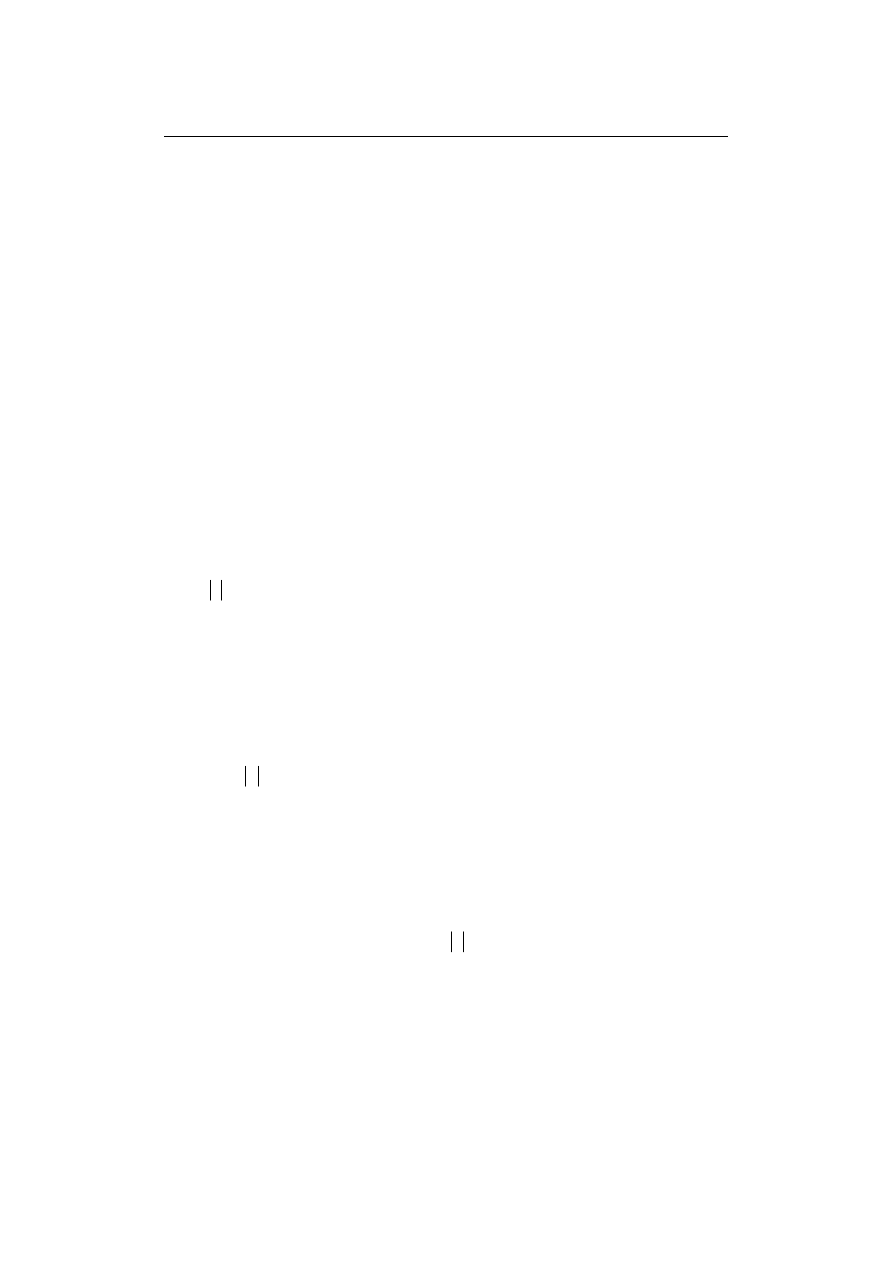
28

Metody numeryczne

Błędy opisu problemu powstają gdy przyjęty do obliczeń model jest tylko
przybliżeniem zjawiska rzeczywistego lub też gdy sformułowane zadanie jest zbyt
skomplikowane do rozwiązania. W pierwszym przypadku przybliżenie wynikać
może z niepełnej wiedzy na temat badanego zjawiska. W drugim przypadku
skomplikowane zadanie zastępowane jest zadaniem odpowiednio uproszczonym
(odpowiednia aproksymacja zadania) dla którego istnieją realne możliwości
rozwiązania.

Błędy zaokrągleń wynikają z niedokładnej reprezentacji liczb rzeczywistych w
maszynach cyfrowych. Biorąc pod uwagę fakt, że w każdym komputerze, bez
względu na sposób reprezentowania liczb rzeczywistych, długość (liczba cyfr w
liczbie rzeczywistej) jest skończona, skończona jest również dokładność zapisu
liczby. Każda liczba, zarówno dana wejściowa jak i wynikowa, jeśli tylko jest
dłuższa od dopuszczalnej zostanie zaokrąglona do wymaganej długości.
Błędy zaokrągleń mogą mieć ogromny wpływ na wynik końcowy. W wielu
przypadkach, w celu otrzymania rozwiązania należy wykonać tysiące czy nawet
miliony operacji arytmetycznych z których każda jest wykonywana na liczbach
przybliżonych a ich wynik podlega kolejnemu zaokrągleniu.

Niech liczby zapisywane będą z dokładnością do k cyfr. Każdą liczbę o

dłuższym formacie r jeśli to możliwe należy zaokrąglić do formatu k. Niech nadto
liczba posiada l cyfr w części całkowitej. Liczba cyfr po przecinku określona jest
zatem przez t = k – l (1.1).

9

0

9

0

,

,

1

2

1

1

1

≤

≤

≤

≤

=

−

+

−

i

i

r

l

r

t

k

t

t

l

l

l

u

c

u

u

u

u

u

c

c

c

x

4

4

4

4

4

4

3

4

4

4

4

4

4

2

1

K

4

4

4

4

3

4

4

4

4

2

1

43

42

1

K

43

42

1

K

(2.1))

Dla zaokrąglenia liczby do długości k mamy:



















≥

+

<

=

+

−

−

+

−

5

10

,

5

,

~

1

2

1

1

1

1

2

1

1

1

t

t

k

t

t

l

l

l

t

k

t

t

l

l

l

u

dla

u

u

u

c

c

c

u

dla

u

u

u

c

c

c

x

4

4

4

4

3

4

4

4

4

2

1

43

42

1

K

43

42

1

K

4

4

4

4

3

4

4

4

4

2

1

43

42

1

K

43

42

1

K

(2.2))

tzn. jeśli cyfra u

t+1

jest mniejsza od 5 wówczas dokonujemy obcięcia po cyfrze u

t

,

w przypadku przeciwnym u

t

zwiększamy o jeden.

Liczbę przybliżoną zgodnie z (2.2) określamy jako:

( )

x

x

sign

x

~

~

=

(2.3))

Zapis liczby (modułu) w postaci (2.1) posiada pewne ograniczenia.

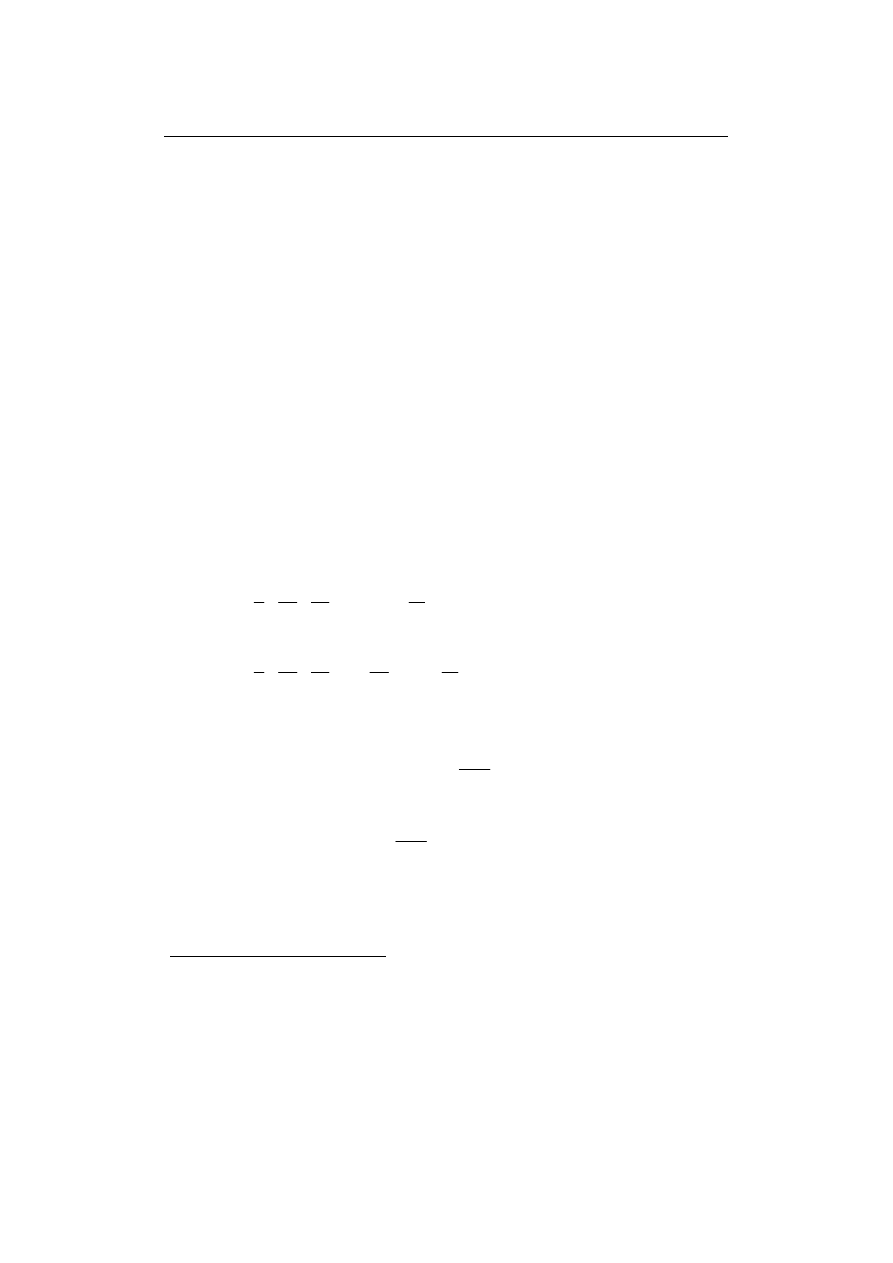
2. Błędy obliczeń komputerowych

29

Warto zauważyć, że jeśli liczba cyfr l w części całkowitej będzie większa od
formatu k, wówczas liczby tej nie można zapisać w tym formacie. Wadę tę można
usunąć stosując inny sposób zapisu liczb rzeczywistych. Zagadnienie to omówiono
w podrozdziale 2.4.

Błędy danych wejściowych.

*)

Z tym typem błędów mamy do czynienia gdy do

obliczeń używamy danych pochodzących z pomiarów czy stosowania wartości
zaokrąglonych stałych matematycznych, ułamków okresowych czy zapisu liczb
niewymiernych: e

≈

2,718,

π

≈

3,1416, 1/3

≈

0,3333 itd.

Poza podanymi wyżej przypadkami należy uwzględnić dane wejściowe dokładne,
ale reprezentowane w komputerze przez liczby maszynowe (zaokrąglane do
ograniczonej i danej w danej reprezentacji liczby miejsc znaczących). Ponadto,
zaokrąglone wyniki w poszczególnych iteracjach stanowiące dane wejściowe do
iteracji następnych również można traktować, jako błędy danych wejściowych
(następnej iteracji).

Błędy obcięcia nazywane również błędami metody wynikają głównie z zastąpienia
działań na wartościach nieskończenie małych przybliżonymi działaniami
skończonymi czy też działań nieskończonych ich przybliżeniem skończonym.
Powstawanie tego rodzaju błędów ma miejsce głównie w przypadkach:
1. Obliczanie wartości funkcji elementarnych z rozwinięcia funkcji w szereg z

konieczności z dokładnością do skończonej liczby wyrazów szeregu.

**)

Należy wyznaczyć wartość e

x

dla danego x. Z rozwinięcia w szereg jest:

∑

∞

=

+

=

+

+

+

+

=

1

3

2

!

1

!

3

!

2

!

1

1

i

i

x

i

x

x

x

x

e

L

,

z konieczności mamy sumę obciętą do n-tego wyrazu szeregu:

∑

=

+

=

+

+

+

+

+

≈

n

i

i

n

x

i

x

n

x

x

x

x

e

1

3

2

!

1

!

!

3

!

2

!

1

1

L

2. Zastąpienie wartości całki sumą skończoną.

Należy obliczyć

0

lim

,

)

(

lim

)

(

0

→













−

=

+

=

∞

→

=

∞

→

∑

∫

n

a

b

h

ih

a

f

h

dx

x

f

n

n

i

n

b

a

Zastępując sumę nieskończoną wartością skończoną n (skończony krok h) obliczamy:

0

,

)

(

)

(

1

0

>

−

=

+

≈

∑

∫

−

=

n

a

b

h

ih

a

f

h

dx

x

f

n

i

b

a

3.

Rozwiązywanie zagadnień metodami iteracyjnymi (kolejne przybliżenia)
dającymi rozwiązanie dokładne tylko, gdy liczba iteracji dąży do nieskończo-
ności.

*)

Często można spotkać określenie błędy początkowe.

**)

Pamiętać należy, że komputery wykonują jedynie elementarne działania arytmetyczne!

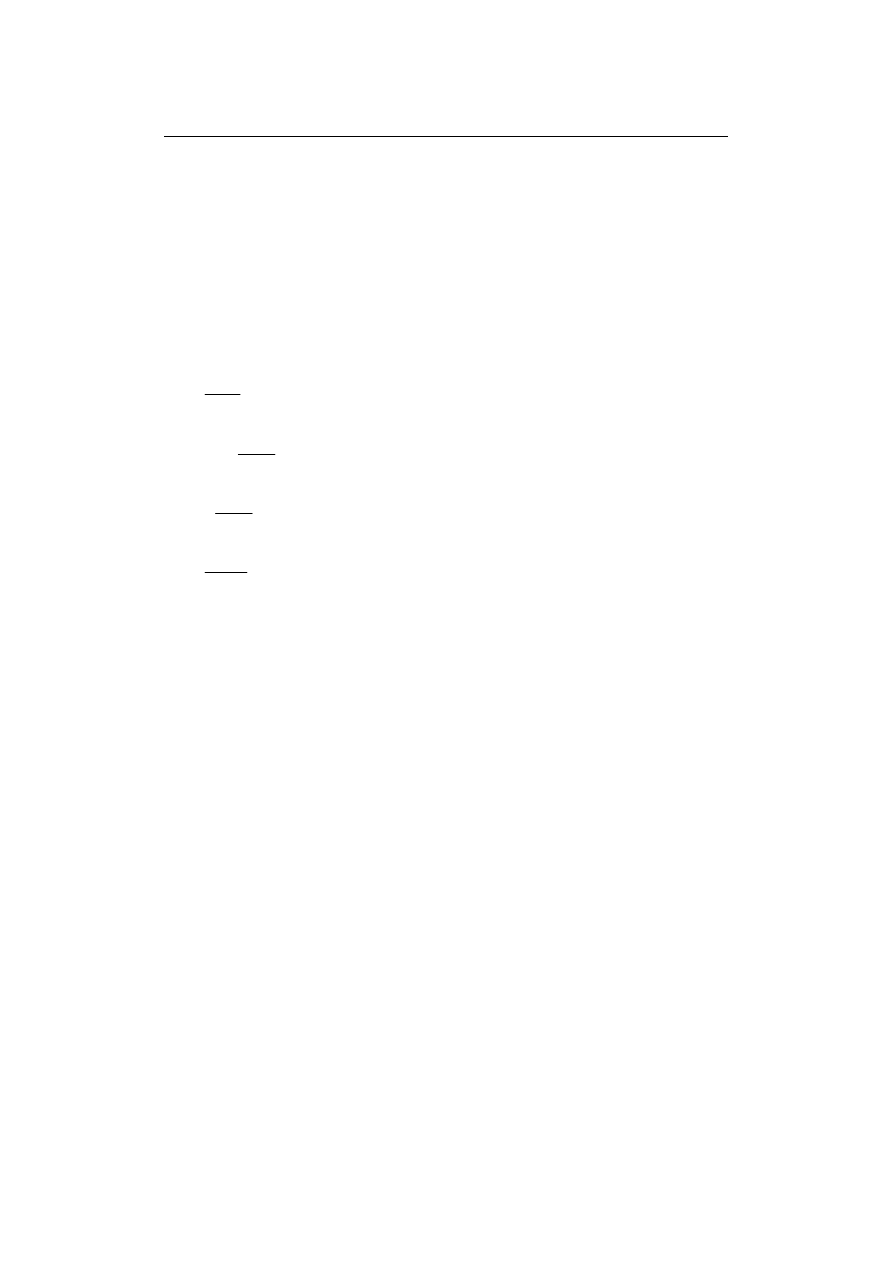
30

Metody numeryczne

Poszukiwane jest x

r

będące rozwiązaniem równania f(x)=0. Dla odpowiedniej funkcji

iteracyjnej jest (patrz podrozdział. 2.1):

( )

( )

(

)

K

K

,

,

,

1

1

2

0

1

0

−

=

=

→

=

→

n

n

x

F

x

x

F

x

x

F

x

x

.

Jeśli metoda jest zbieżna to

r

r

n

n

x

x

F

x

F

=

=

∞

→

)

(

)

(

lim

.

Obcinając obliczenia do skończonej liczby iteracji n mamy przybliżenie:

)

(

1

−

=

≈

n

n

r

x

F

x

x

.

4

Rozwiązywanie zagadnień opisanych równaniami różniczkowymi zastępując
pochodne przybliżonymi ilorazami różnicowymi.

Rozwiązywane jest równanie różniczkowe:

(

) ( )

0

0

,

),

(

)

(

y

x

y

x

x

y

f

dx

x

dy

=

=

co stanowi granicę ilorazu różnicowego:

(

) ( )

0

0

0

,

),

(

)

(

lim

y

x

y

x

x

y

f

x

x

y

x

=

=

→

∆

∆

∆

Dla skończonej wartości przyrostu jest:

(

)

(

)

x

x

y

f

x

x

y

x

x

y

f

x

x

y

),

(

)

(

),

(

)

(

∆

∆

∆

∆

≈

⇒

≈

co prowadzi do zależności rekurencyjnej (metoda Euler’a):

(

)

)

(

),

(

)

(

1

1

1

i

i

i

i

i

i

x

y

y

y

x

x

y

f

x

x

y

∆

∆

∆

+

=

⇒

≈

−

−

−

czyli

(

)

.

,

,

)

(

,

1

1

1

1

i

i

i

i

i

i

i

i

i

y

y

y

x

y

f

x

x

y

y

x

x

x

∆

∆

∆

∆

∆

+

=

=

=

+

=

−

−

−

−

Zauważyć należy, że błędy obcięcia (metody) maleją wraz z ze wzrostem

liczby wykonywanych iteracji (błąd asymptotycznie dążą do zera). Jednocześnie
wzrost liczby wykonywanych operacji prowadzi do kumulacji błędów zaokrągleń.
Jak zatem widać, im później dokonamy obcięcia wówczas z jednej strony
poprawiamy dokładność metody, jednocześnie jednak pogorszymy dokładność
wynikającą z zaokrągleń (rys. 2.1).

Rys. 2.1 Interpretacja błędów metody i zaokrągleń w funkcji liczby iteracji

2. Błędy obliczeń komputerowych

31

W praktyce dla danej metody i rozwiązywanego zagadnienia obliczenia należy
zakończyć w momencie osiągnięcia najwyższej możliwej dokładności (i

opt

).

Określenie kryteriów zakończenia obliczeń (i

opt

), doboru długości kroku jak i

doboru samej metody do rozwiązania określonego zadania tak, aby uzyskać
maksymalną dokładność osiągalną jest zagadnieniem bardzo złożonym i zależnym
od wielu czynników. W praktyce, nie jest możliwe podanie ogólnej zasady
postępowania dla osiągnięcia tego celu. Krok czy moment stopowania algorytmu
najczęściej określany jest w trakcie realizacji obliczeń (badanie aktualnie
osiągniętej dokładności)

*)

.

2.2.

Poj

ę

cia bł

ę

dów bezwzgl

ę

dnego i wzgl

ę

dnego

Niech dalej będzie dana liczba dokładna x (2.1) oraz jej wartość przybliżona

x

~ wyznaczona zgodnie z (2.2).

Błędem bezwzględnym nazywamy wartość:

**)

x

x

x

~

−

=

∆

(2.3)

Zauważmy, że w przypadku zaokrąglenia (2.2) wartość błędu bezwzględnego (2.3)
wynosi:













≥

+

−

=

<

=

+

−

+

−

+

−

+

5

0

0

,

0

1

0

0

,

0

5

0

0

,

0

1

1

1

1

1

t

l

r

t

t

t

t

l

r

t

t

u

dla

u

u

x

u

dla

u

u

x

K

3

2

1

K

3

2

1

K

K

3

2

1

K

∆

∆

(2.4)

Z (2.4) wynika maksymalny błąd bezwzględny (dla zapisu t cyfr po przecinku) z
zastosowaniem reprezentacji liczby rzeczywistej (2.1):

t

x

x

x

−

≤

−

=

10

2

1

~

max

max

∆

(2.5)

Błąd bezwzględny określa wielkość przybliżenia, nie daje jednak informacji o
dokładności. Ten sam błąd np.

∆

x=0,004 jest błędem małym przy przybliżaniu

dużej wartości x (np. dla x=10000,0 błąd stanowi 0,00004%.) i dużym dla małego x
(np. dla x=0,01 jest już równy 40%).
Błąd bezwzględny informuje jedynie o wielkości przybliżenia. O dokładności
informacji dostarcza wartość błędu względnego.

*)

Więcej informacji na temat błędów obliczeń komputerowych znajdzie czytelnik w [S10].

**)

Błąd bezwzględny (2.3) zdefiniowany jest jako moduł różnicy. Często można spotkać

definicje jako różnica z uwzględnieniem znaku. Dla szacowania błędów maksymalnych
przydatna jest definicja postaci (2.3).

32

Metody numeryczne

Błąd bezwzględny

∆

x często nazywany jest poprawką, jeśli wraz z wartością (2.3)

wyznaczymy znak różnicy (pominięcie modułu).

Błędem względnym nazywamy:

x

x

x

x

x

x

~

−

=

=

∆

ε

.

(2.6)

Działania na liczbach przybliżonych mogą prowadzić często do rozwiązań
obarczonych dużym błędem, mimo że dane wejściowe zaburzone były w
niewielkim stopniu.

Dla przykładu niech będzie dany układ równań:







=

−

=

−

52

2

1

2

1

397

6

35

331

5

x

x

x

x

Rozwiązaniem jest x

1

= 3317, x

2

= 50.

Niech układ równań zostanie zaburzony:







=

−

=

−

51

2

1

2

1

397

6

35

331

5

x

x

x

x

Rozwiązanie wynosi wówczas x

1

= 2986, x

2

= 45.

Zaburzony został jeden parametr równań o niecałe. 2%. Zaburzenie to przeniosło się na
rozwiązanie i błąd względny x

1

oraz x

2

sięga 10% !

Powyższy przykład wskazuje, jak wielki wpływ na rozwiązanie może mieć
konieczność stosowania przybliżania liczb w procesie obliczeniowym.

*)

2.3.

Liczby i arytmetyka liczb całkowitych

Rozpatrzmy reprezentacje i arytmetykę liczb całkowitych realizowanych w

komputerach.
Niech liczba całkowita zapisywana jest na n bitach:

**)

0

0

1

1

2

2

1

1

0

1

2

1

2

2

2

2

l

l

l

l

l

l

l

l

n

n

n

n

n

n

n

+

+

+

+

=

−

−

−

−

−

−

L

4

4 3

4

4 2

1

L

.

(2.7)

Wartości liczb całkowitych (co do modułu) muszą mieścić się w zakresie:
– najmniejsza liczba całkowita

*)

Problem przenoszenia się błędów danych na wyniki szerzej został przedstawiony w

podrozdziale 2.5 przy omawianiu propagacji błędów i wskaźników uwarunkowania.

**)

Przy dalszym omawianiu pomija się bit znaku. Na n bitach zapisywana jest liczba!

2. Błędy obliczeń komputerowych

33

0

2

0

2

0

2

0

2

0

0

0

0

0

0

1

2

1

=

×

+

×

+

+

×

+

×

=

−

−

L

4

3

42

1

L

n

n

n

,

(2.8)

– największa liczba całkowita

1

2

2

1

2

1

2

1

2

1

1

1

1

1

0

1

2

1

−

=

×

+

×

+

+

×

+

×

=

−

−

n

n

n

n

L

3

2

1

L

.

(2.9)

Utwórzmy zbiór liczb maszynowych

A

c

zawierający wszystkie liczby całkowite

spełniające (2.7) - (2.9). Wszystkie operacje arytmetyczne wykonywane na
liczbach całkowitych muszą w wyniku zawierać się w tym zbiorze.
Zbiór ten jest podzbiorem zbioru liczb całkowitych. Każda liczba z tego zbioru
zapisana jest dokładnie!
Jeśli wykonujemy operacje arytmetyczne na liczbach całkowitych i wynik zawiera
się z zbiorze liczb maszynowych, wówczas operacja została wykonana dokładnie i
zapisana zostanie bez zaokrągleń.
Ogólnie, jeśli wynik działania jest liczbą całkowitą i zawiera się w

A

c

, wówczas

operacja jest operacją dokładną.
Wyjątek stanowią przypadki operacji:

l

n

A

l

l

z

∉

−

>

+

=

1

2

2

1

,

(2.10)

l

n

A

l

l

z

∉

−

>

×

=

1

2

2

1

.

(2.11)

Wynik (nadmiar liczby całkowitej) nie posiada reprezentacji komputerowej. Innym
przypadkiem są operacje dzielenia w których wynik nie jest liczba całkowitą.

*)

2.4.

Reprezentacja liczb rzeczywistych

2.4.1. Zapis stałopozycyjny

Historycznie liczby rzeczywiste zapisywane były w notacji stałopozycyjnej.

W pierwszych maszynach liczących ten system był dominujący. Przyjmijmy dalej,
ze liczba zapisywana jest na n cyfrach. Dokonajmy podziału na dwie części,
całkowitą n

1

i ułamkową n

2

:

**)

*)

Warto zwrócić uwagę na operacje na tzw. liczbach długich. Jeśli opcjonalnie postawimy

przecinek (np. dwie cyfry końcowe) wówczas operacje będą dokładne z oddzieleniem
groszy (wykluczając dzielenie nie całkowitoliczbowe). Taka reprezentacja stosowana jest w
systemach bankowych gdzie błędy zaokrągleń są bardzo istotne.

**)

Znane są dwa formaty, Drugi omówiony później pozwala na rozszerzenie tej notacji.

Zainteresowany czytelnik znajdzie więcej informacji w pracach [S3 i S4].

34

Metody numeryczne

43

42

1

K

4

4 3

4

4 2

1

K

2

2

1

1

1

2

1

1

1

,

n

n

n

n

n

u

u

u

c

c

c

−

−

(2.12)

Przy powyższym zapisie dla

n=10 i n

1

=4 i

n

2

= 6 mamy:

30,421321=0030,421321,
0,0347321

≈

0000,034732.

W późniejszych urządzeniach liczących przecinek ustawiano tak, aby zawsze
znajdował się pomiędzy częścią całkowitą a ułamkiem (jak wcześniej) ale pierwsza
cyfra (jeśli liczba była większa od jedności) była większa od zera:

30,421321=30,42132100,
0,0347321=0,034732100.

Ten zapis stosowany jest do dnia dzisiejszego w większości prostych kalkulatorów.
Zaletą tego zapisu jest przedstawienie liczby w sposób ogólnie przyjęty w zapisie
ręcznym i jednocześnie pozwalający na ukazanie maksymalnej liczby cyfr
znaczących (przy danej długości liczby

n).

Rozpatrzmy teraz problem błędu zaokrągleń liczb stałopozycyjnych. Niech

liczba będzie zapisana w formacie drugim na

n = 9 cyfrach (z pominięciem znaku):

– Najmniejsza liczba rzeczywista różna od zera (z pominięciem znaku):

43

42

1

43

42

1

n

n

z

0001

...

000

,

0

4

0001

...

000

,

0

≈

=

,

(2.13)

Błąd bezwzględny (2.3) wynosi:

000000004

,

0

~

=

−

=

z

z

z

∆

Natomiast błąd względny w procentach (2.6):

%!

6

,

28

%

100

000000014

,

0

000000004

,

0

%

100

~

≈

=

−

=

z

z

z

z

ε

Natomiast dla liczb dużych jest
– Największa liczba rzeczywista zaokrąglona do 9 cyfr:

43

42

1

43

42

1

n

n

z

999999999

4

,

999999999

≈

=

,

(2.14)

Błąd bezwzględny (2.3) wynosi:

4

,

0

~

=

−

=

z

z

z

∆

Natomiast błąd względny w procentach (2.6):

%!

10

4

%

100

4

,

999999999

4

,

0

%

100

~

8

−

×

≈

=

−

=

z

z

z

z

ε

Powyższe pokazuje jak wielkie znaczenie mają wielkości wartości liczbowych na
błąd względny zaokrągleń w reprezentacji stałopozycyjnej liczb rzeczywistych.

2. Błędy obliczeń komputerowych

35

Niech dalej liczba w zapisie stałopozycyjnym zapisywana jest na n cyfrach w

drugim z przedstawionych formatów. Ponadto niech jest określony zbiór A

r

(A

r

⊂

R)

wszystkich liczb rzeczywistych które można zapisać w tym formacie na n cyfrach.
Każdą liczbę zawartą w tym zbiorze określać będziemy jako liczbę maszynową.
Oznaczmy nadto przez rd(x) przybliżenie liczby rzeczywistej (patrz podrozdział
2.2) do zapisu na n cyfrach.
Najmniejszą co do modułu liczbą jaka może zostać zapisana jest:

{

}

)

1

(

10

001

...

000

,

0

)

rd(

min

inf

−

−

=

=

∈

=

n

n

r

r

A

x

A

43

42

1

.

(2.15)

Największą natomiast jest:

1

10

99

...

9999

)

rd(

max

sup

−

=

=

∈

=

n

n

r

r

A

x

A

4

3

42

1

.

(2.16)

Jeśli dla danej wartości x zachodzi:

r

A

x

sup

)

rd(

>

,

(2.17)

wówczas liczby nie można zapisać w podanym formacie i mamy do czynienia z tak
zwanym nadmiarem stałopozycyjnym.
Jeśli natomiast dla x

≠

0 jest:

r

A

x

inf

)

rd(

<

,

(2.18)

wówczas mówimy o tak zwanym podmiarze stałopozycyjnym.
Często podmiar w dalszych obliczeniach traktowany jest jako zero.

*)

2.4.2. Reprezentacja i arytmetyka zmiennopozycyjna

Wadą przedstawionego wyżej systemu reprezentacji liczb rzeczywistych jest

to, że każda liczba mniejsza od (2.15) jest już podmiarem, każda wieksza od (2.16)
jest traktowana jako nadmiar, a błędy względne zależą od wielkości liczb na
których wykonywane są obliczenia.

We współczesnych komputerach stosowany jest powszechnie zapis zmienno-

pozycyjny liczb rzeczywistych. Zapis ten pozwala na zachowanie maksymalnego
błędu względnego na stałym poziomie niezależnie od wartości liczby.
Ponadto, co jest bardzo istotne w bardziej złożonych obliczeniach rozszerza zakres
liczbowy co pozwala na zmniejszenie ryzyka wystąpienia nadmiaru i podmiaru w
trakcie realizacji obliczeń.

W zapisie zmiennopozycyjnym ogólnie format liczby można przedstawić:

*)

Zastępowanie podmiaru zerem w większości kompilatorów traktowane jest jako opcja.

36

Metody numeryczne

dwójkowym

systemie

w

m

x

m

dziesięzie

systemie

w

m

x

c

c

2

,

10

×

=

×

=

(2.19)

gdzie

m – liczba rzeczywista określająca tzw. mantysę liczby rzeczywistej, c –

liczba całkowita określająca tzw.

cechę liczby.

Mantysa zapisywana jest w formacie liczby rzeczywistej stałopozycyjnej i określa
wartość bez precyzowania dokładnego położenia przecinka. Cecha natomiast
określa (doprecyzuje) położenie przecinka.
Niech dla przykładu liczba będzie zapisywana: mantysa na

t cyfrach gdzie t

1

jest

liczbą cyfr części całkowitej mantysy a

t

2

jest liczbą cyfr ułamka. Ponadto niech

cecha zapisywana jest na

e cyfrach.

Format spełniający te wymagania ma postać:

43

42

1

L

K

4

4

4

4

4

3

4

4

4

4

4

2

1

43

42

1

K

4

4 3

4

4 2

1

e

e

e

c

c

c

t

t

t

t

t

t

u

u

u

m

m

m

1

1

2

2

1

1

1

10

,

2

1

1

1

−

×

−

−

.

(2.20)

Przy powyższym zapisie dla

t=10, t

1

=4 i

t

2

= 6 oraz e=2 mamy:

30,421321=3042,132100

×

10

-02

,

0,0347321

≈

3473,210000

×

10

-05

.

Zmieniając wartości ,

t

1

i

t

2

dla danej długości

t ta sama liczba w zapisie

zmiennopozycyjnym przyjmie różne formy.
W praktyce komputerowej stosowany jest zapis

znormalizowany.

Ogólnie liczba zapisana w formacie

znormalizowanym ma postać:

1

1

,

0

,

10

<

≤

×

m

m

c

.

(2.21)

Co przy zapisie mantysy z pominięciem znaku liczby) na t cyfrach i cechy na e
cyfrach sprowadza (2.20) do postaci:

*)

43

42

1

L

43

42

1

K

e

e

e

c

c

c

t

t

u

u

u

1

1

10

,

0

2

1

−

×

.

(2.22)

Dla wcześniejszych liczb przykładowych mamy:

30,421321=3042,132100

×

10

-02

=0,3042132100

×

10

+02

,

*)

W zapisie znormalizowanym część całkowita jest zawsze równa zero i stanowi wartość

domyślną której nie potrzeba pamiętać.

2. Błędy obliczeń komputerowych

37

0,0347321

≈

3473,210000

×

10

-05

=0,3473210000

×

10

-01

.

Dla maszyny z zapisem znormalizowanym o długości mantysy t i cechy e zbiór
wszystkich liczb które można zapisać w takim formacie będziemy nazywali
zbiorem liczb rzeczywistych maszynowych A

r

(podobnie jak zbiór liczb

maszynowych A

r

dla maszyny pracującej w arytmetyce stałopozycyjnej).

Oznaczmy nadto przez rd(x) przybliżenie liczby rzeczywistej (patrz podrozdział
2.2) do zapisu zmiennopozycyjnego na t cyfrach mantysy i e cyfrach cechy.
Najmniejszą co do modułu liczbą jaka może zostać zapisana jest:

{

}

3

2

1

43

42

1

e

t

r

r

A

x

A

9

...

99

10

000

...

1000

,

0

)

rd(

min

inf

−

=

=

∈

=

.

(2.23)

Największą natomiast jest:

{

}

3

2

1

4

3

42

1

e

t

r

r

A

x

A

9

...

99

10

999

...

999

,

0

)

rd(

max

sup

+

=

=

∈

=

.

(2.24)

Jeśli dla danej wartości x zachodzi:

r

A

x

sup

)

rd(

>

,

(2.25)

wówczas liczby nie można zapisać w podanym formacie i mamy do czynienia z tak
zwanym nadmiarem zmiennopozycyjnym.
Jeśli natomiast dla x

≠

0 jest:

r

A

x

inf

)

rd(

<

,

(2.26)

wówczas mówimy o tak zwanym podmiarze zmiennopozycyjnym.

Rozpatrzmy teraz problem błędu zaokrągleń liczb zmiennopozycyjnych.

Niech liczba będzie zapisana w formacie znormalizowanym z mantysą na t = 7
cyfrach (z pominięciem znaku) oraz cechy na e = 2 cyfrach:
– Najmniejsza liczba rzeczywista z najniższą cechą -99:

99

99

10

1000000

,

0

10

4

1000000

,

0

−

−

×

≈

×

=

4

3

42

1

4

3

42

1

t

t

z

,

(2.27)

Błąd bezwzględny (2.3) wynosi:

99

10

00000004

,

0

~

−

×

=

−

=

z

z

z

∆

Natomiast błąd względny w procentach (2.6):

%

100

10

4

,

0

%

100

10000004

,

0

00000004

,

0

%

100

~

6

×

×

≈

=

−

=

−

z

z

z

z

ε

38

Metody numeryczne

– Największa liczba rzeczywista z cechą -99:

99

99

10

9999999

,

0

10

4

9999999

,

0

−

−

×

≈

×

=

4

3

42

1

4

3

42

1

t

t

z

,

(2.28)

Błąd bezwzględny wynosi:

99

10

00000004

,

0

~

−

×

=

−

=

z

z

z

∆

Natomiast błąd względny w procentach:

%

100

10

4

,

0

%

100

99999994

,

0

00000004

,

0

%

100

~

7

×

×

≈

=

−

=

−

z

z

z

z

ε

Natomiast dla liczb dużych jest
– Najmniejsza liczba rzeczywista z największą cechą +99:

99

99

10

1000000

,

0

10

4

1000000

,

0

+

+

×

≈

×

=

4

3

42

1

4

3

42

1

t

t

z

,

(2.29)

Błąd bezwzględny:

99

10

00000004

,

0

~

+

×

=

−

=

z

z

z

∆

Natomiast błąd względny w procentach:

%

100

10

4

,

0

%

100

10000004

,

0

00000004

,

0

%

100

~

6

×

×

≈

=

−

=

−

z

z

z

z

ε

– Największa liczba rzeczywista z cechą +99:

99

99

10

9999999

,

0

10

4

9999999

,

0

+

+

×

≈

×

=

4

3

42

1

4

3

42

1

t

t

z

,

(2.30)

Błąd bezwzględny wynosi:

99

10

00000004

,

0

~

+

×

=

−

=

z

z

z

∆

Natomiast błąd względny w procentach:

%

100

10

4

,

0

%

100

99999994

,

0

00000004

,

0

%

100

~

7

×

×

≈

=

−

=

−

z

z

z

z

ε

Jak można zauważyć na podstawie (2.27) i (2.29) dla liczby najmniejszej (wartości
mantysy), błąd względny jest stały i niezależny od wartości cechy. Podobnie dla
błędu względnego dla liczb największych ((2.28) i (2.30), przy czym dla liczb
małych błąd jest większy o jeden rząd wielkości.
Powyższe prowadzi do uogólnienia dla liczb w formacie znormalizowanym z
mantysą na

t cyfrach niezależnie od wielkości cechy:

(

)

%

100

10

5

10

5

10

5

,

0

,

1

1

max

max

max

×

×

×

=

×

≤

≤

≤

−

−

−

t

t

t

z

ε

ε

ε

ε

.

(2.31)

2. Błędy obliczeń komputerowych

39

Natomiast błąd bezwzględny zależy od wartości cechy.

Dla operacji zmiennopozycyjnych znamiennym jest brak zachowania praw

łączności i przemienności zachodzących w operacjach na liczbach dokładnych.
Rozpatrzmy prosty przykład [P14]:

Niech dane są liczby zapisane na t=8 cyfrach:

a=0,23371258×10

-4

,

b=0,33678429×10

2

,

c=-0,33677811×10

2

.

Należy wyznaczyć sumę z=a+b+c.
Zgodnie z zasadami arytmetyki istnieją równoważne algorytmy a+(b+c)=(a+b)+c.

*)

W przypadku operacji zmiennopozycyjnej mamy:

fl(a+fl(b+c))=fl(0,23371258×10

-4

+0,61800000×10

-3

)=0,64137126×10

-3

,

fl(fl(a+b)+c))=fl(0,33678452×10

2

-0,33677811×10

2

)=0,64100000×10

-3

.

Wynik dokładny natomiast wynosi:

0,641371258×10

-3

.

Jak można zauważyć otrzymane rozwiązania są różne i odbiegają od wartości
dokładnej, przy czym pierwszy algorytm dla danych w przykładzie jest
dokładniejszy.

**)

2.5.

Propagacja bł

ę

dów, wska

ź

niki uwarunkowania

Jak wynika z przykładu, dwie różne metody matematycznie równoważne

obliczania sumy w rachunku zmiennopozycyjnym mogą dawać różne wyniki. Z
przyczyn numerycznych jest istotne rozróżnienie różnych algorytmów
matematycznie równoważnych i wybór właściwego dla danego zagadnienia.

Przyjmijmy, że zadanie polega na obliczeniu ze skończonej liczby danych

wejściowych x

1

, x

2

, …, x

n

skończonej liczby wyników y

1

, y

2

, …, y

m

.

(

)

m

i

x

x

x

y

n

i

i

,

1

,

,

,

,

2

1

=

=

L

ϕ

.

Podane wyżej funkcje jednoznacznie definiują algorytm obliczania wartości
funkcji y

y

y

y

=

ϕ

(x

x

x

x

). Skończona sekwencja operacji elementarnych algorytmu

odpowiada skończonej sekwencji odwzorowań elementarnych.
Przez operacje elementarne rozumiemy elementarne operacje arytmetyczne
wykonywane przez komputer. Bardziej skomplikowane operacje jak pierwiastko-
wanie czy obliczanie funkcji elementarnych sprowadza się do odpowiedniego
zastąpienia ich sekwencją operacji elementarnych

***)

*)

Prawo łączności i przemienności dodawania.

**)

Dla innych danych dokładniejszy może okazać się algorytm drugi. Przy stosowaniu

arytmetyki zmiennopozycyjnej istotna dla dokładności jest kolejność wykonywania
operacji

***)

Patrz rozdział 1, np. poprzez rozwinięcie funkcji w szereg Maclaurin’a.

40

Metody numeryczne

Dla odwzorowań elementarnych

ϕ

k

istnieją odwzorowania zastępcze w arytmetyce

zmiennopozycyjnej fl(

ϕ

k

) realizowane przez maszynę cyfrową. Błąd operacji

elementarnych realizowanych przez maszynę określony jest przez:

(

)

(

)

(

)

n

k

n

k

k

x

x

x

x

x

x

y

,

,

,

,

,

,

fl

2

1

2

1

L

L

ϕ

ϕ

∆

−

=

,

(2.32)

i traktowany jako błąd zaokrąglenia powstający przy obliczaniu

ϕ

k

(

n

x

x

x

,

,

,

2

1

L

)

*)

.

Niech jest dana funkcja wektorowa y

y

y

y

=

ϕ

(x

x

x

x

) określona przez:

(

)

(

)

(

)

,

,

,

,

,

,

,

,

,

,

2

1

2

1

1

2

1





















=

=

n

m

n

n

x

x

x

x

x

x

x

x

x

L

M

L

L

ϕ

ϕ

ϕ

y

y

y

y

(2.33)

gdzie funkcje

(

)

n

k

x

x

x

,

,

,

2

1

L

ϕ

,

m

k

,

1

=

są ciągłe i różniczkowalne. Niech nadto

n

i

x

i

,

1

,

~

=

będą wartościami przybliżonymi wartości dokładnych

n

i

x

i

,

1

,

=

.

Mamy:

n

i

x

x

x

x

x

x

x

x

i

i

i

i

x

i

i

i

i

,

1

;

~

,

~

=

−

=

=

−

=

∆

ε

∆

,

(2.34)

to znaczy błędy bezwzględne i względne wartości

i

x

~ .

Zastępując wartości dokładne

i

x wartościami przybliżonymi

i

x

~ jako wynik

otrzymamy wartość przybliżoną

(

)

n

i

i

x

x

x

y

~

,

,

~

,

~

~

2

1

L

ϕ

=

a nie

(

)

n

i

i

x

x

x

y

,

,

,

2

1

L

ϕ

=

.

Rozwijając poszczególne funkcje (2.32) w szereg Taylor’a i ograniczając
rozwinięcie do pierwszej pochodnej dla poszczególnych funkcji jest:

(

) (

)

(

)

(

)

(

)

.

,

1

,

,

,

,

,

~

,

,

~

,

,

~

~

1

1

1

1

1

1

m

k

x

x

x

x

x

x

x

x

x

x

x

x

x

y

y

y

i

n

i

i

n

k

n

i

i

n

k

i

i

n

n

k

k

k

=

×

∂

∂

=

∂

∂

×

−

≈

−

=

−

=

∑

∑

=

=

∆

ϕ

ϕ

ϕ

ϕ

∆

K

K

K

K

(2.35)

Inaczej w zapisie wektorowym mamy:
Znając błąd bezwzględny (2.35i podstawiając

(

)

n

k

k

x

x

x

y

~

,

,

~

,

~

~

2

1

L

ϕ

=

oraz (2.34)

błąd względny wyniesie:

*)

Zauważyć należy, ze w przypadku obliczania wartości funkcji elementarnych dochodzi

jeszcze błąd obcięcia wynikający z warunku stopowania algorytmu (np. obliczanie wartości
rozwinięcia funkcji w nieskończony szereg potęgowy).
Dane zaokrąglane są do wartości ze zbioru liczb maszynowych z dokładnością nie gorszą
od dokładności maszynowej, czyli zawierają się w odpowiednich przedziałach. W pracy
[S8] przedstawiono tzw. arytmetyką przedziałową gdzie operacje wykonywane są na
przedziałach zawierających dane a nie na wartościach szczególnych w nich zawartych.
Otrzymane rozwiązania również określane są przez przedział zawierający rozwiązanie.

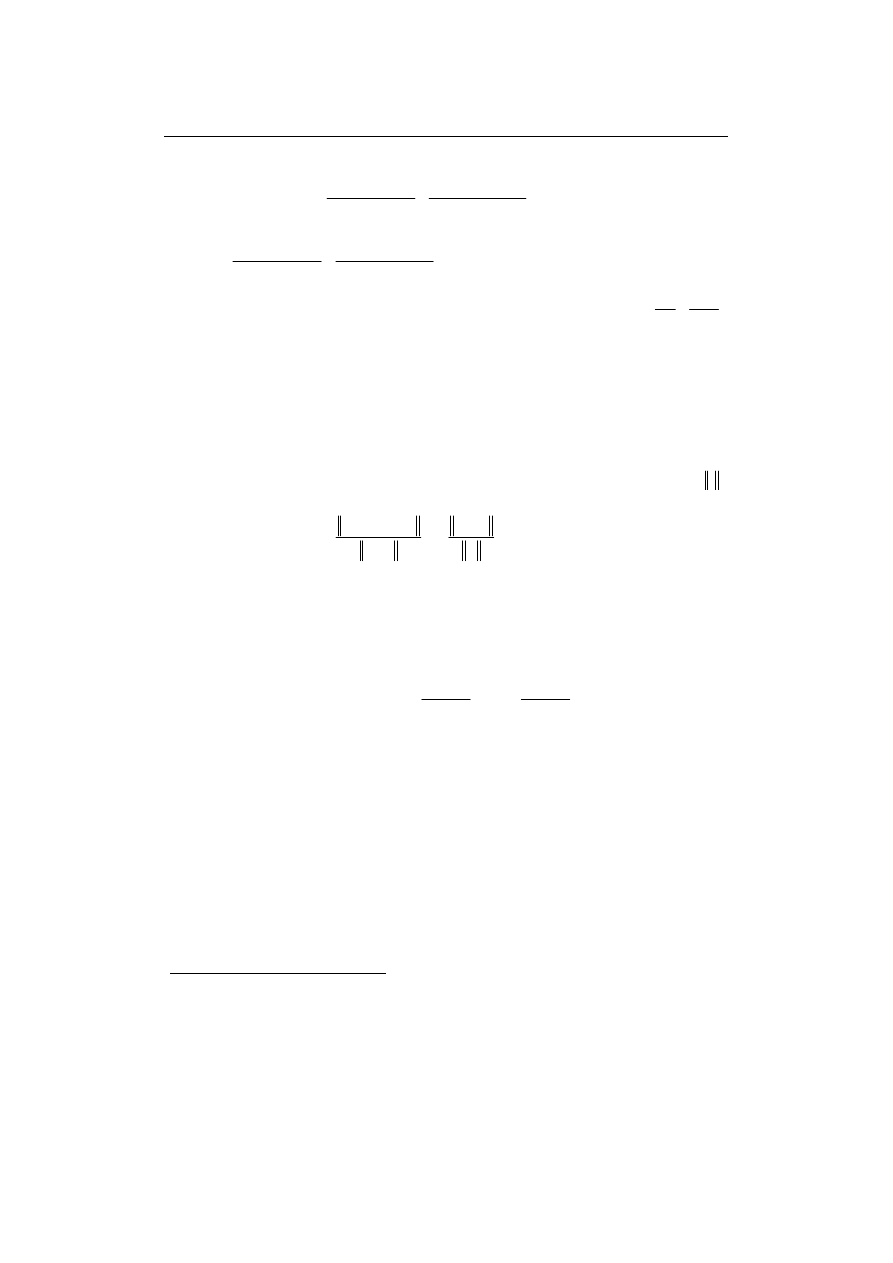
2. Błędy obliczeń komputerowych

41

(

)

(

)

.

,

,

,

,

1

1

1

i

k

x

i

n

k

n

i

n

k

i

y

x

x

x

x

x

x

ε

ϕ

ϕ

ε

×

∂

∂

×

≈

∑

=

K

K

(2.36)

Wartość

(

)

(

)

i

n

k

n

k

i

x

x

x

x

x

x

∂

∂

×

,

,

,

,

1

1

K

K

ϕ

ϕ

określa jak mocno błąd względny danej

x

i

wpływa na błąd względny wartości

y

k

. Współczynniki wzmocnienia

i

k

k

i

x

x

∂

∂

×

ϕ

ϕ

błędów nazywane są

wskaźnikami uwarunkowania. Jeśli wartości bezwzględne

współczynników wzmocnienia są duże, wówczas małe wartości błędów
względnych danych wejściowych generują duże wartości błędu względnego
wyników. Mówimy wówczas, że zadanie jest źle uwarunkowane. Jeśli natomiast
wskaźniki uwarunkowania (współczynniki wzmocnienia błędów) są małe,
wówczas zadanie określamy jako dobrze uwarunkowane.
Często można spotkać się z inną definicją wskaźnika uwarunkowania zadania.
Wskaźnik uwarunkowania określa liczba

c, która dla odpowiednia normy

•

spełnia.

( ) ( )

( )

x

x

x

c

x

x

x

~

~

~

~

−

≤

−

ϕ

ϕ

ϕ

(2.37)

Z zależności (2.36) wynikają współczynniki wzmocnienia błędów dla operacji
elementarnych:

*)

(

)

(

)

(

)

.

;

,

,

1

1

;

/

,

,

1

1

;

,

2

1

2

1

2

1

2

1

2

2

1

1

2

1

2

1

2

1

2

1

2

1

2

1

x

x

y

x

x

y

x

x

y

x

x

x

x

x

x

x

x

x

x

y

x

x

x

x

y

x

x

x

x

y

ε

ε

ε

ϕ

ε

ε

ε

ϕ

ε

ε

ε

ϕ

×

±

±

×

±

≈

±

=

=

×

−

×

≈

=

=

×

+

×

≈

×

=

=

(2.38)

Zauważmy, że operacje mnożenia i dzielenia są operacjami bezpiecznymi. Błąd nie
przekroczy sumy błędów danych wejściowych, a moduły współczynników
wzmocnienia błędu równe są jeden i nie zależą od wartości danych. Oznacza to, ze
błędy danych słabo przenoszą się na wynik.
Dodawanie natomiast jest bezpieczne jeśli dane wejściowe są jednakowych
znaków. W przypadku różnych znaków moduły współczynników wzmocnienia są
większe od jeden. Jeśli dane co do modułów będą prawie równe, wówczas
wzmocnienia błędów będą bardzo duże (suma prawie równa zero generuje dużą
wartość błędu). Jak zatem widać operacja dodawania może być bezpieczna bądź
nadzwyczaj niebezpieczna w zależności od wartości danych!
Podobna sytuacja występuje przy odejmowaniu liczb o tych samych znakach.

*)

Wyprowadzenie jako ćwiczenie pozostawia się czytelnikowi (patrz (2.36).

42

Metody numeryczne

Jeśli dodawanie wykonywane jest na liczbach o tych samych znakach, wówczas
wskaźniki uwarunkowania są mniejsze od jeden.

*)

Mamy wówczas:

{

}

y

x

y

ε

ε

ε

,

max

≤

.

(2.39)

Jeśli powyższe zachodzi mówimy o wygaszanie błędów.

Rozpatrzmy teraz przypadek zachowania się błędów dla dwóch różnych ale

równoważnych algorytmów.
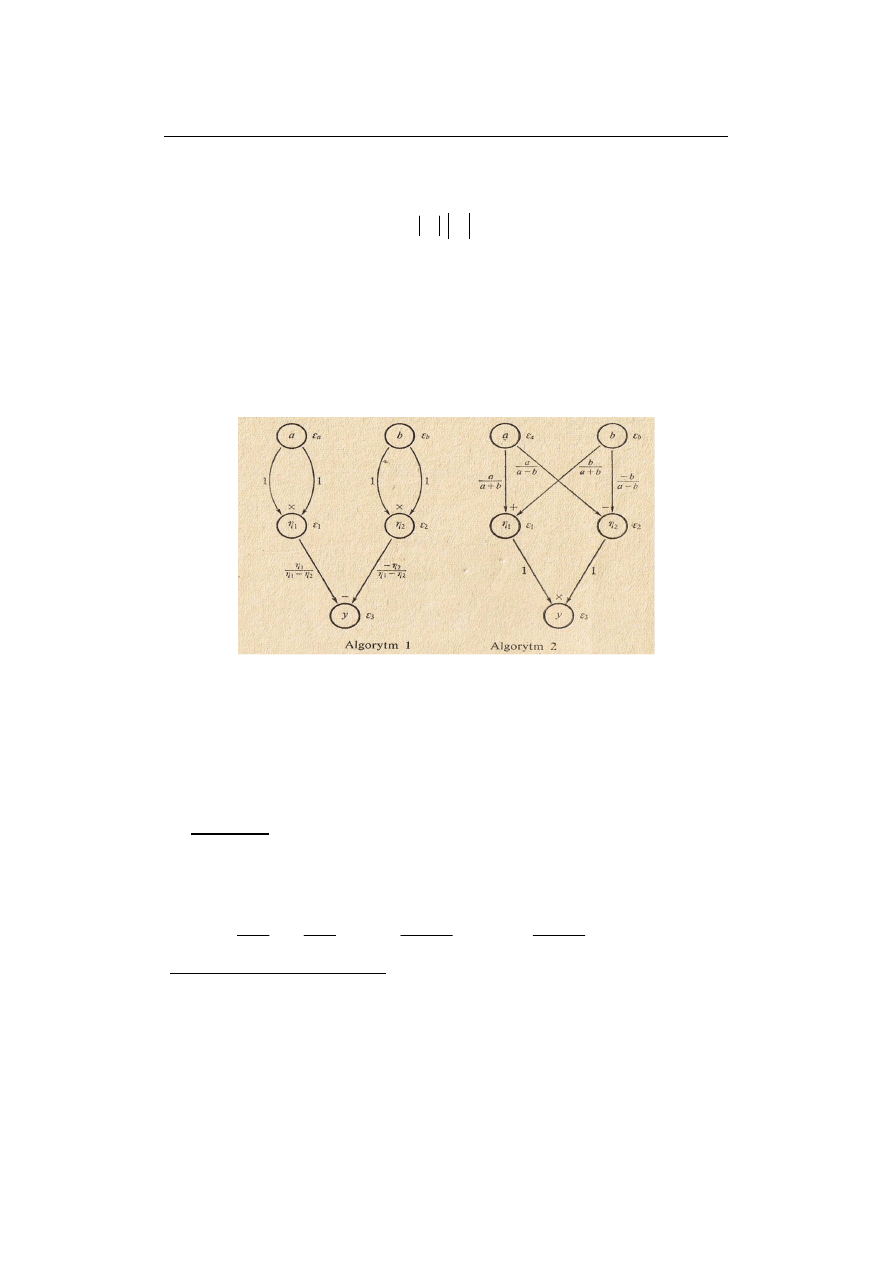
Należy wyznaczyć

y = a

2

-

b

2

Obliczenia można przeprowadzić przy użyciu dwóch równoważnych algorytmów:

Algorytm 1:

y = a

2

-

b

2.

= (

a + b)(a – b).

Algorytm 2:

y = a

2

-

b

2.

= (

a

×

a) - (a

×

b).

Rys. 2.2. Grafy dwóch algorytmów obliczania y = a

2

- b

2.

.

Węzły grafu reprezentują wyniki pośrednie obliczeń, natomiast krawędziom
skierowanym grafu odpowiadają współczynniki wzmocnienia błędu dla
wykonywanych operacji elementarnych.
W każdym węźle dla wyniku pośredniego powstaje nowy błąd wynikający z
przeniesienia błędu danych oraz błąd zaokrąglenia wyniku (

ε

1

,

ε

2

,

ε

3

).

Zgodnie z (2.38) mamy:

Algorytm 1:

(

)

(

)

.

2

2

,

2

1

1

,

2

1

1

.

,

,

3

2

2

2

2

1

2

2

2

3

2

2

1

1

ε

ε

ε

ε

ε

ε

ε

ε

ε

ε

ε

ε

ε

ε

ε

ε

ε

ε

ε

ε

ε

+

+

−

−

+

−

=

+

−

−

−

=

+

=

+

×

+

×

=

+

=

+

×

+

×

=

−

=

×

=

×

=

b

a

v

u

y

b

b

b

v

a

a

a

u

b

a

b

b

a

a

v

u

v

v

u

u

v

u

y

b

b

v

a

a

u

*)

Z analogiczną sytuacją mamy do czynienia przy odejmowaniu liczb o różnych znakach.

2. Błędy obliczeń komputerowych

43

Algorytm 2:

.

1

1

,

,

.

,

,

3

2

1

3

2

1

3

2

1

ε

ε

ε

ε

ε

ε

ε

ε

ε

ε

ε

ε

ε

ε

ε

ε

ε

ε

ε

ε

ε

ε

ε

ε

+

+

+













−

−

+

+













−

+

+

=

=

+

+

×

−

−

×

−

+

+

×

+

+

×

+

=

=

+

×

+

×

=

+

×

−

−

×

−

=

+

×

+

+

×

+

=

×

=

−

=

+

=

b

a

b

a

b

a

v

u

y

b

a

v

b

a

u

b

a

b

b

a

b

b

a

a

b

a

a

b

a

b

b

a

a

b

a

b

b

a

a

b

a

b

b

a

a

b

a

b

b

a

a

v

u

y

b

a

v

b

a

u

Porównując błąd wyniku

ε

y

w obu algorytmach można zauważyć, że jego wartości

są różne dla obu algorytmów i mocno zależą o wartości danych wejściowych.
W zależności od danych dokładniejszy może być pierwszy lub drugi algorytm a
wyniki otrzymane mogą się różnic w obu algorytmach.

Zadania

2.1.

Maszyna pracuje w arytmetyce stałopozycyjnej. Liczby rzeczywiste zapisywane są na
n = 8 cyfrach w zapisie stałopozycyjnym.

Wprowadzono liczby:

x

1

=0,00012345679

x

2

=0,12345

x

3

=12345,123456789

x

4

=12345679876,543

Zapisz podane liczby zaokrąglone do długości liczb maszynowych.
Wyznacz błąd bezwzględny i względny zaokrąglenia.

2.2.

Maszyna pracuje w arytmetyce zmiennopozycyjnej z mantysa na sześciu cyfrach i
cecha dwucyfrową.

Wprowadzono dane:

x

1

=0,00012345679

x

2

=0,12345

x

3

=0,000000000012345

x

4

=12345679876543,21

x

5

=12345,123456789

×

10

10

x

6

=12345679876,543

×

10

-12

Zapisz podane liczby zaokrąglone do długości liczb maszynowych w znormalizowanej
postaci zmiennopozycyjnej.
Wyznacz błąd bezwzględny i względny zaokrąglenia.

2.3.

Dane są znormalizowanymi liczbami zmiennopozycyjnymi o n=8 cyfrach znaczących:
a = 0,23371258

×

10

-4

,

b = 0,33677429

×

10

2

,

44

Metody numeryczne

c = 0,33677811

×

10

-4

.

Wyznaczyć w arytmetyce zmiennopozycyjnej:
z

1

= fl ( a + fl ( b + c )),

z

2

= fl ( fl ( a + b ) +c ).

Wyznacz błąd względny obu algorytmów i porównaj otrzymane wartości.

*)

2.4.

Przyjmując, że pierwiastkowanie można potraktować jako operacje elementarną wy-
znaczyć współczynnik wzmocnienia błędu

ϕ

(x)=x

1/2

. Czy operacja ta jest bezpieczna?

2.5.

Dla danych p i q należy wyznaczyć

q

p

p

y

+

+

−

=

2

używając jednego z dwóch

algorytmów:

Algorytm 1:

.

,

,

,

2

w

p

y

v

w

q

u

v

p

u

+

−

=

=

+

=

=

Algorytm 2:

.

,

,

,

.

2

t

q

y

w

p

t

v

w

q

u

v

p

u

=

+

=

=

+

=

=

Wyznacz wskaźniki uwarunkowania (współczynniki wzmocnienia błędu) obu
algorytmów.

2.6.

Dla algorytmów z zadania 2.5 określić który algorytm jest poprawny w przypadkach:

a. p

≈

q,

b. p

>>

q.

*)

Dokładna wartość wynosi z = 0,6413371258

×

10

-3

.