1

RUCH OBROTOWY BRYŁY

SZTYWNEJ

2

RUCH OBROTOWY BRYŁY SZTYWNEJ

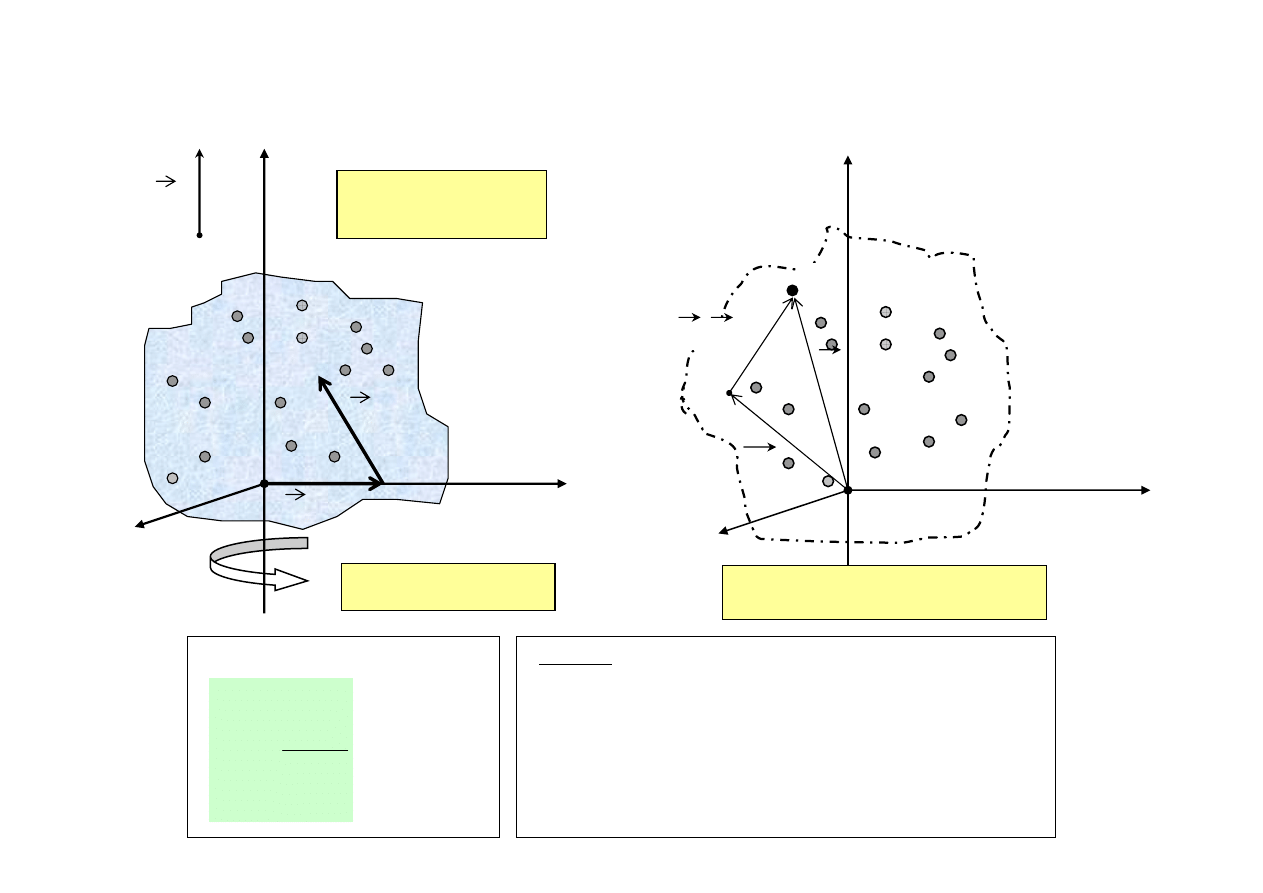
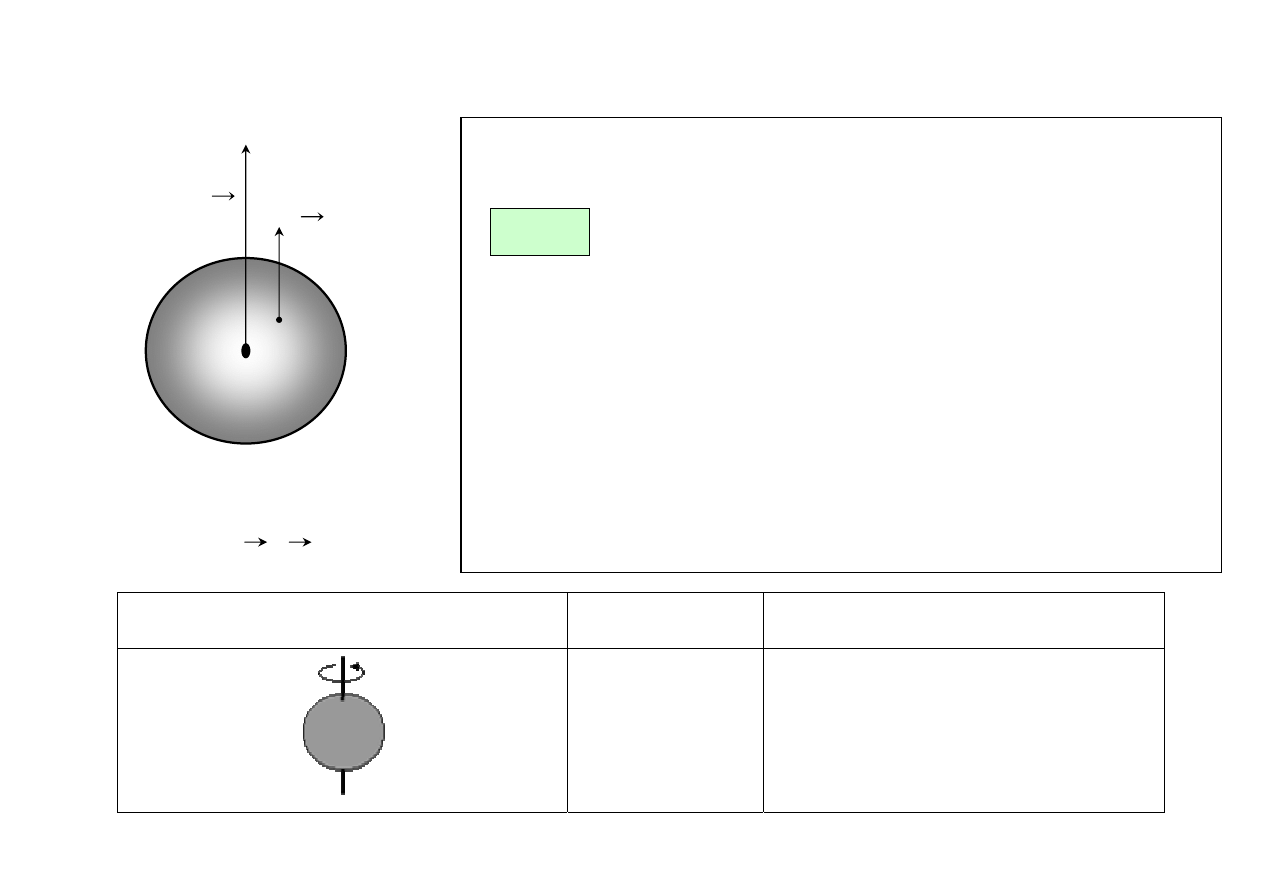
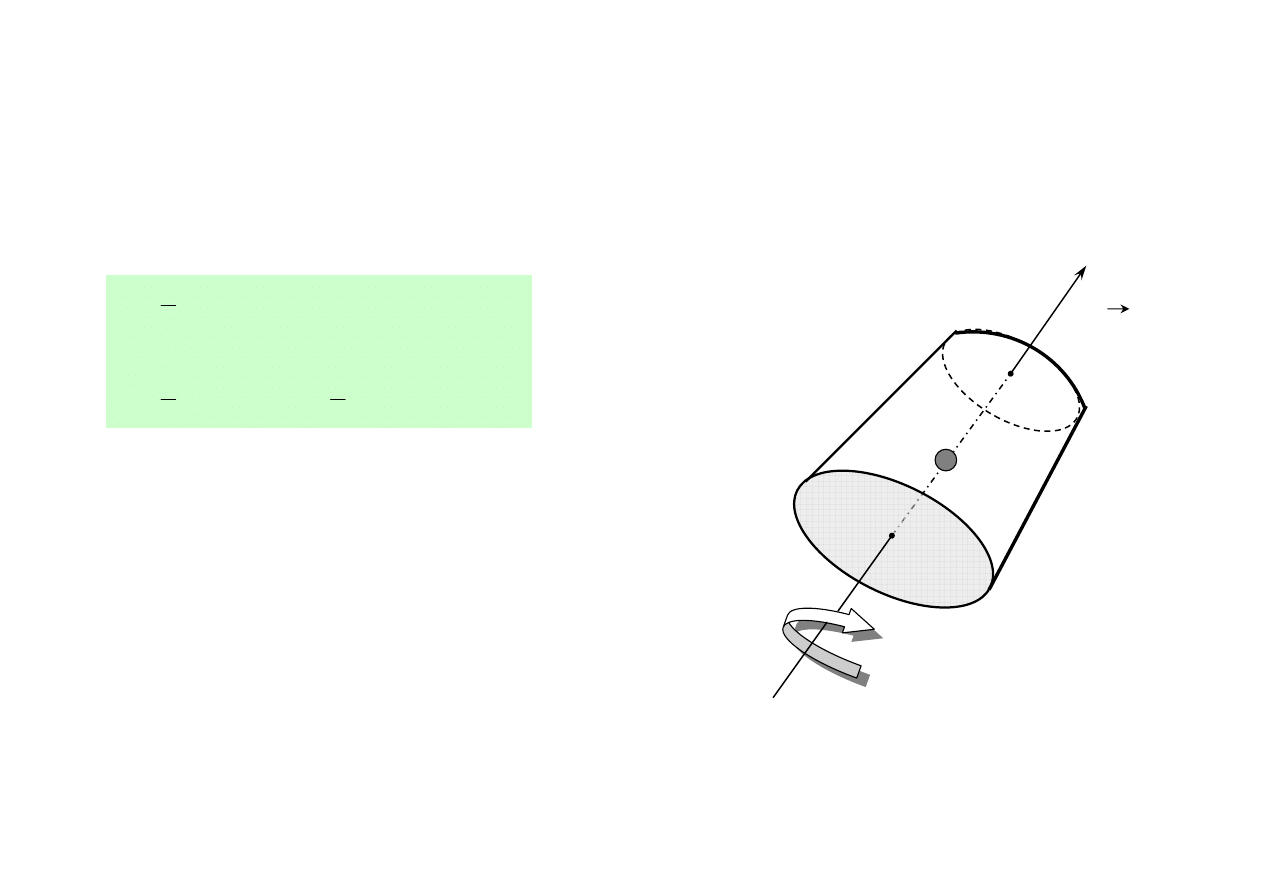
• Ciało Doskonale Sztywne (Bryła Sztywna) = model ciała rzeczywistego = układ „n”
oddziaływujących cząstek których wzajemne odległości nie ulegają zmianie

• Ciało wykonuje ruch obrotowy względem osi obrotu, tj. układu punktów, które znajdują się w spoczynku
• Wektor prędkości kątowej ω jest wektorem, którego kierunek pokrywa się z kierunkiem osi obrotu

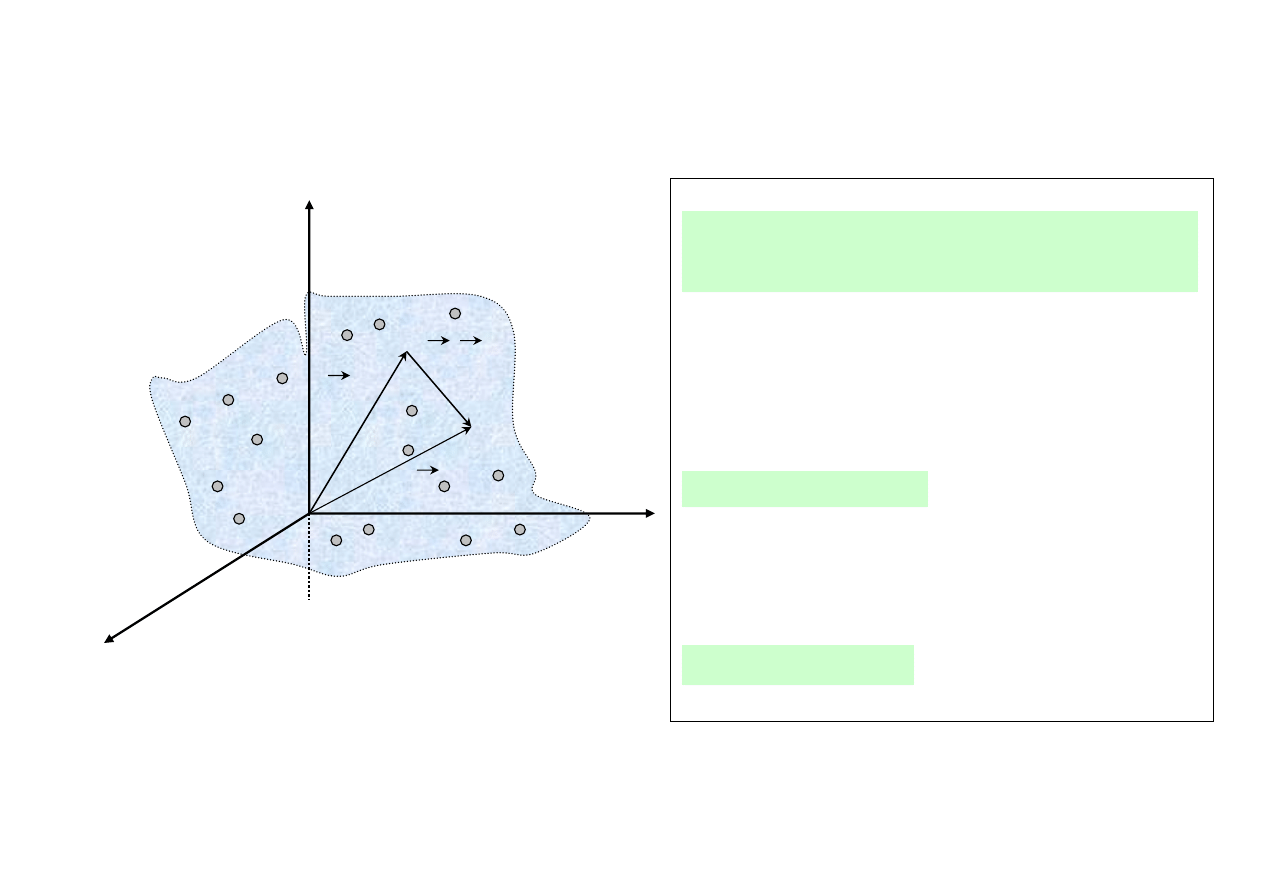
• Wielkości opisujące ruch układu cząstek: n

i

= i - ta cząstka

)

,

,

,

(

ω

i

i

i

v

r

m

r

r

wszystkie cząstki posiadają tę samą prędkość kątową

3

ŚRODEK MASY UKŁADU PUNKTÓW MATERIALNYCH (ŚRODEK MASY BRYŁY SZTYWNEJ)

Rys. 22.

Rys. 23.

Definicja CM (= Center Mass)

∑

∑

=

=

=

n

1

i

i

n

1

i

i

i

CM

m

r

m

R

r

r

(CM)

x

y

z

ω

m

r

i

układ n punktów

materialnych

oś z = oś obrotu

0

v

i

Uwaga: w dalszym zapisie wzorów sumowanie po liczbie

cząstek nie będzie oznaczane wskaźnikami przy znaku

sumy, tzn.

∑

∑

=

=

i

n

1

i

i

x

x

R

CM

r

i

0

z

y

x

r

i

-R

CM

m

i

0

′

0

′ - POCZĄTEK UKŁADU CM

4

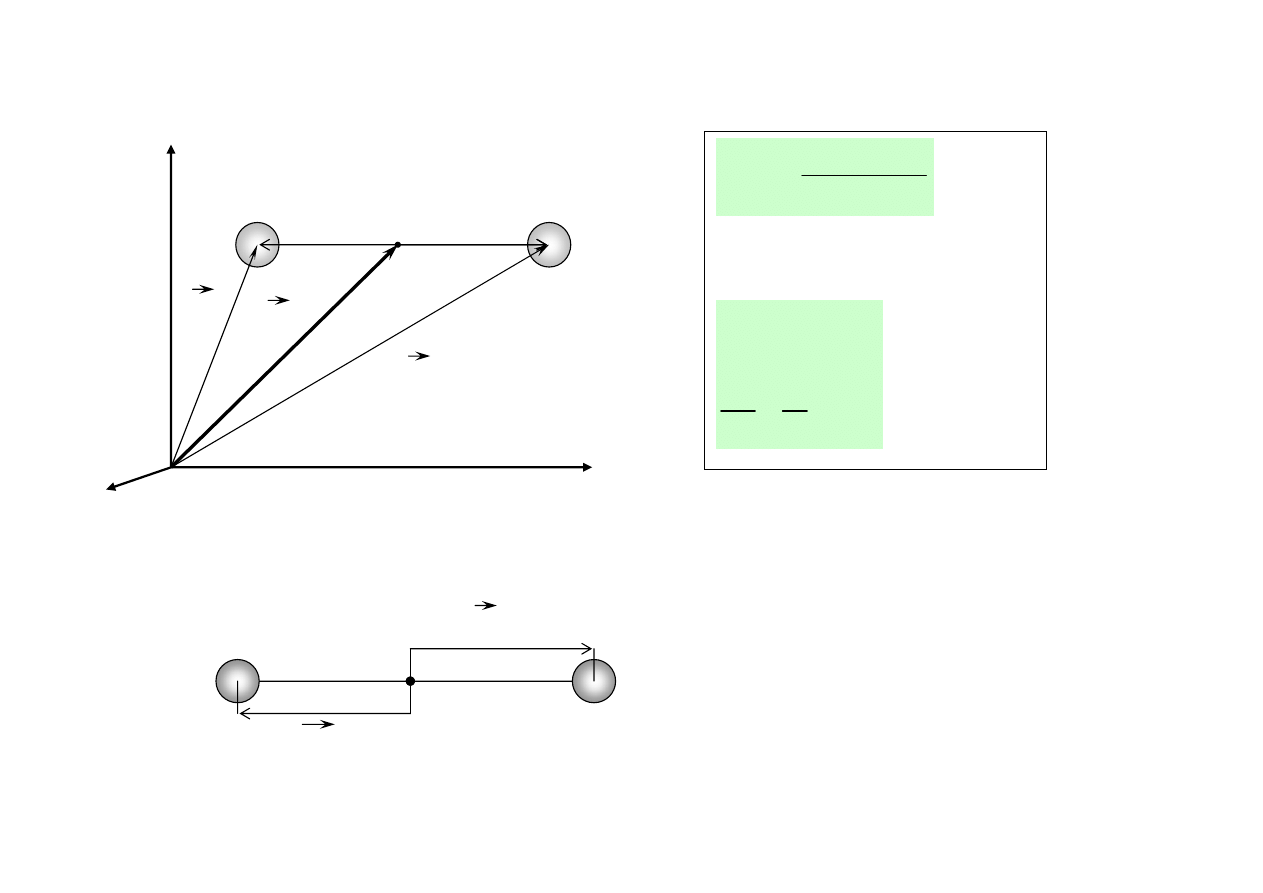
UKŁAD DWÓCH PUNKTÓW MATERIALNYCH (DWÓCH CZĄSTEK), przykład

Rys. 24.

Rys. 25.

m

1

m

2

r

1

r

2

0

′ = CM

R

CM

0

z

y

m

1

m

2

CM

0

′

r

1

r

2

x

2

1

2

2

1

1

CM

m

m

r

m

r

m

R

+

+

=

r

r

r

Gdy początek układu odniesienia

znajduje się w środku masy (O’=CM)

1

2

2

1

2

2

1

1

CM

r

r

m

m

0

r

m

r

m

0

R

=

=

+

=

r

r

r

5

PĘD, MOMENT PĘDU, MOMENT SIŁY

Rys. 26.

Rys. 27.

Punkt materialny

Układ punktów materialnych (bryła sztywna)

Pęd

i

i

i

v

m

p

r

r =

∑

∑

=

=

i

i

i

v

m

p

P

r

r

r

Moment pędu

i

i

i

i

i

i

i

i

r

v

v

r

m

p

r

J

r

r

r

r

r

r

r

r

×

=

×

=

×

=

ϖ

∑

∑

∑

×

=

×

=

=

i

i

i

i

i

i

v

r

m

p

r

J

J

r

r

r

r

r

r

Moment siły

i

i

i

F

r

N

r

r

r

×

=

∑

∑

×

=

=

i

i

i

p

r

N

N

r

r

r

r

0

r

i

m

i

v

i

ω

MOMENT PĘDU

0

m

i

J

i

r

i

v

i

(P

i

)

J

i

⊥ r

i

oraz J

i

⊥ P

i

0

r

i

m

i

v

i

ω

moment pędu

6

ROLA MOMENTU PĘDU I MOMENTU SIŁY W RUCHU OBROTOWYM BRYŁY SZTYWNEJ

• CM = środek masy bryły sztywnej
• R

CM

= wektor położenia środka masy

Rys. 28.

x

y

r

i

R

CM

r

i

- R

CM

0

m

i

0

′

z

P

R

J

J

v

R

m

v

)

R

r

(

m

v

r

m

J

CM

CM

i

CM

i

i

CM

i

i

i

i

i

r

r

r

r

r

r

r

r

r

r

r

r

×

+

=

×

+

×

−

=

×

=

∑

∑

∑

SPIN = moment pędu bryły sztywnej względem

środka masy (własny moment pędu, nie zależy od

układu odniesienia):

∑

×

−

=

i

CM

i

i

CM

v

)

R

r

(

m

J

r

r

r

r

Moment pędu środka masy względem początku

układu (zależy od wyboru układu odniesienia):

P

R

v

m

R

CM

i

i

CM

r

r

r

r

×

=

×

∑

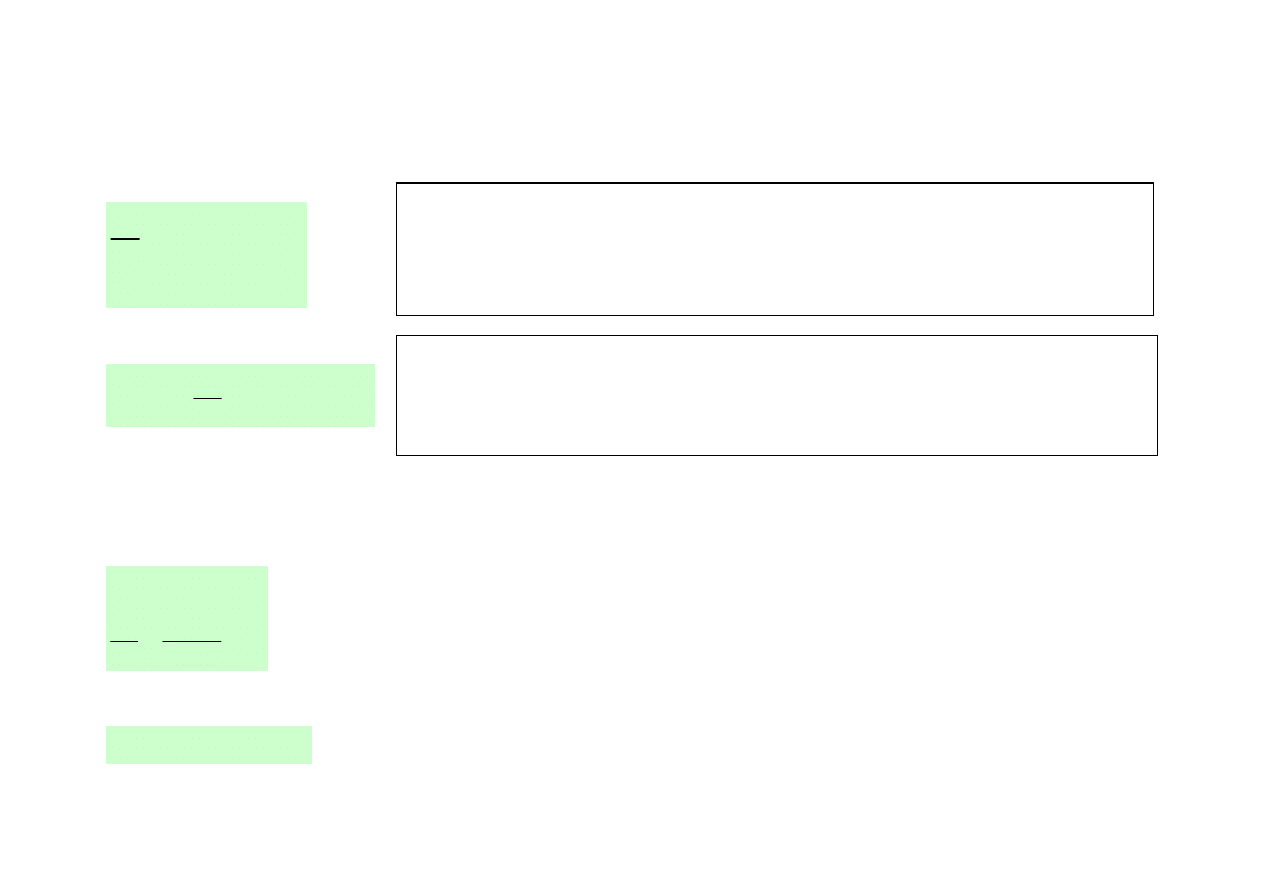
7

RÓWNANIE RUCHU OBROTOWEGO BRYŁY SZTYWNEJ

• Aby wprawić bryłę sztywną w ruch obrotowy należy zadziałać momentem siły

N

r

.

P

R

J

J

N

dt

J

d

CM

CM

r

r

r

r

r

r

×

+

=

=

const

J

0

dt

J

d

0

N

=

→

=

→

≡

r

r

r

• Gdy początek układu odniesienia znajduje się w środku masy CM, całkowity moment pędu równy jest

spinowi. Wówczas:

N

dt

J

d

dt

J

d

0

P

R

CM

CM

r

r

r

r

r

=

=

=

×

oraz

const

J

0

N

CM

=

→

=

r

r

II zasada dynamiki dla ruchu obrotowego.

Zmiana całkowitego momentu pędu przypadająca na jednostkę czasu jest

równa wypadkowemu momentowi sił działającemu na bryłę sztywną.

Prawo zachowania momentu pędu

Gdy na bryłę sztywną nie działa zewnętrzny moment sił, lub wypadkowy moment sił

jest równy zeru, to moment pędu jest wielkością stałą w czasie.

8

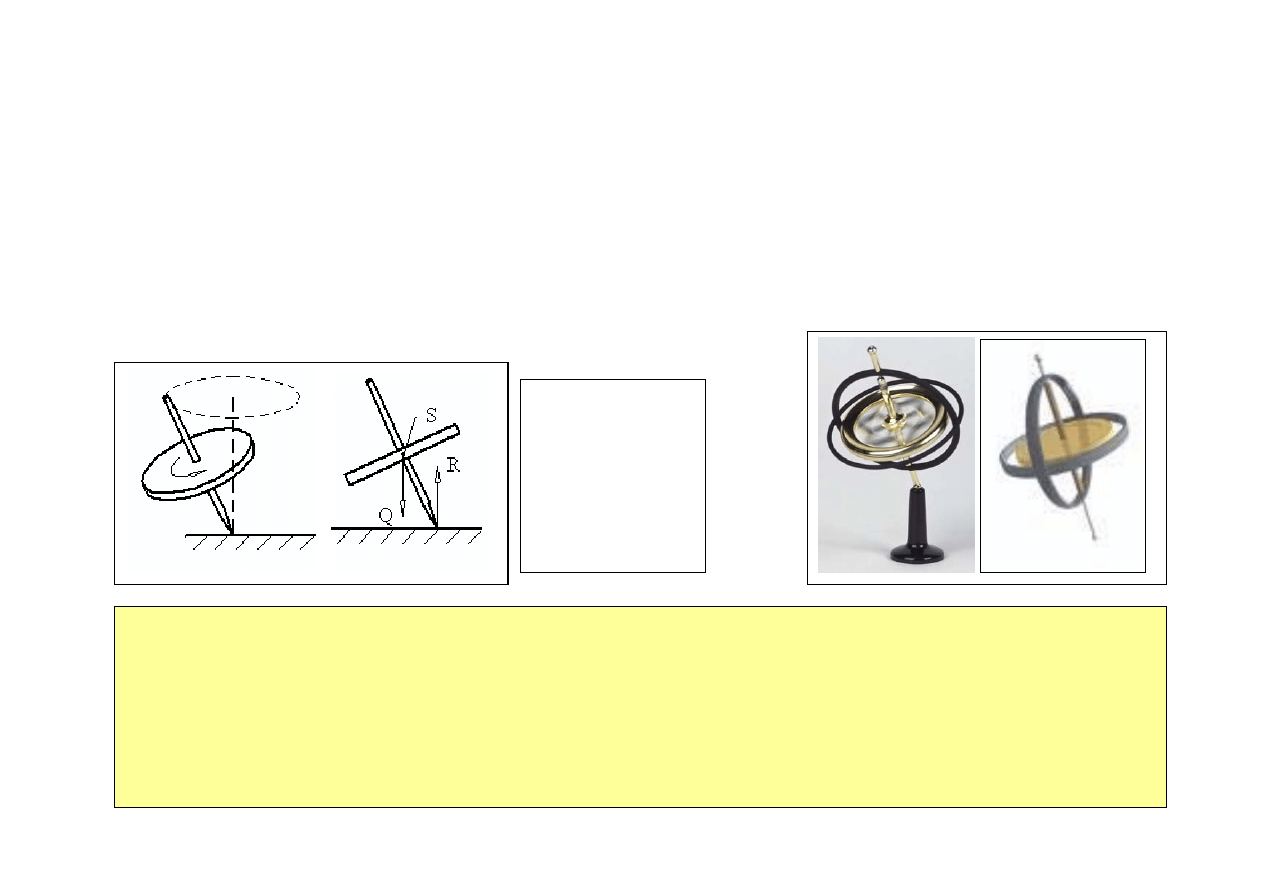
RUCH OBROTOWY BĄKA SYMETRYCZNEGO (ELEMENTARNA TEORIA ŻYROSKOPU)

• Bąk symetryczny = ciało o symetrii osiowej i jednorodnym rozkładzie masy,

np. bąk – zabawka, krążek z bolcami umożliwiającymi przyłożenie momentu sił

• Ruch bąka symetrycznego w polu grawitacyjnym. Bąk wirujący ze stałą prędkością kątową wokół osi

poziomej doznaje działania pary sił: siły ciężkości i reakcji w punkcie podparcia osi, co powoduje, że

moment sił działający na bąka jest różny od zera.

Rys. 29.

• Własności żyroskopu posiada wiele ciał np: ciała niebieskie w tym Ziemia, pociski karabinowe, wirniki

maszyn, koła.

• Żyroskop ma on postać metalowego krążka, który raz wprawiony w ruch obrotowy zachowuje swoje

pierwotne położenie osi obrotu. Żyroskop został wynaleziony w 1852 przez Leona Foucaulta, jako
demonstracja zasady zachowania momentu pędu.

R - siła reakcji

podłoża

Q – moment siły

ciężkości

9

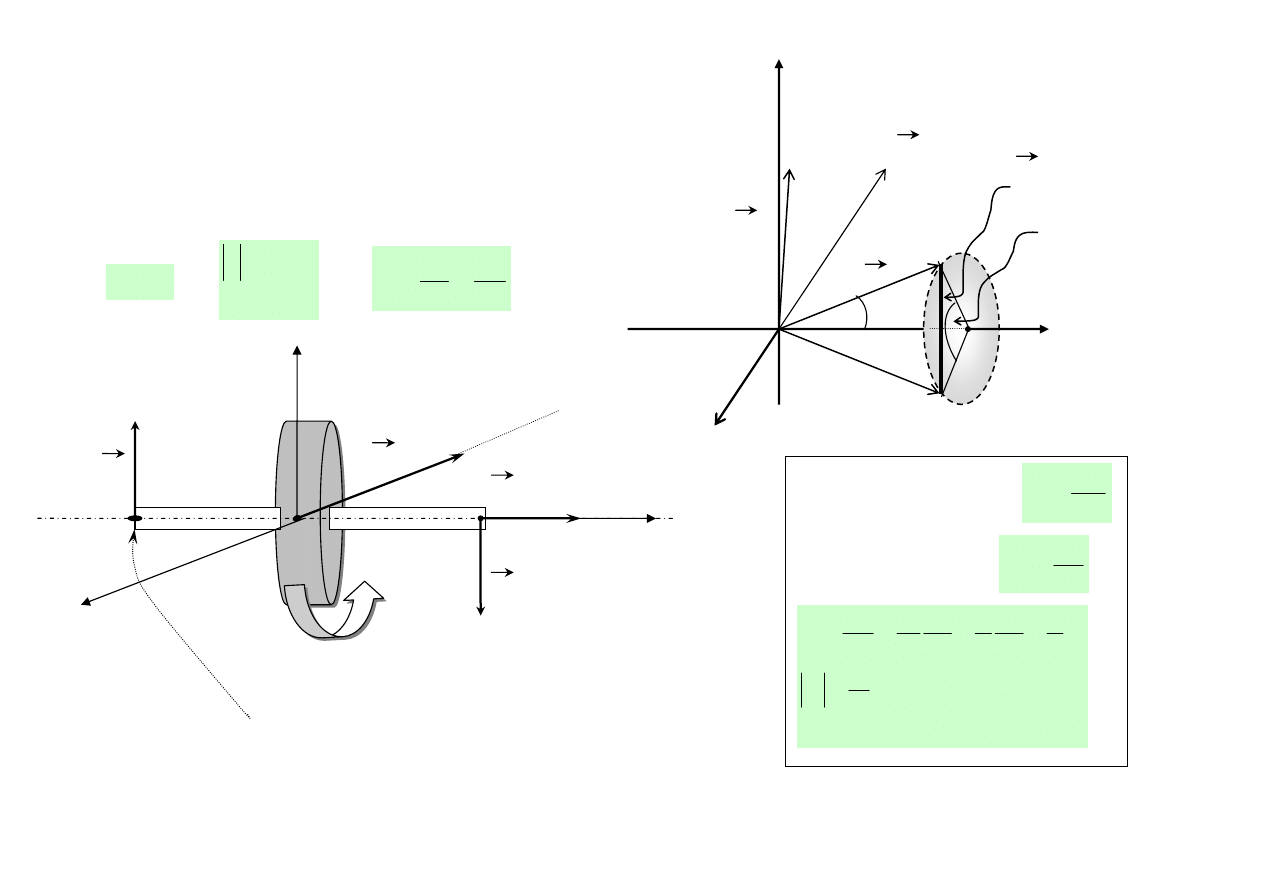
Założenia:

Duża wartość momentu pędu

Moment siły prostopadły do momentu pędu

oraz

0

N

≠

r

,

0

J

const

J

≠

=

r

r

∆

,

t

J

dt

J

d

N

∆

∆

r

r

r

=

=

Rys. 30.

N

F

F

y

x

z

J

(0 = CM)

punkt podparcia

0

y

z

x

Ω

N

J

∆ϕ

∆J

Rys. 31.

Prędkość kątowa precesji:

t

∆

ϕ

∆

Ω

=

w mierze łukowej kąta:

J

J

∆

ϕ

∆

=

J

N

J

N

N

J

1

t

J

J

1

J

J

t

1

t

r

r

r

r

×

=

=

=

=

=

=

Ω

Ω

∆

∆

∆

∆

∆

ϕ

∆

Ω

10

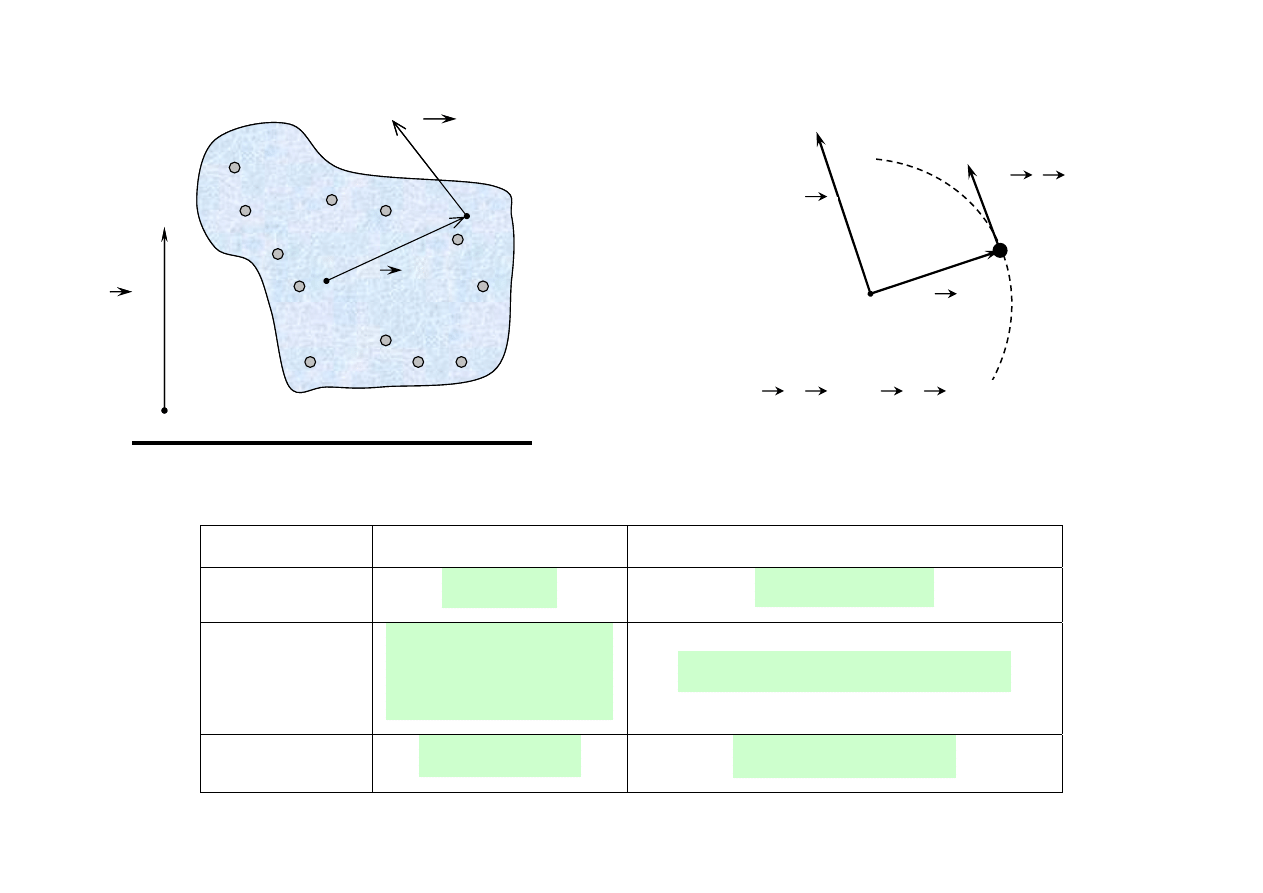
MOMENT BEZWŁADNOŚCI BRYŁY SZTYWNEJ

• Wirująca swobodnie kula jednorodna

Rysunek

Wzór na moment

bezwładności

Opis

I = 0,4mR

2

Kula o promieniu R –

oś obrotu przechodzi przez środek kuli

J

ω

wirująca swobodnie kula jednorodna

zawsze

J

ω

Rys. 32

• Zawsze J jest równoległe do ω. Wówczas moment pędu jest

proporcjonalny do prędkości kątowej.

ω

r

r

I

J

=

gdzie I jest współczynnikiem proporcjonalności. Współczynnik ten nosi

nazwę momentu bezwładności, w tym przypadku momentu

bezwładności kuli. Określa on pewną charakterystyczna cechę ciała –

rozkład masy ciała względem osi obrotu.

• Powyższa relacja pomiędzy J i

ω

jest również słuszna w przypadku ciał o

symetrii osiowej i jednorodnym rozkładzie masy oraz ciał wykonujących

ruch obrotowy względem jednej z tzw. osi głównych ciała.

11

•

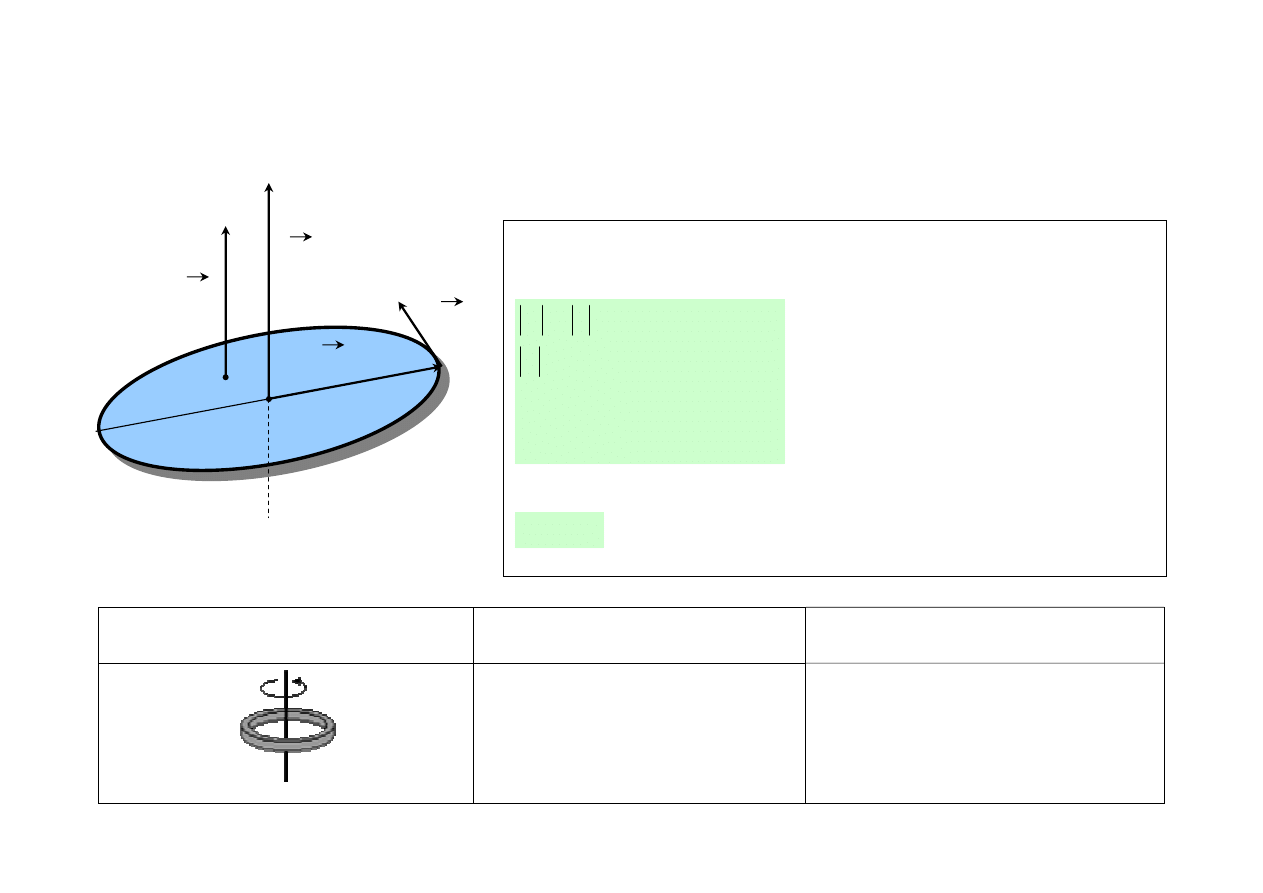
Moment bezwładności obręczy

Cienka obręcz kołowa o masie M i promieniu R wykonująca ruch obrotowy względem osi przechodzącej

przez środek masy i prostopadłej do płaszczyzny obręczy.

Rys. 33

Rysunek

Wzór na moment

bezwładności

Opis

I = mR

2

Pierścień o promieniu R

(także cylinder i obręcz)

R

v

n

r

n

J

ω

oś obrotu

cienka obręcz kołowa o masie M

i promieniu R

M

Prędkość liniowa i kątowa wszystkich Punktów materialnych, z których

składa się obręcz jest taka sama:

ω

ω

2

i

i

i

i

i

MR

MRv

J

v

R

M

)

v

r

(

m

J

R

r

r

v

v

=

=

×

=

×

=

=

⋅

=

=

∑

r

r

r

r

v

r

r

r

Z definicji, moment bezwładności obręczy względem osi obrotu wynosi:

2

MR

I

=

12

•

Ciało sztywne o dowolnym kształcie i dowolnym rozkładzie masy

•

ω

r

r

I

J

=

, gdy J równoległe do

ω

• Na ogół J nie jest równoległe do

ω

. Jest tak w przypadku, gdy wypadkowy ruch obrotowy jest złożeniem

wielu ruchów.

Składowe wektora momentu pędu:

)

J

,

J

,

J

(

J

z

y

x

r

r

r

r

=

Składowe wektora prędkości kątowej:

)

,

,

(

z

y

x

ω

ω

ω

ω

r

r

r

r =

Związek między J i

ω

ma postać równania macierzowego:









































=





















z

y

x

zz

zy

zx

yz

yy

yx

xz

y

xx

z

y

x

I

I

I

I

I

I

I

Ix

I

J

J

J

ω

ω

ω

• Moment bezwładności wyrażony jest za pomocą macierzy bezwładności (tensor bezwładności) o

własnościach:

Wyrazy poza przekątne są symetryczne, tzn.

zy

yz

zx

xz

yx

xy

I

I

,

I

I

,

I

I

=

=

=

Suma wyrazów przekątnych wynosi:

∑

=

+

+

2

i

i

zz

yy

xx

r

m

2

I

I

I

13

•

Ogólne wzory na obliczanie wyrazów macierzy bezwładności mają postać całkową

Rys. 34.

Gęstość materii bryły sztywnej w dowolnym punkcie

wynosi:

)

r

( r

ρ

Wektor położenia ma współrzędne

)

z

,

y

,

x

(

rr

0

x

y

z

r

ρ

Wyrazy przekątne macierzy bezwładności:

∫∫∫

−

=

dV

)

x

r

)(

r

(

I

2

2

xx

r

ρ

Podobna postać mają wzory na I

yy

i I

zz

.

Wyrazy poza przekątne tensora bezwładności:

∫∫∫

∫∫∫

−

=

−

=

xzdV

)

r

(

I

xydV

)

r

(

I

xz

xy

r

r

ρ

ρ

podobna postać mają pozostałe wyrazy.

Ponadto

∫∫∫

=

+

+

dV

r

)

r

(

2

I

I

I

2

zz

yy

xx

r

ρ

oraz wyrazy poza przekątne są symetryczne.

Obliczenia upraszczają się, gdy rozkład masy ciała

posiada wysoka symetrię względem osi obrotu.

14

TWIERDZENIE O OSIACH RÓWNOLEGŁYCH (Twierdzenie Steinera)

• Osie obrotu x i x’ są równoległe i odległe o odcinek a
• Oś x przechodzi przez środek masy CM, M = masa ciała

Rys. 35.

x

1

x

2

a

M

CM

Jakob Steiner

(1796 - 1863)

Twierdzenie:

Moment bezwładności bryły sztywnej względem dowolnej osi obrotu, równoległej do osi

przechodzącej przez środek masy, jest sumą momentu bezwładności względem osi przechodzącej

przez CM i iloczynu masy ciała przez kwadrat odległości między osiami obrotu.

2

x

'

x

Ma

I

I

+

=

15

ENERGIA ROTACJI = ENERGIA KINETYCZNA CIAŁA DOSKONALE SZTYWNEGO W RUCHU

OBROTOWYM

• Ciało doskonale sztywne wykonuje obrót wokół nieruchomego środka masy,
• Całkowita energia kinetyczna ciała jest równa sumie energii kinetycznych poszczególnych punktów
materialnych, z których ciało się składa:

∫∫∫

∑

∑

×

=

×

=

×

=

=

dV

)

r

)(

r

(

2

1

)

r

(

m

2

1

E

r

v

v

m

2

1

E

2

2

i

i

k

i

i

2

i

i

k

r

r

r

r

r

r

r

r

ω

ρ

ω

ω

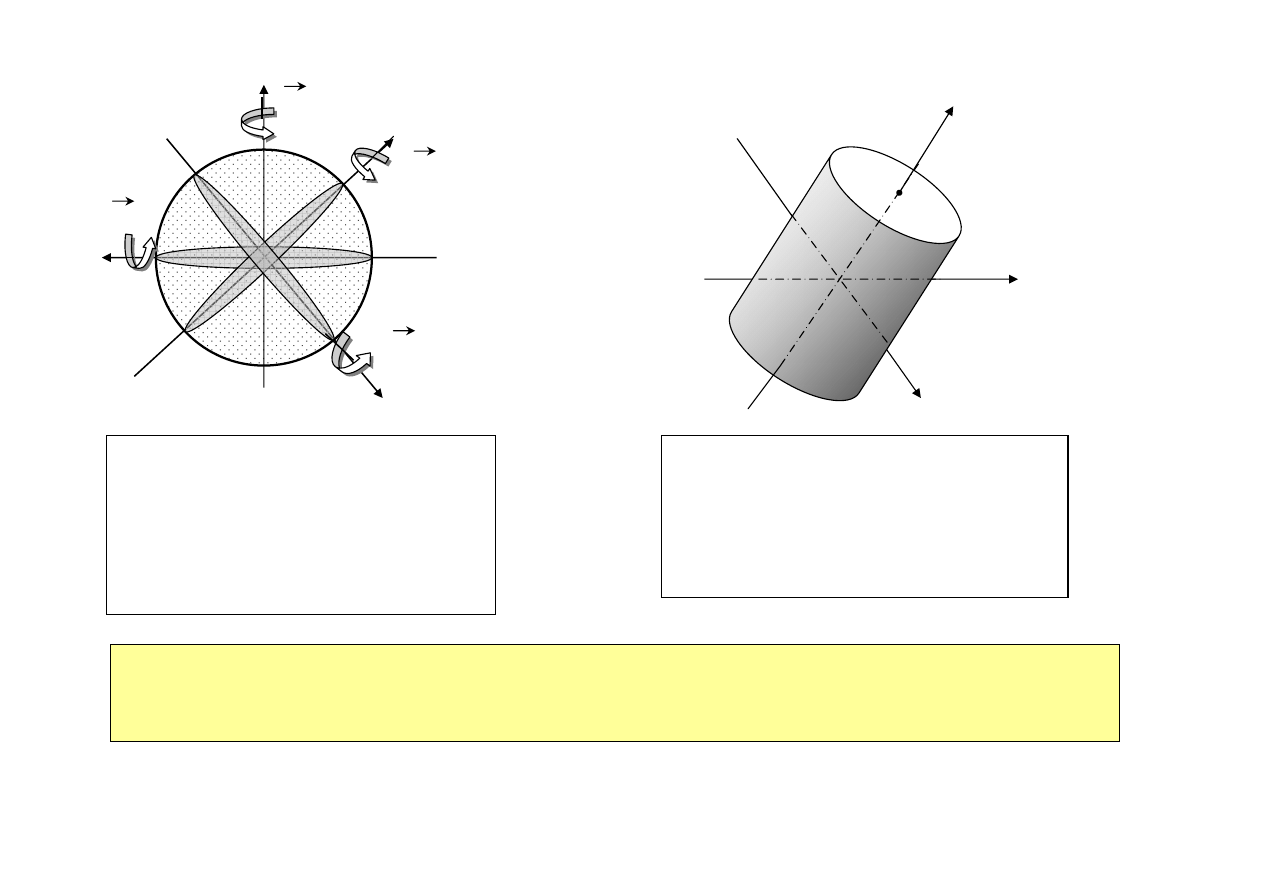
• Ciało o symetrii osiowej (stożek, walec, kula, itp.)

x

ω

Rys. 36.

16

OSIE GŁÓWNE CIAŁA

• Wzór na energię kinetyczną ciała można zapisać w postaci:

[

]

)

I

2

I

2

I

2

I

I

I

2

1

E

yz

z

y

yz

z

y

xy

y

x

zz

2

z

yy

2

y

xx

2

x

k

ω

ω

ω

ω

ω

ω

ω

ω

ω

+

+

+

+

+

=

Wyrażenie powyższe upraszcza się dla ciał o regularnym kształcie w układzie tzw. osi głównych ciała.

• Definicja osi głównych:
W układzie osi głównych wyrażenie na energię kinetyczną przyjmuje postać:

2

3

3

2

2

2

2

1

1

2

z

zz

2

y

yy

2

x

xx

k

I

2

1

I

2

1

I

2

1

I

2

1

I

2

1

I

2

1

E

ω

ω

ω

ω

ω

ω

+

+

=

+

+

=

Indeksy 1, 2, 3 numerują osie główne ciała: osie obrotu o największej, najmniejszej i pośredniej wartości momentu

bezwładności

• W układzie osi głównych moment pędu posiada składowe

(

)

3

3

3

2

2

2

1

1

1

3

2

1

I

J

I

J

I

J

J

.

J

.

J

J

ω

ω

ω

=

=

=

r

r

r

r

2

k

2

2

3

2

2

2

1

3

2

1

J

2

1

E

I

I

I

I

ω

ω

ω

ω

ω

=

=

=

=

=

=

=

I

1

, I

2

, I

3

- główne momenty bezwładności (maksymalny, minimalny, pośredni)

• Jeżeli ciało obraca się wokół którejś z osi głównych, to wektor momentu pędu ciała jest równoległy do

wektora prędkości kątowej.

17

CM

(1)

(2)

(3)

CM

ω

ω

ω

ω

Rys. 37.

Rys. 38.

• Walec jednorodny – oś podłużna i

dwie osie do niej prostopadłe są

osiami głównymi.

• Ciało sztywne wirujące swobodnie wokół osi o maksymalnym lub minimalnym momencie

bezwładności zachowuje stały kierunek tej osi w przestrzeni (zasada działania stabilizatorów).

• Kula, powłoka kulista

o jednorodnym rozkładzie masy –

wszystkie osie przechodzące przez

środek masy są osiami głównymi.

18

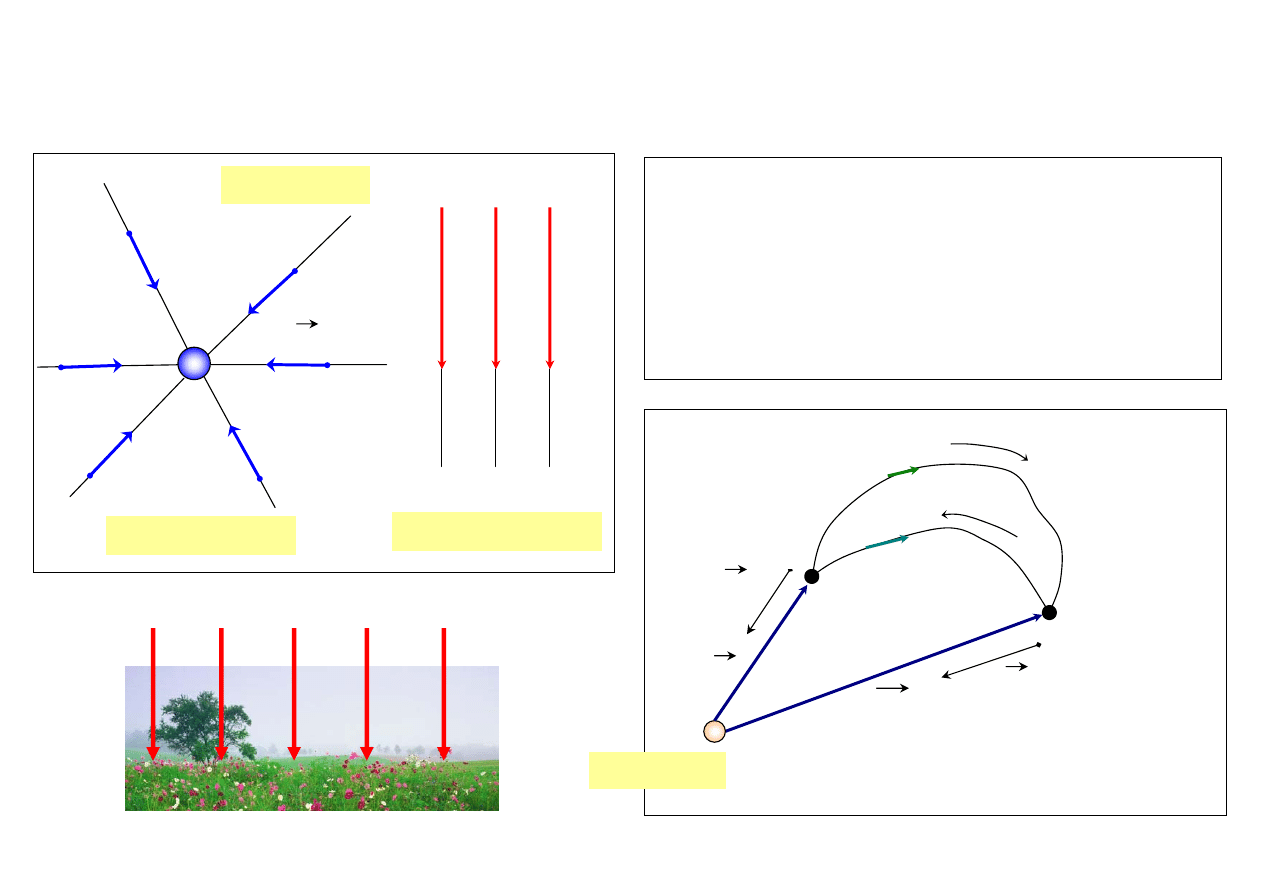
PRAWA ZACHOWANIA W MECHANICE (PĘDU, ENERGII, MOMENTU PĘDU)

•

PRAWO ZACHOWANIA PĘDU

• Całkowity pęd cząstek (ciał) tworzących układ zamknięty (izolowany) pozostaje stały w czasie
UKŁAD IZOLOWANY = układ na który nie działają siły zewnętrzne

[

]

i

i

i

i

i

n

n

3

3

2

2

1

1

v

m

p

)

t

,

t

(

const

v

m

v

m

...

v

m

v

m

v

m

P

r

r

r

r

r

r

r

r

=

+∞

=

−∞

=

=

=

+

+

+

+

=

∑

• Klasycznie, masa i-tej cząstki

m

i

=const

• Relatywistycznie, masa i-tej cząstki wynosi

2

2

i

i

0

i

i

i

c

v

1

1

m

m

−

=

=

γ

γ

0

z

x

r

r

y

v

1

m

1

m

i

v

i

v

2

m

2

r

i

Układ izolowany

Rys.39.

19

•

PRAWO ZACHOWANIA ENERGII

• Całkowita energia izolowanego układu cząstek (ciał) pozostaje stała w czasie
Układ izolowany = układ, który nie wymienia energii z otoczeniem

)

,

(

)

(

+∞

=

−∞

=

=

=

t

t

const

r

E

E

p

k

r

∑

∑

=

=

pi

p

ki

k

E

E

E

E

• Klasycznie, energia kinetyczna i-tej cząstki wynosi:

2

i

i

ki

v

m

2

1

E

=

• Relatywistycznie:

2

i

0

i

ki

c

m

)

1

(

E

−

=

γ

• Energia potencjalna E

p

(r) jest określona dla potencjalnego pola sił, tj. pola sił zachowawczych

(grawitacyjnych, kulombowskich)

•

PRAWO ZACHOWANIA MOMENTU PĘDU

• Całkowity moment pędu izolowanego układu cząstek (ciał) pozostaje stały w czasie
Układ izolowany = układ, na który nie działa zewnętrzny moment sił, lub wypadkowy moment sił jest

równy zeru

0

N

N

)

t,

t

(

p

r

v

r

m

J

J

i

i

i

i

i

i

i

=

=

+∞

=

−∞

=

×

=

×

=

=

∑

∑

∑

∑

r

r

r

r

r

r

r

r

20

RUCH CIAŁ W POTENCJALNYM POLU SIŁ

m

m

F

N

S

Pole centralne

Pole niecentralne

linie sił pola

M

Centralne pole sił - pole sił, w którym linie sił są

półprostymi zbiegającymi się w jednym punkcie, np.

pole grawitacyjne masy punktowej, pole elektrostatyczne

ładunku punktowego. Siła działająca między ciałami jest

zawsze skierowana wzdłuż prostej łączącej ciała.

Rys. 40.

r

1

F

2

F

1

(1)

(2)
m

l

1

l

2

m

M

centrum sił

punkt pola

punkt pola

r

2

Rys.41.

21

POLE GRAWITACYJNE MAS PUNKTOWYCH

• Siłę działającą między dwoma masami punktowymi można zapisać za pomocą wzoru, który wyraża

matematyczna postać prawa powszechnego ciążenia (prawa grawitacji, prawa Newtona).

2

2

11

2

/

10

67

.

6

)

(

kg

m

N

G

r

r

r

Mm

G

r

F

⋅

⋅

=

−

=

−

r

r

r

Rys. 42

r

M

m

F

- F

22

NATĘŻENIE POLA GRAWITACYJNEGO

Rys. 43

M r

F

g

g

M - masa ciała wytwarzającego pole grawitacyjne,

m – masa ciała „próbnego”

Miarą natężenia pola grawitacyjnego jest siła działająca

na ciało o masie jednostkowej, umieszczone w danym

punkcie pola:

m

F

g

r

r =

Gdy oddziaływają masy punktowe, wzór na

g przybiera postać:

r

r

r

M

G

g

2

r

r −

=

Wartość natężenia pola grawitacyjnego opisuje dynamiczne własności pola: zależy tylko od masy ciała

wytwarzającego pole i położenia punktu pola w przestrzeni; nie zależy od własności ciała próbnego.

23

PRACA W POLU GRAWITACYJNYM

• Ciało o masie M wytwarza pole.
W polu tym przemieszczamy masę próbną z punktu 1 do punktu 2.

r

r

)

r

(

F

)

r

(

F

r

r

r

−

=

Praca wykonana podczas przemieszczenia ciała:

)

(

1

1

)

(

2

1

2

3

2

1

2

1

2

1

2

1

rdr

r

d

r

r

r

GMm

r

GMm

r

dr

GMm

r

d

r

r

GMm

r

d

r

F

W

r

r

r

r

r

r

r

r

=

⋅













−

−

=









=

−

=

⋅

−

=

⋅

=

∫

∫

∫

r

r

r

r

r

r

r

• Praca wykonana przez siły pola. Ciało o masie m znajduje się pod wpływem siły grawitacji i jego

położenie końcowe znajduje się bliżej źródła pola M:

0

W

r

r

1

2

>

⇒

<

• Praca wykonana przez siły zewnętrzne. Ciało ulega przemieszczeniu pod wpływem siły zewnętrznej,

powodującej oddalenie ciała od źródła pola :

0

W

r

r

1

2

<

⇒

>

• Siły grawitacyjne są siłami zachowawczymi ⇔ pole grawitacyjne jest polem zachowawczym

∫

∫

∫

=

•

⇒

•

=

•

=

0

r

d

F

r

d

F

r

d

F

W

2

r

)

2

l

(

1

r

2

r

)

1

l

(

1

r

r

r

r

r

r

r

Rys. 44.

r

1

m

l

2

l

1

M

r

2

24

ENERGIA POTENCJALNA CIAŁA W POLU SIŁ GRAWITACYJNYCH

• Praca wykonana w polu grawitacyjnym jest równa różnicy energii potencjalnej ciała w położeniu

początkowym i końcowym

)

r

(

U

)

r

(

U

r

d

F

W

2

1

2

r

1

r

r

r

r

r

−

=

=

∫

• Energia potencjalna ciała określona jest ujemnie













−

−

−

=

−

2

1

2

1

)

(

)

(

r

GMm

r

GMm

r

U

r

U

r

r

r

GMm

r

U

−

=

)

(

• Energia potencjalna ciała znajdującego się poza zasięgiem sił grawitacyjnych (w nieskończoności) jest

równa zeru

r

GMm

dr

)

r

(

F

dr

)

r

(

F

)

r

(

U

0

)

(

U

r

r

−

=

=

−

=

=

∞

∫

∫

∞

∞

Energia potencjalna ciała w danym położeniu (w danym punkcie pola) jest równa pracy jaką trzeba

wykonać, aby ciało przenieść do nieskończoności (poza zasięg sił grawitacji).

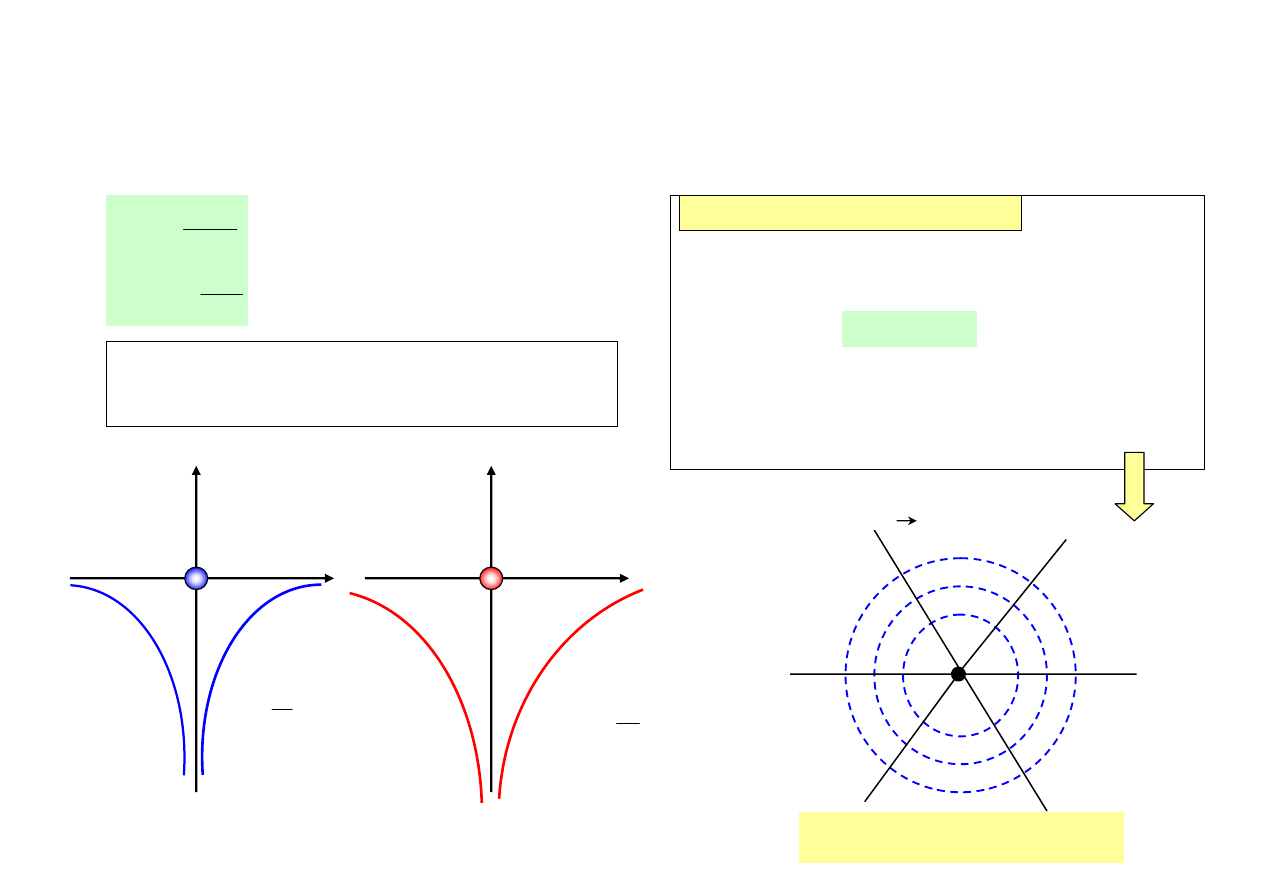
25

POTENCJAŁ POLA GRAWITACYJNEGO

• Potencjał pola grawitacyjnego w odległości r od centrum sił jest równy energii potencjalnej ciała
próbnego o masie jednostkowej znajdującego się w danym punkcie pola

r

GM

)

r

(

U

m

)

r

(

U

)

r

(

−

=

=

r

r

ϕ

Rys. 45.

g (r)

r

M

-

G

2

r

M

- G

r

M

natężenie pola

r

ϕ

(r) lub U(r)

M

potencjał pola

(lub energia potencjalna)

Powierzchnie ekwipotencjalne (powierzchnie

jednakowego potencjału) stanowią zbiory geometryczne

punktów w przestrzeni, w których potencjał pola posiada tę

samą wartość, tzn.

const

)

r

(

=

r

ϕ

Jeżeli pole grawitacyjne wytwarza masa punktowa, to

powierzchnie ekwipotencjalne stanowią powierzchnie kul

współśrodkowych, otaczających masę punktową.

• Potencjał pola opisuje własności statyczne pola:
zasób energii potencjalnej, którą pole zawiera.

M

linie sił

powierzchnia ekwipotencjalna =

powierzchnia kuli

M - masa
punktowa

ϕ

(r) = const.

Rys. 46.

26

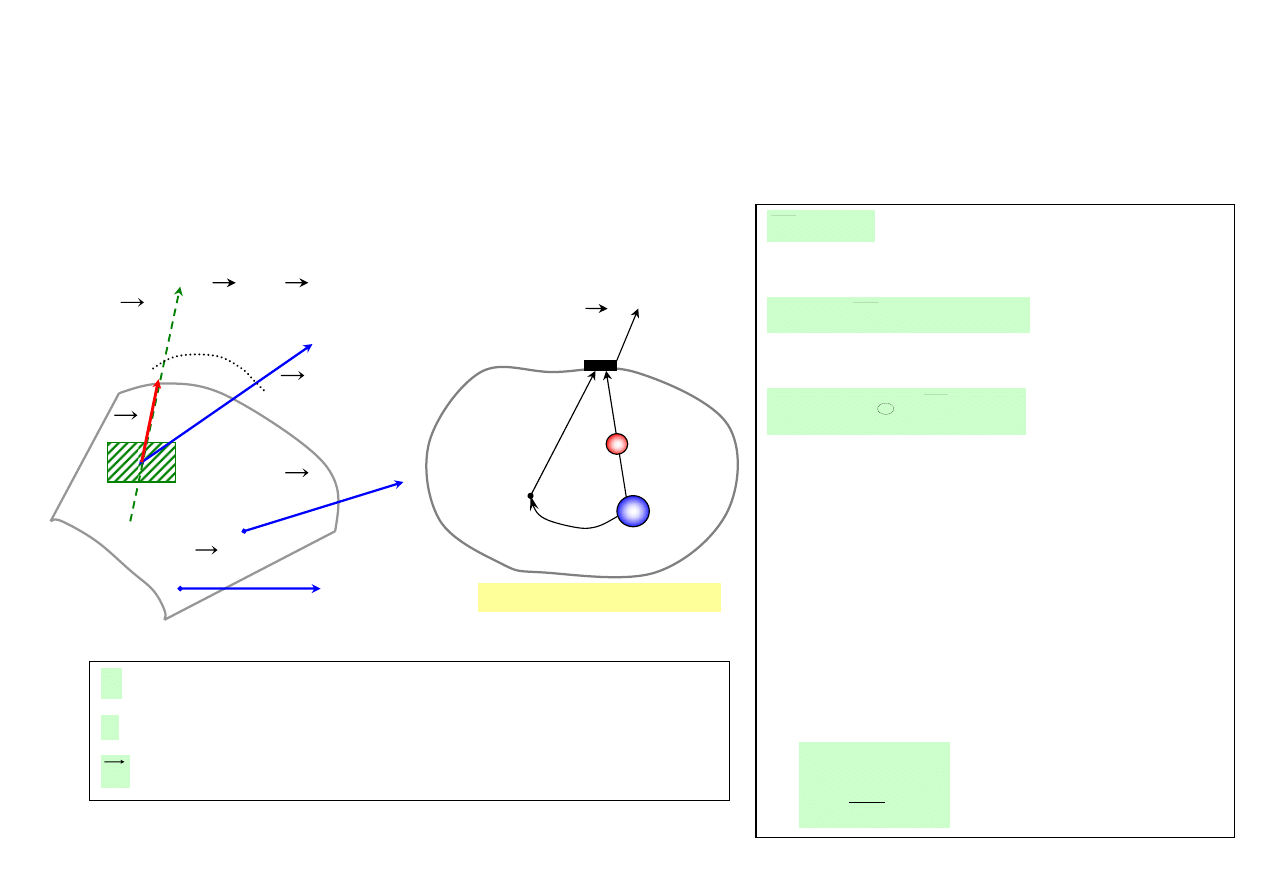
PRAWO GAUSSA DLA POLA GRAWITACYJNEGO

•

Strumień wektora natężenia pola (strumień pola grawitacyjnego) przez dowolna powierzchnię

zamkniętą jest równy iloczynowi masy znajdującej się w obszarze ograniczonym ta powierzchnią przez

(-4

π

G), gdzie G oznacza stałą grawitacji.

Rys. 47.

dS = ds

.

n

M

1

M

2

M

3

dS

S –

powierzchnia zamknięta

S

dS

n

dS

g

g

g

S

gr

- wektor natężenia pola

nr

- wektor jednostkowy o kierunku normalnej do powierzchni

dS

- wektor kierunkowy elementu powierzchni

n

dS

dS

r

⋅

=

• Elementarny strumień pola grawitacyjnego

)

,

cos( n

g

gdS

dS

g

d

r

r

r

=

⋅

=

Φ

Strumień pola przez powierzchnię zamkniętą S

∫

∫∫

−

=

⋅

=

Φ

=

Φ

G

dS

g

d

π

4

r

• Prawo Gaussa stosuje się do wyznaczania

natężenia pola, zwłaszcza w przypadkach

pół wytwarzanych przez układ ciał. W

przypadku pola wytwarzanego przez masę

punktową.

• Prawo Gaussa ma wyjątkowo uproszczoną

postać:

2

2

4

4

r

GM

g

GM

r

g

−

=

−

=

⋅

π

π

27

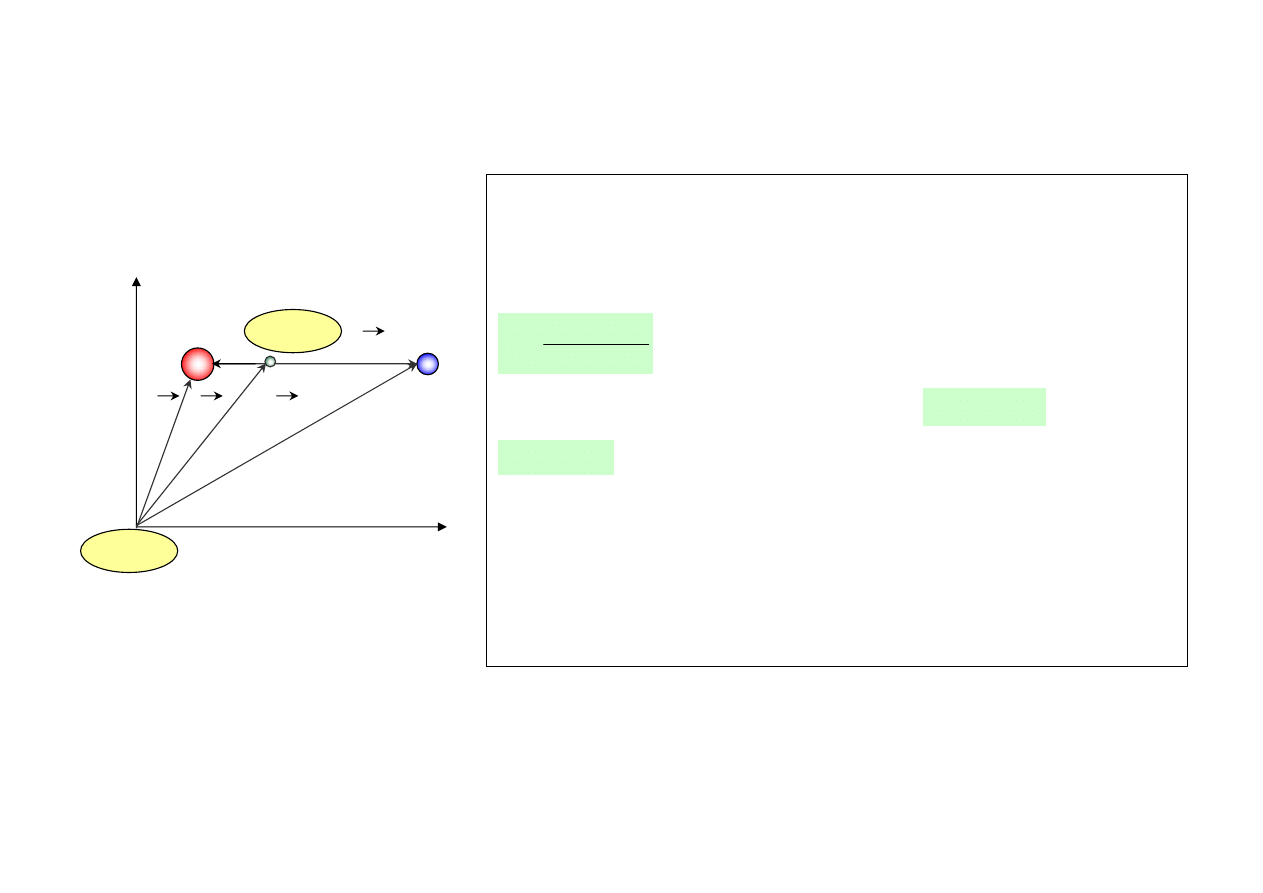
RUCH CIAŁ W POLU SIŁ CENTRALNYCH

• Rozważamy oddziaływanie dwóch ciał o porównywalnych masach w układzie laboratoryjnym i układzie

środka masy

Rys. 48.

0

r

M

LAB

x

y

r

o

r

m

M

CM

r

m

Dwa ciała o masie M i m, ich położenie względem początku układu

laboratoryjnego określają wektory

M

rr

i

m

rr

Położenie środka masy CM wyznacza wektor

0

rr

m

M

r

m

r

M

r

m

M

0

+

+

=

r

r

r

Ciała oddziałują ze sobą siłami centralnymi

)

r

(

F

),

r

(

F

r

r

r

r

−

, gdzie

m

M

r

r

r

r

r

r

−

=

• Wskutek oddziaływania ciała wykonują ruch obrotowy wokół

środka masy, którego opis jest skomplikowany w układzie

laboratoryjnym (wymaga rozwiązania układu różniczkowych

równań ruchu).

28

Rys.49.

M

CM

m

µ

r = r

m

- r

M

• Jeżeli siła jest siłą centralną, to moment tej siły względem

rozważanego środka masy jest równy zeru (ramię siły i jej

kierunek pokrywają się). Z drugiej zasady dynamiki dla

ruchu obrotowego wynika, że moment pędu układu ciał

jest wielkością stałą. Oznacza to również, że ruch jest

płaski (tory ciał leżą w jednej płaszczyźnie).

• Opis ruchu ciał, ich energii, znacznie się upraszcza w układzie środka masy, jeżeli wprowadzimy

ciało o masie zastępczej, tzw. masie zredukowanej, i rozważać będziemy zachowanie się tego ciała.

Sprowadzamy w ten sposób problem opisu ruchu dwóch ciał, oddziaływujących siłami centralnymi,

do problemu opisu ruchu jednego ciała o masie równej masie zredukowanej:

(

)

m

1

M

1

1

m

M

Mm

+

=

+

=

µ

µ

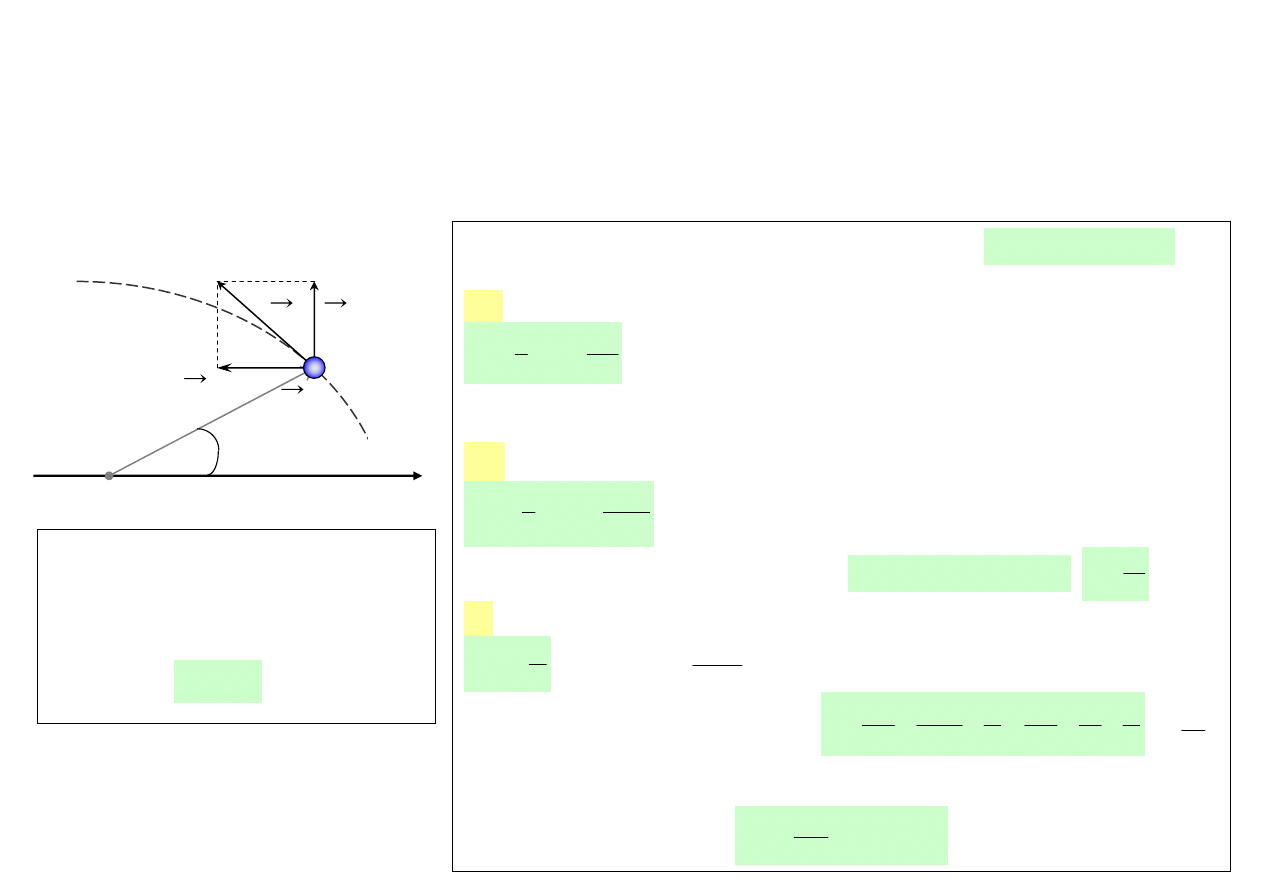
29

ENERGIA CIAŁA W POLU SIŁ CENTRALNYCH

• Układ środka masy ciał, w którym opisujemy ruch masy zredukowanej, stanowić może biegunowy układ

współrzędnych. Masa zredukowana

µ

porusza się po torze krzywoliniowym, a jej chwilowe położenie

wyznacza wektor r i kąt

ϕ

.

Rys. 50.

v

tor

r

ϕ

v

r

v

ϕ

CM

r

µ

Chwilowe wartości prędkości

całkowitej oraz jej składowych, tzw.

radialnej i azymutalnej wynoszą

odpowiednio

ϕ

v

v

v

r

r

r

r

,

,

•

Całkowita energia układu

⇔

energia masy zredukowanej

p

k

kr

E

E

E

E

+

+

=

ϕ

r

k

E

- energia kinetyczna związana z prędkością radialną

µ

µ

2

p

v

2

1

E

2

r

2

r

kr

=

=

(1)

r

r

v

p

µ

=

jest

składową radialną pędu masy zredukowanej

ϕ

k

E

- energia kinetyczna związana z prędkością azymutalną

2

2

2

k

r

2

J

v

2

1

E

µ

µ

ϕ

ϕ

=

=

(2)

Moment pędu jest wielkością stałą w czasie:

const

r

v

r

p

J

=

=

=

ϕ

ϕ

µ

r

J

v

µ

ϕ

=

p

E

- energia potencjalna układu ciał w polu sił centralnych

r

A

E

p

−

=

(3)

)

(

r

GMm

E

p

−

=

•

Energia całkowita masy zredukowanej

r

A

r

B

p

r

A

r

J

p

E

r

r

−

+

=

−

+

=

2

2

2

2

2

2

2

2

µ

µ

µ

µ

2

2

J

B

≡

•

Energia całkowita masy zredukowanej jest funkcją położenia ciała

const

)

r

(

U

2

p

)

r

(

E

2

r

=

+

=

µ

30

Rys. 51.

• Jeżeli jedno z ciał wytwarzających pole grawitacyjne posiada dużą masę tak, że M >> m, to środek

masy układu pokrywa się z położeniem ciała o masie M. Wówczas wartość masy zredukowanej układu

ciał jest w przybliżeniu równa masie ciała mniejszego m, zaś r oznacza odległość ciała m od centrum sił

(M). Warunki te są spełnione np. w naszym układzie planetarnym, modelu planetarnym atomu.

U (r)

E

E

1

0

E

2

r

1

r

2

µ

2

2

p

r

r

2

r

B

r

A

−

• Całkowita energia masy zredukowanej
może być dodatnia lub ujemna. I tak:

Gdy E>0 (np. E

1

) ruch ciała po krzywej

stożkowej otwartej (parabola, hiperbola).

Gdy E<0 (np. E

2

) ruch ciała po

krzywej stożkowej zamkniętej (elipsa,

koło).

Na rysunku r

1

i r

2

oznaczają odległości największego

i najmniejszego oddalenia ciała od centrum sił.

31

SIŁY GRAWITACJI WE WSZECHŚWIECIE

• Kształt Galaktyki, model Hubble’a

Gaz kosmiczny o masie M składający się z pojedynczych obiektów, z których jeden posiada masę np. M

1

.

Masa posiada moment pędu J=const.

Rys. 52.

• Obłok gazu kurczy się pod wpływem oddziaływania grawitacyjnego

Kształt galaktyki (Model Hubble’a)

J

o

M - masa galaktyki
M

1

– masa pojedynczej cząstki

M

1

M

Edwin Powell Hubble

(1889 – 1953)

32

Rys. 53.

r

r

v

v

vr

M

r

v

M

const

J

0

0

1

0

0

1

=

=

=

• Zmiana energii kinetycznej cząstki M

1

wskutek pracy sił grawitacyjnych jest równa zmianie jej energii

potencjalnej i wynosi :

Ep

Ek

r

r

v

M

v

M

v

M

E

k

∆

=

∆













−

=

−

=

∆

1

)

(

2

1

2

1

2

1

2

0

2

0

1

2

0

1

2

1

• Energia potencjalna obiektu M

1

wynosi:

2

0

2

0

1

1

J

g

p

r

r

v

M

2

1

r

GMM

E

E

E













+

−

=

+

=

r

r

o

v

v

o

CM

M

1

gdzie indeks „0” określa wartość prędkości i położenia masy M

1

w chwili t = 0,

wielkości bez indeksu – w dowolnej chwili czasu t

E

p

0

r

τ

min

E

min

E

J

∼ 1 / r

2

E

g

∼ - 1 / r

Rys. 54.

33

• Kurcząc się grawitacyjnie, obłok gazu osiąga stan równowagi. W stanie równowagi cząstki obłoku

posiadają najmniejsza wartość energii potencjalnej (energia potencjalna osiąga minimum). Minimum energii

określa warunek:

0

r

r

v

M

r

M

GM

0

dr

dE

3

2

0

2

0

1

2

1

p

=

−

=

dla r = r

min

GM

r

v

r

2

0

2

0

min

=

Przypuszczalny widok Drogi Mlecznej z boku i z góry z zaznaczonym

położeniem Słońca.

J

Słońce

Słońce

Rys. 55.

• Galaktyka „naprawdę” posiada kształt dysku

• W przypadku naszej Galaktyki r

min

~ 10

20

m

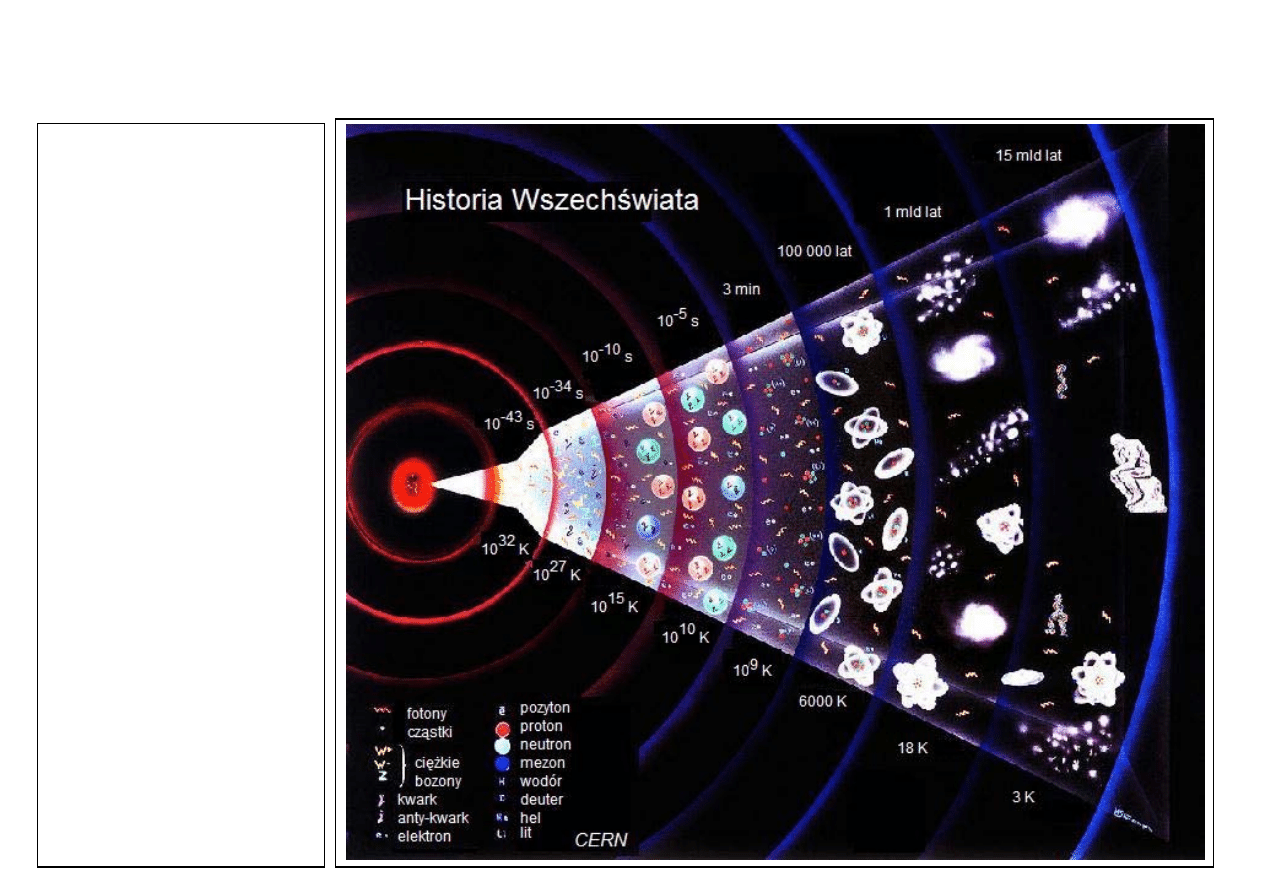
34

NIEKTÓRE PROBLEMY KOSMOLOGII

• rozszerzanie się
Wszechświata

• gęstość krytyczna i los
Wszechświata

• wiek Wszechświata
• wczesny Wszechświat,
jego temperatura, czas

trwania epoki leptonowej i

hadronowej

Kosmologia obejmuje:

- teorię grawitacji,

- fizykę jąder i cząstek

elementarnych,

- termodynamikę,

- fizykę statystyczną.