Modelowanie komputerowe

Modelowanie komputerowe

Arkadiusz Mandowski

Modelowanie komputerowe

Automaty komórkowe (cellular automata)

CA - dyskretne systemy dynamiczne, których zachowanie
jest w pełni określone poprzez lokalne reguły.

Automat komórkowy jest "wymyślonym wszechświatem", w
którym przestrzeń jest reprezentowana poprzez jednorodną
sieć z komórkami zawierającymi niewielką ilość informacji
(właściwości - stan komórki). Czas ma również charakter
dyskretny i jest określony przez kolejne generacje automatu.

Modelowanie komputerowe

Historia automatów komórkowych

•

John von Neumann (1903 -1957) - w latach 1930/40 stworzył teorię gier (z myślą o
ekonomii). Koncepcja automatu samo-powielającego się (kinematic beast -
factory/duplicator/controller/instructions - łącznie 200 000 komórek o 29 stanach).

•

Stanisław Ulam (1909 -1984) - twórca pierwszych gier komputerowych 2-D i 3-D. Gry
strategiczne na różnego rodzaju sieciach komórkowych (np. trójkątne, sześciokątne)
"obiekty geometryczne zdefiniowane rekursywnie".

•

John Horton Conway (1937- ) - matematyk w Gonville and Caius College
(Cambridge) potem Princeton. w 1970 r. uprościł automat von Neumann'a (game of
life). Teoria gier i teoria liczb.

•

Stephen Wolfram (1959 - ) - Eton/Oxford/Caltech; 1974 - pierwszy artykuł, 1979
Ph.D. (Caltech - fizyka teoretyczna). Fizyka wysokich energii, pól kwantowych,
kosmologia, dynamika cieczy. Od 1986 tworzy program Mathematica. 1982 -
klasyfikacja automatów komórkowych 1-D; (2002) książka New kind of science.

Modelowanie komputerowe

Gra w życie (game of life)

Zasady

1.

Przetrwanie: gdy żywa komórka ma 2 lub 3 sąsiadów

2.

Śmierć: gdy żywa komórka ma mniej niż 2 lub więcej niż 3

sąsiadów

3.

Narodziny: gdy martwa komórka ma dokładnie 3 sąsiadów

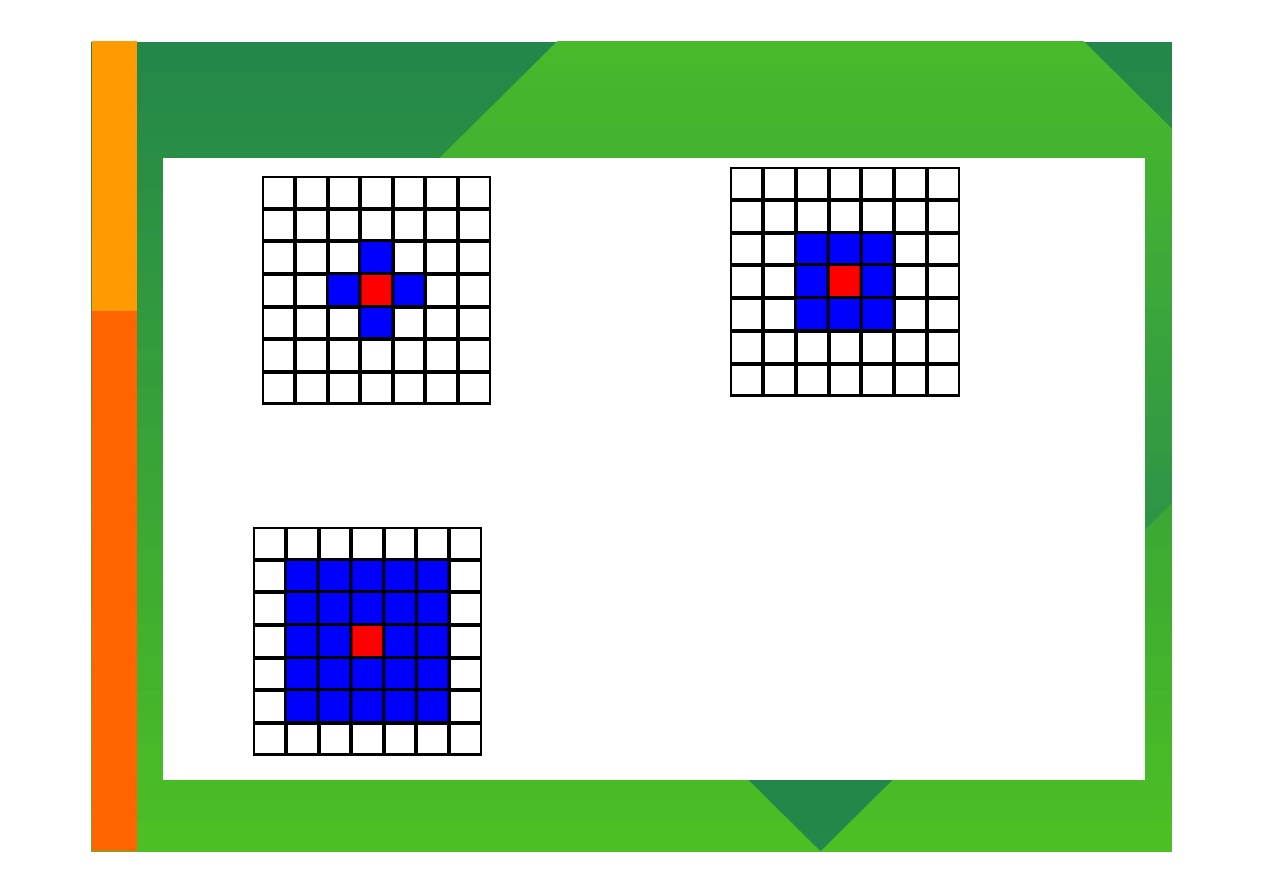
Modelowanie komputerowe

Typy sąsiedztwa (otoczenie - neighborhood)

otoczenie von Neumann’a

rozszerzone otoczenie
Moore’a

otoczenie Moore’a

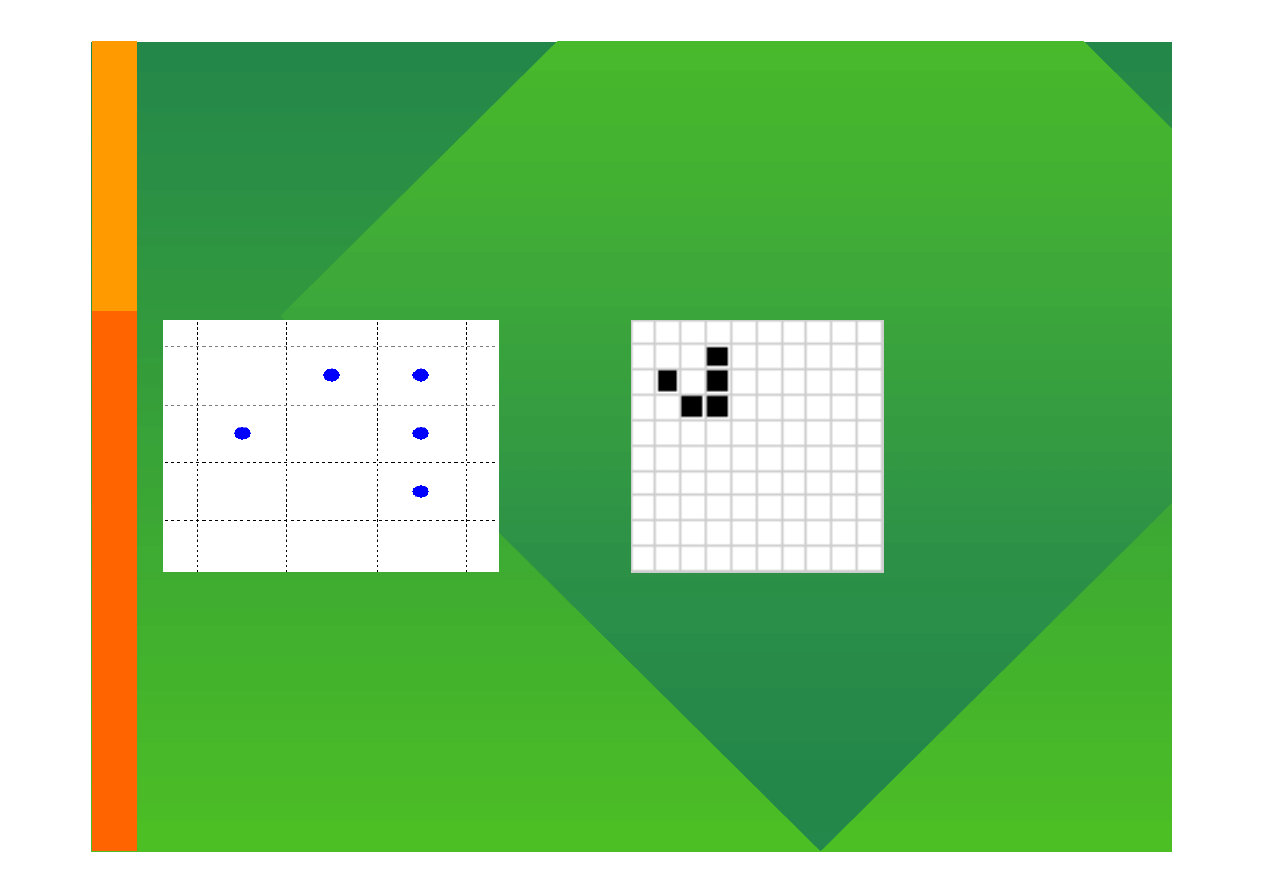
Modelowanie komputerowe

Glider (szybowiec)

Modelowanie komputerowe

Automaty komórkowe – definicja I

• Automat Komórkowy (AK) to sieć N komórek, z których każda jest w

jednym z k stanów w czasie t

• Każda z komórek podlega tym samym prawom rozwoju

• Stan komórki s w czasie t+1 zależy od jej własnego stanu, oraz stanu

pewnej liczby jej sąsiadów w chwili t

• Dla 1-D AK otoczenie komórki składa się z r sąsiadów po każdej

stronie, stąd parametrami AK są k i r

→ k

2r +1

możliwości różnego sąsiedztwa

→ k

k 2r +1

możliwych reguł ewolucji (typów AK)

Modelowanie komputerowe

Automaty komórkowe – definicja II

Zbiór (K, E, S, f) jest nazwany automatem komórkowym, jeżeli:

K jest siecią komórek

(i, j)

4
3
2
1

1 2 3 4

Modelowanie komputerowe

E jest zbiorem stanów elementarnych np:

np. E { zdrowy =

czarny

,

zakażony =

czerwony

,

uzdrowiony =

niebieski

}

S – sąsiedztwo (otoczenie)

i, j+1

i-1, j

i, j

i+1, j

i, j

i, j-1

Moore

Von Neumann

f – funkcja lokalna

nowy stan w
miejscu (i, j) = f ( sąsiedztwo (i, j) )

Modelowanie komputerowe

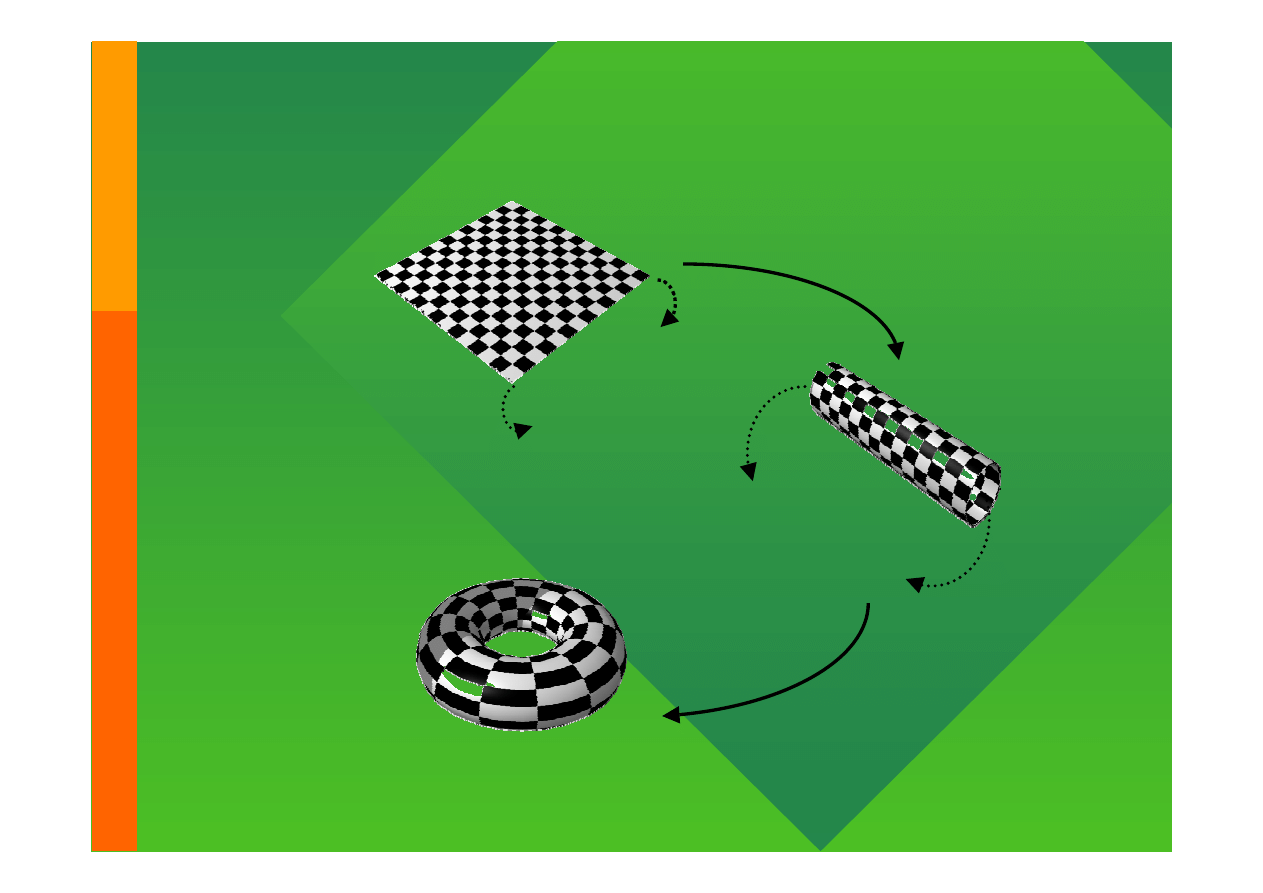
Problem nieskończoności - warunki brzegowe

Ograniczone

Periodyczne

Modelowanie komputerowe

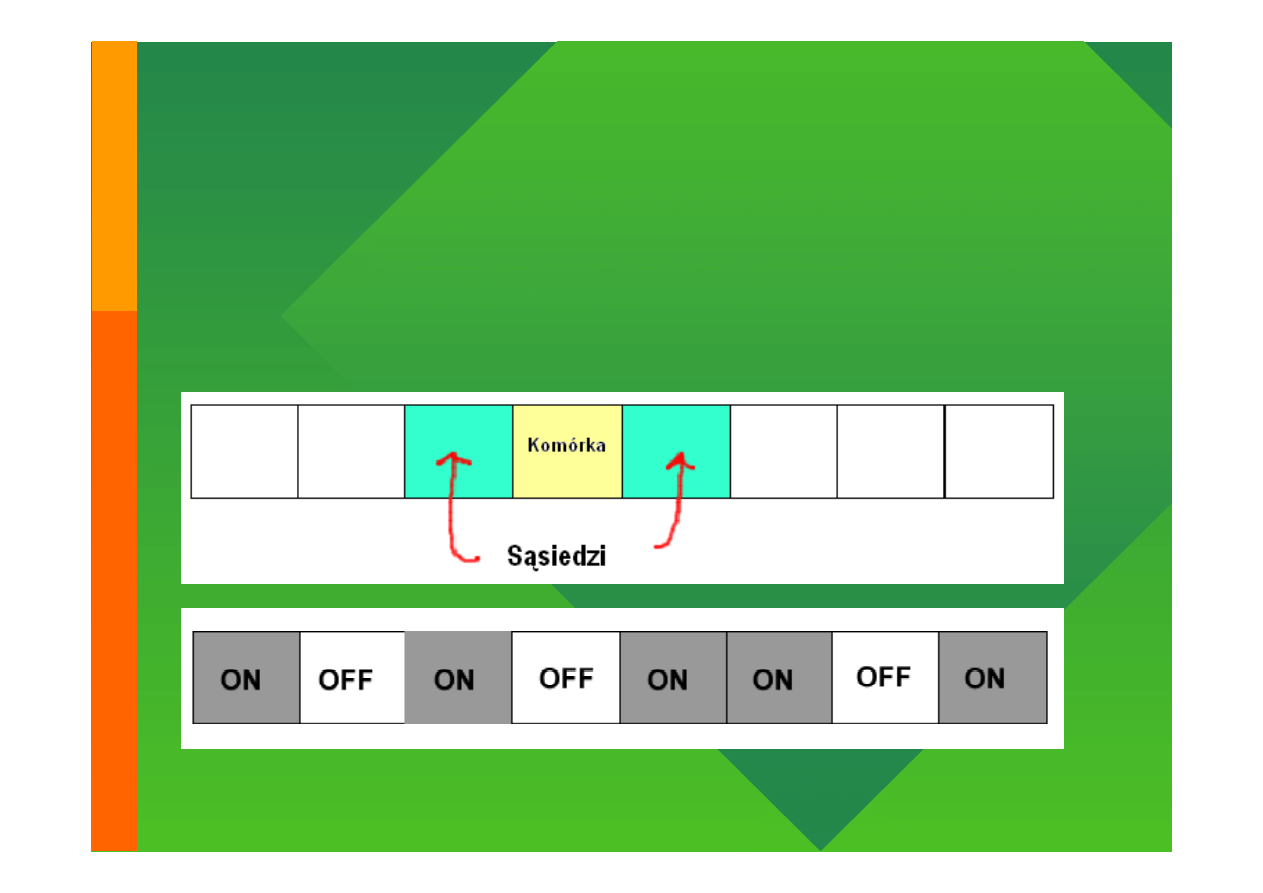
Automaty Jednowymiarowe (1-D)

Modelowanie komputerowe

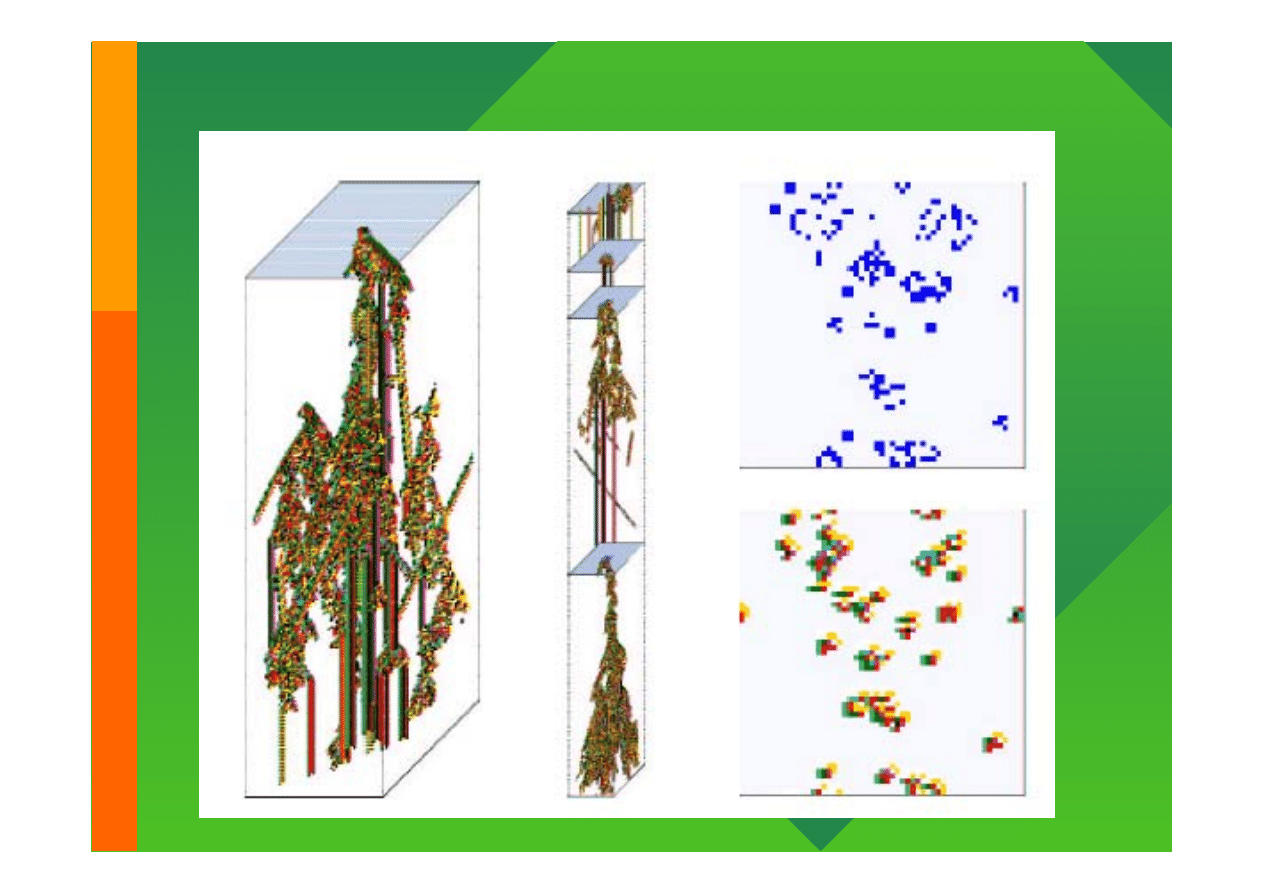
Automaty Dwuwymiarowe (2-D)

Modelowanie komputerowe

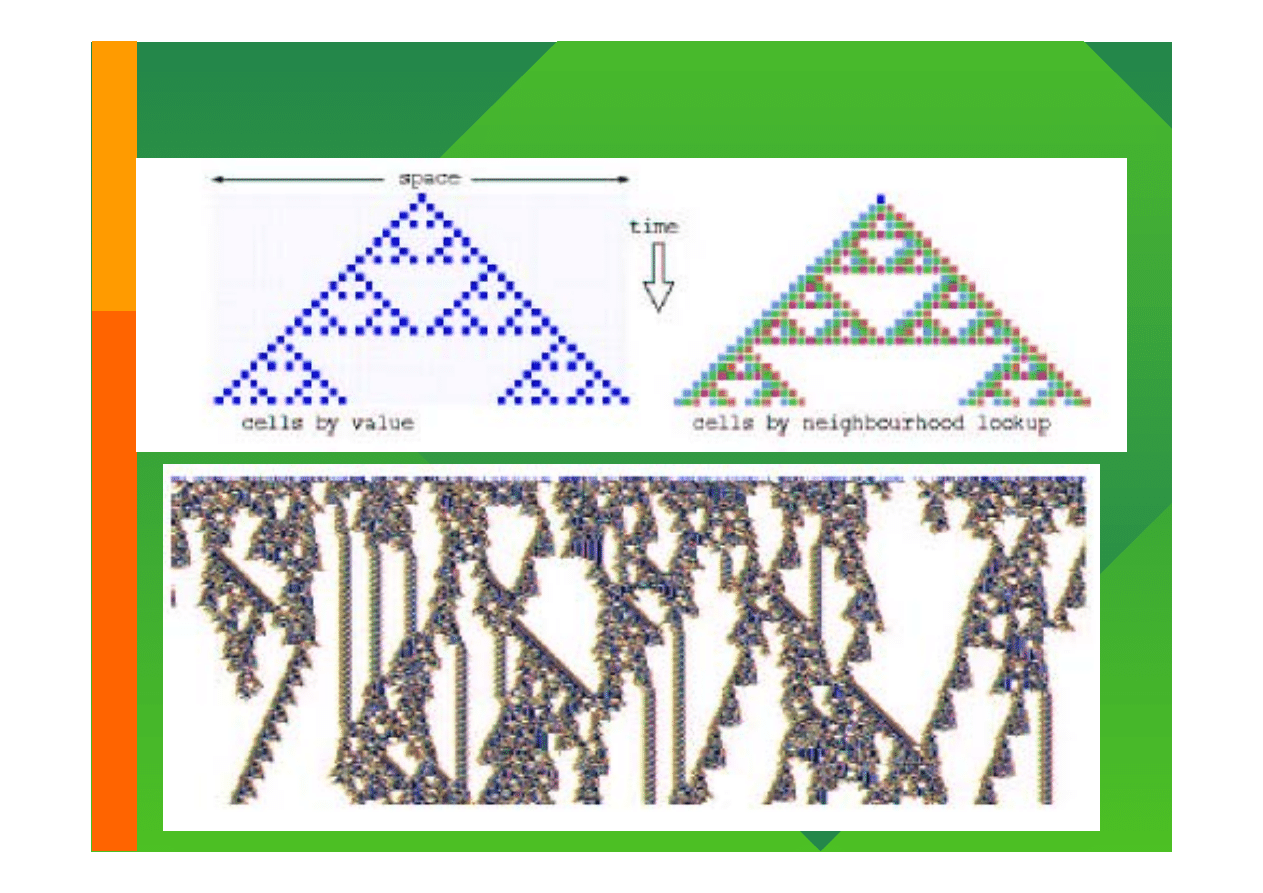
Automaty 1-D (Wolfram)

•

Jednowymiarowa sieć komórek z periodycznymi warunkami

brzegowymi

•

Każda komórka ma dwóch sąsiadów

•

Każda komórka znajduje się w jednym z dwu stanów

(np. 0, 1 – „OFF” i „ON”)

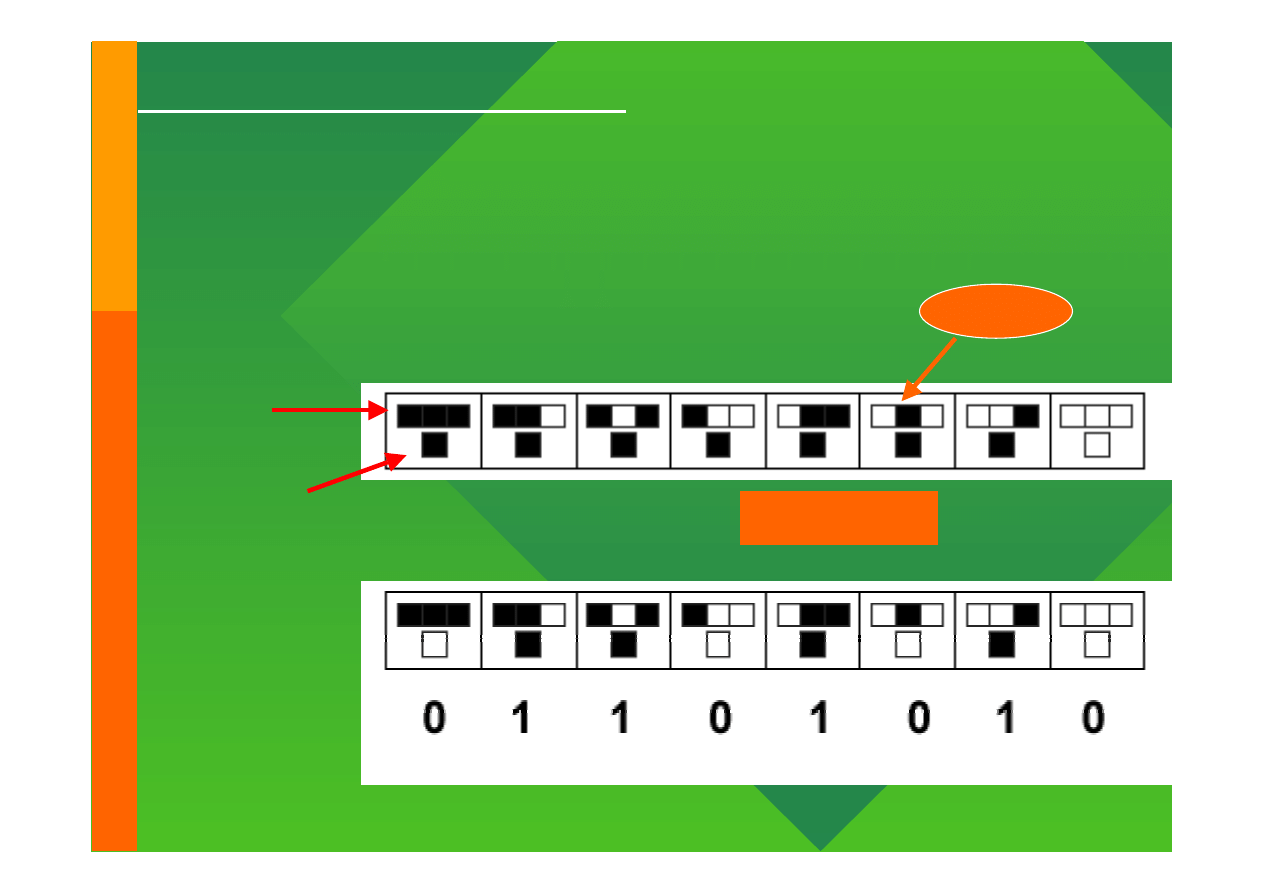
Modelowanie komputerowe

Klasyfikacja automatów 1-D

(CAR – Cellular Automata Rule)

Tryplet

•

Przyszły stan komórki określony jest przez:

–

aktualny stan komórki

–

stan jej sąsiadów

Typ sąsiedztwa

Kolejny krok

2

8

=256 reguł

CAR =

= 01101010|

2

=

= 106

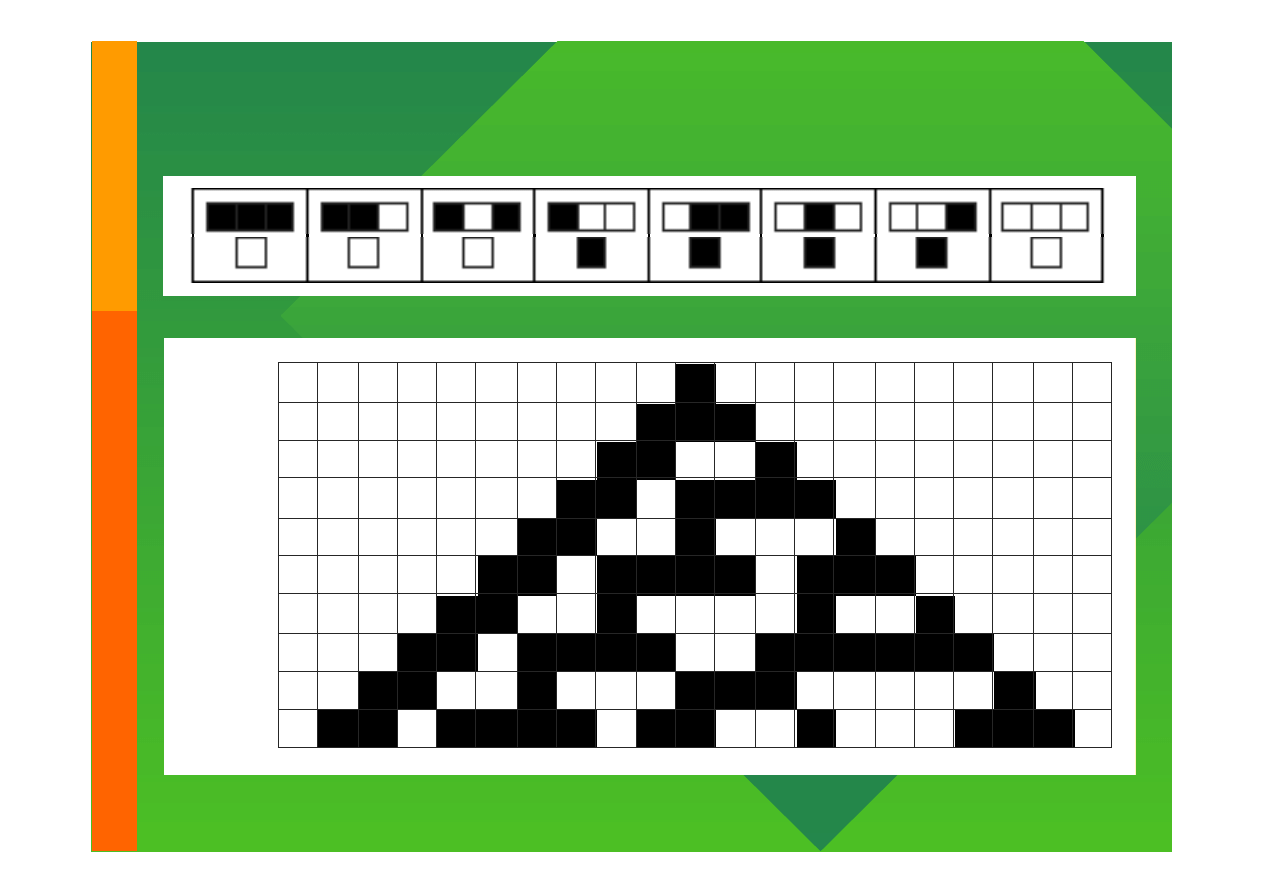
Modelowanie komputerowe

Przykład – CAR30

step 10:

step 9:

step 8:

step 7:

step 6:

step 5:

step 4:

step 3:

step 2:

step 1:

Modelowanie komputerowe

Klasy automatów komórkowych (Wolfram)

• Klasa 1: po skończonej liczbie kroków AK zmierza do

osiągnięcia określonego stanu wychodząc z niemal

każdych warunków początkowych

• Klasa 2: AK wytwarza struktury powtarzające się

periodycznie lub stabilne

• Klasa 3: prawie dla wszystkich warunków

początkowych AK zmierza do struktur aperiodycznych

(chaotycznych), których statystyczne właściwości

upodabniają się do struktur początkowych (samo-

podobieństwo fraktalne)

• Klasa 4: bardziej złożona; po skończonej liczbie

kroków AK zwykle wymiera; może pozostać jedynie

kilka stabilnych lub periodycznych struktur

Modelowanie komputerowe

Wirtualne mrówki Langton’a

1. Zacznij w dowolnym punkcie płaszczyzny euklidesowej

2. Wykonaj krok naprzód

3. Jeżeli stoisz na polu białym pokoloruj je na czerwono i

wykonaj zwrot o 90° w prawo

4. Jeżeli stoisz na polu czerwonym pokoloruj je na biało i

wykonaj zwrot o 90° w lewo

5. Przejdź do kroku 2 i powtarzaj dowolną ilość iteracji

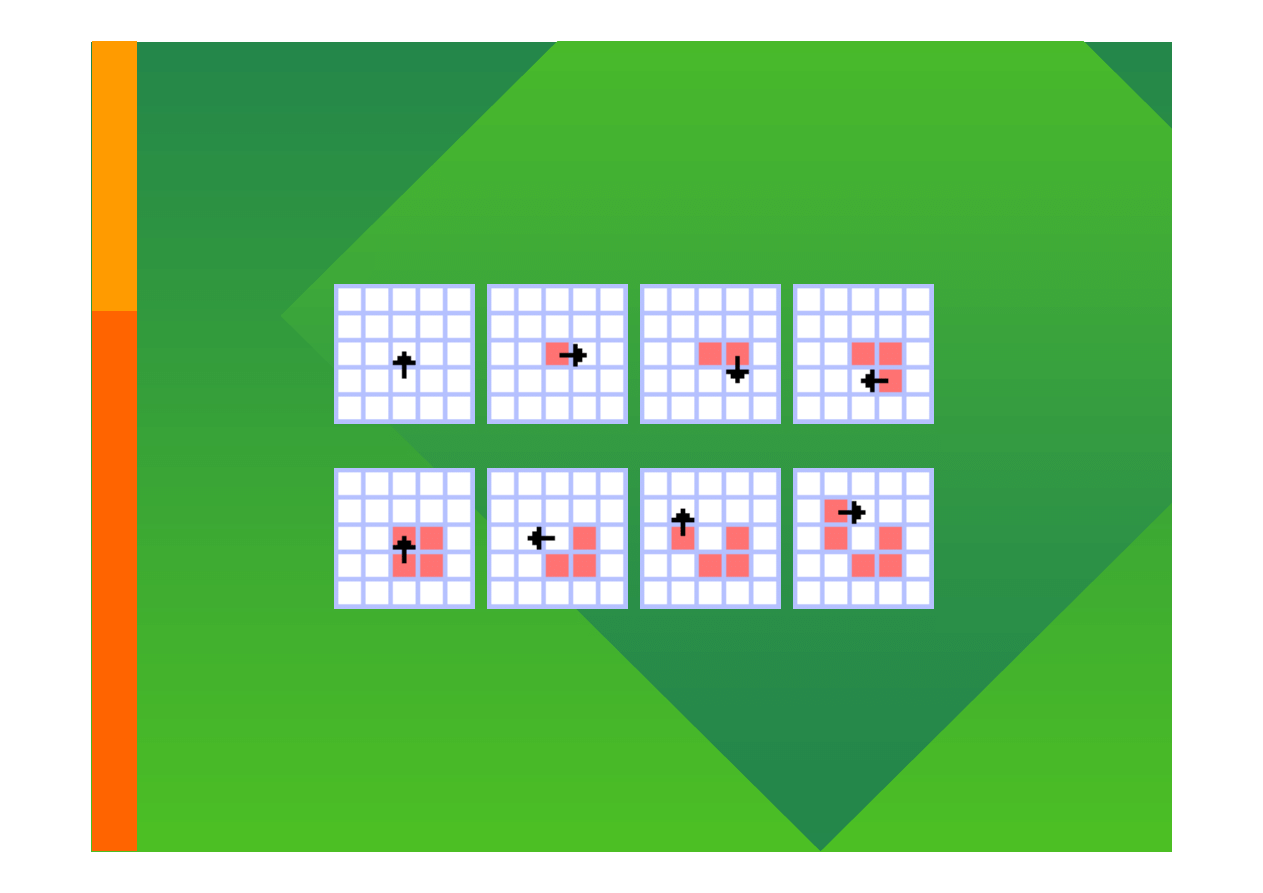
Modelowanie komputerowe

Mrówki Langton’a - przykład

1

2

3

4

5

6

7

8

Modelowanie komputerowe

Mrówki Langton’a - przykład

Pierwsze 10 000 iteracji wydaje się być chaotyczne.

W końcu „mrówki” formują ścieżkę

10 000 it.

12 000 it.

5 000 it.

Modelowanie komputerowe

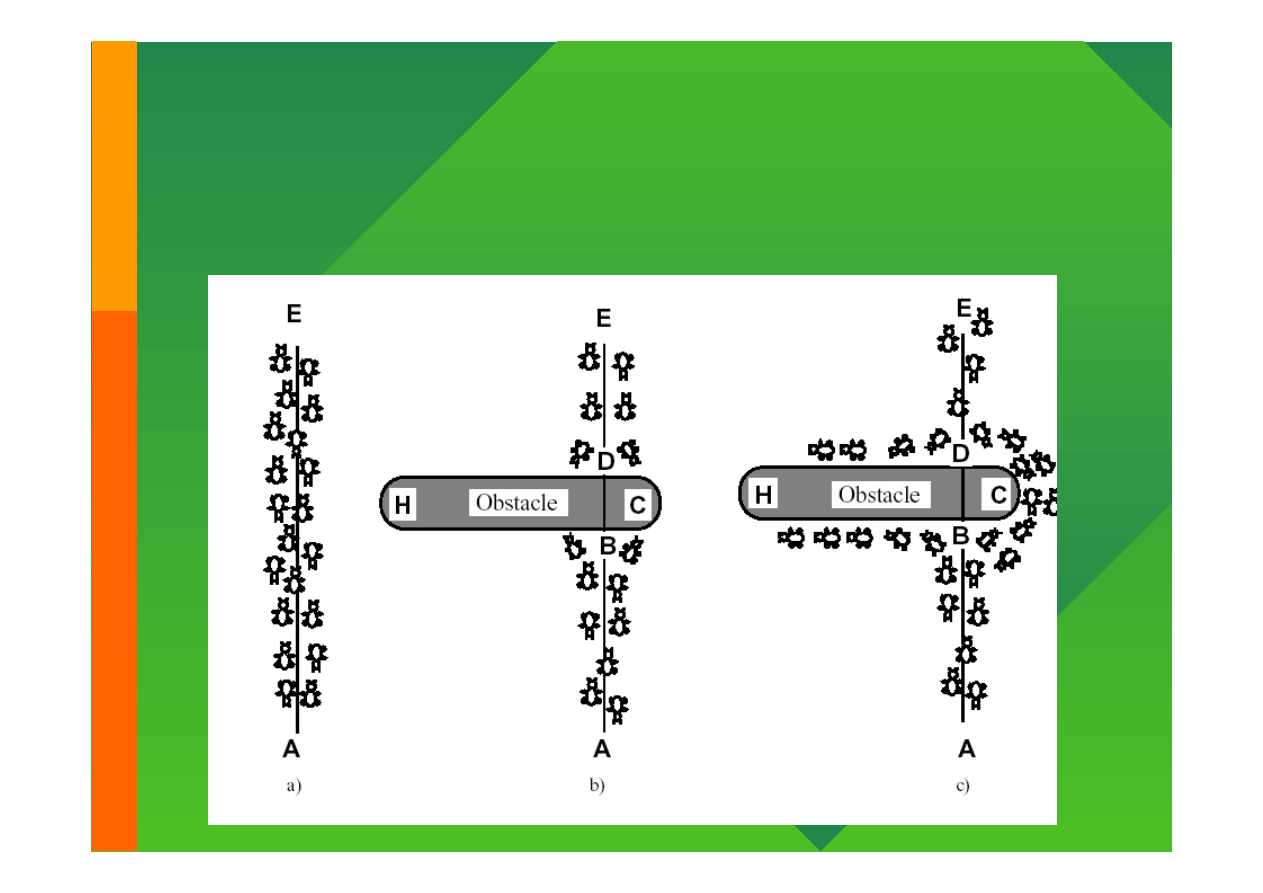
Optymalizacja drogi (Marco Dorigo)

a) Mrówki podążają z A do E.
b) Ustawiamy przeszkodę; mrówka może ją obejść z równym prawdopodobieństwem
c) Na krótszej ścieżce mrówki zostawiają więcej „feromonu”

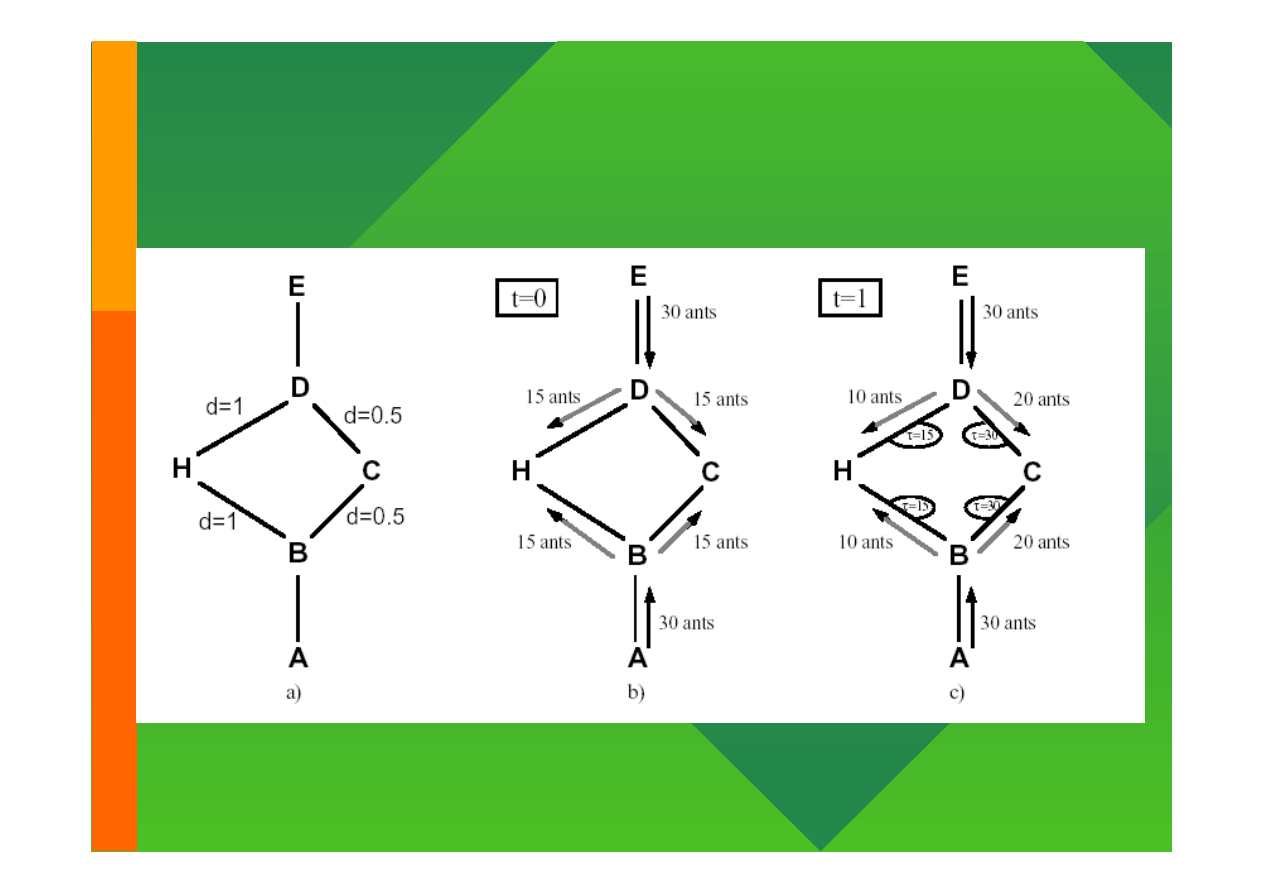
Modelowanie komputerowe

Optymalizacja drogi - zastosowanie