
1
Wykład 1,2
PROGNOZOWANIE WŁAŚCIWOŚCI MATERIAŁÓW
Inżynieria Materiałowa
ALGORYTMY I STRUKTURY DANYCH
1 SSI
Dr hab. inż. Barbara Dębska, prof. PWSZ
Algorytmy i struktury danych
WYKŁAD 1, 2
Złożoność algorytmów
Złożoność algorytmów
Dr hab. inż. Barbara Dębska, prof. PWSZ

2
Wykład 1,2
PROGNOZOWANIE WŁAŚCIWOŚCI MATERIAŁÓW
Inżynieria Materiałowa
ALGORYTMY I STRUKTURY DANYCH
1 SSI
Dr hab. inż. Barbara Dębska, prof. PWSZ
Literatura:
Obowiązujące podręczniki:
1. Niklaus Wirth, „Algorytmy + Struktury Danych = Programy”, WNT,
Warszawa 2000 (1980, 1999)
2. Lech Banachowski, Krzysztof Diks, Wojciech Rytter, „Algorytmy i
Struktury Danych”, WNT, Warszawa 1999 (1996)
3. David Harel, „Rzecz o Istocie Informatyki – Algorytmika”, WNT,
Warszawa 2000 (1992)

3
Wykład 1,2
PROGNOZOWANIE WŁAŚCIWOŚCI MATERIAŁÓW
Inżynieria Materiałowa
ALGORYTMY I STRUKTURY DANYCH
1 SSI
Dr hab. inż. Barbara Dębska, prof. PWSZ
Podręczniki pomocnicze:
1. Banachowski L., Diks K., Rytter W.,”Wprowadzenie do algorytmów”, WNT,
Warszawa 1997
2. Cormen T.H., Leiserson C.E., Rivest R.L., „Algorytmy i struktury danych”,
WNT, Warszawa 1996
3. Wróblewski P., ”Algorytmy, struktury danych i techniki programowania,
Helion”, Gliwice 1996
4. Sobczak W., Malina W., „Metody selekcji i redukcji informacji”, WNT,
Warszawa 1985
5. Aho A.V., Hopcropft J.E., Ullman J.D., „Projektowanie i analiza algorytmów
komputerowych”, PWN Warszawa 1983
6. Banachowski L., Kreczmar A., „Elementy analizy algorytmów”, WNT,
Warszawa 1982

4
Wykład 1,2
PROGNOZOWANIE WŁAŚCIWOŚCI MATERIAŁÓW
Inżynieria Materiałowa
ALGORYTMY I STRUKTURY DANYCH
1 SSI
Dr hab. inż. Barbara Dębska, prof. PWSZ
PODSTAWOWE ZASADY ANALIZY ALGORYTMÓW
Dziedziny na których bazuje teoria tworzenia i analizy algorytmów:
• podstawowe przygotowanie z kombinatoryki i rachunku prawdopodobieństwa
(na poziomie szkoły średniej),
• przekształcenia algebraiczne, sumy ciągów i szeregów, oraz
• umiejętność układania algorytmów w Pascalu.
Analiza algorytmów
– dział informatyki zajmujący się poszukiwaniem
najlepszych algorytmów, które pozwalają rozwiązać postawione zadanie za
pomocą komputera.

5
Wykład 1,2
PROGNOZOWANIE WŁAŚCIWOŚCI MATERIAŁÓW
Inżynieria Materiałowa
ALGORYTMY I STRUKTURY DANYCH
1 SSI
Dr hab. inż. Barbara Dębska, prof. PWSZ
Analiza algorytmów
pozwala uzyskać odpowiedź na pytania:
1. czy problem może być rozwiązany na komputerze w dostępnym czasie i
pamięci? (
złożoność obliczeniowa
, czyli czas działania i ilość zajmowanej
pamięci
),
2. który ze znanych algorytmów należy zastosować? (
okoliczności, w jakich
należy używać algorytmu
, a w jakich nie
),
3. czy jest to algorytm najlepszy? (
optymalność
wybranego algorytmu
),
4. jak wykazać, że stosując dany algorytm, rozwiąże się postawione zadanie?
(
poprawność semantyczna i prostota działania
algorytmu
).

6
Wykład 1,2
PROGNOZOWANIE WŁAŚCIWOŚCI MATERIAŁÓW
Inżynieria Materiałowa
ALGORYTMY I STRUKTURY DANYCH
1 SSI
Dr hab. inż. Barbara Dębska, prof. PWSZ
Złożoność obliczeniowa:
•
złożoność pamięciowa(
zp
), związana z rozmiarem danych wejściowych
(
za jednostkę
zp
przyjmuje się słowo pamięci maszyny cyfrowej
),
•
złożoność czasowa
(
zc
), właściwość samego algorytmu jako metody
rozwiązania problemu – niezależnie od komputera, wybranego języka
programowania czy sposobu zakodowania algorytmu (
za jednostkę
zc
przyjmuje się wykonanie jednej
operacji dominującej
).
Operacja dominująca
– to operacja charakterystyczna dla algorytmu, taka, której
krotność jest proporcjonalna do liczby wykonań wszystkich operacji
jednostkowych w dowolnej komputerowej realizacji algorytmu.
Przykłady operacji dominujących:
1. algorytm sortowania – operacja porównywania dwóch elementów w
porządkowanym zbiorze,
2. obliczanie wartości wielomianu (schemat Hornera) – operacja
arytmetyczna + lub
∗.

7
Wykład 1,2
PROGNOZOWANIE WŁAŚCIWOŚCI MATERIAŁÓW
Inżynieria Materiałowa
ALGORYTMY I STRUKTURY DANYCH
1 SSI
Dr hab. inż. Barbara Dębska, prof. PWSZ
Złożoność obliczeniowa -
jest funkcją rozmiaru zestawu danych wejściowych d.
Przyjęte oznaczenia i definicje wykorzystywane przy obliczaniu złożoności
algorytmu :
n =
⏐d⏐
- rozmiar zestawu danych wejściowych,
D
n
- zbiór zestawów danych wejściowych rozmiaru
n,
t(d)
- liczba operacji dominujących dla zestawu danych wejściowych d,
X
n
- zmienna losowa, której wartością jest
t(d)
dla
d
∈ D
n
,
p
n,k
- rozkład prawdopodobieństwa zmiennej losowej
X
n
, tzn.
prawdopodobieństwo
,
że dla danych rozmiaru
n
algorytm wykona
k
operacji
dominujących (
k
≥0
).

8
Wykład 1,2
PROGNOZOWANIE WŁAŚCIWOŚCI MATERIAŁÓW
Inżynieria Materiałowa
ALGORYTMY I STRUKTURY DANYCH
1 SSI
Dr hab. inż. Barbara Dębska, prof. PWSZ
Rozkład prawdopodobieństwa zmiennej losowej X
n
wyznacza się na
podstawie informacji o zastosowaniach rozważanego algorytmu. Gdy
D
n
jest
skończony, zakłada się, że każdy zestaw danych rozmiaru
n
może pojawić się na
wejściu do algorytmu z jednakowym prawdopodobieństwem.
Pesymistyczna złożoność czasowa algorytmu W(n)
– ilość zasobów
komputerowych, potrzebnych przy „najgorszych danych wejściowych
rozmiaru
n
.
W(n) = sup{t(d) : d
∈D
n
}
Funkcja sup (supremum) oznacza kres górny zbioru liczby operacji
dominujących
t(d)
.

9
Wykład 1,2
PROGNOZOWANIE WŁAŚCIWOŚCI MATERIAŁÓW
Inżynieria Materiałowa
ALGORYTMY I STRUKTURY DANYCH
1 SSI
Dr hab. inż. Barbara Dębska, prof. PWSZ
Oczekiwana złożoność czasowa algorytmu A(n)
– ilość zasobów komputerowych,
potrzebnych przy „typowych” danych wejściowych rozmiaru
n
.
A(n) =
Σ
k
∗
p
n,k
k
≥0
A(n)
–
oznacza wartość oczekiwaną zmiennej losowej
X
n
Pesymistyczna wrażliwość
czasowa algorytmu
∆
(n) –
jest miarą
reprezentatywności funkcji
W(n)
dla wszystkich danych wejściowych rozmiaru
n
.
∆
(n)
=
sup{t(d
i
) - t(d
j
): d
i
, d
j
∈D
n
}

10
Wykład 1,2
PROGNOZOWANIE WŁAŚCIWOŚCI MATERIAŁÓW
Inżynieria Materiałowa
ALGORYTMY I STRUKTURY DANYCH
1 SSI
Dr hab. inż. Barbara Dębska, prof. PWSZ
Oczekiwana wrażliwość
czasowa algorytmu
δ
(n) –
jest miarą
reprezentatywności funkcji
A(n)
dla wszystkich danych wejściowych rozmiaru
n
.
δ
(n) = sqrt (var(X
n
) ) = sqrt(
Σ
(k - A(n))
2
∗
p
n,k
)
k
≥0
var(X
n
)
jest wariancją zmiennej losowej
X
n
.
Im większe są
∆
(n)
i
δ
(n)
, tym
algorytm jest bardziej wrażliwy
na dane
wejściowe.

11
Wykład 1,2
PROGNOZOWANIE WŁAŚCIWOŚCI MATERIAŁÓW
Inżynieria Materiałowa
ALGORYTMY I STRUKTURY DANYCH
1 SSI
Dr hab. inż. Barbara Dębska, prof. PWSZ
Przykład 1.
Oszacować złożoność algorytmu sprawdzającego czy w
N-elementowym
zbiorze
L
liczb naturalnych znajduje się liczba
a
.
Dane wejściowe:
N
- liczebność analizowanego zbioru L,
L [1 . . N]
- zbiór liczb naturalnych,
a
- liczba naturalna, której obecność chcemy sprawdzić.
Dane wyjściowe:
Zmienna logiczna p taka, że p = true
≡ a znajduje się w L[1 . . n].
Algorytm:
begin
j:= 1;
L[N+1] := a;
while L[j]
<> a do j := j + 1;
p := j
<=N
end;
L[j]
<> a

12
Wykład 1,2
PROGNOZOWANIE WŁAŚCIWOŚCI MATERIAŁÓW
Inżynieria Materiałowa
ALGORYTMY I STRUKTURY DANYCH
1 SSI
Dr hab. inż. Barbara Dębska, prof. PWSZ
Obliczenia:
Rozmiar danych wejściowych:
n=N
Operacja dominująca:
L[j]
<> a
Pesymistyczna złożoność czasowa:
W(n)
= n+1
(jeśli nie ma w zbiorze L liczby tożsamej z a)
Pesymistyczna wrażliwość czasowa:
∆(n)
= (n +1) – 1 = n
Rozkład prawdopodobieństwa:
p
n,k
= 1/n dla k=1, 2, ... , n
(prawdopodobieństwo znalezienia się a na każdym z N możliwych miejsc jest takie samo)
Oczekiwana złożoność czasowa:
A(n)
= (n+1)/2
Oczekiwana wrażliwość czasowa:
δ
(n)
= 0.29
∗ n
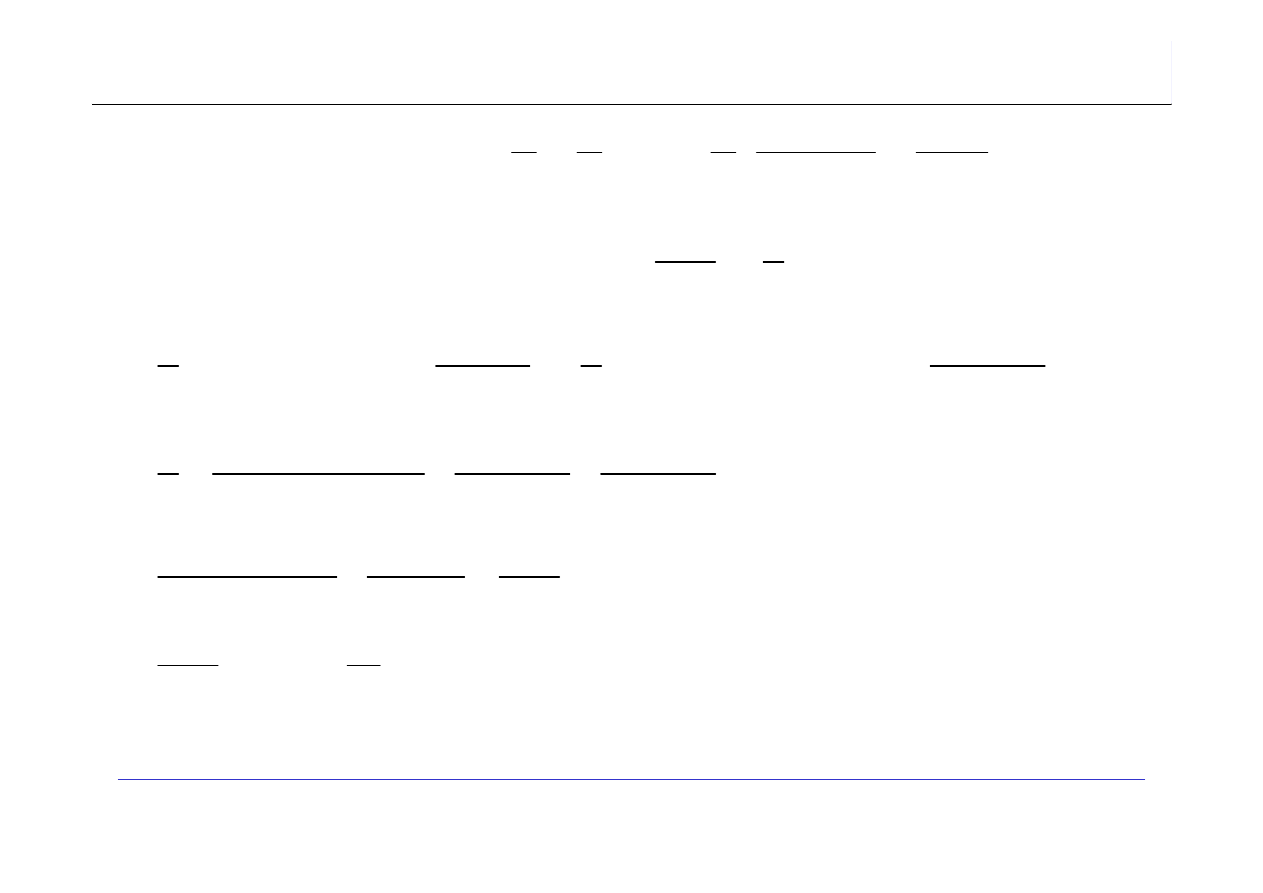
Wszystkie wyznaczone funkcje
W(n),
∆(n)
,
A(n),
i
δ
(n)
są liniowe
.
13
Wykład 1,2
PROGNOZOWANIE WŁAŚCIWOŚCI MATERIAŁÓW
Inżynieria Materiałowa
ALGORYTMY I STRUKTURY DANYCH
1 SSI
Dr hab. inż. Barbara Dębska, prof. PWSZ
(
) (
)
2
2
2
2
2
2
1
1
2
1
2
2
1
2
,
1
2
08333
.
0
)
1
(
12
1
)
1
(
12
1
)
3
3
2
4
(
12
1
4
)
1
(
6
)
1
2
)(
1
(
4
)
1
(
2
)
1
(
6
)
1
2
)(
1
(
1
4
)
1
(
)
1
(
1
4
1
1
1
1
2
1
))
(
(
)
var(
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
k
n
k
n
n
n
k
k
n
n
n
k
p
n
A
k
X
n
k
n
k
n
k
n
k
k
n
n
k
n
⋅
≅
−
⋅
=
−
⋅
+
=
=
−
−
+
⋅
+
=
+
−
+
+
=
=
⎭
⎬
⎫
⎩
⎨
⎧
+
+
+
−
+
+
⋅
⋅
=
=
⎭
⎬
⎫
⎩
⎨
⎧
+
+
⋅
+
−
⋅
=
⎭
⎬
⎫
⎩
⎨
⎧
+
+
+
−
⋅
=
=
⋅
⎟
⎠
⎞
⎜
⎝
⎛
+
−
=
⋅
−
=
∑
∑
∑
∑
∑
=
=
=
=
=
2
1
2
)
1
(
1
1
1
)
(
1
1
1
,
+
=
+
⋅
=
=
⋅
=
⋅
=
∑
∑
∑
=
=
=
n
n
n
n
k
n
n
k
p
k
n
A
n
k
n
k
n
k
k
n
δ
(n) = sqrt (var(X
n
) )
= sqrt (0.08333
∗
n
2
) = 0.29
∗
n

14
Wykład 1,2
PROGNOZOWANIE WŁAŚCIWOŚCI MATERIAŁÓW
Inżynieria Materiałowa
ALGORYTMY I STRUKTURY DANYCH
1 SSI
Dr hab. inż. Barbara Dębska, prof. PWSZ
Przykład 2.
Oszacować złożoność algorytmu wskazującego, który z elementów macierzy A
o rozmiarze NxN najmniej różni się od zadanej liczby b.
Dane wejściowe:
NxN
- liczebność elementów w zadanej macierzy,
A [1 . . N, 1 . . N]
- macierz A,
b
- liczba rzeczywista.
Dane wyjściowe:
k, l
- wskaźniki określające położenie liczby najmniej różniącej się od b
w macierzy A.

15
Wykład 1,2
PROGNOZOWANIE WŁAŚCIWOŚCI MATERIAŁÓW
Inżynieria Materiałowa
ALGORYTMY I STRUKTURY DANYCH
1 SSI
Dr hab. inż. Barbara Dębska, prof. PWSZ
Algorytm:
begin
k := 1;
l :=1;
delta := abs(A[1,1] – b);
for i:= 1 to N do
for j:= 1 to N do begin
roznica := abs(A[i,j] – b);
if roznica = 0 then begin
k := i; l :=j; exit;
end;
if roznica < delta then begin
k := i; l :=j;
delta:=roznica;
end;
end;
end;
roznica < delta

16
Wykład 1,2
PROGNOZOWANIE WŁAŚCIWOŚCI MATERIAŁÓW
Inżynieria Materiałowa
ALGORYTMY I STRUKTURY DANYCH
1 SSI
Dr hab. inż. Barbara Dębska, prof. PWSZ
Obliczenia:
Rozmiar danych wejściowych:
n = N*N
Operacja dominująca:
roznica < delta
Pesymistyczna złożoność czasowa:
W(n)
= n
2
(maksymalna ilość realizacji operacji dominującej)
Pesymistyczna wrażliwość czasowa:
∆(n)
= n
2
– 1
≅ n
2
Rozkład prawdopodobieństwa: p
n,k
= 1/n
2
dla k=1, 2, ... , n
2
(prawdopodobieństwo znalezienia w macierzy A liczby najmniej różniącej się od
liczby b jest takie samo dla wszystkich elementów macierzy A)
(
)
2
1
1
1
1
)
(
2
2
2
1
2
1
2
1
,
2
2
2
+
⋅
=
⋅
=
⋅
=
⋅
=
∑
∑
∑
=
=
=
n
n
n
k
n
n
k
p
k
n
A
n
k
n
k
n
k
k
n
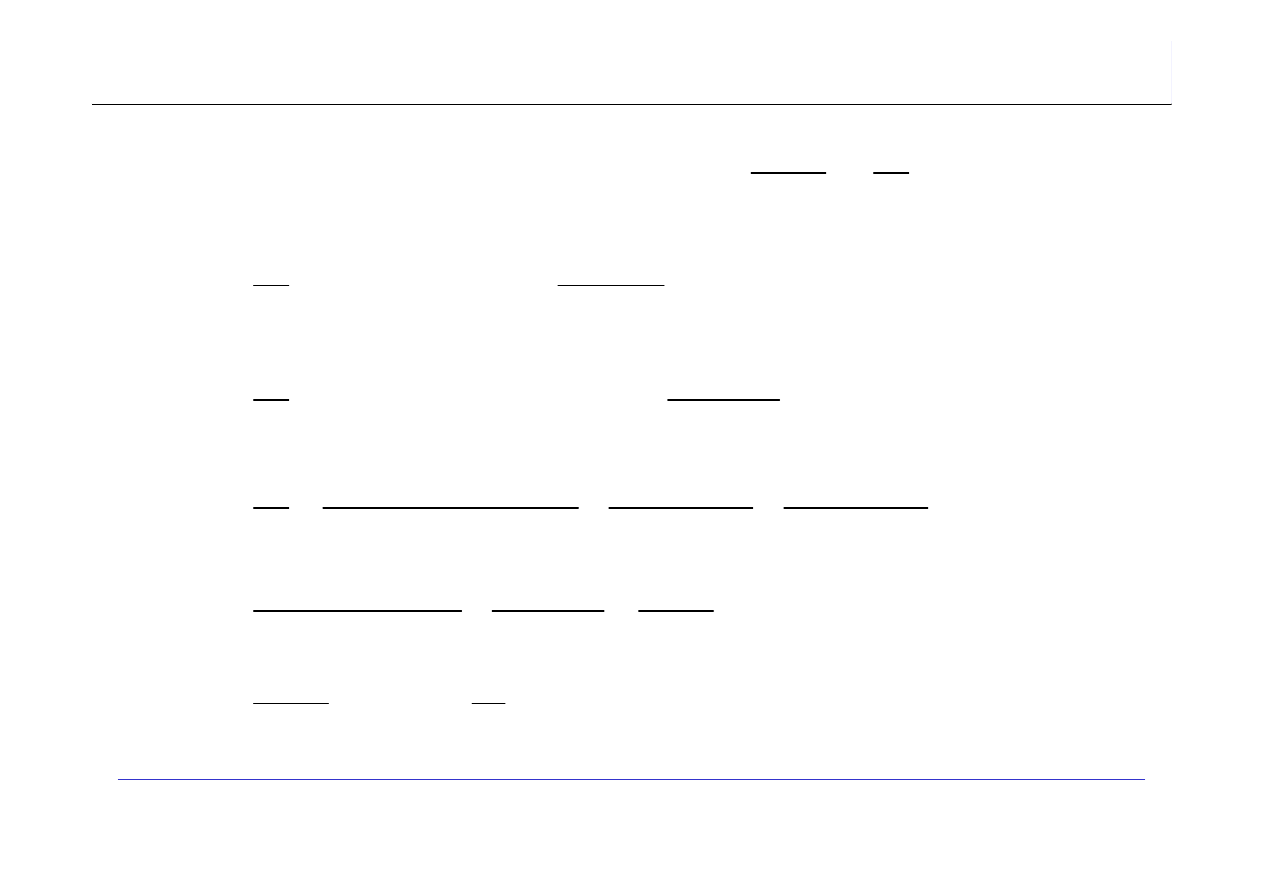
Oczekiwana złożoność czasowa:
A(n)
=
(n
2
+1)/2
=
n
2
/2 + 1/2
17
Wykład 1,2
PROGNOZOWANIE WŁAŚCIWOŚCI MATERIAŁÓW
Inżynieria Materiałowa
ALGORYTMY I STRUKTURY DANYCH
1 SSI
Dr hab. inż. Barbara Dębska, prof. PWSZ
(
) (
)
4
4
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
1
2
1
2
2
1
2
2
2
2
2
1
2
2
2
,
1
2
08333
.
0
)
1
(
12
1
)
1
(
12
1
)
3
3
2
4
(
12
1
4
)
1
(
6
)
1
2
)(
1
(
4
)
1
(
2
)
1
(
6
)
1
2
)(
1
(
1
4
)
1
(
)
1
(
1
4
1
1
1
1
2
1
))
(
(
)
var(
2
2
2
2
2
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
k
n
k
n
n
n
k
k
n
n
n
k
p
n
A
k
X
n
k
n
k
n
k
n
k
k
n
n
k
n
⋅
≅
−
⋅
=
−
⋅
+
=
=
−
−
+
⋅
+
=
+
−
+
+
=
=
⎭
⎬
⎫
⎩
⎨
⎧
+
+
+
−
+
+
⋅
⋅
=
=
⎭
⎬
⎫
⎩
⎨
⎧
+
+
⋅
+
−
⋅
=
=
⎪⎭
⎪
⎬
⎫
⎪⎩
⎪
⎨
⎧
+
+
+
−
⋅
=
=
⋅
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
−
=
⋅
−
=
∑
∑
∑
∑
∑
=
=
=
=
=

18
Wykład 1,2
PROGNOZOWANIE WŁAŚCIWOŚCI MATERIAŁÓW
Inżynieria Materiałowa
ALGORYTMY I STRUKTURY DANYCH
1 SSI
Dr hab. inż. Barbara Dębska, prof. PWSZ
δ(n) = sqrt (var(Xn) )
= sqrt (0.08333
∗ n
4
) = 0.29
∗ n
2
Podsumowanie:
Pesymistyczna złożoność czasowa:
W(n)
= n
2
Pesymistyczna wrażliwość czasowa:
∆(n)
= n
2
– 1
≅ n
2
Oczekiwana złożoność czasowa:
A(n)
= n
2
/2 + 1/2
Oczekiwana wrażliwość czasowa:
δ
(n)
= 0.29
∗ n
2
Wyznaczone funkcje
W(n),
∆(n), A(n),
i
δ
(n)
są zależne od n
2
.

19
Wykład 1,2
PROGNOZOWANIE WŁAŚCIWOŚCI MATERIAŁÓW
Inżynieria Materiałowa
ALGORYTMY I STRUKTURY DANYCH
1 SSI
Dr hab. inż. Barbara Dębska, prof. PWSZ
Przykład 3.
Algorytm sortowania zbioru A={a
1
, a
2
,..., a
n
} zapisano w postaci procedury.
Należy:
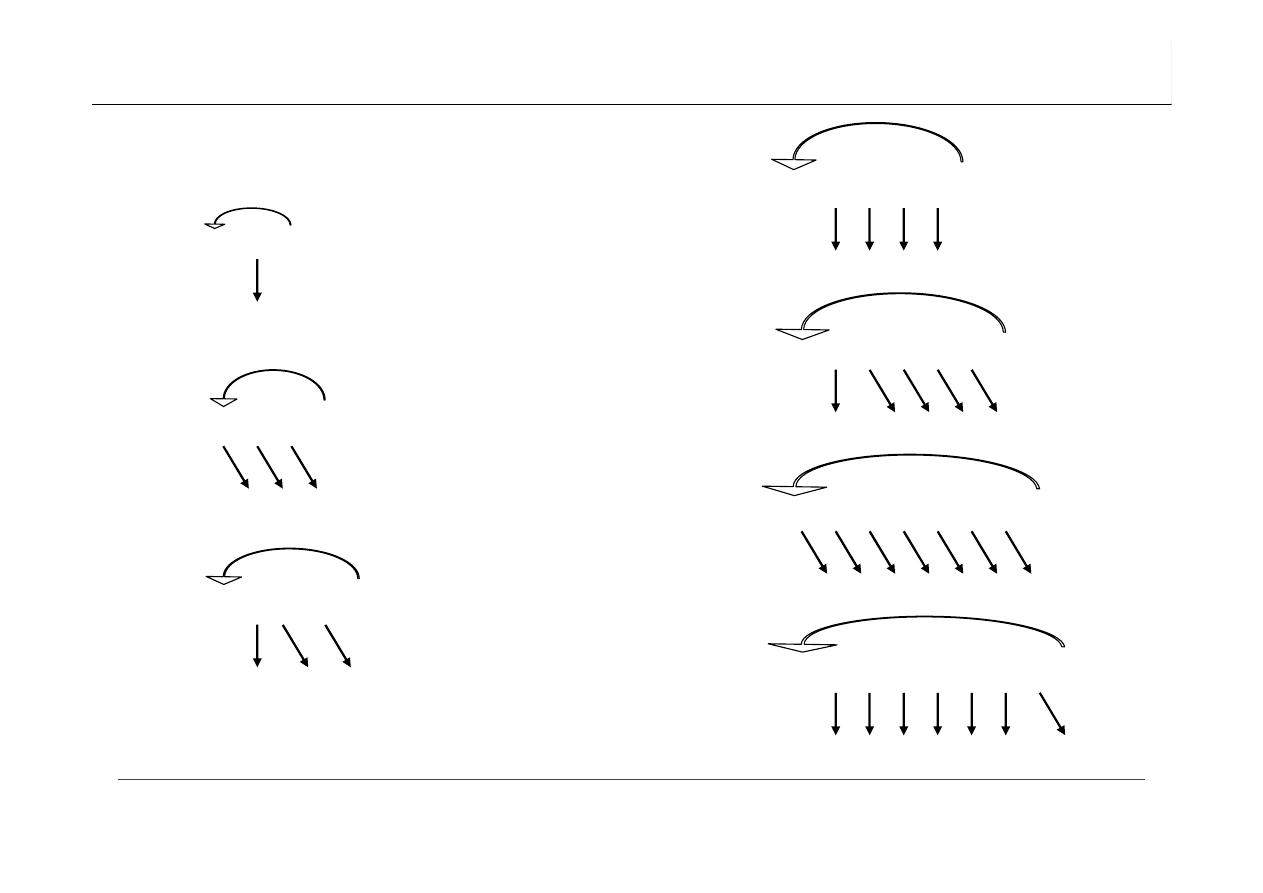
1. Narysować schemat blokowy tego algorytmu.
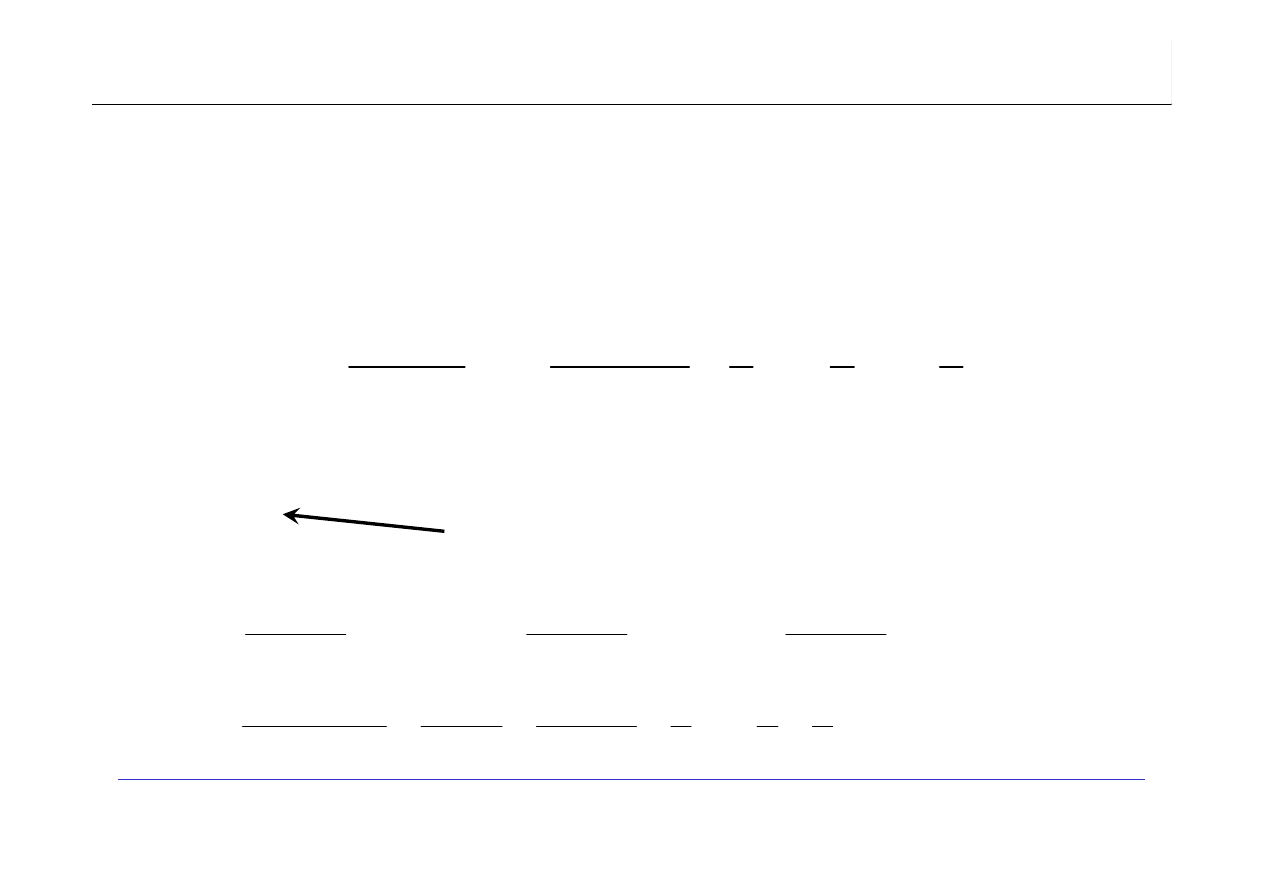
2. Dla przykładowego zbioru liczb dokonać symulacji procesu sortowania.
3. Przeprowadzić analizę metody, tzn. wskazać operację dominującą i obliczyć
wartości czterech wskaźników:
•
pesymistyczna złożoność czasowa W(n)
•
oczekiwana złożoność czasowa A(n)
•
pesymistyczna wrażliwość czasowa
∆(n)
•
oczekiwana wrażliwość czasowa
δ(n)
Zadanie zrealizować dla sortowania:
- przez proste wstawianie
20
Wykład 1,2
PROGNOZOWANIE WŁAŚCIWOŚCI MATERIAŁÓW
Inżynieria Materiałowa
ALGORYTMY I STRUKTURY DANYCH
1 SSI
Dr hab. inż. Barbara Dębska, prof. PWSZ
var i,j,x : inetger;
begin
for
i:=2 to n do begin
x:=a[i]; a[0]:=x;
j:=i-1;
while
x<a[j] do begin
a[j+1]:=a[j];
j:=j-1
end;
a[j=1]:=x
end;
end;
for i:=2 to n do
begin
x:=a[i]; a[0]:=x, j:=j-1;
„wstaw x w odpowiednim
miejscu w a
1
, a
2
,..., a
i
”
end;
21
Wykład 1,2
PROGNOZOWANIE WŁAŚCIWOŚCI MATERIAŁÓW
Inżynieria Materiałowa
ALGORYTMY I STRUKTURY DANYCH
1 SSI
Dr hab. inż. Barbara Dębska, prof. PWSZ
N
N
T
czy
x<a
j
x = a
i
a(0)=x
j = i-1
i:=2
a
j+1
= x
czy
x<a
j
i = i+1
Rozwiązanie:
AD. 1. Schemat
a
j+1
= a
j
j = j-1
T
22
Wykład 1,2
PROGNOZOWANIE WŁAŚCIWOŚCI MATERIAŁÓW
Inżynieria Materiałowa
ALGORYTMY I STRUKTURY DANYCH
1 SSI
Dr hab. inż. Barbara Dębska, prof. PWSZ
AD. 2. A=(44,55,12,42,94,18,06,87)
i=5
a(0)= 94 12 42 44 55
94
18 06 87
12 42 44 55 94 18 06 87
i=6
a(0)= 18 12 42 44 55 94
18
06 87
12 18 42 44 55 94 06 87
i=7
a(0)= 06 12 18 42 44 55 94
06
87
06 12 18 42 44 55 94 87
i=8
a(0)= 87 06 12 18 42 44 55 94
87
06 12 18 42 44 55 87 94
i=2
a(0)= 55 44
55
12 42 94 18 06 87
44 55 12 42 94 18 06 87
i=3
a(0)= 12 44 55
12
42 94 18 06 87
12 44 55 42 94 18 06 87
i=4
a(0)= 42 12 44 55
42
94 18 06 87
12 42 44 55 94 18 06 87
23
Wykład 1,2
PROGNOZOWANIE WŁAŚCIWOŚCI MATERIAŁÓW
Inżynieria Materiałowa
ALGORYTMY I STRUKTURY DANYCH
1 SSI
Dr hab. inż. Barbara Dębska, prof. PWSZ
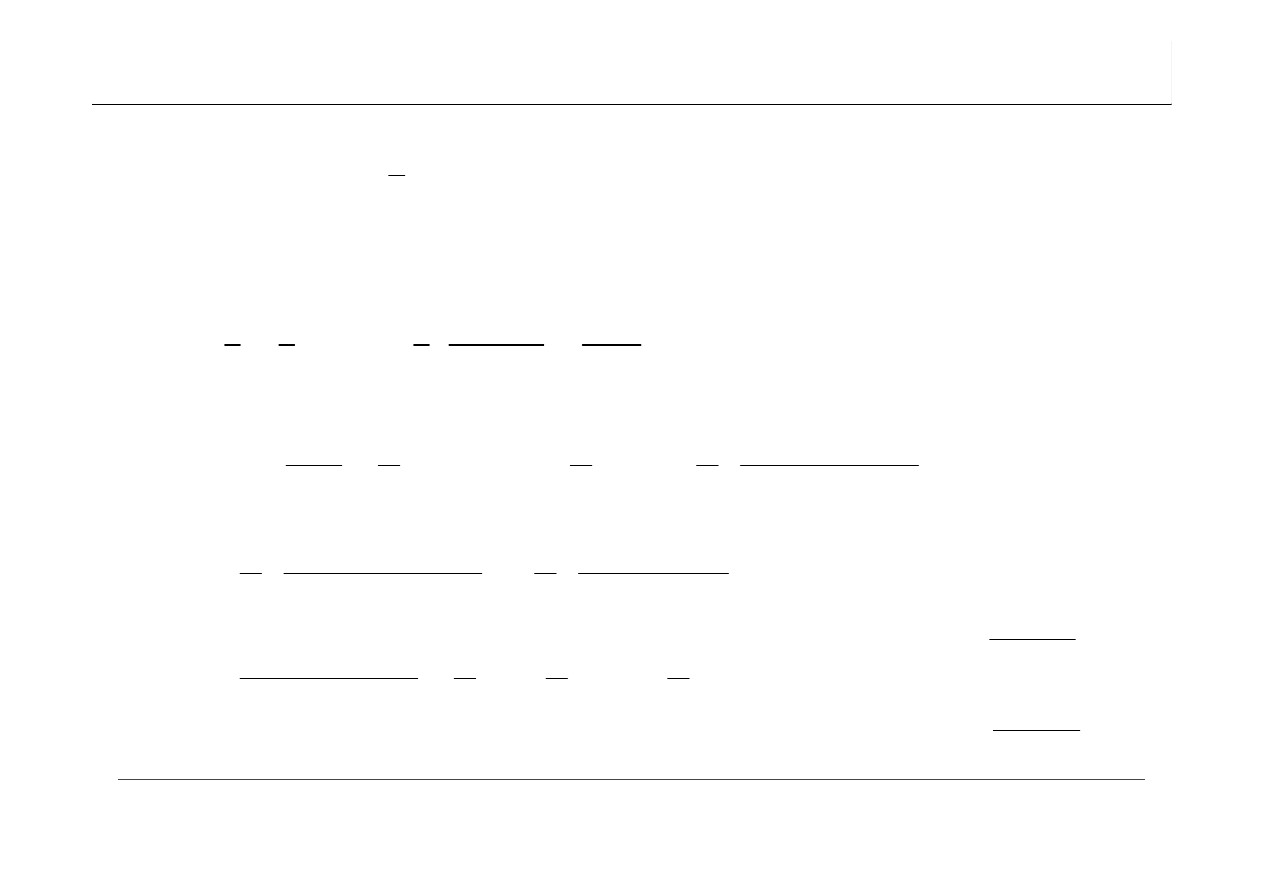
AD. 3. Operacja dominująca: porównanie x < a
j
W(n) -
maksymalna ilość porównań – w każdej pętli zewnętrznej realizuje się
i
wykonań pętli wewnętrznej:
)
(
2
1
1
1
2
1
2
2
1
1
2
)
1
(
)
(
2
2
2
2
n
O
n
n
n
n
n
n
i
n
W
n
i
+
=
−
+
=
−
+
=
−
+
=
=
∑
=
1
)
(
)
(
min
min
−
=
−
=
∆
n
t
t
n
W
n
(jedna operacja porównania w każdym przebiegu pętli zewnętrznej –
przypadek, gdy ciąg jest uporządkowany; wtedy, pętla wewnętrzna
wykonywana jest jeden raz w każdym przebiegu pętli zewnętrznej,
która jest wykonywana (n-1) razy)
)
(
2
1
2
2
1
2
)
1
(
2
2
2
2
)
1
(
1
1
2
)
1
(
)
1
(
1
2
)
1
(
)
(
2
2
2
2
n
O
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
−
=
−
=
−
=
−
=
−
+
=
−
+
=
+
−
−
+
=
−
−
−
+
=
∆
24
Wykład 1,2
PROGNOZOWANIE WŁAŚCIWOŚCI MATERIAŁÓW
Inżynieria Materiałowa
ALGORYTMY I STRUKTURY DANYCH
1 SSI
Dr hab. inż. Barbara Dębska, prof. PWSZ
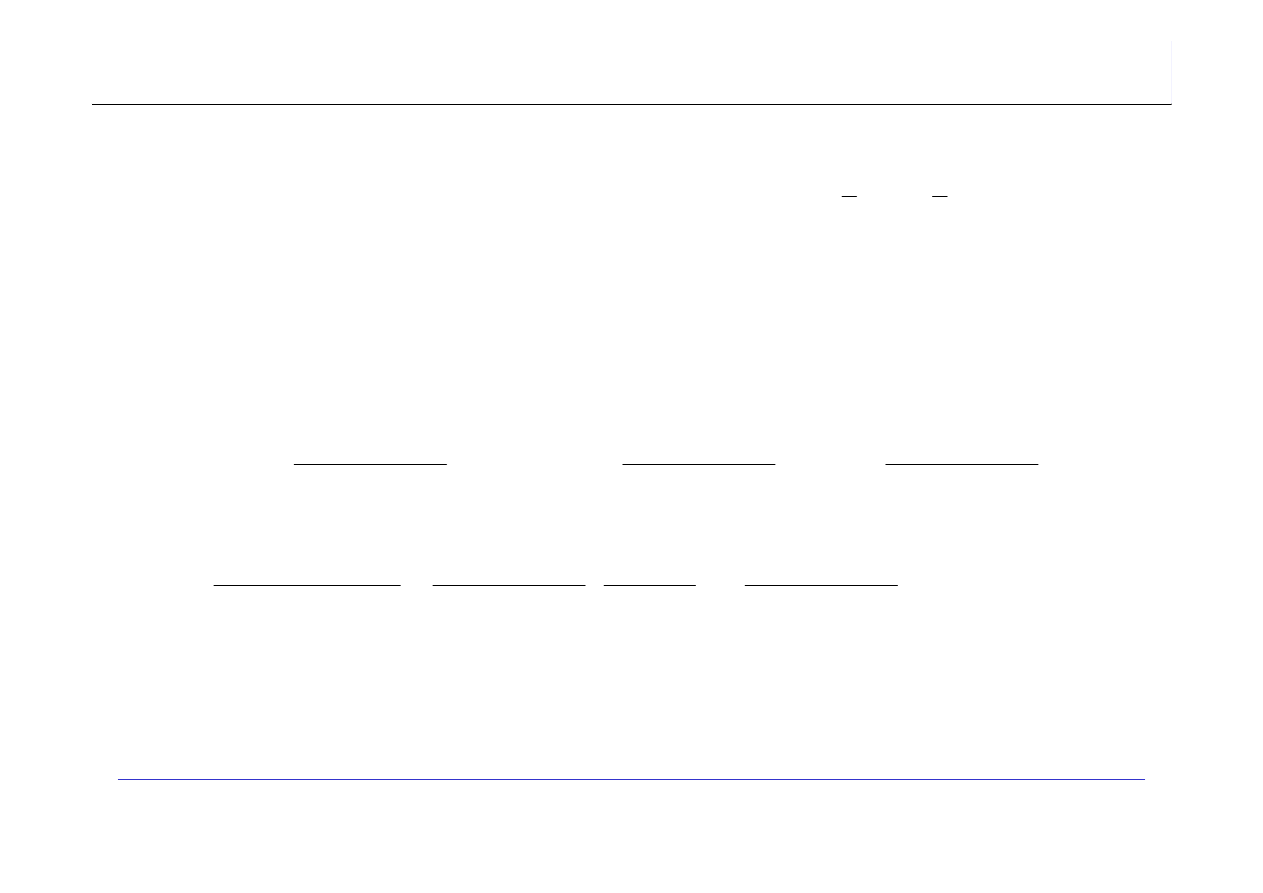
∑ ∑
= =
⋅
=
n
i
i
j
i
j
n
A
2 1
1
)
(
← p=1/i, każde miejsce w ciągu a
1
, ..., a
i
, wystąpienia
a
i
jest jednakowo prawdopodobne
Najpierw obliczamy sumę wewnętrzną:
2
1
2
)
1
(
1
1
1
1
1
+
=
+
⋅
=
⋅
=
⋅
∑
∑
=
=
i
i
i
i
j
i
i
j
i
j
i
j
)
(
4
1
1
4
3
4
1
4
)
1
)(
4
(
2
4
3
2
1
2
6
2
3
2
1
3
2
)
2
)(
1
(
2
1
2
1
)
1
(
2
1
2
1
)
(
2
)
(
2
2
2
1
3
2
2
n
O
n
n
n
n
n
n
n
n
n
n
n
i
i
i
n
A
n
O
n
i
n
i
n
i
+
=
−
+
=
−
+
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
+
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
+
+
=
⎟
⎠
⎞
⎜
⎝
⎛
−
+
+
=
⋅
=
+
⋅
=
+
=
∑
∑
∑
+
=
=
=
3
2
1
1
2
5
3
n
4
2
5
3
n
9
2
1
=
+
−
=
−
=
−
−
=
25
=
16
+
=
∆
25
Wykład 1,2
PROGNOZOWANIE WŁAŚCIWOŚCI MATERIAŁÓW
Inżynieria Materiałowa
ALGORYTMY I STRUKTURY DANYCH
1 SSI
Dr hab. inż. Barbara Dębska, prof. PWSZ
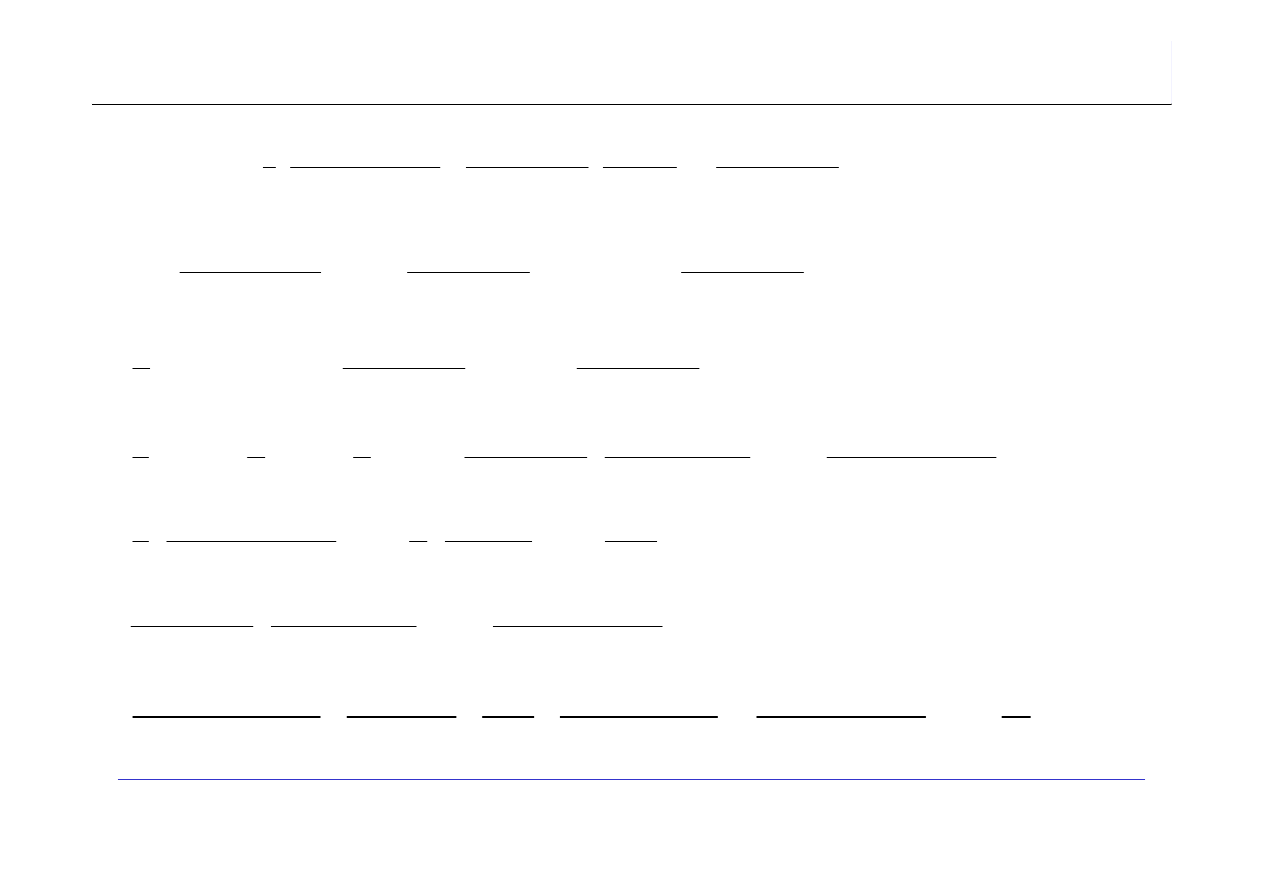
(
)
(
)
(
)
∑ ∑
∑∑
∑∑
=
=
=
=
=
=
−
=
⋅
−
=
⋅
−
=
n
i
i
j
n
i
i
j
k
n
n
i
i
j
n
n
A
j
i
i
n
A
j
p
n
A
j
X
2
1
2
2
1
2
,
2
1
2
)
(
1
1
)
(
)
(
)
var(
Najpierw obliczamy sumę wewnętrzną:
i
n
n
i
i
n
n
i
i
i
i
n
n
j
n
n
j
n
n
j
i
j
i
j
i
j
⋅
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
+
+
+
⋅
−
+
−
+
+
=
=
⋅
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
+
+
−
+
−
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
+
−
∑
∑
∑
=
=
=
2
2
2
2
1
2
1
2
2
2
1
2
4
4
3
2
)
1
(
2
4
3
6
)
1
2
)(
1
(
4
4
3
2
4
3
4
4
3
26
Wykład 1,2
PROGNOZOWANIE WŁAŚCIWOŚCI MATERIAŁÓW
Inżynieria Materiałowa
ALGORYTMY I STRUKTURY DANYCH
1 SSI
Dr hab. inż. Barbara Dębska, prof. PWSZ
(
)
( )
( )
( )
)
(
16
1
...
16
)
1
(
)
4
(
8
)
1
(
)
4
(
6
1
4
2
18
6
3
2
16
)
1
(
)
4
(
3
2
)
2
)(
1
(
4
4
3
6
1
1
2
)
1
(
2
1
1
6
)
1
2
)(
1
(
3
1
16
)
1
(
)
4
(
3
2
)
2
)(
1
(
4
4
3
)
1
(
6
1
2
1
3
1
)
1
(
4
4
3
4
4
3
1
3
2
6
1
4
4
3
)
1
(
4
4
3
6
)
1
2
)(
1
(
4
4
3
2
)
1
(
2
4
3
6
)
1
2
)(
1
(
1
)
var(
4
5
3
2
2
2
2
2
3
3
2
2
3
2
2
2
2
2
2
2
1
3
2
2
2
2
2
2
2
2
2
2
2
2
2
n
O
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
i
i
n
n
n
i
n
n
i
i
n
n
i
n
n
i
i
i
n
n
i
i
n
n
i
i
i
i
X
n
i
n
i
n
i
n
i
n
i
n
i
n
i
n
i
n
+
=
=
−
+
+
−
+
−
−
−
−
+
+
−
+
+
=
=
−
+
+
⎟
⎠
⎞
⎜
⎝
⎛
−
+
+
−
+
−
−
−
+
⎟
⎠
⎞
⎜
⎝
⎛
−
+
+
⎟
⎠
⎞
⎜
⎝
⎛
−
+
+
=
=
−
+
+
⎟
⎠
⎞
⎜
⎝
⎛
−
+
+
−
+
−
−
+
+
=
=
−
⋅
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
+
+
⋅
−
+
−
+
+
=
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
+
+
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
−
+
−
⎟
⎠
⎞
⎜
⎝
⎛
+
+
=
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
+
+
+
⋅
−
+
−
+
+
=
∑
∑
∑
∑
∑
∑
∑
∑
=
=
+
=
=
=
=
=
=

27
Wykład 1,2
PROGNOZOWANIE WŁAŚCIWOŚCI MATERIAŁÓW
Inżynieria Materiałowa
ALGORYTMY I STRUKTURY DANYCH
1 SSI
Dr hab. inż. Barbara Dębska, prof. PWSZ
Podsumowanie:
δ(n) = sqrt (var(Xn) )
)
(
4
1
)
(
)
var(
)
(
2
2
5
n
O
n
n
n
n
+
=
=
δ
δ
Pesymistyczna złożoność czasowa:
W(n)
= 1/2 n
2
+
Ο
(n)
Pesymistyczna wrażliwość czasowa:
∆(n)
= 1/2 n
2
-
Ο
(n)
Oczekiwana złożoność czasowa:
A(n)
= 1/4 n
2
+
Ο
(n)
Oczekiwana wrażliwość czasowa:
δ
(n)
=
Wyznaczone funkcje
W(n),
∆(n), A(n)
są zależne od n2
,
δ (n)
jest zależne od n
5/2
.
)
(
4
1
2
2
5
n
O
n
+

28
Wykład 1,2
PROGNOZOWANIE WŁAŚCIWOŚCI MATERIAŁÓW
Inżynieria Materiałowa
ALGORYTMY I STRUKTURY DANYCH
1 SSI
Dr hab. inż. Barbara Dębska, prof. PWSZ
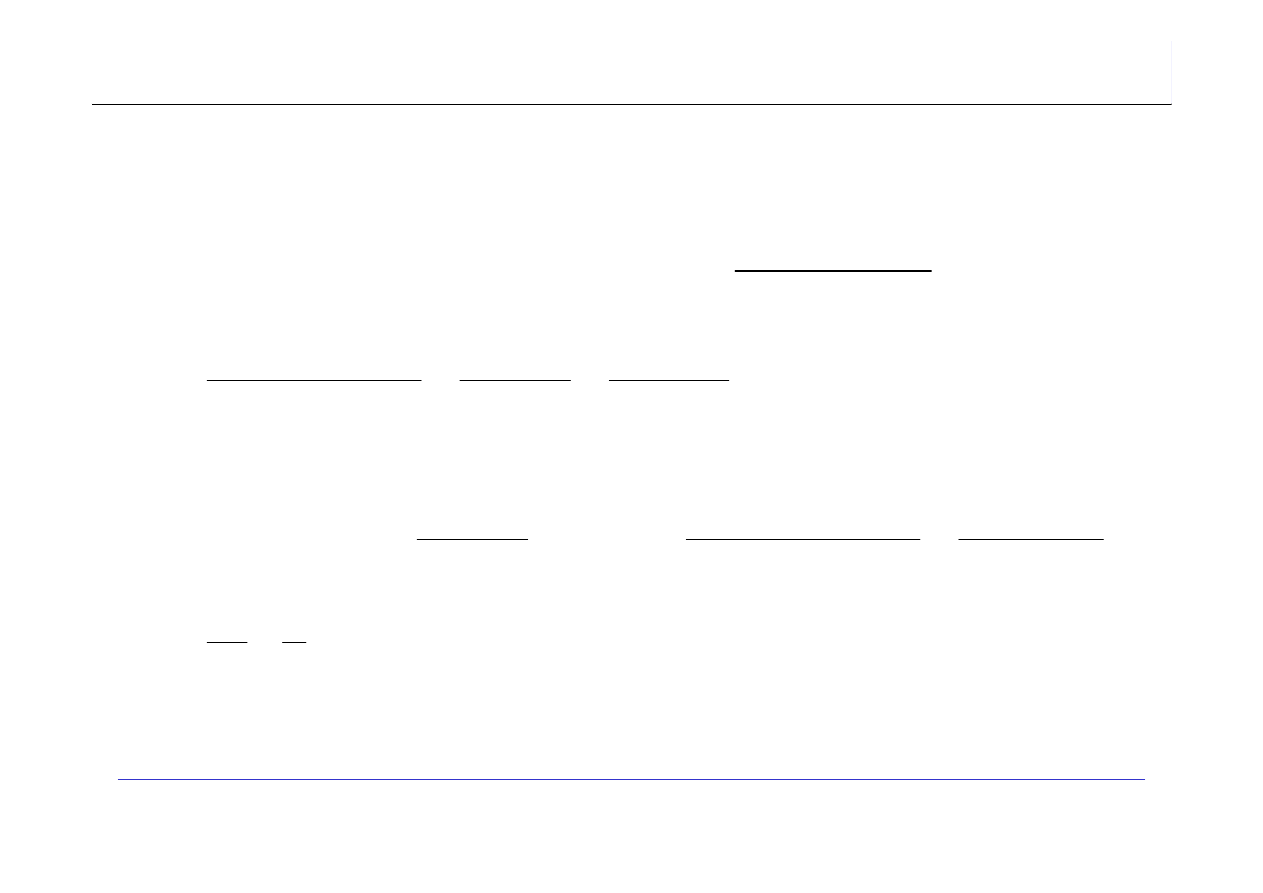
Przykład 4.
Operacje dominujące: podstawienie
a
0
a
1
a
2
j
j
j
i
a
a
stale
x
a
x
a
a
x
=
⎪
⎭
⎪
⎬
⎫
=
=
=
+
+
1
1
0
:
3
2
0
2
⎪
⎭
⎪
⎬
⎫
=
=
=
x
a
x
a
a
x
29
Wykład 1,2
PROGNOZOWANIE WŁAŚCIWOŚCI MATERIAŁÓW
Inżynieria Materiałowa
ALGORYTMY I STRUKTURY DANYCH
1 SSI
Dr hab. inż. Barbara Dębska, prof. PWSZ
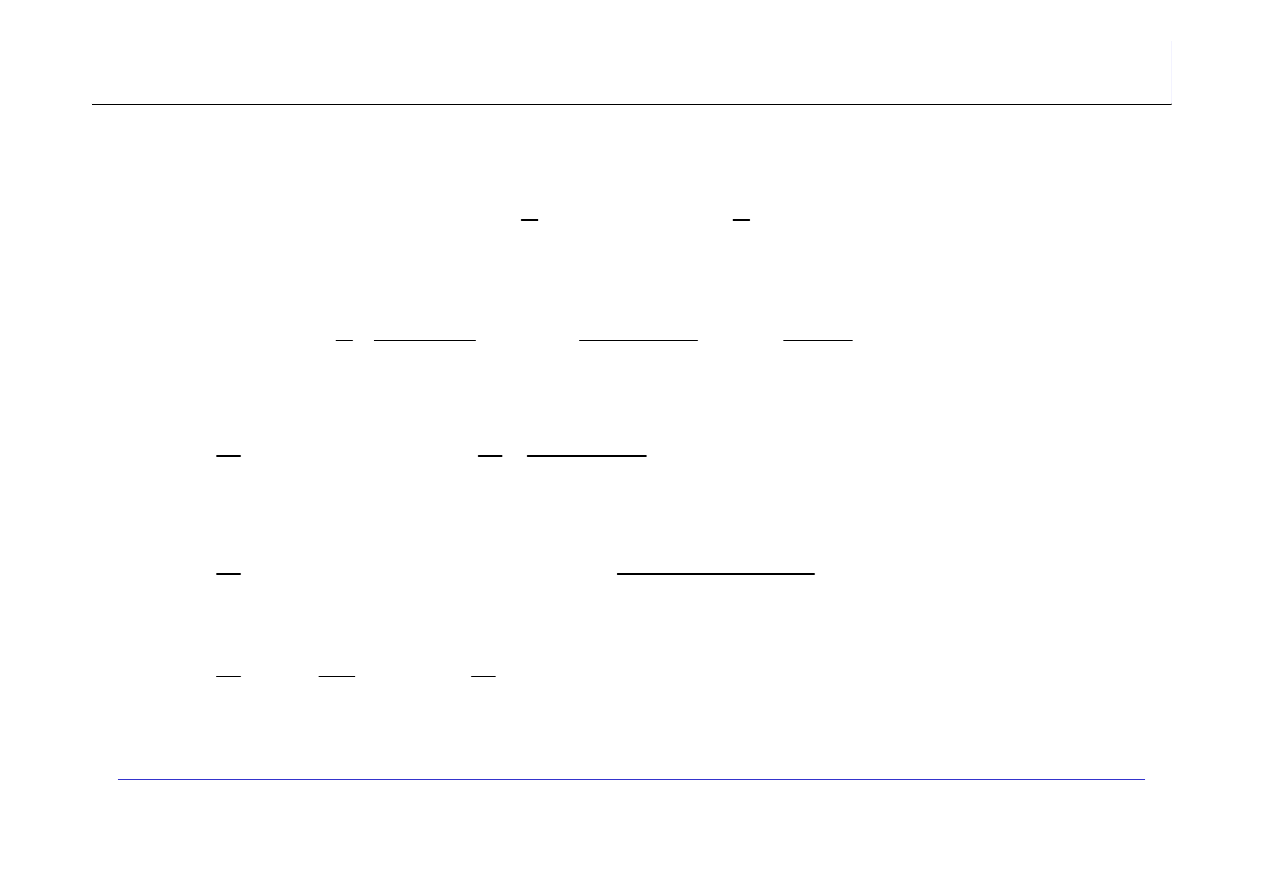
)
(
3
2
2
2
6
2
6
6
5
3
3
2
5
)
1
(
3
)
(
2
)
5
(
2
5
2
6
6
5
)
3
2
1
(
2
)
3
)(
2
(
)
2
(
)
(
2
3
1
2
2
2
2
2
min
min
2
2
2
3
1
2
1
2
2
4
n
O
n
n
n
n
n
n
n
n
n
n
t
W
n
t
n
O
n
n
n
n
n
n
n
n
i
i
i
i
n
W
i
i
n
n
i
n
i
n
i
n
i
=
+
−
=
=
+
−
=
+
−
+
=
+
−
+
=
−
=
∆
−
=
=
+
=
+
=
−
+
+
=
=
+
+
−
+
+
=
−
=
=
+
=
+
=
+
−
∑
∑
∑
∑
=
+
=
=
+
=
30
Wykład 1,2
PROGNOZOWANIE WŁAŚCIWOŚCI MATERIAŁÓW
Inżynieria Materiałowa
ALGORYTMY I STRUKTURY DANYCH
1 SSI
Dr hab. inż. Barbara Dębska, prof. PWSZ
)
(
4
1
3
4
11
4
1
4
12
11
)
10
10
2
(
4
1
)
1
(
5
1
2
)
1
(
2
1
5
2
1
2
5
2
1
4
2
)
1
(
1
2
1
2
1
2
)
(
2
2
2
2
2
2
2
2
2
2
2
1
2
1
n
O
n
n
n
n
n
n
n
n
n
n
n
i
i
i
i
i
i
j
i
i
j
n
A
n
i
n
i
n
i
n
i
n
i
n
i
i
j
n
i
i
j
+
=
−
+
=
=
−
+
=
−
+
−
+
=
=
⎟
⎠
⎞
⎜
⎝
⎛
−
+
−
+
=
⎟
⎠
⎞
⎜
⎝
⎛
+
=
=
+
=
+
+
=
⎟
⎠
⎞
⎜
⎝
⎛
+
⋅
+
=
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛ ⋅
+
=
∑ ∑
∑
∑
∑
∑
∑
∑
∑
=
=
=
=
=
=
=
=
=

31
Wykład 1,2
PROGNOZOWANIE WŁAŚCIWOŚCI MATERIAŁÓW
Inżynieria Materiałowa
ALGORYTMY I STRUKTURY DANYCH
1 SSI
Dr hab. inż. Barbara Dębska, prof. PWSZ
Document Outline
Wyszukiwarka
Podobne podstrony:
filozofia-str wyk, Filozofia
wprowadzenie do sztucznej inteligencji-wyk łady (10 str), Administracja, Administracja, Administracj
str.tyt, TBS Wrocław Wojanowska, Etap I, ETAP I - PROJEKT WYK, Drogi
2 1 IX 1 STR TYT WYK MOP Krzyza Nieznany (2)
str.tyt, TBS Wrocław Wojanowska, Etap I, ETAP I - PROJEKT WYK, Drogi
Rys do wyk 1 Str 1
więcej podobnych podstron