70
Grafy – podstawowe pojęcia
Graf jest najbardziej złożoną strukturą dynamiczną. W
przeciwieństwie do drzewa i listy, które są szczególnymi
przypadkami grafów, nie nakładamy tu żadnych ograniczeń,
jeśli chodzi o łuki łączące węzły grafu, mogą one występować
w dowolnej ilości, łącząc poszczególne węzły w dowolny
sposób. Dodatkowo w grafach dopuszczamy przetwarzanie
(dodawanie i usuwanie) łuków, niezależnie od przetwarzania
węzłów. Wszystko to stwarza duże problemy, jeśli chodzi o
reprezentacje grafów w pamięci komputera. Istnieje wiele
reprezentacji o różniących się własnościach.
Przykładowe zastosowania grafów:
• analiza sieci elektrycznych, ale też sieci komputerowych,
• zagadnienia segmentacji programów i
wieloprzetwarzania,
• zagadnienia planowania w badaniach operacyjnych,
• identyfikacja struktur molekularnych w chemii
organicznej.
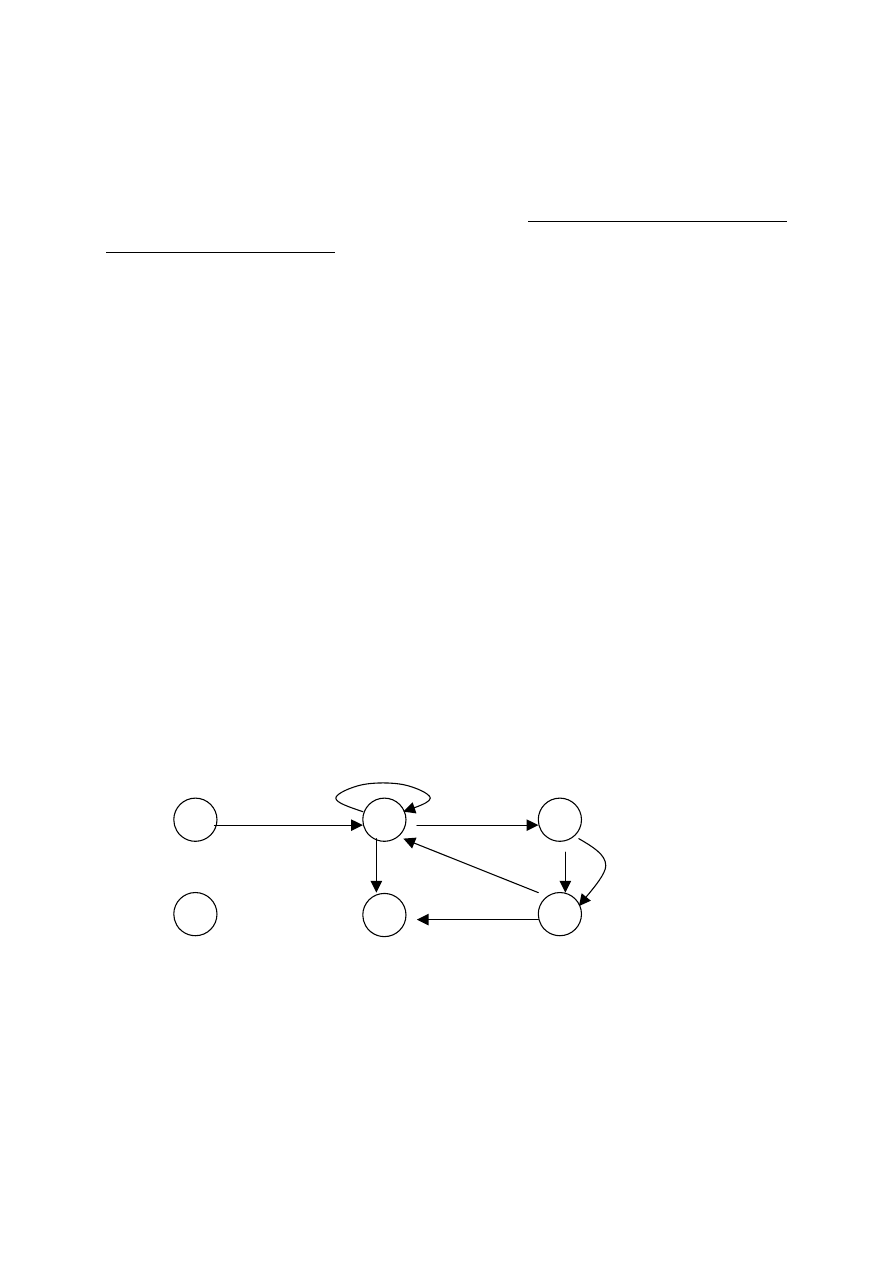
Rys. 42. Przykładowy graf
1
2
3
5
4
6
71
Podstawowe pojęcia:
1. Graf, w którym wszystkie krawędzie są krawędziami
skierowanymi, nazywamy grafem skierowanym, albo
zorientowanym, w przeciwnym przypadku – grafem
nieskierowanym.
2. Ścieżką w grafie nazywać będziemy ciąg możliwych do
przejścia, wierzchołków, np. (2, 3, 4).
3. Cyklem będzie ścieżka, zaczynająca się i kończąca tym
samym wierzchołkiem, np. (2, 3, 4, 2).
4. Graf nie zawierający żadnych cykli nazywać będziemy
grafem acyklicznym, w przeciwnym przypadku –
grafem cyklicznym
.
5. Kolejną, ważną z punktu widzenia wielu algorytmów
grafowych, jest spójność grafu. Oto definicje:
Graf nieskierowany nazywać będziemy spójnym,
jeśli między dwoma dowolnymi węzłami istnieje
przynajmniej jedna, łącząca je ścieżka. W
przeciwnym przypadku – graf nieskierowany
nazywać będziemy niespójnym.
Graf skierowany nazywać będziemy spójnym, jeśli
po odrzuceniu skierowania, między dwoma
dowolnymi węzłami istnieje przynajmniej jedna,
łącząca je ścieżka.
72
Graf skierowany nazywać będziemy silnie
spójnym, jeśli między dwoma dowolnymi węzłami
istnieje przynajmniej jedna. łącząca je ścieżka.
Przykładowy graf skierowany z rys. 42, po
odrzuceniu węzła z etykietą 6, jest grafem
spójnym, natomiast nie jest grafem silnie spójnym
– brak, na przykład, ścieżki od węzła 5 do 3.
6. Graf, w którym każdej krawędzi przypisano pewną
wartość (wagę), nazywać będziemy grafem ważonym.
Waga może reprezentować, na przykład, koszt
przejścia między dwoma węzłami.
7. Grafem płaskim nazywać będziemy narysowany na
płaszczyźnie
graf,
w
którym
między
dwoma
dowolnymi
wierzchołkami
narysować
można
przynajmniej jedną krawędź. Przykładowy graf z
rys. 42 jest takim grafem płaskim.
Grafy – metody reprezentacji w pamięci
Poniżej zostaną przedstawione trzy, najczęściej spotykane,
najważniejsze reprezentacje grafów.
Macierz sąsiedztwa
Macierz sąsiedztwa (adjacency matrix) jest reprezentacją
tablicową, statyczną. Jej zaletą jest szybki, bezpośredni dostęp
do krawędzi (a więc możliwość łatwego ich przetwarzania),
wielką wadą natomiast, wynikający ze statyczności - brak
możliwości łatwego przetwarzania (dodawania lub usuwania)
węzłów.
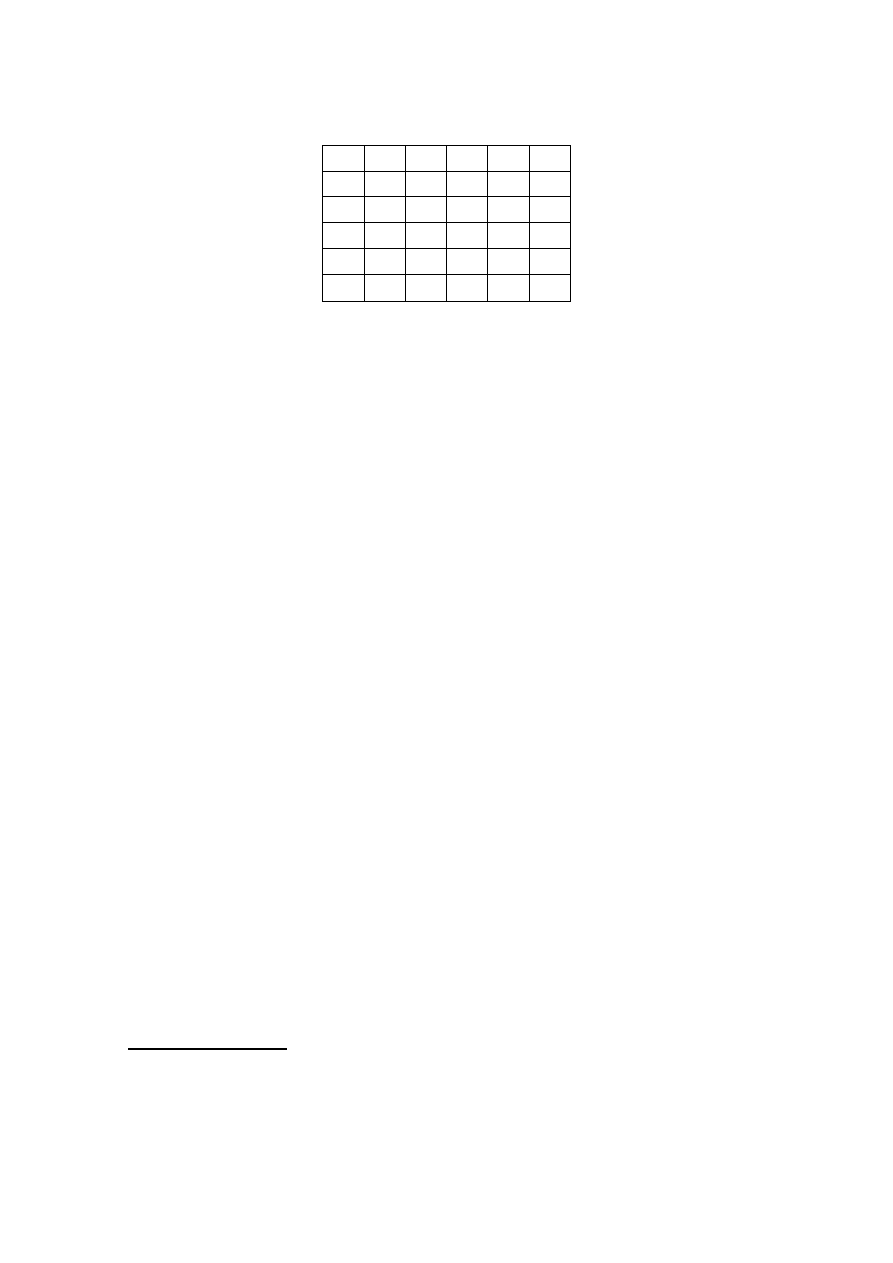
73
1 2 3 4 5 6
1
2
3
4
5
6
Rys. 43. Reprezentacja przykładowego grafu, którego
model przedstawiono na rys. 42, w postaci bitowej
macierzy sąsiedztwa
Oznaczmy przez n ilość węzłów grafu, oraz przez m – ilość
jego krawędzi. Bitowa macierz sąsiedztwa będzie macierzą
kwadratową o rozmiarach n x n zawierającą jedynki na
skrzyżowaniu
odpowiednich
wierszy
i
kolumn
(dla
reprezentowania krawędzi) i zera w pozostałych miejscach.
Ponieważ zajętość pamięci w tej reprezentacji zależy tylko
od ilości węzłów (jest proporcjonalna do n
2
), reprezentacja
dobrze nadaje się do przechowywania informacji o grafach
gęstych, dla których
(n/m) << 1.
W reprezentacji grafu nieskierowanego w postaci macierzy
sąsiedztwa jedynki występują symetrycznie względem
głównej przekątnej, dlatego też zwykle przechowuje się tylko
informacje zawarte nad, lub pod główną przekątną, co
pozwala zmniejszyć zajętość pamięci prawie o połowę,
kosztem niewielkiego wydłużenia czasu dostępu.
Lista krawędzi
Lista krawędzi, jak sama nazwa wskazuje, przechowuje
informacje tylko o krawędziach, podobnie zresztą jak macierz
1
1
1
1
1
1
1
74
sąsiedztwa. Jest to jednak struktura dynamiczna, jej rozmiary
są wyznaczone przez rzeczywistą ilość krawędzi.
1
2
2 2 3 4 4
2
2
3 5 4 2 5
Rys. 44. Reprezentacja przykładowego grafu,
przedstawionego na rys. 42, w postaci listy
krawędzi. Każdy z elementów listy zawiera etykiety
krawędzi: węzła wyjściowego (górny wiersz), oraz
docelowego (dolny wiersz),.
Oto jak wyglądają zalety i wady tej reprezentacji, pokazane
w sposób skondensowany:
• zajętość pamięci zależy tylko od ilości krawędzi i jest
proporcjonalna do m, reprezentacja nadaje się więc
wybitnie do przechowywania informacji o grafach
rzadkich, dla których
(n/m) >>1,
• dodawanie, lub usuwanie węzłów jest możliwe,
pociąga za sobą jedynie konieczność modyfikacji listy
krawędzi
(usunięcie
elementów
listy
krawędzi
odpowiadających
krawędziom
wychodzącym
i
dochodzącym do usuwanego węzła),
• istnieje możliwość reprezentacji krawędzi zapętlonych i
równoległych (każdej krawędzi odpowiada bowiem
odrębny element listy krawędzi). Podobnie - dodając do
elementów listy krawędzi pole, przechowujące wagę
krawędzi, można reprezentować grafy ważone,
• zajętość pamięci dla grafów nieskierowanych wzrasta
natomiast
dwukrotnie
w
stosunku
do
grafów
skierowanych, trzeba bowiem w liście krawędzi
reprezentować możliwość poruszania się w obu
kierunkach miedzy węzłami grafu.
75
Lista incydencji
Najbardziej uniwersalną, o najlepszych własnościach,
wydaje się być reprezentacja, którą nazwiemy listą incydencji.
Jest to struktura w pełni dynamiczna, z możliwością
przechowywania (i przetwarzania) w jednej strukturze
wszystkich informacji, dotyczących zarówno krawędzi, jak i
węzłów.
Za taką uniwersalność płacimy jednak względnie dużym
stopniem skomplikowania struktury, z czym jednak nie musi
wiązać się, jak zobaczymy, skomplikowanie algorytmów.
W strukturze, przechowującej pełną informację o grafie,
występują dwa rodzaje rekordów. Zdefiniujmy najpierw
postać rekordów, przechowujących informacje dotyczące
węzłów grafu:
struct VERT
{ int klucz;
int old;
ELEM * eref;
VERT * nextv;
};
Zawierają one, oprócz etykiety węzła o nazwie klucz,
wskazanie eref do początku listy rekordów, opisujących
krawędzie
wychodzące
z
danego
węzła
(rekordy
odpowiadające krawędziom są typu ELEM), oraz wskazanie
nextv do następnego węzła w liście węzłów. Znaczenie pola
old zostanie wyjaśnione później.
Rekordy
drugiego
rodzaju
przechowują
informacje
dotyczące krawędzi. Są one typu:
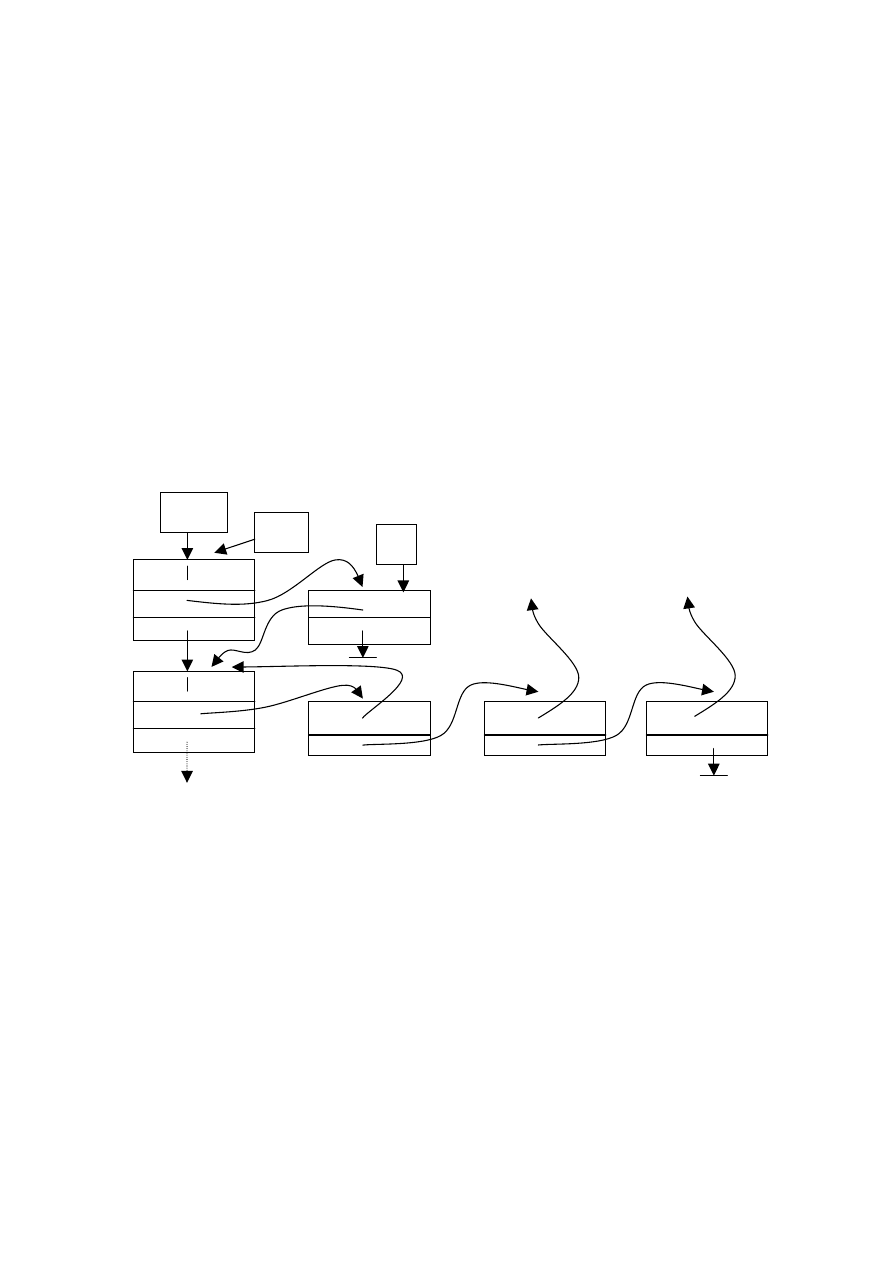
76
struct ELEM
{ VERT * vref;
ELEM * nexte;
};
gdzie: vref jest wskazaniem węzła, do którego wiedzie
dana krawędź,
nexte jest wskazaniem kolejnego rekordu w liście
krawędzi wychodzących z tego samego węzła.
Poniższy rysunek przedstawia początkowa część struktury
przykładowego grafu z rys. 42
old do węzła 3 do węzła 5
old
Rys. 45 Reprezentacja części przykładowego grafu w
postaci listy incydencji
Oto cechy tej reprezentacji:
• zajętość pamięci zależy w równym stopniu od ilości
węzłów grafu, jak i od ilości jego krawędzi, i jest
proporcjonalna do sumy ( n + m ), taka reprezentacja
nadaje się więc do przechowywania dowolnych grafów,
o ile rozmiary grafu nie są zbyt duże, wtedy bowiem
zaczyna odgrywać rolę czas dostępu sekwencyjnego,
1
2
graf
ptr
k
77
• dodawanie, lub usuwanie zarówno węzłów, jak i
krawędzi, jest możliwe i łatwe,
• zajętość pamięci dla grafów nieskierowanych wzrasta i
jest proporcjonalna do ( n + 2 * m ), dwukrotnie
bowiem wzrasta ilość rekordów reprezentujących
krawędzie,
• najważniejszą jednak zaletą tej reprezentacji jest jej
listowy charakter (w istocie jest to lista list), co daje
szansę stosowania prostych algorytmów obsługi, i to
zarówno rekurencyjnych, jak też iteracyjnych.
Algorytm szukania w głąb dla grafu
Algorytm szukania w głąb jest podstawowym algorytmem
grafowym. Jego konstrukcja oparta jest o schemat ogólny tak
zwanych algorytmów z powrotami, zwanych niekiedy
wyszukiwaniem wyczerpującym. Schemat ten zostanie
bardziej szczegółowo omówiony w dalszej części wykładu.
Poza tym, algorytm szukania w głąb jest kolejnym
przykładem rekurencyjnego algorytmu typu „dziel i
zwyciężaj”. Jego zasada została już omówiona przy okazji
algorytmu sortowania tablic QuickSort.
Poniżej przedstawiono pełną postać algorytmu szukania w
głąb dla grafu w formie rekurencyjnej funkcji, zapisanej w
notacji C/C++ i wykorzystującej podane wcześniej definicje
struktur. Przy okazji zauważmy, że cechą charakterystyczną
tych algorytmów jest umieszczona wewnątrz ciała funkcji
pętla iteracyjna, zawierająca rekurencyjne wywołanie.
78
Załóżmy, że podobnie jak w drzewie binarnym, chcemy
wykonać pewną operację Q(ptr) na wszystkich węzłach
zupełnie dowolnego grafu skierowanego. W tym celu należy
dokonać wywołania SEARCH ( graf ); niżej zdefiniowanej
rekurencyjnej funkcji
void SEARCH( VERT * ptr)
{
if ( not old ) // 1
{ ptr →
→
→
→ old =1; Q( ptr ); // 2
ELEM * k = ptr →
→
→
→ eref; // 3
while (k) // 4
{ SEARCH( k →
→
→
→ vref ); // 5
k = k →
→
→
→ nexte; // 6
}
}
}
Szczegółowa analiza działania tego algorytmu wykaże, że
odwiedzenie wszystkich węzłów grafu zawsze powiedzie się,
jeśli będzie to graf silnie spójny, w przeciwnym przypadku,
może się nie powieść.
W jaki sposób działa ten algorytm ?
Kolejne węzły są wybierane z listy krawędzi danego węzła
(linia 5). Jeśli wybrany węzeł nie był jeszcze odwiedzony
(linia 1), zaznaczamy jego odwiedzenie wpisując jedynkę w
jego pole old i wykonując na nim operację Q (linia 2), a
następnie zabieramy się do przeglądania jego listy krawędzi
(linie 3 i 4), nie kończąc przeglądania listy krawędzi węzła
poprzedniego (sic !).
79
W ten sposób poruszamy się w głąb grafu. Po zakończeniu
przeglądania jednak każdej listy krawędzi, wycofujemy się
rekurencyjnie, powracając do przeglądania listy incydencji
węzła poprzedniego.
Zauważmy, że kolejność występowania węzłów w liście
węzłów nie ma żadnego znaczenia. Dalej – powiązanie
węzłów w listę wydaje się zbyteczne (nie korzystaliśmy
przecież ze wskaźnika nextv). Ale to tylko pozór. Jest ono
konieczne, ponieważ w trakcie przetwarzania grafu może, po
kolejnej operacji, okazać się, że do któregoś z węzłów nie
dochodzi żadna krawędź, ani żadna z niego nie wychodzić
(węzeł o etykiecie 6 w naszym przykładowym grafie), albo też
po prostu graf przestanie być grafem silnie spójnym (nawet
jeśli przedtem był). Sytuacje takie powodują „omijanie”
niektórych węzłów w trakcie rekurencyjnego wywoływania
algorytmu.
Dzięki utrzymywaniu wszystkich węzłów grafu w liście
węzłów możemy w niżej podany sposób
VERT * k = graf;
while ( k ) { SEARCH( k ); k = k →
→
→
→ nextv; }
zapobiec omijaniu niektórych węzłów. Nie należy jednak,
przed każdym cyklem przeglądania grafu, zapominać o
wyzerowaniu pola old.
Algorytm szukania w głąb dla grafu, mimo swoich
skromnych rozmiarów (tylko 6 linii poleceń !), posiada wielką
siłę i możliwości. Na jego kanwie można zaproponować wiele
algorytmów obsługujących grafy. Oto przykłady:
80
• wyszukiwanie węzła o zadanych cechach,
• wyszukiwanie węzła o najmniejszej (największej)
wartości klucza,
• wyszukiwanie najkrótszej ścieżki do węzła o zadanych
cechach,
• wyszukiwanie wszystkich ścieżek do węzła o zadanych
cechach,
• badanie cykliczności grafu,
• badania spójności i silnej spójności grafu,
• badanie płaskości grafu,
• itd.
Poza tym, lista incydencji umożliwia łatwe, dynamiczne
dostawianie i usuwanie węzłów grafu.
Wszystko to uzyskujemy dzięki stosowaniu algorytmów
rekurencyjnych do rekurencyjnych struktur danych.
Zadania do samodzielnego rozwiązania:
1. Wykaż, że metoda preorder dla drzewa binarnego jest
szczególnym przypadkiem algorytmu szukania w głąb
dla grafu, gdy ten ostatni degeneruje się do takiego
drzewa.
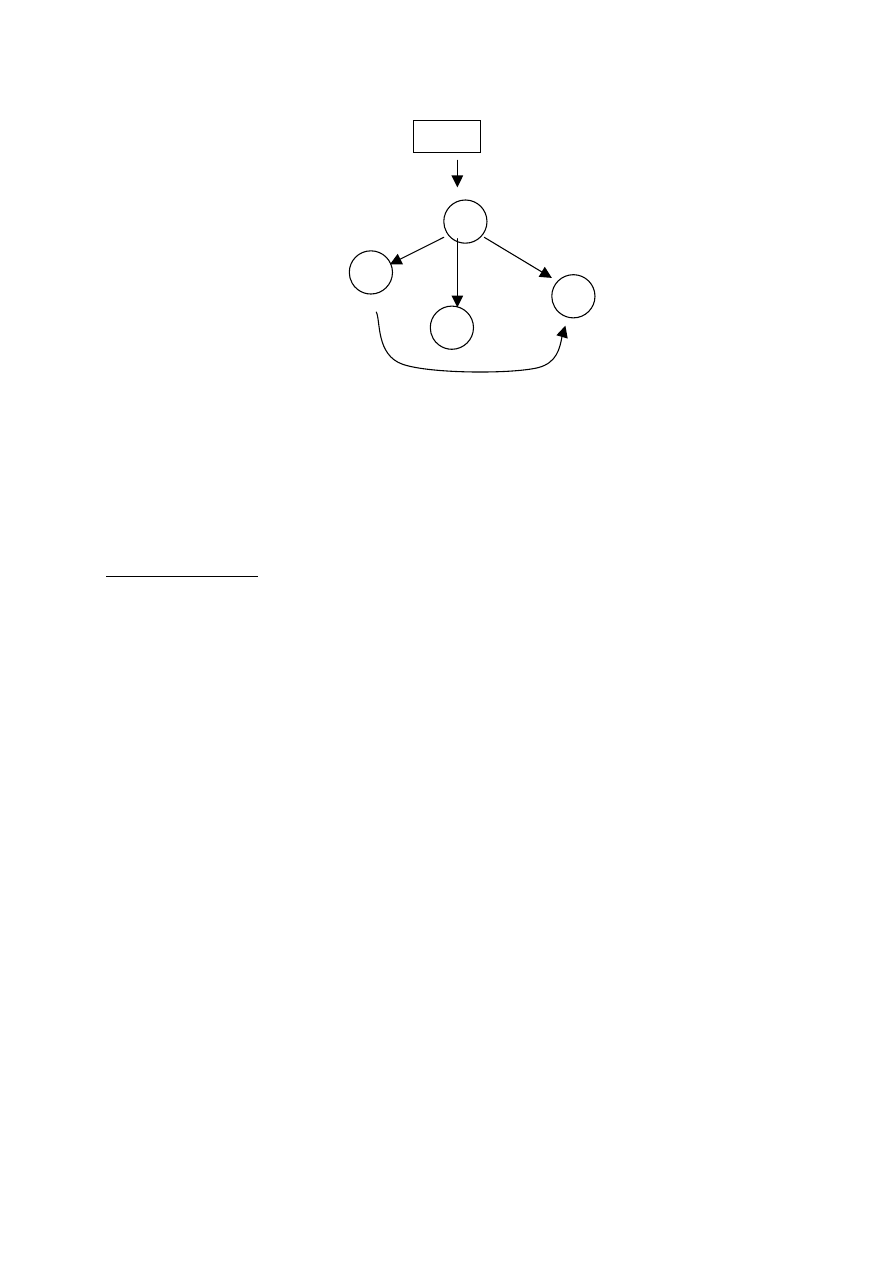
2. Jaka będzie kolejność wykonywania wybranej operacji
w poniższym grafie, po wywołaniu procedury szukania
w głąb, począwszy od węzła o etykiecie 7 ? Rozważ
wszelkie możliwe rozwiązania.
3. Dodaj minimalną ilość krawędzi do poniższego grafu
tak, aby graf ten stał się grafem silnie spójnym.
81
Kodowanie mieszające
Opisana poniżej metoda przechowywania i wyszukiwania
elementów będzie miała praktyczny sens, jeśli zbiór
potencjalnych kluczy identyfikujących te elementy jest
zbiorem o bardzo dużej liczności. W takich sytuacjach
bowiem omawiane dotychczas metody, łącznie z drzewem
binarnych poszukiwań, nie zapewnią nam dostatecznie dużej
efektywności algorytmów wyszukiwania.
Dla przykładu, wspomniane drzewo binarnych poszukiwań,
stanie się drzewem silnie nie wyważonym i efektywność
wyszukiwania w takim drzewie zbliży się do efektywności
wyszukiwania liniowego w liście liniowej.
Wyobraźmy sobie, że w pewnym systemie używa się haseł o
długości 10 liter wykorzystując alfabet języka polskiego.
Wszystkich możliwych haseł (być może potencjalnych kluczy
użytkowników tego systemu) będzie 33
10
, to jest około
1.5 * 10
15
haseł. Jeżeli liczba użytkowników nie jest zbyt
duża, opłacalnym będzie zastosowanie systemu, który
najpierw dokona „wstępnej selekcji” tych użytkowników,
szufladkując każdego z nich do odrębnych przegródek.
graf
7
1
9
3
82
Zadanie szufladkowania może być wykonane za pomocą
metody, zwanej kodowaniem mieszającym, lub transformacją
kluczową. W literaturze można też spotkać terminy mieszanie
liniowe, lub haszowanie dla określenia opisywanej teraz
metody, lub jej odmian.
Ponieważ jest bardzo wiele różnych zastosowań tej metody,
jak również wiele jej odmian, najpierw opiszemy problem
możliwie ogólnie a następnie omówimy jedną z jej
implementacji, opartej o struktury listowe.
Niech U będzie pewnym uniwersum, tj. dowolnym,
skończonym zbiorem (na przykład zbiorem haseł) o dużej
liczności. Przez A
i
⊂
⊂
⊂
⊂ U oznaczmy dowolny i-ty podzbiór (tzw.
katalog) zbioru U, natomiast przez m << | U | oznaczmy liczbę
tych katalogów. Wszystkie katalogi są zbiorami rozłącznymi.
Nie muszą one zawierać elementów uniwersum U. Natomiast
dowolny element x ∈
∈
∈
∈ U, jeśli się pojawi, musi być
zakwalifikowany w sposób jednoznaczny do jednego i tylko
jednego katalogu.
Przez h(x) oznaczmy funkcję o szczególnych własnościach
(tak zwaną funkcję transformującą lub funkcję haszującą),
której zadaniem będzie przydzielanie w sposób jednoznaczny
dowolnemu elementowi x ∈
∈
∈
∈ U określonego katalogu A
i
.
Będzie to więc funkcja
h: U → { 1, 2, 3, . . . , m }
z uniwersum U w zbiór liczb naturalnych, będących
numerami katalogów.
83
Funkcja haszująca powinna spełniać dwa podstawowe
warunki:
- przyjmować wartości ze zbioru { 1, 2, 3, . . . , m } w
sposób możliwie równomierny,
- koszt liczenia tej funkcji musi być stały, to jest
niezależny od x ∈
∈
∈
∈ U i możliwie najniższy.
Pierwszy z tych warunków sprowadza się do żądania, aby dla
każdego x ∈
∈
∈
∈U prawdopodobieństwo otrzymania określonej
wartości i ∈
∈
∈
∈{ 1, 2, 3, . . . , m } było mniej więcej stałe, to jest
niezależne od samej wartości i.
Cała trudność w efektywnym zastosowaniu kodowania
mieszającego polega na znalezieniu odpowiedniej do danego
problemu, a jednocześnie spełniającej oba postawione
warunki, funkcji haszującej.
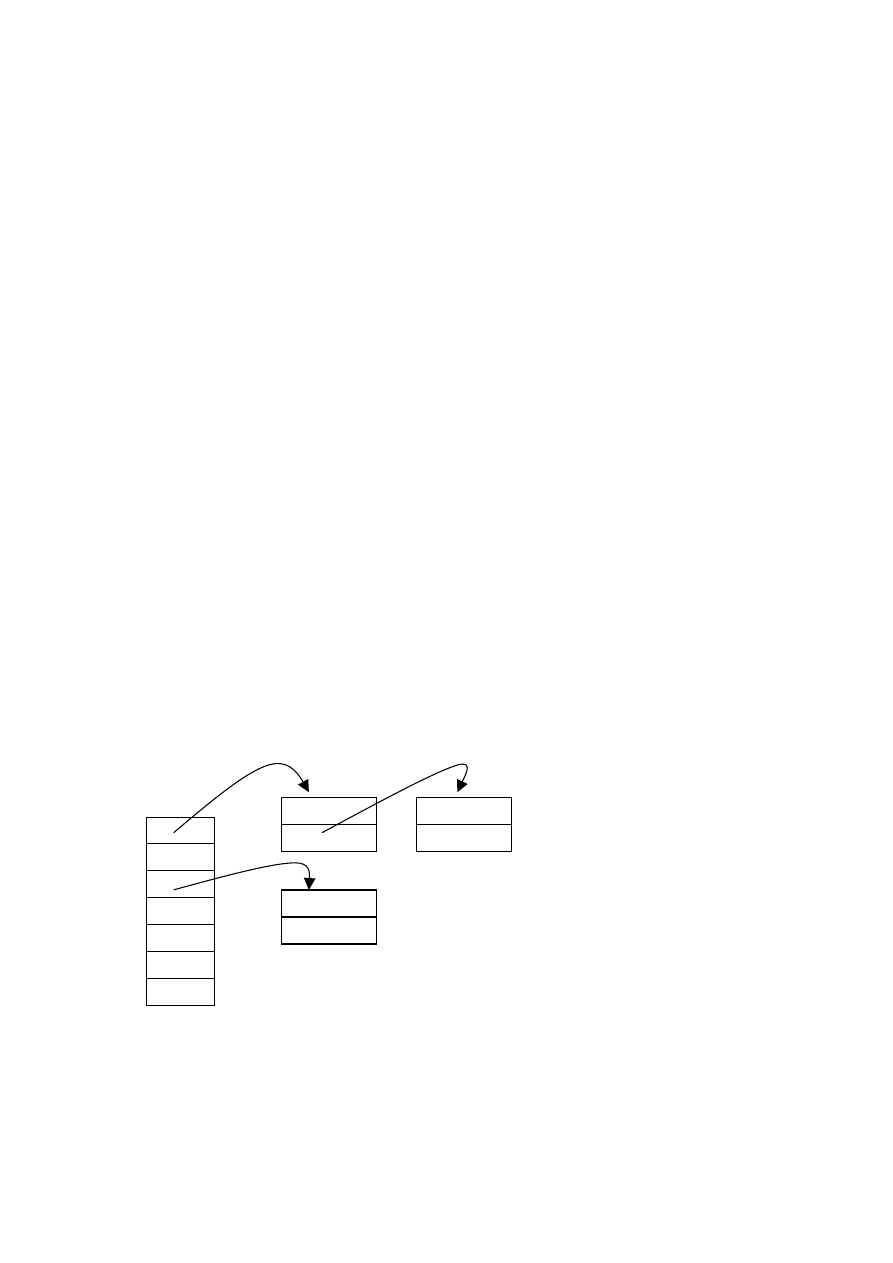
Poniższy rysunek przedstawia ideę implementacji metody
kodowania mieszającego z wykorzystaniem list liniowych.
H
”
1
2
m
Rys. 46. Kodowanie mieszające wykorzystujące listy liniowe
Tablica H, indeksowana numerami katalogów, przechowuje
wskaźniki do list liniowych z elementami uniwersum U.
Null
Null
Null
Null
Null
”dobrze”
Null
”całość”
Null
”kot”
84
Wstawienie nowego elementu do tej struktury sprowadza się
do obliczenia, za pomocą funkcji haszującej, wartości indeksu
i ∈
∈
∈
∈{ 1, 2, 3, . . . , m }, a następnie umieszczenia tego elementu
w liście wskazywanej przez element tablicy H[i].
Podobnie przebiega wyszukanie elementu o kluczu równym
zadanej wartości x. Najpierw oblicza się przy pomocy funkcji
haszującej wartość i a następnie przegląda listę wskazywaną
przez H[i] w celu ostatecznego wyszukania elementu. W celu
przyspieszenia wyszukiwania warto jest poszczególne listy
utrzymywać w stanie uporządkowania.
Algorytmy z powrotami
Algorytm szukania w głąb dla grafu jest typowym
przykładem szerszej klasy algorytmów, zwanych algorytmami
z powrotami lub wyszukiwaniem wyczerpującym.
Są to algorytmy rekurencyjne, które w swoim ciele zawierają,
zamiast warunkowych wywołań rekurencyjnych, pętlę
iteracyjną, z której wnętrza następują dopiero wywołania
rekurencyjne.
Pojedyncze
wywołanie
algorytmu
rekurencyjnego może więc spowodować ciąg kolejnych
wywołań rekurencyjnych (wszystkie wywołania z tego
samego poziomu) nadzorowanych przez pętlę iteracyjną. Pętla
ta musi być tak skonstruowana, aby dla każdego
dopuszczalnego zestawu danych zapewnić spełnienie w
pewnym momencie warunku stopu, przerywając ten ciąg
wywołań.
Algorytmy z powrotami wykorzystywane są nie tylko do
rozwiązywania problemów, dających się łatwo przedstawić w
postaci grafu, ale w szeregu innych dziedzinach wiążących się
ściśle z informatyką, takich jak: teoria automatów,
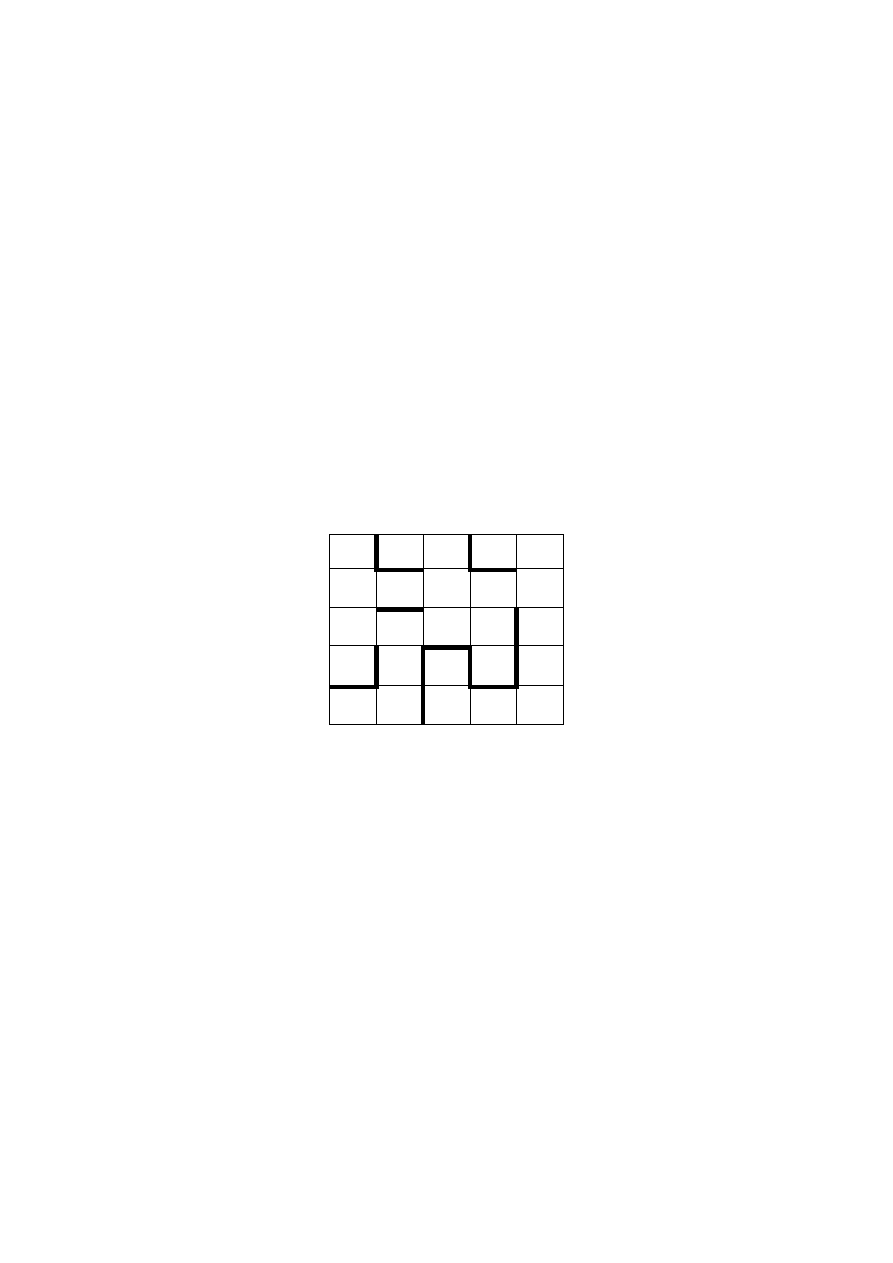
85
projektowanie i analiza sieciowych systemów operacyjnych,
przetwarzanie
równoległe,
wykorzystanie
logiki
w
programowaniu, problemy kodowania, czy wreszcie – gry
komputerowe.
Klasa algorytmów z powrotami opisana została już dawno
opisana w literaturze, gdzie została zilustrowana szeregiem
klasycznych problemów, takich jak: szukanie wyjścia z
labiryntu, problem ośmiu hetmanów, droga skoczka
szachowego, problem komiwojażera, problem doboru,
problem plecakowy.
Klasę algorytmów z powrotami omówimy na przykładzie
problemu szukania wyjścia z labiryntu.
Rys. 47 Labirynt zawierający 25 ponumerowanych pól z
widocznymi przegrodami, uniemożliwiającymi
przejście między niektórymi polami
W labiryncie, przedstawionym na rys. 47 można przechodzić
między sąsiednimi polami po liniach prostych. Zadanie polega
na szukaniu drogi między dwoma dowolnymi polami
labiryntu.
Tak
postawiony
problem
trzeba
jednak
uszczegółowić, można bowiem szukać odpowiedzi na
następujące pytania:
- czy taka droga w ogóle istnieje ?
- jeśli tak, to czy takich różnych dróg jest więcej ?
- jeśli tak, to która z nich jest najkrótsza ?
21 22 23 24 25
16 17 18 19 20
11 12 13 14 15
6
7
8
9 10
1
2
3
4
5
86
Mówiąc ogólnie metoda powrotów polega na próbach
rozszerzenia pewnego rozwiązania częściowego. W każdym
kroku, jeśli rozszerzenie aktualnego rozwiązania częściowego
nie jest możliwe, powraca się do „krótszego” rozwiązania
częściowego i ponownie próbuje się je rozszerzyć.
Tak więc można szukać drogi miedzy dwoma dowolnymi
polami labiryntu kierując się następującymi zasadami:
1. z danego pola mogę zawsze wybrać dopuszczalne, nie
badaną jeszcze pole sąsiednie,
2. jeśli będąc w określonym polu stwierdzę, że nie istnieje
dopuszczalne, nie badana jeszcze pole sąsiednie,
zmuszony jestem cofnąć się na pole, z którego
wykonałem poprzedni ruch i próbować z tego pola
realizować punkt 1.
Znane
są
dwie,
różne
reprezentacje
pozwalające
zaimplementować przedstawioną wyżej ideę algorytmu z
powrotami:
1. implementacja oparta na zbiorach,
2. implementacja w postaci drzewa.
Implementacja algorytmu z powrotami oparta na zbiorach
Niech A
i
będzie zbiorem kandydatów związanych z punktem i
(w naszym przypadku z polem labiryntu o
numerze i). Zbiór
ograniczeń, związanych z punktem i oznaczmy przez O
i
.
Wtedy
S
i
= A
i
- O
i
jest zbiorem dopuszczalnych kandydatów, związanych z
punktem i.
87
Dla
przykładowego
pola
o
numerze
13
labiryntu,
przestawionego na rys. 47 będzie:
A
13
= { 8, 12, 14, 18} O
13
= { 8 } S
13
= { 12, 14, 18}
Na ogół zbiory A
i
można generować automatycznie. Tak też
jest i w naszym przykładowym labiryncie – są to dwu-, trzy-
lub czteroelementowe zbiory o wartościach różniących się o 1,
lub o 5 od wartości i.
Natomiast zbiory O
i
są albo z góry zadane i na ogół nie
zmieniają się w trakcie realizacji algorytmu, albo (w
przypadku bardziej ogólnym) są generowane dla punktu i (a
często i dla najbliższego jego otoczenia), na bieżąco w trakcie
realizacji algorytmu. Tak się dzieje, na przykład, w większości
zręcznościowych gier komputerowych.
Rozwiązaniem częściowym jest częściowy wektor rozwiązań
(a
1
, a
2
, . . . , a
k
), zawierający nie powtarzające się numery
punktów i reprezentujący częściową, dopuszczalną drogę z
punktu wyjściowego a
1
do punktu a
k
. Przykładem rozwiązania
częściowego dla rozważanego labiryntu może być wektor
( 1, 2, 7, 12, 13, 14, 19, 20 ).
Próba rozszerzenia rozwiązania częściowego polegać będzie
na wyborze ze zbioru S
k
kolejnego kandydata, rozszerzając
rozwiązanie częściowe do (a
1
, a
2
, . . . , a
k,
a
k+1
) a następnie
sprawdzenie, czy w ten sposób osiągamy rozwiązanie
końcowe ( w naszym przykładzie – dochodzimy do pola
docelowego labiryntu ). Jeśli nie – kontynuujemy rozszerzanie
rozwiązania częściowego wybierając kolejnego kandydata ze
zbioru S
k+1
. Dla zaznaczenia, że przejście z punktu a
k,
do
a
k+1
miało już miejsce i w przyszłości nie powinno już być badane,
usuwamy ze zbioru S
k
kandydata S
k+1
.
88
Takie poruszanie się w głąb labiryntu musimy przerwać, jeśli
napotkamy pusty zbiór S
k
. Wtedy algorytm usuwa z
rozwiązania częściowego kandydata a
k
, wybierając kolejnego
kandydata ze zbioru S
k-1
. Gdyby i ten zbiór okazał się pusty,
trzeba usunąć z rozwiązania częściowego punkt a
k-1
, próbując
rozszerzyć to rozwiązanie punktem ze zbioru S
k-2
.
Poniżej przedstawiono w pseudokodzie ogólną postać
algorytmu
z
powrotami.
Przystosowanie
algorytmu,
zapisanego w pseudokodzie do rozwiązywania pewnych
konkretnych problemów polegać będzie na uszczegółowieniu
sformułowań zapisanych w języku naturalnym i ich zapisie na
poziomie języka programowania. Przedtem należy wybrać
oczywiście odpowiednią reprezentację danych.
void próbuj( )
{ zapoczątkuj wybieranie kandydatów;
do
{ wybierz następnego kandydata;
if (dopuszczalny)
{ zapisz go;
if (rozwiązanie niepełne)
{ próbuj( );
// próba wykonania następnego kroku
if (nie ma następnego kandydata)
usuń poprzedni zapis;
}
}
} while ( rozwiązanie niepełne
and jest następny kandydat);
}
Rys. 48 Ogólna postać algorytmu z powrotami zapisana w
pseudokodzie
89
Ćwiczenia do samodzielnego wykonania:
1. W jaki sposób i dlaczego przy pomocy algorytmu z
powrotami można stwierdzić, że między dwoma polami
labiryntu nie istnieje żadna droga ?
2. W jaki sposób należy zmodyfikować algorytm z
powrotami, aby:
a) znajdował on wszystkie drogi miedzy dwoma
dowolnymi polami labiryntu,
b) znajdował on najkrótszą drogę spośród
wszystkich możliwych dróg labiryntu.
3. Zastąp w ogólnym algorytmie z powrotami wszystkie
sformułowania w języku naturalnym przez odpowiednie
polecenia w języku programowania tak, aby algorytm
ten znajdował drogę między dwoma dowolnymi polami
a i b labiryntu.