Instrukcja IEF Algorytmy i struktury danych

Laboratorium 2: ”Przeszukiwanie tekstów” cd.

1. Algorytm KMP (Knuth, Morris Pratt).

Algorytm KMP opublikowany został w roku 1976 i stanowi rozwinięcie algorytmu naiwnego. Algorytm
naiwny wykonuje wiele powtarzających się przeszukiwań, nie wykorzystując w przypadku niezgodności
któregoś znaku wzorca informacji wcześniej przebadanej. W algorytmie KMP wykorzystywana jest
informacja o możliwości wykonania przesunięcia wzorca o więcej niż jeden znak.
i – indeks tekstu
j – indeks wzorca
N – długość tekstu
M - długość wzorca.

•

tworzenie tablicy przesunięć

Tablica przesunięć (zwyczajowo nazwana next) wykorzystywana jest w algorytmie KMP do
wyznaczania maksymalnych bezpiecznych przesunięć wzorca względem przeszukiwanego tekstu.
Tworzona jest według następującego algorytmu:
a)

next[0]=-1

j=1

b)

umieść kopię pierwszych j znaków wzorca pod fragmentem wzorca złożonym z pierwszych j liter
wzorca, przesuniętych w prawo o jeden znak

c)

przesuwaj te kopię w prawo do chwili gdy:

-

wszystkie nakładające znaki są identyczne, lub

-

nie ma nakładających się znaków

d)

next[j] jest równe liczbie nakładających się znaków

j=j+1
jeśli j jest równe długości wzorca – stop,

w przeciwnym wypadku skocz do punktu b).

next[0]=-1;

for(i=0,j=-1;i<M-1;i++,j++,next[i]=j)

while((j>=0)&&(wzor[i]!=wzor[j]))

j=next[j];

•

algorytm KMP - wykorzystanie tablicy przesunięć

a)

i=0 j=0

b)

wyznaczyć tablicę przesunięć next dla danego wzorca

c)

dopóki text[i]=wzor[j] i nie przeszukano całego tekstu zwiększ i oraz j o jeden

d)

jeśli przeszukano cały tekst, wtedy możliwe są dwa przypadki:

jeśli j=M to wzorzec zaczyna się na pozycji i-M,

w przeciwnym przypadku wzorzec nie został znaleziony

e)

ponieważ tekst[i]!=wzor[j], więc należy skoczyć do c) zmieniając j na next[j]. Jeśli j=-1, należy
zwiększyć i oraz j o jeden i również skoczyć do c).

for(i=0,j=0;i<N && j<M; i++, j++)

while((j>=0) && (tekst[i]!=wzor[j]))

j=next[j];

if(j==M)

printf("\nwzor zaczyna sie od indeksu %d\n",i-M+1);

else

printf("\n brak wzorca w tekscie\n");

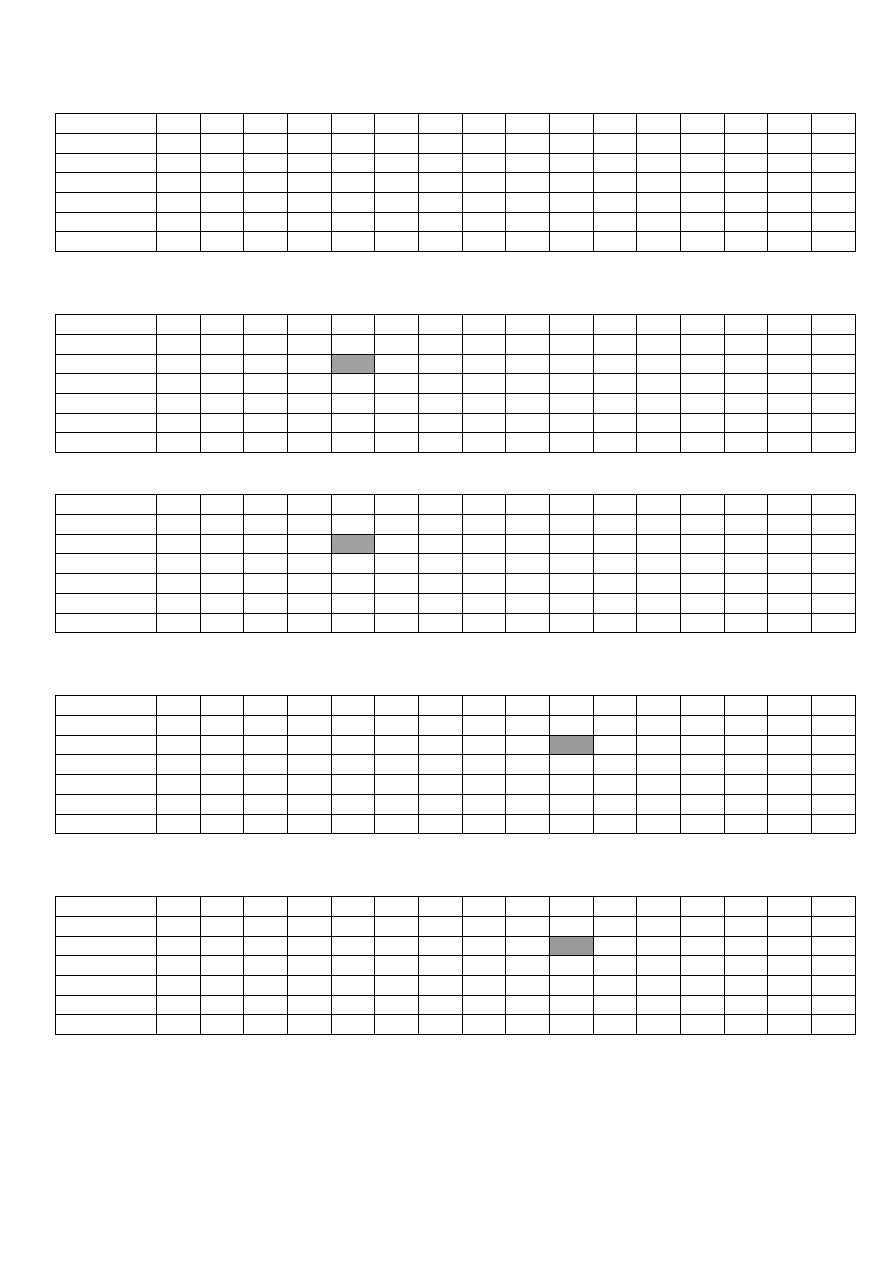
Przykład

Znaleźć wzorzec BABAABBB w tekście BABABAABBABAABBB

indeks T

0

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

i

↓

tekst T

B

A

B

A

B

A

A

B

B

A

B

A

A

B

B

B

wzorzec W

B

A

B

A

A

B

B

B

j

↑

indeks W

0

1

2

3

4

5

6

7

next

-1

0

0

1

2

0

1

1

Ponieważ znaki text[i] i wzor[j] są zgodne, następuje przesunięcie i oraz j aż do momentu stwierdzenia
niezgodności lub znalezienia całego wzorca.
W przykładzie niezgodność występuje na pozycji 4:

indeks T

0

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

i

↓

tekst T

B

A

B

A

B

A

A

B

B

A

B

A

A

B

B

B

wzorzec W

B

A

B

A

A

B

B

B

j

↑

indeks W

0

1

2

3

4

5

6

7

next

-1

0

0

1

2

0

1

1

Z tego powodu konieczne jest przesunięcie wzorca tak, aby znak o indeksie next[4] (czyli 2), oznaczony
pismem pogrubionym znalazł się pod znakiem o indeksie i (oznaczonym kolorem szarym):

indeks T

0

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

i

↓

tekst T

B

A

B

A

B

A

A

B

B

A

B

A

A

B

B

B

wzorzec W

B

A

B

A

A

B

B

B

j

↑

indeks W

0

1

2

3

4

5

6

7

next

-1

0

0

1

2

0

1

1

Ponieważ znaki tekstu o indeksach od 4 do 8 są zgodne z odpowiednimi znakami (od 2 do 6) wzorca, więc
następuje przesunięcie indeksów i oraz j zgodnie z c). Różne znaki występują na pozycji 9:

indeks T

0

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

i

↓

tekst T

B

A

B

A

B

A

A

B

B

A

B

A

A

B

B

B

wzorzec W

B

A

B

A

A

B

B

B

j

↑

indeks W

0

1

2

3

4

5

6

7

next

-1

0

0

1

2

0

1

1

Z tego powodu konieczne jest przesunięcie wzorca (poprzez zmianę j) tak, aby znak o indeksie next[7]
(czyli 1), oznaczony pismem pogrubionym znalazł się pod znakiem o indeksie i (oznaczonym kolorem
szarym):

indeks T

0

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

i

↓

tekst T

B

A

B

A

B

A

A

B

B

A

B

A

A

B

B

B

wzorzec W

B

A

B

A

A

B

B

B

j

↑

indeks W

0

1

2

3

4

5

6

7

next

-1

0

0

1

2

0

1

1

Ponieważ wszystkie pozostałe znaki są zgodne z wzorcem, wzorzec został odnaleziony na pozycji 16-8=8.
Wartość 8 wynika z wartości indeksu i o jeden większej od długości napisu.

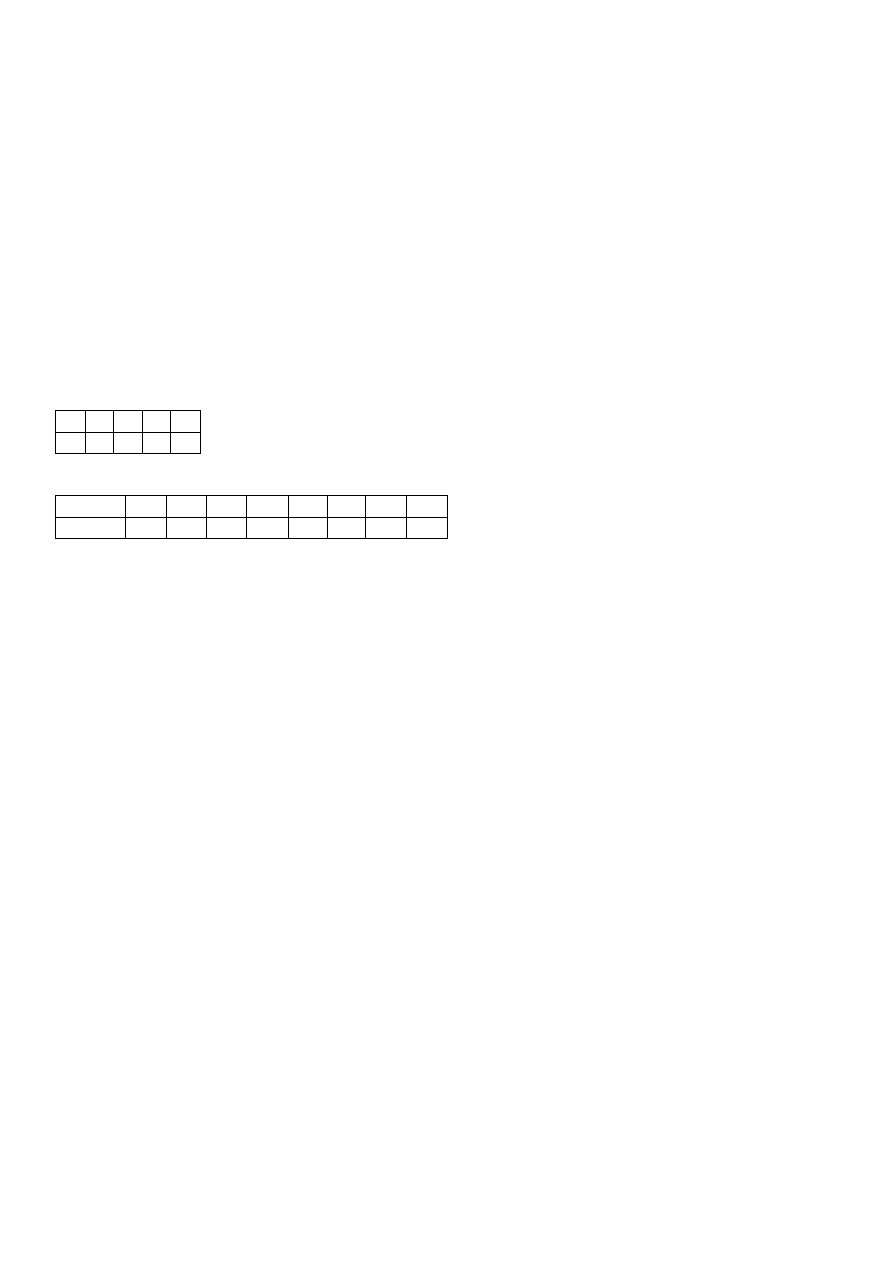
2. Algorytm BM (Boyera i Moore’a)

W algorytmie tym w przeciwieństwie do algorytmu KMP porównywany jest ostatni znak wzorca. Jeśli
badany znak ( o indeksie i) tekstu nie wchodzi w skład wzorca, możliwe jest przesunięcie indeksu i o
długość wzorca. Jeśli znak ten występuje – konieczne jest przesunięcie wzorca tak, aby znak ten znalazł się
pod odpowiadającym mu znakiem wzorca.
K - maksymalna ilość różnych liter w tekście i we wzorcu (zakładamy, że występują tylko duże litery)

•

tworzenie tablicy przesunięć

for(i=0;i<K;i++)

shift[i]=M;

for(i=0;i<M;i++)

shift[wzor[i]-'A']=M-i-1;

Przykład:

wzorzec ABGBD

tekst ABCDEFGH

A B G B D

0 1 2 3 4

długość wzorca wynosi 5
Zawartość tablicy shift

k

‘A’ ‘B’ ‘C’ ‘D’ ‘E’ ‘F’ ‘G’ ‘H’

shift[k]

4

1

5

0

5

5

2

5

•

algorytm BM - wykorzystanie tablicy przesunięć

a)

wyznaczyć tablicę przesunięć shift dla danego wzorca

b)

jeśli długość wzorca > długość tekstu – stop, nie znaleziono

c)

rozpocząć przeszukiwanie od ostatniej litery wzorca i odpowiadającej jej literze tekstu i=M-1, j=M-1

d)

dopóki j>=0 wykonuj

dopóki i-ty znak tekstu oraz j-ty znak wzorca różnią się, wykonuj

używając tablicy shift wyznacz przesunięcie x odpowiadające znakowi T[i]

jeśli M-j>x, zwiększ i o wartość M-j;

w przeciwnym przypadku – zwiększ i o wartość przesunięcia x

jeśli i jest większe lub równe od długości tekstu – stop, wzorca nie znaleziono

ustaw j na ostatni znak wzorca

zmniejsz i oraz j o jeden

e)

odnaleziono wzorzec na pozycji i+1

for(i=M-1,j=M-1;j>=0 ; i--, j--)

while(tekst[i]!=wzor[j])

{

x=shift[tekst[i]-'A'];

if(M-j>x)

i+=M-j;

else

i+=x;

if(i>=N)

{

printf("\nbrak\n");

return 0;

}

}

printf("\nwzor zaczyna sie od indeksu %d\n",i+1);

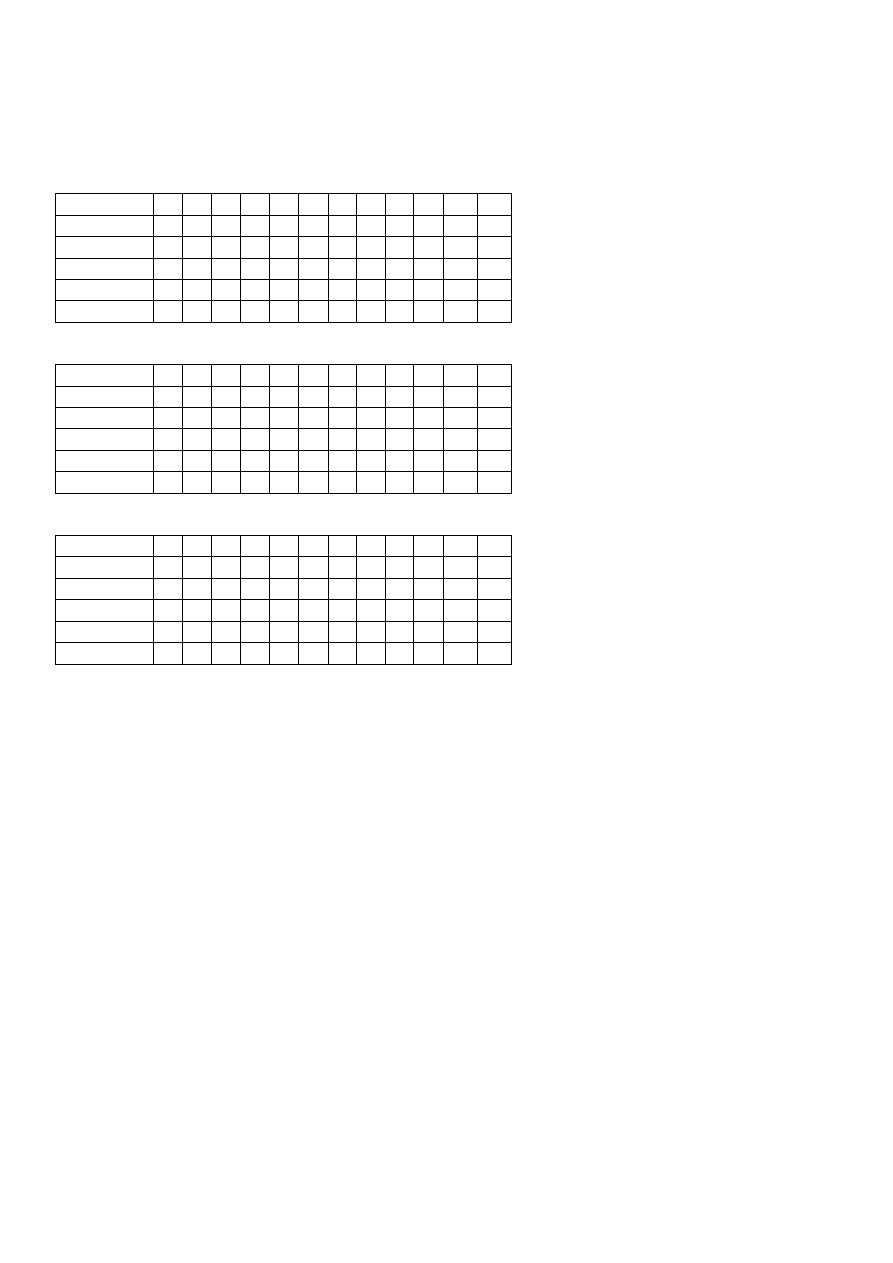
Przykład:

wzorzec: ABGBD

tekst: ABGHHABGBDEH

M=5 N=12 M ≤ N - poszukiwania można rozpocząć od i=j=4

indeks T

0 1 2 3 4 5 6 7 8 9 10 11

i

↓

tekst T

A B G H H A B G B D E

H

wzorzec W A B G B D

j

↑

indeks W

0 1 2 3 4

Ponieważ j>0 i znaki H i D różnią się, więc należy wyznaczyć przesunięcie x=shift[‘H’]=5. Ponieważ
warunek 5-4>5 nie jest spełniony i=4+5=9;

indeks T

0 1 2 3 4 5 6 7 8 9 10 11

i

↓

tekst T

A B G H H A B G B D E

H

wzorzec W

A B G B D

j

↑

indeks W

0 1 2 3 4

Ponieważ i-ty znak tekstu i j-ty znak wzorca są identyczne, więc należy zbadać poprzedni znak,
zmniejszając je o jeden:

indeks T

0 1 2 3 4 5 6 7 8 9 10 11

i

↓

tekst T

A B G H H A B G B D E

H

wzorzec W

A B G B D

j

↑

indeks W

0 1 2 3 4

Postępując analogicznie okaże się, że wzorzec został odnaleziony.

3.

Zadania

do wykonania

:

•

Proszę napisać program, który wczytuje dowolny tekst oraz wzorzec. Szuka wzorca algorytmem
KMP. Uogólnić algorytm, aby znajdował wszystkie wzorce, ich ilość, albo ich brak.

•

Proszę napisać program, który wczytuje dowolny tekst oraz wzorzec. Szuka wzorca algorytmem BM.
Uogólnić algorytm, aby znajdował wszystkie wzorce, ich ilość, albo ich brak.