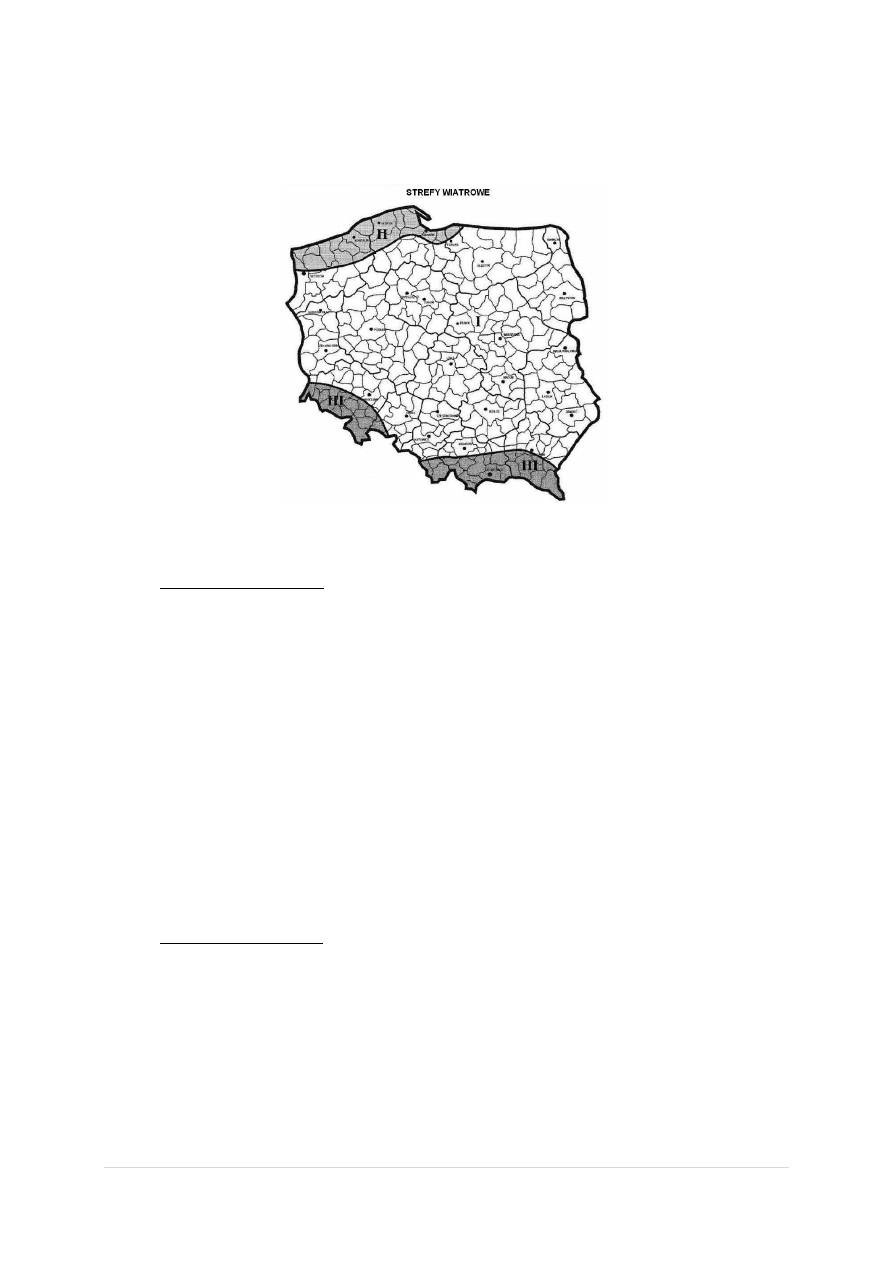
1.1 Obciążenie wiatrem

Zgodnie z PN-EN 1991-1-4, Polska podzielona jest na 3 strefy wiatrowe. Przedstawia je poniższa mapa

Sieradz leży w I strefie wiatrowej. Wysokośd nad poziomem morza to 124 m n.p.m., tak więc zgodnie
z PN-EN podstawowa bazowa prędkośd wiatru 𝑣

𝑏,0

to 22 𝑚/𝑠

Bazowa prędkośd wiatru

Wartośd bazowa prędkości wiatru, przedstawia się wzorem:

𝑣

𝑏

= 𝑣

𝑏,0

∗ 𝐶

𝑑𝑖𝑟

∗ 𝐶

𝑠𝑒𝑎𝑠𝑜𝑛

gdzie:

𝐶

𝑑𝑖𝑟

– współczynnik, pozwalający uwzględnid kierunek wiatru. Przyjmujemy 𝐶

𝑑𝑖𝑟

= 1,0

𝐶

𝑠𝑒𝑎𝑠𝑜𝑛

- współczynnik do obliczania konstrukcji tymczasowych lub znajdujących się w stanie

budowy, jeśli w analizie można uwzględnid porę roku. Z uwagi na brak danych, przyjmujemy
𝐶

𝑠𝑒𝑎𝑠𝑜𝑛

= 1,0

Tak więc bazowa prędkośd wiatru to:

𝑣

𝑏

= 𝑣

𝑏,0

∗ 𝐶

𝑑𝑖𝑟

∗ 𝐶

𝑠𝑒𝑎𝑠𝑜𝑛

= 22 𝑚/𝑠 ∗ 1,0 ∗ 1,0 = 22 𝑚/𝑠

Średnia prędkośd wiatru

Średnia prędkośd wiatru przedstawia się wzorem:

𝑣

𝑚

𝑧 = 𝑐

𝑟

𝑧 ∗ 𝑐

𝑜

𝑧 ∗ 𝑣

𝑏

Gdzie:

𝑐

𝑟

𝑧 - współczynnik chropowatości

𝑐

𝑜

𝑧 - współczynnik rzeźby terenu



Wyższa częśd hali:

Wyznaczenie współczynnika chropowatości:

𝑧

𝑚𝑖𝑛

≤ 𝑧 ≤ 𝑧

𝑚𝑎𝑥

𝑐

𝑟

𝑧 =

𝑘

𝑟

∗ ln

𝑧

𝑧

0

→ 𝑑𝑙𝑎 𝑧

𝑚𝑖𝑛

≤ 𝑧 ≤ 𝑧

𝑚𝑎𝑥

𝑐

𝑟

𝑧

𝑚𝑖𝑛

→ 𝑑𝑙𝑎 𝑧 ≤ 𝑧

𝑚𝑖𝑛

𝑧 = 12 𝑚 - wysokośd konstrukcji nad poziomem gruntu

𝑧

𝑚𝑖𝑛

= 5𝑚 - dla kategorii III terenu

𝑧

𝑚𝑎𝑥

= 200 𝑚

𝑧

0

= 0,3 𝑚 - dla kategorii III terenu

𝑧

𝑚𝑖𝑛

= 5 𝑚 ≤ 𝑧 = 12 𝑚 ≤ 𝑧

𝑚𝑎𝑥

= 200 𝑚

Tak więc

𝑐

𝑟

𝑧 = 𝑘

𝑟

∗ ln

𝑧

𝑧

0

𝑘

𝑟

= 0,19 ∗

𝑧

0

𝑧

0,𝐼𝐼

0,07

= 0,19 ∗

0,3 𝑚

0,05 𝑚

0,07

= 0,215

𝑐

𝑟

𝑧 = 12 = 0,215 ∗ ln

12 𝑚

0,3 𝑚

= 𝟎, 𝟕𝟗

Wyznaczenie współczynnika rzeźby terenu:

Przyjmujemy 𝑐

𝑜

𝑧 = 1,0

𝒗

𝒎

𝒛 = 𝑐

𝑟

𝑧 ∗ 𝑐

𝑜

𝑧 ∗ 𝑣

𝑏

= 0,79 ∗ 1,0 ∗ 22 𝑚/𝑠 = 𝟏𝟕, 𝟑𝟖 𝒎/𝒔



Niższa częśd hali

𝑧 = 10,5 𝑚 - wysokośd konstrukcji nad poziomem gruntu

𝑧

𝑚𝑖𝑛

= 5𝑚 - dla kategorii III terenu

𝑧

𝑚𝑎𝑥

= 200 𝑚

𝑧

0

= 0,3 𝑚 - dla kategorii III terenu

𝑧

𝑚𝑖𝑛

= 5 𝑚 ≤ 𝑧 = 10,5 𝑚 ≤ 𝑧

𝑚𝑎𝑥

= 200 𝑚

Tak więc

𝑐

𝑟

𝑧 = 𝑘

𝑟

∗ ln

𝑧

𝑧

0

𝑘

𝑟

= 0,19 ∗

𝑧

0

𝑧

0,𝐼𝐼

0,07

= 0,19 ∗

0,3 𝑚

0,05 𝑚

0,07

= 0,215

𝑐

𝑟

𝑧 = 10,5 = 0,215 ∗ ln

10,5 𝑚

0,3 𝑚

= 𝟎, 𝟕𝟔

Wyznaczenie współczynnika rzeźby terenu:

Przyjmujemy 𝑐

𝑜

𝑧 = 1,0

𝒗

𝒎

𝒛 = 𝑐

𝑟

𝑧 ∗ 𝑐

𝑜

𝑧 ∗ 𝑣

𝑏

= 0,76 ∗ 1,0 ∗ 22 𝑚 𝑠

= 𝟏𝟔, 𝟕𝟐 𝒎 𝒔

Intensywnośd turbulencji



Wyższa częśd hali

𝐼

𝑉

𝑧 =

𝑘

𝑙

𝑐

𝑜

𝑧 ∗ 𝑙𝑛 𝑧

𝑧

0

𝑑𝑙𝑎 𝑧

𝑚𝑖𝑛

≤ 𝑧 ≤ 𝑧

𝑚𝑎𝑥

gdzie:

𝑘

𝑙

- współczynnik turbulencji. Zalecana wartośd to 𝑘

𝑙

= 1,0

𝑰

𝑽

𝒛 =

𝑘

𝑙

𝑐

𝑜

𝑧 ∗ 𝑙𝑛 𝑧

𝑧

0

=

1

1 ∗ 𝑙𝑛

12 𝑚

0,3 𝑚

= 𝟎, 𝟐𝟕



Niższa częśd hali

𝐼

𝑉

𝑧 =

𝑘

𝑙

𝑐

𝑜

𝑧 ∗ 𝑙𝑛 𝑧

𝑧

0

𝑑𝑙𝑎 𝑧

𝑚𝑖𝑛

≤ 𝑧 ≤ 𝑧

𝑚𝑎𝑥

𝑰

𝑽

𝒛 =

𝑘

𝑙

𝑐

𝑜

𝑧 ∗ 𝑙𝑛 𝑧

𝑧

0

=

1

1 ∗ 𝑙𝑛

10,5 𝑚

0,3 𝑚

= 𝟎, 𝟐𝟖

Wartośd szczytowa ciśnienia prędkości



Wyższa częśd hali

𝑞

𝑝

𝑕 = 1 + 7 ∗ 𝐼

𝑉

𝑧 ∗

1
2

𝜌 ∗ 𝑣

𝑚

𝑧

2

𝜌 = 1,25

𝑘𝑔

𝑚

3

𝑔ę𝑠𝑡𝑜ś𝑐 𝑝𝑜𝑤𝑖𝑒𝑡𝑟𝑧𝑎

𝑞

𝑝

𝑕1 = 1 + 7 ∗ 𝐼

𝑉

𝑧 ∗

1
2

𝜌 ∗ 𝑣

𝑚

𝑧

2

= 1 + 7 ∗ 0,27 ∗

1
2

∗ 1,25 𝑘𝑔 𝑚

3

∗ 17,38 𝑚 𝑠

2

= 545,6 𝑁 𝑚

2

= 0,546 𝑘𝑁 𝑚

2



Niższa częśd hali

𝑞

𝑝

𝑕2 = 1 + 7 ∗ 𝐼

𝑉

𝑧 ∗

1
2

𝜌 ∗ 𝑣

𝑚

𝑧

2

= 1 + 7 ∗ 0,28 ∗

1
2

∗ 1,25 𝑘𝑔 𝑚

3

∗ 16,72 𝑚 𝑠

2

= 517,2 𝑁 𝑚

2

= 0,517 𝑘𝑁 𝑚

2

Ciśnienie wiatru

Ciśnienie wiatru działające na powierzchnie zewnętrzne konstrukcji, wyraża się wzorem:

𝑤

𝑒

= 𝑞

𝑝

𝑕 ∗ 𝑐

𝑝𝑒 ,10



Ściany zewnętrzne

Wiatr na ściany zewnętrzne może działad od czoła bądź też z boku.

o Od czoła:

𝑏 = 24,25 𝑚

𝑕 = 12 𝑚

𝑕 ≤ 𝑏

o Od wyższego boku:

𝑏 = 96 𝑚

𝑕 = 12 𝑚

𝑕 ≤ 𝑏

o Od niższego boku:

𝑏 = 96 𝑚

𝑕 = 10,5 𝑚

𝑕 ≤ 𝑏

Jak widad z rysunku, w obu przypadkach obciążenie wiatrem ścian będzie równomierne.

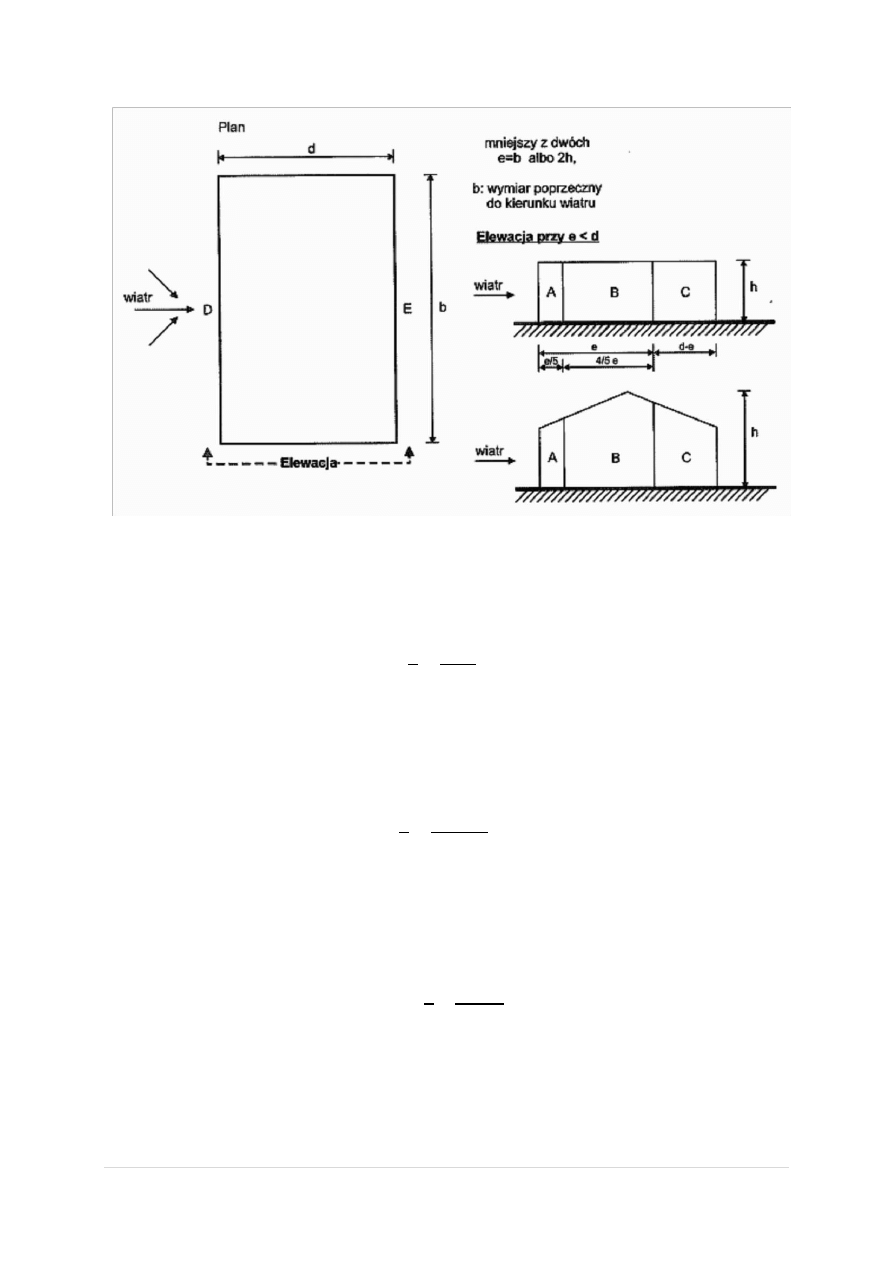
o Od czoła:

𝑒 = 𝑚𝑖𝑛

𝑏 = 24,25 𝑚

2𝑕 = 2 ∗ 12 𝑚 = 24 𝑚

= 24 𝑚

𝑑 = 96 𝑚

𝑒 < 𝑑

𝑕
𝑑

=

12 𝑚
96 𝑚

= 0,125 ≤ 0,25

o Od wyższego boku:

𝑒 = 𝑚𝑖𝑛

𝑏 = 96 𝑚

2𝑕 = 2 ∗ 12 𝑚 = 24 𝑚

= 24 𝑚

𝑑 = 25,75 𝑚

𝑒 < 𝑑

𝑕
𝑑

=

12 𝑚

25,75 𝑚

= 0,466 ≈ 0,25

o Od niższego boku:

𝑒 = 𝑚𝑖𝑛

𝑏 = 96 𝑚

2𝑕 = 2 ∗ 10,5 𝑚 = 21 𝑚

= 21 𝑚

𝑑 = 25,75 𝑚

𝑒 < 𝑑

𝑕
𝑑

=

10,5 𝑚

21 𝑚

= 0,5 ≈ 1

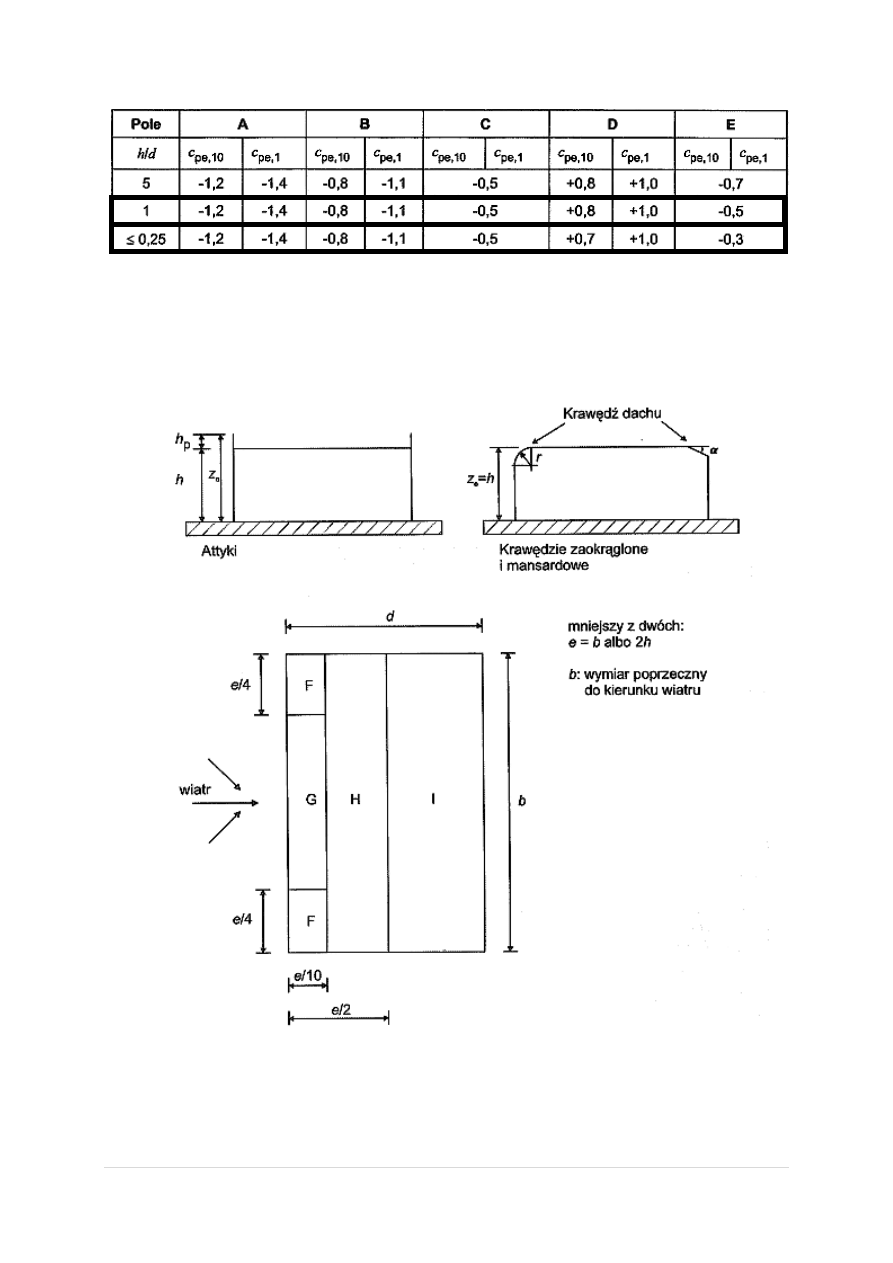
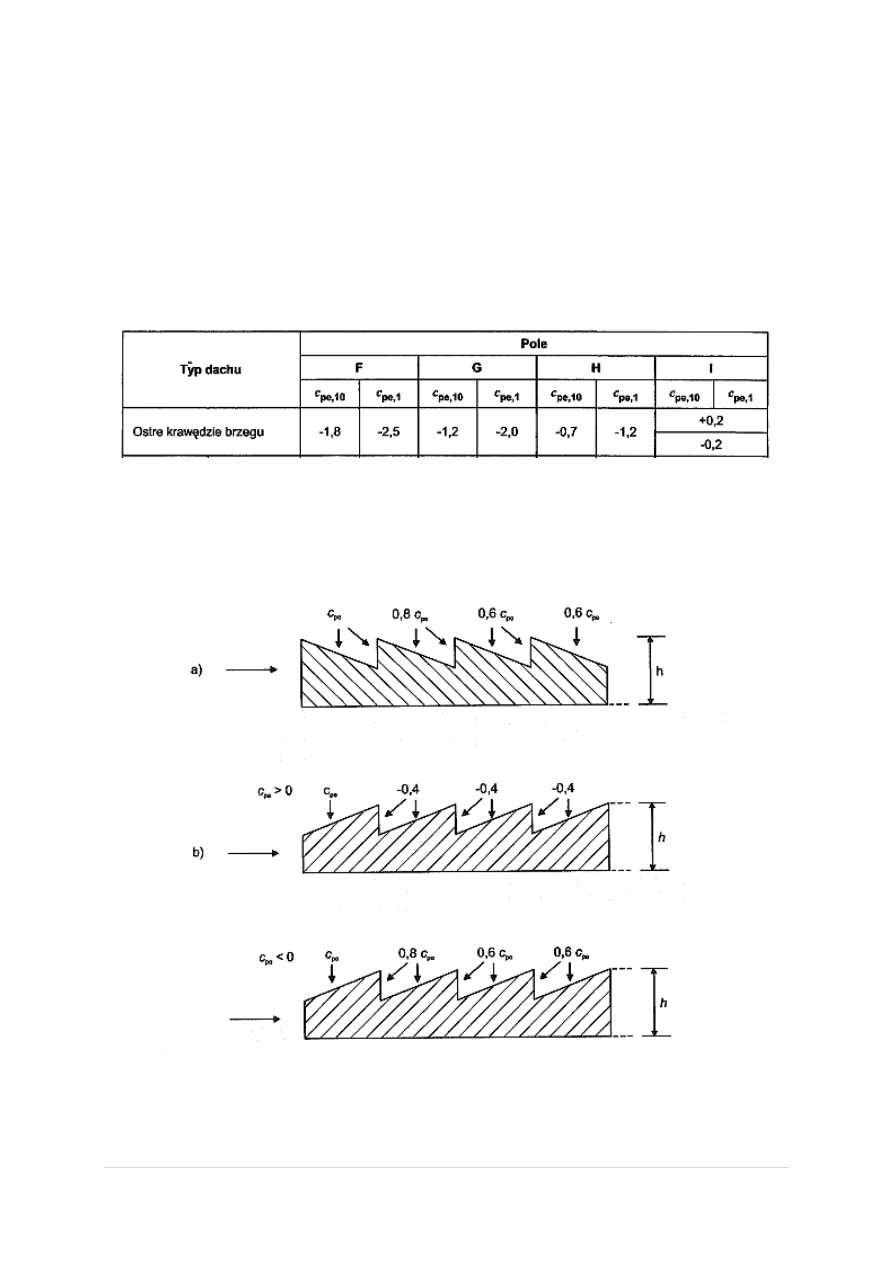
Poniższa tabela przedstawia zalecane wartości współczynnika ciśnienia zewnętrznego dla ścian
pionowych budynków w rzucie prostokąta:



Poład dachowa

Projektowana hala to hala dwunawowa. Dach lewej nawy nachylony jest do poziomu pod kątem 4

o

,

natomiast prawej – pod kątem 3

o

. Można więc przyjąd, że obydwie nawy mają dach płaski(



<5

o

)

o Od czoła:

𝑒 = 𝑚𝑖𝑛

𝑏 = 24,25 𝑚

2𝑕 = 2 ∗ 12 𝑚 = 24 𝑚

= 24 𝑚

o Od wyższego boku:

𝑒 = 𝑚𝑖𝑛

𝑏 = 96 𝑚

2𝑕 = 2 ∗ 12 𝑚 = 24 𝑚

= 24 𝑚

o Od niższego boku:

𝑒 = 𝑚𝑖𝑛

𝑏 = 96 𝑚

2𝑕 = 2 ∗ 10,5 𝑚 = 21 𝑚

= 21 𝑚

Poniższa tabela przedstawia zalecane wartości współczynnika ciśnienia zewnętrznego dla dachów
płaskich:

Z racji tego, iż hala jest dwunawowa – jej dach nie jest jednolity. Jedna jego częśd jest wyższa od
drugiej. Należy uwzględnid to w obliczeniach obliczając dach zgodnie z PN-EN 1991 jak dach
wielospadowy, zmieniając wartości współczynników ciśnienie zewnętrznego C

pe

według podanych

schematów:

𝑤

𝑒

= 𝑞

𝑝

𝑕1 ∗ 𝑐

𝑝𝑒 ,10

= 0,546 𝑘𝑁/𝑚

2

∗ 𝑐

𝑝𝑒 ,10

𝑤

𝑒

= 𝑞

𝑝

𝑕2 ∗ 𝑐

𝑝𝑒 ,10

= 0,517 𝑘𝑁/𝑚

2

∗ 𝑐

𝑝𝑒 ,10

Wariant I -

wiatr od

czoła

Ściany

Pole

A

B

C

D

E

C

pe,10

-1,2

-0,8

-0,5

0,7

-0,3

w

e (h1)

-0,655

-0,437

-0,273

0,382

-0,164

Poład

dachowa

Pole

F

G

H

I

I

C

pe,10

-1,8

-1,2

-0,7

-0,2

0,2

w

e

-0,983

-0,655

-0,382

-0,109

0,109

Wariant II -

wiatr od

wyższego

boku

Ściany

Pole

A

B

C

D

E

C

pe,10

-1,2

-0,8

-0,5

0,7

-0,3

w

e(h1)

-0,655

-0,437

-0,273

0,382

-0,164

Poład

dachowa

Pole

F

G

H

I

I

C

pe,10

-1,8

-1,2

-0,7

-0,2*0,8

0,2*0,8

w

e

-0,983

-0,655

-0,382

-0,087

0,087

Wariant III -

wiatr od
niższego

boku

Ściany

Pole

A

B

C

D

E

C

pe,10

-1,2

-0,8

-0,5

0,8

-0,5

w

e(h2)

-0,620

-0,414

-0,256

0,414

-0,256

Poład

dachowa

Pole

F

G

H

I

I

C

pe,10

-1,8

-1,2

-0,7

-0,2*0,8

0,2*0,8

w

e

-0,983

-0,655

-0,382

-0,087

0,087