1

w w w. o p e r o n . p l

Modele odpowiedzi do arkusza Próbnej Matury z OPERONEM

Matematyka

Poziom podstawowy

Listopad 2010

W kluczu są prezentowane przykładowe prawidłowe odpowiedzi. Należy również uznać odpowiedzi ucznia, jeśli są
inaczej sformułowane, ale ich sens jest synonimiczny wobec schematu, oraz inne odpowiedzi, nieprzewidziane
w kluczu, ale poprawne.

Za każdą prawidłową odpowiedź zdający otrzymuje 1 punkt.

Nr

zad.

1.

2.

3.

4.

5.

6.

7.

8.

9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25.

Odp. A

C

B

A

C

B

C

D

D

A

C

C

A

C

C

D

B

C

B

C

D

A

D

A

D

Zadania zamknięte

Zadania otwarte

Numer

zadania

Zdający otrzymuje po 1 punkcie

Suma

punktów

26.

gdy pogrupuje wyrazy do postaci, z której łatwo można przejść do postaci iloczynowej np.:

i na tym poprzestanie lub dalej popełni błąd

(

2)

6 (

2)

0

x x

x

2

+

-

+

=

1 pkt

gdy wyznaczy bezbłędnie wszystkie rozwiązania równania:

, ,

x

6

3

=

x

6

2

= -

2

x

1

= -

2 pkt

27.

gdy poprawnie określi znak czynnika liniowego i poda rozwiązanie

i na

tym poprzestanie lub dalej popełni błąd

(

,

)

x

3

3

!

-

+

1 pkt

gdy poda rozwiązanie nierówności

i uwzględni je w ostatecznej odpowiedzi

albo

i

(

5)

0

x

>

2

-

(

3, 5)

(5,

)

,

3

-

+

x

5

!

(

3,

)

x

3

!

-

2 pkt

28.

gdy obliczy wyróżnik podanego trójmianu kwadratowego:

i na tym poprzestanie lub dalej popełni błąd

4

k

k

2

D =

+

1 pkt

gdy zauważy, że

dla każdego

, zatem

dla

, co oznacza, że

równanie ma dwa pierwiastki

0

k >

0

>

D

0

k >

4

0

k

k >

2

+

2 pkt

29.

sposób I

gdy korzystając z własności funkcji trygonometrycznych poda układ równań:

i na tym poprzestanie lub dalej popełni błąd

cos

sin

sin

cos

2

1

2

2

a

a

a

a

=

+

=

*

1 pkt

2

w w w. o p e r o n . p l

Matematyka. Poziom podstawowy

Próbna Matura z OPERONEM i „Gazetą Wyborczą”

Numer

zadania

Zdający otrzymuje po 1 punkcie

Suma

punktów

gdy rozwiąże otrzymany układ poprawnie i otrzyma

, a następnie, korzystając

z podanego w treści zadania warunku

– kąt ostry, wybierze rozwiązanie

i zauważy, że

jest liczbą niewymierną

cos

5

1

2

a =

cos

5

1

a =

a

5

1

2 pkt

29.

sposób II

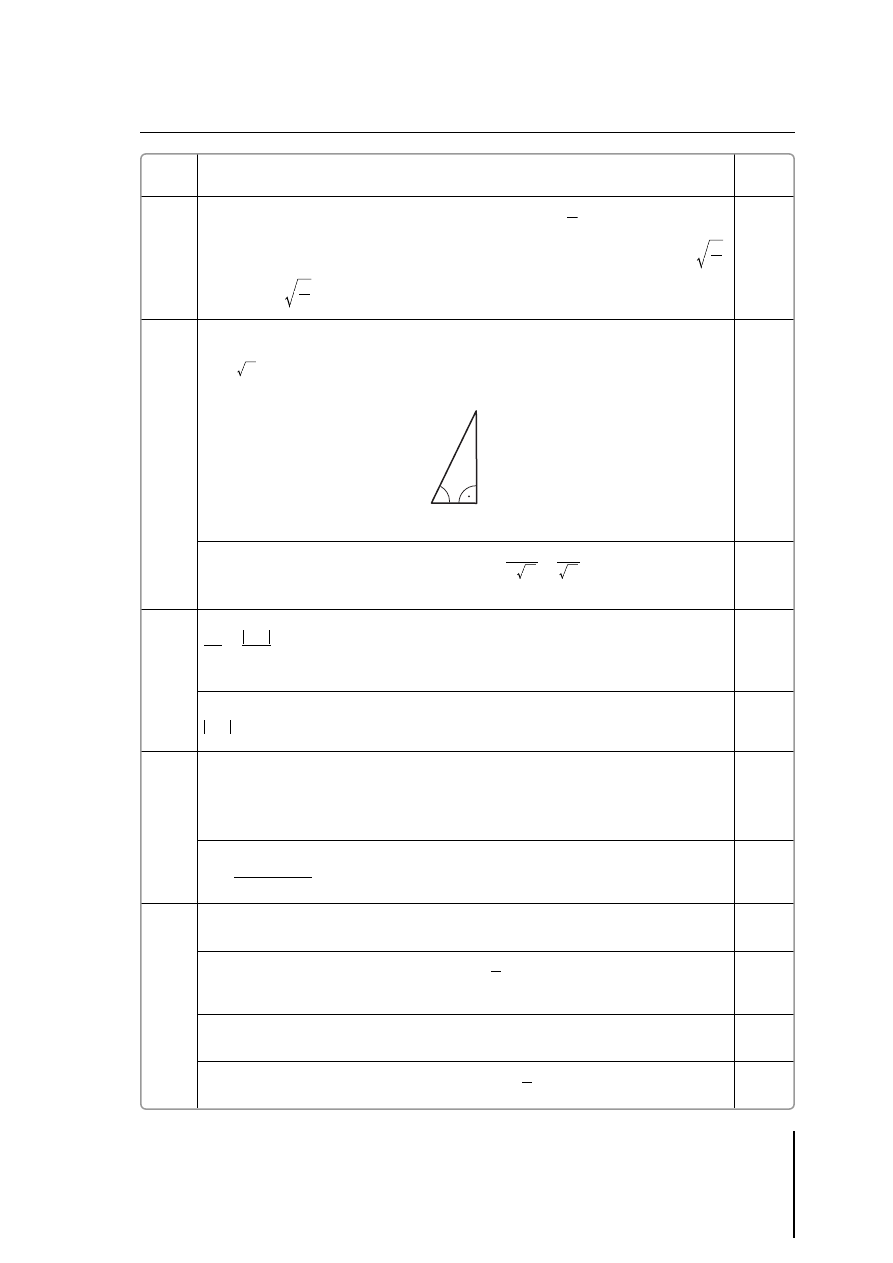
gdy zbuduje trójkąt prostokątny, w którym

i obliczy długość

przeciwprostokątnej tego trójkąta:

i na tym poprzestanie lub dalej popełni błąd

2

tg a =

r

x 5

=

1 pkt

gdy skorzysta z definicji cosinusa i zapisze

i zauważy, że jest to

liczba niewymierna

cos

x

x

5

5

1

a =

=

2 pkt

30.

gdy zastosuje twierdzenie Talesa do zapisania odpowiedniej proporcji, np.:

i na tym poprzestanie lub dalej popełni błąd

DE

10

12

4

=

1 pkt

gdy obliczy długość odcinka

:

DE

4,8

DE =

2 pkt

31.

gdy pra wi dło wo po dzie li tra pez na dwa trój ką ty rów no ra mien ne pro sto kąt ne (o przy pro -

sto kąt nych dłu go ści i ką

cie ostrym

) i pro sto kąt (o bo kach i

)

oraz po praw nie ob li czy wy so kość tra pe zu i na tym

po

prze sta nie lub da lej po -

peł ni błąd

10 cm

3 cm

°

45

a =

3 cm

3

h

cm

=

1 pkt

gdy poprawnie obliczy pole trapezu:

(

)

cm

2

(

)

39

P

2

10

16

3

$

=

+

=

2 pkt

32.

gdy poprawnie obliczy krawędź podstawy:

i na tym poprzestanie lub dalej

popełni błąd

10

a =

1 pkt

gdy poprawnie obliczy wysokość ściany bocznej:

,

i na tym

poprzestanie lub dalej popełni błąd

13

h =

10

65

h

2

1

$

=

2 pkt

gdy poprawnie obliczy wysokość ostrosłupa:

i na tym poprzestanie lub dalej

popełni błąd

12

H =

3 pkt

gdy poprawnie obliczy objętość tego ostrosłupa:

100 12

400

V

3

1

$

$

=

=

4 pkt

2x

r

x

a

3

w w w. o p e r o n . p l

Matematyka. Poziom podstawowy

Próbna Matura z OPERONEM i „Gazetą Wyborczą”

Numer

zadania

Zdający otrzymuje po 1 punkcie

Suma

punktów

33.

gdy narysuje odpowiednie drzewko lub zapisze:

56

X =

1 pkt

gdy opisze odpowiednie gałęzie drzewka lub wypisze zdarzenia sprzyjające:

,

,

cz b

]

g

,

b cz

]

g

2 pkt

gdy zapisze odpowiednią sumę, korzystając z drzewka, lub określi liczbę zdarzeń

sprzyjających:

6 2 2

24

$

$

=

3 pkt

gdy poprawnie na podstawie drzewka obliczy prawdopodobieństwo:

lub zastosuje model klasyczny do obliczenia

prawdopodobieństwa:

( )

P A

8

6

7

2

7

6

8

2

7

3

$

$

=

+

=

( )

P A

56

24

7

3

=

=

4 pkt

34.

gdy wprowadzi odpowiednie oznaczenia i zapisze równanie wynikające z treści zadania:

– pierwsza liczba,

– druga liczba,

x

1

x +

(

1)

6

x

x

$

+

=

1 pkt

gdy zapisane równanie przekształci do postaci, z której można łatwo obliczyć pierwiastki:

6

0

x

x

2

+ -

=

2 pkt

gdy obliczy wyróżnik trójmianu:

oraz znajdzie pierwiastki:

,

3

x

1

= -

25

D =

x

2

2

=

3 pkt

gdy znajdzie dwie pary liczb spełniające warunki zadania:

,

lub popełni błąd w obliczeniach, ale dalej konsekwentnie wykonuje obliczenia

(2, 3)

(

3,

2)

-

-

4 pkt

gdy znajdzie sumy liczb:

,

i sformułuje odpowiedź: suma tych liczb jest równa

lub

5

-

2

3

5

+

=

3

(

2)

5

- + -

= -

5

5 pkt