ZESPÓŁ LABORATORIÓW TELEMATYKI TRANSPORTU
ZAKŁAD TELEKOMUNIKACJI W TRANSPORCIE
WYDZIAŁ TRANSPORTU
POLITECHNIKI WARSZAWSKIEJ
LABORATORIUM
Telekomunikacji Kolejowej
INSTRUKCJA DO ĆWICZENIA NR 5
Kompresja danych
© TwTWTPW, DO UŻYTKU WEWNĘTRZNEGO
Warszawa 2013

Ćw. nr 5 – Kompresja danych 2013-11-09
Laboratorium Telekomunikacji Kolejowej
Zakład Telekomunikacji w Transporcie Wydziału Transportu Politechniki Warszawskiej
1
1.
Cel ćwiczenia
Celem ćwiczenia jest prezentacja procesu kompresji danych, na przykładzie obróbki
plików o różnej zawartości – różnej naturze danych.
Zakres ćwiczenia obejmuje obserwację, ocenę oraz rejestrację podstawowych dla
procesu kompresji danych parametrów, a w szczególności:
- współczynnik kompresji,
- rozkład statystyczny danych w zbiorze,
- entropia zbioru,
- teoretyczna minimalna wielkość pliku po kompresji,
- teoretyczny maksymalny współczynnik kompresji,
- sprawność kompresji popularnych programów archiwizujących.
2.
Wykaz wykorzystanych przyrządów i oprogramowania
- komputer PC z systemem Windows 98/NT/2000/XP,
- programy kompresujące:
A – WinZIP,
B – WinRAR,
C – WinACE.
- program Kompresja danych do analizy statystycznej plików (rys. 3.1),
- program graficzny IrfanView do kompresji JPG,
- zestaw plików poddawanych kompresji (patrz p. 5).
3.
Program Kompresja danych
Program
przeznaczony
jest
do
wyznaczania
podstawowych
własności
probabilistycznych dowolnych zbiorów danych. Do jego podstawowych funkcji należy:
- odczyt dowolnego zbioru danych,
- określenie wielkości zbioru danych (w bajtach),
- określenie częstości występowania wszystkich znaków we wskazanym zbiorze
danych i przedstawienie ich w postaci graficznej (histogramu),
Ćw. nr 5 – Kompresja danych 2013-11-09
Laboratorium Telekomunikacji Kolejowej
Zakład Telekomunikacji w Transporcie Wydziału Transportu Politechniki Warszawskiej
2
- eksport (zapis) wykresu w postaci pliku BMP,
- obliczenie entropii wejścia zbioru danych,
- wyznaczenie teoretycznej minimalnej wielkości zbioru wyjściowego (po
kompresji),
- wyznaczenie teoretycznego maksymalnego współczynnika kompresji dla danego
zbioru danych.
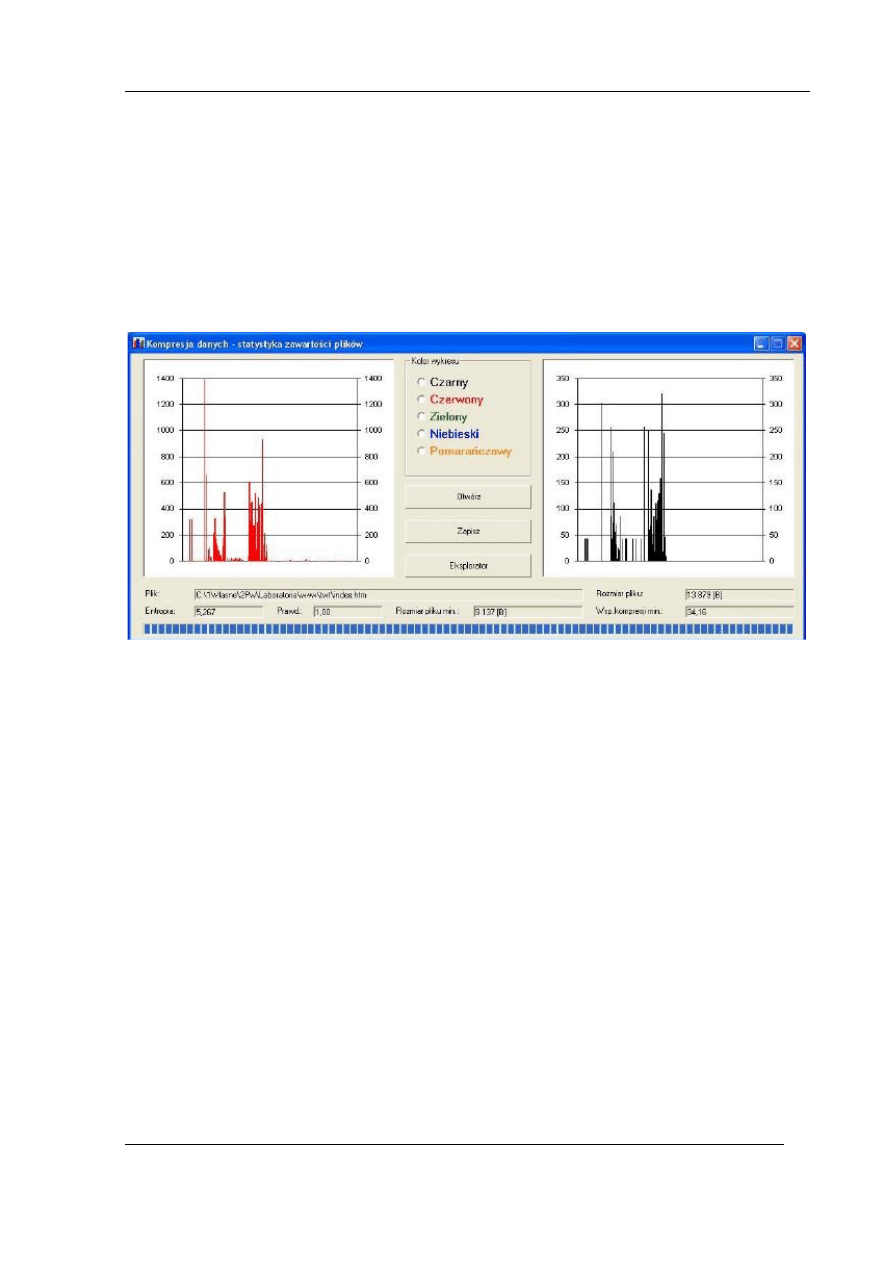
Rys. 3.1 Program Kompresja danych do analizy statystycznej plików
Obsługa programu jest bardzo prosta, a jego instalacja przebiega w typowy dla systemu
Windows sposób (setup.exe, katalog programu, itd.). Po naciśnięciu klawisza Otwórz pojawia
się typowe dla Windows okno dialogu. Wskazujemy dowolny plik danych, którego statystykę
zamierzamy określić. Program przystępuje do analizy pliku, a przebieg procesu
sygnalizowany jest zmianami zapełnienia paska postępu, u dołu okna programu. Po
zakończeniu analizy program, po lewej stronie okna, wyświetla wykres częstości
występowania poszczególnych znaków w pliku danych. Poniżej prezentowane są wszystkie
odczytane i obliczone dane: ścieżka pliku danych, jego rozmiar, entropia wejścia, teoretyczna
minimalna wielkość zbioru wyjściowego i teoretyczny maksymalny współczynnik kompresji
dla tego zbioru. Obliczana wielkość prawdopodobieństwa (pole Prawd.) służy jedynie celom
kontrolnym – powinna zawsze wynosić „1,00”, w przypadku różnicy większej niż 0,01 należy
powiadomić prowadzącego.

Ćw. nr 5 – Kompresja danych 2013-11-09
Laboratorium Telekomunikacji Kolejowej
Zakład Telekomunikacji w Transporcie Wydziału Transportu Politechniki Warszawskiej
3
Po kliknięciu na jedno z pól koloru w ramce Kolor wykresu następuje przeniesienie
wykresu z lewej strony okna na prawą, z jednoczesną zmianą jego koloru na wskazany.
Wygodnie, dla celów późniejszej analizy, jest przypisać określony kolor dla określonego typu
danych wejściowych, np. czarny dla zbioru nie skompresowanego, czerwony dla ZIP, itd. Po
naciśnięciu klawisza Zapisz pojawia się typowe dla Windows okno dialogu. Określamy
położenie (ścieżkę) i nazwę pliku BMP, w którym zostanie zapisany wykres. UWAGA!!!
Zapisywany jest wykres z prawej strony okna programu, a więc po przypisaniu mu koloru
wykresu. Wykres ten jest wyświetlany nadal po otwarciu kolejnego zbioru danych, aż do
kolejnego wyboru koloru wykresu. Takie rozwiązanie pozwala już na bieżąco kontrolować
przebieg ćwiczenia i porównywać wykresy kolejnych plików danych. Wykresy zapisywane są
w rozdzielczości dostosowanej do programu przeznaczonego dla wykonania sprawozdania.
Klawisz Eksplorator służy do wywołania Eksploratora Windows z poziomu, którego
łatwo dokonuje się operacji kompresji zbiorów.
4.
Wprowadzenie teoretyczne
Kompresja jest tanim (może nawet najtańszym) sposobem/procesem zmniejszenia
objętości danych wejściowych (źródłowych), w taki sposób, aby zajmowały one jak najmniej
miejsca. Dekompresją nazywamy proces odwrotny do kompresji, polegający na odtworzeniu
z danych wyjściowych (skompresowanych) danych wejściowych. W zależności od rodzaju
kompresji dane odtworzone (zdekompresowane) odpowiadają danym wejściowym w 100%
(kompresja bezstratna) lub jedynie z pewnym przybliżeniem (kompresja stratna). Kompresja
bezstratna stosowana jest wszędzie tam, gdzie zmiana nawet jednego bitu danych może
wywołać negatywne skutki - np. w plikach wykonywalnych EXE, dokumentach DOC,
arkuszach XLS. Kompresja stratna stosowana jest tam, gdzie dopuszczalne jest powstanie
różnicy między danymi wejściowymi a odtworzonymi, głównie w kompresji obrazów i
dźwięków - np. JPEG, MPEG, MP3. Pośrednim skutkiem kompresji może być wzrost
szybkości transmisji danych – mniejsza ilość danych zostanie przecież przesłana w krótszym
czasie niż większa przy wykorzystaniu tego samego pasma transmisyjnego. Tym samym
kompresja danych stała się jednym z fundamentalnych zagadnień transmisji danych, w
niektórych przypadkach umożliwiając wręcz jej realizację – np. w transmisji obrazu.
Realizacja kompresji możliwa jest dzięki tzw. redundancji (nadmiarowości) informacji
zawartej w danych źródłowych oraz dzięki różnym zależnościom w strukturze danych. Każdą
kompresję charakteryzuje tzw. współczynnik kompresji k, wyrażony wzorem (4.1):

Ćw. nr 5 – Kompresja danych 2013-11-09
Laboratorium Telekomunikacji Kolejowej
Zakład Telekomunikacji w Transporcie Wydziału Transportu Politechniki Warszawskiej
4
%
100
we
wy
we
L
L
L
k
(4.1)
gdzie:
we
L - rozmiar danych wejściowych,
wy
L
- rozmiar danych wyjściowych.
Wielkość współczynnika kompresji może zmieniać się od 0 do 100% i zależy od
przyjętego algorytmu (metody) kompresji oraz od zawartości zbioru. O ile pierwsza
przyczyna nie wymaga komentarza, to druga może nie być już tak oczywista. Metody
kompresji danych ogólnie dzielimy na obliczeniowe i statystyczne. Obliczeniowe dokonują
kompresji poprzez mniej lub bardziej złożone obliczenia matematyczne, których bazą jest
zbiór danych wejściowych. Nie poszukują jednak powiązań między samymi danymi.
Statystyczne zaś dostosowują algorytm kompresji do zawartości zbioru danych wejściowych,
częstości występowania poszczególnych elementów, znaków, symboli, fraz, itp. W ogólnym
ujęciu metody statystyczne dają zawsze lepsze rezultaty (większe współczynniki kompresji)
niż obliczeniowe. Wymagają jednak określenia częstości występowania poszczególnych
elementów zbioru wejściowego, a więc wymagają znajomości całego zbioru danych
wejściowych przed rozpoczęciem procesu kompresji. Fakt ten dyskwalifikuje je z zastosowań
w transmisji danych, gdzie na ogół występuje strumień a nie zbiór danych. Problem ten
rozwiązano poprzez połączenie metod obliczeniowych i statystycznych w metody, które
„przewidują” charakter strumienia danych na podstawie analizy jego wcześniej odebranej
części. Dzięki współczynnikowi kompresji możemy w prosty sposób określić podatność
zbioru wejściowego na kompresję – większy współczynnik kompresji, to większa podatność i
odwrotnie. Jest to jednak możliwe już po procesie kompresji. Ponieważ wielkość
współczynnika kompresji może zależeć od przyjętej metody kompresji, to nie można
wykluczyć, że przy zastosowaniu innego algorytmu jego wartość uległaby zwiększeniu, a
rozmiar danych wyjściowych dalszemu zmniejszeniu. Przydatna byłaby, więc możliwość
oceny podatności zbioru danych wejściowych na kompresję jeszcze przed rozpoczęciem
zasadniczego procesu kompresji. Jest to możliwe dzięki tzw. entropii wejścia
(współczynnikowi chaosu zbioru), określającej właśnie podatność na kompresję i obliczanej
ze wzoru (4.2):
Ćw. nr 5 – Kompresja danych 2013-11-09
Laboratorium Telekomunikacji Kolejowej
Zakład Telekomunikacji w Transporcie Wydziału Transportu Politechniki Warszawskiej
5
i
n
i
i
we
z
P
z
P
E
2
1
log
(4.2)
gdzie:
i
z
P
- prawdopodobieństwo występowania znaku z
i
,
2
log - logarytm o podstawie 2, podstawa 2 wynika z binarnego, 0 lub 1 systemu kodowania,
n
- ilość różnych znaków, np. 256 dla kodu 8-bitowego.
Dodatkowo z własności prawdopodobieństwa wynika, że musi być spełniony warunek
(4.3) dla którego suma prawdopodobieństw występowania wszystkich znaków P(z
i
) musi być
równa jedności:
1
1
n
i
i
z
P
(4.3)
Łatwo zauważyć, że obliczona wartość entropii ma bardzo duże znaczenie praktyczne:
Entropia duża (duża przypadkowość danych, chaos, losowość):
maksimum informacji,
minimum podatności na kompresję.
Entropia mała (uporządkowanie danych, wyraźna przewaga części danych):
mniej informacji,
większa podatność na kompresję.
Entropia zdążająca do minimum (przewaga jednych danych, brak innych):
minimum informacji,
maksymalna podatność na kompresję.
Obliczona entropia wejścia pozwala nie tylko na ocenę podatności zbioru wejściowego
na kompresję. Dzięki niej można też w prosty sposób obliczyć (4.4) teoretyczny minimalny
rozmiar danych wyjściowych (po kompresji) za pomocą metody probabilistycznej – opartej
na rozkładzie statystycznym źródła:
l
E
L
L
we
we
min
(4.4)

Ćw. nr 5 – Kompresja danych 2013-11-09
Laboratorium Telekomunikacji Kolejowej
Zakład Telekomunikacji w Transporcie Wydziału Transportu Politechniki Warszawskiej
6
gdzie:
we
L - rozmiar danych wejściowych,
we
E - entropia wejścia,
l – podstawa kodowania (pojedynczych) danych np. 8 bitów dla kodu ASCII
Stąd, równie łatwo, można wyliczyć (4.5) teoretyczny maksymalny współczynnik
kompresji:
%
100
min
max
we
we
L
L
L
k
(4.5)
Kompresja jest tym bardziej wydajna (mniejszy zbiór danych wyjściowych), im
bardziej rozmiar danej reprezentującej konkretny znak jest zbliżony do entropii wejścia. W
roku 1948 Claude E. Shannon udowodnił, że nie można wygenerować krótszego kodu
(używając metod probabilistycznych), niż wyznacza sama entropia. Inaczej mówiąc, nie
można opracować metody kompresji, która byłaby jeszcze bardziej wydajna i dawałaby
mniejszy zbiór danych wyjściowych od ich wyznaczonego teoretycznego minimalnego
rozmiaru L
min
. W praktyce przeważająca większość metod probabilistycznych nie jest w
stanie nawet dorównać wartości L
min
. Należy jednak pamiętać, że większość powszechnie
wykorzystywanych współczesnych metod kompresji jedynie w części swojego działania
wykorzystuje statystykę zbioru, która stanowi bazę do dalszych działań.
5.
Uwagi praktyczne
Większość obserwacji i operacji dokonywana jest przy wykorzystaniu jedynie
Eksploratora Windows, programu laboratoryjnego Kompresja danych, programu graficznego
IrfanView oraz programów kompresujących (patrz p. 2). Oprócz nich w ćwiczeniu występuje
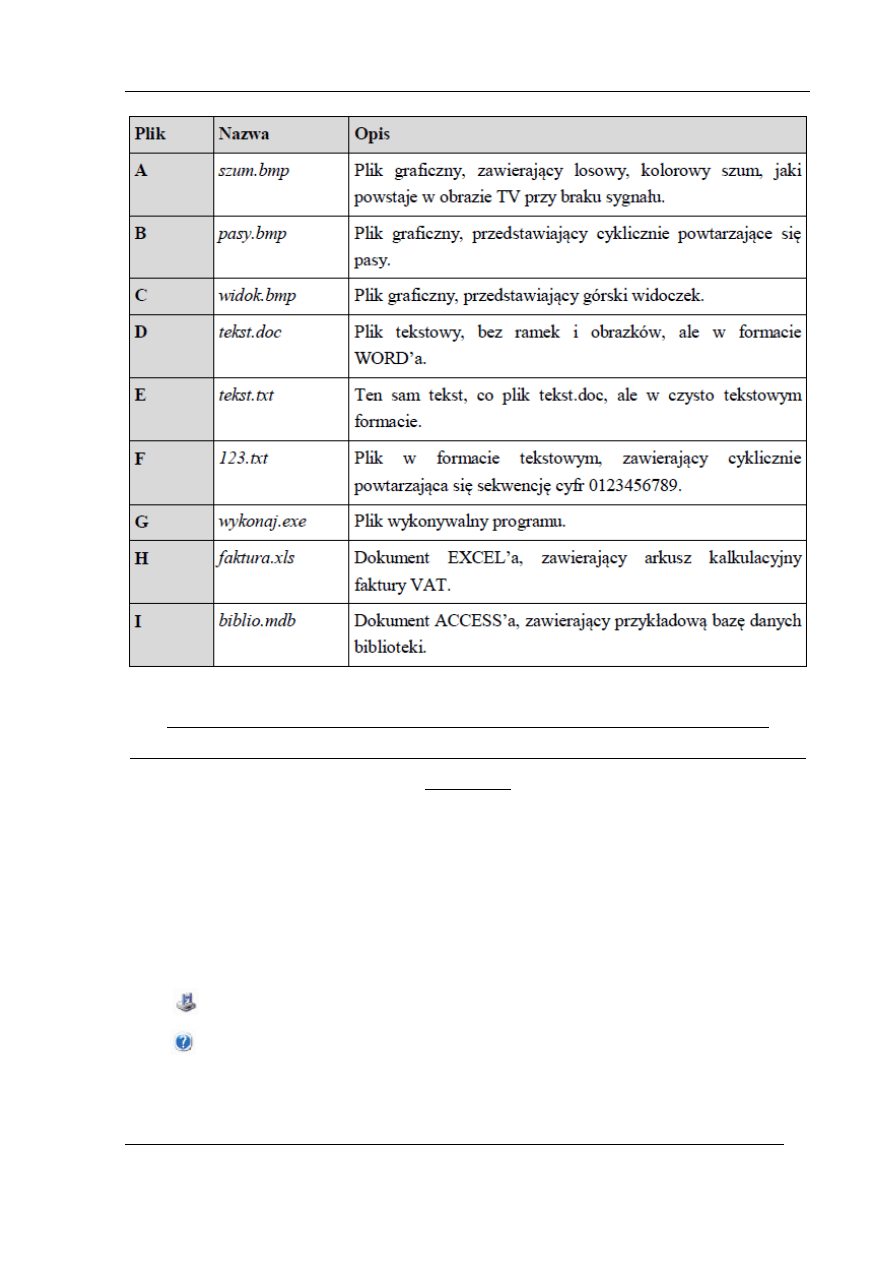
zestaw plików, które poddawane są kompresji:
Ćw. nr 5 – Kompresja danych 2013-11-09
Laboratorium Telekomunikacji Kolejowej
Zakład Telekomunikacji w Transporcie Wydziału Transportu Politechniki Warszawskiej
7
UWAGA!!! Istnieje kilka zestawów o identycznych nazwach ww. plików, więc lepiej
wykonywać ćwiczenie samodzielnie i nie opierać się na wcześniejszych opracowaniach (patrz
regulamin)!
Podczas kompresji plików graficznych BMP do formatu JPG należy zawsze i za
każdym razem otworzyć źródłowy plik BMP i dopiero go skompresować.
Dla zwiększenia przejrzystości instrukcji przyjęto wykorzystanie prostych skrótów
graficznych:
- zapisz dane do pliku na dysku,
- pytanie, na które odpowiedź musi znaleźć się w sprawozdaniu.

Ćw. nr 5 – Kompresja danych 2013-11-09
Laboratorium Telekomunikacji Kolejowej
Zakład Telekomunikacji w Transporcie Wydziału Transportu Politechniki Warszawskiej
8
Pod żadnym pozorem nie należy „upraszczać” ćwiczenia i próbować wykonywać operacji
jednocześnie z kilku punktów instrukcji. Jest to najszybsza droga do pomyłki w identyfikacji
przebiegów i wyników, co skutkuje odrzuceniem sprawozdania.
6.
Przebieg ćwiczenia
6.1. Zapoznaj się z obsługą programów wykorzystywanych podczas ćwiczenia. Programy
kompresujące najlepiej jest wywoływać z poziomu Eksploratora Windows.
6.2. W programie IrfanView poddaj kompresji JPG wszystkie pliki graficzne BMP dla
współczynnika jakości 80, 50 i 30. Jako nazwę tworzonego pliku przyjmij nazwę
oryginalną powiększoną o wartość współczynnika jakości, np. szum80.jpg.
Pamiętaj, żeby po każdym zapisaniu pliku JPG, przed zapisem z nową wartością
współczynnika jakości, otworzyć na nowo oryginalny plik BMP.
6.3. Każdy z wymienionych w p. 5 plików oraz utworzone pliki JPG poddaj kolejno
kompresji każdym z programów wymienionych w p. 2.
6.4. Otwórz plik kompresja.xls, zawierający arkusz Excel’a dla zestawienia wyników
ćwiczenia. Zapisz ten plik pod nazwą zawierającą datę wykonania ćwiczenia, typ
studiów (DZ, ZA, SMU), grupę i semestr.
6.5. Uruchom program Kompresja danych. Otwórz kolejno każdy z plików źródłowych i
odpowiadające im pliki skompresowane. W arkuszu XLS zapisz wszystkie dane
dotyczące plików.
Zapisz na dysku histogramy plików.
6.6. Dokonaj analizy otrzymanych wyników. Jak wpływa współczynnik jakości na wielkość
pliku JPG?
Jak wpływa „treść” pliku graficznego i tekstowego na podatność na
kompresję?
Jaka jest zależność między entropią wejścia pliku a współczynnikiem
kompresji?
Kiedy plik jest najbardziej podatny na kompresję?
Który z
programów kompresujących wykazuje największą sprawność kompresji – ich pliki
wynikowe są najmniejsze?
7.
Wykonanie sprawozdania
Nie należy umieszczać w sprawozdaniu podstaw teoretycznych, opisów stanowiska
laboratoryjnego, ani wykorzystanego oprogramowania.

Ćw. nr 5 – Kompresja danych 2013-11-09
Laboratorium Telekomunikacji Kolejowej
Zakład Telekomunikacji w Transporcie Wydziału Transportu Politechniki Warszawskiej
9
Sprawozdanie musi zawierać wszystkie wyniki pomiarów i obliczeń oraz wszystkie
zarejestrowane histogramy, prezentowane w logicznym ciągu (np. plik nie skompresowany i
skompresowany kolejnymi programami). Każdy wynik i wykres musi być opatrzony
numerem punktu instrukcji wg, którego został zarejestrowany. Każdy histogram musi być
opatrzony opisem, wyjaśniającym, co przedstawia i jakiego pliku dotyczy. W sprawozdaniu
muszą się znaleźć odpowiedzi na wszystkie postawione w instrukcji pytania, ponumerowane
wg punktów, w których zostały postawione. Zarówno opisy, jak i odpowiedzi, mają być
zwięzłe, ale przedstawione pełnymi zdaniami.
Wnioski powinny zawierać podsumowanie przeprowadzonych pomiarów i obliczeń.
Szczególny nacisk należy położyć na zaprezentowanie różnic i podobieństw pomiędzy
histogramami plików nie skompresowanych, a skompresowanych z jednoczesnym
odniesieniem do ich zawartości. Sednem ćwiczenia jest znalezienie związku między
podatnością pliku danych wejściowych na kompresję a jego zawartością, a więc i statystyką.
8.
Literatura
Heim K., Metody kompresji danych, MIKOM 2000,
Sayood K., Kompresja danych - wprowadzenie, RM 2002,
Skarbek Wł. (pod redkakcją), Multimedia. Algorytmy i standardy kompresji, PLJ 1998,
Plucińska A., Pluciński E., Rachunek Prawdopodobieństwa, Statystyka matematyczna,
Procesy stochastyczne, WNT 2000.
Wyszukiwarka
Podobne podstrony:
Cw 5 Kompresja danych
Kompresja danych (FAQ), Informatyka -all, INFORMATYKA-all
kompresja danych
Cw 5 Struktury Danych Materiały dodatkowe
Kodowanie i kompresja danych
ćw zapisywanie danych
19. Archiwizacja i kompresja danych, Semestr 1
SII 16 Kompresja danych
Kompresja danych (FAQ), Informatyka -all, INFORMATYKA-all
kompresja danych
Cw 5 Struktury Danych Materiały dodatkowe
Cw 5 Struktury Danych Instrukcja
08 archiw kompres danych
archiwizery i kompresory danych (7 str)
metody kompresji danych
ćw 34 LabView Obsługa programu rejestracji danych
więcej podobnych podstron