1

Sprawdzian 2 Grupa A

© Copyright by Wydawnictwa Szkolne i Pedagogiczne sp. z o.o.

Matematyka. Poznać, zrozumieć. Kształcenie w zakresie podstawowym



Liceum i technikum

Klasa 2

Zadanie 1. (0–1)
Wskaż poprawne dokończenie zdania.
Dany jest trójkąt równoboczny

ABC

, w którym długość wysokości wynosi

3 3

. Punkty

M N L

, ,

są środkami boków trójkąta

ABC

. Obwód trójkąta

MNL

jest równy

 



A. 9 



B.

9 3

 



C. 13,5 



D. 18

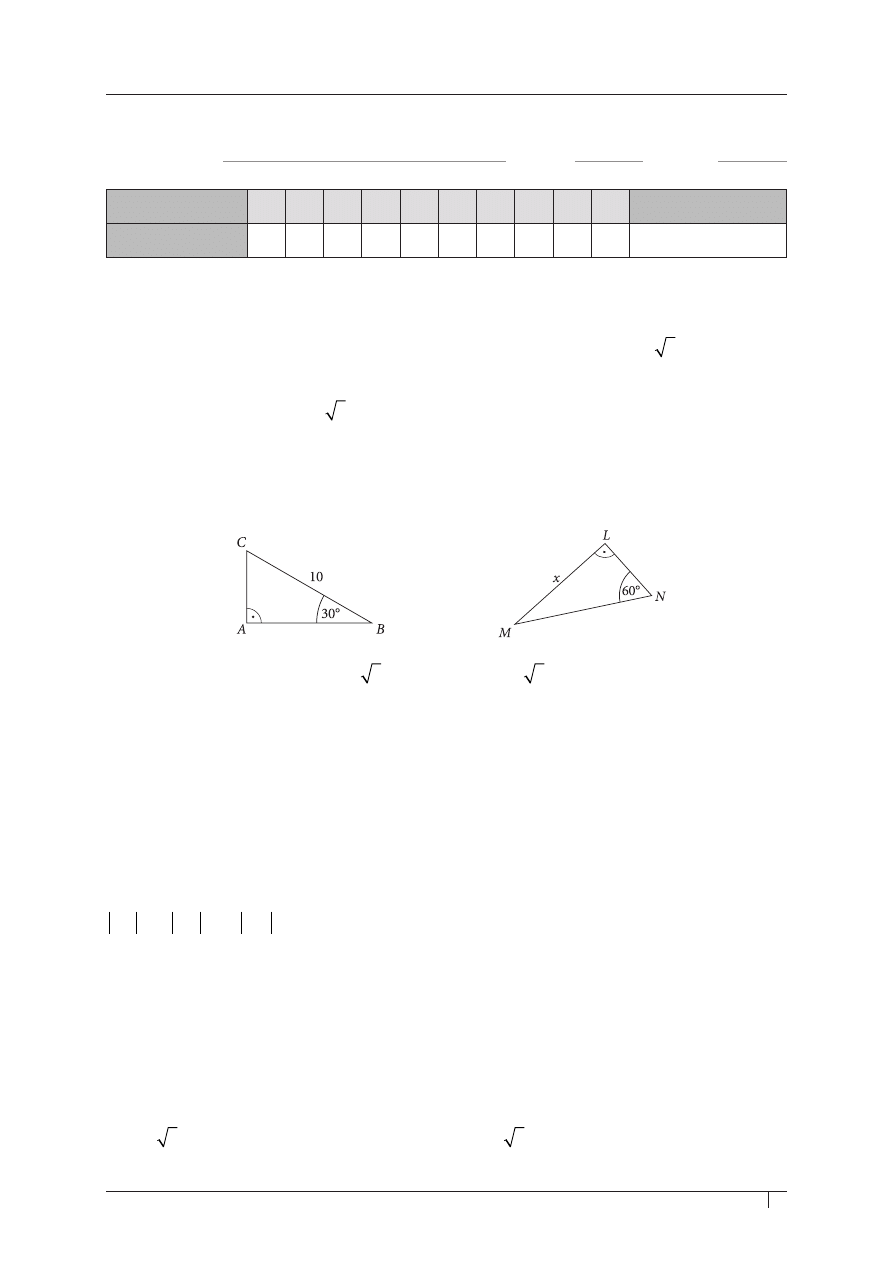
Zadanie 2. (0–1)
Wskaż poprawne dokończenie zdania.
Jeśli trójkąty

ABC MNL

i

są przystające, wówczas

 



A.

x = 5

 



B.

x = 10 3

 



C.

x = 5 3

 



D.

x = 10

Zadanie 3. (0–1)
Wskaż poprawne dokończenie zdania.
Powierzchnia parku wynosi 8 ha. Na planie w skali 1 : 500 powierzchnia ta zajmuje
 



A. 320 cm

2

 



B. 32 cm

2

 



C. 32 dm

2

 



D. 0,32 m

2

Zadanie 4. (0–1)
Wskaż poprawne dokończenie zdania.
Dany jest trapez równoramienny

ABCD

, gdzie bok AB jest równoległy do boku CD oraz

AB

CD

AD

=

=

=

9

6

5

,

i

. Przedłużenia ramion przecinają się w punkcie P. Obwód trójkąta

DPC

wynosi

 



A.

20

 



B.

26

 



C.

29

 



D.

39

Zadanie 5. (0–1)
Wskaż poprawne dokończenie zdania.
Długość boku rombu jest równa 10 i miara jego kąta rozwartego wynosi

120



. Długość dłuższej

przekątnej tego rombu jest równa

 



A.

5 3

 



B.

10

 



C.

10 3

 



D.

12

Imię i nazwisko

_____________________________

Klasa

_______

Ocena

_______

Numer zadania

1

2

3

4

5

6

7

8

9

10

Suma punktów

Liczba punktów

Grupa A

Sprawdzian 2

Matematyka. Poznać, zrozumieć. Kształcenie w zakresie podstawowym



Liceum i technikum

Klasa 2

2

Sprawdzian 2 Grupa A

© Copyright by Wydawnictwa Szkolne i Pedagogiczne sp. z o.o.

Zadanie 6. (0–4)
Oceń prawdziwość każdego zdania.
Zaznacz P, jeśli zdanie jest prawdziwe, lub F, jeśli jest fałszywe.
Dany jest prostokątny trójkąt równoramienny, w którym długość podstawy jest równa

8 2

.

I. Długość promienia okręgu wpisanego w ten trójkąt jest równa

4 4 2

−

. 



P  F

II. Długości środkowych tego trójkąta są równe

4 5 4 5 4 2

,

,

. 



P  F

III. Środek ciężkości tego trójkąta jest oddalony od wierzchołka

kąta prostego o

8
3

2

. 



P  F

IV. Dwusieczna kąta ostrego dzieli ramię tego trójkąta na odcinki

długości

8 2 1 8 2

2

−

(

)

−

(

)

i

. 



P  F

Zadanie 7. (0–2)
Dany jest trójkąt prostokątny o przyprostokątnych długości

a a

i 2

. Wykaż, że odległość środka

ciężkości tego trójkąta od wierzchołka kąta prostego jest równa

a 5

3

.

Zapisz uzasadnienie.

Zadanie 8. (0–2)
Wysokość poprowadzona z wierzchołka kąta prostego w trójkącie prostokątnym dzieli

przeciwprostokątną na odcinki długości 3 i 6. Oblicz obwód tego trójkąta.
Zapisz wszystkie obliczenia i sformułuj odpowiedź.

Odpowiedź:

___________________________________________________________

3

Sprawdzian 2 Grupa A

© Copyright by Wydawnictwa Szkolne i Pedagogiczne sp. z o.o.

Matematyka. Poznać, zrozumieć. Kształcenie w zakresie podstawowym



Liceum i technikum

Klasa 2

Zadanie 9. (0–3)
Z wierzchołka C trójkąta

ABC

poprowadzono dwusieczną, która podzieliła bok

AB

na

odcinki o długościach 5 i 7. Długość boku

BC

jest o 4 krótsza od długości boku

AC

. Oblicz

obwód trójkąta

ABC

.

Zapisz wszystkie obliczenia i sformułuj odpowiedź.

Odpowiedź:

___________________________________________________________

Zadanie 10. (0–4)
Dany jest równoległobok o polu równym

12 3

i kącie rozwartym o mierze

120



. Obwód tego

równoległoboku wynosi 20. Oblicz długości boków tego równoległoboku.
Zapisz wszystkie obliczenia i sformułuj odpowiedź.

Odpowiedź:

___________________________________________________________