F1-87
©J. Kalisz, WAT, 2006
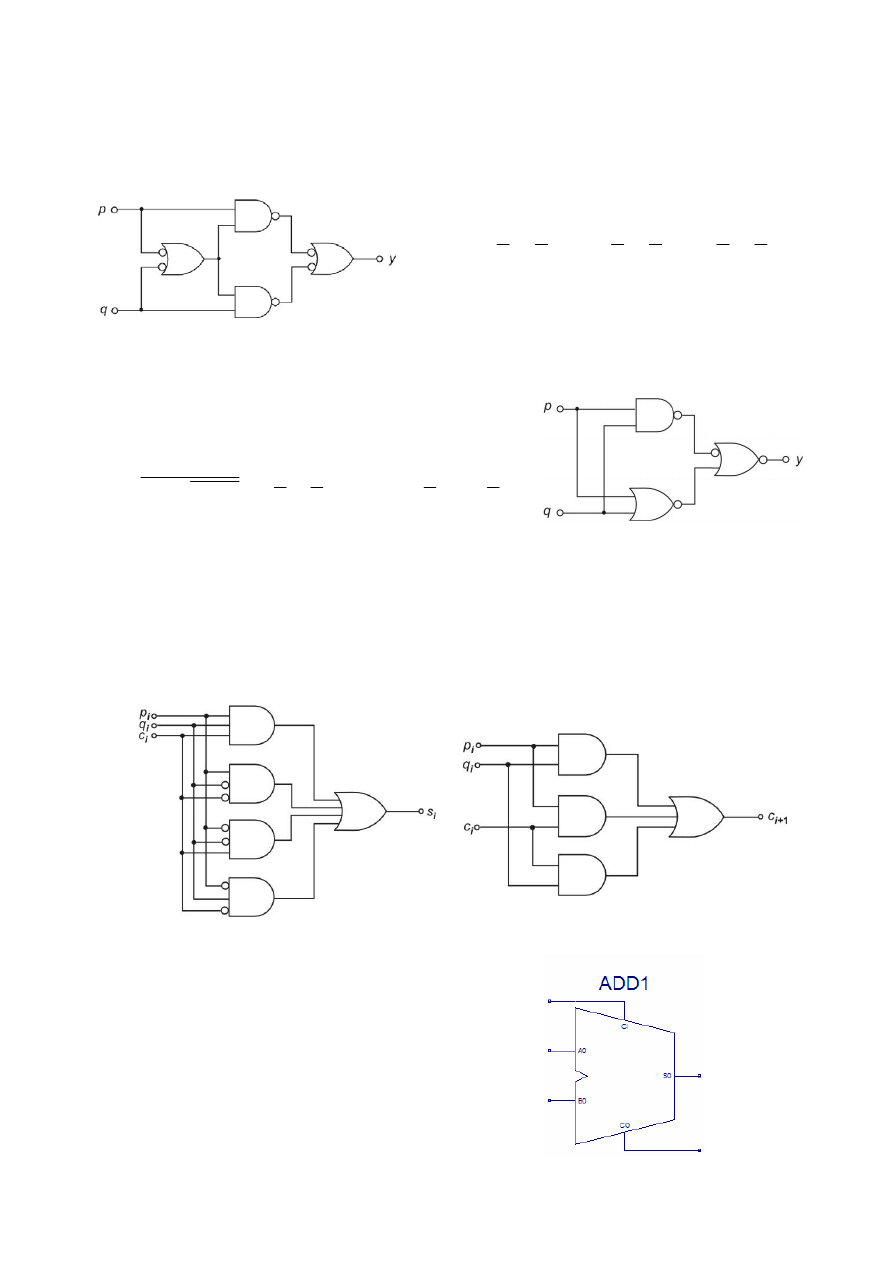
Budowa logiczna sumatora
• Bramka XOR może być realizowana
trójpoziomowo
,
na przykład z użyciem 4 bramek NAND
(
)
(
)
y
pq
pq
p p
q
q p
q
=
+
=
+
+
+
• Wtedy funkcja
s
i
jest realizowana przez
6
poziomów (opóźnień)
bramkowych, a funkcja
c
i
+1
przez
5
poziomów
Prostsza budowa bramki XOR z
użyciem trzech bramek
z inwersją
►
(
)(
)
y
pq
p
q
p
q p
q
pq
pq
=
+ + =
+
+
=
+
• W technologii CMOS można zbudować proste i szybkie bramki XOR
►
prosty i szybki sumator CMOS z bramkami XOR
•
Najprostszy logicznie
jest schemat z bramkami NAND reprezentujący
zminimalizowane formy boolowskie sumatora
• Symbol graficzny sumatora 1-bitowego w
systemie projektowym
Xilinx ISE 7.1
Porty przeniesień:
CI –
Carry Input
–
wejście przeniesienia
CO –
Carry Output
– wyjście przeniesienia