1) Temat zadania

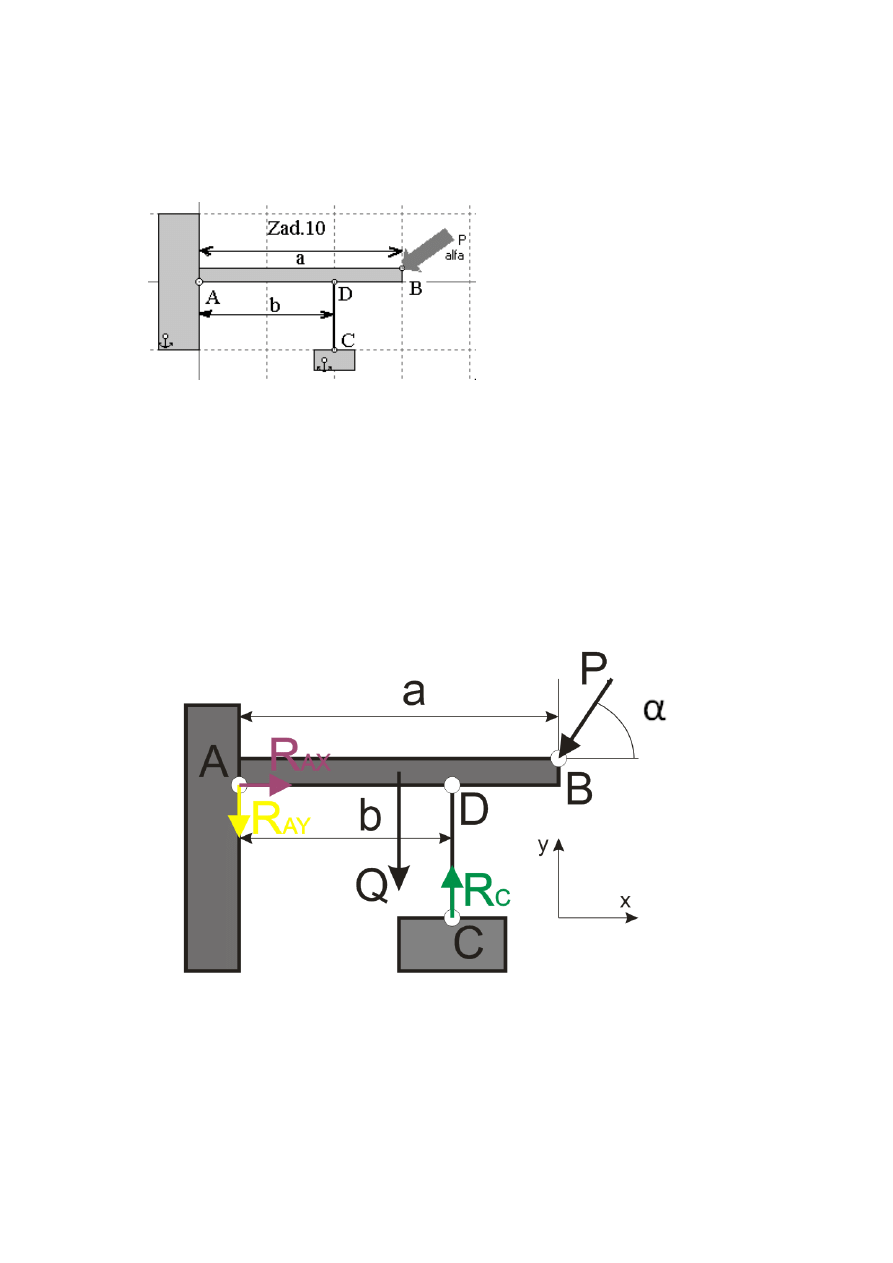
Dźwignia o wadze Q jest
na końcu zamocowana
przegubowo, natomiast w
odległości b jest podparta
pionowym prętem.

Rys. 1 Schemat układu

Polecenia do wykonania:

1. Dla danych: P, α, a, b, Q - wyznacz w Mathcadzie reakcje.
Oto przykładowe dane: P=10N; Q=5,88N; a=3m; b=2m oraz wyniki: Ra=8,66; Rc=11
2. Sporządź wykresy dla zbadania zależności reakcji Ra i Rc od α
3. Przyjmując sensowne dane (np. P=50kG) oraz materiał, oblicz jaki przekrój poprzeczny
(kwadratowy) powinien mieć pręt aby nie uległ wyboczeniu.
4. Zakładając, że α jest zmienną losową o rozkładzie normalnym, przyjmij parametry tego
rozkładu (na podstawie uzyskanych już wyników). Sporządź wykresy dystrybuanty i gęstości
prawdopodobieństwa oraz wyznacz w Mathcadzie prawdopodobieństwo wyboczenia .

2) Schemat geometrii i przewidywanego rozkładu sił

Rys. 2 Schemat układu z przyjętymi siłami reakcji

3) Równania statyki

DANE:

SZUKANE:

Rax, Ray, Rc

P

10 N

⋅

:=

Q

5.88 N

⋅

:=

a

3 m

⋅

:=

b

2 m

⋅

:=

α

45 deg

⋅

:=

RAX

1 N

⋅

:=

RAY

1 N

⋅

:=

RC

1 N

⋅

:=

Given

RAX

P cos α

( )

⋅

−

0

=

RAY

RC

+

P sin α

( )

⋅

−

0

=

RC b

⋅

Q

a

2

⋅

−

P sin α

( )

⋅

a

⋅

−

0

=

Find RAX RAY

,

RC

,

(

)

7.071

7.946

−

15.017

















N

=

RC

P sin α

( )

⋅

a

⋅

Q

a

2

⋅

+













b

:=

RA

P cos α

( )

⋅

(

)

2

P sin α

( )

⋅

P sin α

( )

⋅

a

⋅

Q

a

2

⋅

+













b

−

































2

+

:=

RA

10.636 N

=

RC

15.017 N

=

4) Wykres obrazujący zależności reakcji Ra i Rc od α

α1

0 deg

⋅

10 deg

⋅

,

90 deg

⋅

..

:=

RC α1

(

)

P sin α1

(

)

⋅

a

⋅

Q

a

2

⋅

+













b

:=

RA α1

(

)

P cos α1

(

)

⋅

(

)

2

P sin α1

(

)

⋅

P sin α1

(

)

⋅

a

⋅

Q

a

2

⋅

+













b

−

































2

+

:=

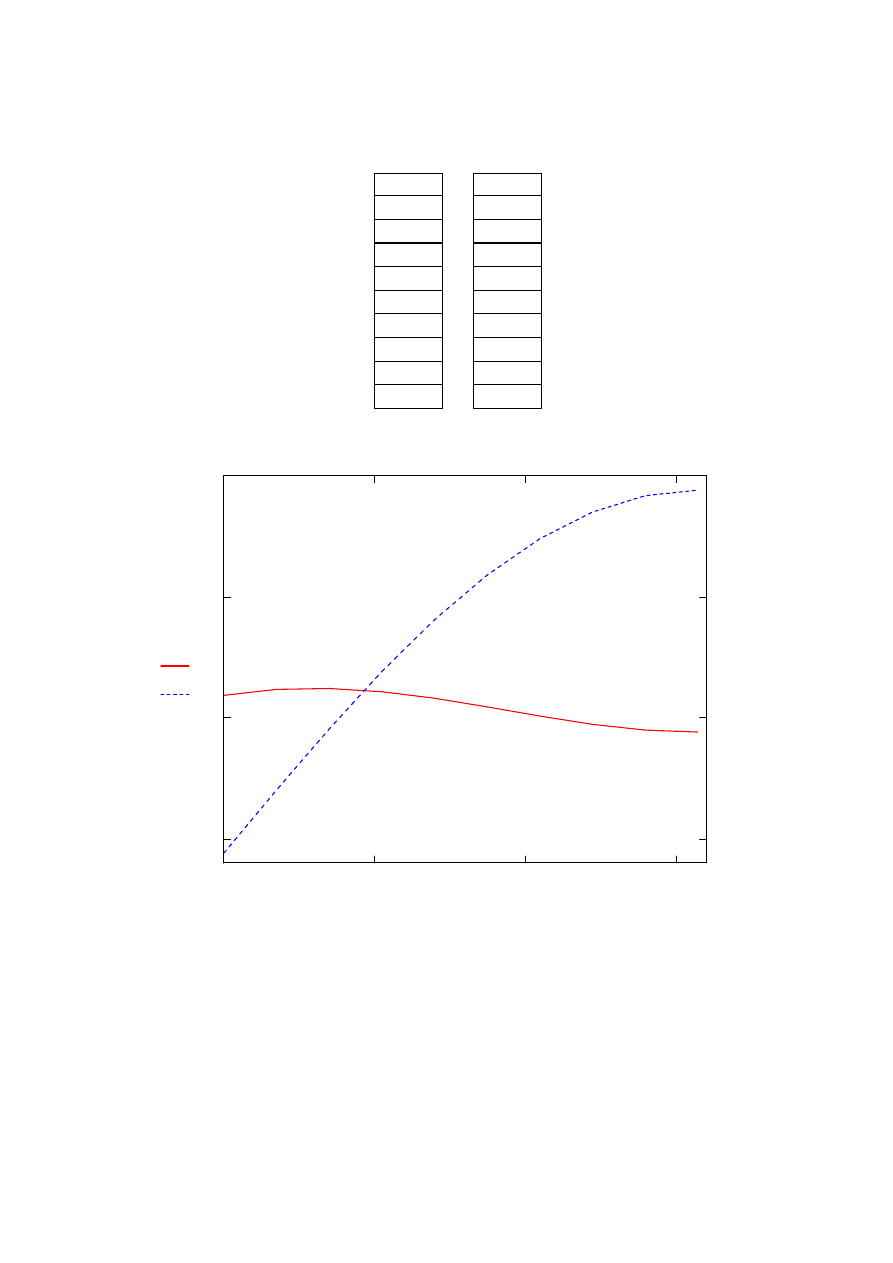
RA α1

(

)

10.929

11.173

11.214

11.079

10.808

10.451

10.069

9.729

9.494

9.41

N

=

RC α1

(

)

4.41

7.015

9.54

11.91

14.052

15.901

17.4

18.505

19.182

19.41

N

=

0

0.5

1

1.5

5

10

15

20

RA α1

(

)

RC α1

(

)

α1

Wykres. 1 Wykres obrazujący zależności reakcji Ra i Rc od kąta α