PROGRAM WYKŁADU

Wstęp do matematyki dyskretnej

Semestr IV, 30 godz. wykł. + 30 godz. ćw.

opracował: M. Woźniak

W

YKŁAD 1

(

TYDZIEŃ 1)

1. Elementy teorii grafów.
2. Grafy proste.
3. Tw. o uściskach dłoni.
4. Digrafy, multigrafy.
5. Izomorfizm. Ścieżki, cykle.
6. Spójność.
7. Drzewa.
8. Dopełnienie.
9. Iloczyn kartezjański.
10.Zastosowanie do problemu sztywności kratownic

W

YKŁAD 2

(

TYDZIEŃ 2)

1. Skojarzenia w grafach dwudzielnych.
2. Skojarzenie z

do

.

3. Problem małżeństw.
4. Tw. Halla.
5. Wierzchołki wolne (słabe) i skojarzone (mocne), ścieżki przemienne i powiekszające.
6. Tw. Berge'a.
7. Dowód tw. Halla.

W

YKŁAD 3

(

TYDZIEŃ 3)

1. Znajdywania maksymalnego skojarzenia.
2. Algorytm (dający przy okazji minimalne pokrycie).
3. Tw. Königa (o dwugrafach).
4. Tw. Königa-Egervary'ego (o macierzach 0-1).
5. Problem przydziału zadań

W

YKŁAD 4

(

TYDZIEŃ 4)

1. Macierze permutacyjne i bistochastyczne.
2. Tw. Birkhoffa-von Neumanna.
3. Tw. o szczęściu i monogamii.
4. Problem stabilności małżeństw.
5. Algorytm

W

YKŁAD 5

(

TYDZIEŃ 5)

1. Zbiory częściowo uporządkowane.
2. Diagramy Hassego.
3. Łańcuchy i antyłańcuchy.

4. Tw. Dilwortha.
5. Wzmianka o innych twierdzeniach minimaksowych (Forda-Fulkersona, Mengera).

W

YKŁAD 6

(

TYDZIEŃ 6)

1. Ciągi rekurencyjne.
2. Ciąg Fibonacciego.
3. Równania rekurencyjne liniowe o stałych ach.
4. Przykłady.

W

YKŁAD 7

(

TYDZIEŃ 7)

1. Funkcje tworzące (zwykłe i wykładnicze).
2. Przykłady zastosowań.

W

YKŁAD 8

(

TYDZIEŃ 8)

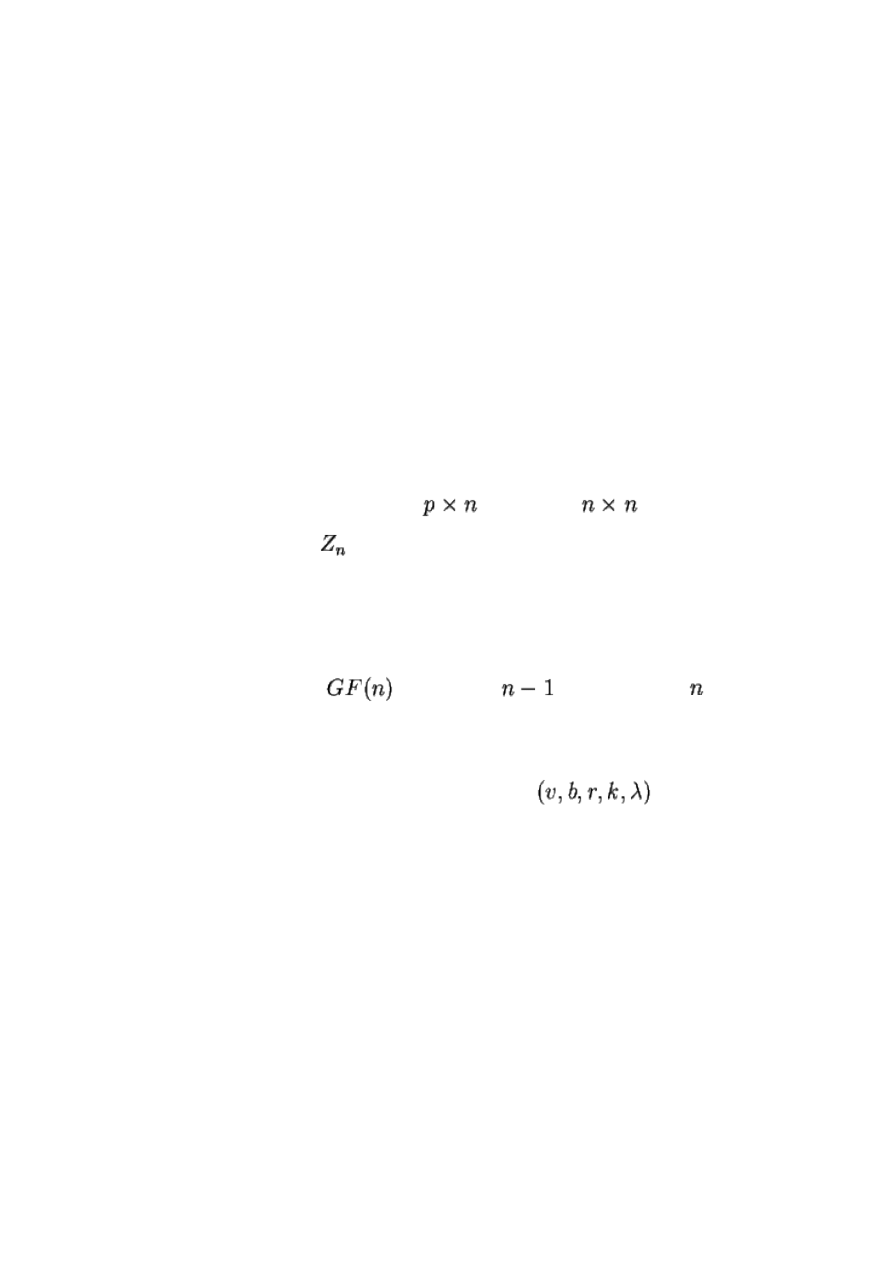
1. Kwadraty i prostokąty łacińskie.
2. Twierdzenie o rozszerzaniu prostokąta

do kwadratu

.

3. Zastosowanie pierścieni

.

W

YKŁAD 9

(

TYDZIEŃ 9)

1. Problem 36 oficerów.
2. Wzajemnie ortogonalne łacińskie kwadraty (WOŁKi).
3. Zastosowanie ciał Galois

do tworzenia

WOŁKów rzędu .

W

YKŁAD 10

(

TYDZIEŃ 10)

1. Konfiguracje kombinatoryczne (BIBD) o parametrach

.

2. Podstawowe związki między parametrami.
3. Macierz konfiguracji.
4. Nierówność Fishera.
5. Konfiguracje symetryczne (kwadratowe).

W

YKŁAD 11

(

TYDZIEŃ 11)

1. Tworzenie konfiguracji.
2. Konfiguracje a WOŁKi.
3. Zbiory różnicowe.
4. Konfiguracje dualne.
5. Konfiguracje a rozkłady grafów.

W

YKŁAD 12

(

TYDZIEŃ 12)

1. Kody wykrywające i korygujące błedy.

2. Waga słowa.
3. Odległość Hamminga.
4. Kody grupowe.
5. Kodowanie macierzowe.

W

YKŁAD 13

(

TYDZIEŃ 13)

1. Wykorzystanie konfiguracji do tworzenia kodów.
2. Przykład kodu doskonałego.
3. Interpretacja geometryczna (kostka).

W

YKŁAD 14

(

TYDZIEŃ 14)

1. Problemy komunikacji w grafach.
2. Kostka jako minimalny graf dyfuzji.

W

YKŁAD 15

(

TYDZIEŃ 15)

1. Podsumowanie.

Literatura uzupełniającaw języku polskim:

1. V. B

RYANT

, Aspekty kombinatoryki, WN-T, Warszawa 1993.

2. G. B

IRKHOFF I

T.C. B

ARTEE

, Współczesna algebra stosowana, PWN, Warszawa 1983.

3. W. L

IPSKI

, Kombinatoryka dla programistów, WN-T, Warszawa 1989.

4. W. L

IPSKI I

W. M

AREK

, Analiza kombinatoryczna, PWN, Warszawa 1986.

5. Z. P

ALKA I

A. R

UCIŃSKI

, Wykłady z kombinatoryki, WN-T, Warszawa 1998.

6. K.A. R

OSS I

C.R.B. W

RIGHT

, Matematyka dyskretna, PWN, Warszawa 199?.

7. R.J. W

ILSON

, Wprowadzenie do teorii grafów, PWN, Warszawa 1985.

8. M. W

OŹNIAK

, Dyfuzja informacji w grafach, Wyd. AGH (skrypt 1475), Kraków 1996.

9. M. W

OŹNIAK

, Wprowadzenie do problemów komunikacjiw grafach, Wyd. AGH, Kraków

1999.