MO

Z4/4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH – ZADANIE 4

1

Z4/4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH –

ZADANIE 4

Z4/4.1. Zadanie 4

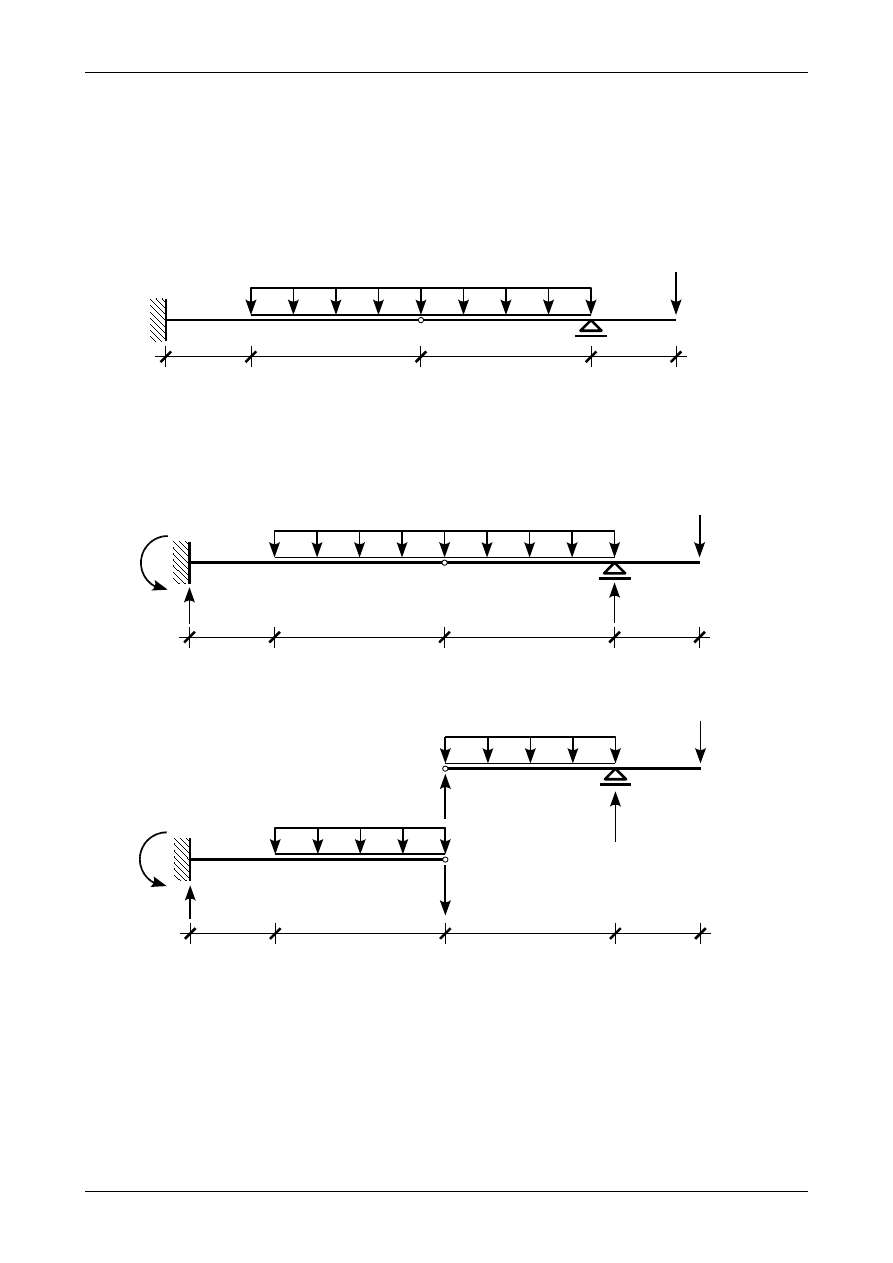
Narysować metodą punktów szczególnych wykresy sił przekrojowych dla belki złożonej

przedstawionej na rysunku Z4/4.1. Wymiary belki podane są w metrach.

A

B

C

D

E

[m]

1,0

2,0

2,0

1,0

16,0 kN/m

18,0 kN

Rys. Z4/4.1. Belka złożona

Analiza kinematyczna belki złożonej przedstawionej na rysunku Z4/4.1 znajduje się w zadaniu 3.

Zgodnie z tamtym zadaniem rysunek Z4/4.2 i Z4/4.3 przedstawiają wartości i zwroty reakcji podporowych.

A

B

C

D

E

[m]

1,0

2,0

2,0

1,0

16,0 kN/m

18,0 kN

85,0 kNm

39,0 kN

43,0 kN

Rys. Z4/4.2. Prawidłowe wartości i zwroty reakcji w belce złożonej

A

B

C

[m]

1,0

2,0

2,0

1,0

16,0 kN/m

C

D

E

18,0 kN

16,0 kN/m

43,0 kN

7,0 kN

7,0 kN

39,0 kN

85,0 kNm

Rys. Z4/4.3. Prawidłowe wartości i zwroty reakcji we wszystkich podporach belki złożonej

Z4/4.2. Wykres siły poprzecznej

Zgodnie z rozdziałem 4 w przedziałach BC i CD siła poprzeczna będzie funkcją liniową natomiast w

pozostałych przedziałach będzie miała wartość stałą. Moment skupiony w utwierdzeniu 85,0 kNm oraz
przegub rzeczywisty C nie będą wpływały na wartość siły poprzecznej. Pionowe reakcje na podporach A i D
będą powodowały skok siły poprzecznej o wartości bezwzględnej równej danej reakcji.

Rysowanie wykresu siły poprzecznej zaczniemy od punktu A. W punkcie tym działa reakcja o

wartości 39,0 kN do góry. Siła poprzeczna w tym punkcie wynosi więc

Dr inż. Janusz Dębiński

Zaoczni

MO

Z4/4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH – ZADANIE 4

2

T

A

=39,0 kN

.

(Z4/4.1)

W przedziale AB nie działa żadne obciążenie ciągłe więc siła poprzeczna ma w całym przedziale oraz

z lewej strony punktu B wartość stałą równą

T

AB

=T

B



L



=39,0 kN

.

(Z4/4.2)

W punkcie B nie działa żadna siła więc siła poprzeczna z prawej strony punktu B znajdującego się w

przedziale AB będzie miała wartość

T

B



P



=39,0 kN

.

(Z4/4.3)

W przedziale BC działa obciążenie ciągłe równomiernie rozłożone o wartości 16,0 kN/m w dół więc

siła poprzeczna w tym przedziale będzie liniowo opadać a w punkcie C tego przedziału wynosi

T

C



L



=39,0−16,0⋅2,0=7,0kN

.

(Z4/4.4)

Jak widać siła poprzeczna na obu końcach przedziału BC ma wartości tych samych znaków. W przedziale
tym nie będzie ona miała więc miejsca zerowego.

Przegub rzeczywisty C nie będzie wpływał na wartość siły poprzecznej więc z prawej strony punktu C

siła poprzeczna wynosi

T

C



P



=7,0kN

.

(Z4/4.5)

W przedziale CD działa obciążenie ciągłe równomiernie rozłożone o wartości 16,0 kN/m w dół więc

siła poprzeczna w tym przedziale będzie liniowo opadać a w punkcie D tego przedziału wynosi

T

D



L



=7,0−16,0⋅2,0=−25,0 kN

.

(Z4/4.6)

Jak widać siła poprzeczna na obu końcach przedziału CD ma wartości przeciwnych znaków. W przedziale
tym będzie ona miała więc miejsce zerowe. Zgodnie ze wzorem (4.125) jego odległość od punktu C wynosi

x

L

=

7,0

16,0

=0,4375m

(Z4/4.7)

natomiast od punktu B, zgodnie ze wzorem (4.126) miejsce zerowe znajduje się w odległości

x

P

=

25,0
16,0

=1,563 m

.

(Z4/4.8)

Dr inż. Janusz Dębiński

Zaoczni

MO

Z4/4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH – ZADANIE 4

3

W punkcie D działa reakcja o wartości 43,0 kN w górę. Wartość siły poprzecznej z prawej strony

punktu D wynosi więc

T

D



P



=−25,043,0=18,0 kN

.

(Z4/4.9)

W przedziale DE nie działa żadne obciążenie ciągłe więc siła poprzeczna ma w całym przedziale

wartość stałą równą

T

DE

=18,0 kN

.

(Z4/4.10)

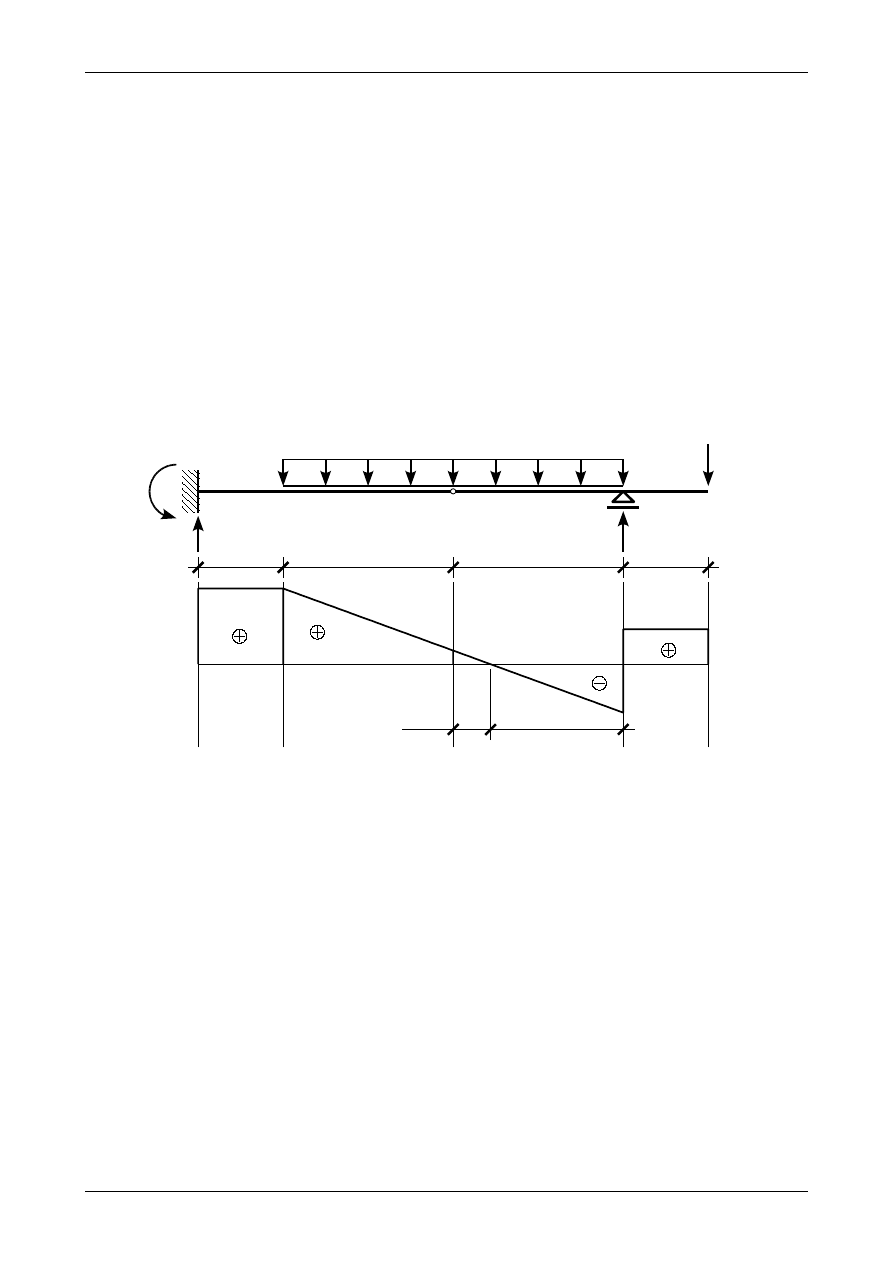
Rysunek Z4/4.4 przedstawia ostateczną postać wykresu siły poprzecznej w całej belce złożonej

wyznaczonego metodą punktów charakterystycznych.

A

B

C

D

E

[m]

1,0

2,0

2,0

1,0

16,0 kN/m

18,0 kN

85,0 kNm

39,0 kN

43,0 kN

T(x) [kN]

39,0

7,

0

25

,0

18,0

0,4375

1,563

Rys. Z4/4.4. Wykres siły poprzecznej w belce złożonej

Z4/4.3. Wykres momentu zginającego

Zgodnie z rozdziałem 4 w przedziałach BC i CD moment zginający będzie funkcją kwadratową

natomiast w pozostałych przedziałach będzie funkcją liniową. Moment skupiony 85,0 kNm spowoduje skok
momentu zginającego w punkcie A. Poza tym wykres momentu będzie w całej belce ciągły. Moment
zginający w przegubie rzeczywistym C będzie miał wartość zero. W dalszej części, przy obliczaniu wartości
momentu zginającego w punktach charakterystycznych, siły, które kręcą zgodnie z założonym momentem
będziemy zapisywać z minusem, siły które kręcą przeciwnie z plusem.

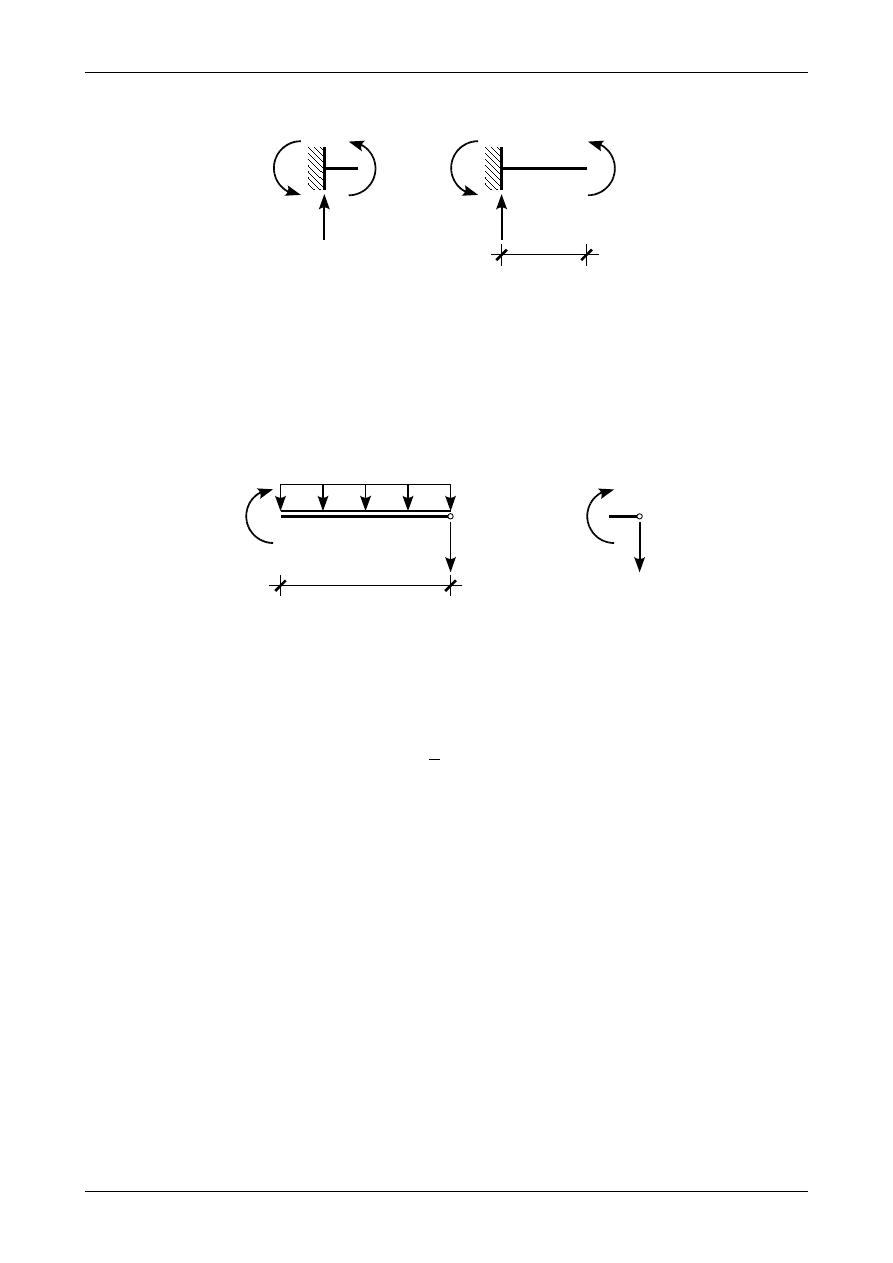
Rysunek Z4/2.5 a) przedstawia moment zginający w punkcie A. Zgodnie z tym rysunkiem moment ten

ma wartość

M

A

=−85,0 kNm

.

(Z4/4.11)

Znak minus oznacza, że rozciąga on górną część belki.

Rysunek Z4/4.5 b) przedstawia moment zginający w punkcie B z lewej strony. Zgodnie z tym

rysunkiem moment ten ma wartość

Dr inż. Janusz Dębiński

Zaoczni

MO

Z4/4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH – ZADANIE 4

4

A

1,0

39,0 kN

85,0 kNm

M

B

(L)

[m]

A

39,0 kN

85,0 kNm

M

A

a)

b)

Rys. Z4/4.5. Momenty zginające na obu końcach przedziału AB

M

B



L



=39,0⋅1,0−85,0=−46,0 kNm

.

(Z4/4.12)

Znak minus oznacza, że rozciąga on górną część belki.

C

2,0

16,0 kN/m

7,0 kN

M

B

(P)

C

7,0 kN

M

C

(L)

[m]

a)

b)

Rys. Z4/4.6. Momenty zginające na na obu końcach przedziału BC

Rysunek Z4/4.6 a) przedstawia moment zginający w punkcie B z prawej strony. Zgodnie z tym

rysunkiem moment ten ma wartość

M

B



P



=−7,0⋅2,0−16,0⋅2,0⋅

1
2

⋅2,0=−46,0 kNm

.

(Z4/4.13)

Moment ten jest równy momentowi wyznaczonemu ze wzoru (Z4/2.12). Znak minus oznacza, że rozciąga on
górną część belki.

Rysunek Z4/4.6 b) przedstawia moment zginający w punkcie C z lewej strony. Zgodnie z tym

rysunkiem moment ten ma wartość

M

C



L



=0,0 kNm

.

(Z4/4.14)

Zgodnie z rysunkiem Z4/4.4 w przedziale BC siła poprzeczna nie posiada miejsca zerowego. W

związku z tym nie będziemy wyznaczali ekstremum funkcji kwadratowej, które to znajduje się już poza
przedziałem BC.

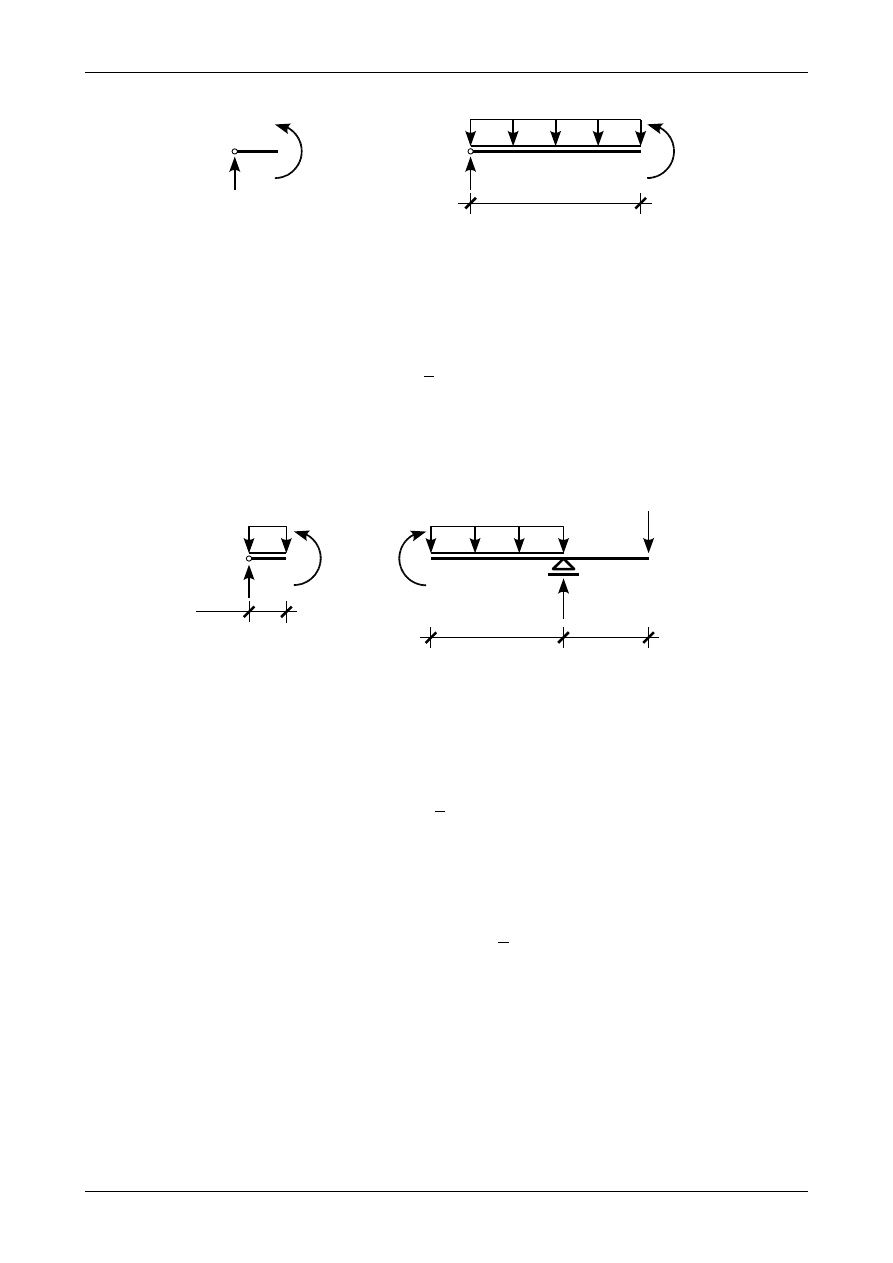
Rysunek Z4/4.7 a) przedstawia moment zginający w punkcie C z prawej strony tego punktu. Zgodnie

z tym rysunkiem moment ten ma wartość

M

C



P



=0,0 kNm

.

(Z4/4.15)

Dr inż. Janusz Dębiński

Zaoczni

MO

Z4/4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH – ZADANIE 4

5

2,0

16,0 kN/m

7,0 kN

M

D

(L)

C

7,0 kN

M

C

(P)

C

[m]

a)

b)

Rys. Z4/4.7. Momenty zginające na na obu końcach przedziału CD

Rysunek Z4/4.7 b) przedstawia moment zginający w punkcie D z lewej strony podpory. Zgodnie z tym

rysunkiem moment ten ma wartość

M

D



L



=7,0⋅2,0−16,0⋅2,0⋅

1
2

⋅2,0=−18,0 kNm

.

(Z4/4.16)

Znak minus oznacza, że rozciąga on górną część belki.

D

E

[m]

1,0

16,0 kN/m

18,0 kN

43,0 kN

1,563

C

[m]

0,4375

16,0 kN/m

7,0 kN

M

1

M

1

a)

b)

Rys. Z4/4.8. Ekstremalny moment zginający w przedziale CD

Rysunek Z4/4.8 przedstawia ekstremalny moment zginający w przedziale CD. Zgodnie z rysunkiem

Z4/4.8 a) wynosi on

M

1

=7,0⋅0,4375−16,0⋅0,4375⋅

1

2

⋅0,4375=1,531 kNm

(Z4/4.17)

Zgodnie z rysunkiem Z4/4.8 b) wynosi on

M

1

=43,0⋅1,563−18,0⋅



1,0

1,563



−16,0⋅1,563⋅

1

2

⋅1,563=1,531 kNm

.

(Z4/4.18)

Jak widać ekstremalne momenty zginające w przedziale CD obliczone dla lewej i prawej części belki CE są
takie same. Znak plus oznacza, że rozciąga on dolną część belki.

Rysunek Z4/4.9 a) przedstawia moment zginający w punkcie D z prawej strony tego punktu. Zgodnie

z tym rysunkiem moment ten ma wartość

M

B



P



=−18,0⋅1,0=−18,0 kNm

.

(Z4/4.19)

Dr inż. Janusz Dębiński

Zaoczni

MO

Z4/4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH – ZADANIE 4

6

E

1,0

18,0 kN

M

D

(P)

[m]

E

18,0 kN

M

E

a)

b)

Rys. Z4/4.9. Momenty zginające na na obu końcach przedziału DE

Moment ten jest równy momentowi wyznaczonemu ze wzoru (Z4/4.16) Znak minus oznacza, że rozciąga on
górną część belki.

Rysunek Z4/4.9 b) przedstawia moment zginający w punkcie E. Zgodnie z tym rysunkiem moment ten

ma wartość

M

E

=0,0 kNm

.

(Z4/4.20)

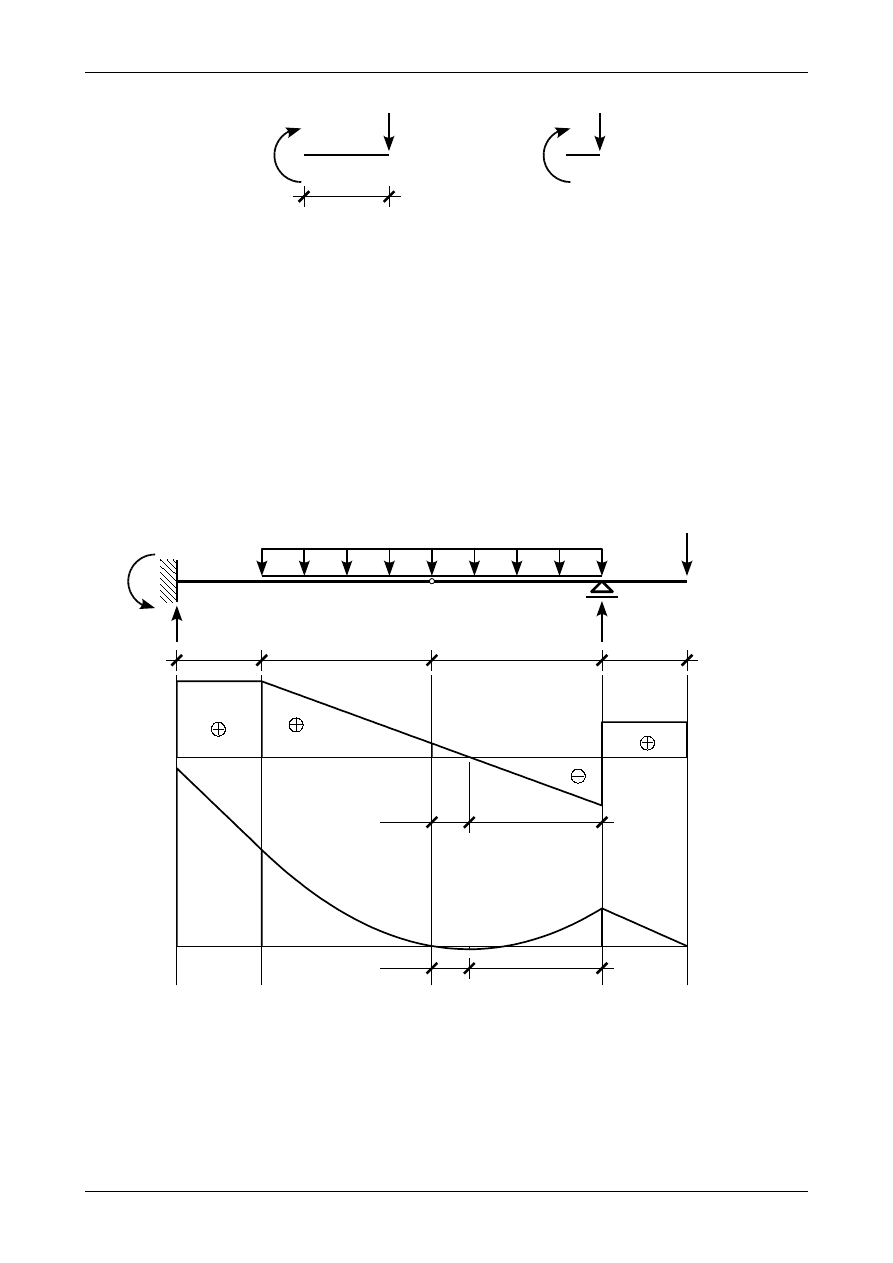
Rysunek Z4/4.10 przedstawia ostateczne wykresy siły poprzecznej i momentu zginającego w belce

złożonej wyznaczone metodą punktów charakterystycznych.

A

B

C

D

E

[m]

1,0

2,0

2,0

1,0

16,0 kN/m

18,0 kN

85,0 kNm

39,0 kN

43,0 kN

T(x) [kN]

M(x) [kNm]

39,0

7,

0

25

,0

18,0

85

,0

46

,0

0,

0

18

,0

0,

0

0,4375

1,563

0,4375

1,563

1,

53

1

Rys. Z4/4.10. Ostateczne wykresy siły poprzecznej i momentu zginającego wyznaczone metodą punktów

charakterystycznych

Dr inż. Janusz Dębiński

Zaoczni