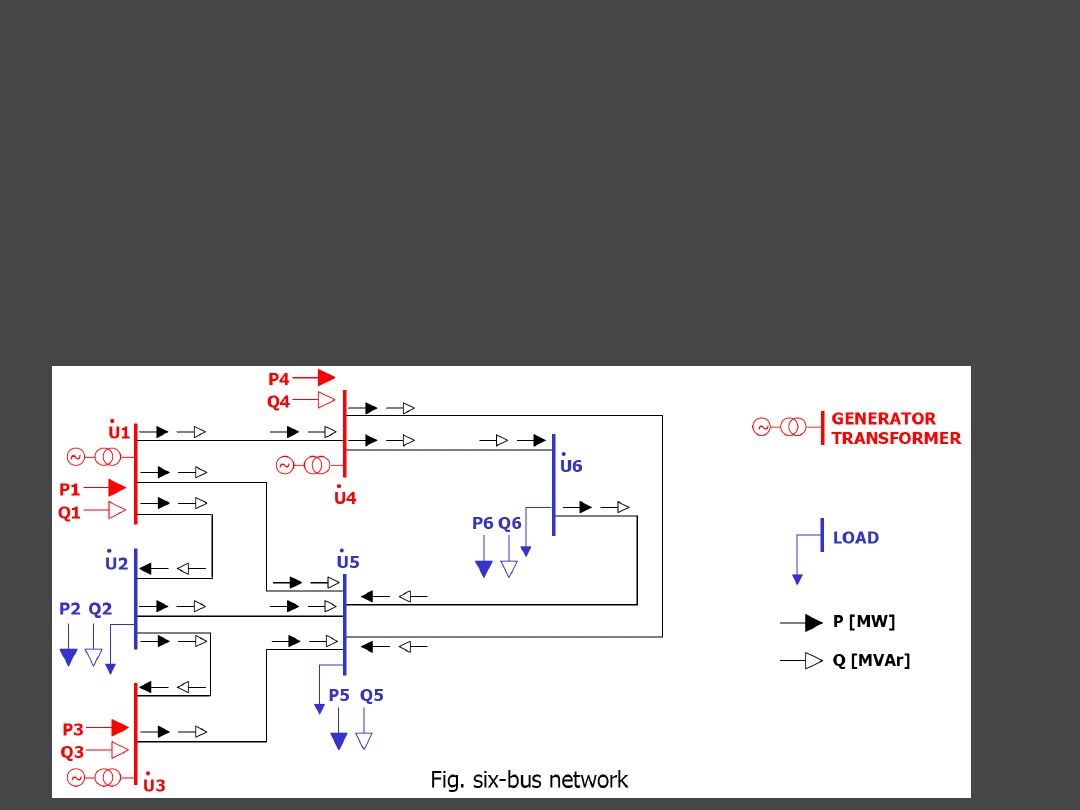
1
3 Current and Power Distribution in Branches and
Network Power Losses Determination
Steady state solution in power system consists of two steps:
1. calculation of voltages in individual network nodes,
2. calculation of current and power distributions and determination of
losses in network.
If we know voltages in individual nodes, we can evaluate current or power
distribution and losses in networks using Ohm’s and Kirchhoff’s law.

2
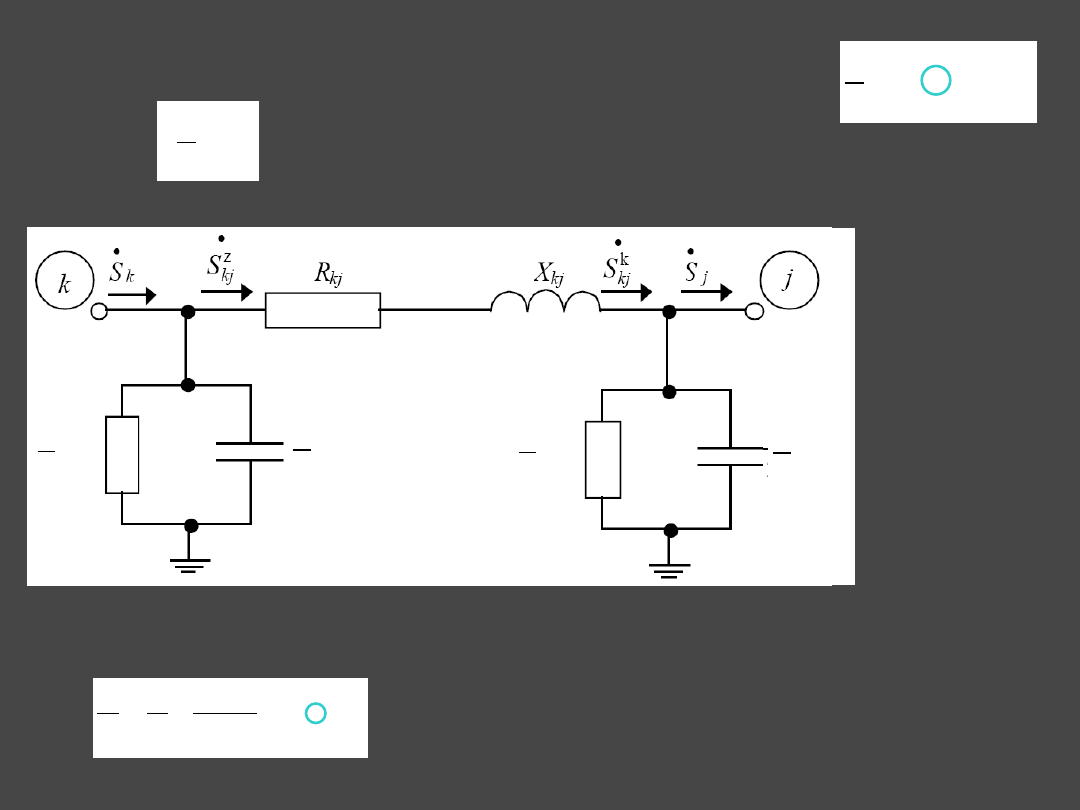
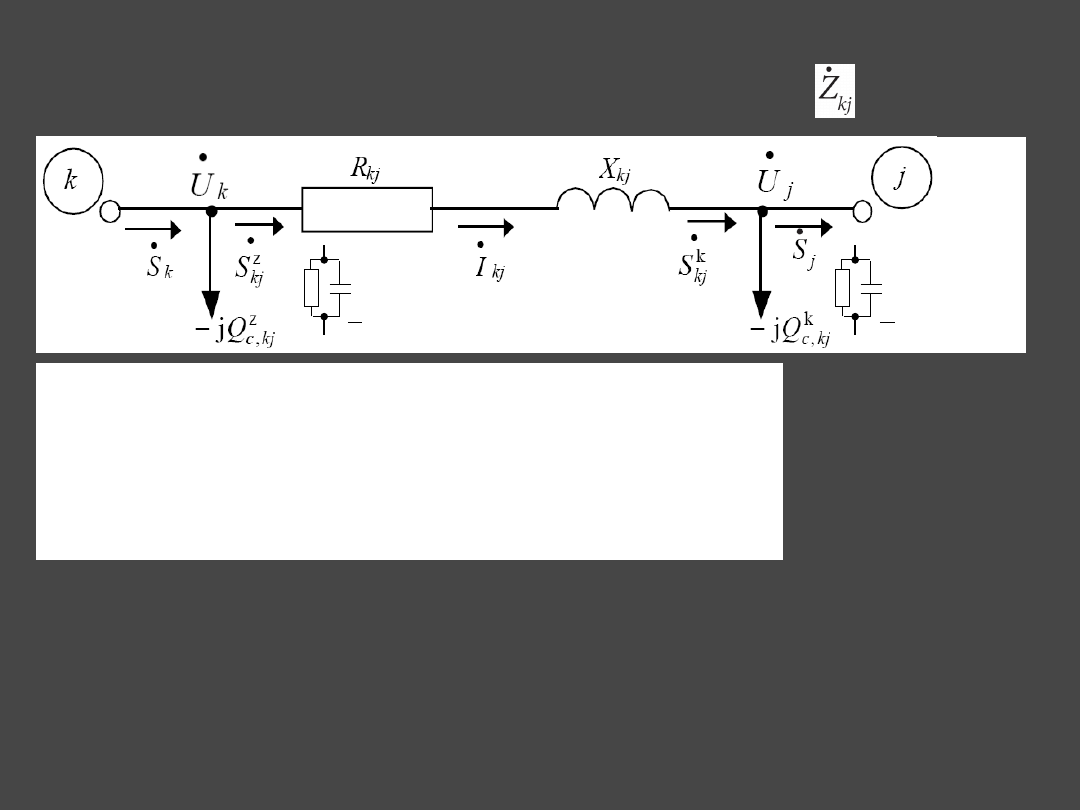
3.1 Current distribution in branches
The phase current flowing in series part of the line, according to Ohm’s law is:
kj
j
k
kj
j
k
kj
Y
U
U
Z
U
U
I
3
1
.
3
where
j
k
U
U
,
- phase to phase voltage of the nodes
k
and
j
,
kj
kj
kj
X
R
Z
j
- series impedance of branch
kj
,
1
kj
kj
Z
Y
- element of node admittance matrix , it is admitance
between nodes
k
and
j
(with the negative sign).
Y
kj
c
B
,
2
1
kj
c
B
,
2
1
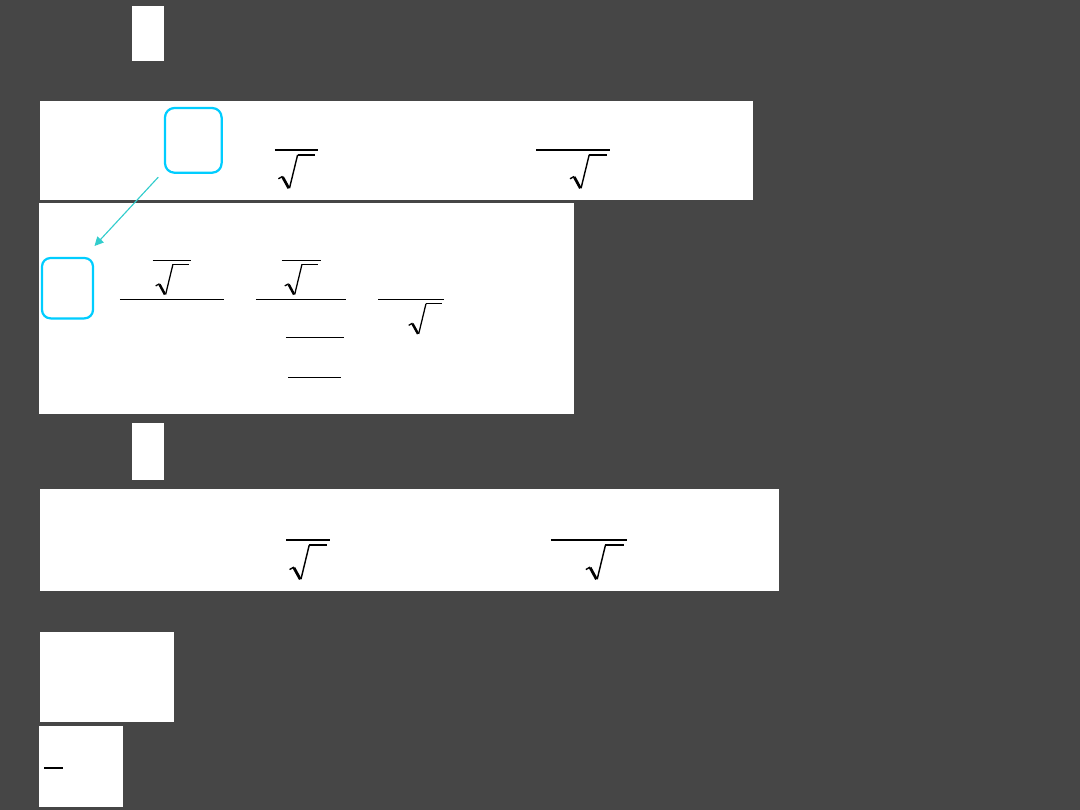
3
Current flowing from the node
k
into the lines
kj
according to I. Kirchhoff’s
Current Law is determined as:
k
I
kj
c
k
kj
j
k
z
kj
c
kj
k
B
U
Y
U
U
I
I
I
,
,
j
3
.
2
1
3
1
where
kj
c
B
,
2
1
- phase capacity current at the begin (end) of the line
kj
,
- one half capacity susceptance of line
kj
Current flowing from line
kj
into node
j
is determine as:
j
I
kj
c
j
kj
j
k
k
kj
c
kj
j
B
U
Y
U
U
I
I
I
,
,
j
3
.
2
1
3
1
kj
c
k
kj
c
k
kj
c
k
z
kj
c
B
U
B
U
X
U
I
,
,
,
2
/
,
j
3
.
2
1
2
1
j
-
3
j
-
3
k
kj
c
z
kj
c
I
I
,
,
,
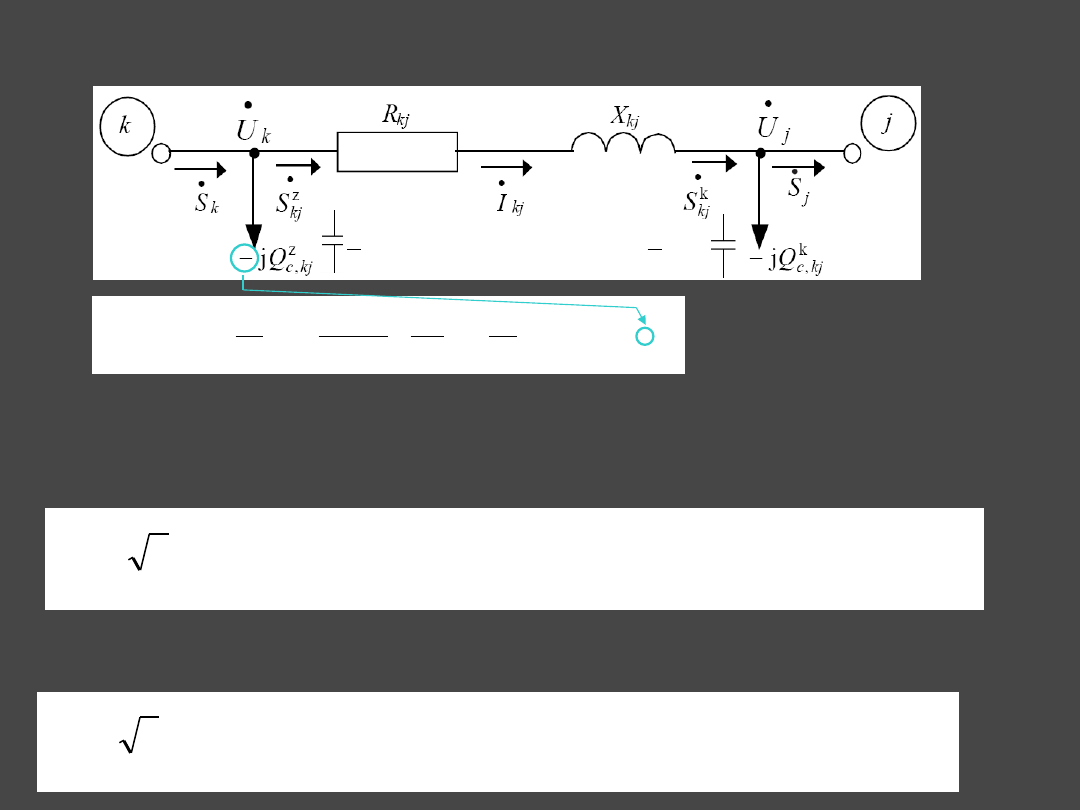
4
3.2 Power distribution in branches
Three-phase electric power at the begin of series impedance of line
kj
, i.e. flowing
from node
k
into
j
:
j
k
kj
k
kj
kj
j
k
k
kj
k
z
kj
U
U
Y
U
Y
Y
U
U
U
I
U
S
*
*
2
*
*
*
.
.
3
Three-phase electric power at the end of series impedance of line
kj
:
2
*
*
*
*
*
*
*
.
.
.
.
.
.
.
3
j
kj
k
j
kj
kj
j
k
j
kj
j
k
kj
U
Y
U
U
Y
Y
U
U
U
I
U
S
kj
c
B
,
2
1
kj
c
B
,
2
1
c
c
2
f
c
2
f
c
2
f
*
c
f
*
f
c
*
f
*
f
c
*
f
j
j
j
j
j
Q
B
U
X
U
X
U
X
U
U
Z
U
U
I
U
S
note:
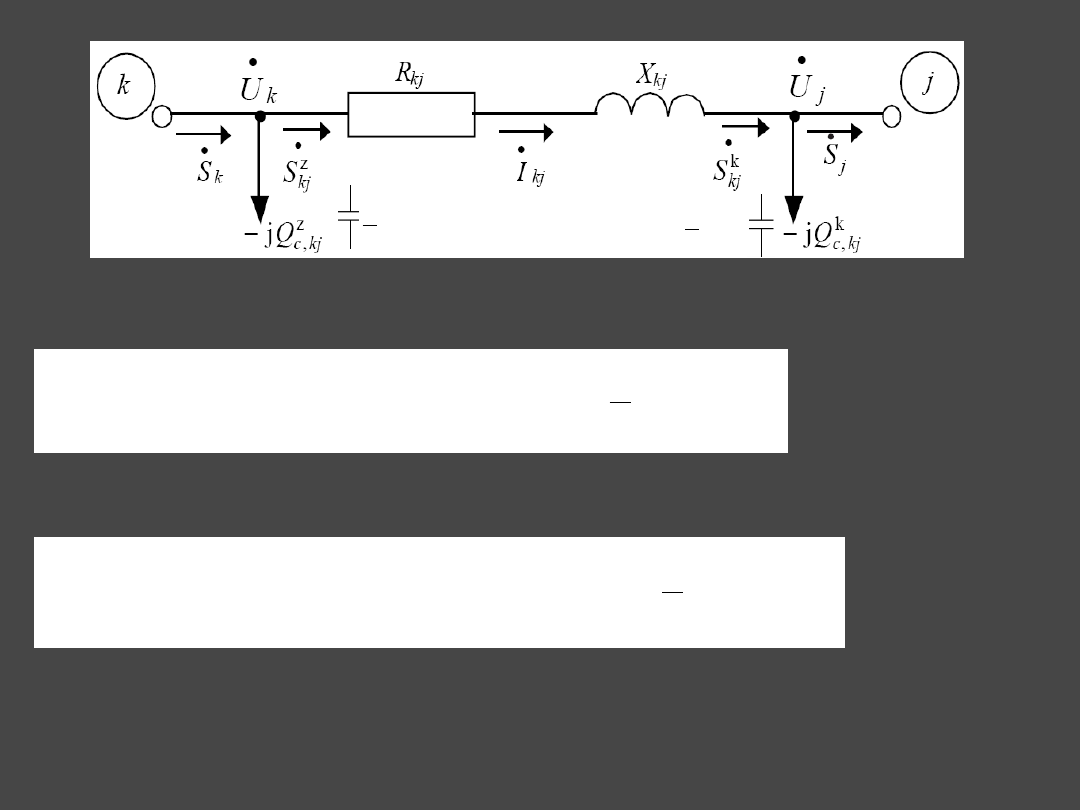
5
Electric power flowing from node
k
into lines
kj
is:
kj
c
kj
j
k
k
z
kj
c
z
kj
k
B
U
Y
U
U
U
Q
S
S
k
,
2
*
*
*
,
j
.
2
1
j
Electric power flowing into node
j
from line
kj
is:
kj
c
j
kj
j
k
j
k
kj
c
k
kj
j
B
U
Y
U
U
U
Q
S
S
,
2
*
*
*
,
j
2
1
j
kj
c
B
,
2
1
kj
c
B
,
2
1
6
In case of consideration of conductance as well, then we obtain
instead of .
kj
c
B
,
2
1
j
kj
G
2
1
kj
G
2
1
kj
c
B
,
2
1
kj
c
B
,
2
1
note:
c
c
j
j
1
1
1
B
G
X
R
Z
kj
c
kj
B
G
,
j
2
1
7
3.3 Network Electric Power Losses Determination
kj
j
k
j
k
kj
j
k
j
kj
j
k
k
k
kj
z
kj
Y
U
U
U
U
Y
U
U
U
Y
U
U
U
S
S
*
*
*
*
*
*
*
*
*
Power losses in series part of line
kj
,
i.e
.
losses at impedance are:
z
kj
g
P
,
k
kj
g
P
,
kj
c
kj
B
G
,
j
2
1
kj
c
kj
B
G
,
j
2
1

8
Electric power losses in line
kj
are losses both in the:
- series part of line
- shunt admittance of line at the begin and at the
end of the line.
If we summarize these relations for all branches of the EPN, then we receive the
expressions for total power losses in the power system:
2
j
,kj
c
kj
z
kj
B
G
Y
z
kj
k
kj
Y
Y
k
kj
c
k
kj
g
z
kj
c
z
kj
g
k
kj
z
kj
k
kj
c
k
kj
g
k
kj
z
kj
c
z
kj
g
z
kj
j
k
kj
Q
P
Q
P
S
S
Q
P
S
Q
P
S
S
S
S
,
,
,
,
,
,
,
,
j
j
j
j
We can evaluate them as follows:
Active power losses in line
kj
:
)
(
real
S
P
kj
S
S
Reactive power ”losses” in line
kj
:
)
(
imag
S
Q
(only
„
+” sign)
(
„
+” or
„
-” sign)
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron