PRzeglĄd budowlany 

9/2010

28

konstRukcje – elementy – mateRiały

a

R

tyk

uł

y

 PR

oblemowe

W  nr  6/2008  „Przeglądu  Budo­

wlanego”  opublikowano  artykuł 

Autorów, dotyczący współczynnika 

przewodzenia  ciepła  zasolonych 

materiałów  ściennych,  w  którym 

zaproponowano  określenie  war­

tości  obliczeniowych  tego  współ­

czynnika  za  pomocą  wskaźni­

ków  poprawkowych  uzyskanych 

metodą  podziału  soli  na  grupy 

na  podstawie  stopnia  ich  wpły­

wu na przewodność cieplną mate­

riału.  We  wspomnianym  artykule 

nie  podano  opisu  modelowania 

procesu  przewodzenia  ciepła. 

Ze względu na żywe zainteresowa­

nie Czytelników tematem, w niniej­

szej  pracy,  Autorzy  prezentują 

zasady opracowania modelu mate­

matycznego  przewodności  ciepl­

nej  materiału  kapilarno­porowate­

go zawierającego wilgoć i sole.

1. Wprowadzenie

Przyczyną  gromadzenia  się  soli 

w ścianach zewnętrznych obiektów 

murowanych  może  być  oddzia­

ływanie  wód  gruntowych,  pyłów 

przemysłowych,  opadów  atmos­

ferycznych,  a  także  materiałów 

uzupełniających  braki  rodzime­

go  materiału  muru.  W  większości 

przypadków,  największy  wpływ 

mają zmineralizowane wody grun­

towe  przenikające  w  części  nad­

ziemne budynków w wyniku znisz­

czenia  izolacji  przeciwwilgociowej 

pomiędzy  fundamentem  a  ścianą 

[1–3]. W efekcie, w głąb materiału 

ściany  przedostają  się  łatwo  roz­

Prof. dr hab. inż. Valeriy ezerskiy, dr inż. marta kosior-kazberuk, Politechnika białostocka

Modelowanie procesu przewodzenia 

ciepła w zasolonych materiałach 

ściennych

puszczalne  sole,  takie  jak  NaCl, 

CaCl

2

,  MgCl

2

,  Na

2

SO

4

 ,  MgSO

4

 

i  inne.  Nawet  przy  braku  widocz­

nych  poważnych  zniszczeń  ścian 

zewnętrznych  średnia  zawartość 

soli  w  murze  z  cegły  nierzadko 

stanowi 3–4% (wagowo), a w war­

stwach  zewnętrznych  –  kilkakrot­

nie więcej. Sole mogą występować 

w  postaci  roztworu  lub  w  stanie 

stałym.

Obecność soli w porach powoduje 

istotne zmiany charakterystyk ciepl­

nych materiału ściennego, a przede 

wszystkim wartości współczynnika 

przewodzenia  ciepła  [4–6].  Przy 

opracowaniu projektów restauracji 

i rekonstrukcji obiektów, rozwiąza­

nie takich problemów jak poprawa 

stanu  wilgotnościowego  i  ocieple­

nie dodatkowe ścian wymaga infor­

macji  o  zmianach  przewodności 

cieplnej materiału w rzeczywistych 

warunkach eksploatacji.

Przyjmując, że przewodność ciepl­

na  roztworów  wodnych  większo­

ści  soli  jest  mniejsza,  a  przewod­

ność  cieplna  kryształów  soli  jest 

10–20­krotnie  większa  od  prze­

wodności  cieplnej  czystej  wody, 

można  przypuszczać,  że  wpływ 

soli na przewodność cieplną mate­

riału ściennego jest złożony i zale­

ży  od  rodzaju  soli  oraz  jej  stanu 

skupienia.

W  pracy  przedstawiono  opis 

modelu  matematycznego  prze­

wodności  cieplnej  zawilgoconego 

muru  zawierającego  sole,  a  także 

wyniki  badania  zmian  współczyn­

nika przewodzenia ciepła zawilgo­

conej cegły ceramicznej oraz muru 

ceglanego zawierających pospolitą 

sól  NaCl,  przeprowadzonych  przy 

wykorzystaniu modelu.

Zastosowanie  modelowania  mate­

matycznego  pozwala  uwzględ­

niać  realną  strukturę  zasolonego 

materiału  ściennego,  wymaga 

mniejszych nakładów finansowych 

i czasu w porównaniu do podejścia 

eksperymentalnego.  Oprócz  tego, 

proponowana  metoda  pozwa­

la  uniknąć  niedokładności,  które 

mają  miejsce  przy  eksperymen­

talnym  określaniu  współczynnika 

przewodzenia  ciepła  związanych 

z  niekontrolowanymi  migracjami 

roztworów  i  zmianami  stanu  sku­

pienia soli w trakcie przygotowania 

i badania próbek.

2. Podstawy teoretyczne mode-

lowania przewodności cieplnej 

zasolonych  materiałów  ścien-

nych

W  najbardziej  złożonych  warun­

kach eksploatacji przegród budow­

lanych w materiale ściennym może 

znajdować się roztwór wodny soli, 

mieszanina  pary  wodnej  i  powie­

trza oraz kryształy soli [7, 8].

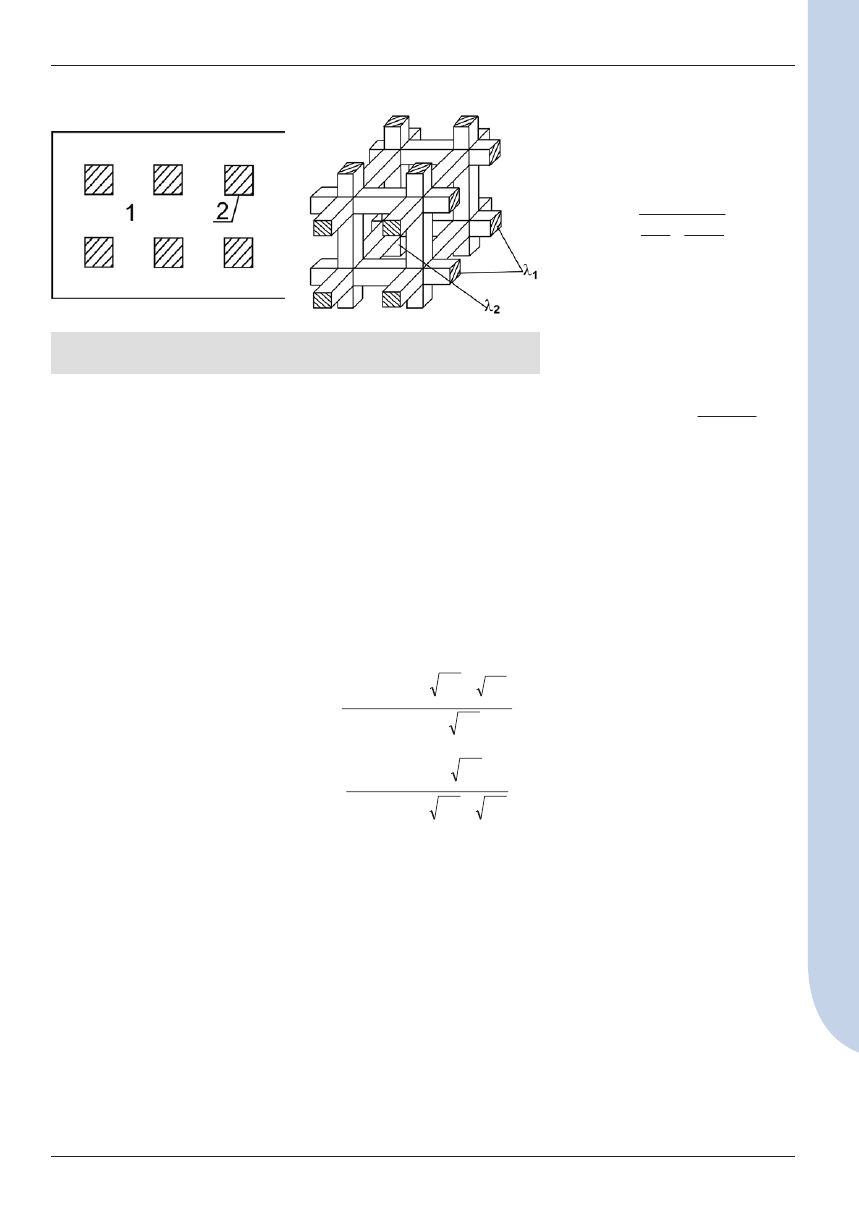
Materiały ścienne i wodne roztwory 

soli  będące  ciałami  heterogenicz­

nymi różnią się między sobą struk­

turą. Według Dulniewa [9], twarde 

materiały  kompozytowe  (cegła, 

beton)  mają  strukturę  z  zamknię­

tymi wtrąceniami jednego materia­

łu  w  drugim.  Natomiast  roztwory 

soli, wg tej samej klasyfikacji, mają 

PRzeglĄd budowlany 

9/2010

konstRukcje – elementy – mateRiały

29

a

R

tyk

uł
y

 PR
oblemowe

strukturę  o  wzajemnie  przenikają­

cych się składnikach.

Badając  przewodność  cieplną 

układów,  ich  chaotyczną  struktu­

rę zastępuje się uporządkowanym 

modelem, który powinien wyrażać 

podstawowe  właściwości  geome­

tryczne  rozpatrywanej  struktury, 

a  także  uwzględniać  wszystkie 

czynniki  wpływające  na  proces 

przenoszenia  ciepła.  W  dowolnej 

uporządkowanej strukturze można 

wyróżnić  element  podstawowy, 

którego  powtarzanie  pozwala 

utworzyć  całą  objętość  struktury 

wyjściowej  (rys.  1).  Po  obliczeniu 

efektywnej  przewodności  cieplnej 

elementu  podstawowego,  jej  war­

tość  można  rozszerzyć  na  całą 

uporządkowaną strukturę.

Ścisłe  sformułowanie  problemu 

określenia  efektywnej  przewod­

ności  cieplnej  układu  sprowadza 

się  do  analizy  pola  temperaturo­

wego  występującego  w  systemie 

ciał  i  wymaga  rozwiązania  złożo­

nych  układów  równań.  W  tym  celu 

powszechnie  stosuje  się  zasadę 

uogólnionego  przewodzenia,  ba­ 

zującą na analogii pomiędzy równa­

niami różniczkowymi stacjonarnego 

strumienia  ciepła,  prądu  elektrycz­

nego, indukcji elektrycznej i magne­

tycznej czy ruchu masy. Na podsta­

wie  tej  zasady  autorzy  prac  [9–11] 

otrzymali  przybliżone  wyrażenia 

określające efektywną przewodność 

cieplną  systemów  dwuskładniko­

wych o zróżnicowanej strukturze.

Po  analizie  i  ocenie  przybliżonych 

zależności  opracowanych  przez 

różnych  badaczy,  Autorzy  wybrali 

i przedstawili tylko te z nich, które 

charakteryzują  się  dużą  dokład­

nością  oceny  opisywanego  zjawi­

ska.  Te  zależności  zostały  wyko­

rzystane  do  opracowania  modelu 

przewodzenia  ciepła  zasolonego 

materiału.

Współczynnik przewodzenia ciepła 

materiału  z  zamkniętymi  wtrące­

niami  można  obliczyć  wg  wzorów 

przedstawionych w pracach [9, 10]: 

(

)

5

,

0

u

a

λ

λ

λ

+

=

   (1)

( )

(

)

3

2

2

3

2

3

2

2

1

1

1

1

1

1

m

m

m

a

⋅

−

−

⎥⎦

⎤

⎢⎣

⎡

⋅

⎟

⎠

⎞

⎜

⎝

⎛ −

−

−

=

ν

ν

λ

λ

  (2)

(

)

(

)

3

2

2

3

2

2

3

2

2

1

1

1

1

m

m

m

u

⋅

⎟

⎠

⎞

⎜

⎝

⎛ −

−

+

⎥⎦

⎤

⎢⎣

⎡

⋅

−

+

=

ν

ν

ν

ν

λ

λ

  (3)

gdzie:
l

a

,  l

u

  –  efektywne  przewodności 

cieplne  systemu,  odpowiednio 

przy  adiabatycznym  i  izotermicz­

nym  przecięciu  elementu  podsta­

wowego,
l

1

,  l

2

  –  współczynniki  przewodze­

nia  ciepła,  odpowiednio  składnika 

ciągłego  i  składnika  rozproszone­

go, przy czym ν

 = l

1

/l

2

m

2

  –  stężenie  objętościowe  skład­

nika rozproszonego.

Do  obliczeń  efektywnej  przewod­

ności  cieplnej  dwuskładnikowej 

twardej  mieszaniny  z  zamkniętymi 

wtrąceniami  proponuje  się  zależ­

ność,  zaczerpniętą  z  pracy  [11], 

która  zapewnia  wysoką  dokład­

ność  zarówno  przy  małej,  jak 

i dużej koncentracji wtrąceń,

⎥

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎢

⎣

⎡

−

−

−

−

=

3

1

1

1

1

2

2

1

m

m

ϑ

λ

λ

  (4),

gdzie ϑ

 = l

2

/l

1

.

Efektywną  przewodność  cieplną 

materiału zawierającego dwa wza­

jemnie  przenikające  się  składniki, 

przy  ϑ  >  0,  można  z  wystarczają­

cą dokładnością ocenić wg wzoru 

cytowanego w pracy [9]:

(

)

(

)

⎥

⎦

⎤

⎢

⎣

⎡

+

−

−

+

−

+

=

c

c

c

c

c

c

a

ϑ

ϑ

ϑ

λ

λ

1

1

2

1

2

2

1

  (5)

gdzie:

c

 – funkcja porowatości, którą obli­

cza się wg wzoru:

c

 = 0,5 + A cos(ϕ/3),

270° ≤ ϕ ≤ 360°,

dla 

m

2

 ≤ 0,5, A = – 1,  

ϕ

 = arccos(1–2m

2

),

dla 0,5 < m

2

 ≤ 1, A = 1,

ϕ

 = arccos(2m

2

 

–1),

l

1

,  l

2

  –  współczynniki  przewodze­

nia  ciepła,  odpowiednio  pierwsze­

go i drugiego komponentu,

m

2

  –  stężenie  objętościowe  skład­

nika.

Przedstawione  wzory  pozwalają 

również  obliczyć  efektywną  prze­

wodność cieplną mieszaniny skła­

dającej się z trzech i więcej skład­

ników.  W  tym  przypadku  struktu­

rę  mieszaniny  wieloskładnikowej 

kolejno  sprowadza  się  do  struk­

tury  dwuskładnikowej.  Kolejność 

uwzględniania  wtrąceń  może  być 

dowolna.  Jednakże,  przestawienie 

numeracji indeksów elementu pod­

stawowego  i  wtrąceń  we  wzorach 

(2),  (3),  (4)  jest  niedopuszczalne 

ze  względu  na  geometryczne  róż­

nice komponentów.

Przewodność  cieplną  roztworów 

solnych można najdokładniej okre­

ślić stosując prawo cieplne miesza­

niny  dwóch  cieczy:  rozpuszczalni­

ka (wody) i hipotetycznego roztwo­

ru  soli  o  100%  stężeniu.  Strukturę 

takiego układu można przedstawić 

w  postaci  modelu  o  składnikach 

przenikających  się  wzajemnie. 

a)

b)

Rys. 1. Modele systemów heterogenicznych: a) struktura z wtrąceniami: 1 – skład-

nik ciągły, 2 – wtrącenia; b) struktura ze składnikami wzajemnie przenikającymi się

PRzeglĄd budowlany 

9/2010

30

konstRukcje – elementy – mateRiały

a

R

tyk

uł

y

 PR

oblemowe

Zmienioną  przewodność  cieplną 

soli w hipotetycznym roztworze l

u

 

można określić wg wzoru [10]:

( )

6

5

2

10

3

,

9

−

−

⋅

⋅

⋅

=

M

T

p

st

u

ρ

λ

  (6)

gdzie:

M

 – masa molekuły soli,

P

  –  liczba  atomów  w  molekule 

soli,

T

st

 – temperatura topnienia soli, K

r

 – gęstość soli, kg/m

3

.

Mając  wartość  l

u

,  określoną 

na  podstawie  wzoru  (6),  można 

obliczyć przewodność cieplną roz­

tworu l

r

 dowolnej soli w dowolnym 

rozpuszczalniku  o  przewodności 
l

1

, stosując wzór (5).

Obecność  wilgoci  lub  roztworów 

wodnych  soli  w  przestrzeni  poro­

wej  materiałów  ściennych  znacz­

nie komplikuje proces przewodze­

nia ciepła. Para wodna znajdująca 

się w porach materiału, przekazu­

je  ciepło  przez  dyfuzję  od  ciepłej 

do  chłodniejszej  powierzchni  ele­

mentu.  Przy  czym,  na  chłodniej­

szej powierzchni odbywa się kon­

densacja  wilgoci  z  wydzieleniem 

ilości ciepła równej ciepłu wytwo­

rzenia pary wodnej. Współczynnik 

przewodzenia  ciepła  mieszaniny 

powietrza  i  pary  l

pw

  w  porach 

materiału  można  określić  wg 

wzoru [10]:

(

)

t

t

o

pw

q

c

c

d

⋅

−

+

=

2

1

λ

λ

 

(7)

gdzie:
l

0

  –  współczynnik  przewodze­

nia  ciepła  suchego  powietrza,  W/

(m

2

K),

d

t

 – współczynnik dyfuzji pary wod­

nej  w  powietrzu  o  temperaturze  t, 

m

2

/s,

D

c  =  (c

1

  –  c

2

)

  –  różnica  stężeń 

pary  wodnej  w  powietrzu  przy 

gradiencie temperatury 1K,

q

t

  –  ciepło  parowania  wody 

w temperaturze t, J/kg.

Obecność  roztworu  soli  w  porach 

materiału  powoduje  zmianę  skła­

dowej  dyfuzyjnej  strumienia  cie­

pła,  ponieważ  sole,  obniżając 

prężność  pary  wodnej,  wpływają 

na  różnicę  stężenia  pary  wodnej 

D

c

.  Intensywność  tego  wpływu 

zależy  od  rodzaju  soli  oraz  stęże­

nia  roztworu.  Największy  wpływ 

na  Dc  wykazują  roztwory  nasyco­

ne.  Zmianę  Dc,  w  tym  przypadku, 

można  przyjąć  jako  proporcjonal­

ną do punktu higroskopijności roz­

tworu nasyconego soli

 ϕ

n

r

.

Sole  mają  również  wpływ  na  cie­

pło  parowania  wody  z  roztworów. 

Ciepło  parowania  jednego  mola 

wody  z  roztworu  DH

r

,  kJ/mol 

w  danej  temperaturze  można 

wyznaczyć ze wzoru:

n

h

h

H

H

w

r

1

2

Δ

−

Δ

+

Δ

=

Δ

 (8)

gdzie:
D

H

w

 

–  ciepło  parowania  jednego 

mola wody w danej temperaturze, 

kJ/mol,
D

h

2

 

–  Dh

1

 

–  różnica  entalpii  roz­

tworów,  odpowiednio  końcowego 

i wyjściowego, kJ/mol,

n

  –  liczba  wyparowanych  moli 

wody.

Przyjmując, że współczynnik dyfu­

zji pary wodnej w powietrzu d

t

 przy 

zadanej  temperaturze  nie  zależy 

od rodzaju soli ani stężenia roztwo­

ru, można zapisać wzór, który okre­

śla  współczynnik  przewodzenia 

ciepła mieszaniny pary i powietrza 

w porach materiału zawierającego 

roztwór soli:

w

r

n

r

t

o

rd

H

H

c

d

Δ

⋅

Δ

⋅

⋅

Δ

⋅

+

=

100

ϕ

λ

λ

 (9)

Uwzględniając obecność roztworu 

nasyconego  soli  oraz  mieszani­

ny  pary  i  powietrza  w  materia­

le,  substancję  w  porach  można 

rozpatrywać  jako  dwuskładnikowy 

system  o  strukturze  z  wtrącenia­

mi.  Zauważmy,  że  wzory  (2)  i  (3) 

zapewniają  górne  i  dolne  osza­

cowanie  składowej  dyfuzyjnej 

współczynnika  przewodzenia  cie­

pła  mieszaniny  pary  i  powietrza. 

W celu otrzymania bardziej dokład­

nej  oceny  do  drugiego  składni­

ka  tych  wzorów  należy  wprowa­

dzić  współczynnik  poprawkowy, 

zależny od zawilgocenia materiału 

i  dobierany  na  podstawie  porów­

nania  obliczeniowych  wartości 

przewodności  cieplnej  materiału 

z wartościami eksperymentalnymi. 

Wartości  współczynników  przewo­

dzenia ciepła kryształów soli przyj­

muje się na podstawie danych lite­

raturowych  lub  można  je  obliczyć 

wg  wzorów  zaproponowanych 

przez Missenarda [10].

Podany opis przewodności cieplnej 

materiału  kapilarno­porowatego 

wskazuje,  że  zbudowanie  ścisłej 

zależności współczynnika przewo­

dzenia ciepła materiału zasolonego 

od  wszystkich  znaczących  czyn­

ników  jest  zadaniem  złożonym. 

Stąd,  w  celu  uzyskania  informa­

cji  o  współczynniku  przewodzenia 

ciepła  materiału  zasolonego  celo­

we jest zastosowanie modelowania 

matematycznego  i  przeprowadze­

nie  eksperymentu  obliczeniowego 

za pomocą modelu.

3.  Model  matematyczny  prze-

wodności  cieplnej  zawilgoco-

nego i zasolonego muru cegla-

nego

Celem opracowania modelu mate­

matycznego  było  zbadanie  zależ­

ności współczynnika przewodzenia 

ciepła materiałów ściennych (cegły 

ceramicznej  i  muru  ceglanego) 

od  zawartości  wilgoci  oraz  rodza­

ju  i  zawartości  soli  w  materiale. 

Czynniki te w pełni wyrażają cechy 

charakterystyczne związane z eks­

ploatacją  elementów  ściennych 

obiektów  murowanych  i  poddają 

się dostatecznie dokładnej kontroli 

podczas  badań  terenowych  stanu 

ścian.

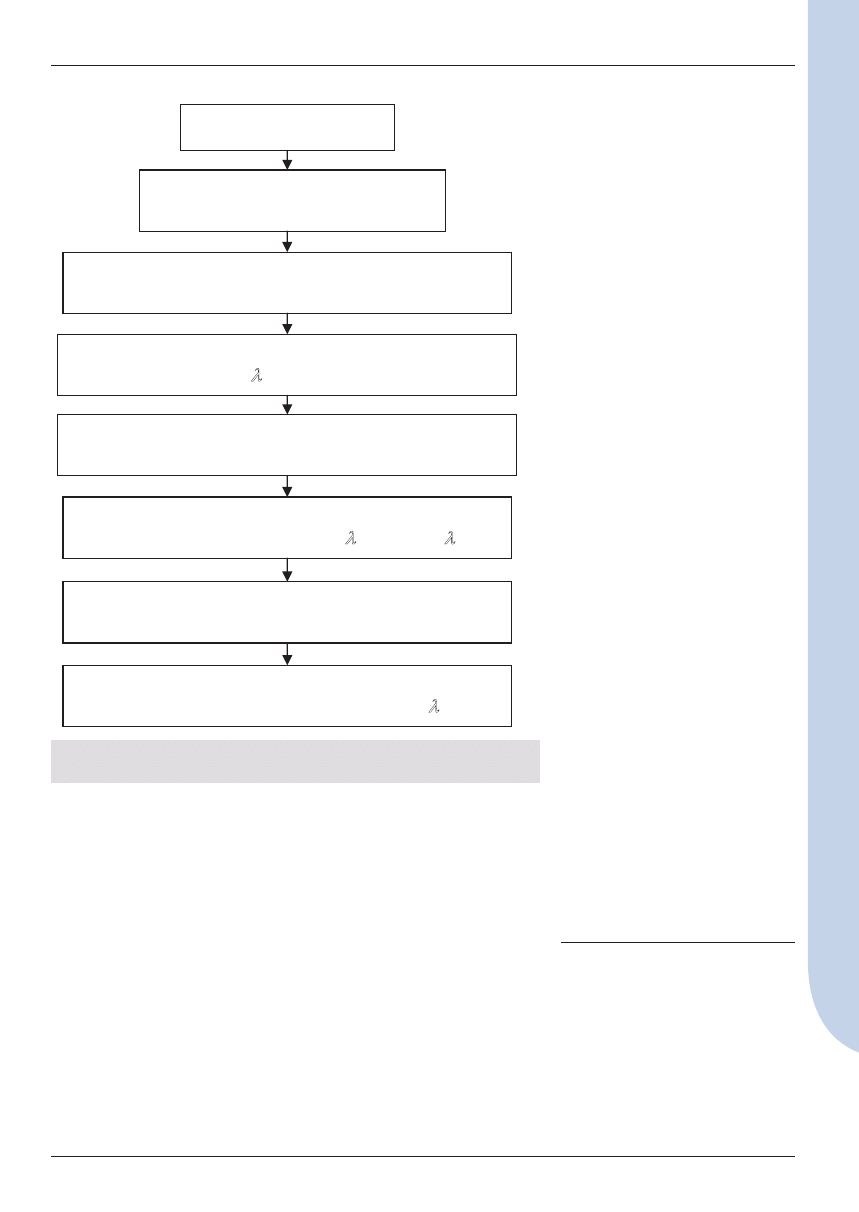
Algorytm modelu matematycznego 

obejmuje cztery główne bloki obli­

czeń.  W  pierwszym  bloku  oblicza 

się  współczynnik  przewodzenia 

ciepła  substancji  w  porach  l

wp

. 

W blokach drugim, trzecim i czwar­

tym  –  odpowiednio,  współczynnik 

przewodzenia  ciepła  cegły  cera­

micznej  l

cs

,  zaprawy  cementowej 

l

zs

 i muru ceglanego l

ms

, uwzględ­

niając obecność wilgoci i soli.

Współczynnik  przewodzenia  cie­

pła  substancji  w  porach  oblicza 

się biorąc pod uwagę stan skupie­

nia  jej  składników.  Rozpatruje  się 

PRzeglĄd budowlany 

9/2010

konstRukcje – elementy – mateRiały

31

a

R

tyk

uł
y

 PR
oblemowe

osiem  wariantów  składu  substan­

cji  w  porach.  W  pierwszym,  naj­

prostszym przypadku przyjmuje się 

wypełnienie  porów  tylko  suchym 

powietrzem. W ostatnim wariancie, 

w skład substancji w porach wcho­

dzi  mieszanina  pary  i  powietrza, 

roztwór nasycony i kryształy soli.

Uogólniony  schemat  blokowy  obli­

czania  współczynnika  przewodze­

nia ciepła zasolonego muru cegla­

nego przedstawiono na rysunku 2.

W  trakcie  przekształcania  algorytmu 

obliczeniowego  w  opis  matema­

tyczny  procesu  przenikania  ciepła, 

wprowadzono  dodatkowe  wzory 

i  założenia,  które  dotyczą  składni­

ków substancji w porach, ich stanu 

skupienia i stężeń objętościowych.

Założono,  że  przenikanie  cie­

pła  poprzez  dyfuzję  pary  wodnej 

ma miejsce wówczas, gdy w kapi­

larach  materiału  rozpocznie  się 

kondensacja  wilgoci,  która  może 

zwilżać  strefy  powierzchni  porów 

wokół otworów wylotowych kapilar, 

a  układ  może  być  rozpatrywany 

jako tak zwany schemat Krischera 

[12]. Jako wartość graniczną wilgot­

ności  w  przyjęto  wilgotność  sorp­

cyjną w

80

 przy względnej wilgotno­

ści powietrza ϕ

p 

= 80%, określoną 

dla materiału badanego za pomo­

cą izoterm sorpcji. Oczywiste jest, 

że  po  całkowitym  wypełnieniu 

porów  wodą  lub  roztworem  skła­

dowa  dyfuzyjna  strumienia  ciepła 

zniknie, a przy pewnym objętościo­

wym  stężeniu  wody  lub  roztworu 

m

2w

 w stosunku do objętości porów 

m

2p

,  składowa  ta  osiągnie  maksy­

malną  wartość.  Przyjęto,  że  taki 

stan  nastąpi,  gdy  m

2wr

 

=

 

0,5  m

2p

. 

W obliczeniach przyjęto założenie, 

że przy zawartości wilgoci w mate­

riale  w

r

  mniejszej  od  wilgoci  sorp­

cyjnej, przy określonej wilgotności 

względnej  powietrza  ϕ

p

  odpowia­

dającej  punktowi  higroskopijności 
ϕ

g

 badanej soli, roztwory solne nie 

powstają.

W  celu  opisu  zmiany  stanu  sku­

pienia  soli  wprowadzono  pojęcie 

roztworu  quasi­rzeczywistego, 

którego  stężenie  c

k

r

 

przewyższa 

wartość  stężenia  roztworu  nasy­

conego c

r

. Założono, że przy speł­

nieniu  warunku  c

k

r

 

>  c

n

 

w  porach 

zaczyna się krystalizacja soli. Przy 

obliczaniu  stężeń  objętościowych 

składników  substancji  w  porach 

uwzględniono  właściwości  fizyko­ 

­chemiczne  soli  i  ich  roztworów, 

porowatość  badanego  materiału, 

zawartości  masowe  wilgoci  i  soli, 

a także opisane wyżej założenie.

Przewodność  cieplną  substancji 

w  porach,  bez  uwzględniania  soli 

krystalicznej,  obliczono  wg  wzoru 

(1).  Kryształy  soli  wraz  ze  szkiele­

tem  materiału  rozpatrywano  jako 

dwuskładnikową  mieszaninę  twar­

dą,  której  przewodność  cieplną 

określono  wg  wzoru  (4).  W  etapie 

końcowym  obliczono  przewodno­

ści  cieplne  zawilgoconych  mate­

riałów  zawierających  sole  –  cegły 

ceramicznej i zaprawy cementowej 

– wg wzoru (1), a muru ceglanego 

– wg wzoru (4).

4. Dane do badania przewodno-

ści cieplnej za pomocą modelu 

matematycznego

Model  matematyczny  w  formie 

ujednoliconego  cyklicznego  algo ­ 

rytmu  obliczeniowego  zrealizowa­

no w postaci programu za pomocą 

którego przeprowadzono ekspery­

ment  obliczeniowy.  Jako  zmienne 

niezależne przyjęto zawartości wil­

goci  i  soli  w  materiale  ściennym. 

Realizując  eksperyment  oblicze­

niowy  uwzględniono:  cegłę  cera­

Wprowadzenie danych 

Ocena  stanu  skupienia  substancji 

w porach materiału 

Określenie stężeń objętościowych składników 

substancji w porach materiału 

Obliczenie współczynnika przewodzenia ciepła 

substancji w porach 

λ

wp

, zakładając różne jej stany 

 

Określenie stężeń objętościowych składników 

materiałów:

 

cegły ceramicznej, zaprawy cementowej

 

Obliczenie współczynnika przewodzenia ciepła 

materiałów:

 

cegły ceramicznej 

λ

cs

; zaprawy 

λ

zs

 

Określenie stężeń objętościowych składników układu: 

cegła ceramiczna + zaprawa cementowa 

Obliczenie współczynnika przewodzenia ciepła układu: 

cegła ceramiczna + zaprawa cementowa 

λ

ms

 

Rys.  2.  Uogólniony  schemat  blokowy  obliczania  współczynnika  przewodzenia 

ciepła zasolonego muru

PRzeglĄd budowlany 

9/2010

32

konstRukcje – elementy – mateRiały

a

R

tyk

uł

y

 PR

oblemowe

miczną o porowatości 50% i gęsto­

ści 1300 kg/m

3

 oraz materiały skła­

dowe  muru  ceglanego:  zaprawę 

cementową  i  cegłę  ceramiczną 

o  gęstości  1800  kg/m

3

,  porowa­

tości  31%  i  współczynniku  prze­

wodzenia  ciepła  szkieletu  2,326 

W/(mK).  Jako  sól,  wprowadzono 

NaCl o współczynniku przewodze­

nia ciepła kryształów 8,3 W/(mK).

W  wyniku  eksperymentu  oblicze­

niowego  otrzymano  dane  o  prze­

wodności cieplnej mieszaniny pary 

wodnej i powietrza, roztworów soli 

oraz  substancji  w  porach  dla  róż­

nych wariantów jej składu, a także 

dane dotyczące cegły ceramicznej, 

zaprawy cementowej i muru cegla­

nego  w  zależności  od  zawartości 

wilgoci  (od  0  do  9%)  i  soli  NaCl 

(od 0 do 6,5%) w materiale.

5. Analiza wyników badania

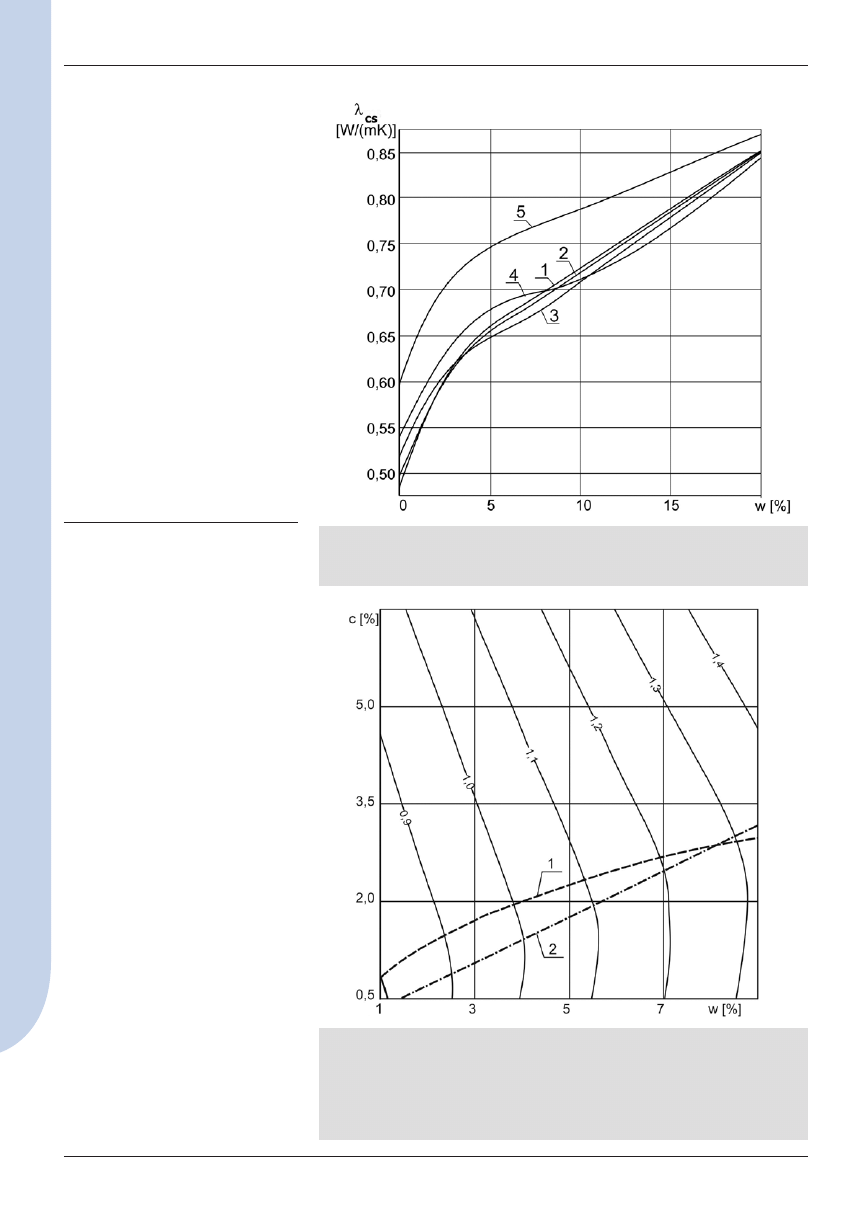
Wyniki  obliczeń  współczynnika 

przewodzenia  ciepła  cegły  cera­

micznej  o  gęstości  1300  kg/m

3

 

l

cs

  dla  wybranych  punktów  roz­

patrywanej  przestrzeni  czynników 

przedstawiono na rysunku 3.

Analizując  wykres  zależności  na 

rysunku 3, stwierdzono, że współ­

czynnik przewodzenia ciepła cegły 

ceramicznej, w porach której znaj­

duje  się  powietrze  i  kryształy  soli, 

wzrasta  liniowo  wraz  ze  wzrostem 

zawartości  NaCl.  Szybkość  tego 

wzrostu  zależy  nie  tylko  od  prze­

wodności  cieplnej  kryształów  soli, 

lecz także od porowatości materia­

łu  i  gęstości  kryształów,  ponieważ 

gęstość  kryształów  określa  stęże­

nie  objętościowe  soli  w  porach. 

Wypełnienie solą przestrzeni poro­

wej do 6,5% masy materiału zwięk­

sza  wartość  współczynnika  prze­

wodzenia ciepła cegły o 25%.

Obecność  wilgoci  w  materiale  

zmienia  charakter  wpływu  soli  na 

współczynnik  l

cs

  cegły.  W  porach 

materiału  powstają  roztwory  so­ 

li,  których  współczynnik  prze­

wodzenia  ciepła  zmniejsza  się 

wraz  ze  wzrostem  ich  stężenia. 

Zmniejszenie  ilości  soli  krystalicz­

nej  i  zwiększenie  objętości  roz­

tworu odbywa się stopniowo wraz 

Rys. 3. Współczynnik przewodzenia ciepła l

cs

, W/(mK) cegły ceramicznej o gęsto-

ści  1300  kg/m

3

  w  zależności  od  zawartości  wilgoci  w,  %  oraz  soli  (NaCl)  c,  %: 

1 – c = 0; 2 – c =1%; 3 – c = 2%; 4 – c = 4%; 5 – c = 8%

Rys. 4. Izolinie współczynnika przewodzenia ciepła l

ms

 , W/(mK) muru ceglanego 

r

 = 1800 kg/m

3

 zawierającego NaCl przy zmianie zawartości wilgoci w, % i soli c, %: 

1 – linia zerowego wpływu soli, powyżej której przy określonej wilgotności obecność 

soli powoduje zwiększenie wartości współczynnika przewodzenia ciepła; 2 – linia 

rozdziału faz substancji wewnątrz porów, powyżej której w porach materiału znajduje 

się roztwór nasycony i kryształy soli, poniżej – roztwór nienasycony

PRzeglĄd budowlany 

9/2010

konstRukcje – elementy – mateRiały

33

a

R

tyk

uł
y

 PR
oblemowe

ze  wzrostem  zawilgocenia  mate­

riału. W rezultacie, efekt zwiększe­

nia  przewodności  cieplnej  cegły 

spowodowany  obecnością  krysz­

tałów  soli  pochłania  efekt  zmniej­

szenia  przewodności  spowodo­

wany  powstaniem  roztworów  soli 

i zmniejszeniem wartości składowej 

dyfuzyjnej  przenikania  ciepła  l

rd

. 

Moment pełnego pochłaniania jed­

nego efektu przez drugi następuje 

przy  pewnej  zawartości  soli  kry­

stalicznej  i  roztworu  nasyconego. 

Wówczas,  przewodność  cieplna 

cegły  zawierającej  wilgoć  i  sole, 

nie  różni  się  od  przewodności 

cieplnej  cegły  zawilgoconej  bez 

soli  (pod  warunkiem  jednakowej 

w  nich  zawartości  wilgoci).  Przy 

wzroście  zawilgocenia,  ilość  roz­

tworu  nasyconego  zwiększa  się 

kosztem rozpuszczania kryształów 

soli.  Przy  pełnej  rozpuszczalności 

kryształów  soli  efekt  zmniejszenia 

wartości  l

cs

  cegły  jest  najwięk­

szy.  Jednakże,  zmiana  wartości 

współczynnika  przewodzenia  cie­

pła nie przekracza 5% w stosunku 

do współczynnika dla cegły nieza­

solonej.

Dalszy  wzrost  zawilgocenia  mate­

riału  prowadzi  do  rozcieńczenia 

roztworu  w  wyniku  czego  przy  tej 

samej  wilgotności  wartość  współ­

czynnika  przewodzenia  ciepła 

cegły  zasolonej  zbliża  się  do  war­

tości współczynnika dla cegły nie­

zasolonej.  Jednakże,  taki  proces 

może  mieć  miejsce  przy  ograni­

czonej zawartości soli w materiale 

(7–8%  masowo),  ponieważ  przy 

większym  zasoleniu  i  przy  ogra­

niczonej  objętości  porów,  wilgoci 

pochłanianej  przez  materiał  cegły, 

może  nie  wystarczyć  do  całkowi­

tego rozpuszczenia soli. Wówczas 

efekt  zmniejszenia  przewodności 

cieplnej nie będzie miał miejsca.

Największe  znaczenie  praktyczne 

ma  analiza  współczynnika  prze­

wodzenia  ciepła  muru  ceglanego 

w  zakresie  dopuszczalnej  wilgot­

ności  eksploatacyjnej  w  okresie 

zimowym. Według danych literatu­

rowych  dopuszczalne  zawilgoce ­ 

nie  muru  z  cegły  ceramicznej  wy­ 

nosi  2–3%  [1].  Obliczenia  prze­

prowadzone  przy  zastosowaniu 

modelu  wykazały,  że  przy  takim 

zawilgoceniu  współczynnik  prze­

wodzenia  ciepła  muru  zaczy­

na  wzrastać  przy  zawartości  soli 

NaCl  przekraczającej  1,3÷1,7%, 

co  pokazano  na  rysunku  4.  Dalej, 

zwiększenie  zawartości  soli  o  1% 

powoduje  przyrost  wartości  l

ms

 

o około 0,04 W/(mK). Na przykład, 

przy  wilgotności  muru  w  =  3% 

i zawartości NaCl c=6,5%, współ­

czynnik  l

ms

  wynosi  1,11  W/(mK), 

co  o  blisko  20%  przewyższa  war­

tość  współczynnika  przewodzenia 

ciepła muru, który nie zawiera soli 

(l

cs

 = 0,93 W/(mK)).

Należy  uwzględnić,  że  opisany 

wyżej  efekt  zmniejszenia  l

ms

  (tj. 

poprawa  właściwości  materiału 

ściennego)  ma  określoną  ogra­

niczoną  wartość  zależną  tylko 

od  zdolności  roztworu  do  obniża­

nia przewodności cieplnej miesza­

niny cieczy i pary wodnej w porach 

materiału.

Natomiast  efekt  zwiększenia  war­

tości l

ms

 (tj. pogorszenie właściwo­

ści materiału) zależy przede wszy ­ 

stkim  od  stężenia  objętościowego 

soli  krystalicznej  w  porach.  Stęże­

nie  objętościowe  soli  jest  teore­

tycznie  nieograniczone,  ponieważ 

sól  zapełniwszy  przestrzeń  poro ­ 

wą  może  dosłownie  otoczyć  ma ­ 

teriał.  Dlatego  w  obliczeniach 

cieplnych  zasolonych  ścian  zale­

ca  się  brać  pod  uwagę  tylko  te 

wartości  l

ms

,  które  przy  tej  samej 

wilgotności  przekraczają  wartość 

współczynnika  przewodzenia  cie­

pła materiału niezasolonego.

6. Wnioski

1.  Przeprowadzona  analiza  wyka­

zała wysoką efektywność wykorzy­

stania  modelowania  matematycz­

nego  do  oceny  i  prognozowania 

współczynnika  przewodzenia  cie­

pła materiałów ściennych podlega­

jących oddziaływaniu soli.

2.  Analiza  wyników  eksperymen­

tu  obliczeniowego  wykazała  zło­

żoną  zależność  pomiędzy  warto­

ścią  współczynnika  przewodzenia 

ciepła  ceramicznych  materiałów 

ściennych  a  rodzajem  soli,  zawar­

tością wilgoci i soli w porach oraz 

stanem skupienia soli.

3.  Stwierdzono,  że  w  warunkach 

dopuszczalnego zawilgocenia eks­

ploatacyjnego  muru  ceglanego 

(2÷3%)  jego  współczynnik  prze­

wodzenia ciepła zaczyna wzrastać 

przy  zawartości  NaCl  większej  niż 

1,3÷1,7%.  Dalszy  przyrost  warto­

ści współczynnika wynosi 0,04 W/

(mK) przy wzroście zawartości soli 

w materiale o 1%.

BiBliografia

[1] Hoła J., Matkowski Z., Wybrane problemy 

dotyczące zabezpieczeń przeciwwilgocio­

wych ścian w istniejących obiektach murowa­

nych Mat. XXIV Konferencji Naukowo­ 

­Technicznej „Awarie Budowlane”, Szczecin­

Międzyzdroje, 26–29 maja 2009, s. 73–92

[2] Kunzel H. M., Kiessel K., Calculation 

of heat and moisture transfer in exposed 

building components. International Journal of 

Heat and Mass Transfer, 1997, Vol. 40,  

s. 159–167

[3] Ahl J., Salt diffusion in brick structures. 

Journal of Material Science, 2003, Vol. 38, 

s. 2055–2061

[4] Solymez M. S., On the effective thermal 

conductivity of building bricks. Building and 

Environment, 1999, Vol. 34, s. 1–5

[5] Dawson D. M., Briggs A., Prediction of the 

thermal conductivity of insulation materials. 

Journal of Material Science, 1981, Vol. 16, 

s. 3346–3356

[6] Alawadhi E. M., Thermal analysis of 

a building brick containing phase change 

material. Energy and Building, 2008, Vol. 40, 

s. 351–357

[7] Lubelli B., Van Hees R. P. J., Brocken 

H. J. P., Experimental research on 

hygroscopic behaviour of porous specimens 

contaminated with salts. Construction and 

Building Materials, 2004, Vol. 18, s. 339–348

[8] Espinosa R. M., Franke L., Deckelmann 

G., Phase changes of salts in porous 

materials: Crystallization, hydration and 

deliquescence. Construction and Building 

Materials, 2008, Vol. 22, s. 1758–1773

[9] Dulniev G. N., Zarichniak Yu. P., 

Tieploprovodnost’ smiesei i kompozy­

cionnych materialov. Spravochnaja kniga – 

L., Energia, 1974, s. 264

[10] Missenard A., Conductivite thermique des 

solidem, liquides, gaz et de leurs melanges. 

Editions Eyrolles, Paris, 1985, 340 s.

[11] Odelevskiy W. I., Raschet 

obobshchennoj provodimosti geterogennych 

sistem. Zh.T.F. 1951, 21, s. 667–685

[12] Krischer O., Rohnalter H., Die 

Wärmeübertragung durch Diffusion des 

Wasserdampfes in den Poren von Baustoffen 

unter Einwirkung eines Temperaturgefälles. 

Gesundheits – Ingenieur, Berlin, 1937 – N 41, 

s. 39–46