Zadania z oryginalną numeracją pochodzą z Informatora o egzaminie maturalnym od 2010 roku
z matematyki (zdawanej jako przedmiot obowiązkowy) – Zbiór przykładowych zadań maturalnych.

Tydzień 7.

Przed przystąpieniem do rozwiązywania zadań skorzystaj z

tablic

matematycznych 10. Planimetria.

Promień SA jest w punkcie styczności prostopadły do stycznej. Stąd

Trójkąt ABS jest równoramienny, czyli

Odp. B

Miara kąta środkowego jest dwa razy większa od miary kąta wpisanego opartych na tym samym łuku.
Jeśli miarę kąta wpisanego oznaczymy x, to x + 2x = 180

o

. Zatem x = 60

o

, a miara kąta środkowego 120

o

.

Odp. C

Suma miar kątów wewnętrznych przy ramieniu trapezu wynosi 180

o

. Możemy ułożyć prosty układ

równań, w którym x, y oznaczają miary kątów wewnętrznych przy ramieniu trapezu, przy czym x przy
krótszej podstawie.

Stąd, 2x = 220

o

, czyli x = 110

o

.

Odp. B

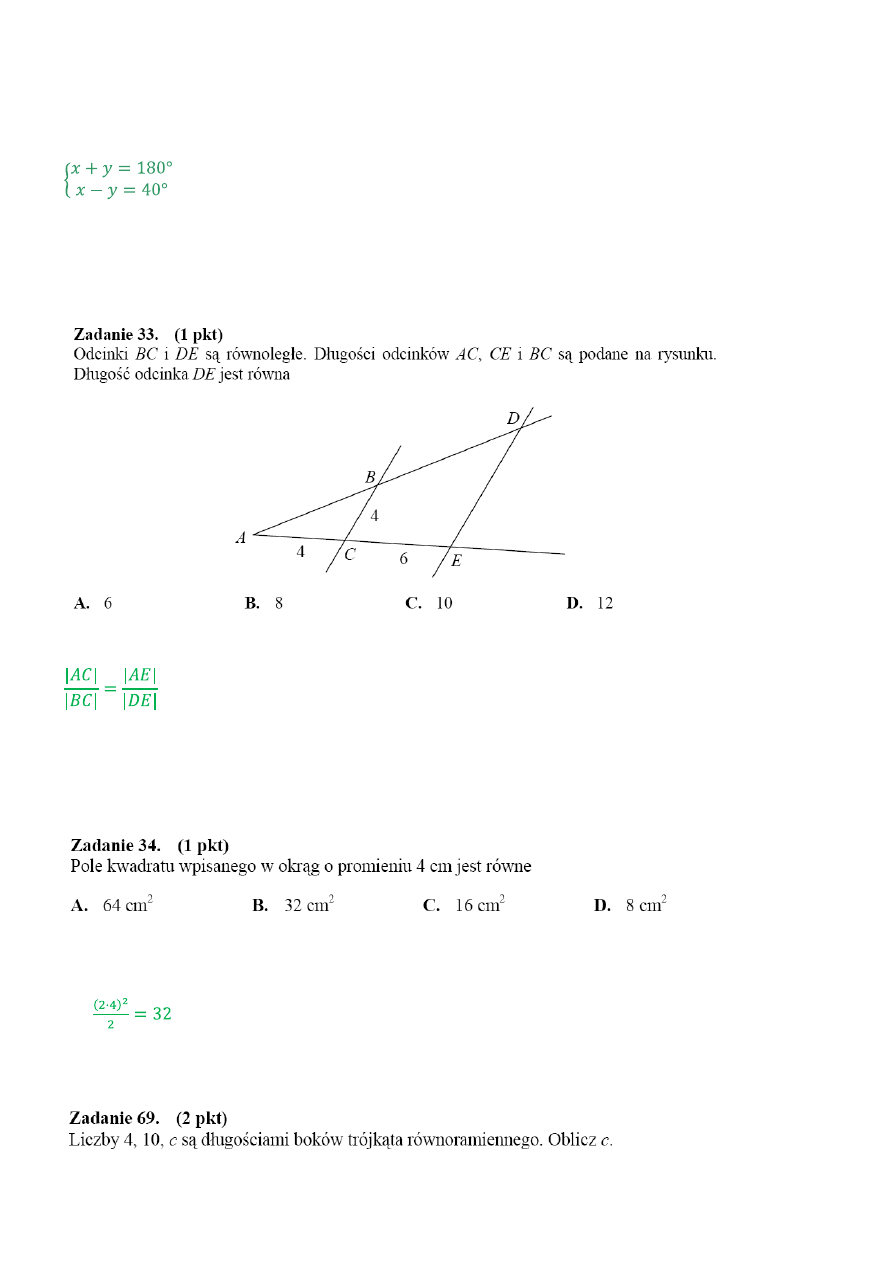
Korzystając z twierdzenia Talesa zapisujemy następującą proporcję.

Po podstawieniu danych liczbowych i rozwiązaniu prostego równania otrzymujemy |DE| = 10.

Odp. C

Przekątna kwadratu wpisanego w okrąg jest równa średnicy tego okręgu. Korzystając ze wzoru na pole
rombu, gdy dane są przekątne otrzymujemy

P =

Odp. B

Trójkąt o podanych długościach boków jest równoramienny, gdy c = 4 lub c = 10.

Teraz musimy sprawdzić warunek trójkąta. Trójkąt o bokach długości 4, 4, 10 nie istnieje, ponieważ
4 + 4 < 10. Długości boków szukanego trójkąta są równe 4, 10, 10.

Podobnie jak w zadaniu 69. c = 6 lub c = 10. W tym przypadku istnieją dwa trójkąty: jeden o bokach
długości 6, 6, 10 oraz 6, 10, 10.

Musimy rozważyć trzy przypadki.
I – przeciwprostokątna ma długość 6, co jest niemożliwe, bo przeciwprostokątna nie może być krótsza od
przyprostokątnej (długość 10)

II – przeciwprostokątna ma długość c

III – przeciwprostokątna ma długość 10

Korzystając z twierdzenia Pitagorasa otrzymujemy
6

2

+ 10

2

= c

2

6

2

+ c

2

= 10

2

c =

c = 8

c = 2

Obw

ABCD

= 50 cm

Obw

ABD

= 46 cm

Obw

BCD

= 36 cm

Obw

ABCD

= Obw

ABD

+ Obw

BCD

– 2|BD|

50 = 46 + 36 – 2|BD|

|BD| = 16 cm

A

B

C

D

10

20

20

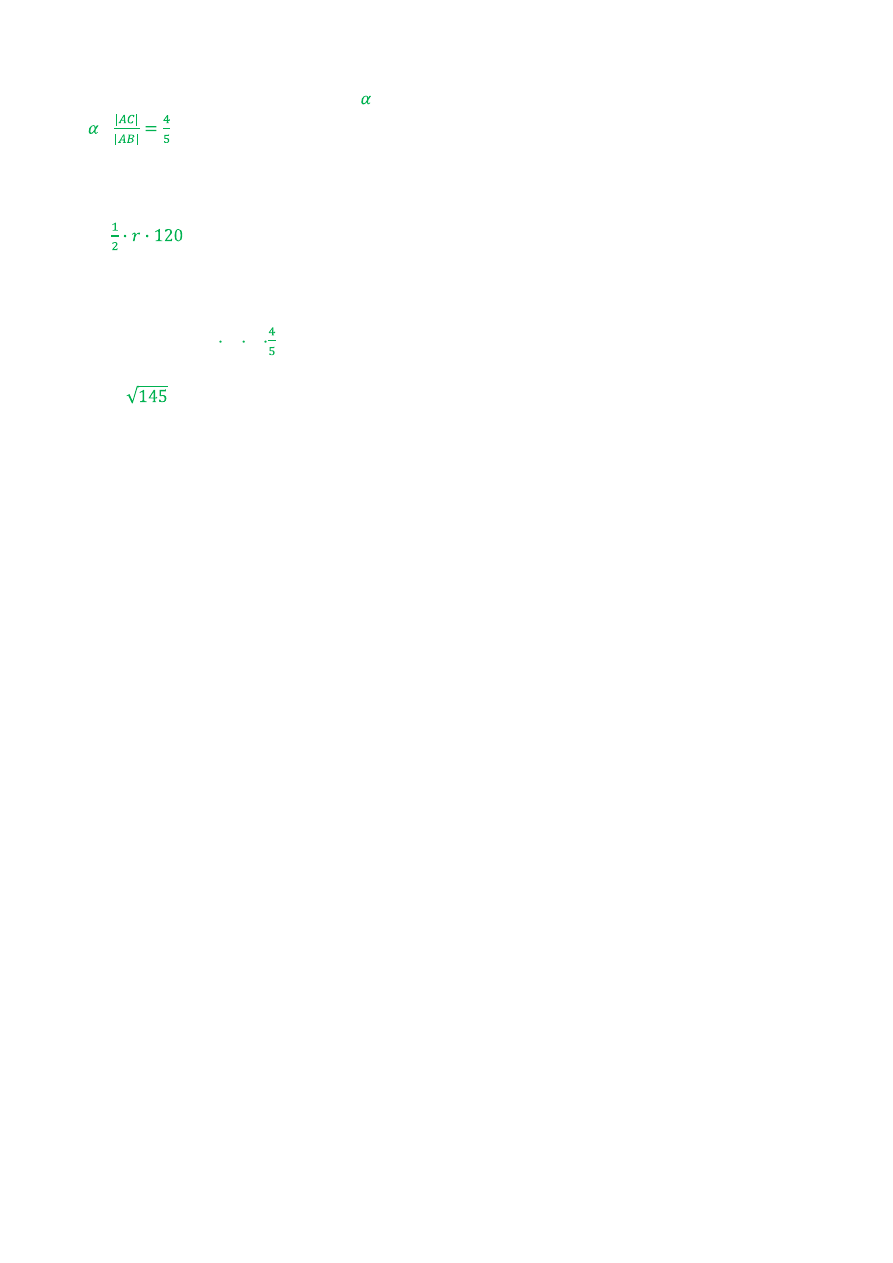
Możemy skorzystać z twierdzenia cosinusów.
(1) |CM|

2

= |CA|

2

+ |AM|

2

– 2|AC||AM|cos

cos =

Aby wyznaczyć |AM| musimy wcześniej obliczyć BM, a do tego przyda się nam promień okręgu
wpiasanego w trójkąt.
P

ABC

= 600

P

ABC

=

= 60r

Z porównania otrzymanych wyrażeń otrzymujemy, że r = 10.
Znając promień możemy uzupełnić rysunek o długości niektórych odcinków.
Wracamy do (1) i po podstawieniu wartości liczbowych otrzymujemy

|CM|

2

= 40

2

+ 30

2

– 2 30 40

|CM|

2

= 580

|CM| = 2