
LISTA 3
ZADANIE 1
a) −817
10
= −1⋅817
10
= −1 ⋅ 01101110001
U2
= 10010001111
U2
b)
1321
10
=010100101001
U2
c)
10111101
2
= 010111101
U2
=
d)
1011101
U2
=1100111
SD
=1100 101
SD
e)
1011101
−2
=10 11101
SD
Krzysztof Adamski :: http://mr-k.namyslow.eu.org
1
817
1
408
0
204
0
102
0
51
1
25
1
12
1
6
0
3
1
1
1
0
metoda Bootha
1
0
0
1
0
0
0
1
1
1
1
0
-1 0
1
-1 0
0
1
0
0
0
-1
metoda Bootha-McSorleya
1
1
0
0
1
0
0
0
1
1
1
1
0
0
-1 0
1
-1 0
0
1
0
0
0
-1
1321 1
660
0
330
0
165
1
82
0
41
1
20
0
10
0
5
1
2
0
1
1
0
metoda Bootha
0
1
0
1
0
0
1
0
1
0
0
1
0
1
-1 1
-1 0
1
-1 1
-1 0
1
-1
metoda Bootha-McSorleya
0 1 0 1 0 0 1 0 1 0 0 1 0
0 1 0 1 0 1 0 -1 -1 0 0 1
metoda Bootha
0
1
0
1
1
1
1
0
1
0
1
-1 1
0
0
0
-1 1
-1
metoda Bootha-McSorleya
0
0
1
0
1
1
1
1
0
1
0
0
1
0
-1 0
0
0
-1 0
1
metoda Bootha
1
0
1
1
1
0
1
0
-1 1
0
0
-1 1
-1
metoda Bootha-McSorleya
1
1
0
1
1
1
0
1
0
0
-1 1
0
0
-1 0
1
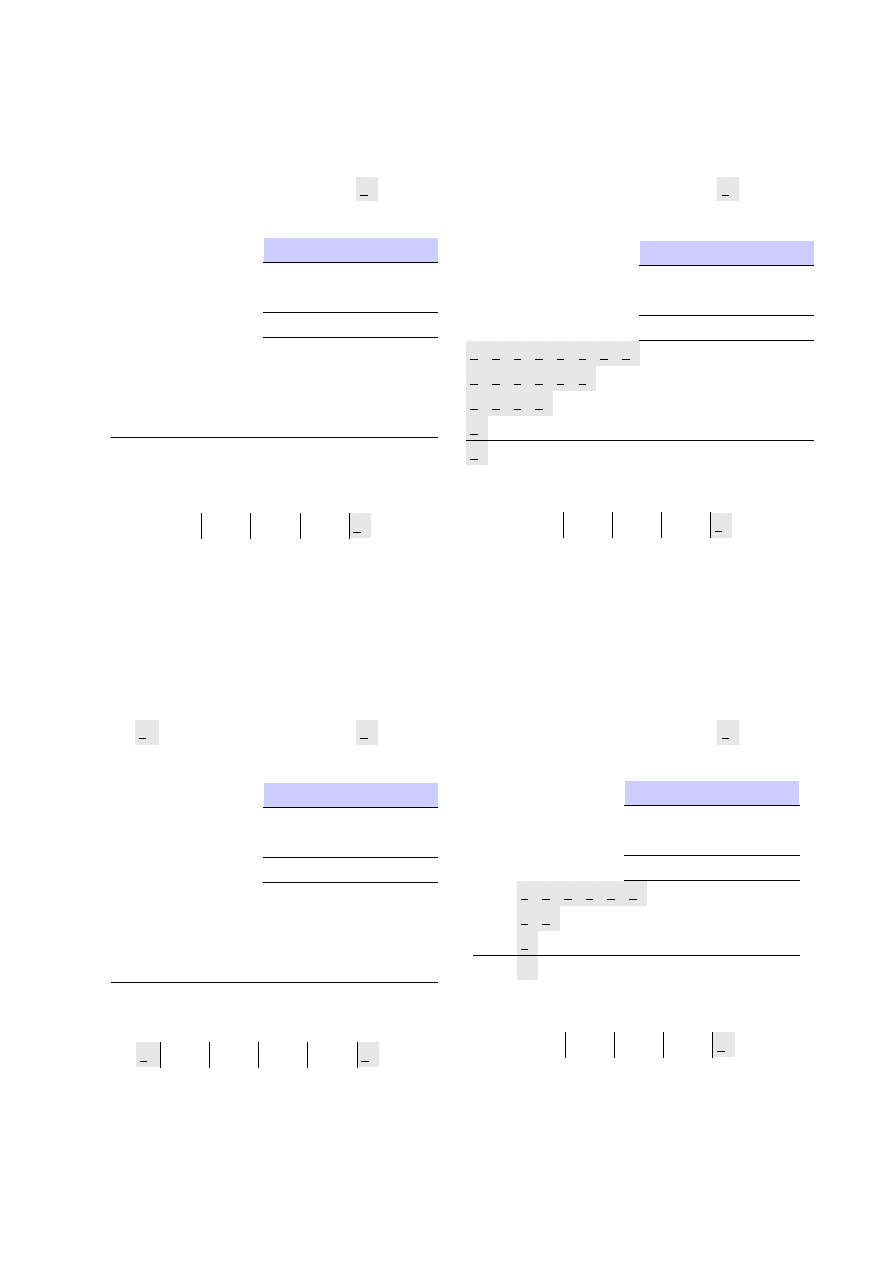
ZADANIE 2
Należy pamiętać, że przekodowywanie wykonujemy na liczbach w systemie U2, więc w A musimy dodać bit
rozszerzenia
A – dwójkowy naturalny
B – U2
a)
Liczba SD po przekodowaniu algorytmem Bootha-
McSorleya jest identyczna jak ta po przekodowaniu
algorytmem Bootha więc nie potrzeby liczyć tego samego.
a)
Liczba SD po przekodowaniu algorytmem Bootha-
McSorleya jest identyczna jak ta po przekodowaniu
algorytmem Bootha więc nie potrzeby liczyć tego samego.
b)
Znów po przekodowaniu metodą Bootha-McSorleya,
liczba SD jest ta sama więc nie ma co liczyć.
b)
Znów po przekodowaniu metodą Bootha-McSorleya,
liczba SD jest ta sama więc nie ma co liczyć.
Krzysztof Adamski :: http://mr-k.namyslow.eu.org
2
metoda Bootha
0
1
1
1
0
0
1
1
0
1
0
0
-1 0
1
0
-1
0 0 1 1 1 0 1 1
1 1 0 0 0 1 0 1
0 1 1 1 0 0 1 1
1 0 0 -1 0 1 0 -1
0 0 1 1 1 0 1 1
1 1 0 0 0 1 0 1
0 0 1 1 1 0 1 1
1 1 0 0 0 1 0 1
1 1 0 1 0 0 1 0 1 1 1 1 1 1 1
metoda Bootha-McSorleya
0
1
1
1
0
0
1
1
0
1
0
0
-1 0
1
0
-1
metoda Bootha
0
1
1
1
0
0
1
1
0
1
0
0
-1 0
1
0
-1
0 0 1 1 1 0 1 1
1 1 0 0 0 1 0 1
0 1 1 1 0 0 1 1
1 0 0 -1 0 1 0 -1
0 0 0 0 0 0 0 0 0 0 1 1 1 0 1 1
1 1 1 1 1 1 1 1 0 0 0 1 0 1
0 0 0 0 0 0 1 1 1 0 1 1
1 1 1 0 0 0 1 0 1
1 1 1 0 0 1 0 1 0 1 1 1 1 1 1 1
metoda Bootha-McSorleya
0
1
1
1
0
0
1
1
0
1
0
0
-1 0
1
0
-1
1 0 0 0 1 1
0 1 1 1 0 1
1 1 0 1 1 1 1 0
1 0 -1 1 0 0 0 -1 0
1 0 0 0 1 1
0 1 1 1 0 1
1 0 0 0 1 1
0 1 1 1 1 1
1 0 1 0 1 1 1 0 1 0 0 1 1 0
metoda Bootha-McSorleya
1
1
0
1
1
1
1
0
0
0
-1 1
0
0
0
-1 0
1 0 0 0 1 1
0 1 1 1 0 1
1 1 0 1 1 1 1 0
0 -1 1 0 0 0 -1 0
1 1 1 1 1 1 1 0 0 0 1 1
0 0 0 1 1 1 0 1
1 1 0 0 0 1 1
1 1 0 1 0 0 0 1 0 0 1 1 0
metoda Bootha
0
1
1
0
1
1
1
1
0
0
1
0
-1 1
0
0
0
-1 0
metoda Bootha-McSorleya
0
1
1
0
1
1
1
1
0
0
1
0
-1 1
0
0
0
-1 0
metoda Bootha
1
1
0
1
1
1
1
0
0
0
-1 1
0
0
0
-1 0
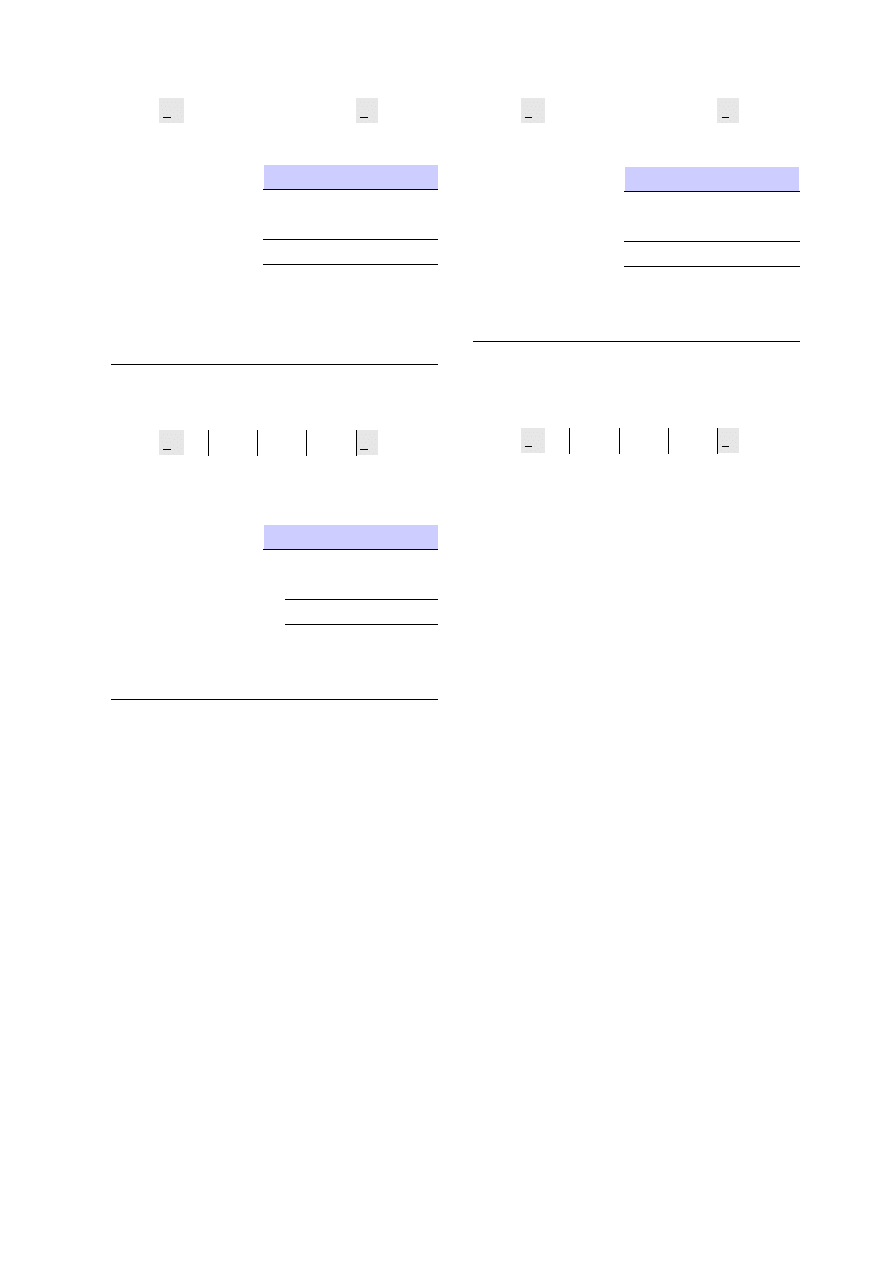
c)
c)
Po przekodowaniu metodą Bootha-McSorleya, liczba SD
jest ta sama więc nie ma co liczyć.
Krzysztof Adamski :: http://mr-k.namyslow.eu.org
3
metoda Bootha
0
1
0
1
1
1
1
1
0
1
-1 1
0
0
0
0
-1
0 1 0 1 1 1
1 0 1 0 0 1
1 0 1 1 1 1 1
1 -1 1 0 0 0 0 -1
0 1 0 1 1 1
1 0 1 0 0 1
0 1 0 1 1 1
1 0 1 0 0 1
1 1 1 1 1 0 1 1 1 0 1 1 1
metoda Bootha-McSorleya
0
1
0
1
1
1
1
1
0
0
1
1
0
0
0
0
-1
0 1 0 1 1 1
1 0 1 0 0 1
1 0 1 1 1 1 1
1 1 0 0 0 0 -1
0 1 0 1 1 1
1 0 1 0 0 1
1 0 1 0 0 1
1 1 1 1 0 1 1 1 0 1 1 1
metoda Bootha
1
1
0
1
1
1
1
1
0
0
-1 1
0
0
0
0
-1
0 1 0 1 1 1
1 0 1 0 0 1
1 0 1 1 1 1 1
0 -1 1 0 0 0 0 -1
0 1 0 1 1 1
1 0 1 0 0 1
0 1 0 1 1 1
1 0 1 0 1 1 1 1 0 1 1 1
metoda Bootha-McSorleya
1
1
0
1
1
1
1
1
0
0
-1 1
0
0
0
0
-1
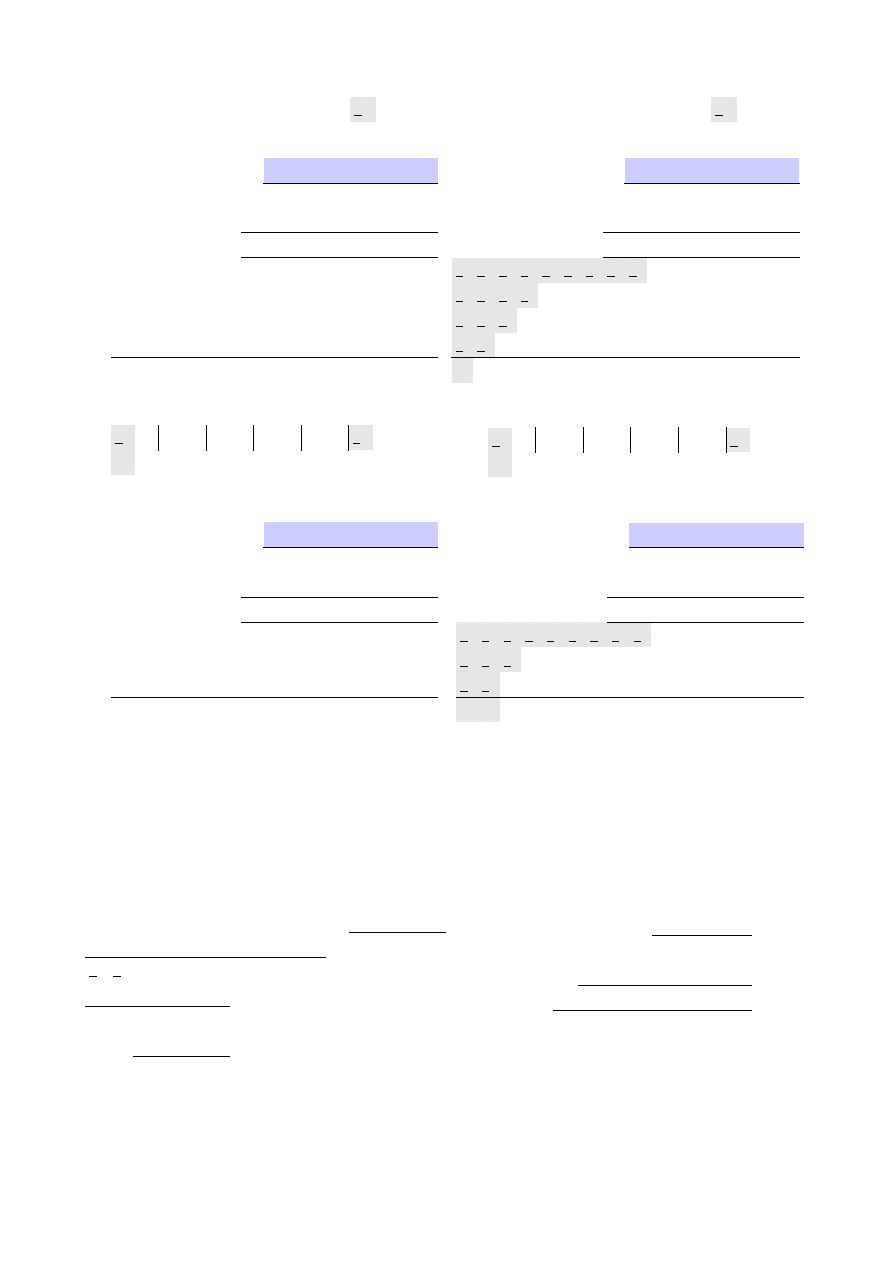
d)
ZADANIE 3
a) 01010011
U2
: 1011
U2
= 10000,01
U2
Krzysztof Adamski :: http://mr-k.namyslow.eu.org
4
metoda Bootha
0
1
0
1
1
1
1
1
0
0
1
-1 1
0
0
0
0
-1 0
metoda Bootha-McSorleya
0 0 1 0 1 1 1 1 1 0 0
0 1 0 -1 0 0 0 0 -1 0
metoda Bootha
0
1
0
1
1
1
1
1
0
0
1
-1 1
0
0
0
0
-1 0
1 0 1 1 0 1
0 1 0 0 1 1
0 1 0 1 1 1 1 1 0
1 -1 1 0 0 0 0 -1 0
1 1 1 1 1 1 1 1 1 1 0 1 1 0 1
0 0 0 0 0 1 0 0 1 1
1 1 1 1 0 1 1 0 1
0 0 0 1 0 0 1 1
1 0 0 0 1 1 1 0 0 0 0 1 1 0 1 0
metoda Bootha-McSorleya
0 0 1 0 1 1 1 1 1 0 0
0 1 0 -1 0 0 0 0 -1 0
1 0 1 1 0 1
0 1 0 0 1 1
0 1 0 1 1 1 1 1 0
1 -1 1 0 0 0 0 -1 0
1 0 1 1 0 1
0 1 0 0 1 1
1 0 1 1 0 1
0 1 0 0 1 1
1 0 1 1 1 0 1 0 0 1 1 0 1 0
1 0 1 1 0 1
0 1 0 0 1 1
0 1 0 1 1 1 1 1 0
1 0 -1 0 0 0 0 -1 0
1 0 1 1 0 1
1 1 0 1 1 0 1
0 1 0 0 1 1
0 1 1 1 1 0 1 0 0 1 1 0 1 0
1 0 1 1 0 1
0 1 0 0 1 1
0 1 0 1 1 1 1 1 0
1 0 -1 0 0 0 0 -1 0
1 1 1 1 1 1 1 1 1 1 0 1 1 0 1
1 1 1 1 1 0 1 1 0 1
0 0 0 1 0 0 1 1
1 0 0 0 1 1 1 0 0 0 0 1 1 0 1 0
0 1 0 1
1 1 0 0 0 0, 0 1
0 0 0 1 0 1 0 0 1 1 :
1 0 1 1
+ 1 0 1 1
1 1 0 1 1
-
1 1 0 1 1
0 0 0 0 0 0 1 1 0 0
0
1
0
1
1
0
1
1
×
1
0
0
0
0
0
1
0
1
0
1
0
1
0
0
0
0

b) 1010011
U2
: 01011
U2
= 1011,11
U2
c) 576
U10
: 176
U10
= 7,590
U10
d) 424
U10
: 824
U10
= 7,590
U10
Krzysztof Adamski :: http://mr-k.namyslow.eu.org
5
0 1 0 1 1 0 1
1 0 1 1, 1 1
1 1 0 1 0 0 1 1 :
0 1 0 1 1
+ 0 1 0 1 1
0 1 0 1 0 1
-
0 1 0 1 1
0 1 0 1 0 1
-
0 1 0 1 1
0 1 0 1 0 0
-
1 0 1 1
0 1 0 0 1 0
0 4 2 4
9 7, 5 9 0
9 5 7 6 :
1 7 6
+ 1 7 6
1 3 3 6
-
1 2 3 2
0 1 0 4 0
-
8 8 0
1 6 0 0
-
1 5 8 4
1 6 0
1 7 6
9 7, 5 9 0
0 4 2 4 :
8 2 4
+ 8 2 4
8 6 6 4
-
8 7 6 8
9 8 9 6 0
-
9 1 2 0
9 8 4 0 0
-
9 8 4 1 6
9 8 4 0
wielokrotności dzielnika
1
9824
2
9648
3
9472
4
9296
5
9120
6
98844
7
98768
8
98592
9
98416
1
0
1
0
1
0
1
0
1
1
×
1
0
1
1, 1
0
1
0
1
1
0
1
0
1
1
0
1
0
1
1
1
0
1
0
1
0
1
0
0
1
1
1
0, 1
8
2
4
0
1
7
6
×
9
7, 5
9
0
0
0
1
5
8
4
0
0
0
8
8
0
0
1
2
3
2
9
8
2
4
9
5
7
5, 8
4
0
1
7
6
9
8
2
4
×
9
7, 5
9
9
9
9
8
4
1
6
9
9
9
1
2
0
9
8
7
6
8
0
1
7
6
0
0
4
2
4, 1
6

e) 6465
U10
: 353,5
U10
= 90
U10
f) 6465
U8
: 353,5
U8
= 74,75
U8
g) 5465
U10
: 150,7
U10
= 69,90
U10
h) 2465
U8
: 753,5
U8
= 676,4
U8
Krzysztof Adamski :: http://mr-k.namyslow.eu.org
6
3 5 3 5
9 0, 0 0
6 4 6 5 :
3 5 3, 5
+ 3 5 3 5
0
1
3
1
3
7
4, 7
5
6
4
6
5
:
3
5
3, 5
+ 3
5
3, 5
2
2
2
2
0
-
1
6
5
6
4
3
4
3
4
0
-
3
1
6
1
3
2
5
2
5
0
4 5 3 5
9 6 9, 9 0
9 5 4 6 5 :
1 5 0, 7
+ 1 5 0 7
1 0 5 3 5
-
9 0 4 2
1 4 9 3 0
-
1 3 5 6 3
1 3 6 7 0
-
1 3 5 6 3
1 0 7 0
wielokrotności dzielnika
1
353,5
2
727,2
3
1302,7
4
1656,4
5
2232,1
6
2605,6
7
3161,3
wielokrotności dzielnika
1
753,5
2
727,2
3
702,7
4
7656,4
5
7632,1
6
7605,6
7
7561,3
6
4
6
5
3
5
3, 5
×
9
0
6
4
6
5
6
4
6
5, 0
4
2
4
3
3
5
3, 5
×
7
4, 7
5
2
2
3
2
1
3
1
6
1
3
1
6
5
6
4
4
2
4
3
6
4
6
2, 0
5
1
8
4
9
3
1
5
0, 7
×
9
6
9, 9
0
1
3
5
6
3
1
3
5
6
3
9
0
4
2
8
4
9
3
9
5
4
6
3, 9
3
0
0 2 4 3
7 6 7 6, 4
0 0 2 4 6 5 :
7 5 3, 5
+ 7 5 3, 5
7 5 6 1 6
-
7 6 0 5 6
7 5 4 0 5
-
7 5 6 1 3
7 5 7 2 0
-
7 6 0 5 6
7 6 4 2 0
1
0
1
4
6
7
6, 4
×
7
5
3, 5
7
7
7
7
2
7
0
4
7
7
7
3
7
2
0
7
7
2
7
0
4
0
1
0
1
4
0
0
2
3
6
5, 0
4
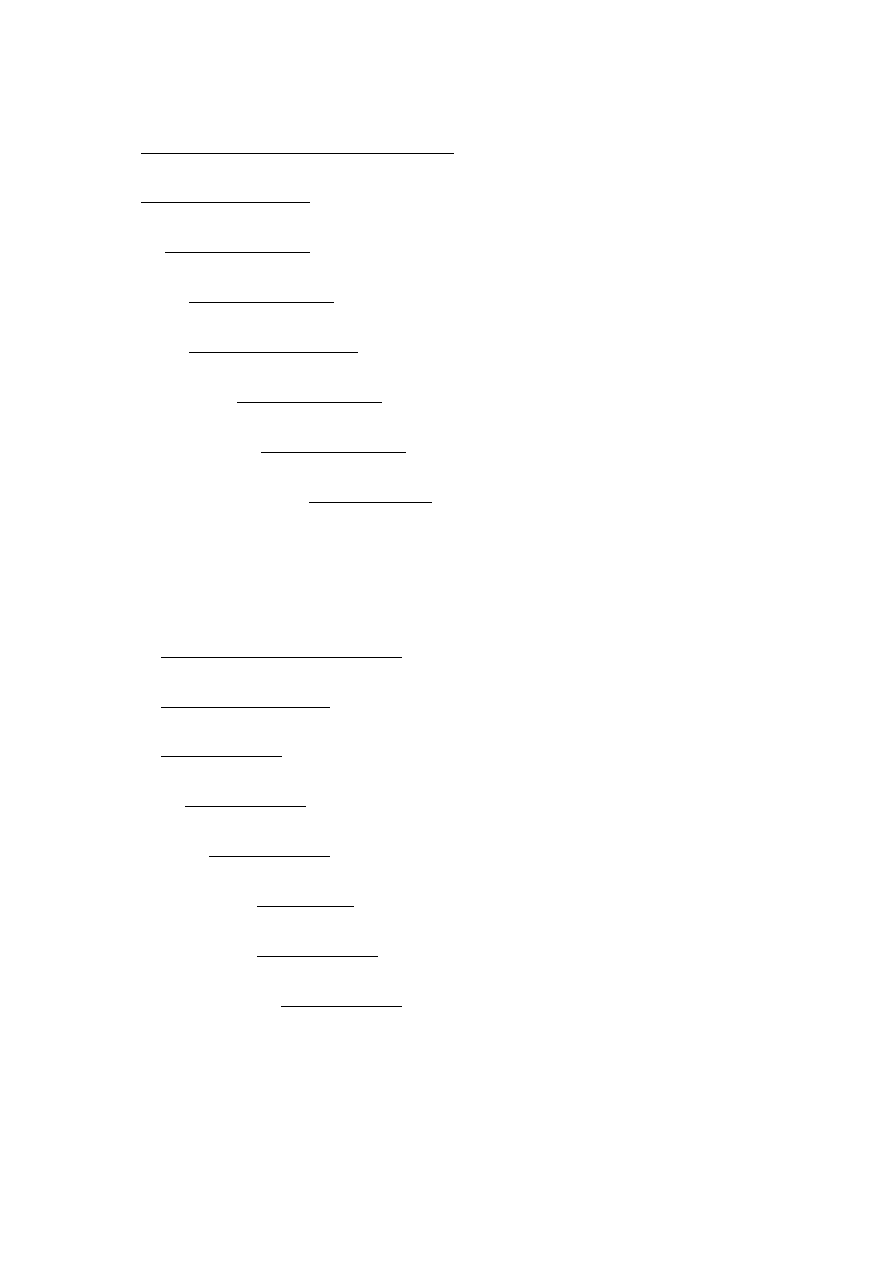
ZADANIE 4 (wykonywanie sprawdzeń sobie darowałem, czasem liczyłem więcej bitów niż potrzeba..)
a) 110101
U2
: 011011
U2
= 1,100101
U2
b) 011101
U2
: 110111
U2
= 100,1100
U2
Krzysztof Adamski :: http://mr-k.namyslow.eu.org
7
0 0 1 0 1 1
1, 1 0 0 1 0
1
1 1 0 1 0 1 :
0 1 1 0 1
1
+ 0 1 1 0 1 1
0 1 0 0 0 0 0
-
0 1 1 0 1 1
0 0 1 0 1 0
-
0 1 1 0 1 1
1 0 1 1 1 1 0
+
0 1 1 0 1 1
1 1 1 1 0 0 1 0
+
0 1 1 0 1 1
0 0 1 1 0 1 0
-
0 1 1 0 1 1
1 1 1 1 1 1 0
+
0 1 1 0 1 1
0 1 1 0 0 1
0
0 0 1 0 0
1
1 0 0, 1 1 0 0
0 0 1 1 1 0 1 :
1 1 0 1 1
1
+ 1 0 1 1 1
1 1 1 0 0
-
1 0 1 1 1
0 1 0 1 1
+ 1 0 1 1 1
0 0 1 0 0
+
1 0 1 1 1
1 1 0 1 1 0
-
1 0 1 1 1
1 1 1 1 1 0
-
1 0 1 1 1
0 0 1 1 1 0
+
1 0 1 1 1
0 0 1 0 1 0
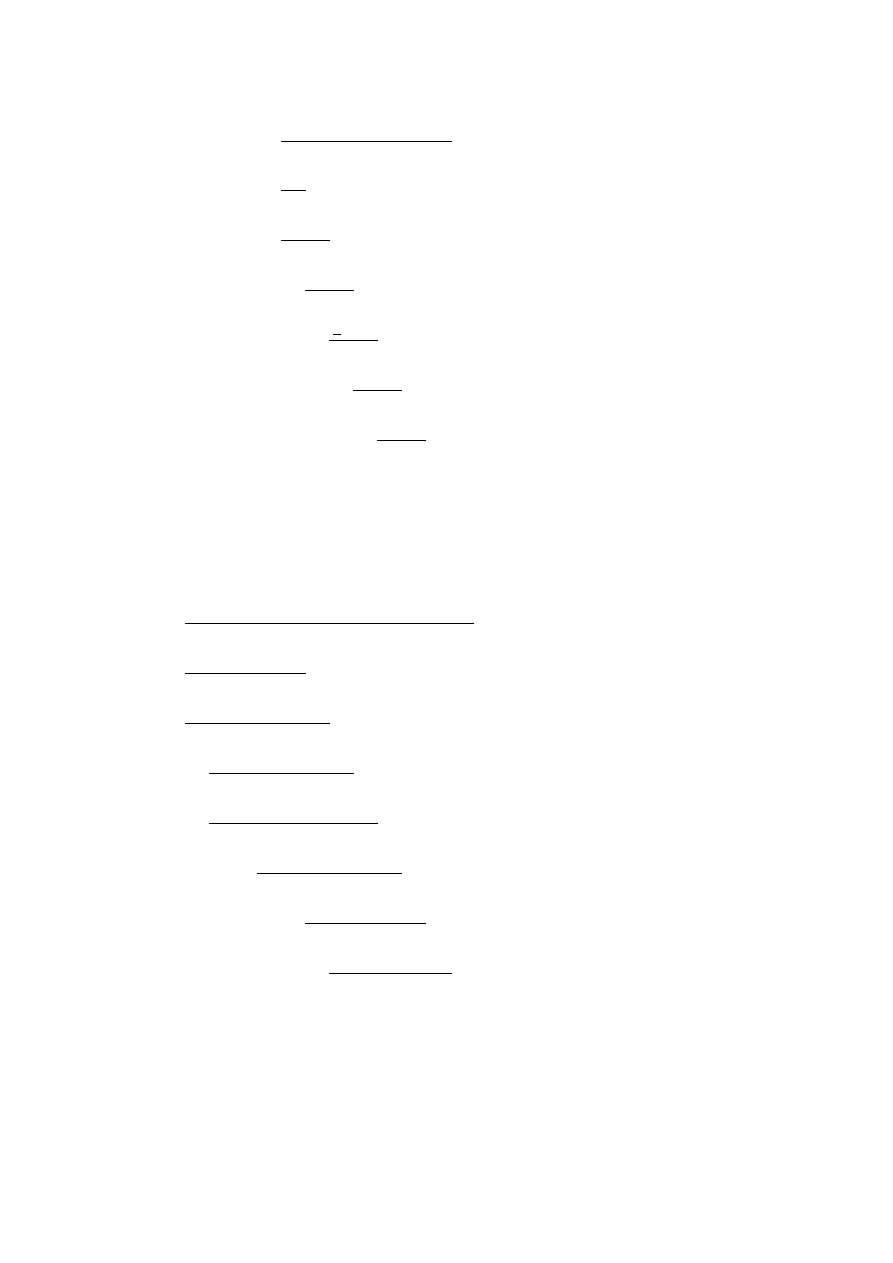
c) 101001
U2
: 11111
U2
= 010110
U2
d) 101001
U2
: 10011
U2
= 01,11000
U2
Krzysztof Adamski :: http://mr-k.namyslow.eu.org
8
0 1 0 1 1 0
1 0 1 0 0 1 :
1
-
1
0 0
+
1
1 1
-
1
0 0 0
+
1 1
1 0
-
1
1 1
-
1
0 0 0
0 1 0 1 1 1
0 1 1 0
1
0 1, 1 1 0 0
0
1 0 1 0 0 1 :
1 0 0 1
1
-
1 0 0 1 1
0 0 0 0 1 1
+
1 0 0 1 1
1 0 1 1 0 0
-
1 0 0 1 1
1 1 0 0 1 0
-
1 0 0 1 1
1 1 1 1 1 0
-
1 0 0 1 1
0 1 0 1 1 0
+
1 0 0 1 1
0 1 0 0 1 0
+
1 0 0 1 1
0 0 1 0 1
0
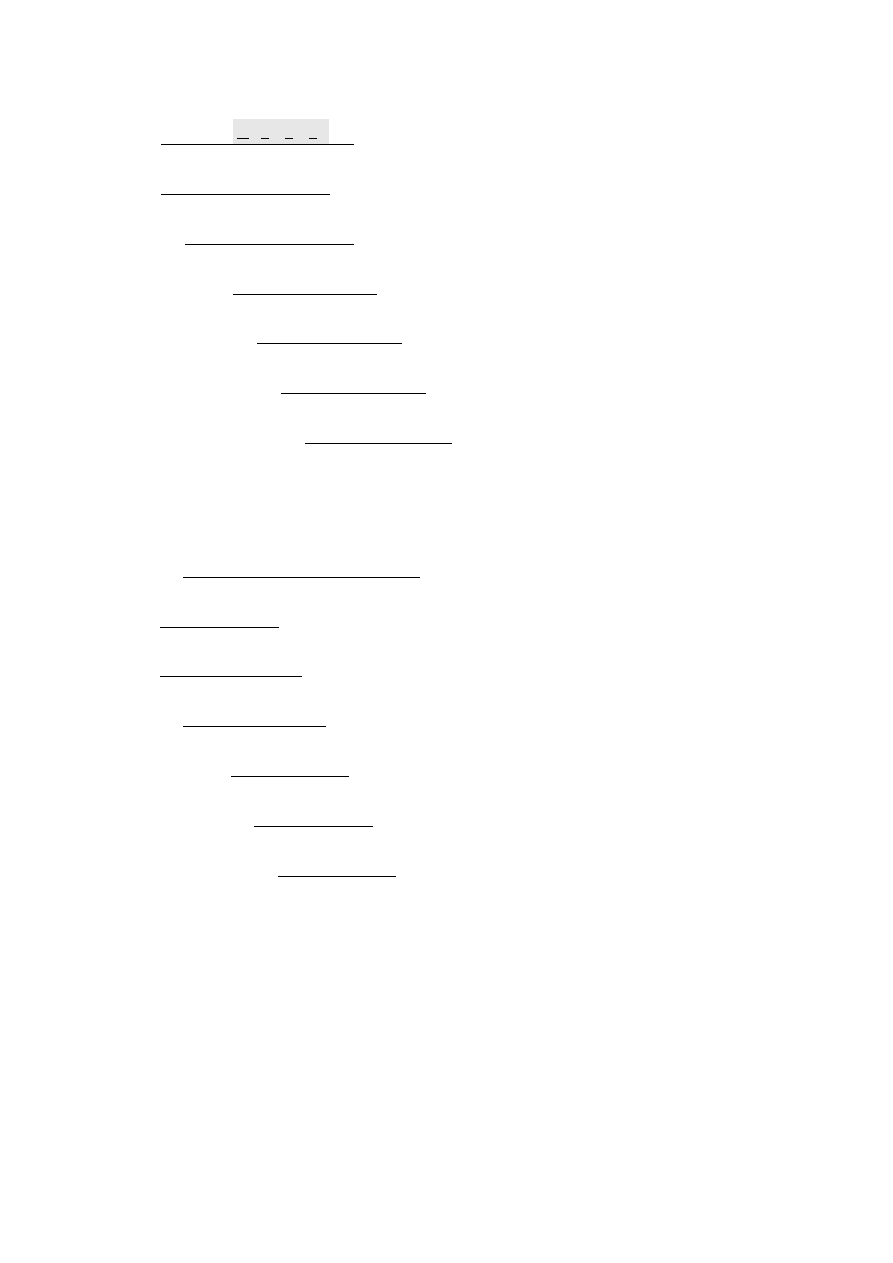
e)
1,10101
U2
: 01101,1
U2
= 1,111100101
U2
f) 0,11101
U2
: 110,111
U2
= 1,00110
U2
Krzysztof Adamski :: http://mr-k.namyslow.eu.org
9
0 0 1 0 1 1
1, 1 1 1 1 0 0
1 0
1
1, 1 0 1 0 1 :
0 1 1
0 1, 1
+
0 1 1 0 1, 1
0 0 0 1 0 1 0
-
0 1 1 0 1 1
1 0 1 1 1 1 0
+ 0 1 1 0 1 1
1 1 1 0 0 1 0
+
0 1 1 0 1 1
0 0 1 1 0 1
0
-
0 1 1 0 1
1
1 1 1 1 1
1 0
+
0 1 1 0
1 1
0 1 1 0
0 1
0
0 0 1 0 0 1
1, 0 0 1 1 0
0, 1 1 1 0 1 :
1 1 0, 1 1 1
+
1 0, 1 1 1
1 1 1 1 0 0
-
1 1 0 1 1 1
0 0 0 1 0 1 1
+
1 0, 1 1 1
0 0 0 1 0 0
+
1 0 1 1 1
1 1 0 1 1 0
-
1 0 1 1 1
1 1 1 1 1 0
-
1 0 1 1 1
0 0 1 1 1 0
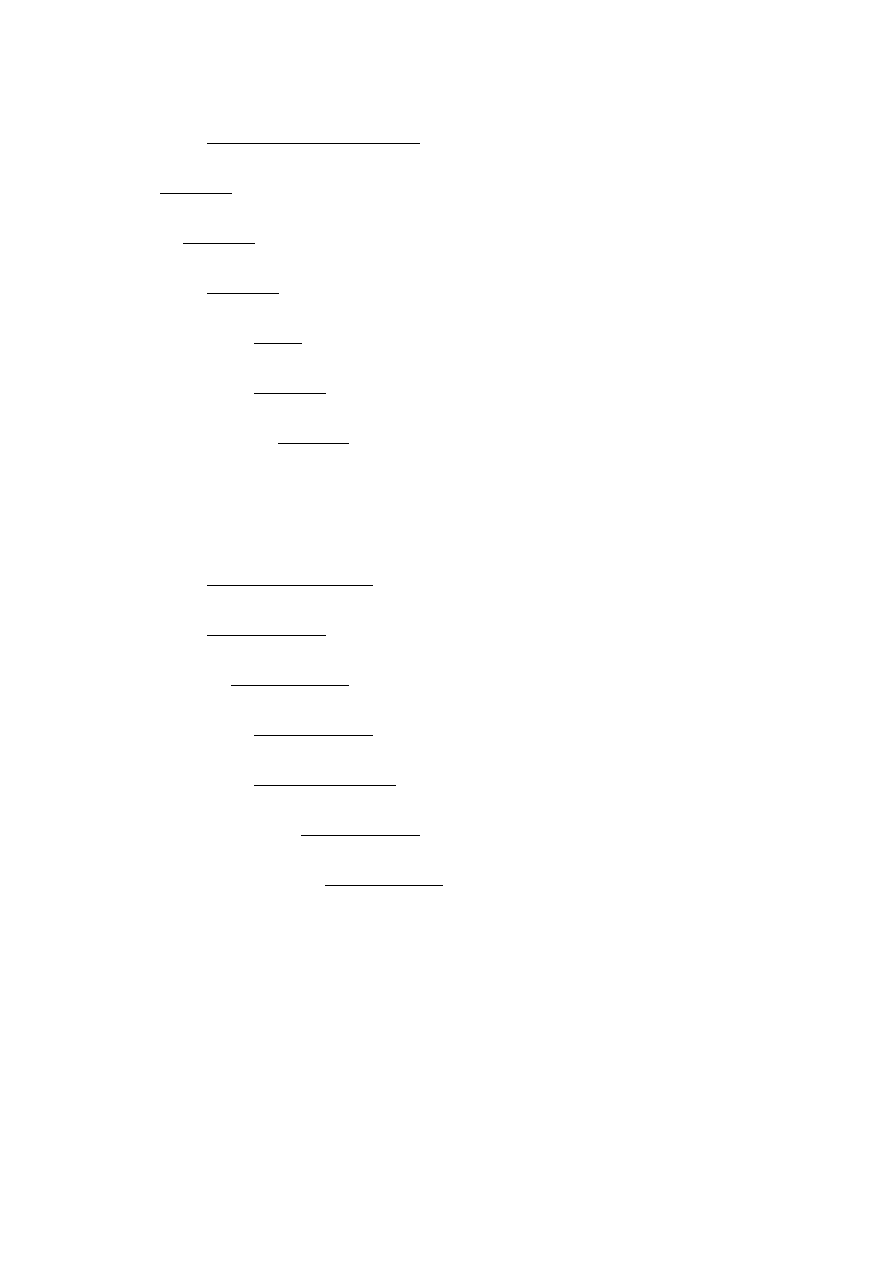
g) 1010,01
U2
: 111,11
U2
= 010110
U2
h) 101001
U2
:100,11
U2
= 0111,00
U2
Krzysztof Adamski :: http://mr-k.namyslow.eu.org
10
0 1 0 1 1 1
0 0 0 0 1
0 1 0 1 1 0
1 0 1 0, 0 1 :
1 1 1, 1 1
-
1, 1 1
0 0 0 0
+
1 1 1
1 1 1 1
-
1 1 1
0 0 0 0
+
1 1
1 1 0
-
1 1 1
1 1 1 1
-
1 1 1
0 0 0
0 1 0 1 1 1
0 1 1 0 1
0 1 1 1, 0 0
1 0 1 0 0 1 :
1 0 0, 1 1
-
1 0 0, 1 1
0 0 0 0 1 1
+
1 0 0 1 1
1 0 1 1 0 0
-
1 0 0 1 1
1 1 0 0 1 0
-
1 0 0 1 1
1 1 1 1 1 1 0
-
1 0 0 1 1
0 1 0 1 1 0
+
1 0 0 1 1
0 1 0 0 1 0
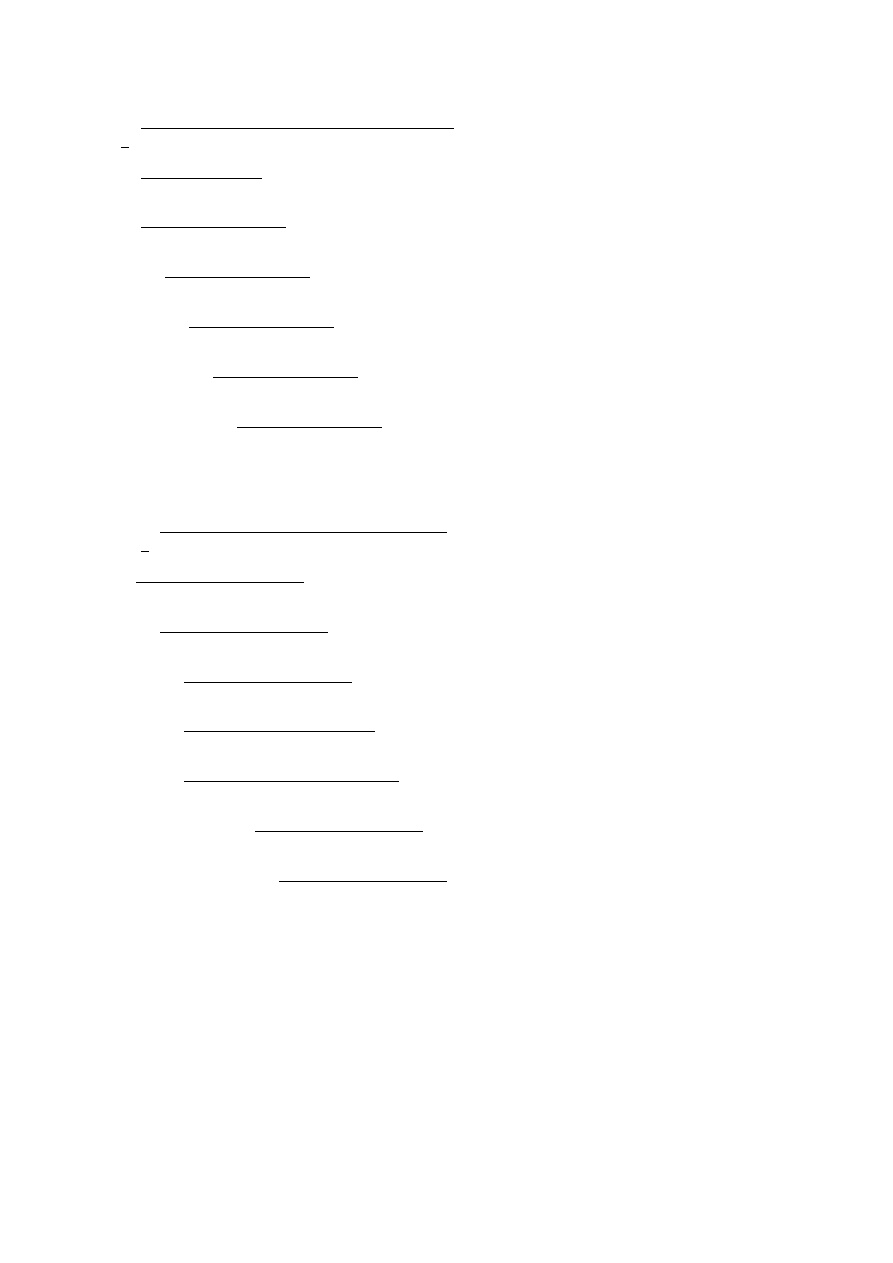
ZADANIE 5 (wykonywanie sprawdzeń sobie darowałem, czasem liczyłem więcej bitów niż potrzeba..)
a) 110101
2
: 011011
2
= 1,1111
2
b) 011101
2
: 110111
2
= 0,10001
2
Krzysztof Adamski :: http://mr-k.namyslow.eu.org
11
0 1, 1 1 1 1
0 1 1 0 1 0 1 :
0 1 1 0 1
1
-
0 1 1 0 1 1
1 1 1 1 1 1
+ 0 1 1 0 1 1
0 1 1 0 1 0 0
-
0 1 1 0 1 1
0 1 1 0 0 1 0
-
0 1 1 0 1 1
0 1 0 1 1 1 1
-
0 1 1 0 1 1
0 1 0 1 0 0 0
-
0 1 1 0 1 1
0 1 1 0 1 0
0, 1 0 0 0 0 1
0 0 1 1 1 0 1 :
0 1 1 0 1 1 1
-
0 1 1 0 1 1 1
1 1 0 0 1 1 0 0
+
0 1 1 0 1 1 1
0 0 0 0 0 1 1 0
-
0 1 1 0 1 1 1
1 0 0 1 1 1 1 0
+
0 1 1 0 1 1 1
1 1 0 1 0 1 0 1 0
+ 0 0 0 1 1 0 1 1 1
1 1 1 1 0 0 0 0 1 0
+
0 1 1 0 1 1 1
1 1 1 1 0 0 1 0
+
0 1 1 0 1 1 1
0 1 0 1 0 0 1 0
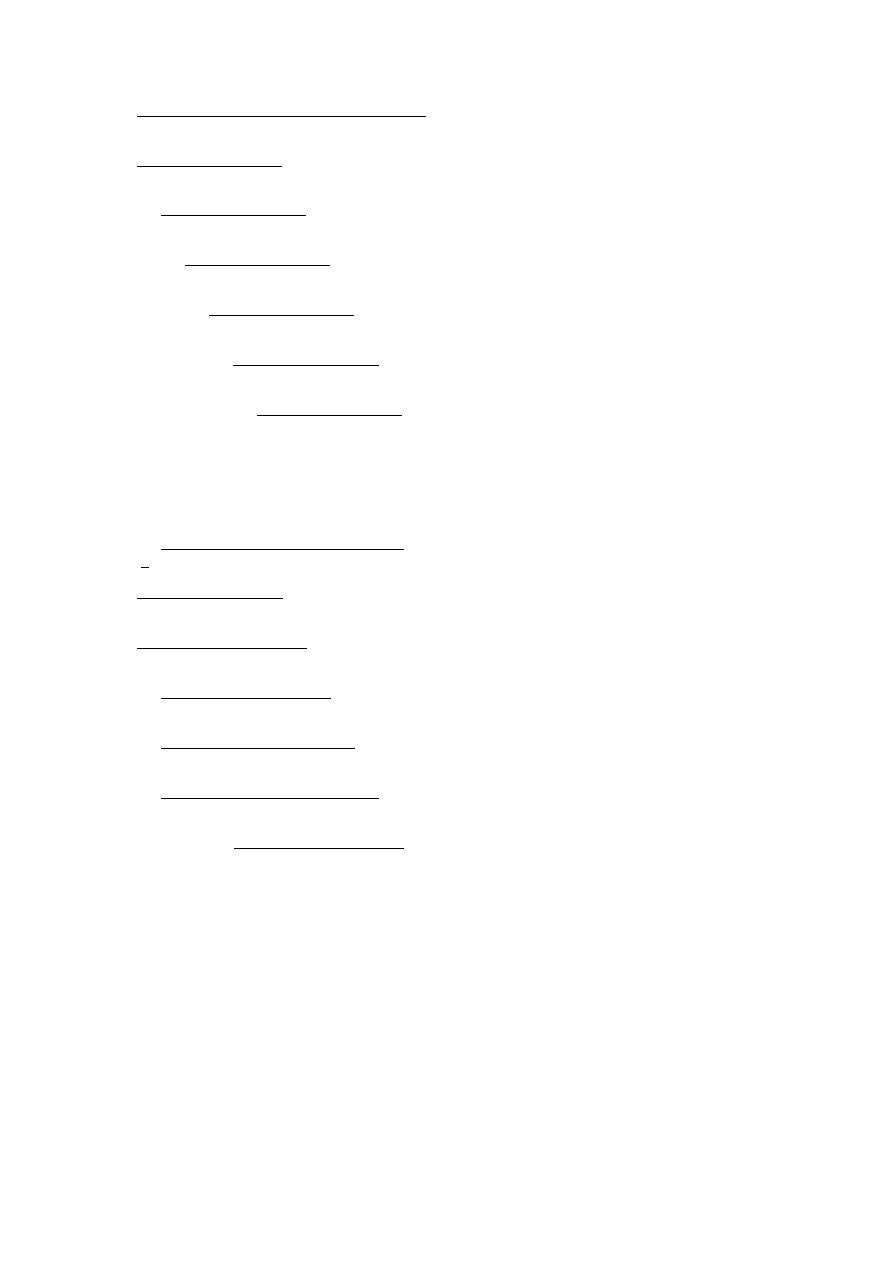
c) 101001
2
: 11111
2
= 01,0101
2
d) 101001
2
: 10011
2
= 010,001
2
Krzysztof Adamski :: http://mr-k.namyslow.eu.org
12
0 1, 0 1
0 1
0 1 0 1 0 0 1 :
0 1
1 1 1
1
-
0 1 1 1 1 1
1 1 0 1 0 1 1
+
0 1 1 1 1 1
0 0 1 0 1 0 0
-
0 1 1 1 1 1
1 1 0 1 0 1 0
+
0 1 1 1 1 1
0 0 1 0 0 1 0
-
0 1 1 1 1 1
1 1 0 0 1 1
0
+
0 1 1 1 1
1
0 0 0 1 0
1 0
0
1
0, 0
0
1
0
0
1
0
1
0
0
1
:
0
1
0
0
1
1
-
0
1
0
0
1
1
1
1
0
1
1
1
0
+
0
1
0
0
1
1
0
0
0
0
0
1
1
-
0
0
1
0
0
1
1
1
1
1
0
0
0
0
0
+
0
1
0
0
1
1
1
1
1
1
0
0
1
1
0
+
0
1
0
0
1
1
1
1
1
0
0
1
0
+
0
1
0
0
1
1
0
0
1
0
1
0
1
0

e)
1,10101
2
: 01101,1
2
=0,0001111
2
f) 0,11101
2
: 110,111
2
= 0,001
2
Krzysztof Adamski :: http://mr-k.namyslow.eu.org
13
0, 0 0 0 1 1 1 1
0 1, 1 0 1 0 1 :
0 1 1
0 1, 1
-
0 1 1 0 1, 1
1 1 1 1 1 1 1
+
0 1 1 0 1 1
0 1 1 0 1 0 0
-
0 1 1 0 1 1
0 1 1 0 0 1 0
-
0 1 1 0 1 1
0 1 0 1 1 1 0
-
0 1 1 0 1 1
0 1 0 0 1 1 0
0, 0 0 1 0 0 0 0
0 0, 1 1 1 0 1 :
0 1 1 0, 1 1 1
-
0 1 1 0, 1 1 1
1 0 0 1 1 0 0
+ 0 1 1 0 1 1 1
0 0 0 0 0 1 1 0
-
0 1 1 0 1 1 1
1 0 0 1 1 1 1 0
+
0 1 1 0 1 1 1
1 0 1 0 1 0 1 0
+
0 1 1 0 1 1 1
1 1 0 0 0 0 1 0
+
0 1 1 0 1 1 1
1 1 1 0 0 1 0

g) 1010,01
2
: 111,11
2
= 1,0101
2
h) 101001
2
:100,11
2
= 1000,1
2
Krzysztof Adamski :: http://mr-k.namyslow.eu.org
14
0 1, 0 1 0 1
0 1 0 1 0, 0 1 :
0 1 1 1, 1 1
-
0 1 1 1, 1 1
1 0 1 0 1 1
+
0 1 1 1 1 1
0 1 0 1 0 0
-
0 1 1 1 1 1
1 0 1 0 1 0
+ 0 1 1 1 1 1
0 1 0 0 1 0
-
0 1 1 1 1 1
1 0 0 1 1 0
+ 0 1 1 1 1 1
0 0 1 0 1 0
0 1 0 0 0, 1
0 0 1 0 1 0 0 1 :
0 1 0 0, 1 1
-
0 1 0 0, 1 1
1 0 1 1 1 0
+ 0 1 0 0 1 1
0 0 0 0 1 1
-
1 0 0 1 1
1 0 0 0 0 0
+ 0 1 0 0 1 1
1 0 0 1 1 0
+
1 0 0 1 1
1 1 0 0 1 0
+ 0 1 0 0 1 1
0 1 0 1 0
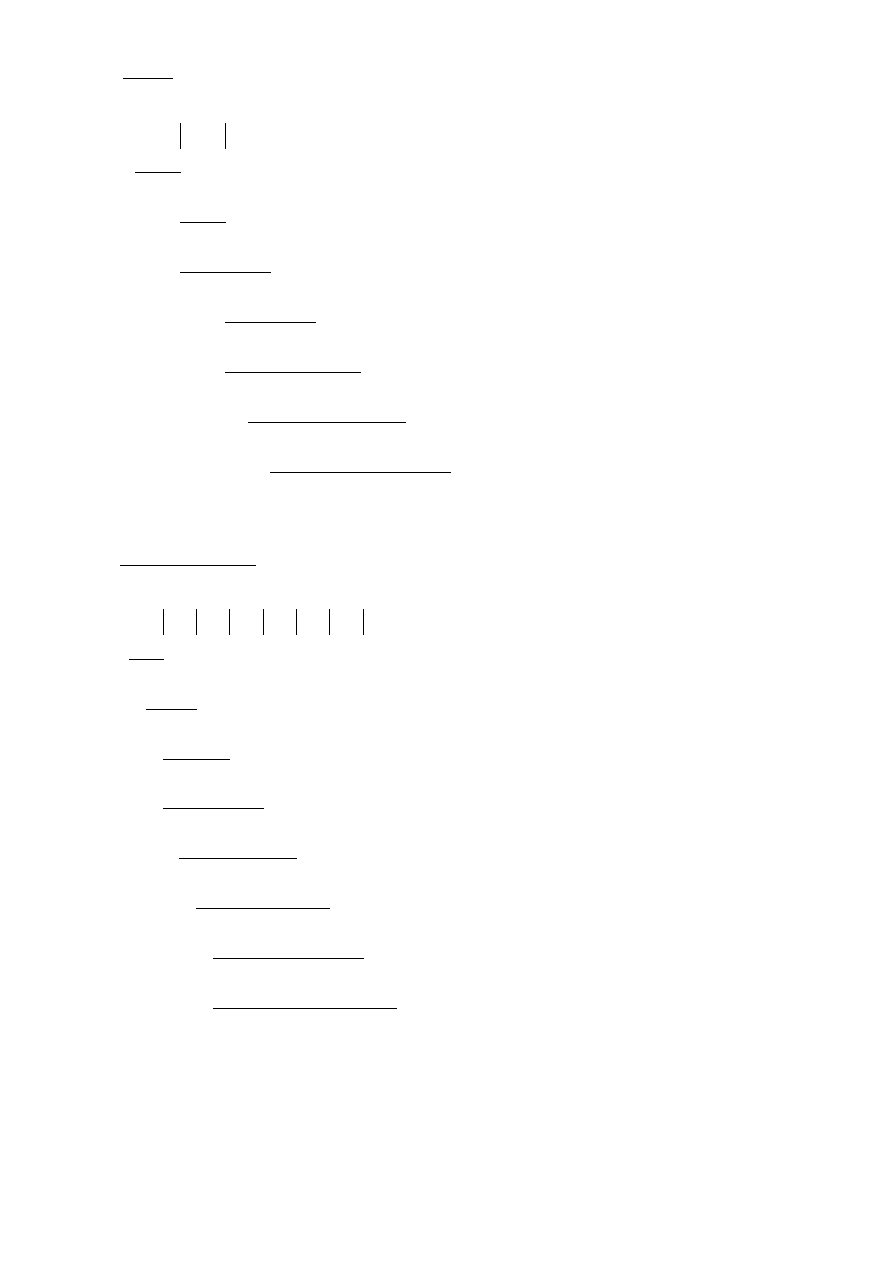
ZADANIE 6 (trzecią i czwartą resztę odczytajcie sami)
a)
123456
7
= 304,1466
7
b)
1010 0010 0111 1100
2
= 11001011
2
Krzysztof Adamski :: http://mr-k.namyslow.eu.org
15
1 2 3 4 5 6
7
= 3 0 4, 1 4 6 6
-
1 2
3×3=12
0 0 3 4
-
0 0
60×0=0
3 4 5 6
-
3 3 2 2
604×4=3322
1 3 4 0 0
-
6 1 1 1
6111×1=6111
4 2 5 6 0 0
-
3 3 4 5 3 2
61124×4=334532
6 1 0 3 5 0 0
-
5 2 0 1 5 4 1
611316×6=5201541
6 0 1 4 2 6 0 0
-
5 2 0 1 6 2 3 1
6113256×6=5123336
5 1 2 3 3 3 6
1 0 1 0 0 0 1 0 0 1 1 1 1 1 0 0 = 1 1 0 0 1 0 1 1
- 0 1
1×1=1
1 1 0
- 1 0 1
101×1=101
1 0 0
-
0
1100×0=0
1 0 0 1 0
-
0
11000×0=0
1 0 0 1 0 0 1
-
1 1 0 0 0 1
110001×1=110001
0 1 1 0 0 0 1 1
-
0
1100100×0=0
0 1 1 0 0 0 1 1 1 1
-
1 1 0 0 1 0 0 1
11001001×1=11001001
0 1 1 0 0 0 1 1 0 0 0
-
1 1 0 0 1 0 1 0 1
110010101×1=110010101
1 1 0 0 0 0 0 1 1
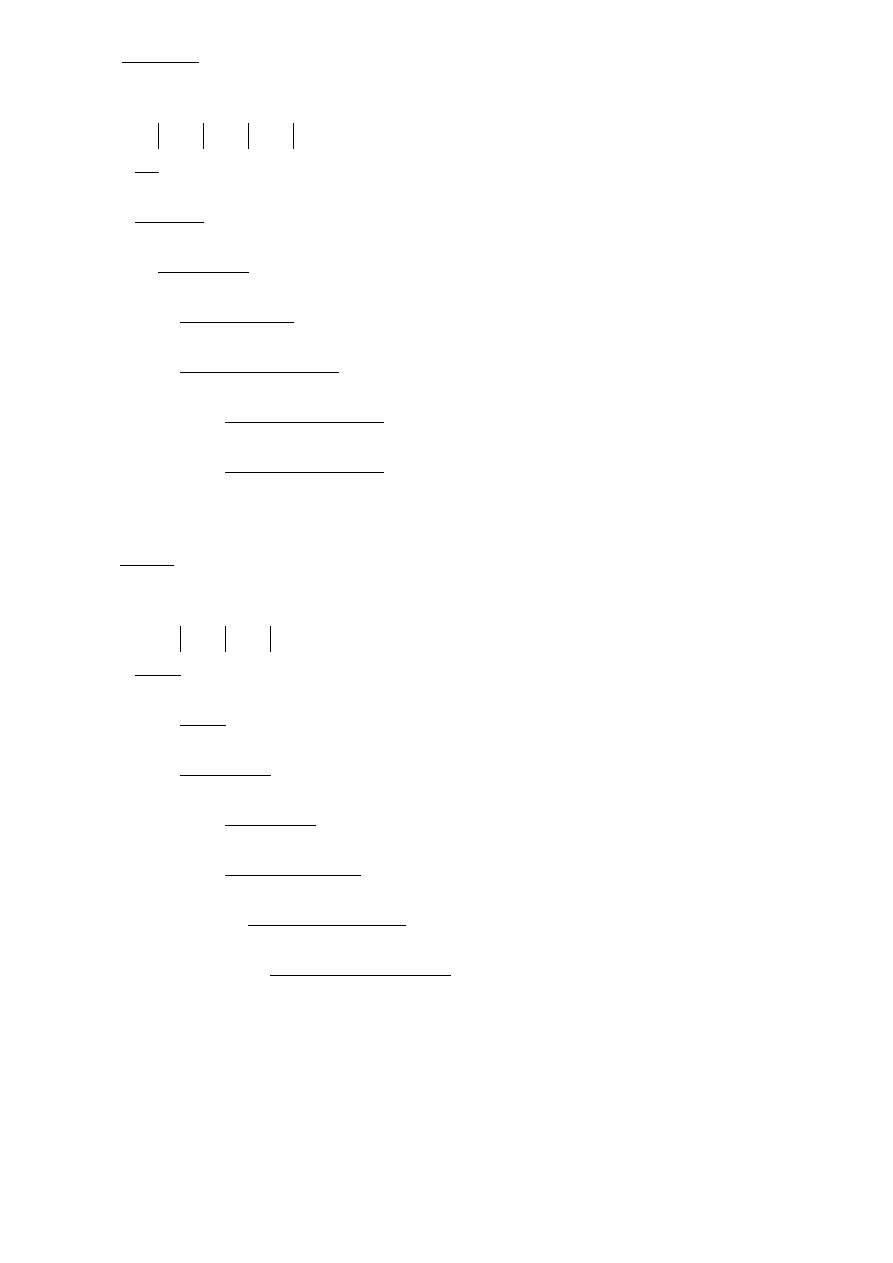
c)
987654321
10
= 31426,96
10
d)
123,456
7
= 11,11117
Krzysztof Adamski :: http://mr-k.namyslow.eu.org
16
9 8 7 6 5 4 3 2 1 = 3 1 4 2 6, 9 6
-
9
3×3=9
0 8 7
-
6 1
61×1=61
2 6 6 5
-
2 4 9 6
624×4=2496
1 6 9 4 3
-
1 2 5 6 4
6282×2=12564
4 3 7 9 2 1
-
3 7 7 0 7 6
62846×6=377076
6 0 8 4 5 0 0
-
5 6 5 6 7 6 1
628529×9=5656761
4 2 7 7 3 9 0 0
-
3 7 7 1 2 3 1 6
6285386×6=37712316
5 0 6 1 5 8 4 0 0
1 2 3, 4 5 6 0 = 1 1, 1 1 1 1 4
-
1
1×1=1
0 0 2 3
-
2 1
21×1=21
2 4 5
-
2 2 1
221×1=221
2 4 6 0
-
2 2 2 1
2221×1=2221
2 3 6 0 0
-
2 2 2 2 1
22221×1=22221
1 3 4 6 0 0
-
0
222220×0=0
1 3 4 5 0 0 0 0
1 2 2 2 2 2 3 2
2222224×4=1222232
-
1 2 2 4 4 3 5

e)
10100 0100,1111 100
2
= 10010,00
2
ZADANIE 7
a) Q
3
=123
7
r
3
=3456
7
246X×X ≤ 3456
7
=> X=1
2461
7
×1
7
=2461
7
Q
4
=1231
7
r
4
=(3456
7
-2462
7
)×100
7
+ YY
7
= 664YY
7
2462X×X ≤ 662YY
7
=> X=2
24622
7
×2
7
=52544
7
Dwie kolejne cyfry to
1 i
2 .
b) Q
3
=123
10
r
3
=3456
10
246X×X ≤ 3456
10
=> X=1
2461
10
×1
10
=2461
10
Q
4
=1231
10
r
3
=(3456
10
-2461
10
)×100
10
+ YY
10
=995YY
10
2462X×X ≤ 992YY
10
=> X=4
24624
10
×4
10
=98496
10
Dwie kolejne cyfry to
2 i
8 .
c) Q
3
=101
2
r
3
=11101
2
1010X×X ≤ 11101
2
=> X=1 10101
2
×1
2
=10101
2
Q
3
=1011
2
r
4
=(11101
2
-10101
2
) ×100
2
+YY
2
= 1000YY
2
10110X×X ≤ 1000YY
2
=> X=0
Dwie kolejne cyfry to
1 i
0 .
ZADANIE 8
(nie wiem czemu prof. Biernat napisał w podpowiedzi, że możliwych jest wiele rozwiązań. Moim sposobem wychodzi
dokładnie jedno i wydaje mi się, że inne być nie może)
a) Q
4
= 12,34
7
r
4
=0
r
3
=2464×4=13552
7
52
7
r
2
=243×3+135=1230
7
30 52
7
r
1
=22×2+12=56
7
56,30 52
7
r
0
=1×1+0=1
1 56,30 52
7
Wartością liczby pierwiastkowanej jest
156,3052
7.
b) Q
4
= 1,234
10
r
4
=0
r
3
=2464×4=9856
10
56
10
r
2
=243×3+98=827
10
27 56
10
r
1
=22×2+8=52
10
52 27 56
10
r
0
= 1×1+0=1
1,52 27 56
10
Wartością liczby pierwiastkowanej jest
1,522756
10.
Krzysztof Adamski :: http://mr-k.namyslow.eu.org
17
1 0 1 0 0 0 1 0 0, 1 1 1 1 1 0 0 = 1 0 0 1 0, 0 0
- 1
1×1=1
0 0 1
-
0
100×0=0
1 0 0
-
0
1000×0=0
1 0 0 0 1
- 1 0 0 0 1
10001×1=10001
0 0 0
-
0
100100×0=0
0 1 1
-
0
1001000×0=0
1 1 1 1
-
0
10010000×0=0
1 1 1 1

c) Q
4
=1101
2
r
4
=0
r
3
=11001×1=11001
2
01
2
r
2
=1100×0 + 110=110
2
10 01
2
r
1
=101×1 + 1 = 110
2
10 10 01
2
r
0
= 1×1+1=10
2
10 10 10 01
2
Wartością liczby pierwiastkowanej jest
10101001
2.
ZADANIE 9
Nie było mowy na temat pierwiastkowania metodą restrykcyjną na wykładzie i ćwiczeniach więc zakładam, że na
kolokwium tego nie będzie.
Krzysztof Adamski :: http://mr-k.namyslow.eu.org
18
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron