Sławomir Kulesza

[e-mail]

Cyfrowe przetwarzanie sygnałów (6)

Wykład dla studentów I roku (N)SMU WMiI

Specjalność: Techniki multimedialne

1 (44)

Ogólna postać równania różnicowego

Ogólna postać liniowego równania różnicowego ze stałymi współczynnikami jest

następująca:

y [n]=−

∑

k=1

N

a

k

⋅

y [n−k ]

∑

k=0

M

b

k

⋅

x [n−k ]

Lub równoważnie:

∑

k=0

N

a

k

⋅

y [n−k ]=

∑

k =0

M

b

k

⋅

x [ n−k ] ;a

0

≡

1

gdzie: liczba N jest rzędem równania różnicowego lub też rzędem układu.

Odpowiedź układu rekursywnego w chwili n jest więc kombinacją liniową

wcześniejszych próbek odpowiedzi {y[n-1], y[n-2], ..., y[n-N]}, jak też bieżącej

i wcześniejszych próbek pobudzenia {x[n], x[n-1], ..., x[n-M]}.

2 (44)

Rozwiązanie równania różnicowego o stałych współczynnikach

Znając zależność wej-wyj układu LTI wyrażoną w postaci równania różnicowego

o stałych współczynnikach, naszym celem będzie rozwiązanie tego równania,

czyli wyrażenie odpowiedzi y[n] jako jawnej funkcji pobudzenia oraz warunków

początkowych (wyeliminowanie rekurencji):

y [n]= f



x [ n] , y [−1]



Zasadniczo istnieją dwie metody rozwiązania tego problemu:

–

metoda bezpośrednia – poszukiwanie rozwiązania w postaci sumy:

y [n]= y

a

[

n] y

b

[

n]

–

metoda pośrednia (z-transformaty).

3 (44)

Całkowite rozwiązanie równania różnicowego

Procedura rozwiązywania równań różnicowych jest zbliżona do tej, jaką stosuje

się do rozwiązywania równań różniczkowych o stałych współczynnikach.

Odpowiedź układu poszukuje się zatem w postaci sumy dwóch niezależnych

składników, które łącznie dają rozwiązanie całkowite:

y [n]= y

h

[

n] y

p

[

n]

Składowa y

h

[n] to rozwiązanie jednorodne (dla x[n] = 0), zaś składowa y

p

[n] jest

rozwiązaniem szczególnym (dla określonego, niezerowego pobudzenia).

4 (44)

Rozwiązanie jednorodne równania różnicowego

Rozwiązanie jednorodne równania różnicowego jest rozwiązaniem otrzymanym

przy braku pobudzenia:

∀

n∈Z

x [n]=0

Jednorodne równanie różnicowe ma więc postać:

∑

k=0

N

a

k

⋅

y [n−k ]=0

Postulujemy wykładniczą postać rozwiązania jednorodnego:

y

h

[

n]=

n

Skąd otrzymujemy, że:

∑

k=0

N

a

k

⋅

n−k

=

n−N





N



a

1

⋅

N −1



...a

N −1

⋅

a

N



=

0

5 (44)

Wielomian:



N



a

1

⋅

N −1



...a

N −1

⋅

a

N

nazywany jest wielomianem charakterystycznym układu. Posiada on

w ogólności N-pierwiastków zespolonych {λ

1

, λ

2

,... , λ

N

}.

Załóżmy chwilowo, że pierwiastki są rozdzielone (nie powtarzają się) – ogólna

postać rozwiązania jednorodnego równania różnicowego jest następująca:

y

h

[

n]=c

1

⋅

1

n



c

2

⋅

2

n



...c

N

⋅

N

n

gdzie współczynniki rozwinięcia c

1

...c

N

wyznacza się na podstawie warunków

początkowych. Ponieważ jednocześnie założyliśmy, że pobudzenie jest równe

zero, powyższe równanie jest równe odpowiedzi swobodnej układu y

zi

[n].

W przypadku pierwiastków wielokrotnych (np. m-krotnego λ

1

) mamy:

y

h

[

n]=



c

1

⋅

1

n



c

2

⋅

n⋅

1

n



...c

m

⋅

n

m−1



1

n





c

m1

⋅

m1

n



...c

N

⋅

N −m

n

6 (44)

Ex.: Wyznaczyć rozwiązanie jednorodne układu danego równaniem różnicowym:

y [n]a

1

⋅

y [n−1]=x [n]

Postulujemy rozwiązanie jednorodne (dla x[n] = 0) w postaci wykładniczej:

y

h

[

n]=

n

Podstawiając do wzoru wyjściowego otrzymamy:



n



a

1

⋅

n−1

=

n−1





a

1



=

0

Skąd otrzymujemy, że pierwiastkiem wielomianu charakterystycznego jest:



1

=−

a

1

Rozwiązanie jednorodne ma więc postać:

y

h

[

n]=c

1

⋅

1

n

=

c

1

−

a

1



n

7 (44)

Rozwiązanie szczególne równania różnicowego

Rozwiązanie szczególne równania różnicowego y

p

[n] jest rozwiązaniem

otrzymanym dla konkretnego pobudzenia x[n]:

∑

k=0

N

a

k

⋅

y

p

[

n−k ]=

∑

k =0

M

b

k

⋅

x [n−k ] ;a

0

≡

1

Procedura obliczania rozwiązania szczególnego wychodzi z założenia, że

przyjmuje ono taką samą postać jak pobudzenie, tzn. jeśli x[n] jest ciągiem stałym,

y

p

[n] również jest stały; jeśli x[n] jest sinusoidalny, y

p

[n] jest sinusoidalny itd.

Założenie to jest wynikiem liniowości omawianych układów.

8 (44)

Ex.: Wyznaczyć rozwiązanie szczególne równania różnicowego:

y [n]a

1

⋅

y [n−1]= x [n];∣a

1

∣

1

dla pobudzenia w postaci skoku jednostkowego:

x [n]=u[n]

Postulujemy rozwiązanie szczególne w postaci:

y

p

[

n]= A⋅u[n]

Po podstawieniu do równania wyjściowego otrzymujemy:

A⋅u [n]a

1

⋅

A⋅u[n−1]=u[n]

Skąd dla wszystkich n≥1 otrzymujemy:

A



1a

1



=

1

Rozwiązanie szczególne ma zatem postać:

y

p

[

n]=

1

1a

1

u[n]

9 (44)

Odpowiedź swobodna i wymuszona

Znając rozwiązanie jednorodne i ogólne równania różnicowego można wyznaczyć

odpowiedź swobodną i wymuszoną układu. Odpowiedź swobodna y

zi

[n] jest

obliczana przy braku pobudzenia, zaś odpowiedź wymuszona y

zs

[n] jest obliczona

dla określonego pobudzenia, przy wyzerowanych wszystkich warunkach

początkowych.

Całkowite rozwiązanie równania różnicowego ma wówczas postać:

y [n]= y

zi

[

n] y

zs

[

n]

10 (44)

Ex.: Wyznaczyć odpowiedź swobodną i wymuszoną układu:

y [n] y [n−1]−6y [n−2]=x [n]

dla pobudzenia skokowego i zadanych warunków początkowych:

x [n]=8 u[n] ; y [−1]=1 ; y [−2]=−1

Znajdźmy najpierw rozwiązanie jednorodne w postaci y

h

[n] = λ

n

:



n



n−1

−

6

n−2

=

n−2





2

−

6



=

n−2





3



−

2



=

0

Stąd rozwiązanie jednorodne wynosi:

y

h

[

n]=c

1



−

3



n



c

2



2



n

11 (44)

Obliczmy teraz rozwiązanie szczególne dla zadanego pobudzenia:

y

p

[

n]= A

Wówczas po podstawieniu do równania wyjściowego otrzymamy:

A A−6A=8 u[n]

Skąd, dla n≥0 mamy, że:

y

p

[

n]= A=−2

Rozwiązanie całkowite ma więc postać:

y [n]=c

1



−

3



n



c

2



2



n

−

2

12 (44)

Odpowiedź swobodną wyznaczymy z rozwiązania jednorodnego dobierając stałe

c

1

oraz c

2

na podstawie warunków początkowych:

y [0]=6y [−2]− y [−1]=−7
y [1]=6y [−1]− y [0]=13

y [0]=c

1



c

2

y [1]=−3 c

1



2 c

2

Po rozwiązaniu układu równań otrzymujemy, że:

c

1

=−

5.4 ; c

2

=−

1.6

Odpowiedź swobodna układu ma więc postać:

y

zi

[

n]=−5.4⋅−3

n

−

1.6⋅2

n

; n≥0

13 (44)

Odpowiedź wymuszoną obliczymy z rozwiązania całkowitego, dobierając stałe c

1

oraz c

2

tak, aby uzyskać wyzerowanie warunków początkowych. Podstawiając

zerowe warunki początkowe do równania wyjściowego otrzymamy, że:

y [0]=x [0]=8
y [1]= x [1]− y [0]=0

Zatem:

y [0]=c

1



c

2

−

2=8

y [1]=−3 c

1



2 c

2

−

2=0

Skąd otrzymujemy, że:

c

1

=

3.6 ; c

2

=

6.4

Stąd odpowiedź wymuszona przy zerowych warunkach początkowych wynosi:

y

zs

[

n]=3.6⋅−3

n



6.4⋅2

n

−

2 ; n≥0

14 (44)

Odpowiedź impulsowa rekursywnych układów LTI

Odpowiedź impulsowa h[n] układów LTI została zdefiniowana jako odpowiedź na

pobudzenie impulsowe. W przypadku rekursywnych układów LTI odpowiedź

wymuszona dana jest jako splot:

y

zs

[

n]=

∑

k =0

n

h[k ]⋅x [n−k ] ; n≥0

Co dla pobudzenia impulsowego redukuje się do:

y

zs

[

n]=

∑

k =0

n

h[k ]⋅[n−k ]=h[n]

Odpowiedź impulsowa h[n] jest więc tożsama odpowiedzi wymuszonej na

pobudzenie impulsem jednostkowym x[n] = δ[n].

15 (44)

Wyznaczanie odpowiedzi impulsowej

Z wcześniejszych rozważań wynika, iż całkowita odpowiedź rekursywnego układu

LTI opisywanego równaniem różnicowym składa się z dwóch części: rozwiązania

równania jednorodnego (przy zerowym pobudzeniu) oraz rozwiązania

szczególnego dla określonego pobudzenia.

W przypadku pobudzenia impulsowego x[n] = 0 dla wszystkich n > 0, a zatem

rozwiązanie szczegółowe również jest równe zero: y

p

[n] = 0. W takim przypadku

odpowiedź impulsowa może zostać wyznaczona na podstawie rozwiązania

jednorodnego, po dopasowaniu współczynników c

k

tak, aby spełniały one

wymaganie zerowych warunków początkowych.

16 (44)

Ex.: Wyznaczyć odpowiedź impulsową h[n] układu:

y [n] y [n−1]−6y [n−2]=x [n]

Rozwiązanie jednorodne ma postać:

y

h

[

n]=c

1



−

3



n



c

2



2



n

; n≥0

Konieczność zerowania się warunków początkowych prowadzi do wniosku, że:

y [0]=c

1



c

2

=

1

y [1]=−3 c

1



2 c

2

=−

1

Skąd otrzymujemy, że:

c

1

=

0.6

c

2

=

0.4

Odpowiedź impulsowa ma więc postać:

h[n]=



0.6



−

3



n



0.4



2



n



u[ n]

17 (44)

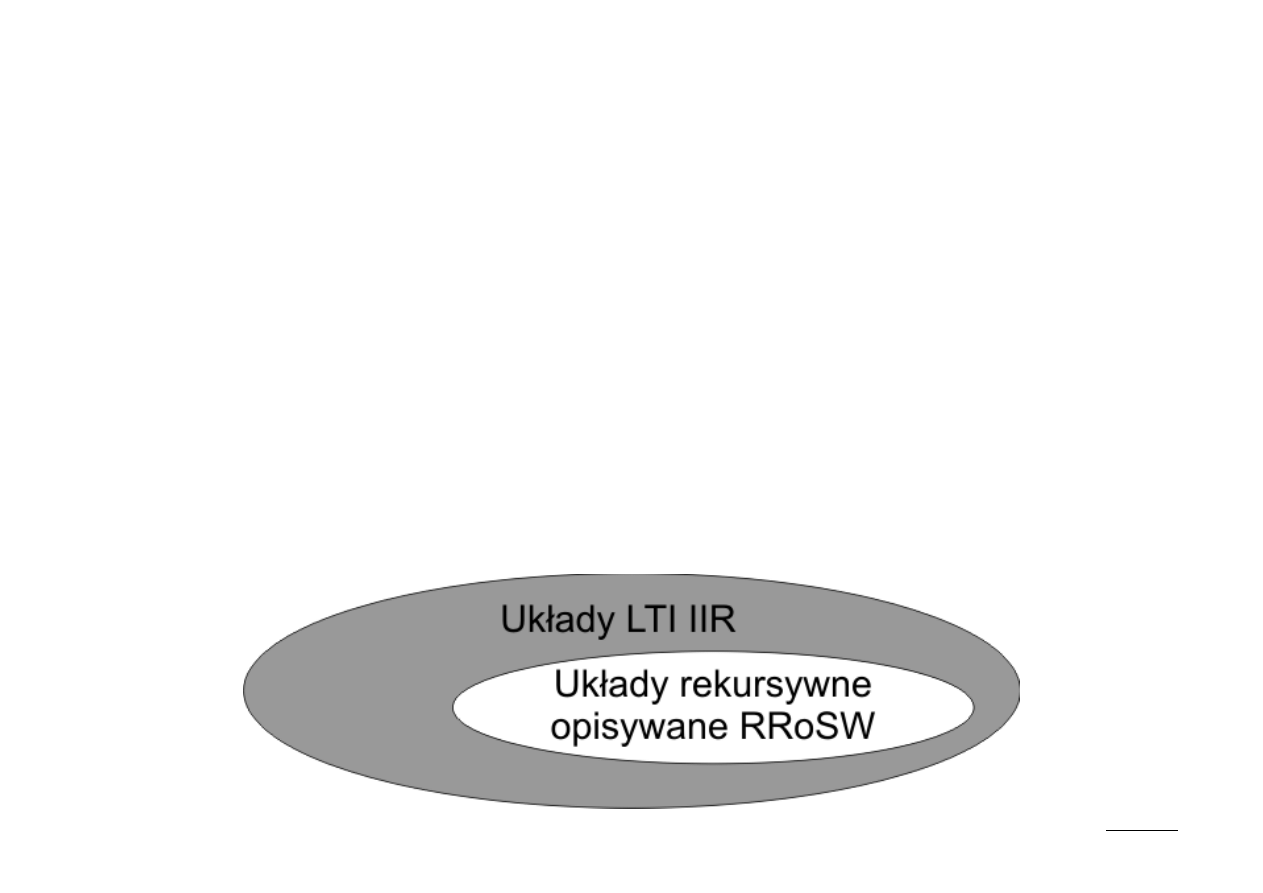
Długość odpowiedzi filtrów rekursywnych

Z dotychczasowej analizy wypływa wniosek, iż odpowiedzi impulsowe układów

rekursywnych są z natury nieskończone, a więc są to układy IIR. Istotnie,

rekursywny charakter równań różnicowych o stałych współczynnikach powoduje,

że opisywane przez nie układy są układami IIR.

Nie jest prawdziwe twierdzenie odwrotne: nie każdy układ LTI IIR daje się opisać

równaniami różnicowymi o stałych współczynnikach (sprawdź np. h[n] = n

-2

·u[n]),

co oznacza, że układy rekursywne opisywane równaniami różnicowymi o stałych

współczynnikach są zaledwie podzbiorem wszystkich układów LTI IIR.

18 (44)

Stabilność filtrów rekursywnych

Jeśli układ jest opisywany liniowym równaniem różnicowym N-tego rzędu,

wówczas rozwiązanie równania jednorodnego ma postać:

y

h

[

n]=

∑

k =1

N

c

k



k

n

gdzie milcząco założyliśmy, że wszystkie pierwiastki wielomianu

charakterystycznego są rozdzielone.

Odpowiedź impulsowa takiego układu ma identyczną formę:

h[n]=

∑

k=1

N

c

k



k

n

gdzie współczynniki {c

k

} dobierane są dla spełnienia warunków początkowych:

y [−N ]= y [−N 1]=...= y [−1]=0

19 (44)

Otrzymana postać odpowiedzi impulsowej pozwala w prosty sposób powiązać

stabilność układu opisywanego równaniem różnicowym N-tego rzędu

z wartościami pierwiastków wielomianu charakterystycznego.

Warunek stabilności w sensie BIBO wymaga bezwzględnej sumowalności

odpowiedzi impulsowej, co w przypadku układów rekursywnych oznacza, że:

∑

n=0

∞

∣

∑

k =1

N

c

k



k

n

∣

≤

∑

k=1

N

∣

c

k

∣

∑

n=0

∞

∣

k

∣

n

Warunkiem koniecznym i wystarczającym do tego, aby przyczynowy układ IIR

opisywany RRoSW był stabilny, jest:

∀

k ∈[1, N ]

∣

k

∣

1

20 (44)

W przypadku pierwiastków wielokrotnych zachodzi (L-krotny pierwiastek λ

1

):

1

h[n]=



c

¿

nc

2

n

1

n



...c

L

n

L−1



1

n





c

L1



2

n



...c

N



N − L1

n

=



∑

k=1

L

c

k

⋅

n

k −1

⋅

1

n



∑

j=1

N −L

c

L j

⋅

j1

n



Co daje następujący warunek stabilności BIBO:

∑

n=0

∞



∣

∑

k =1

L

c

k

⋅

n

k −1

⋅

1

n



∑

j=1

N −L

c

L j

⋅

j1

n

∣



≤

≤

∑

n=0

∞



∑

k =1

L

∣

c

k

∣⋅∣

n∣

k −1

⋅∣

1

∣

n



∑

j=1

N − L

∣

c

L j

∣⋅∣

j1

∣

n



Przy silniejszej zbieżności ciągu wykładniczego niż potęgowego, warunek

stabilności jest identyczny jak w przypadku pierwiastków rozdzielonych.

21 (44)

Ex.: Sprawdzić stabilność filtru rekursywnego opisanego równaniem:

y [n]−3y [n−1]−4y [n−2]=x [n]2x[n−1]

Wielomian charakterystyczny ma postać:



n−2





2

−

3−4



=

n−2





1



−

4



=

0

Rozwiązanie jednorodne ma więc postać:

y

h

[

n]=



c

1

−

1

n



c

2



4

n



⋅

u[ n]

Wyznaczmy wartości c

1

oraz c

2

, przy zerowych warunkach początkowych:

y [0]=c

1



c

2

=

1

y [1]=−c

1



4 c

2

=

5

Skąd mamy, że odpowiedź impulsowa ma postać:

h[n]=



−

1
5

−

1

n



6
5



4

n



⋅

u[n]

Układ jest niestabilny w sensie BIBO, bowiem |-1| ≥ 1 oraz |4| ≥ 1.

22 (44)

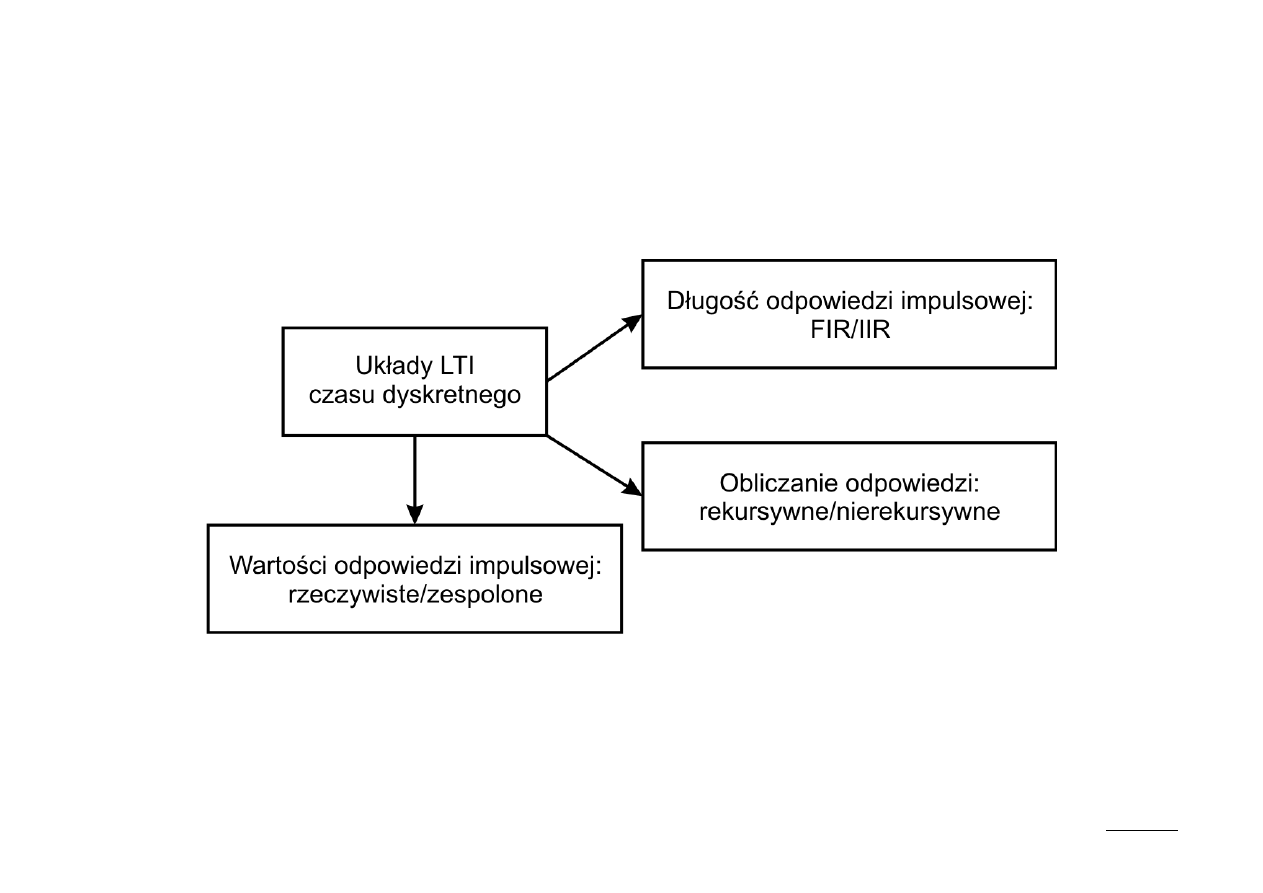
Klasyfikacja układów LTI czasu dyskretnego

23 (44)

Korelacja sygnałów czasu dyskretnego

Miarą podobieństwa pary sygnałów o skończonej energii x[n], y[n] jest sygnał

korelacji wzajemnej (cross-correlation) r

xy

[n] zdefiniowany jako:

r

xy

[

n]=

∑

k=−∞

∞

x [k ]⋅y [k −n]; n∈ℤ

Parametr n (tzw. lag) opisuje przesunięcie czasowe pomiędzy sygnałami. Sygnał

y[n] jest przesunięty względem sygnału odniesienia x[n] o n-próbek w prawo

dla dodatnich n i n-próbek w lewo dla ujemnych n.

Podobieństwo do splotu jest złudne, bowiem korelacja jest operacją całkowicie

odmienną. Splot pozwala wyliczyć odpowiedź układu o znanej charakterystyce

przy znanym pobudzeniu, natomiast korelacja wzajemna pozwala odnaleźć

podobieństwo sygnału analizowanego y[n] do zdefiniowanego wzorca x[n].

24 (44)

Przemienność korelacji wzajemnej

Jeśli zamienimy rolami sygnał analizowany i wzorcowy, wówczas korelacja

wzajemna przyjmie postać:

r

yx

[

n]=

∑

k =−∞

∞

y [k ]⋅x [k −n]=

∑

j=−∞

∞

y [ jn]⋅x [ j]=

∑

k =−∞

∞

x [ k ]⋅y [k n]

Skąd otrzymujemy, że:

r

yx

[

n]=r

xy

[−

n]

Wynikiem zamiany kolejności sygnałów w korelacji wzajemnej jest więc ciąg, który

jest ciągiem zawiniętym w stosunku do korelacji wyjściowej. Z tego względu r

xy

[n]

zawiera identyczną informację co r

yx

[n] na temat podobieństwa sygnałów x[n] oraz

y[n], dając swobodę interpretacji tego, co jest wzorcem, a co sygnałem

porównywanym.

25 (44)

Ex.: Wyznaczyć korelację wzajemną oraz splot ciągów:

x [n]=[... 0,0 ,2 ,−1,3,7 , 1,2 ,−3,0 ,0 ,...]

y [n]=[... 0,0,1 ,−1,2 ,−2, 4,1 ,−2,5,0 ,0 , ...]

Obliczmy najpierw próbkę r

xy

[0]:

r

xy

[

0]=

[

2 −1 3

7

1

2 −3 0

1 −1 2

−

2

4 1 −2 5

...

...

...

...

... ...

...

...

2

1

6 −14 4

2

6

0

]

r

xy

[

0]=

∑

k =−∞

∞

x [ k ]⋅y [k ]=216−14426=7

26 (44)

Obliczmy teraz próbkę r

xy

[-1]:

r

xy

[−

1]=

[

0

2

−

1

3

7



1

2

−

3

0

1 −1

2

−

2



4

1 −2

5

0

...

...

...

...

... ...

...

...

...

0 −2 −2 −6 28 1 −4 −15 0

]

r

xy

[−

1]=

∑

k=−∞

∞

x [k ]⋅y [k 1]=0

Obliczmy teraz próbkę r

xy

[+1]:

r

xy

[

1]=

[

2 −1

3

7



1

2 −3

0

0

0

1

−

1

2 −2 4

1

−

2 5

...

...

...

...

...

...

...

...

...

0 −1 −3 14 −2 8 −3

0

0

]

r

xy

[

1]=

∑

k =−∞

∞

x [ k ]⋅y [k −1]=13

27 (44)

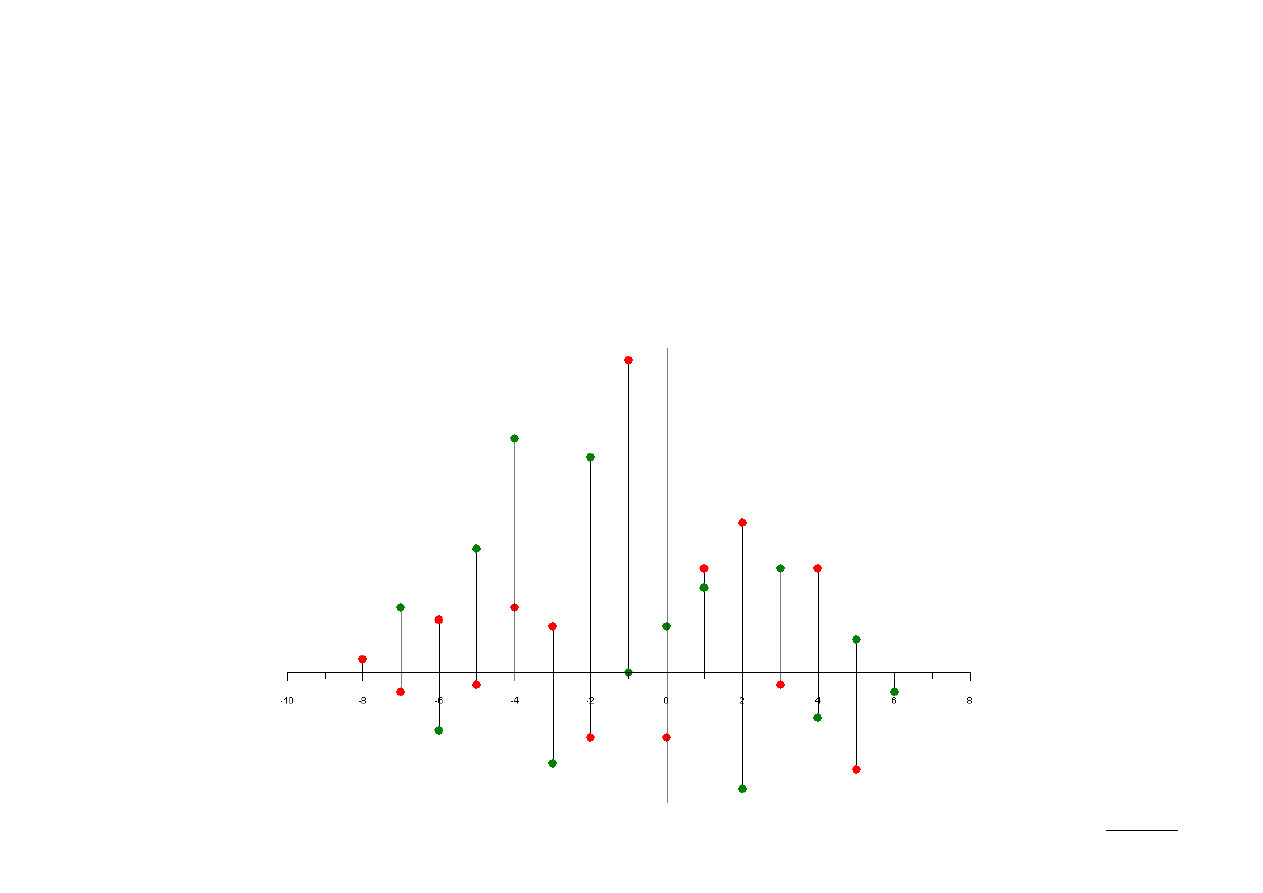
Korelacja wzajemna sygnałów x[n] i y[n] jest więc ciągiem:

r

xy

[

n]=[10,−9,19 ,36 ,−14,33,0 ,7 ,13,−18,16 ,−7,5 ,−3]

Splot tych samych sygnałów jest z kolei ciągiem:

x [n]∗y [n]=[2,−3,8 ,−2,10 ,7 ,−10,48 , 

−

10,16 ,23 ,−2,16 ,−15]

28 (44)

Obliczanie korelacji i splotu

Pomimo zasadniczej różnicy pomiędzy operacją obliczania splotu i korelacji

wzajemnej dwóch sygnałów, podobieństwo matematyczne pozwala

przeprowadzać te operacje w podobny sposób:

–

przy splocie jeden z ciągów jest zawijany, potem przesuwany, mnożony przez

drugi ciąg i wreszcie wszystkie próbki iloczynów są sumowane,

–

przy korelacji sekwencja działań jest identyczna, za wyjątkiem zawijania ciągu.

Można zatem korelację obliczyć przy pomocy procedury obliczającej splot,

wykorzystując fakt, że:

r

xy

[

n]=x [n]∗y [−n]

29 (44)

Korelacja własna

Oprócz korelacji wzajemnej, definiuje się także korelację własną sygnału x[n]

(autocorrelation):

r

xx

[

n]=

∑

k=−∞

∞

x [k ] x [ k −n]

Zauważmy przy tym, że:

r

xx

[

0]=

∑

k =−∞

∞

x

2

[

k ]=E

x

co jest równe energii sygnału x[n].

Korelacja własna ciągu rzeczywistego x[n] jest ponadto ciągiem parzystym:

r

xx

[

n]=

∑

k=−∞

∞

x [k ]⋅x [k −n]=

∑

j=−∞

∞

x [ j]⋅x [ jn]=r

xx

[−

n]

30 (44)

Korelacje ciągów skończonych

W przypadku ciągów o skończonej długości wyrażenia na korelację własną

i wzajemną ulegają znaczącemu zawężeniu jeśli chodzi o granice sumowania.

W szczególności, jeśli ciągi x[n] oraz y[n] są ciągami przyczynowymi o długości N,

wówczas wyrażenia na korelację własną i wzajemną przyjmują postać:

r

xy

[

n]=

∑

k=−N 1

N −1

x [k ]⋅y [ k−n]

r

xx

[

n]=

∑

k =−N 1

N −1

x [k ]⋅x [ k −n]

31 (44)

Własności korelacji własnej i wzajemnej

Niech dany jest ciąg będący kombinacją liniową dwóch ciągów x[n] oraz y[n]

o skończonej energii:

w [n]=a⋅x [n]b⋅y [ n−k ]

gdzie a oraz b są stałymi, zaś k jest przesunięciem pomiędzy ciągami.

Energia sygnału w[n] wynosi:

∑

j=−∞

∞



a⋅x [n]b⋅y [n−k ]



2

=

...

...=a

2

∑

j=−∞

∞

x

2

[

n]b

2

∑

j=−∞

∞

y

2

[

n−k ]2 ab

∑

−∞

∞

x [n]⋅y [n−k ]=...

...=a

2

r

xx

[

0]2 ab r

xy

[

k ]b

2

r

yy

[

0]≥0

32 (44)

Zakładając, że b≠0 otrzymujemy:

r

xx

[

0]



a
b



2



2 r

xy

[

k ]



a
b





r

yy

[

0]≥0

Otrzymaliśmy równanie kwadratowe, które może mieć co najwyżej jeden

pierwiastek. Wyznacznik tego równania musi być zatem niedodatni:

4



r

xy

2

[

k ]−r

xx

[

0]⋅r

yy

[

0]



≤

0

Skąd wynika zależność pomiędzy korelacją własną a wzajemną:

∣

r

xy

[

k ]∣≤



r

xx

[

0]⋅r

yy

[

0]

Powyższy wynik narzuca górne ograniczenie na wartość korelacji wzajemnej

dwóch sygnałów. Zakładając, że y[n] = x[n] otrzymamy, że:

∣

r

xx

[

k ]∣≤r

xx

[

0]

Co oznacza, że korelacja własna osiąga maksimum dla zerowego przesunięcia.

33 (44)

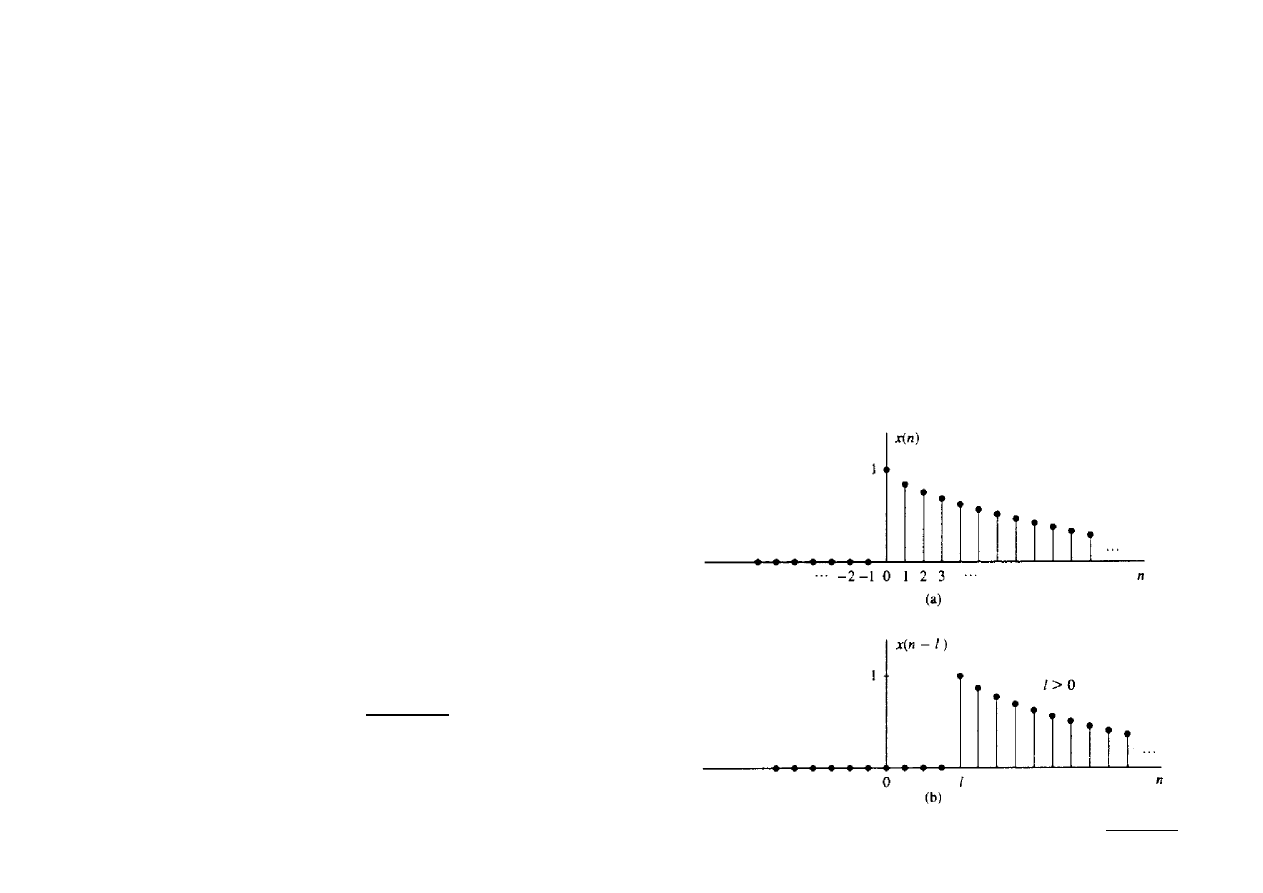
Ex.: Wyznaczyć korelację własną sygnału:

x [n]=a

n

⋅

u[n] ;0a1

Ponieważ sygnał x[n] jest nieskończony, korelacja własna również będzie ciągiem

nieskończonym.

Rozważmy dwa przypadki:

–

k ≥ 0, wówczas:

r

xx

[

k ]=

∑

j=k

∞

x [ j ]⋅x [ j−k ]=

∑

j=k

∞

a

j

⋅

a

j−k

Powyższy szereg jest zbieżny do:

r

xx

[

k ]=

a

k

1−a

2

⋅

u[k ]

34 (44)

–

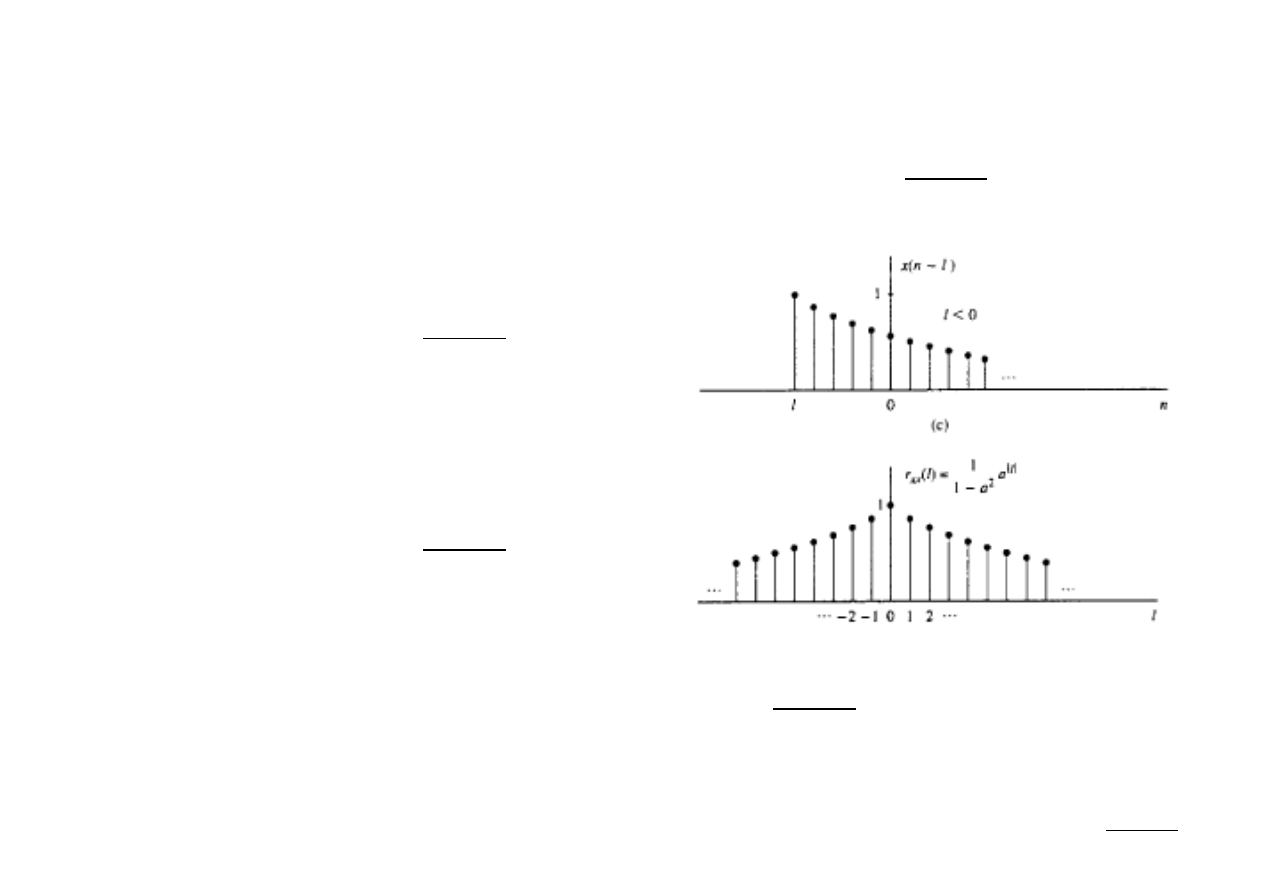
z drugiej strony, jeśli k < 0, wówczas:

r

xx

[

k ]=

∑

j=0

∞

x [ j ]⋅x [ j−k ]=

∑

j=0

∞

a

j

⋅

a

j−k

=

a

−

k

1

1−a

2

Ponieważ jednak k < 0, więc:

r

xx

[

k ]=a

∣

k∣

1

1−a

2

Łącząc rozwiązania dla dodatnich

i ujemnych k otrzymujemy w sumie, że:

r

xx

[

k ]=a

∣

k∣

1

1−a

2

Zauważmy, że:

r

xx

[

k ]=r

xx

[−

k ] ; r

xx

[

0]=

1

1−a

2

35 (44)

Korelacje ciągów okresowych

Do tej pory zajmowaliśmy się korelacjami sygnałów o skończonej energii. Obecnie

wprowadzimy definicję korelacji sygnałów o skończonej mocy, w tym

w szczególności sygnałów okresowych.

Niech x[n] oraz y[n] będą sygnałami o skończonej mocy. Ich korelacja wzajemna

dana jest w postaci:

r

xy

[

k ]= lim

M ∞

1

2M1

∑

j=−M

M

x [ j ]⋅y [ j−k ]

Jeśli z kolei x[n] = y[n] otrzymamy wyrażenie na korelację własną:

r

xx

[

k ]= lim

M ∞

1

2M1

∑

j=−M

M

x [ j ]⋅x [ j−k ]

36 (44)

Jeśli w szczególności sygnały x[n] oraz y[n] będą okresowe z okresem N,

powyższe sumy korelacyjne liczone w przedziale nieskończenie szerokim będą

okresowo równe sumom liczonym po pojedynczym okresie:

r

xy

[

k ]=

1

N

∑

j=0

N −1

x [ j ]⋅y [ j−k ]

r

xx

[

k ]=

1

N

∑

j=0

N −1

x [ j ]⋅x [ j−k ]

Czynnik 1/N występujący w powyższych sumach można traktować jak czynnik

normalizacyjny.

37 (44)

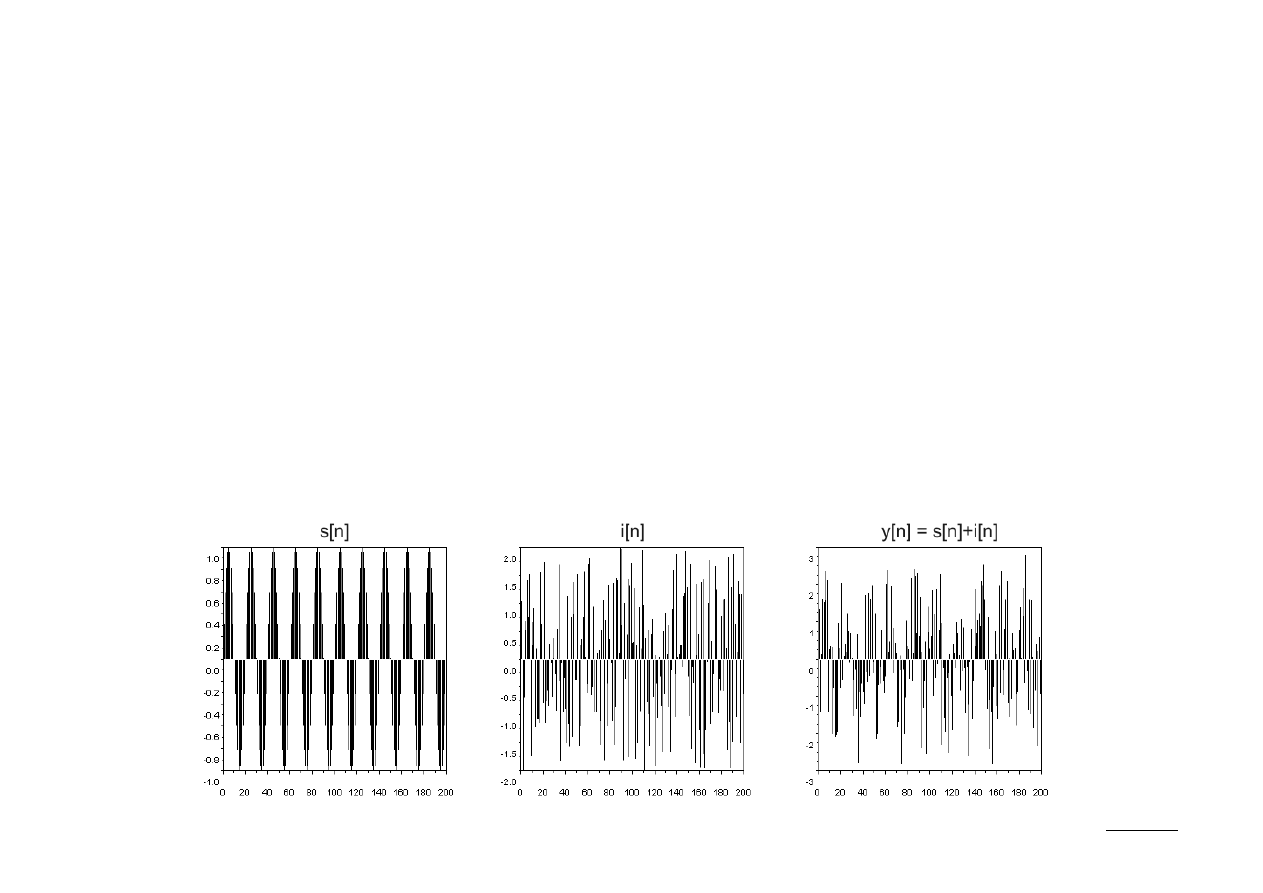
Zastosowania korelacji – wykrywanie okresowości

Funkcje korelacji często wykorzystuje się do wykrywania regularności

(okresowości) sygnałów użytecznych zakłóconych np. sygnałem szumu.

Niech sygnał y[n] dany jest w postaci:

y [n]=s[n]i [n]

gdzie: s[n] jest użytecznym sygnałem okresowym o nieznanym okresie N, zaś i[n]

reprezentuje losowe zakłócenie/szum (interference, noise).

Załóżmy, że obserwujemy y[n] w przedziale znacznie dłuższym niż okres N.

38 (44)

Obliczmy korelację własną zakładając tymczasowo, że okres wynosi M:

r

yy

[

k ]=

1

M

∑

j=0

M −1

y [ j ]⋅y [ j−k ]

Po podstawieniu jawnej postaci sygnału otrzymamy:

r

yy

[

k ]=1

M

∑

j=0

M −1



s[ j]i [ j]



⋅



s[ j−k ]i [ j−k ]



=

...

...= 1

M



∑

j=0

M −1

s [ j ] s[ j−k ]

∑

j =0

M −1



s[ j]i[ j−k ]i [ j ] s[ j−k ]

∑

j=0

M −1

i [ j ]i [ j−k ]



=

...

...=r

ss

[

k ]r

si

[

k ]r

is

[

k ]r

ii

[

k ]

39 (44)

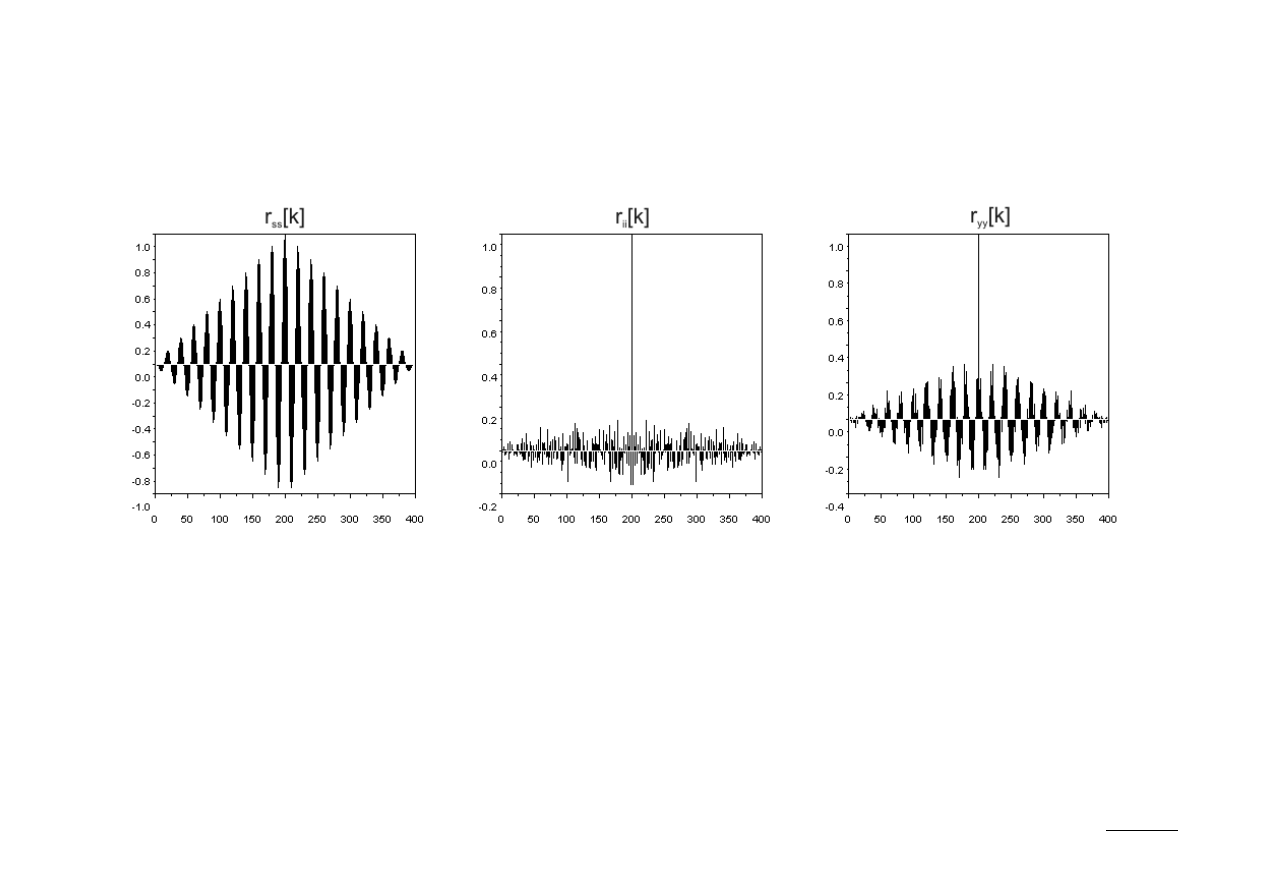
Otrzymaliśmy wynik mówiący, że:

r

yy

[

k ]=r

ss

[

k ]r

si

[

k ]r

is

[

k ]r

ii

[

k ]

Wyraz r

ss

[k] to korelacja własna sygnału użytecznego s[n], okresowa z lokalnymi

maksimami ulokowanymi dla k = 0, N, 2N itd. Korelacje wzajemne r

si

[k] oraz r

is

[k]

są względnie małe, ponieważ oba sygnały nie są ze sobą w żaden sposób

powiązane. Korelacja własna szumu r

ii

[k] osiąga maksimum dla k=0, lecz z uwagi

na losowość szumu szybko zanika dla zwiększających się przesunięć k.

40 (44)

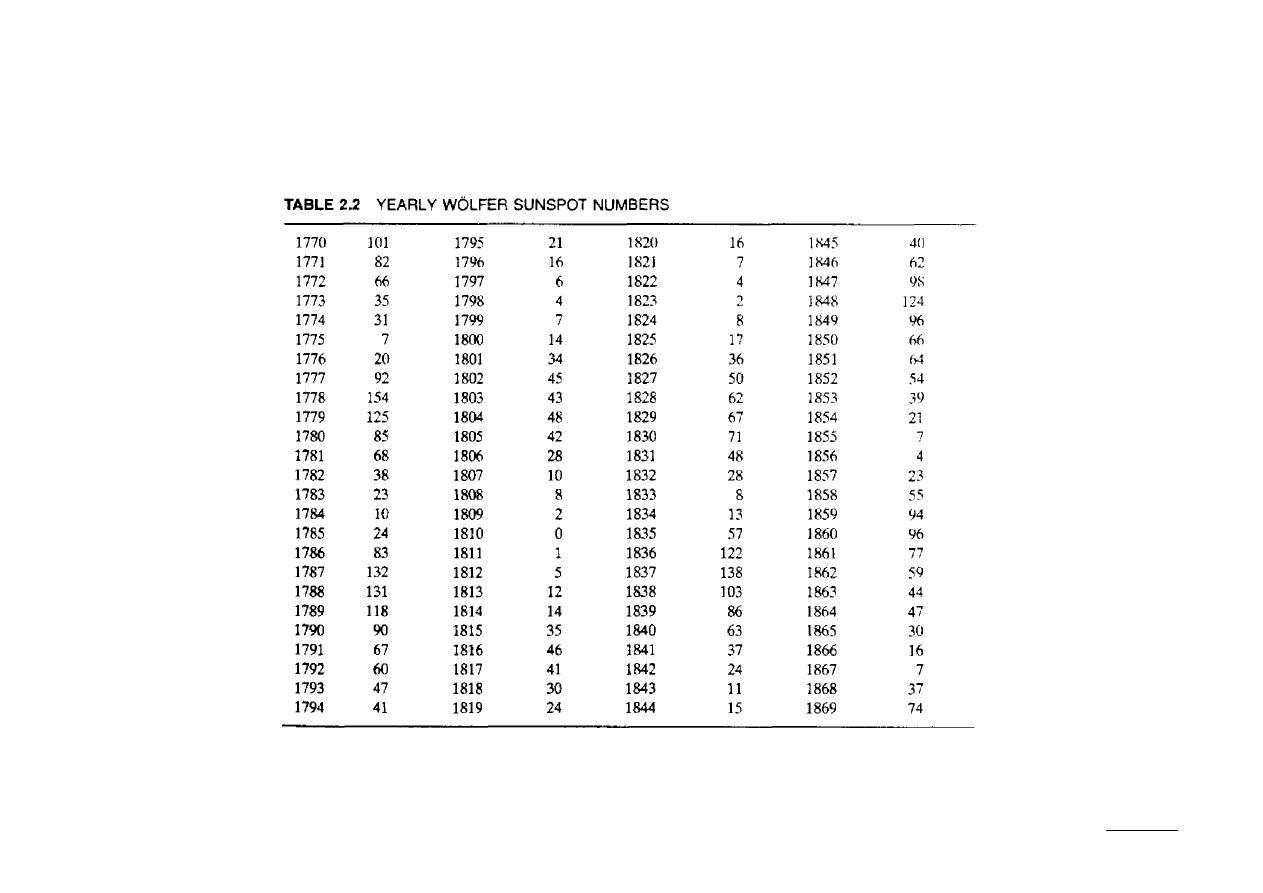
Ex.: Wykrywanie okresowej aktywności Słońca poprzez pomiar ilości plam.

Pomiary ilości plam na Słońcu (plam Wölfera) w latach 1770-1869:

41 (44)

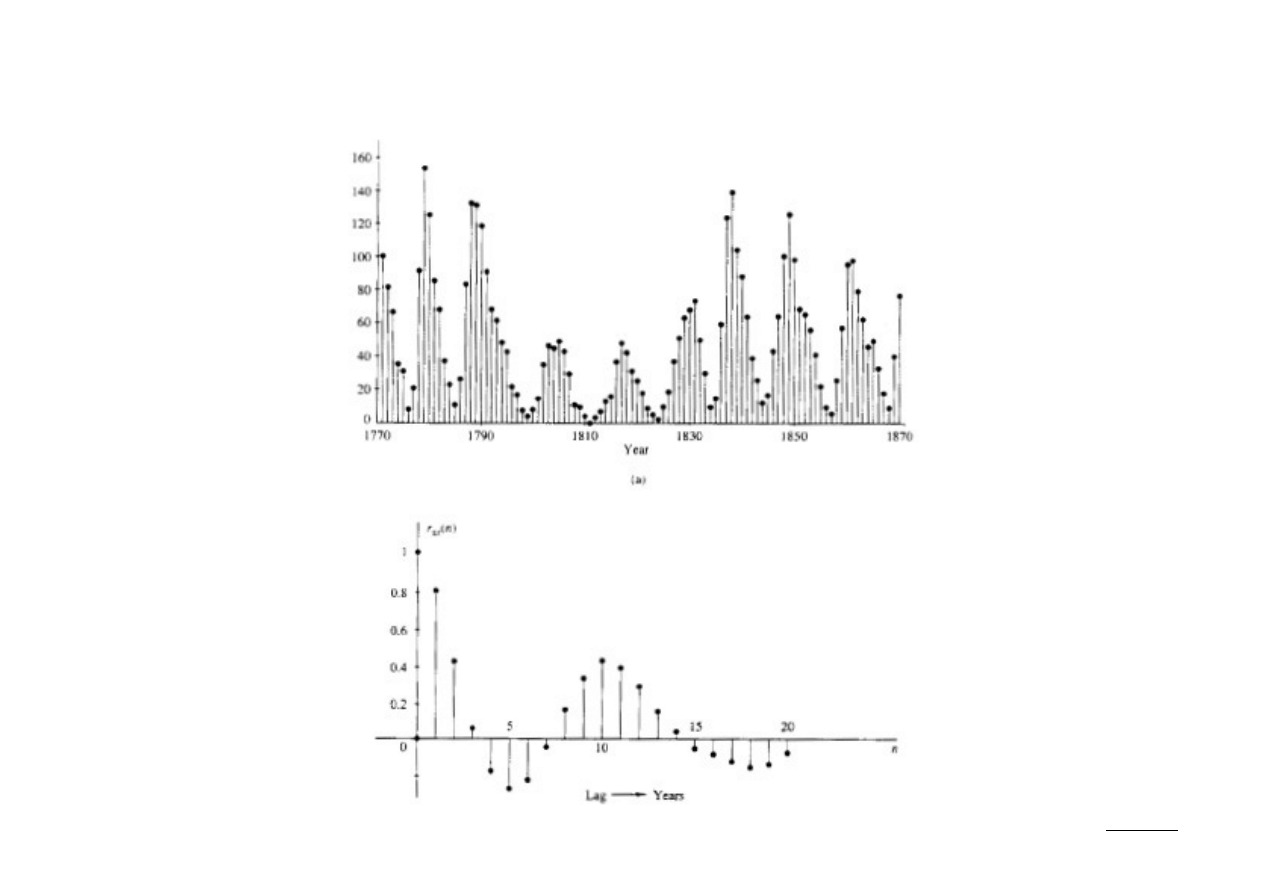
Wykres ilości plam w[n] (aktywności słonecznej) oraz wykres autokorelacji r

ww

[k].

42 (44)

Korelacje zależności wejściowo-wyjściowych

Załóżmy, że sygnał x[n] o korelacji własnej r

xx

[k] podano na wejście układu LTI o

odpowiedzi impulsowej h[n]. Odpowiedź układu wynosić będzie:

y [n]=h[n]∗x [n]=

∑

j=−∞

∞

h[ j]⋅x [n− j]

Korelacja wzajemna pomiędzy pobudzeniem i odpowiedzią wyniesie:

r

yx

[

k ]= y [k ]∗x [−k ]=



h[ k ]∗x [k ]



∗

x [−k ]=h[ k ]∗



x [k ]∗x [−k ]



r

yx

[

k ]=h[k ]∗r

xx

[

k ]

r

xy

[

k ]=h[−k ]∗r

xx

[

k ]

Wynika stąd, że korelacja wzajemna pobudzenia i odpowiedzi układu jest

splotem odpowiedzi impulsowej z korelacją własną pobudzenia.

43 (44)

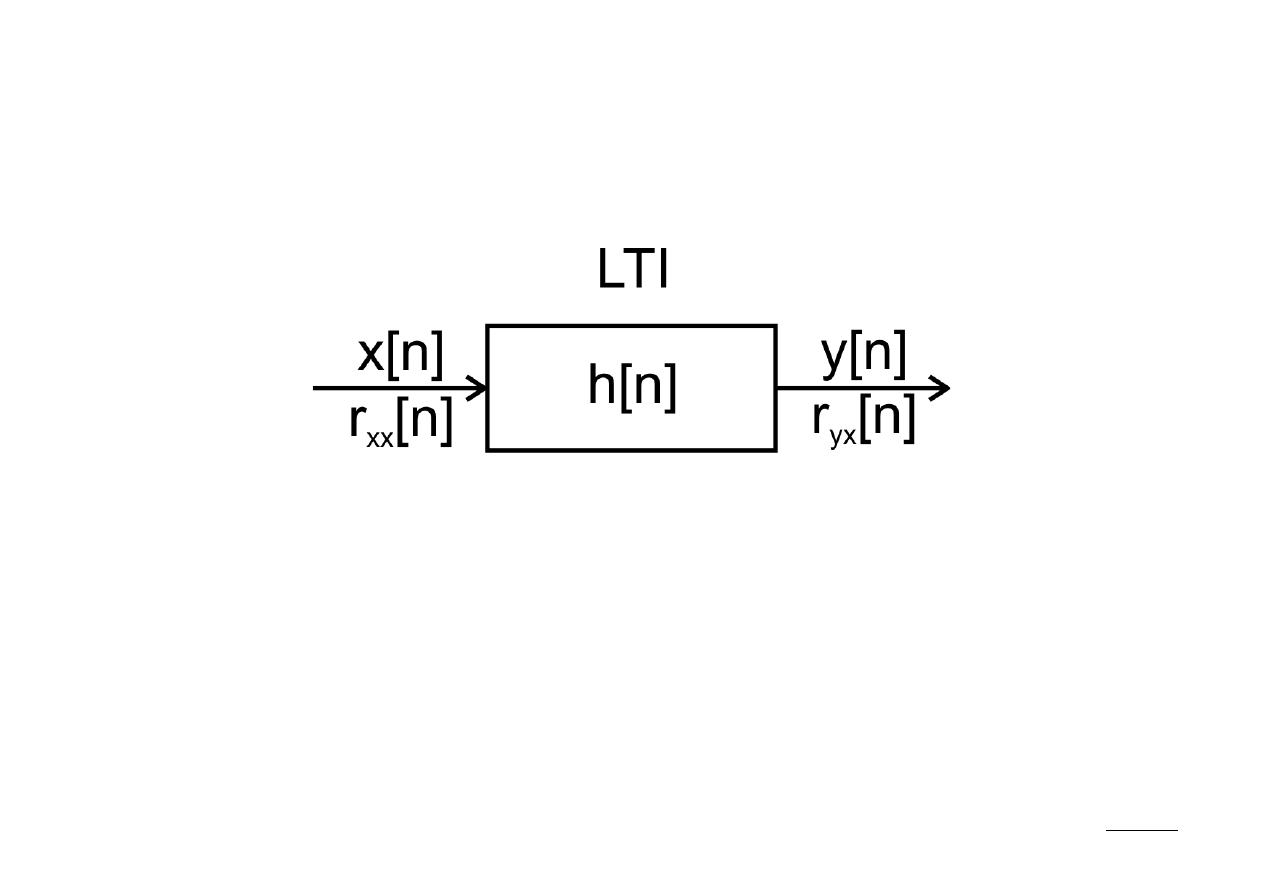
Z drugiej strony, z własności splotu wynika, że odpowiedzią układu na pobudzenie

sygnałem r

xx

[k] będzie r

xy

[k]:

Korelacja własna odpowiedzi wyniesie z kolei:

r

yy

[

k ]= y [ k ]∗y [−k ]=...=r

hh

[

k ]∗r

xx

[

k ]

Oznacza to, że układ nie zmienia charakteru pobudzenia (sygnał o skończonej

energii bądź mocy).

44 (44)