Zadanie 1

Opis: Należało narysować odpowiedź układu o czystym sprzężeniu zwrotnym. Główna ścieżka

zawierała element proporcjonalny o K

R

=4 i obiekt o transmitancji

3

)

1

(

)

(

Ts

K

s

G

o

+

=

i K

o

=1 i T=2s.

Wymuszenie było stałe w przedziale od 0 do 10 i wynosiło 1 a następnie było równe 2

Wykonanie:

clc

clear

all

Kr=4;

Ko=1;

T=2;

L1=[Kr*Ko];

M1=[T^3 3*T^2 3*T 1];

[L,M]=cloop(L1,M1);

printsys(L,M,

's'

);

t=0:0.01:50;

y1=1*ones(1,1001);

y2=2*ones(1,4000);

y=[y1,y2];

[q,w]=lsim(L,M,y,t);

okno=figure(1);

set(okno,

'menubar'

,

'none'

);

set(okno,

'name'

,

'zadanie 1'

);

plot(t,y);

hold

on

plot(t,q,

'r'

);

grid

on

xlabel(

'czas'

);

ylabel(

'wymuszenie i odpowiedz'

);

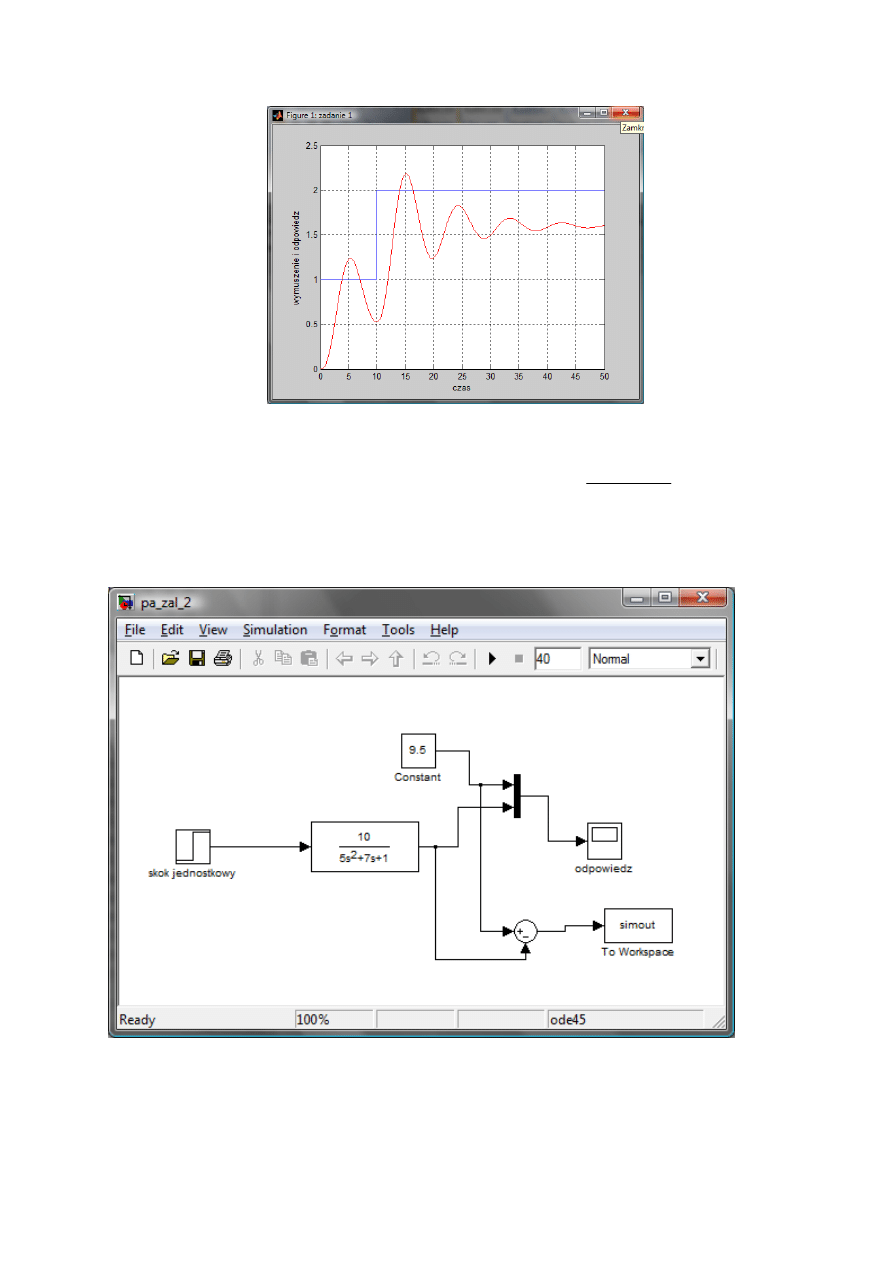
Zadanie 2

Opis: Należało wyznaczyć czas regulacji obiektu o transmitancji

1

7

5

10

)

(

2

+

+

=

s

s

s

G

przy 5%

odchyłce

Wykonanie:

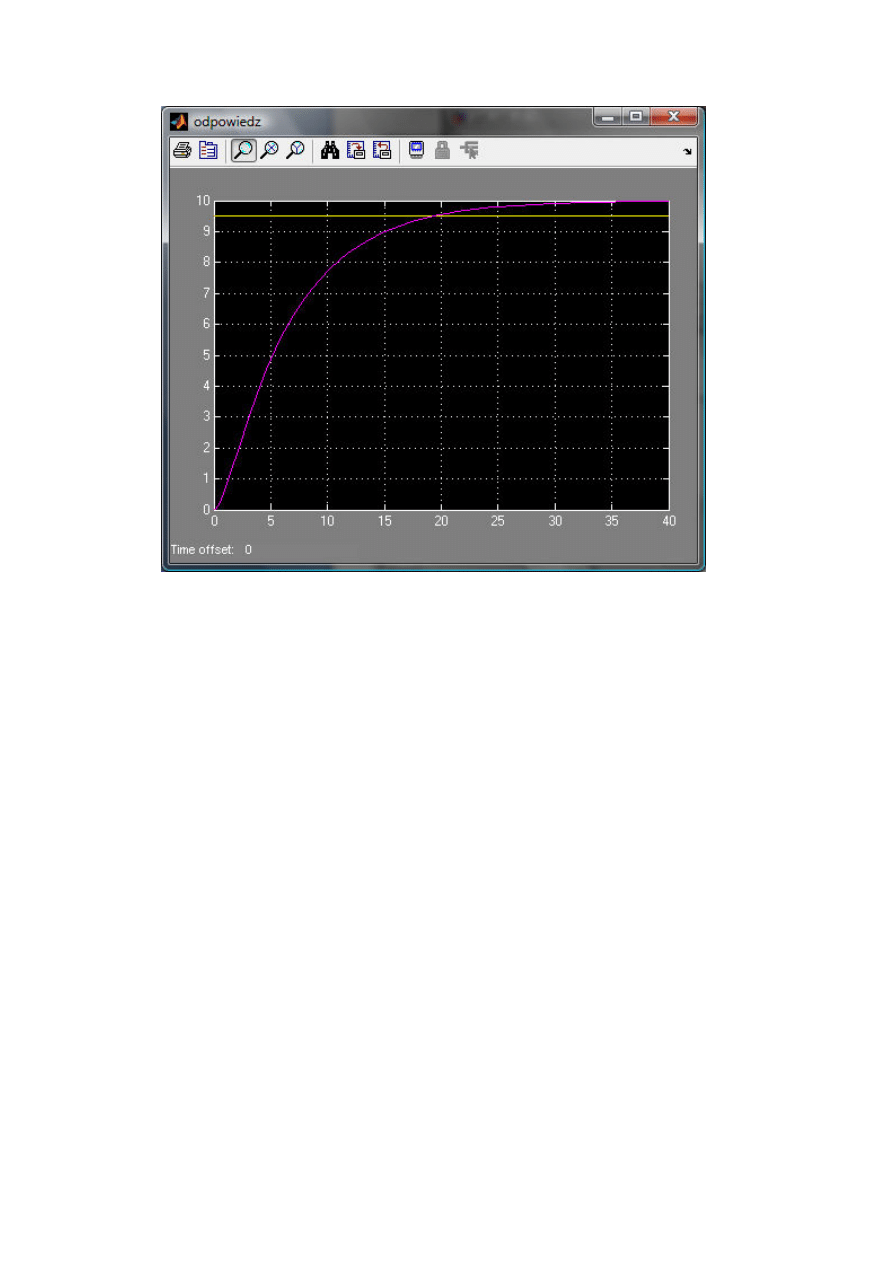
Sygnał dąży do 10 więc jego 95% to 9,5

Parametry skoku: czas skoku=0, wartość początkowa=0, wartość końcowa=1

Po odjęciu otrzymujemy różnicę sygnałów która będzie ujemna gdy sygnał przekroczy 9,5

Wybieramy eksport jako „Structure with Time”

Wpisujemy w linii komend: simout.signals.values i szukamy elementu najbliższego zeru.

Znajdujemy jego pozycję w wektorze wartości (u nas to było np. 18)

Wyświetlamy odpowiadającą tej wartości chwilę czasu: simout.time(18) i na ekranie pojawia

się czas regulacji