
Podstawy Ochrony
Nazwisko: _______________________
Informacji (POI)
Rok/grupa: _______________________
Zima 2012/2013
Ć
wiczenie laboratoryjne V
Implementacja i analiza algorytmów szyfrowych
kryptografii asymetrycznej
To jest laboratorium ćwiczeniowe. Należy jest wykonać w czasie trwania zajęć. Zadanie
to nie powinno zająć więcej czasu niż czas trwania laboratorium. Jeśli zadanie zostanie
zakończone wcześniej, to można kontynuować prace dotyczące poprzedniego
laboratorium lub pracy semestralnej.
1. Wstęp
Przedmiotem laboratorium jest zaimplementowanie i przetestowanie w środowisku
PARI/GP trzech następujących algorytmów szyfrowych:
− algorytmu szyfrowania i podpisu cyfrowego RSA
− algorytmu uzgadniania kluczy Diffie-Hellmana
− algorytm szyfrowania i podpisu cyfrowego ElGamala.
1.1 Algorytm szyfrowania RSA
RSA jest najszerzej używanym kryptosystemem klucza publicznego, nazwanym tak na
cześć jego odkrywców R. Rivesta, A. Shamira i L. Adlemana. Jego użycie zapewnia
zarówno poufność, jak też możliwość tworzenia podpisów cyfrowych, zaś jego
bezpieczeństwo jest oparte na trudności rozwiązania problemu faktoryzacji liczby
całkowitej.
Algorytm Generowanie kluczy do szyfrowania kluczem publicznym RSA
STRESZCZENIE: każdy podmiot tworzy klucz publiczny RSA i
odpowiadający mu klucz prywatny. Każdy podmiot A powinien wykonać
następujące czynności:
1. Wygenerować dwie duże losowe (i różne) liczby pierwsze p i q, każda w
przybliżeniu o tym samym rozmiarze.
2. Obliczyć n = pq i
φ
= (p – 1)(q – 1)
.
3. Wybrać losowa liczbę całkowitą e, 1 < e <
φ
, taką że nwd(e,
φ
) = 1.
4. Użyć rozszerzonego algorytmu Euklidesa (Algorytm 2.107) do obliczenia
unikalnej liczby całkowitej d, 1 < d <
φ
, takiej że ed
≡
1 (mod
φ
)
.
5. Kluczem publicznym podmiotu A jest (n, e), zaś jego kluczem
prywatnym (n, d).

POI
Zima, 2012/2013
Ć
wiczenie laboratoryjne V
strona 2
Algorytm Szyfrowanie kluczem publicznym RSA
STRESZCZENIE: B szyfruje wiadomość m przesyłaną podmiotowi A, który ją
deszyfruje.
1. Szyfrowanie. B powinien wykonać następujące czynności:
(a) Uzyskać autentyczny klucz publiczny (n, e) podmiotu A.
(b) Przedstawić wiadomość m jako liczbę całkowitą z przedziału [0, n-1].
(c) Obliczyć c = m
e
mod n
.
(d) Wysłać szyfrogram c podmiotowi A.
2. Deszyfrowanie. Podmiot A, aby odtworzyć tekst m na podstawie c,
powinien wykonać następujące czynności:
(a) Użyć klucza prywatnego d do odtworzenia m = c
d
mod n.
1.2 Algorytm podpisu cyfrowego RSA z załącznikiem
Przestrzenią wiadomości oraz przestrzenią szyfrogramów schematu RSA szyfrowania
kluczem publicznym RSA jest zbiór Z
n
= {0, 1, 2, ..., n-1}, gdzie n = pq jest iloczynem
dwóch losowo wybranych różnych liczb pierwszych. Schemat podpisu RSA jest
deterministycznym schematem podpisu cyfrowego, zapewniającym odtworzenie
wiadomości.
Algorytm Generowanie klucza w schemacie podpisu RSA
STRESZCZENIE: każdy podmiot A generuje klucz publiczny RSA i
odpowiadający mu klucz prywatny. Każdy podmiot A powinien wykonać, co
następuje:
3. Wygenerować dwie różne losowe liczby pierwsze o dużej wartości p i q,
każda w przybliżeniu o tym samym rozmiarze.
4. Obliczyć n = pq i
φ
= (p -1)(q - 1).
5. Wybrać losową liczbę całkowitą e, 1< e <
φ
taką, że nwd(e,
φ
) = 1.
6. Zastosować rozszerzony algorytm Euklidesa do obliczenia unikalnej liczby
całkowitej d, 1< d <
φ
takiej, że ed
≡ 1 (mod
φ
).
7. (n, e) jest publicznym kluczem pomiotu A, zaś d jest jego kluczem
prywatnym.
Algorytm Tworzenie podpisu RSA z załącznikiem i jego weryfikacja
STRESZCZENIE: podmiot A podpisuje wiadomość m
∈
M.
Dowolny podmiot
B
może zweryfikować podpis użytkownika A, a następnie odtworzyć z podpisu
wiadomość m.
1. Tworzenie podpisu. Podmiot A powinien wykonać, co następuje:
a) Obliczyć wartość skrótu
m
~
= h
(m).
b) Obliczyć s =
m
~
d
mod n.
c) Podpisem podmiotu A jest s.
2. Weryfikacja. Aby zweryfikować podpis A, podmiot B powinien wykonać,

POI
Zima, 2012/2013
Ć
wiczenie laboratoryjne V
strona 3
co następuje:
a) Pobrać autentyczny klucz publiczny (n, e) podmiotu A.
b) Obliczyć
m
~
= s
e
mod n.
c) Obliczyć wartość skrótu '
m
~ = h(m).
d) Zweryfikować czy
m
~
= '
m
~ ; jeśli
m
~
≠ '
m
~
,
to odrzucić podpis.
1.3 Algorytm uzgadniania kluczy Diffie-Hellmana
Algorytm uzgadniania kluczy Diffie-Hellmana zapewnił pierwsze praktyczne
rozwiązanie problemu dystrybucji kluczy, pozwalając dwóm stronom, które nigdy
wcześniej się nie spotkały ani nie udostępniały sobie materiału kluczowego, ustanowić
wspólny sekret poprzez wymianę wiadomości w kanale otwartym. Bezpieczeństwo
algorytmu opiera się na trudności problemu Diffie-Hellmana oraz powiązanego problemu
obliczenia logarytmu dyskretnego.
Algorytm uzgadniania kluczy Diffie-Hellmana
STRESZCZENIE: A i B wysyłają sobie wiadomość kanałem otwartym. W
efekcie ustanawiają współdzielony sekret K znany obu stronom, A i B.
1) Jednorazowa konfiguracja (set-up). Wybierana jest właściwa liczba
pierwsza p oraz generator α należący do
*
n
Z
,
taki że (2 ≤ α ≤ p-2).
2) Komunikaty protokołu.
A → B : α
x
mod p (1)
A ← B : α
y
mod p (2)
3) Działanie protokołu. Wykonaj następujące kroki za każdym razem gdy
potrzebny jest klucz współdzielony.
a) A wybiera sekretną liczbę losową x, taką że 1≤ x ≤ p – 2, i wysyła B
wiadomość (1)
b) B wybiera sekretną liczbę losową y, taką że 1≤ y ≤ p – 2, i wysyła A
wiadomość (2)
c) B otrzymuje α
x
i oblicza klucz współdzielony jako K=( α
x
)
y
mod p
d) A otrzymuje α
y
i oblicza klucz współdzielony jako K=( α
y
)
x
mod p
1.4 Algorytm szyfrowania ElGamala
Schemat ElGamala szyfrowania kluczem publicznym może być rozpatrywany jako
uzgadnianie kluczy Diffiego-Hellmana w trybie przesyłania klucza. Jego bezpieczeństwo
jest oparte na trudności rozwiązania problemu logarytmu dyskretnego oraz problemu
Diffiego-Hellmana.
Algorytm Generowanie kluczy do szyfrowania kluczem publicznym ElGamala
STRESZCZENIE: każdy podmiot tworzy klucz publiczny i odpowiadający mu
klucz prywatny. Każdy podmiot A powinien wykonać następujące czynności:
1. Wygenerować dużą liczbę losową p oraz utworzyć generator
α
grupy
multiplikatywnej
*
n
Z
liczb całkowitych modulo p.
2. Wybrać liczbę losową a, 1
≤ a ≤ p-2 i obliczyć
α
a
mod p
.
3. Kluczem publicznym podmiotu A jest (p,
α
, y
); zaś jego kluczem
prywatnym a.
POI
Zima, 2012/2013
Ć
wiczenie laboratoryjne V
strona 4
Algorytm Szyfrowanie ElGamala
STRESZCZENIE: B szyfruje wiadomość m przesyłaną podmiotowi A, który ją
deszyfruje.
1. Szyfrowanie. B powinien wykonać następujące czynności:
(a) Pobrać autentyczny klucz publiczny (p,
α
, y
) podmiotu A.
(b) Przedstawić wiadomość m jako liczbę całkowitą z zakresu {0, 1, ..., n-
1}
.
(c) Wybrać liczbę losową k, 1
≤ k ≤ p-2.
(d) Obliczyć
γ =
α
k
mod p
oraz
δ = m (y)
k
mod p
.
(e) Wysłać szyfrogram c = (
γ, δ) podmiotowi A.
2. Deszyfrowanie. Podmiot A, aby odtworzyć tekst m na podstawie c,
powinien wykonać następujące czynności:
(a) Użyć klucza prywatnego a do obliczenia
γ
p-1-a
mod
p
(zauważmy:
ak
a
a
p
−
−
−
−
=
=
α
γ
γ
1
).
(b) Odtworzyć m, obliczając (
γ
-a
)
δ mod p.
1.5 Algorytm podpisu cyfrowego ElGamala
Schemat podpisu ElGamala jest mechanizmem podpisu randomizowanego. Tworzy on
podpisy cyfrowe z załącznikiem dla wiadomości binarnych o dowolnej długości i
wymaga użycia funkcji skrótu h: {0, 1}*
→ Z
q
, gdzie p jest dużą liczbą pierwszą.
Algorytm Generowanie klucza w schemacie podpisu ElGamala
STRESZCZENIE: każdy podmiot generuje klucz publiczny i odpowiadający
mu klucz prywatny. Każdy podmiot A powinien wykonać, co następuje:
1. Utworzyć losową liczbę pierwszą p o dużej wartości i generator
α
multiplikatywnej grupy Z
q
* (stosując algorytm 4.84).
2. Wybrać losową liczbę całkowitą a taką, że 1
≤ a ≤ p -2.
3. Obliczyć y =
α
a
mod p.
4. Kluczem publicznym podmiotu A jest (p,
α
, y), zaś jego kluczem
prywatnym
α
.
Algorytm Tworzenie podpisu ElGamala i jego weryfikacja
STRESZCZENIE: podmiot A podpisuje binarną wiadomość m o dowolnej
długości. Dowolny podmiot B może zweryfikować podpis podmiotu A stosując
jego klucz publiczny.
1. Tworzenie podpisu. Użytkownik A powinien wykonać, co następuje:
(a) Wybrać losową tajną liczbę całkowitą k, 1
≤ k ≤ p - 2, spełniającą
zależność nwd(k, p - 1) =1.
(b) Obliczyć r =
α
k
mod p.
POI
Zima, 2012/2013
Ć
wiczenie laboratoryjne V
strona 5
(c) Obliczyć k
-1
mod (p - 1).
(d) Obliczyć s = k
-1
{h(m) - ar} mod (p - 1).
(e) Podpisem podmiotu A wiadomości m jest para (r, s).
2. Weryfikacja. Aby zweryfikować podpis (r, s) podmiotu A złożony na
wiadomości m, podmiot B powinien wykonać, co następuje:
(a) Pobrać autentyczny klucz publiczny (p,
α
, y).
(b) Zweryfikować czy 1
≤ r ≤ p - 1; jeśli warunek ten nie jest spełniony, to
odrzucić podpis.
(c) Obliczyć v
1
= y
r
r
s
mod p.
(d) Obliczyć h(m) i v
2
=
α
h(m)
mod p.
(e) Zaakceptować podpis wtedy i tylko wtedy, gdy v
1
= v
2
.
2. Opis pakietu PARI/GP
PARI/GP jest komputerowym systemem algebraicznym dostosowanym do badań w
zakresie teorii liczb. Może być używany jako potężny kalkulator biurkowy, jako
narzędzie wspomagające studentów w nauce teorii liczb, lub jako środowisko
programistyczne do studiowania teoretycznych kryptosystemów numerycznych.
PARI/GP jest dostępny bez opłat i może być pobrany ze strony:
http://pari.math.u-bordeaux.fr
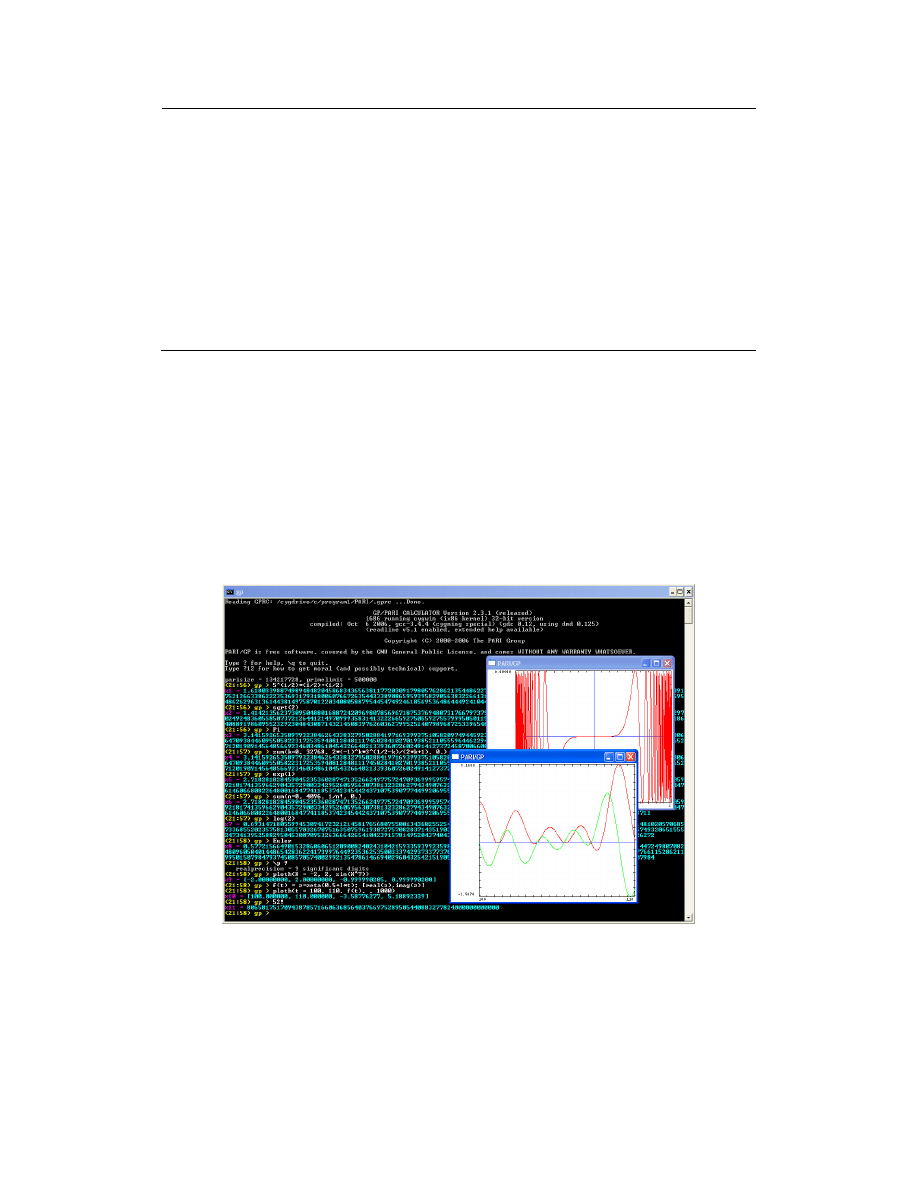
Domyślny interfejs PARI/GP jest oparty o linię poleceń, ale są też dostępne interfejsy
graficzne. Rys. 1 przedstawia przykładową sesję PARI/GP pod Linux i Windows.
Rys. 1 Ilustracja interfejsu pakietu PARI/GP
Poniżej
przedstawiono
podstawowe
informacje
o
wbudowanych
funkcjach
obliczeniowych oraz języku programowania.
2.1 Instrukcje sterujące
if(a, {seq1 }, {seq2 }): oblicza sekwencję wyrażeń seq1 jeśli a jest niezerowe, w
przeciwnym razie oblicza wyrażenie seq2. Oczywiście, seq1 albo seq 2 mogą być puste:

POI
Zima, 2012/2013
Ć
wiczenie laboratoryjne V
strona 6
if (a,seq)
oblicza seq jeśli a jest różne od zera (nie trzeba pisać drugiego przecinka), i nie
robi nic w przeciwnym razie.
if (a,,seq)
oblicza seq jeśli a jest równe zero, i nie robi nic w przeciwnym razie. Ten sam
rezultat można uzyskać za pomocą operatora ! (negacja): if (!a,seq).
for(X = a, b, seq): oblicza seq, dla zmiennej X zmienianej w przedziale od a do b. Jeśli
a>b, to nie jest wykonywana żadna operacja.
Należy pamiętać, że w konstrukcji tpyu
for (X = a,b, seq)
zmienna X jest lokalna dla pętli, co prowadzi do potencjalnie nieprzewidywalnego zachowania:
gp > n = 5;
gp > for (n = 1, 10, if (coś_ciekawego(), break););
gp > \\ w tym momencie n jest równe 5 !
Jeśli sekwencja seq modyfikuje indeks pętli, to pętla jest modyfikowana następująco:
gp > for (n = 1, 10, n += 2; print(n))
3
6
9
12
until(a, seq): oblicza seq dopóki a nie jest równe 0 (np. dopóki a jest prawdziwe). Jeśli a
pierwotnie nie jest równe 0, to seq jest obliczany raz (warunek jest sprawdzany po
wykonaniu seq, a nie przed jak w while).
while(a, seq): gdy a jest niezerowe, oblicza sekwencję wyrażeń seq. Sprawdzenie
warunku jest wykonywane przed obliczaniem seq, stąd jeśli a jest pierwotnie równe zero,
seq
nie będzie obliczony wcale.
2.2 Podstawowe funkcje obliczeniowe
bezout(x, y): znajduje takie dwie minimalne liczby całkowita u i v, że
x * u + y * v = nwd(x, y). Oba argumenty muszą być całkowite lub oba muszą być
wielomianami, a wynik jest wektorem z trzema elementami u, v i nwd(x, y).
lift(x, {v}): zawraca element x = a mod n z Z/nZ dla a z Z, podobnie zwraca reszty
wielomianowe w przypadku wykonywania operacji obliczania reszty z dzielenia dwóch
wielomianów (o ile v jest pominięte). Na przykład:
gp > lift(Mod(5,3))
%1 = 2
gp > lift(3 + O(3^9))
%2 = 3
gp > lift(Mod(x,x^2+1))
%3 = x
gp > lift(x * Mod(1,3) + Mod(2,3))
%4 = x + 2
gp > lift(x * Mod(y,y^2+1) + Mod(2,3))
%5 = y*x + Mod(2, 3) \\ czy to rozumiesz?
gp > lift(x * Mod(y,y^2+1) + Mod(2,3), x)
%6 = Mod(y, y^2+1) * x + Mod(2, y^2+1)

POI
Zima, 2012/2013
Ć
wiczenie laboratoryjne V
strona 7
z
nprimroot(n): zwraca generator dla (Z/nZ)
*
, zawsze gdy druga grupa jest cykiczna (n =
4 lub n = 2p
k
lub n = p
k
, gdzie p jest nieparzystą liczbą pierwszą, a k
≥ 0).
2.3 Funkcje użytkownika:
W pakiecie PARI można na bieżąco definiować funkcje, które można później
wielokrotnie wywoływać. Na przykład, poniższa funkcja oblicza rekurencyjnie wartość
silni:
f(n) = if(n<0,print("Zly
argument!”),if(n==0,return(1),return(n*f(n-1))))
Jak łatwo zauważyć, bardzo szybko wyrażenia te, szczególnie nawiasy, są niemożliwe do
ś
ledzenia. Byłoby o wiele prościej, gdyby zapisywać swoje funkcje i/lub program w
odrębnym pliku i ładować go do PARI. Można najpierw napisać to co potrzebujesz w
edytorze tekstowym (dla komputerów z Windows: użyj notatnika) bez uruchamiania
PARI a następnie zapisz plik.
Na przykład, powiedzmy, że masz następujący plik o nazwie fact.gp:
f(n) = {
if(n<0,
print("Zly argument!"),
if(n==0,
return(1),
return(n*f(n-1))
)
)
}
Wówczas można wczytać funkcję z pliku i i wywoływać ją:
gp > \r c:\pari\fact.gp
gp > f(3)
%2 = 6
3. Przykłady implementacji algorytmu RSA
Poniżej przedstawiono dwa przykłady implementacji algorytmu szyfrowania RSA.
W pierwszym z przykładów zastosowano bezpośrednie, ale nieefektywne potęgowanie w
arytmetyce modularnej. Z kolei w drugim z przykładów najpierw zaimplementowano
algorytm szybkiego potęgowani modularnego, a następnie wykorzystano go w
obliczeniach.
Uwaga 1. Bezpośrednie potęgowanie w arytmetyce modularnej jest nie tylko
nieefektywne, ale może prowadzić także do przepełnienia stosu.
Uwaga 2. Algorytm szybkiego potęgowania wyrażeń y = g
x
mod n
ma postać:
Algorytm Powtarzany algorytm potęguj-i-mnóż do potęgowania w Z
n
.
WEJŚCIE: a
∈
Z
n
, liczba całkowita 0≤k<n, której reprezentacja binarna ma
postać Σ
t
i=0
k
i
2
i
.
WYJŚCIE: a
k
mod n
1. Ustaw b ←1. Jeśli k=0 to return(b).

POI
Zima, 2012/2013
Ć
wiczenie laboratoryjne V
strona 8
2. Ustaw A←a.
3. Jeśli k
0
=1
to ustaw b←a.
4. Dla i od 1 do t wykonaj:
4.1. Ustaw A←A
2
mod n
4.2. Jeśli k
i
= 1 to ustaw b←A · b mod n.
5.
Return(b).
Przykład 1 (bez zastosowania algorytmu szyfrowania):
gp > p=nextprime(random(10^30)) \\ wybiera losową liczbę
pierwszą mniejszą niż 10^30
%1 = 738873402423833494183027176953
gp > q=nextprime(random(10^25))
%2 = 3787776806865662882378273
gp > setrand(2) \\ aby zmienić punkt startowy generatora liczb
losowych
%3 = 2
gp > p=nextprime(random(10^30))
%4 = 420829752590518623220964128931
gp > q=nextprime(random(10^25)) \\ dla bezpieczeństwa, lepiej
wybierać liczby pierwsze różnych rzędów.
%5 = 118661898673302028252493
gp > n=p*q
%6 = 49936457460606882603937486236150029895426667874174983
gp > e=random(n)
%7 = 27911888897893919924427824802746641865747755531264298
gp > phin=(p-1)*(q-1)
%8 = 49936457460606882603937065406278777478130144881793560
gp > while(gcd(e,phin)!=1, e=e+1) \\ by zapewnić liczby
względnie pierwsze
gp > e \\ jak widać, jest o 1 większa
%9 = 27911888897893919924427824802746641865747755531264299
gp > d=lift(Mod(e,phin)^(-1)) \\ lift zmienia wejście w liczbę
całkowitą,
NIE jest już liczbą mod e
%10 = 24004316919709947998922871438864307780709766943417672
gp > (e*d)%phin \\ zawsze dobrze to sprawdzić
%11 = 1
gp > log(n)/log(27) \\ podaje liczę znaków które możemy
zaszyfrować
%12 = 36.81692875661933554457136534
gp > m=5+21*27+12*27^2+5*27^3+18*27^4 \\ szyfrowany tekst
m=EULER
%13 = 9673673

POI
Zima, 2012/2013
Ć
wiczenie laboratoryjne V
strona 9
gp > E(x)=lift(Mod(x,n)^e) \\ szyfruje przy użyciu danych
powyżej
(00:29) gp > D(x)=lift(Mod(x,n)^d) \\ Deszyfruje przy użyciu
danych powyżej
(00:29) gp > secret=E(m) \\ To jest szyfrogram
%14 = 24150232700102980434440083538785706321933018688396212
gp > D(secret) \\ Przy odrobinie szczęścia, to powinniśmy
otrzymać "EULER"
%15 = 9673673
gp > m+O(27^5) \\ Odtworzenie znaków tekstu jawnego "EULER"
%16 = 5 + 21*27 + 12*27^2 + 5*27^3 + 18*27^4 + O(27^5)
gp > factor(n)
%18 =
[118661898673302028252493 1]
[420829752590518623220964128931 1]
(00:42) gp > ##
*** last result computed in 28,190 ms.
Przykład 2 (z zastosowaniem algorytmu szybkiego potęgowania):
Algorytm szybkiego potęgowania został zaimplementowany następująco:
/* Potęgowanie modulo przez powtarzane podnoszenie do kwadratu.
*/
/* Obliczamy a^b mod n. */
modexp (a, b, n) = {
local(d, bin );
d = 1;
bin = binary (b);
for (i = 1, length (bin),
d = Mod(d*d, n);
if (bin[i] == 1,
d = Mod(d*a, n);
);
);
return (d);
}
Po zapisaniu powyższego algorytmu w pliku modexp.gp można użyć go w poniższej
implementacji algorytmu szyfrowania RSA, a następnie zaszyfrowania tekstu
HELLOWORLD
. Przyjmuje się przy tym, że szyfrowane są kody ASCII odpowiadające
poszczególnym znakom szyfrowanego tekstu (zwróć uwagę, że jest to inny sposób
szyfrowania tekstu niż ten, który został zastosowany w przykładzie 1). Odpowiednie
kody ASCII można znaleźć w poniższej tabeli.

POI
Zima, 2012/2013
Ć
wiczenie laboratoryjne V
strona 10
Rys. 1 Tabela podstawowych kodów ASCII
Szyfrowanie tekstu HELLOWORLD przebiega następująco:
gp > p = (2^31) - 1
%6 = 2147483647
gp > isprime(p)
%7 = 1
gp > q = (2^61) - 1
%8 = 2305843009213693951
gp > isprime(q)
%9 = 1
gp > n = p*q
%10 = 4951760154835678088235319297
gp > e = random(eulerphi(n));
gp > while (gcd(e, eulerphi(n)) != 1, e = random(eulerphi(n)))
gp > e
%12 = 4048613754158036308925952619
gp > bezout(e, eulerphi(n))
%13 = [-2467255312924178983708448021,
2017255175378597045689617010, 1]
gp > Mod(-2467255312924178983708448021, eulerphi(n))
%14 = Mod(2484504839605656093165693679,
4951760152529835076874141700)
gp > d = 2484504839605656093165693679
%15 = 2484504839605656093165693679
gp > Mod(d * e, eulerphi(n))
%16 = Mod(1, 4951760152529835076874141700)
gp > m = 72697676798779827668
%17 = 72697676798779827668
gp > Mod(m^e, n)
*** length (lg) overflow
gp > \r c:\pari\modexp.gp
gp > modexp(m, e, n)

POI
Zima, 2012/2013
Ć
wiczenie laboratoryjne V
strona 11
%18 = Mod(359367672514946173472712696,
4951760154835678088235319297)
gp > c = 359367672514946173472712696
%19 = 359367672514946173472712696
gp > modexp(c, d, n)
%22 = Mod(72697676798779827668, 4951760154835678088235319297)
5. Ćwiczenia
Czynności wstępne:
• Ćwiczenie można wykonywać w środowisku MS Windows lub Linux Ubuntu.
• W przypadku systemu MS Windows należy sprawdzić, czy pakiet PARI/GP jest
zainstalowany w systemie. Jeśli nie, to należy pobrać program spod adresu
http://pari.math.u-bordeaux.fr i zainstalować.
• W przypadku systemu Linux Ubuntu należy utworzyć nową lub uruchomić
istniejącą maszynę wirtualną Linux Ubuntu w programie Virtual Box z
domyślnymi ustawieniami.
• Z menu Oracle VirtualBox wybrać Ustawienia, a następnie za pomocą opcji
zarejestrować nośnik USB.
• Po zainstalowaniu i uruchomieniu systemu Linux Ubuntu przejść do konsoli
i zainstalować pakiet PARI/GP
$ sudo apt-get install pari-gp pari-doc
Zadania do wykonania
1. Zaimplementować algorytm podpisu cyfrowego RSA z załącznikiem (patrz
rozdz.1.2), podpisać cyfrowo swoje imię i nazwisko, a następnie zweryfikować
podpis. Uwaga! Przyjąć, że używana w tym algorytmie funkcja skrótu jest
funkcja tożsamościową, a weryfikacja podpisu zwraca prawdę lub fałsz.
2. Zaimplementować
algorytm
szyfrowania
ElGamala
(patrz
rozdz.1.4),
zaszyfrować swoje imię i nazwisko, a następnie na podstawie uzyskanego
kryptogramu uzyskać pierwotny tekst jawny.
3. Zaimplementować algorytm podpisu cyfrowego ElGamala z załącznikiem (patrz
rozdz.1.5), podpisać cyfrowo swoje imię i nazwisko, a następnie zweryfikować
jego poprawność.
4. Zaimplementować schemat uzgadniania kluczy Diffie-Hellmana i na wybranych
przykładach pokazać jego poprawność. Następnie uzgodniony klucz proszę
zastosować w roli klucza prywatnego w algorytmie szyfrowania ElGamala i
zaszyfrować najpierw za jego pomocą swoje imię i nazwisko, zaś później dane te
odszyfrować.
Problemy do dyskusji
1. Dlaczego problem znalezienia logarytmu dyskretnego (indeksu) jest problemem
trudnym obliczeniowym? Pokaż przykładowe obliczenia za pomocą pakietu PARI
wraz z czasami obliczeń dla liczb o różnych rozmiarach (w bitach). Uwaga.
Zaimplementuj własne rozwiązanie problemu logarytmu dyskretnego, a następnie

POI
Zima, 2012/2013
Ć
wiczenie laboratoryjne V
strona 12
w celu porównania czasów obliczeń skorzystaj z funkcji znlog, wbudowanej w
pakiet PARI.
2. Omów podstawowe trudności napotkane podczas implementacji algorytmów
z rozdz.1.
Sprawozdanie z ćwiczenia
W trakcie ćwiczenia należy notować wszystkie czynności oraz uzyskiwane wyniki. Po
zakończeniu ćwiczenia należy przygotować sprawozdanie z przebiegu ćwiczenia,
zawierające m.in. krótki opis ćwiczenia, uzyskane wyniki oraz podsumowanie i wnioski
z ćwiczenia.
Literatura
1. Alfred J. Menezes, Paul C. van Oorschot, Scott A. Vanstone Kryptografia
stosowana
, WNT 2005
2. J. Pieprzyk, T. Hardjono, J. Seberry Teoria bezpieczeństwa systemów
komputerowych
, Wydawnictwo Helion, 2005.
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron