
Elektrotechnika
Podstawy Automatyki 1
ODPOWIEDZI
1
PODSTAWY AUTOMATYKI 1 – ĆWICZENIA
- odpowiedzi
lista zadań nr 1
Transformata Laplace’a
1. (Korzystając wprost z definicji znaleźć transformatę Laplace’a funkcji)
a.
s
s
s
Y
3
2
)
(
2
c.
3
2
)
(
s
s
Y
b.
s
s
s
Y
2
1
)
(
2
d.
s
s
s
Y
1
3
2
)
(
2. (Dana jest odpowiedź na impuls Diraca (funkcja wagi)
)
(t
g
. Znaleźć transmitancję
operatorową
)
(s
G
)
a.
4
3
3
2
)
(
s
s
s
G
d.
3
3
2
2
1
2
)
(
2
3
s
s
s
s
G
b.
1
1
2
2
3
3
)
(
s
s
s
s
G
e.
4
2
1
2
)
(
2
s
s
s
G
c.
2
3
1
4
)
(
3
s
s
s
G
f.
2
2
1
2
)
(
s
s
s
G
3. (Dana jest odpowiedź układu na skok jednostkowy
)
(
1
t
y
. Znaleźć transmitancję
operatorową
)
(s
G
)
a.
2
1
4
)
(
s
s
s
G
c.
2
1
)
(
2
s
s
s
s
G
b.
2
2
2
)
(
s
s
s
G
d.
1
)
(
2
2
s
e
s
s
G
s
4. (Dana jest transmitancja operatorowa obiektu
)
(s
G
. Wyznaczyć odpowiedź układu na
impuls Diraca (funkcję wagi)
)
(t
g
)
a.
)
(
4
9
)
(
2
4
t
e
e
t
g
t
t
1
d.
)
(
)
(
2
2
t
e
te
t
g
t
t
1
b.
)
(
5
7
)
(
4
5
t
e
e
t
g
t
t
1
e.
)
(
3
2
7
)
(
2
3
3
t
e
e
te
t
g
t
t
t
1
c.
)
(
1
)
(
t
e
t
g
t
1
f.
)
(
2
5
,
0
)
(
2
t
te
e
t
t
g
t
t
1

Elektrotechnika
Podstawy Automatyki 1
ODPOWIEDZI
2
5. (Obiekt opisany jest równaniem różniczkowym. Wyznaczyć transmitancję operatorową
)
(s
G
oraz odpowiedź układu na impuls Diraca (funkcję wagi)
)
(t
g
)
a.
5
1
4
)
(
s
s
s
s
G
)
(
75
,
0
25
,
0
)
(
5
t
e
e
t
g
t
t
1
b.
4
2
2
4
)
(
s
s
s
s
G
)
(
7
3
)
(
4
2
t
e
e
t
g
t
t
1
c.
4
1
2
3
)
(
s
s
s
s
G
)
(
3
10
3
1
)
(
4
t
e
e
t
g
t
t
1
6. (Obiekt opisany jest równaniem różniczkowym. Wyznaczyć transmitancję operatorową
)
(s
G
oraz odpowiedź układu na skok jednostkowy
)
(
1
t
y
)
a.
3
1
)
(
s
s
G
)
(
3
1
3
1
)
(
3
1
t
e
t
y
t
1
b.
2
2
)
(
s
s
G
)
(
1
)
(
2
1
t
e
t
y
t
1
c.
4
1
1
)
(
2
s
s
s
s
s
G
)
(
12
13
3
1
4
1
)
(
4
1
t
e
e
t
y
t
t
1
7. (Znaleźć transmitancję
)
(s
G
czwórnika elektrycznego)
a.
1
)
(
Ts
Ts
s
G
R
L
T
b.
1
1
)
(
Ts
s
G
RC
T
c.
1
)
(
2
RCs
LCs
RCs
s
G
d.
2
2
1
1
)
(
LCs
LCs
s
G
Elektrotechnika
Podstawy Automatyki 1
ODPOWIEDZI
3
PODSTAWY AUTOMATYKI 1 – ĆWICZENIA
- odpowiedzi
lista zadań nr 2
Charakterystyki czasowe i częstotliwościowe układów ciągłych
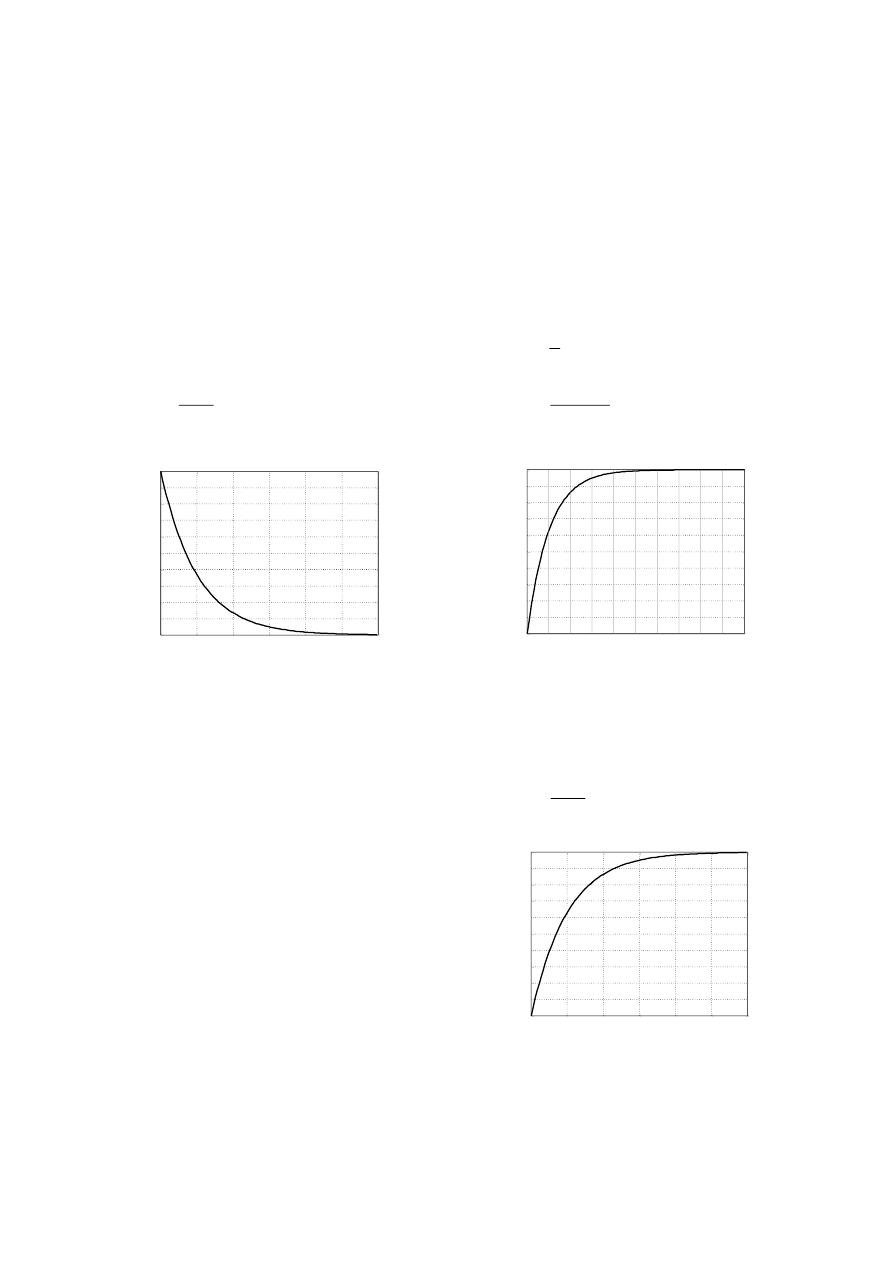
1. (Wykreślić charakterystykę impulsową obiektów opisanych transmitancją operatorową
)
(s
G
)
a.
5
)
(
s
G
)
(
5
)
(
t
t
g
c.
s
s
G
2
)
(
)
(
2
)
(
t
t
g
1
b.
2
1
)
(
s
s
G
d.
1
2
5
)
(
s
s
s
G
Time [s]
A
m
pl
it
ud
e
Impulse Response
0
0.5
1
1.5
2
2.5
3
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
2 4 6 8 10 12 14 16 18 20
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
Time [s]
A
m
pl
it
ud
e
Impulse Response
2. (Wykreślić charakterystykę odpowiedzi na skok jednostkowy obiektów opisanych
transmitancją operatorową identyczną jak w zadaniu I)
a.
5
)
(
s
G
5
)
(
1
t
y
b.
2
1
)
(
s
s
G
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
0.5
Time [s]
A
m
pl
it
ud
e
0.5
1
1.5
2
2.5
3
Step Response
Elektrotechnika
Podstawy Automatyki 1
ODPOWIEDZI
4
c.
s
s
G
2
)
(
d.
1
2
5
)
(
s
s
s
G
Time [s]
A
m
pl
it
ud
e
Step Response
0
0.2
0.4
0.6
0.8
1
0.5
1
1.5
2
2.5
Time [s]
A
m
pl
it
ud
e
Step Response
0
2 4 6 8 10 12 14 16 18 20
10
20
30
40
50
60
70
80
90
100
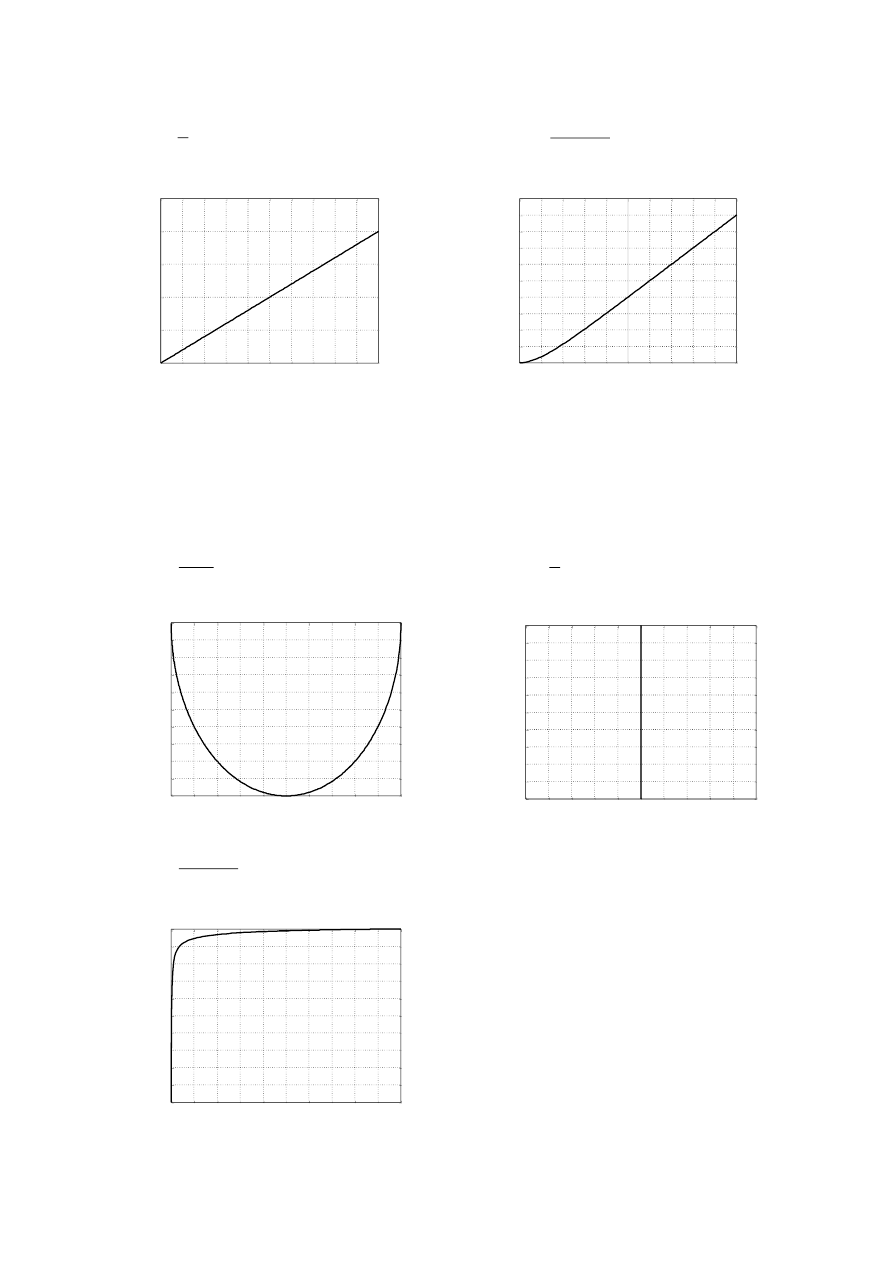
3. (Wykreślić charakterystykę amplitudowo – fazową (Nyquista) obiektów opisanych
transmitancją operatorową identyczną jak w zadaniu I)
a.
5
)
(
s
G
punkt o paramatrach
5
Re
j
G
,
0
Im
j
G
b.
2
1
)
(
s
s
G
c.
s
s
G
2
)
(
0
0.1
0.2
0.3
0.4
0.5
-0.25
-0.20
-0.15
-0.10
-0.05
0
Real Axis
Im
ag
in
ar
y
A
xi
s
Nyquist Diagram
-0.8
-0.4
0
0.4
0.8
-200
-160
-120
-80
-40
0
Real Axis
Im
ag
in
ar
y
A
xi
s
Nyquist Diagram
d.
1
2
5
)
(
s
s
s
G
-10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0
-500
-400
-300
-200
-100
0
Real Axis
Im
agi
na
ry
A
xi
s
Nyquist Diagram
Elektrotechnika
Podstawy Automatyki 1
ODPOWIEDZI
5
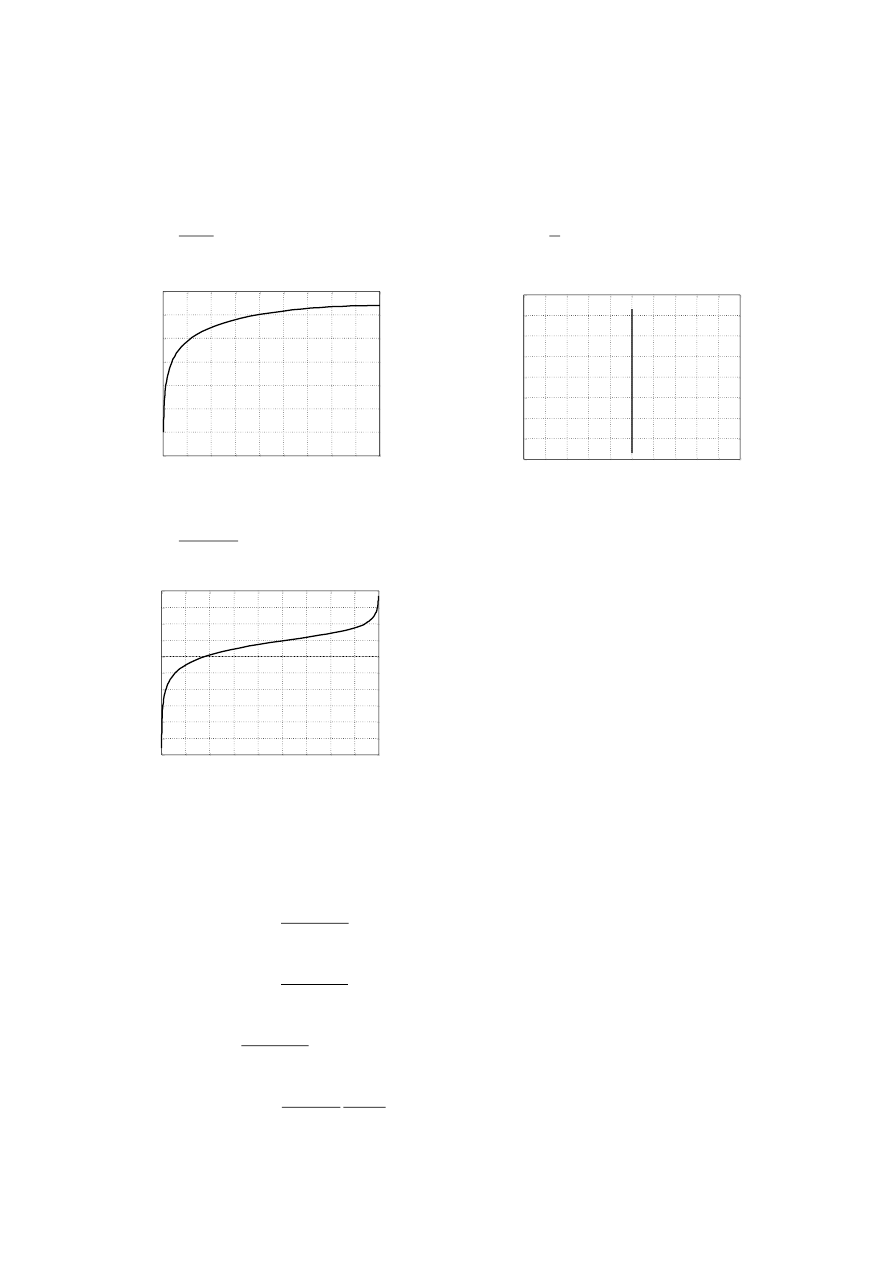
4. (Wykreślić logarytmiczną charakterystykę amplitudowo – fazową (na karcie Nicholsa)
obiektów opisanych transmitancją operatorową identyczną jak w zadaniu I)
a.
5
)
(
s
G
punkt o paramatrach
dB
98
,
13
L
,
0
arg
j
G
b.
2
1
)
(
s
s
G
c.
s
s
G
2
)
(
Open-Loop Phase [deg]
O
pe
n-
L
oop
G
ai
n
[d
B
]
Nichols Charts
-80 -70 -60 -50 -40 -30 -20 -10 0
-70
-60
-50
-40
-30
-20
-10
0
Open-Loop Phase [deg]
O
pe
n-
L
oop
G
ai
n
[d
B
]
Nichols Charts
-91
-90
-89
-60
-40
-20
0
20
40
60
80
d.
1
2
5
)
(
s
s
s
G
Open-Loop Phase [deg]
O
pe
n-
L
oo
p
G
ai
n
[d
B
]
Nichols Charts
-180
-160
-140
-120
-100
-100
-80
-60
-40
-20
0
20
40
60
80
6. (Wyznaczyć transmitancję operatorową
)
(s
G
dla układów, których uproszczone
logarytmiczne charakterystyki modułu dane są na rysunkach)
a.
2
1
10
1
1
100
100
)
(
s
s
s
G
b.
2
3
1
1
10
1
1
100
100
)
(
s
s
s
s
G
c.
1
01
,
0
1
10
1
10000
)
(
2
s
s
s
s
G
d.
1
01
,
0
1
1
1
10
1
1
1000
10
)
(
s
s
s
s
s
G

Elektrotechnika
Podstawy Automatyki 1
ODPOWIEDZI
6
e.
5
,
0
1
1
,
0
1
1
10
1
)
(
s
s
s
s
G
f.
2
1
01
,
0
1
1
1
,
0
1
1
1
10
1
1
100
100
)
(
s
s
s
s
s
s
G

Elektrotechnika
Podstawy Automatyki 1
ODPOWIEDZI
7
PODSTAWY AUTOMATYKI 1 – ĆWICZENIA
- odpowiedzi
lista zadań nr 3
Algebra schematów blokowych układów ciągłych. Uchyby ustalone
1. (Wyznaczyć transmitancję zastępczą układów jak na rysunkach)
a.
2
1
3
1
1
G
G
G
G
G
d.
4
3
2
1
2
1
1
G
G
G
G
G
G
G
b.
1
G
e.
5
2
4
3
2
4
1
G
G
G
G
G
G
G
G
c.
4
2
3
2
1
1
G
G
G
G
G
G
f.
5
2
4
6
1
3
2
1
1
G
G
G
G
G
G
G
G
G
2. (Dana jest transmitancja układu otwartego
)
(
12
s
G
. Obliczyć wartość uchybów położenia,
prędkości i przyspieszenia)
a.
2
,
0
p
e
v
e
a
e
g.
0
p
e
0
v
e
4
a
e
b.
0
p
e
2
,
0
v
e
a
e
h.
0
p
e
0
v
e
0
a
e
c.
0
p
e
0
v
e
2
,
0
a
e
i.
2
,
0
p
e
v
e
a
e
d.
5
,
0
p
e
v
e
a
e
j.
0
p
e
0
v
e
100
a
e
e.
6
,
0
p
e
v
e
a
e
k.
25
,
0
p
e
v
e
a
e
f.
0
p
e
5
,
1
v
e
a
e
l.
0
p
e
0
v
e
5
,
0
a
e
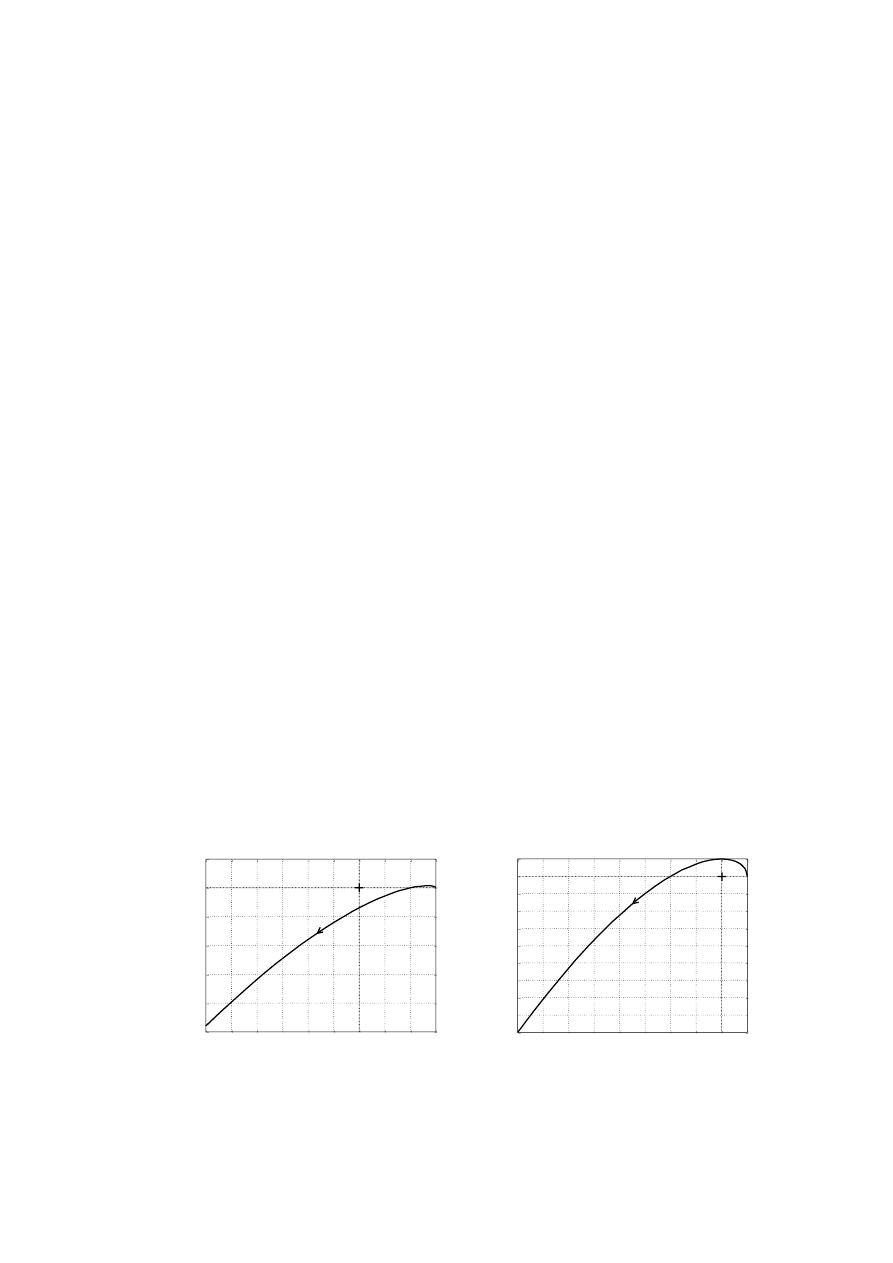
Elektrotechnika
Podstawy Automatyki 1
ODPOWIEDZI
8
PODSTAWY AUTOMATYKI 1 – ĆWICZENIA
- odpowiedzi
lista zadań nr 4
Stabilność układów ciągłych cz.1
1. (Korzystając z kryterium Routh’a zbadać stabilność układu o transmitancji podanej poniżej.
Określić liczbę biegunów w prawej i w lewej półpłaszczyźnie)
a. [5.00 4.00 0.50 -6.00 1.00]
T
układ niestabilny: 2 bieguny w prawej półpłaszczyźnie, 2 bieguny w lewej
b. [1.00 4.00 2.50 0.40 1.00]
T
układ stabilny: 0 biegunów w prawej półpłaszczyźnie, 4 bieguny w lewej
c. [1.00 5.00 6.00 0.1 -6.00]
T
wystąpił zerowy element 1-szej kolumny, przyjęto
1
,
0
układ niestabilny: 1 biegun w prawej półpłaszczyźnie, 3 bieguny w lewej
d. [3.00 2.00 -0.50 1.00]
T
układ niestabilny: 2 bieguny w prawej półpłaszczyźnie, 1 biegun w lewej
e. [1.00 2.00 1.00 4.00]
T
układ stabilny: 0 biegunów w prawej półpłaszczyźnie, 3 bieguny w lewej
f. [5.00 1.00 -4.00 1.00]
T
układ niestabilny: 2 bieguny w prawej półpłaszczyźnie, 1 biegun w lewej
2. (Dana jest transmitancja
)
(
12
s
G
układu otwartego (ze sztywnym sprzężeniem zwrotnym).
Wykorzystując kryterium Michajłowa zbadać czy układ zamknięty jest stabilny)
a. niestabilny
b. stabilny
-5 -4 -3 -2 -1
0
1
2
3
-20
-15
-10
-5
0
5
Real(M)
Im
ag
(M
)
-14 -12 -10 -8 -6 -4 -2 0
2
-16
-14
-12
-10
-8
-6
-4
-2
0
2
Real(M)
Im
ag
(M)
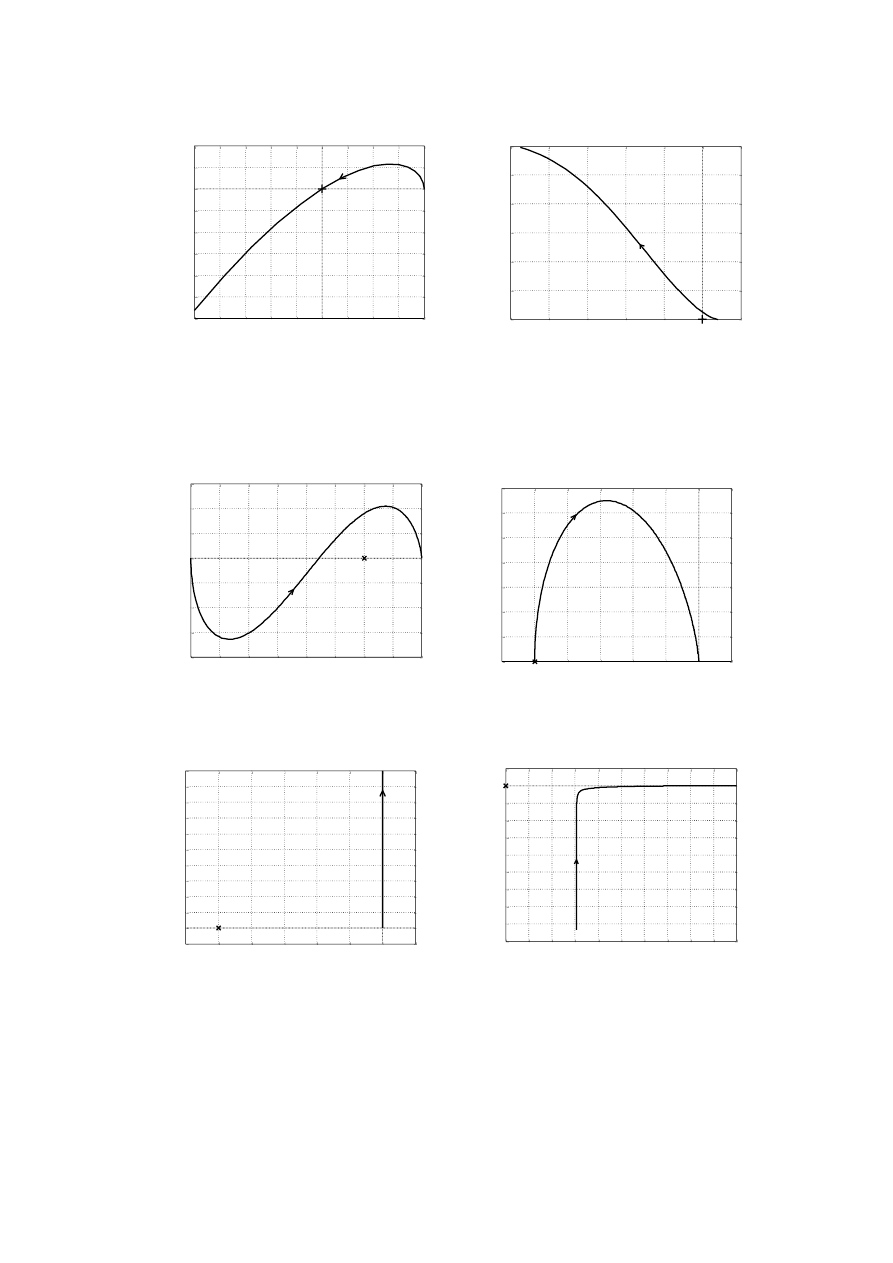
Elektrotechnika
Podstawy Automatyki 1
ODPOWIEDZI
9
c. granica stabilności
d. stabilny
-2
-1
0
1
2
-5
-4
-3
-2
-1
0
1
2
Real(M)
Im
ag
(M
)
-20
-15
-10
-5
0
5
0
1
2
3
4
5
6
Real(M)
Im
ag
(M
)
3. (Dana jest transmitancja
)
(
12
s
G
układu otwartego. Wykorzystując kryterium Nyquista
zbadać czy układ zamknięty jest stabilny)
a. niestabilny
b. niestabilny
-4 -3.5 -3 -2.5 -2 -1.5 -1 -0.5 0
-0.3
-0.2
-0.1
0
0.1
0.2
0.3
Real(G12)
Im
ag
(G
12
)
-1 -0.8 -0.6 -0.4 -0.2
0
0.2
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
Real(G12)
Im
ag
(G
12)
c. niestabilny
d. stabilny
-1 -0.8 -0.6 -0.4 -0.2
0
0.2
0
200
400
600
800
1000
Real(G12)
Im
ag
(G
12
)
-1
-0.8
-0.6
-0.4
-0.2
0
-80
-70
-60
-50
-40
-30
-20
-10
0
10
Real(G12)
Im
ag
(G
12)
4. (Dana jest transmitancja
)
(
12
s
G
układu otwartego. Wykorzystując kryterium Nyquista
zbadać dla jakiego k układ zamknięty jest stabilny)
a. k < 512
c. k < 240
b. k < 32
d. k < 4

Elektrotechnika
Podstawy Automatyki 1
ODPOWIEDZI
10
PODSTAWY AUTOMATYKI 1 – ĆWICZENIA
- odpowiedzi
lista zadań nr 5
Stabilność układów ciągłych cz.2
1. (Dana jest transmitancja
)
(
12
s
G
układu otwartego. Wykorzystując kryterium logarytmiczne
zbadać czy układ zamknięty jest stabilny)
a. układ zamknięty stabilny
1,732
1
,
dB
-1,16
1
L
,631
1
2
,
06
,
3
)
(
arg
2
12
j
G
b. układ zamknięty stabilny
,464
3
1
,
dB
144
,
2
1
L
,094
3
2
,
99
,
2
)
(
arg
2
12
j
G
c. układ zamknięty niestabilny
0,573
1
,
dB
3,18
1
L
2,236
2
,
02
,
12
)
(
arg
2
12
j
G
2. (Dana jest transmitancja
)
(
12
s
G
układu otwartego. Obliczyć zapas fazy i wzmocnienia dla
układu zamkniętego)
a. układ. zamknięty stabilny,
1,732
1
,
dB
,021
6
dB
K
,
,233
1
2
,
o
7,1
2
b. układ zamknięty stabilny,
014
,
1
1
,
dB
068
,
1
dB
K
,
0,866
2
,
o
,8
0
2
c. układ zamknięty stabilny,
928
,
6
1
,
dB
08
,
24
dB
K
, brak
2
dla którego
1
)
(
2
12
j
G
,
czyli
d. układ zamknięty stabilny, brak
1
dla którego
)
(
arg
2
12
j
G
, czyli
K
brak
2
dla którego
1
)
(
2
12
j
G
, czyli
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron