
METODY
MECHANIKI KWANTOWEJ

1.
Mechanika kwantowa (QM)
a) Funkcja falowa i równanie Schrödingera
b)
Układ wielu cz
ą
stek
c)
Przybli
ż
enie Borna-Oppenheimera
d)
Orbitale molekularne
e)
Metody ab initio a półempiryczne
2.
Silniki obliczeniowe dla QM
METODY MECHANIKI KWANTOWEJ
Modelowanie i symulacje molekularne
METODY MECHANIKI KWANTOWEJ
Modelowanie i symulacje molekularne
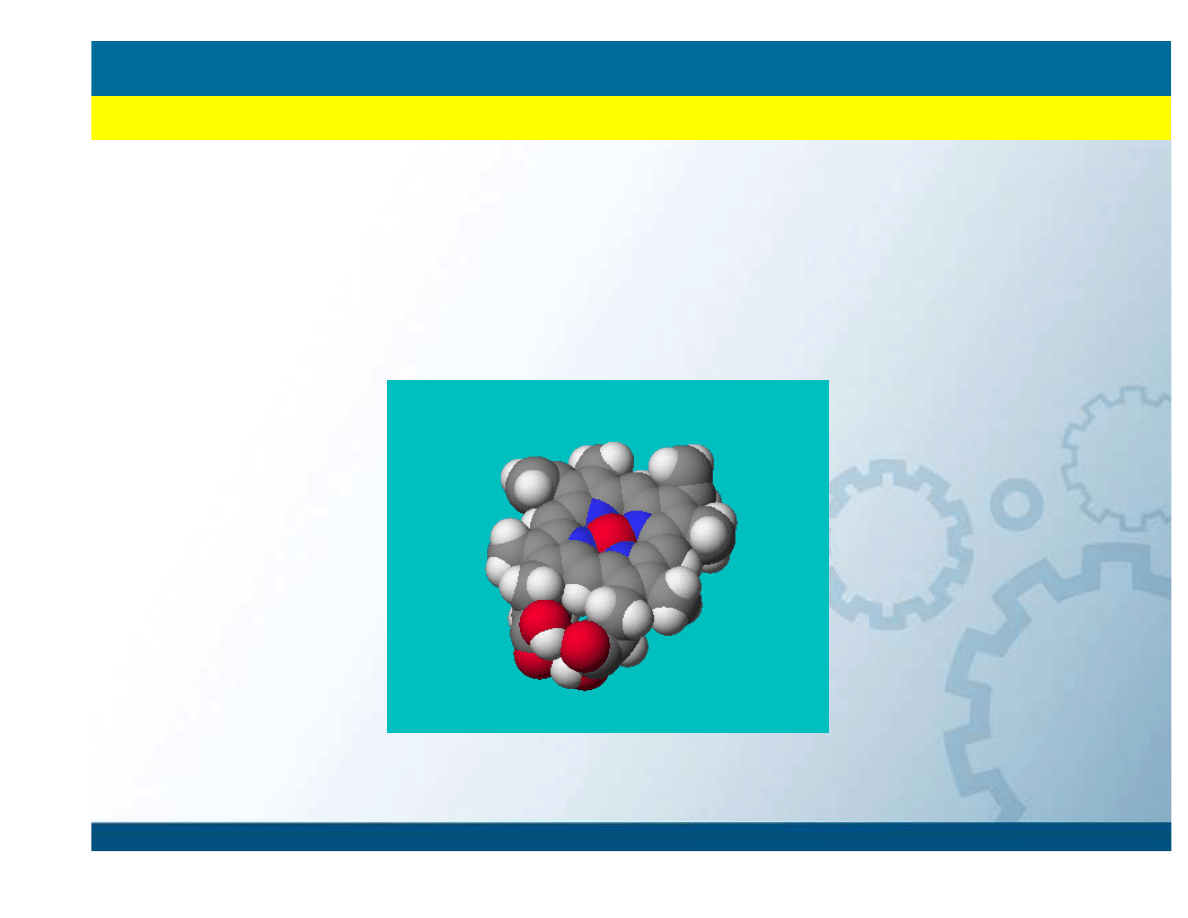
IDEA MECHANIKI KWANTOWEJ
Modelowanie i symulacje molekularne
• Cz
ą
steczka jest zespołem oddziałuj
ą
cych ze sob
ą
j
ą
der atomowych i
elektronów poruszaj
ą
cych si
ę
zgodnie z prawami mechaniki kwantowej
• Opis układu poprzez równanie Schrödingera

METODY MECHANIKI KWANTOWEJ
Równanie Schrödingera
„The underlying physical laws necessary for the
mathematical theory of a large part of physics and the
whole of chemistry are thus completely known.”
[P. A. M. Dirac, Proc. Roy. Soc. (London) 123, 714 (1929)].
Ψ
=
ΗΨ
E
Wej
ś
cie:
Hamiltonian H opisuje energi
ę
cz
ą
stek i oddziaływa
ń
pomi
ę
dzy nimi
Wyj
ś
cie:
E – warto
ść
całkowitej energii układu (molekuły, nanostruktury)
Ψ
Ψ
Ψ
Ψ
- funkcja falowa opisuj
ą
ca stan układu (molekuły, nanostruktury)
METODY MECHANIKI KWANTOWEJ
Równanie Schrödingera
Mechanika kwantowa opisuje du
żą
cz
ęść
fizyki i cał
ą
chemi
ę
!

K
n
(R) – całkowita energia kinetyczna j
ą
der
K
e
(r) – całkowita energia kinetyczna elektronów
V
ee
(r,r) – energia potencjalna oddziaływa
ń
mi
ę
dzyelektronowych
V
ne
(R,r) - energia potencjalna oddziaływa
ń
j
ą
der z elektronami
V
nn
(R,R) - energia potencjalna oddziaływa
ń
mi
ę
dzyj
ą
drowych
)
,
(
)
,
(
)
,
(
)
(
)
(
)
,
(
R
R
V
r
R
V
r
r
V
r
K
R
K
r
R
nn
ne
ee
e
n
+
+
+
+
=
Η
R – opisuje poło
ż
enia j
ą
der
r - opisuje poło
ż
enia elektronów
Całkowita energia:
METODY MECHANIKI KWANTOWEJ
Równanie Schrödingera
METODY MECHANIKI KWANTOWEJ
Równanie Schrödingera
Przybli
ż
enie Borna-Oppenheimera:
Hamiltonian elektronowy :
)
,
(
)
,
(
)
(
)
(
r
R
V
r
r
V
r
K
r
ne
ee
e
el
+
+
=
Η
)
(
)
(
)
(
r
E
r
r
el
el
el
el
Ψ
=
Ψ
Η
J
ą
dra poruszaj
ą
si
ę
znacznie wolniej ni
ż
elektrony
METODY MECHANIKI KWANTOWEJ
Równanie Schrödingera
METODY MECHANIKI KWANTOWEJ
Równanie Schrödingera
Hamiltonian j
ą
drowy:
)
(
)
,
(
)
(
)
(
R
E
R
R
V
R
K
R
el
nn
n
+
+
=
Η
Elektrony poruszaj
ą
si
ę
znacznie szybciej ni
ż
j
ą
dra i w zwi
ą
zku z tym
szczegółowy opis ich ruchu mo
ż
na zast
ą
pi
ć
opisem ich
ś
rednich poło
ż
e
ń
)
(
)
(
R
E
r
el
el
=
Η
(Hiper)powierzchnia energii
potencjalnej
Przybli
ż
enie Borna-Oppenheimera:
)
(R
V
PES
METODY MECHANIKI KWANTOWEJ
Równanie Schrödingera

)
(
)
(
)
(
R
V
R
K
R
H
PES
n
+
=
)
(R
V
T
E
+
=
Podobie
ń
stwo do mechaniki klasycznej,
gdzie:
V(R) - pola siłowe dedukowane z teorii i
parametryzowane z oblicze
ń
teoretycznych
lub z danych eksperymentalnych
V
PES
(R) – wymaga rozwi
ą
zania równania
Schr. dla ka
ż
dego R
)
(R
V
PES
Wystarczy do oblicze
ń
Single Point i Geometry Optimization
)
(R
K
n
+
Nale
ż
y uwzgl
ę
dni
ć
w kwantowych obliczeniach dynamiki
molekularnej
METODY MECHANIKI KWANTOWEJ
Równanie Schrödingera

Funkcje falowe orbitali molekularncych
Slater Type Orbitals (STOs)
(w metodach półempirycznych)
LCAO-MO (Linear Combination of Atomic Orbitals – Molecular Orbital)
∑
Φ
=
Ψ
ν
ν
ν
i
i
C
C
ν
i
- współczynnik okre
ś
laj
ą
cy wag
ę
ν
-go orbitalu
atomowego w i-tym orbitalu molekularnym
Gaussian Type Orbitals (GTOs)
(w metodach ab initio)
METODY MECHANIKI KWANTOWEJ
Sk
ą
d posta
ć
orbitali atomowych
Φ
Φ
Φ
Φ
νννν
?
Funkcje falowe orbitali molekularnych
METODY MECHANIKI KWANTOWEJ
Jak konstruowa
ć
orbitale molekularne?
Z rozwi
ą
zania r. Schr. dla atomu wodoru
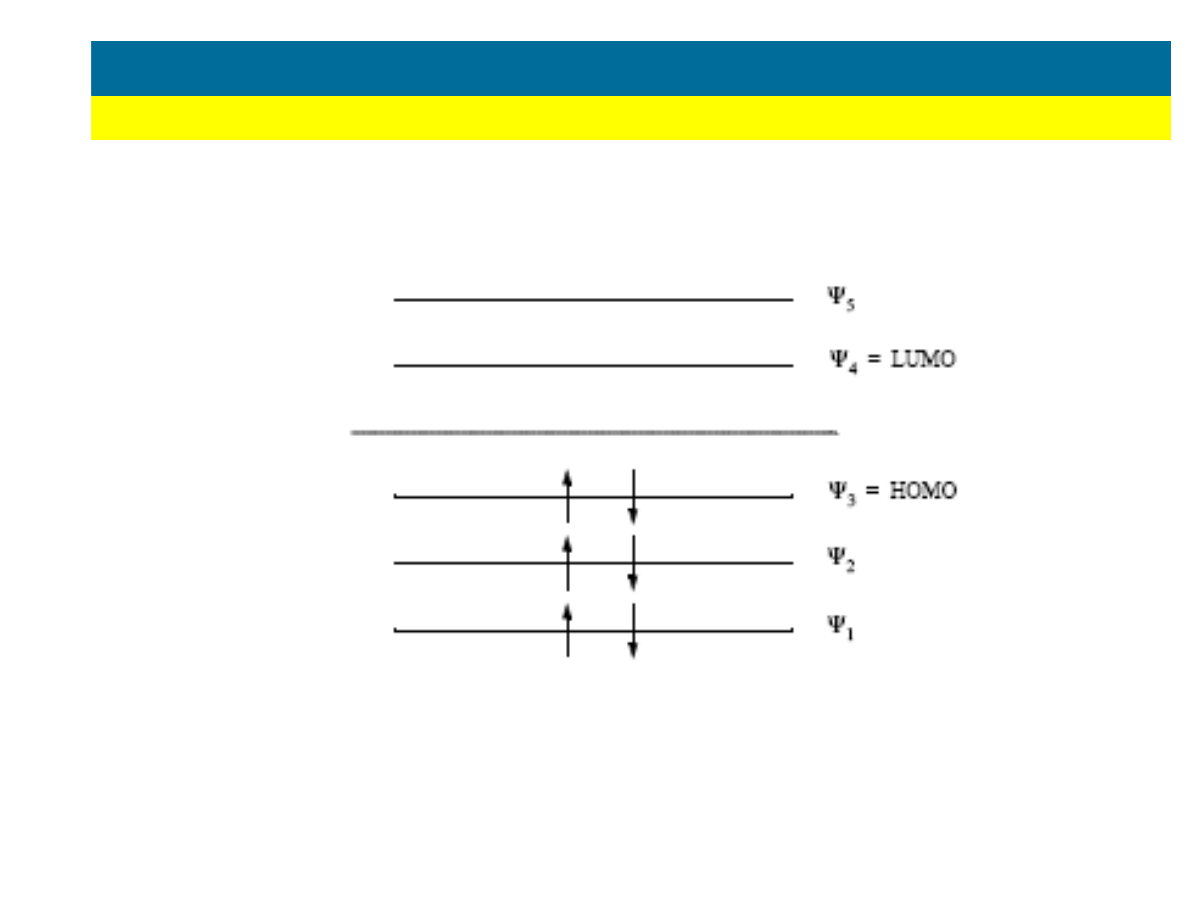
Diagramy energetyczne orbitali
METODY MECHANIKI KWANTOWEJ
Diagramy energetyczne orbitali
METODY MECHANIKI KWANTOWEJ
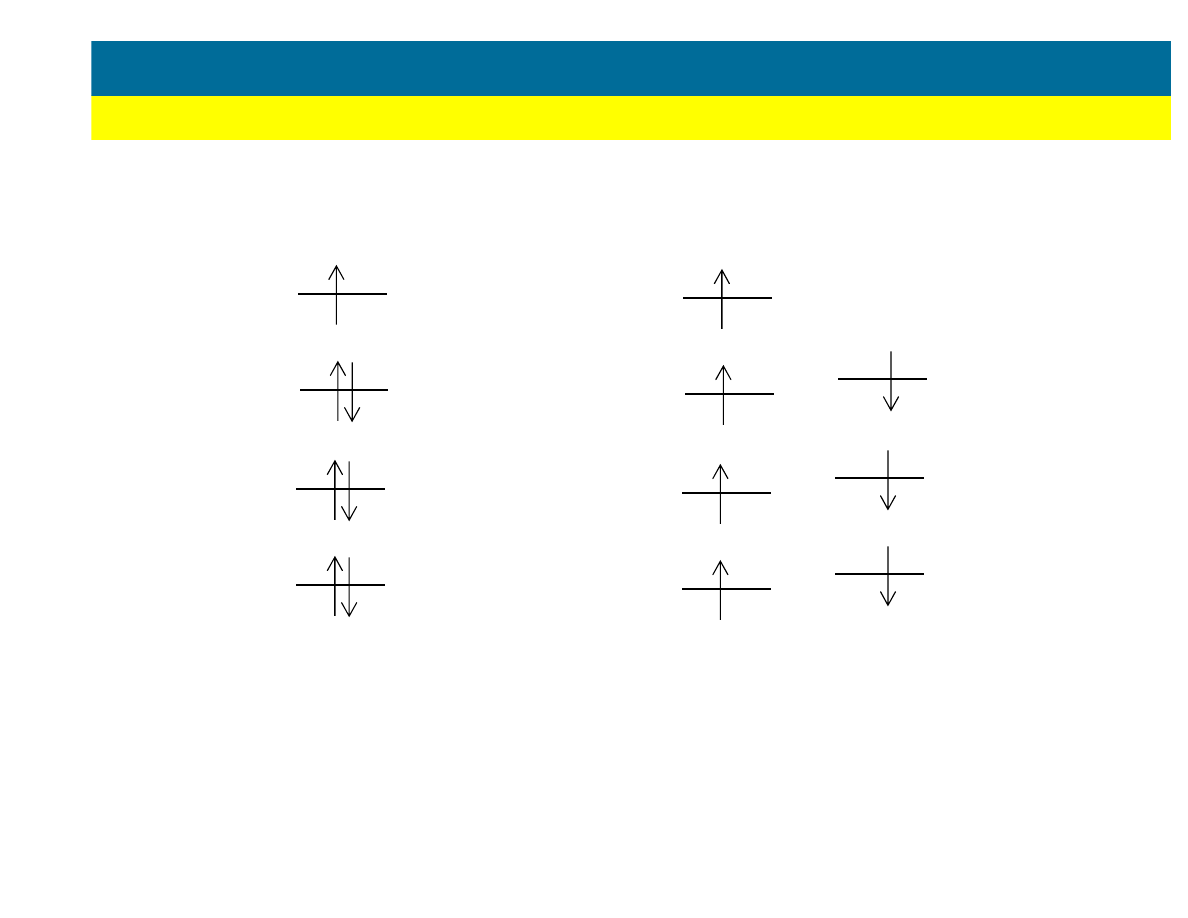
Restricted Hartree Fock (RHF)
Unrestricted Hartree Fock (UHF)
(wi
ę
kszo
ść
stabilnych cz
ą
steczek
organicznych)
(wolne rodniki, niestabilne nanostruktury,
tak
ż
e cz
ą
steczki o du
ż
ej symetrii, np. O
2
)
Diagramy energetyczne orbitali
METODY MECHANIKI KWANTOWEJ
ψ
1
ψ
2
ψ
3
ψ
4
ψ
1
α
ψ
2
α
ψ
3
α
ψ
4
α
ψ
1
β
ψ
2
β
ψ
3
β

MM
QM
Układ molekularny
Zespół atomów
oddziaływuj
ą
cych ze sob
ą
poprzez pola siłowe
Zespół j
ą
der i elektronów
poruszaj
ą
cych si
ę
zgodnie z prawami
QM
Podstawa
teoretyczna
Fizyka Newtonowska
Równanie Schrödingera
Dane wej
ś
ciowe
Wzór strukturalny,
grupy chemiczne,
rodzaje atomów, ich
hybrydyzacja,
typy wi
ą
za
ń
(wielokrotno
ść
)
Wzór strukturalny
Dane wyj
ś
ciowe -
wyniki
Zoptymalizowana geometria
(konformacja)
Zoptymalizowana geometria,
wielokrotno
ś
ci wi
ą
za
ń
, momenty
dipolowe, orbitale molekularne,
wła
ś
ciwo
ś
ci elektronowe itp
Typ energii dla
optymalizacji
geometrii
Energia wzgl
ę
dna (steryczna)
Energie termodynamiczne i/lub
energia całkowita zale
ż
nie od metody
Mechanika kwantowa a molekularna (klasyczna)
METODY MECHANIKI KWANTOWEJ

Metody ab initio (z pierwszych zasad)
- obliczaj
ą
wszystkie elektrony wł
ą
czaj
ą
c elektrony rdzenia atomowego
Metody półempiryczne
- obliczaj
ą
tylko elektrony walencyjne, natomiast elektrony rdzenia brane s
ą
pod uwag
ę
w sposób po
ś
redni (np. cz
ęś
ciowo ekranuj
ą
ładunek j
ą
dra
atomowego), korzysta si
ę
z parametrów empirycznych
Metody ab initio a półempiryczne
METODY MECHANIKI KWANTOWEJ
Metody ab initio a półempiryczne
METODY MECHANIKI KWANTOWEJ
Teoria funkcjonałów g
ę
sto
ś
ci (ang. Density Functional Theory, DFT)
- nie okre
ś
la si
ę
funkcji falowej tylko tzw. funkcjonał g
ę
sto
ś
ci elektronowej
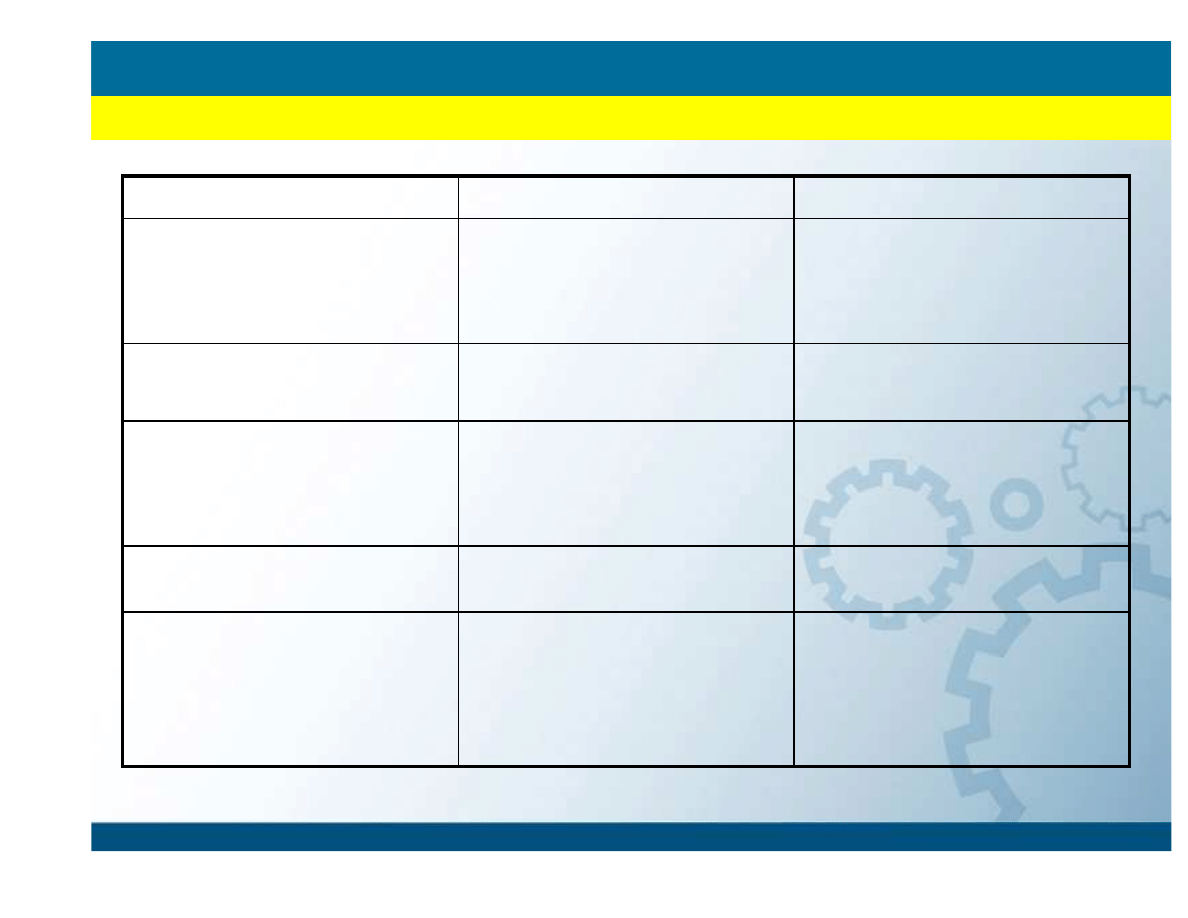
Półempiryczne
Ab initio
Traktowanie elektronów
Tylko walencyjne
wszystkie wł
ą
czaj
ą
c
rdzeniowe
Orbitale atomowe
Slater Type Orbitals (STOs)
Gaussian Type Orbitals
(GTOs)
Parametry
Empiryczne lub policzone
metodami Ab initio
Szybko
ść
i dokładno
ść
Szybsze
Zwykle dokładniejsze
Stosowane do układów:
Du
ż
ych nanostruktur i
cz
ą
steczek, w tym polimerów
i biomolekuł
Małych i
ś
rednich
cz
ą
steczek, głównie
nieorganicznych, ale z
rozwojem metod i sprz
ę
tu
coraz wi
ę
kszych
Metody ab initio a półempiryczne
METODY MECHANIKI KWANTOWEJ
Metody ab initio a półempiryczne
METODY MECHANIKI KWANTOWEJ

Powszechnie stosowane w pakietach obliczeniowych:
• ExtHückel
• MOPAC (AM1, PM3, PM5)
• ZINDO
• DGauss (ab initio)
Silniki obliczeniowe
METODY MECHANIKI KWANTOWEJ
Silniki obliczeniowe
METODY MECHANIKI KWANTOWEJ
Silniki obliczeniowe
METODY MECHANIKI KWANTOWEJ
Silniki obliczeniowe
METODY MECHANIKI KWANTOWEJ

ExtHückel
MOPAC
ZINDO
Based on the Extended
Hückel theory
Molecular Orbital Package by
James Stewart
Prof. M.C. Zerner’s Intermediate
Neglect of Differenctial Overlap
program
Prosty i szybki, ale
ograniczenie liczby
atomów (do 150)
Zło
ż
ony z empiryczn
ą
parametryzacj
ą
,
Specjalna wersja dla układów
supramolekularnych (dziesi
ą
tki
tysi
ę
cy atomów
Zło
ż
ony z teoretyczn
ą
(ab initio)
parametryzacj
ą
Tylko Single Point bez
optymalizacji geometrii
Z optymalizacj
ą
,
Lepszy ni
ż
ZINDO do wyznaczania
struktury i obliczania energii
Z optymalizacj
ą
Parametry dla
wszystkich pierwiastków
Parametry w tablicach
Dla wi
ę
cej pierwiastków ni
ż
MOPAC
Tylko niektóre
wła
ś
ciwo
ś
ci
elektronowe
Wi
ę
kszo
ść
wła
ś
ciwo
ś
ci
elektronowych
Wi
ę
kszo
ść
wła
ś
ciwo
ś
ci
elektronowych, wł
ą
czaj
ą
c widma
elektronowe (specjalna procedura
dla stanów wzbudzonych)
Całkowita energia
molekularna [a.u.]
Ciepło tworzenia (entalpia)
[kcal/mol] przy 25ºC
Całkowita energia molekularna
[a.u.] przy 0K
Półempiryczne silniki obliczeniowe
METODY MECHANIKI KWANTOWEJ

MOPAC
QUANTUM MECHANICS
Hamiltoniany powszechnie u
ż
ywane w MOPACu:
• AM1
• PM3
• PM5

Całkowita energia molekularna (Total molecular energy)
– energia konieczna do rozseparowania cz
ą
steczki na izolowane j
ą
dra i
elektrony
Ciepło (entalpia) tworzenia = TE cz
ą
steczki – TE atomów
Ciepło reakcji = TE produktu – TE reaktantów
1 a.u. = 1 Ha = 627.51 kcal/mol = 27,2 eV
Energia
METODY MECHANIKI KWANTOWEJ
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron