
Egzamin dla Aktuariuszy z 15 czerwca 2002 r.
Matematyka Finansowa
Zadanie 1
÷
ø
ö
ç
è
æ
=
+
=
÷
ø
ö
ç
è
æ
=
+
=
ò
ò
t
II
s
II
t
I
s
I
ds
t
t
A
ds
t
t
A
0
0
exp
2
)
(
exp
2
1
)
(
δ
δ
Z tego wynika:
ò
ò
=
+
=
÷÷
ø
ö
çç
è
æ
+
t
II
s
t
I
s
ds
t
ds
t
0
0
)
2
ln(
2
1
ln
δ
δ
Po obustronnym obliczeniu pochodnych mamy:
t
t
t
t
t
t
t
II
t
I
t
+
=
−
−
=
⋅
+
=
2
1
4
16
2
4
4
1
2
1
1
2
δ
δ
Czyli:
)
2
(
8
48
4
4
4
16
2
4
3
2
2
1
2
2
t
t
t
t
t
t
t
t
t
t
+
=
+
−
→
−
−
=
+
Po podniesieniu obustronnym do kwadratu mamy:
0
144
40
9
6
2
3
4
=
+
−
+
−
t
t
t
t
4 jest pierwiastkiem i nie ma ujemnych więc dzielimy przez t-4
36
2
2
3
−
+
−
→
t
t
t
Znowu nie ma ujemnych i 4 jest pierwiastkiem, znowu dzielimy przez t-4 i otrzymujemy:
0
bo
e
rozwiąozwi
jedyne
4
0
9
2
2
<
∆
=
→
>
+
+
t
t
t
Zadanie 2
I.
NIE bo:
m
i
m
i
i
mi
v
i
m
t
m
t
m
≠
+
=
∂
∂
→
+
=
å
=
2
1
)
(
)
1
(
1
II.
TAK bo
1
2
)
1
(
)
1
(
)
1
(
1
)
1
(
1
klamrowy
nawias
−
−
−
=
∂
∂
→
−
+
−
−
−
−
−
=
n
n
n
n
d
n
d
d
n
d
d
d
d
III.
NIE bo
2
)
1
(
)
1
ln(
)
1
(
)
1
ln(
i
i
i
i
i
i
i
i
a
a
n
n
+
+
+
−
=
∂
∂
→
+
=
[
]
)
1
ln(
)
1
(
)
1
ln(
)
1
(
)
1
(
2
i
i
i
i
i
i
v
LEWA
n
+
+
−
+
+
−
=
LEWA
PRAWA
≠
Zadanie 3
ef
i
v
v
a
a
X
L
1
1
1
=
−
=
=
∞
∞
∞
∞
∞
=
=
=
=
a
X
ZAD
a
X
ZAD
a
X
L
ZAD
1
2
2
1
1
1
0
9
,
0
9
,
0
1
2
2
1
1
1
'
9
,
0
9
,
0
%
10
X
X
a
X
a
X
a
X
ZAD
=
→
=
=
−
=
∞
∞
∞
...
...
9
,
0
9
,
0
1
2
3
1
2
1
X
X
X
X
a
L
X
=
=
=
∞
...
...
9
,
0
1
,
0
2
1
,
0
1
1
2
1
1
∞
∞
⋅
+
=
+
=
a
X
X
WP
a
X
X
WP
L
ZAD
a
L
X
ZAD
X
WP
i
i
i
i
i
i
i
9
,
0
9
,
0
1
,
0
1
1
=
=
+
=
→
∞
−
−
Spłacony kapitał:
1
1
1
9
,
0
1
,
0
9
,
0
9
,
0
−
−
−
=
−
=
−
=
i
i
i
i
i
i
L
L
L
ZAD
ZAD
SK
ef
i
i
i
i
i
i
i
i
i
i
i
Li
v
v
L
L
L
a
L
L
ZAD
X
SK
WP
I
1
1
1
1
1
1
1
9
,
0
)
1
)(
9
,
0
(
9
,
0
1
,
0
9
,
0
1
,
0
9
,
0
9
,
0
1
,
0
1
,
0
−
−
−
−
∞
−
−
−
=
−
=
=
⋅
−
⋅
+
=
−
+
=
−
=
22700
1
,
0
2
,
2
5000
10
32
,
1
2
,
1
1
,
1
9
,
0
5000
1
,
1
10
9
,
0
1
1
1
1
≈
⋅
=
→
ï
î
ï
í
ì
→
=
+
=
=
=
å
å
å
−
∞
=
−
∞
=
I
L
i
L
i
I
Li
L
i
I
I
ef
ef
i
i
ef
ef
i
i
i
Zadanie 4
ï
ï
î
ïï
í
ì
−
=
−
+
=
+
+
+
⋅
+
=
+
+
+
⋅
+
=
3000
6
4
12
.
3
)
(
7
,
0
2
,
1
.
2
)
...
(
.
1
12
9
6
3
12
12
12
6
3
12
012
,
0
012
,
0
;
12
X
K
Y
X
OD
v
v
v
v
Y
v
Xa
K
v
v
v
Y
v
Xa
K

12
12
3
12
5
,
0
3
,
0
.
2
7
,
0
.
1
)
...
(
5
,
0
2
,
0
.
2
2
,
1
.
1
a
K
X
v
v
v
K
Y
=
→
−
⋅
+
+
=
→
−
⋅
Wstawiamy do 3:
1,2%
i
stopie
przy
liczone
to
)
...
(
5
,
0
8
,
0
5
,
0
8
,
1
1
3000
12
3
12
12
=
+
+
−
−
=
→
v
v
v
a
K
Oznaczenia:
A - w I roku
B - w II roku
X
AY
B
Y
X
B
A
3
4
12
12
12
=
→
=
1%
stopa
tu
-
12
12
12
Ba
v
Aa
K
+
=
920
3
01
,
1
1
3
01
,
0
;
12
12
01
,
0
;
12
12
12
12
≈
÷
ø
ö
ç
è
æ
+
=
→
+
=
a
X
Y
a
K
A
a
X
AY
v
Aa
K
Zadanie 5
107
59
55
54
51
50
2
99
51
50
2
5
...
)
5
49
...
5
(
...
)
5
53
...
5
(
)
5
54
...
5
(
...
)
5
51
...
5
(
)
5
50
...
5
(
...
)
5
2
5
(
5
5
...
)
5
49
...
5
(
)
5
50
...
5
(
...
)
5
2
5
(
5
v
v
v
v
v
v
v
v
II
v
v
v
v
v
I
B
A
+
+
⋅
+
+
+
+
⋅
+
+
+
+
⋅
+
+
+
+
⋅
+
+
+
⋅
+
+
+
+
⋅
+
+
=
+
+
⋅
+
+
+
⋅
+
+
+
+
⋅
+
+
=
4
4
4
4
4
3
4
4
4
4
4
2
1
4
4
4
4
4
4
4
3
4
4
4
4
4
4
4
2
1
å
å
=
=
−
−
+
+
+
+
=
+
=
54
51
58
55
8
piechotęi
"
na
liczymy
sumy
te
)
109
)(
108
(
2
5
)
1
(
2
5
k
k
k
k
v
k
k
kv
k
B
v
A
II
B
A
I
i
ć
wyprowadz
mozna
to
-
1
50
2
2
5
51
2
50
50
50
ú
ú
û
ù
ê
ê
ë
é
−
−
−
+
=
v
v
a
Ia
Ia
A
B=5576-A
5700
.....
8
≈
+
=
B
v
A
II
Zadanie 6
02
,
0
e
- zwrot w ci
ą
gu 3 miesi
ę
cy =
25
,
0
08
,
0
⋅
e
i
ψ
- cena instrumentu pierwotnego daj
ą
cego 1,2 lub 0,8
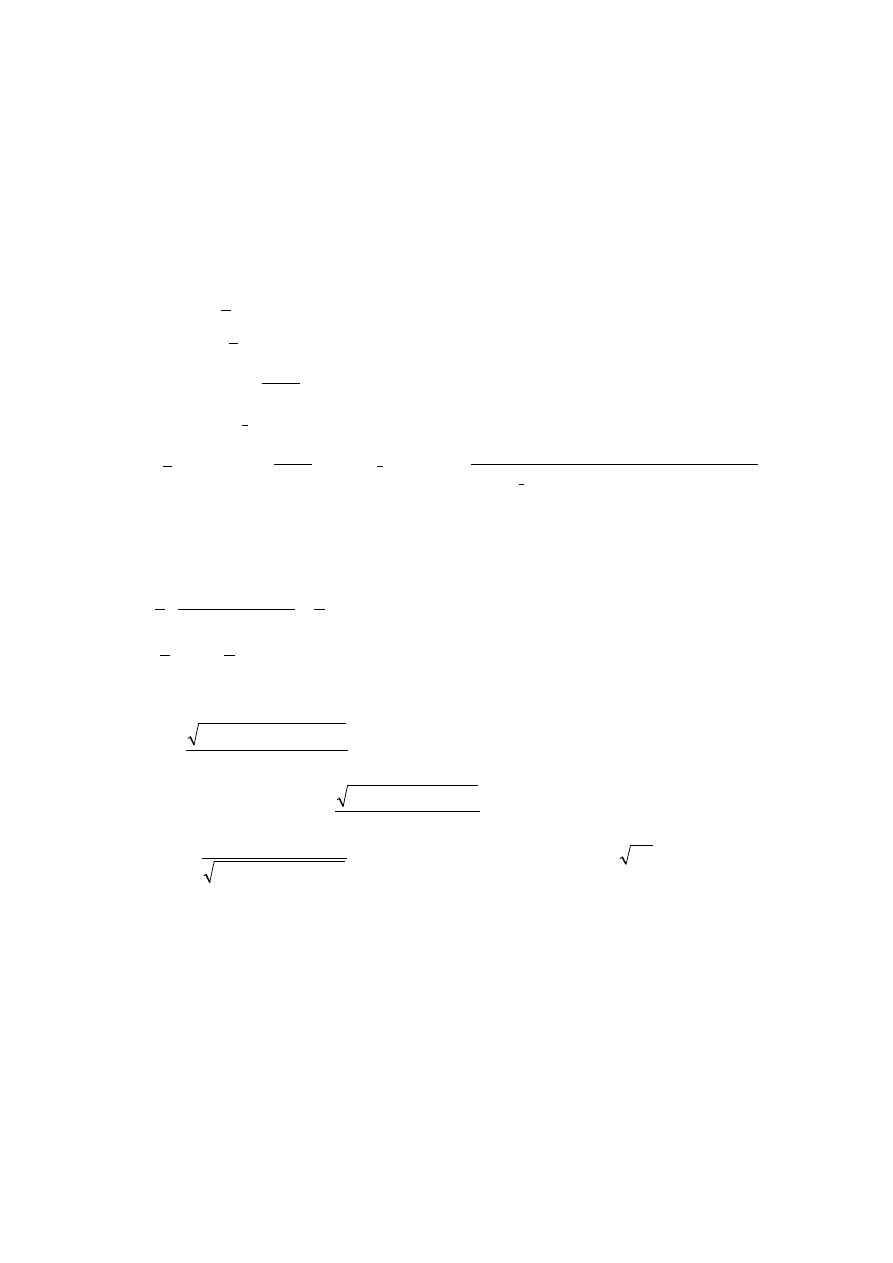
Z teorii wiemy:
1
2
1
02
,
0
2
1
1
)
(
1
8
,
0
2
,
1
ψ
ψ
ψ
ψ
ψ
→
î
í
ì
=
+
=
+
e
%
55
02
,
0
1
1
≈
=
e
P
ψ
Zadanie 7
20
;
20
1500
5
,
1
1500
j
j
v
ja
P
+
⋅
=
15
;
15
1500
5
,
1
1500
5
j
j
v
ja
P
+
⋅
=
5
5
3000
)
1
(
3000
i
v
i
KW
=
+
=
08
,
0
;
5
2000
5
a
KW
P
=
+
( )
(
)
5
,
0
1
2250
)
(
1500
2000
3000
2000
3000
1500
2250
3
5
3
5
08
,
0
;
5
5
08
,
0
;
5
5
15
;
15
≈
−
−
−
=
→
=
+
+
j
j
i
i
j
j
v
v
a
v
a
v
v
ja
Zadanie 8
(
)
ò
ò
+
+
+
=
+
+
+
=
8
12
6
ln
3
1
...
24
24
6
3
1
2
4
6
6
3
5
t
t
t
t
t
t
t
t
δ
ò
ò
=
→
=
=
+
=
−
=
1
0
1
0
5
,
0
5
,
1
)
exp(
1
5
,
1
ln
8
ln
3
1
27
ln
3
1
i
i
s
s
δ
δ
ò
÷
÷
ø
ö
ç
ç
è
æ
+
+
+
=
T
s
T
T
T
0
3
2
4
6
2
8
12
6
ln
δ
2
8
12
6
)
5
,
0
1
(
)
(
)
(
)
(
3
2
4
6
+
+
+
−
+
=
−
=
t
t
t
t
t
B
t
A
t
f
(
)
3
3
5
3
5
3
2
4
6
.....
8
8
2
0
8
8
2
8
12
6
(....)
5
,
0
5
,
0
)
(
=
+
+
→
=
+
+
+
+
+
−
=
′
t
t
t
t
t
t
t
t
t
t
f
i podnosimy do
trzeciej pot
ę
gi obustronnie
4
6
8
2
4
8
10
12
2
4
2
4
6
4
6
8
6
8
10
8
10
12
3
96
160
24
64
192
144
36
12
)
64
64
16
128
128
32
96
96
24
32
32
8
4
4
(
8
t
t
t
t
t
t
t
t
t
t
t
t
t
t
t
t
t
t
t
t
t
t
t
+
+
+
+
+
+
+
+
=
=
+
+
+
+
+
+
+
+
+
+
+
+
+
+
Z tego wynika,
ż
e
5
,
0
1
8
3
=
→
=
t
t
Zadanie 9
10
8
9
10
)
1
(
7
)
(
)
1
(
4
)
1
(
2
)
1
(
)
(
i
i
X
i
i
i
i
P
+
=
+
+
+
+
+
=
Mo
ż
na naszkicowa
ć
wykres:
Analogicznie dla banku B:
10
8
9
10
)
1
(
7
)
(
)
1
(
4
)
1
(
2
)
1
(
)
(
j
j
X
j
j
j
j
P
+
=
+
+
+
+
+
=
St
ą
d:
1
1
1
1
)
(
8
)
(
i
i
i
P
i
i
BC
i
P
−
−
=
−
≈
′
Z rysunku wida
ć
,
ż
e
1
7
8
7
8
32
7
8
18
7
8
10
7
8
4
7
8
2
7
8
8
1
7
8
1
,
0
7
,
0
8
,
0
9
,
0
8
,
0
9
,
0
1
,
0
1
−
÷
ø
ö
ç
è
æ
+
÷
ø
ö
ç
è
æ
+
÷
ø
ö
ç
è
æ
+
÷
ø
ö
ç
è
æ
÷
ø
ö
ç
è
æ
−
÷
ø
ö
ç
è
æ
−
−
=
→
−
÷
ø
ö
ç
è
æ
=
i
i

Analogicznie:
1
7
10
7
10
32
7
10
18
7
10
10
7
10
4
7
10
2
7
10
10
1
,
0
7
,
0
8
,
0
9
,
0
8
,
0
9
,
0
−
÷
ø
ö
ç
è
æ
+
÷
ø
ö
ç
è
æ
+
÷
ø
ö
ç
è
æ
+
÷
ø
ö
ç
è
æ
÷
ø
ö
ç
è
æ
−
÷
ø
ö
ç
è
æ
−
−
=
j
Z tego :
35
,
11
)
1
(
4
)
1
(
2
)
1
(
8
9
10
≈
+
+
+
+
+
+
+
+
=
j
i
j
i
j
i
ODP
Zadanie 10
Z parytetu opcji kupna i sprzeda
ż
y:
S
dK
P
C
=
+
−
C - cena opcji kupna
P - cena opcji sprzeda
ż
y
d - dyskonto w okresie =
np.
1
1
n
r
+
K - cena wykonania
S - bie
żą
ca cena akcji
obliczone
100
4
3
1
1
7
,
4
2
,
6
95
4
1
1
2
,
2
2
,
5
r
r
r
→
⋅
+
+
−
=
⋅
+
+
−
Po podstawieniu wychodzi około 96,29
Wyszukiwarka
Podobne podstrony:
2002.06.15 matematyka finansowa
2002 06 15 prawdopodobie stwo i statystykaid 21643
2011 06 20 matematyka finansowaid 27373
2001 06 02 matematyka finansowaid 21606
2002 06 15
2008.06.02 matematyka finansowa
2002 10 12 matematyka finansowaid 21647
2001.06.02 matematyka finansowa
1 2000.01.15 matematyka finansowa
2006 06 05 matematyka finansowaid 25460
2010 03 15 matematyka finansowaid 26987
2002.06.15 prawdopodobie stwo i statystyka
2011.06.20 matematyka finansowa
2008.12.15 matematyka finansowa
2002.06.15 pra
1 2000 06 17 matematyka finansowaid 8918
2008 12 15 matematyka finansowaid 26464
2008 06 02 matematyka finansowaid 26453
więcej podobnych podstron