Inżynieria Środowiska

2011/12

Materiały

do wykładu 5

03 11 2011

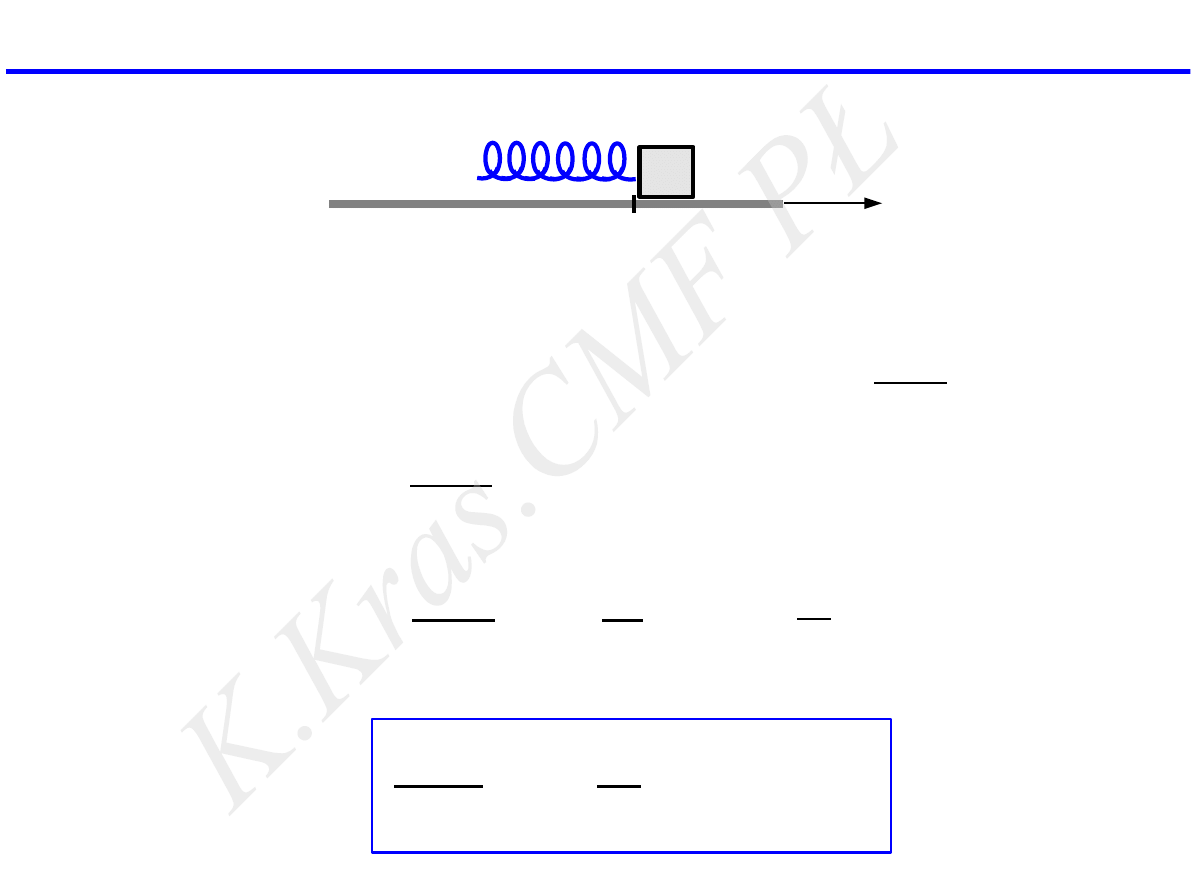
m a = −k x

d

2

x

dt

2

= −

k

m

x = −ω

2

x

m

d

2

x

dt

2

= −

k x

a =

d

2

x

dt

2

dynamiczne równanie oscylatora harmonicznego

drganie harmoniczne proste

oscylator harmoniczny prosty

d

2

x

dt

2

= −

k

m

x

k

m

= ω

2

k

m

x

x=0

x(t) = Asin(ωt+ϕ)

kinematyczne równanie oscylatora harmonicznego

x(t)

A

(ω

t+ϕ)

ϕ

wychylenie z położenia równowagi

amplituda (

maksymalne wychylenie z położenia równowagi)

faza drgania

faza początkowa

ω =

2 π

T

=

2 π f =

√

k

m

częstość kątowa (kołowa) drgania

okres drgania

f =

1

T

częstotliwość drgania

T

x = Asin (ω t+ϕ)

V = Aω cos(ω t+ϕ)

a = − A ω

2

sin(ω t+ϕ) = −ω

2

x

F = −k x = −m ω

2

x

ruch harmoniczny prosty

siła

wychylenie z położenia równowagi

prędkość

przyspieszenie

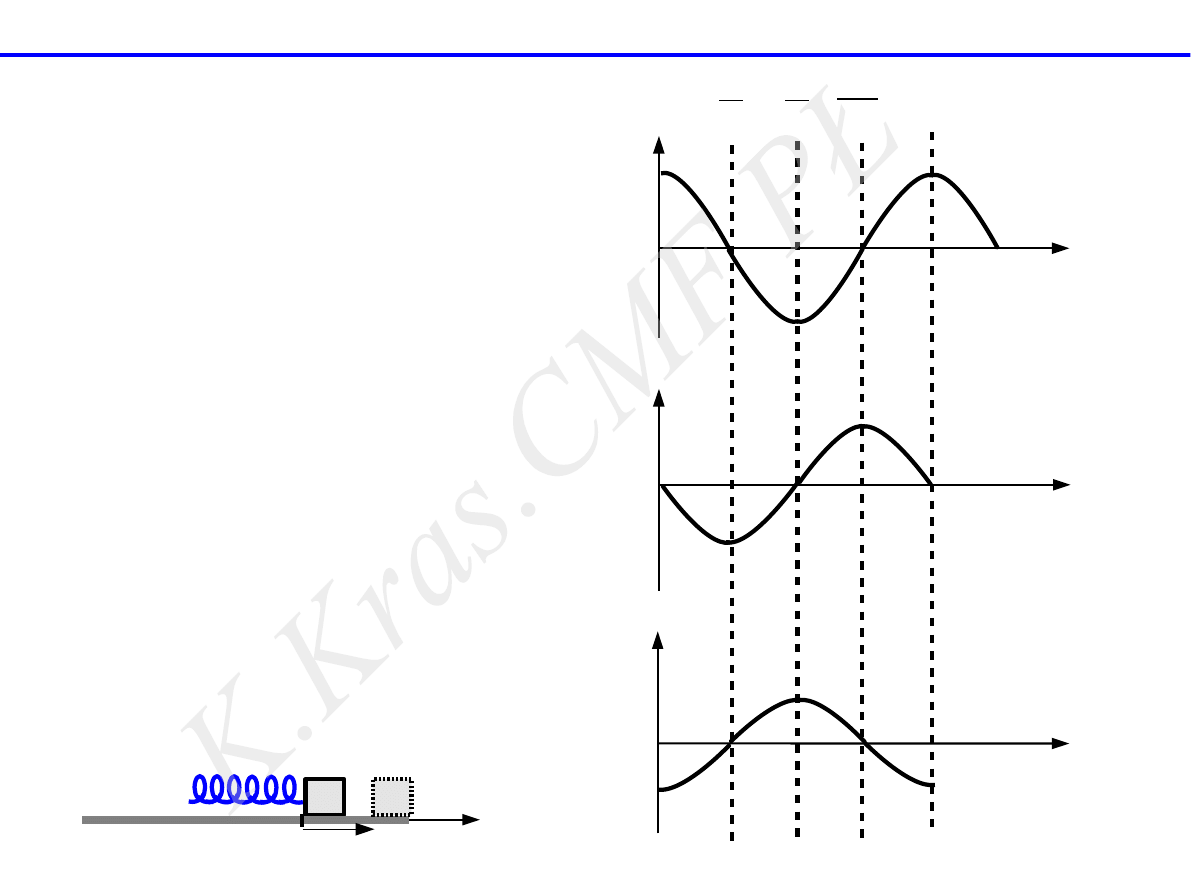
T

4

T

2

3T

4

T

x

V

a

x = Asin(ωt+ϕ)

V = Aω cos(ω t+ϕ)

a = −ω

2

x

ruch harmoniczny prosty

t

t

t

k

m

x

0

m

x = Acos(ωt+ϕ)

t

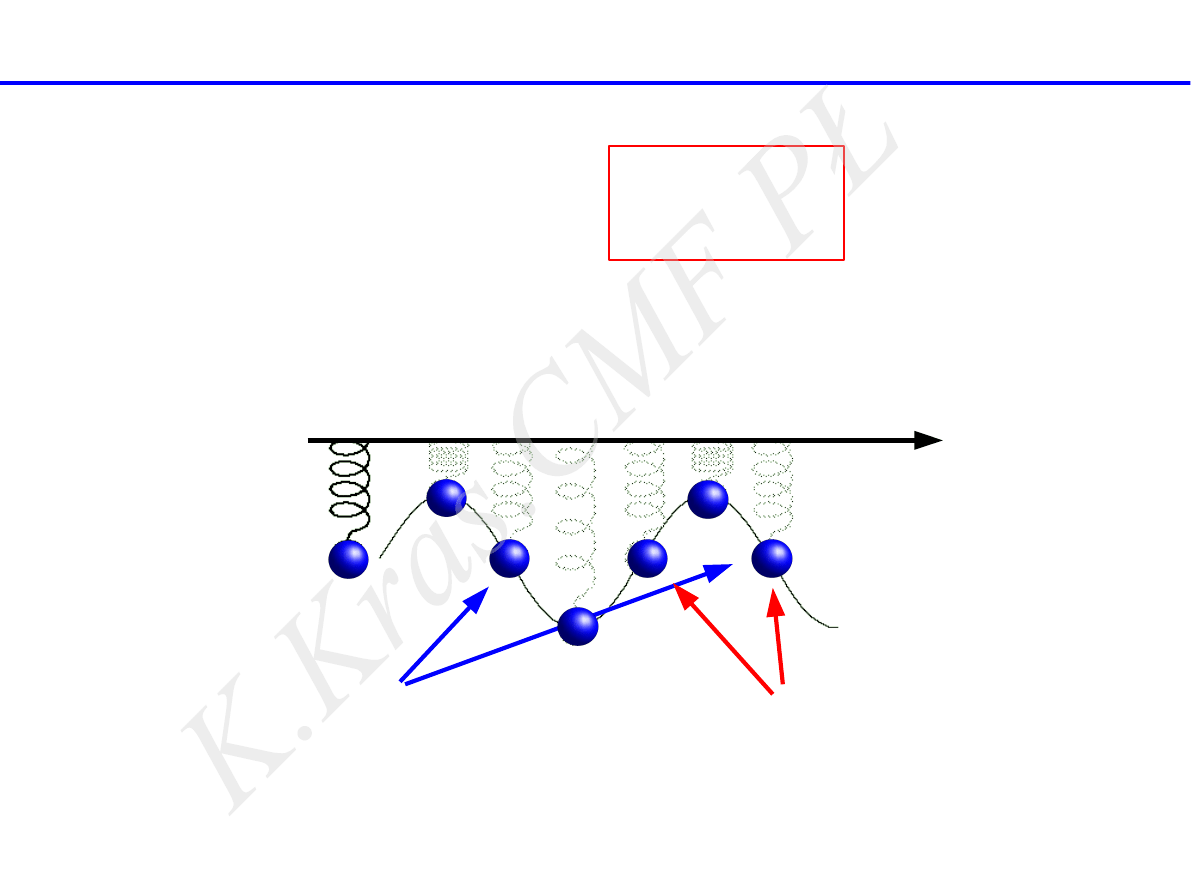
fazy
zgodne

fazy
przeciwne

faza drgania

ruch harmoniczny prosty – faza drgań

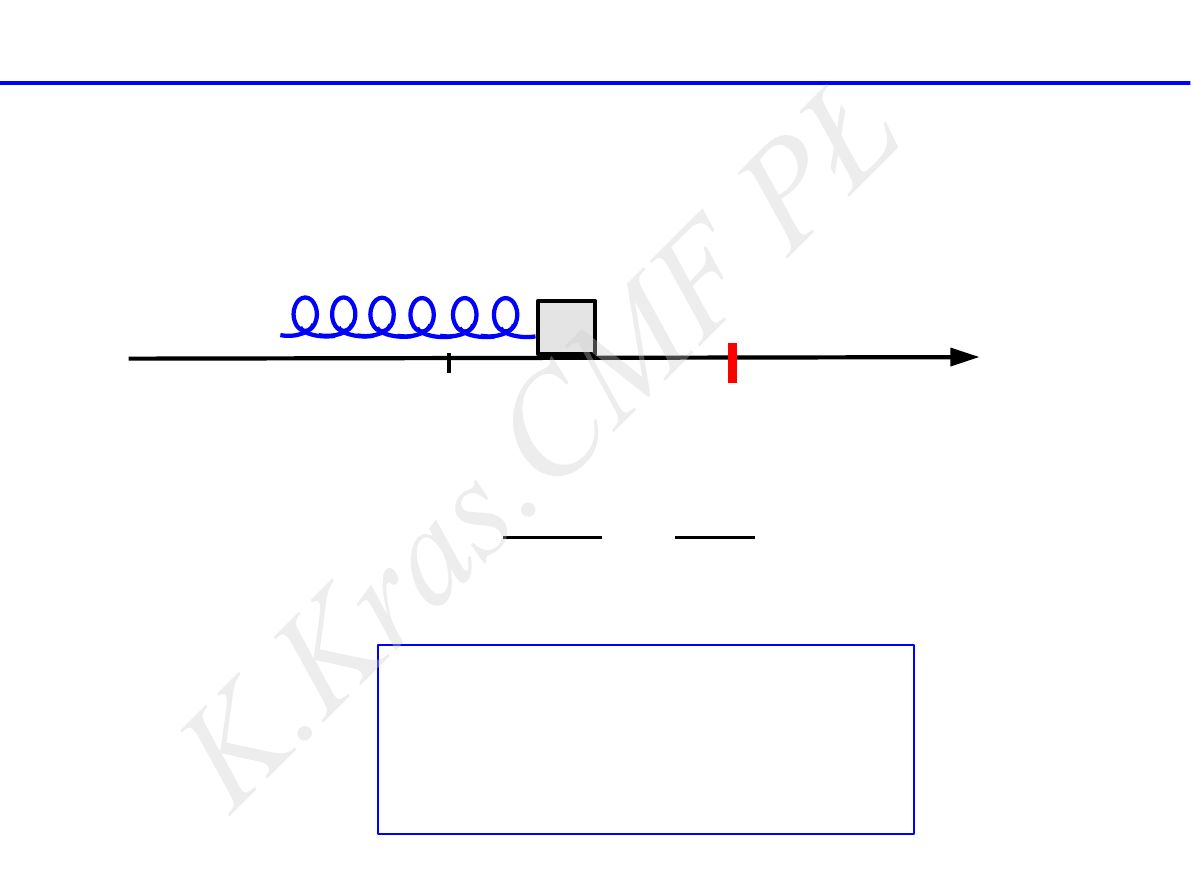
x=0

X

A

V ( A) = 0

E

c

=

E

k

+

E

p

=

mV

2

2

+

k x

2

2

=

const

x = 0 V = V

max

x = x

max

=

A V = 0

ruch harmoniczny prosty – energia

k

m

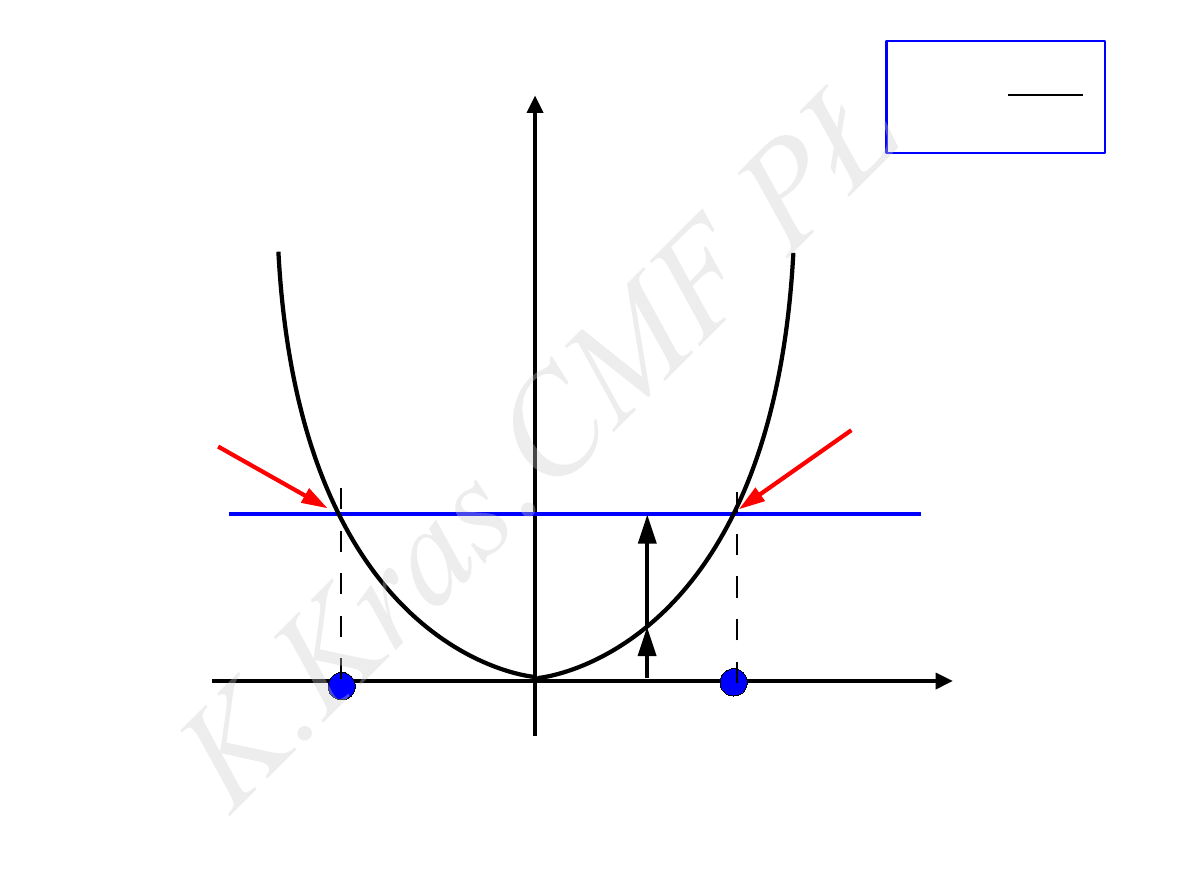
x

E

p

E

c

=

E

p

−

A

A

E

k

E

p

E

p

=

k x

2

2

E

c

=

const

E

c

=

E

p

k

k

x

koniec

nieodkształconej

sprężyny

położenie równowagi

koniec

nieodkształconej

sprężyny

położenie równowagi

s

s =

mg

k

odkształcenie statyczne

mg

- siła stała

m

m

x

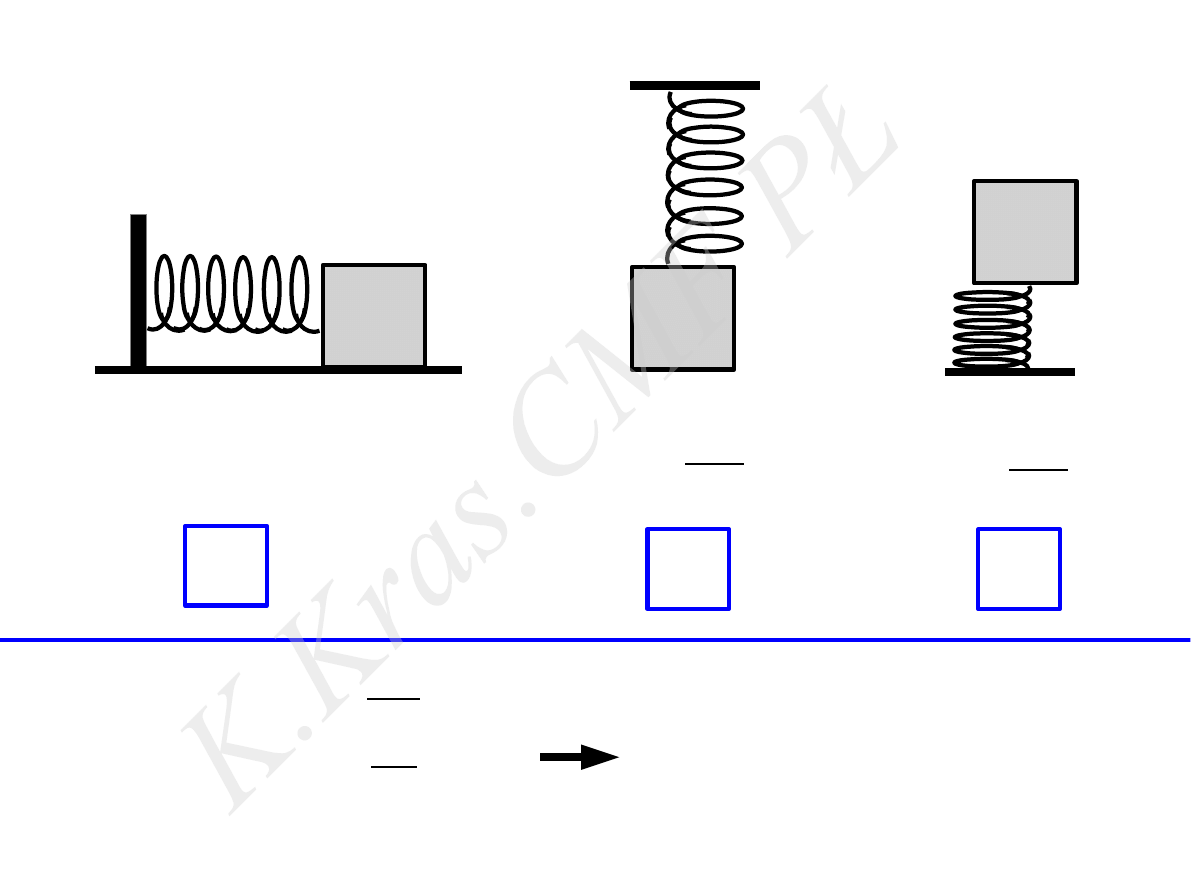
m

k

m

k

m

k

s =

mg

k

s =

mg

k

s = 0

T

1

T

2

T

3

T

1

=

T

2

=

T

3

T = 2 π

√

m

k

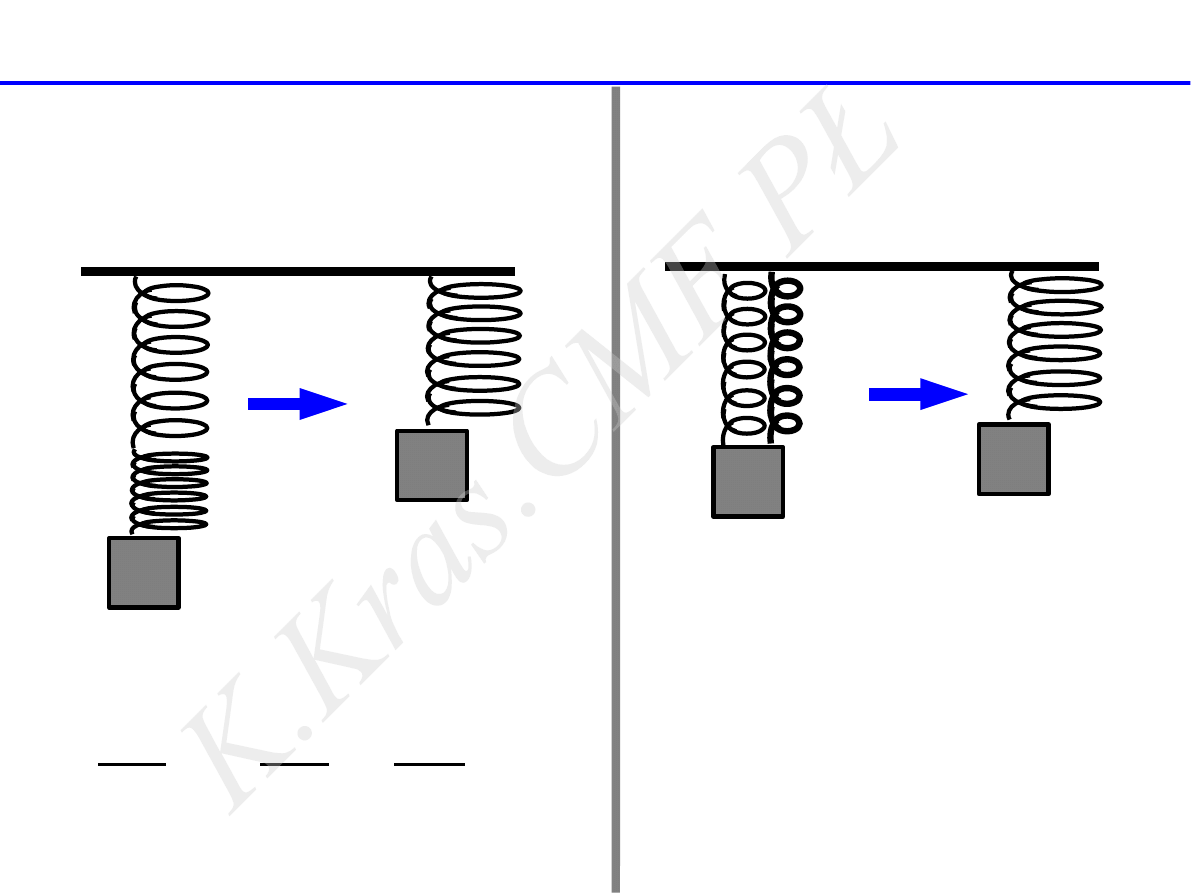
k

1

k

2

połączenie szeregowe

k

s

m

m

k

1

k

2

k

r

m

m

połączenie równoległe

1

k

s

=

1

k

1

+

1

k

2

k

r

=

k

1

+

k

2

połączenie sprężyn

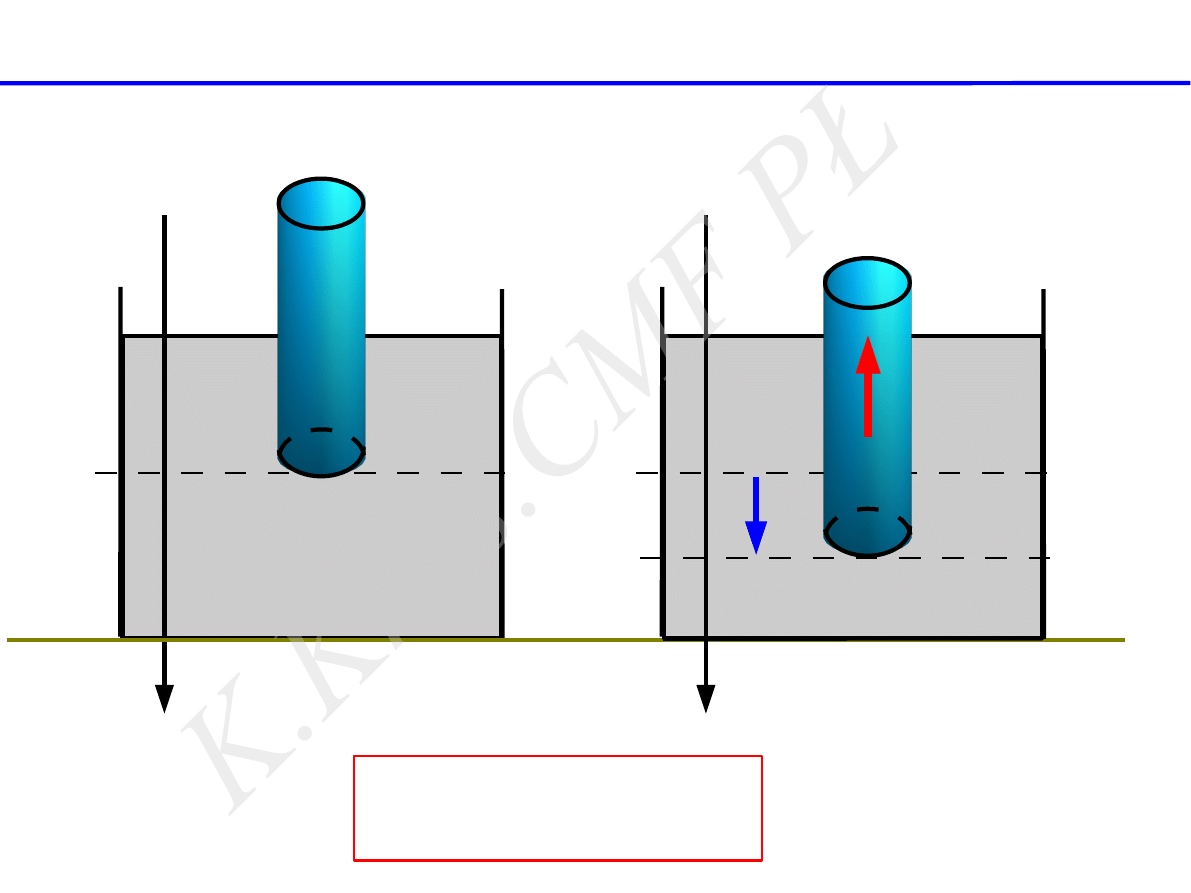
x

0

x

0

x

ρ

ρ

F

w

F

w

= − ρ

g D x

położenie równowagi

wychylenie z położenia równowagi

D

D

siła wyporu

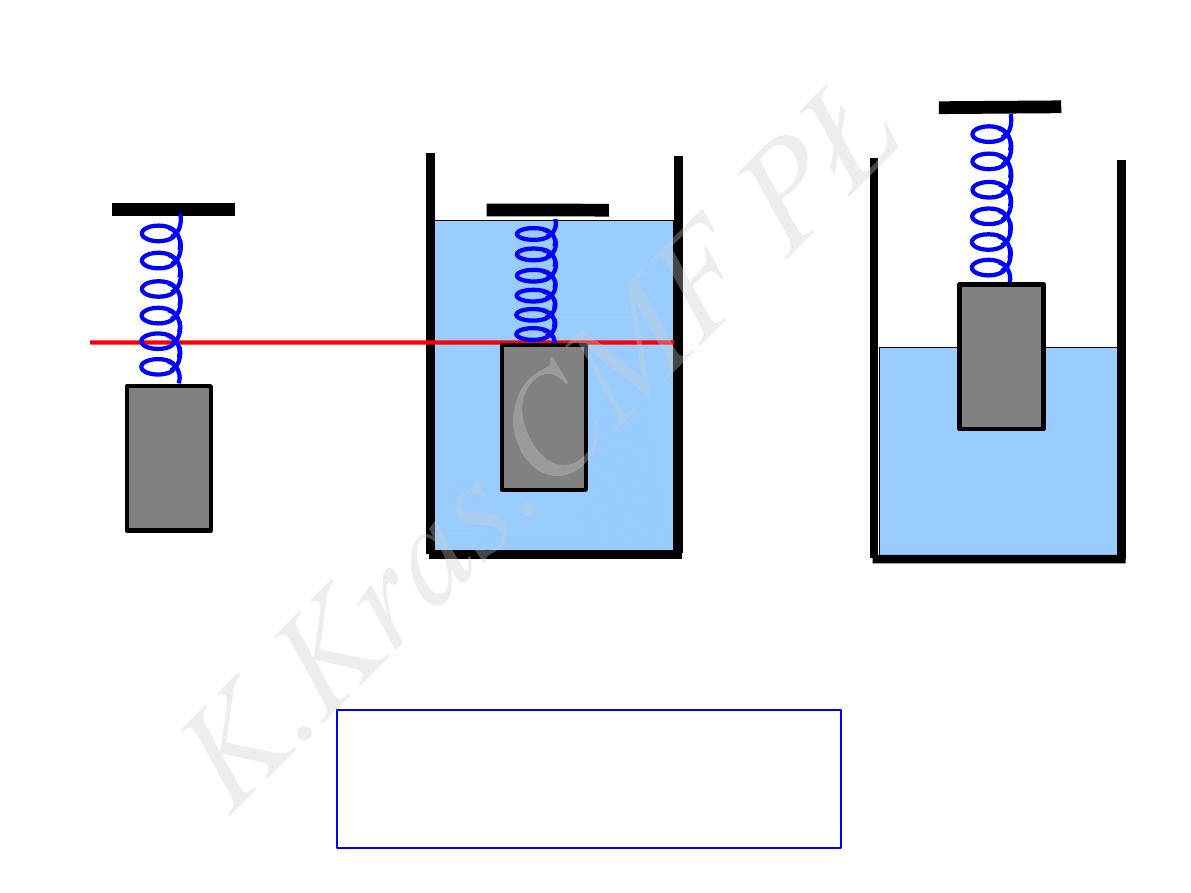
T

1

T

2

T

1

=

T

2

≠

T

3

k

T

3

k

F

w

=

const

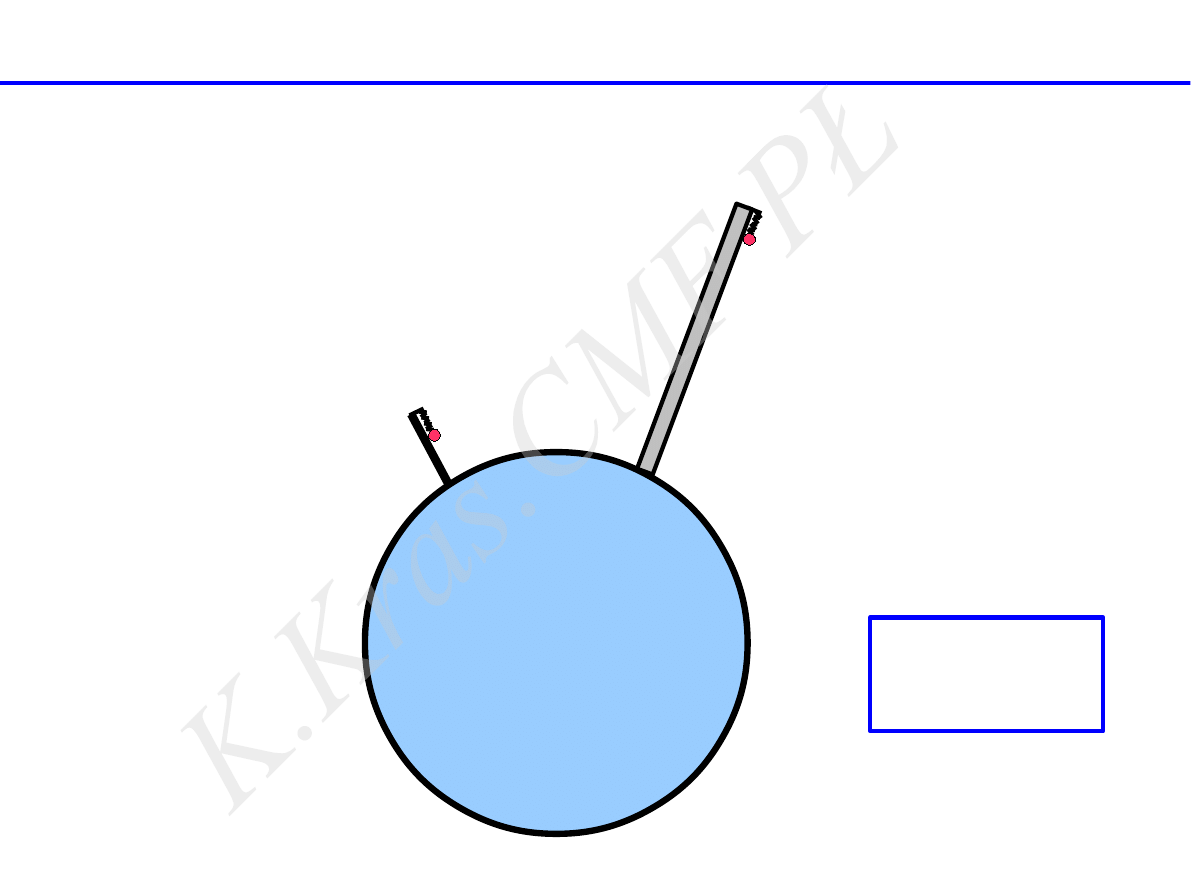
g

1

=

const

g

2

=

const

T

1

T

2

T

1

=

T

2

h

H

H ≫h

„małe” drgania na wieży

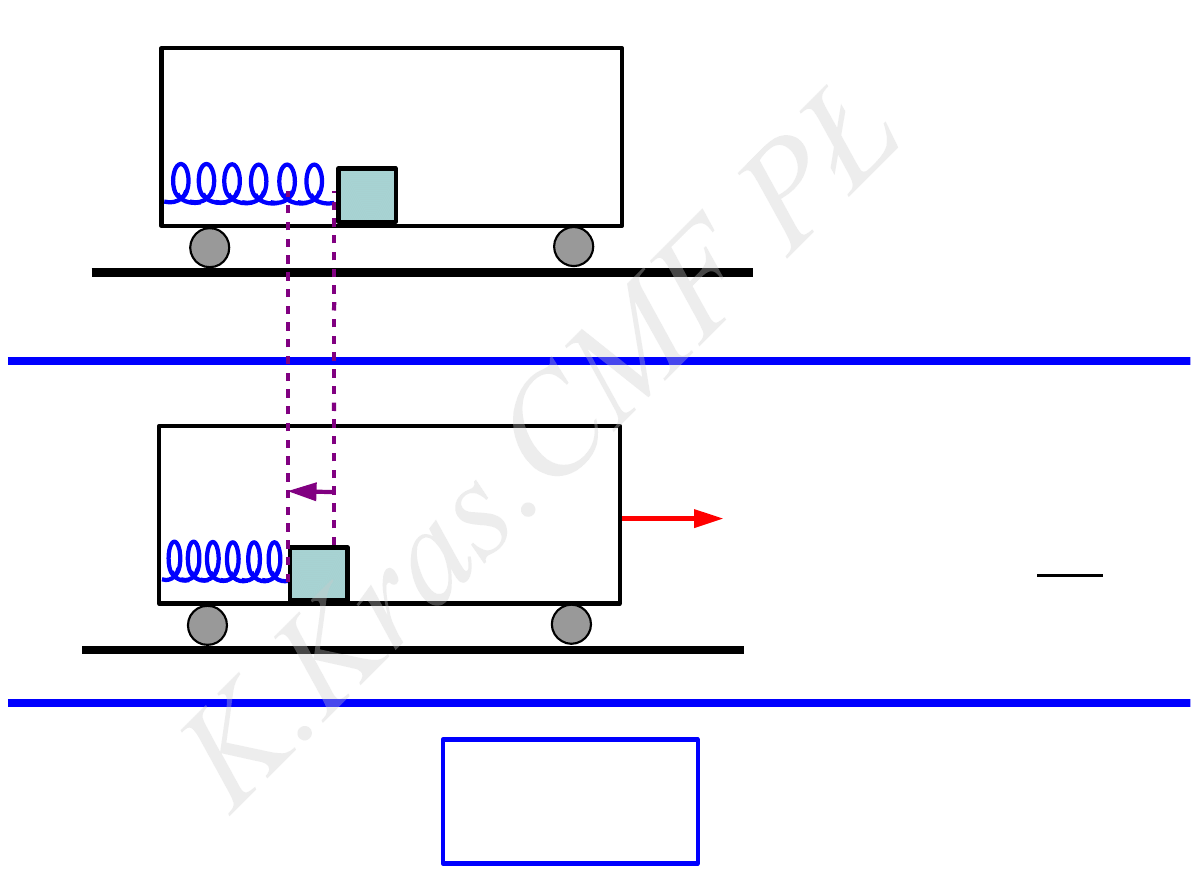
k

m

k

m

⃗p = const

T

1

T

2

T

1

=

T

2

s

s =

mp

k

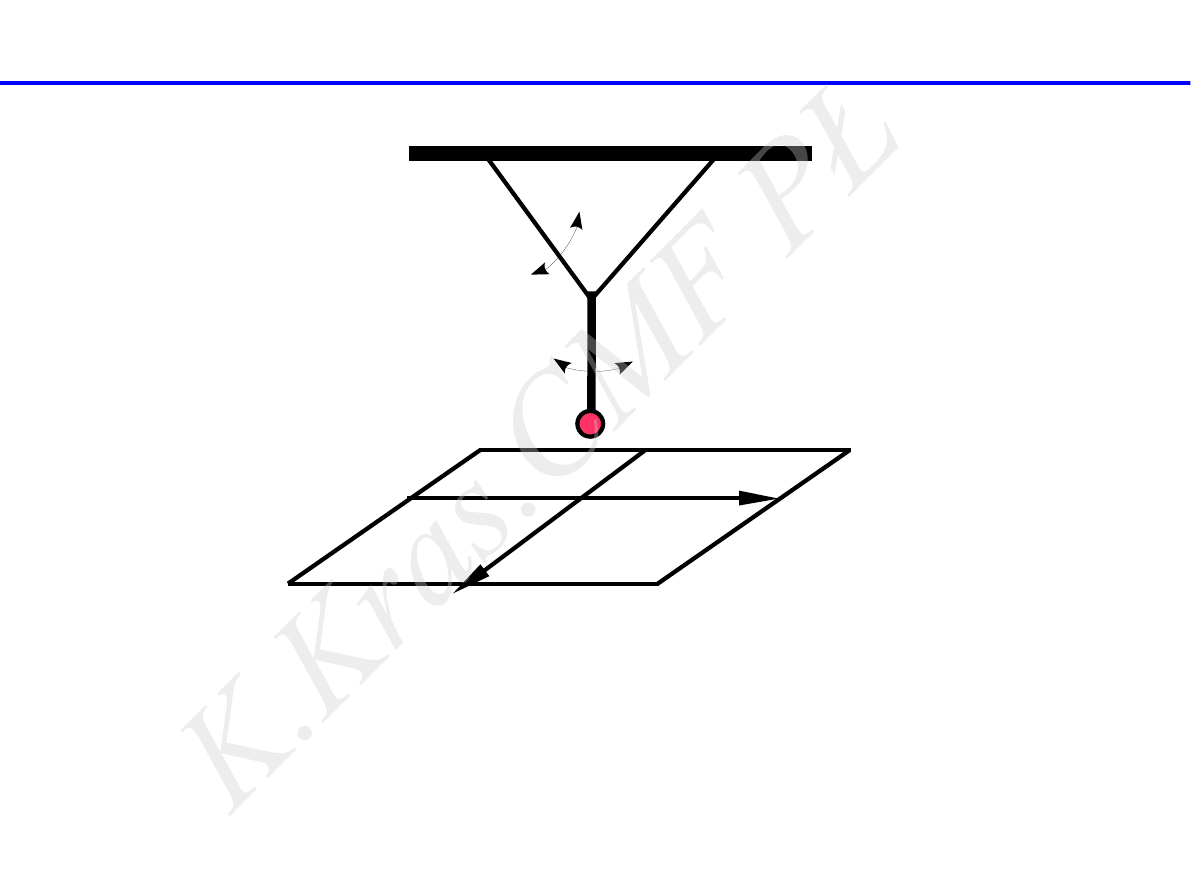
składanie drgań prostopadłych

x = Asin (ω

1t

+ϕ

1

)

y = B sin (ω

2

t+ϕ

2

)

x

y

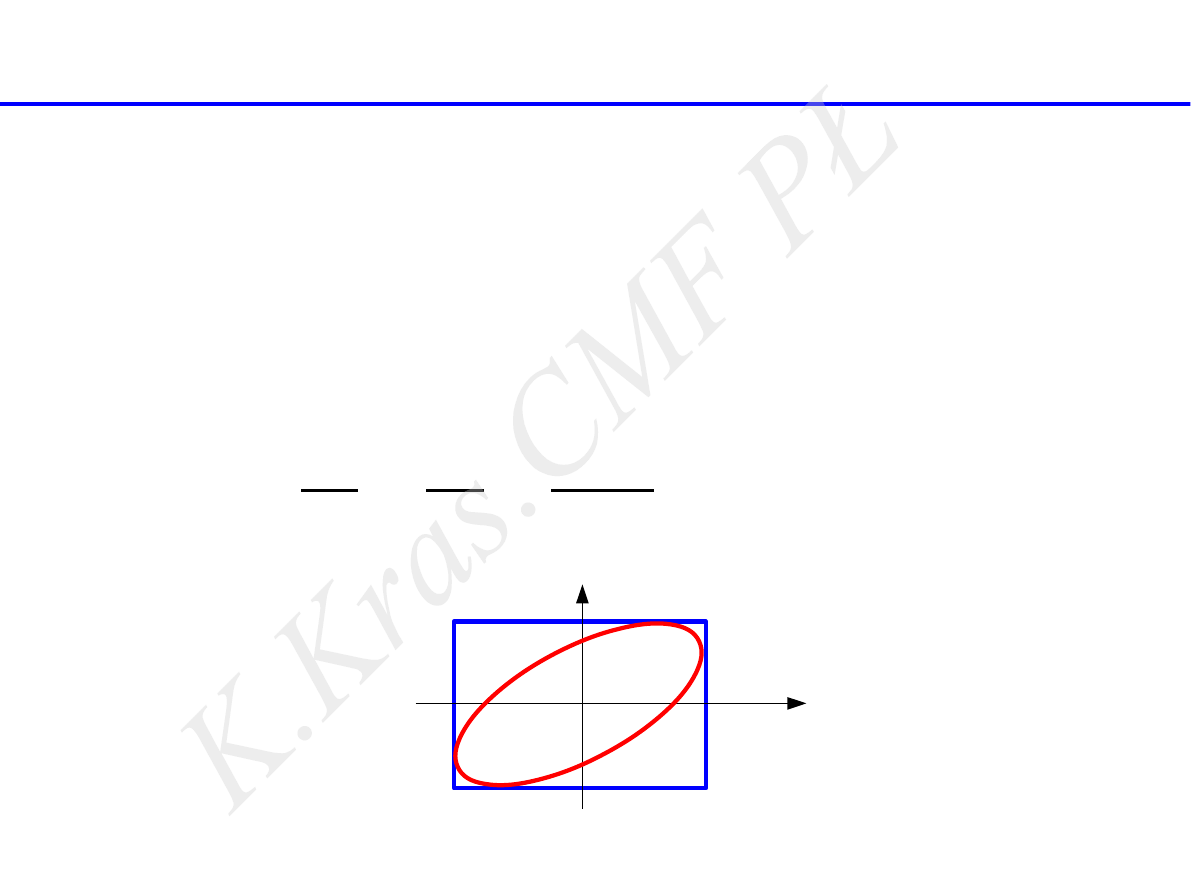
złożenie drgań harmonicznych prostopadłych

równe pulsacje

parametryczne równania toru

x = Acos(ωt )

y = B cos(ωt−ϕ)

równanie toru

x

2

A

2

+

y

2

B

2

−

2 x y

A B

cos ϕ = sin

2

ϕ

x

y

A

B

x

−

A

−

B

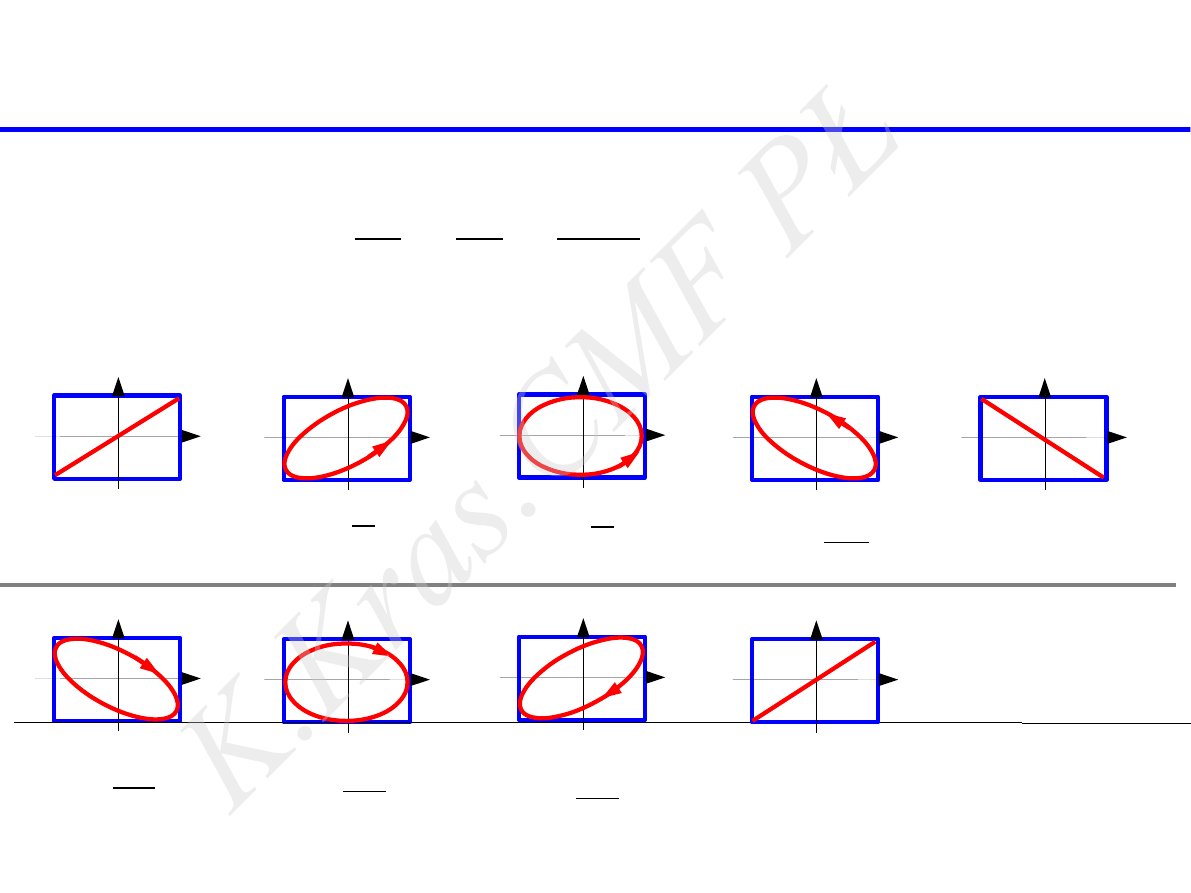
złożenie drgań harmonicznych prostopadłych

równe pulsacje

x

2

A

2

+

y

2

B

2

−

2 x y

A B

cos ϕ = sin

2

ϕ

y

A

B

x

−

A

−

B

y

A

B

x

−

A

−

B

y

A

B

x

−

A

−

B

y

A

B

x

−

A

−

B

y

A

B

x

−

A

−

B

y

A

B

x

−

A

−

B

y

A

B

x

−

A

−

B

y

A

B

x

−

A

−

B

y

A

B

x

−

A

−

B

ϕ=

0

ϕ=π

4

ϕ=π

2

ϕ=

3 π

4

ϕ=π

ϕ=

5π

4

ϕ=

3 π

2

ϕ=

7 π

4

ϕ=

2 π

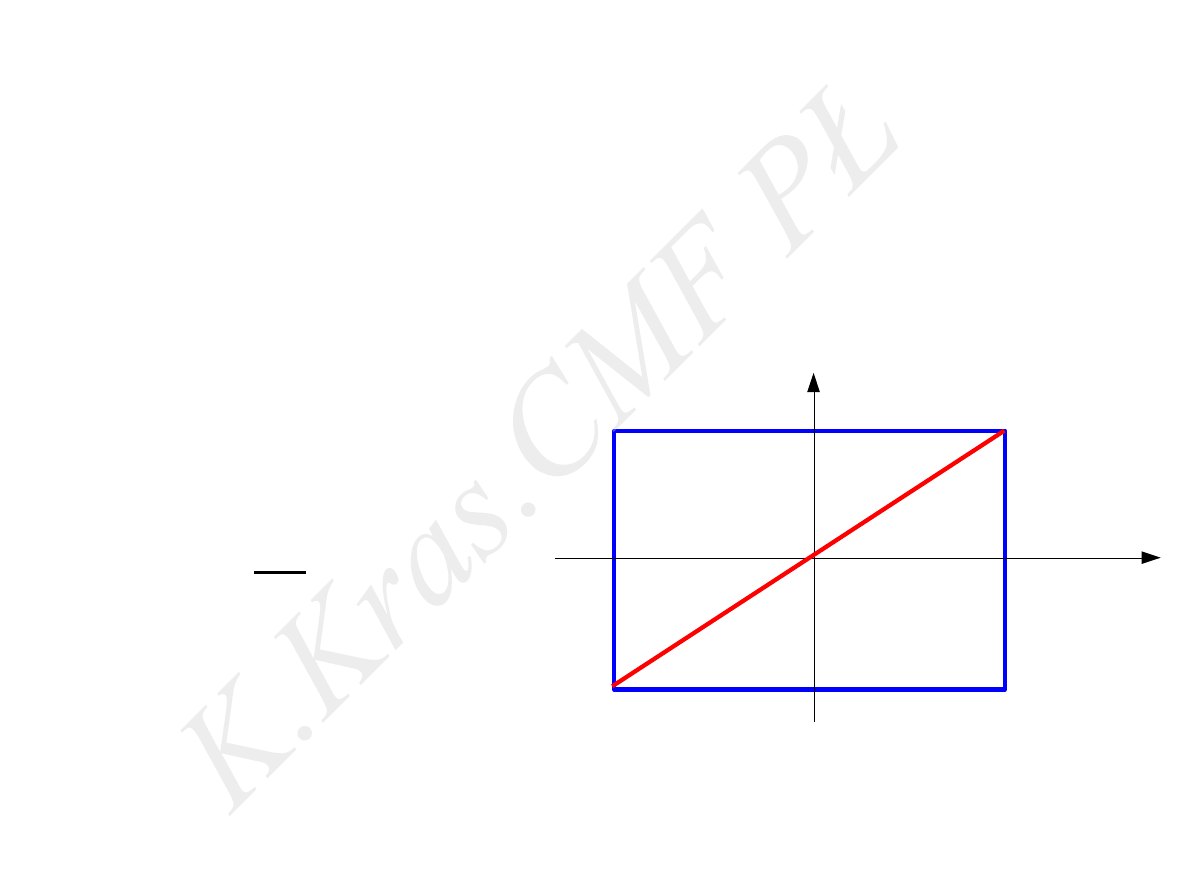
x = Asin(ω t)

y = Bsin(ωt)

y =

B

A

x

x

y

A

B

x

−

A

−

B

parametryczne równania toru

równanie toru

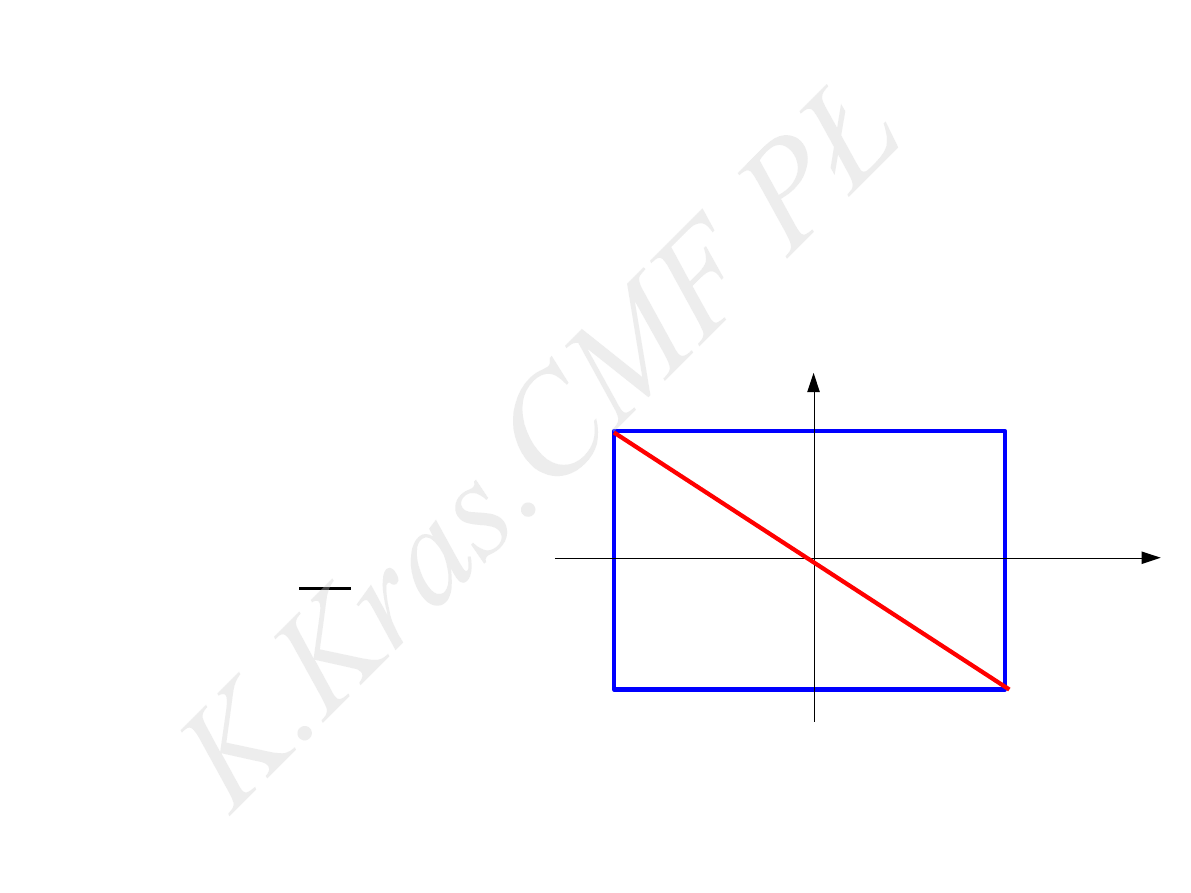
x = Asin(ω t)

y = Bsin (ωt+π)

y =−

B

A

x

x

y

A

B

x

−

A

−

B

parametryczne równania toru

równanie toru

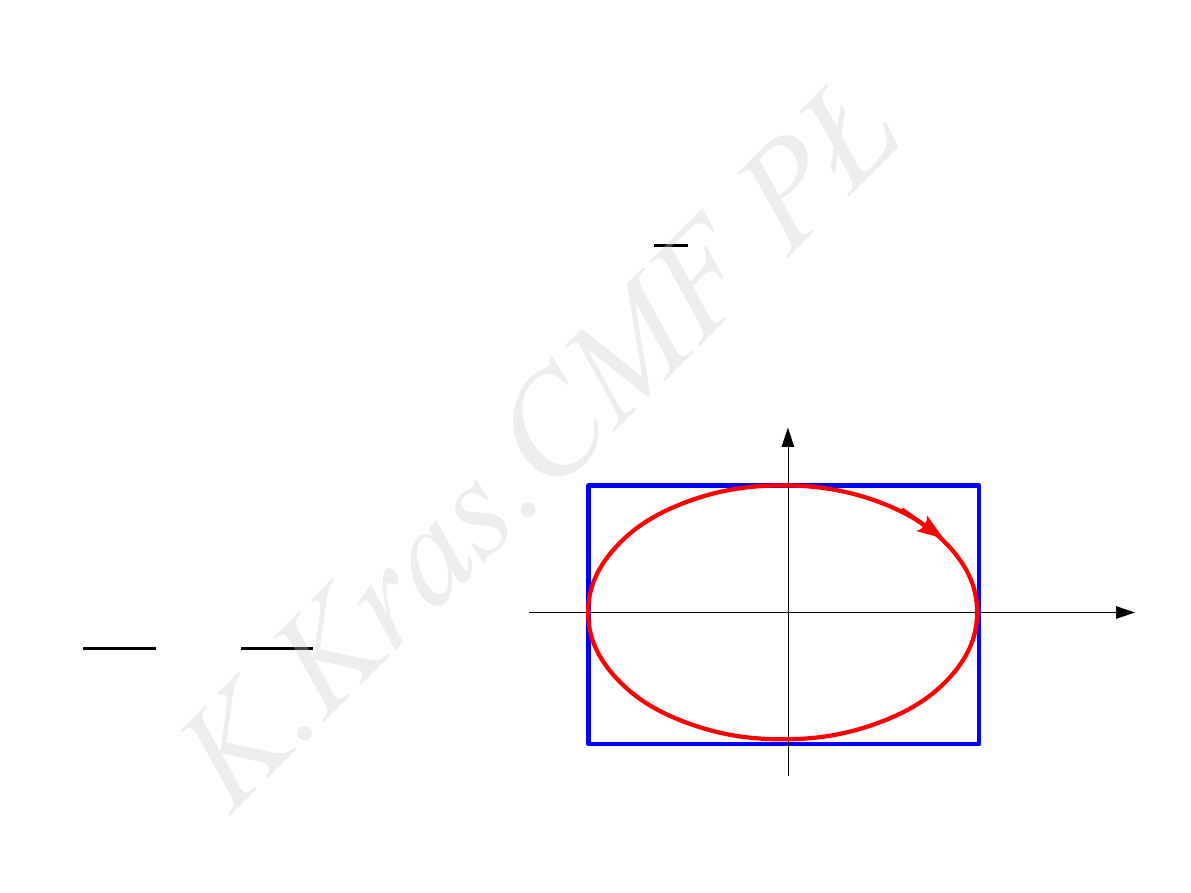
x = Asin(ω t)

y = B sin (ωt+

π

2

)

x

2

A

2

+

y

2

B

2

=

1

x

y

A

B

x

−

A

−

B

parametryczne równania toru

równanie toru

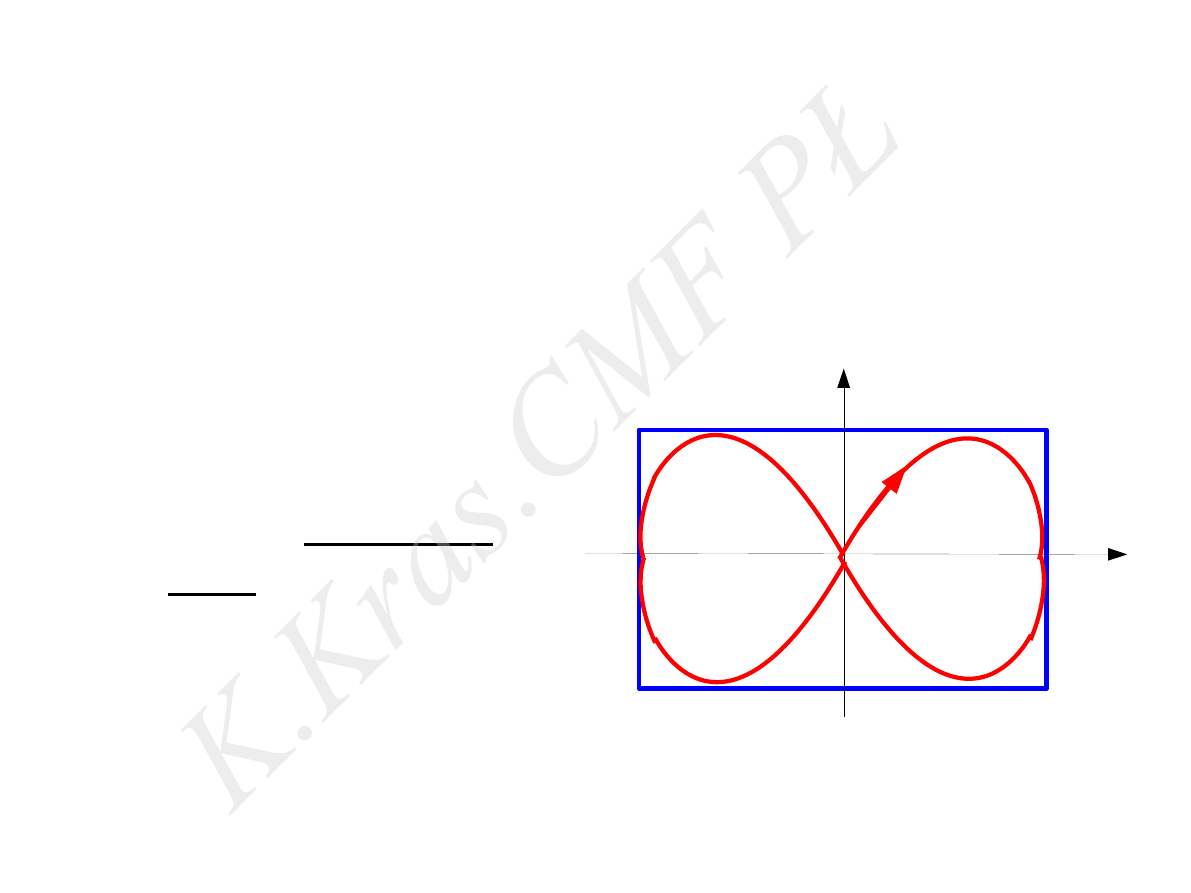
x = Asin(ω t)

y = Asin(2ω t)

y =

2 x

A

√

A

2

−

x

2

x

y

A

B

−

A

−

B

parametryczne równania toru

równanie toru