
Politechnika Warszawska
Instytut Automatyki i Robotyki
Prof. dr hab. inż. Jan Maciej Kościelny
PODSTAWY AUTOMATYKI
część 10
Struktury układów regulacji
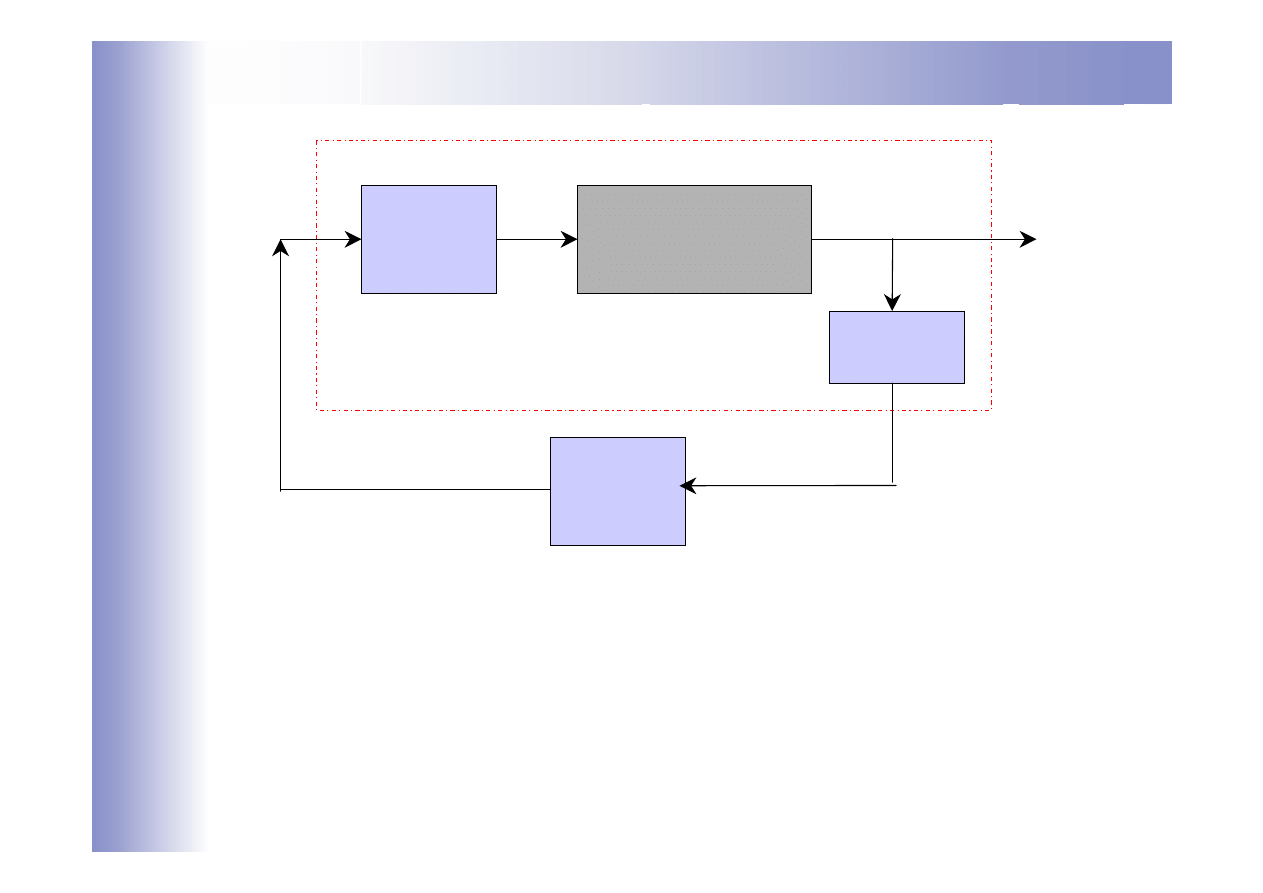
Obiekt regulacji
Regulator
Obiekt
regulacji
Przetwornik
pomiarowy
Element
wykonawczy
y
u
Własności zespołów wykonawczych i przetworników pomiarowych
włączone są do obiektu. Transmitancja obiektu opisuje więc
wypadkowe własności połączenia:
zespół wykonawczy + obiekt + przetwornik pomiarowy
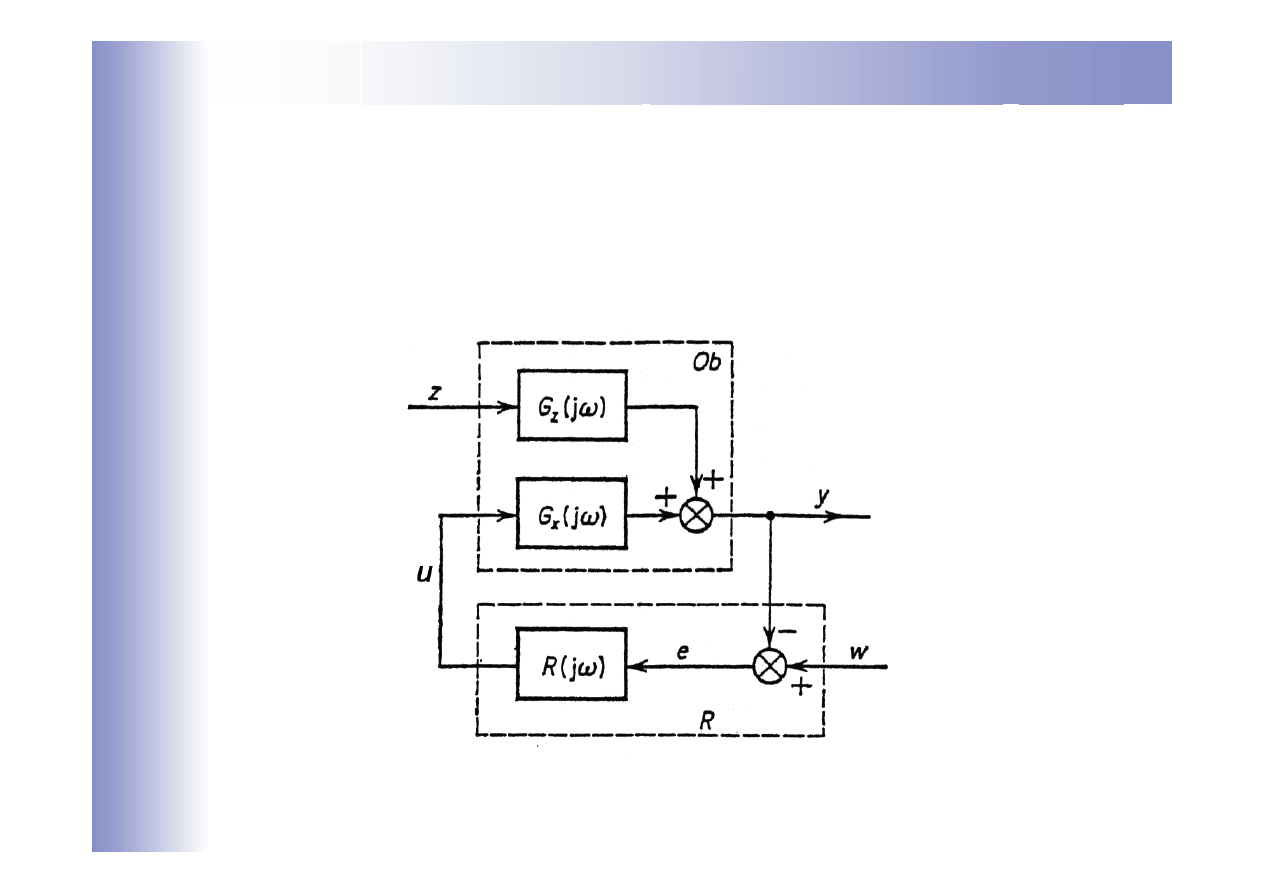
Uogólniona struktura jednoobwodowa
Transmitancja G
x
(s), opisująca związek pomiędzy sterowaniem u i
wyjściem y, może być inna niż transmitancja G
z
(s), opisująca związek
pomiędzy zakłóceniem z i wyjściem y

Regulacja kaskadowa
• franc. cascade = wodospad stopniowany
• w automatyce – regulacja w kolejnych obwodach
Kiedy stosujemy
Regulacja kaskadowa jest celowa dla obiektów:
•wieloinercyjnych,
•o stałych rozłożonych
•z opóźnieniem transportowym (w części G
2
),
Warunkiem utworzenia kaskadowego układu regulacji jest istnienie
w obiekcie mierzalnej pomocniczej wielkości regulowanej y
p
, która
szybciej reaguje na to zakłócenie niż główna wielkość regulowana y.
Regulacja kaskadowa jest celowa dla obiektów:
•wieloinercyjnych,
•o stałych rozłożonych
•z opóźnieniem transportowym (w części G
2
),
Warunkiem utworzenia kaskadowego układu regulacji jest istnienie
w obiekcie mierzalnej pomocniczej wielkości regulowanej y
p
, która
szybciej reaguje na to zakłócenie niż główna wielkość regulowana y.
G
1
G
2
y
p
y
u
OBIEKT
)
(
)
(
)
(
2
1
s
G
s
G
s
G
o
=
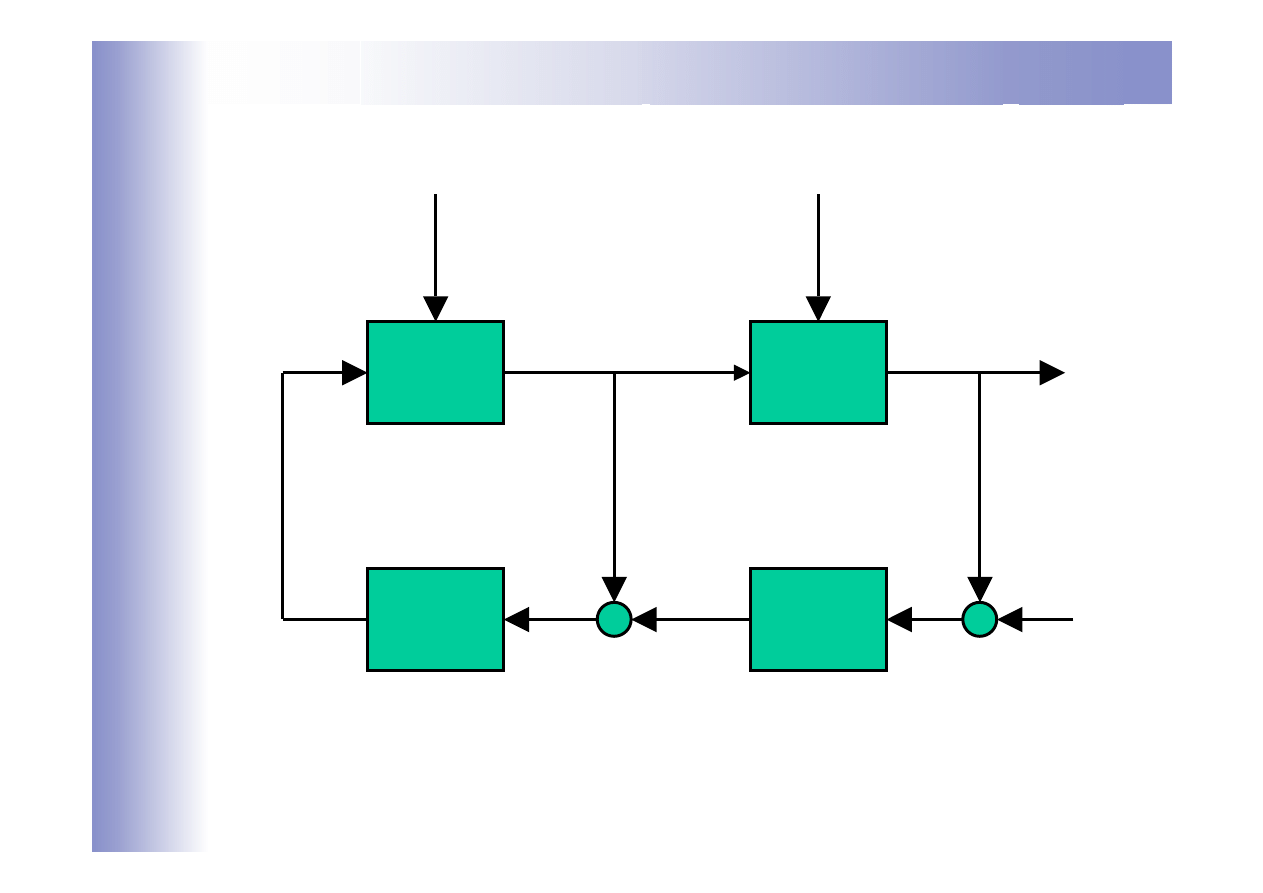
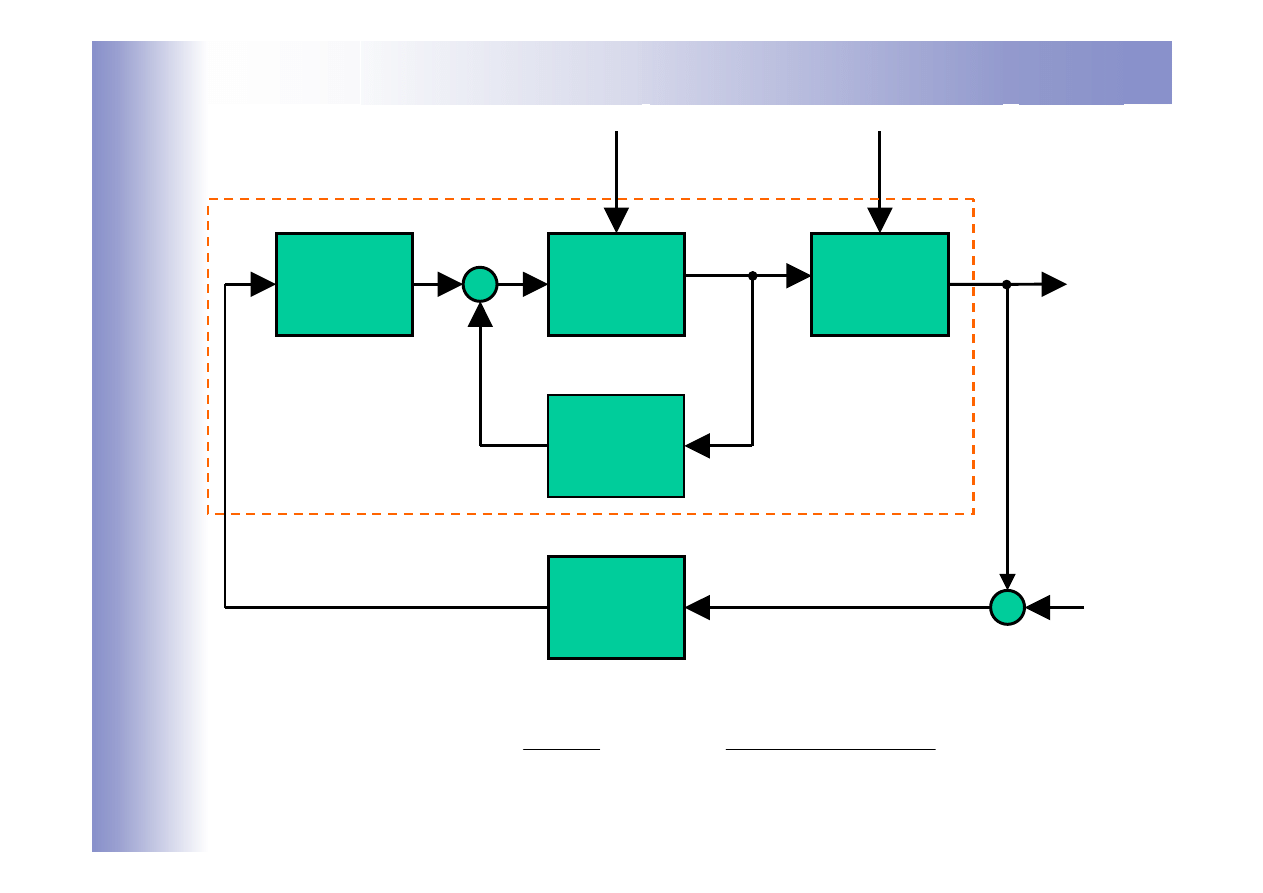
Schemat kaskadowego układu regulacji
G
1
G
2
R
2
R
1
-
+
-
+
z
1
z
2
y
y
0
u
1
u
2
y
p
e
Regulator pomocniczy
Regulator główny
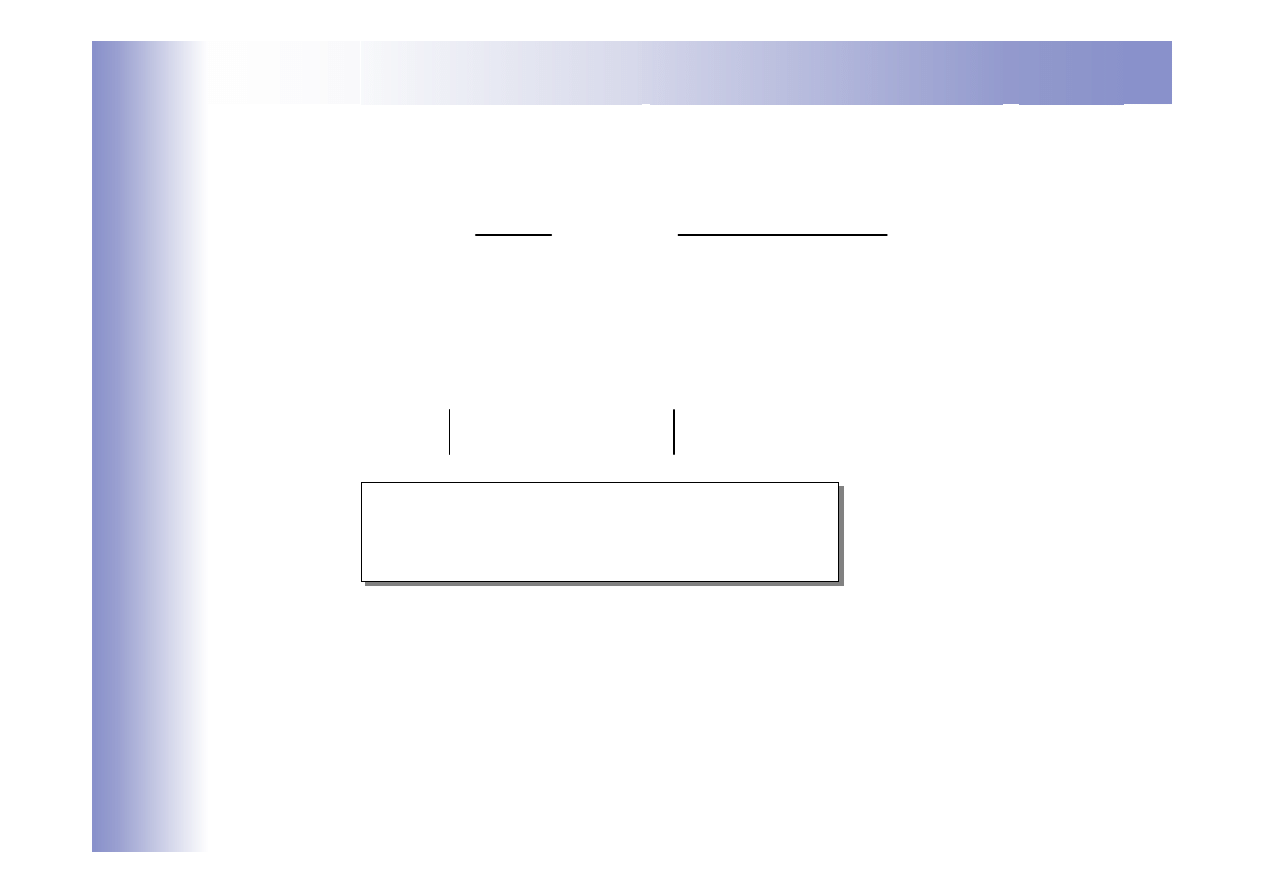
Schemat zmodyfikowany
+
-
+
-
G
1
G
2
R
2
R
1
z
1
z
2
y
y
0
u
1
u
2
y
p
R
2
e
Obiekt zmodyfikowany
)
(
)
(
1
)
(
)
(
)
(
)
(
)
(
)
(
2
1
2
1
2
1
.
s
R
s
G
s
R
s
G
s
G
s
u
s
y
s
G
m
ob
+
=
=
Neutralizacja właściwości dynamicznych
części G
1
obiektu
1
)
(
)
(
2
1
>>
ω
ω
j
R
j
G
)
(
)
(
1
)
(
)
(
)
(
)
(
)
(
)
(
2
1
2
1
2
1
.
s
R
s
G
s
R
s
G
s
G
s
u
s
y
s
G
m
ob
+
=
=
w paśmie częstotliwości, w którym zachodzi:
)
(
)
(
2
.
ω
ω
j
G
j
G
m
ob
≈
Linearyzacja charakterystyki statycznej
Charakterystyka statyczna obiektu: y
p
=f(u
2
)
Charakterystyka zmodyfikowana: y
p
=f(A)
u
2
=A-B → A=u
2
+B
y
0
G
1
+
-
R
2
R
2
G
2
R
1
A
B
y
p
y
+
-
e
u
1
z
1
z
2
u
2
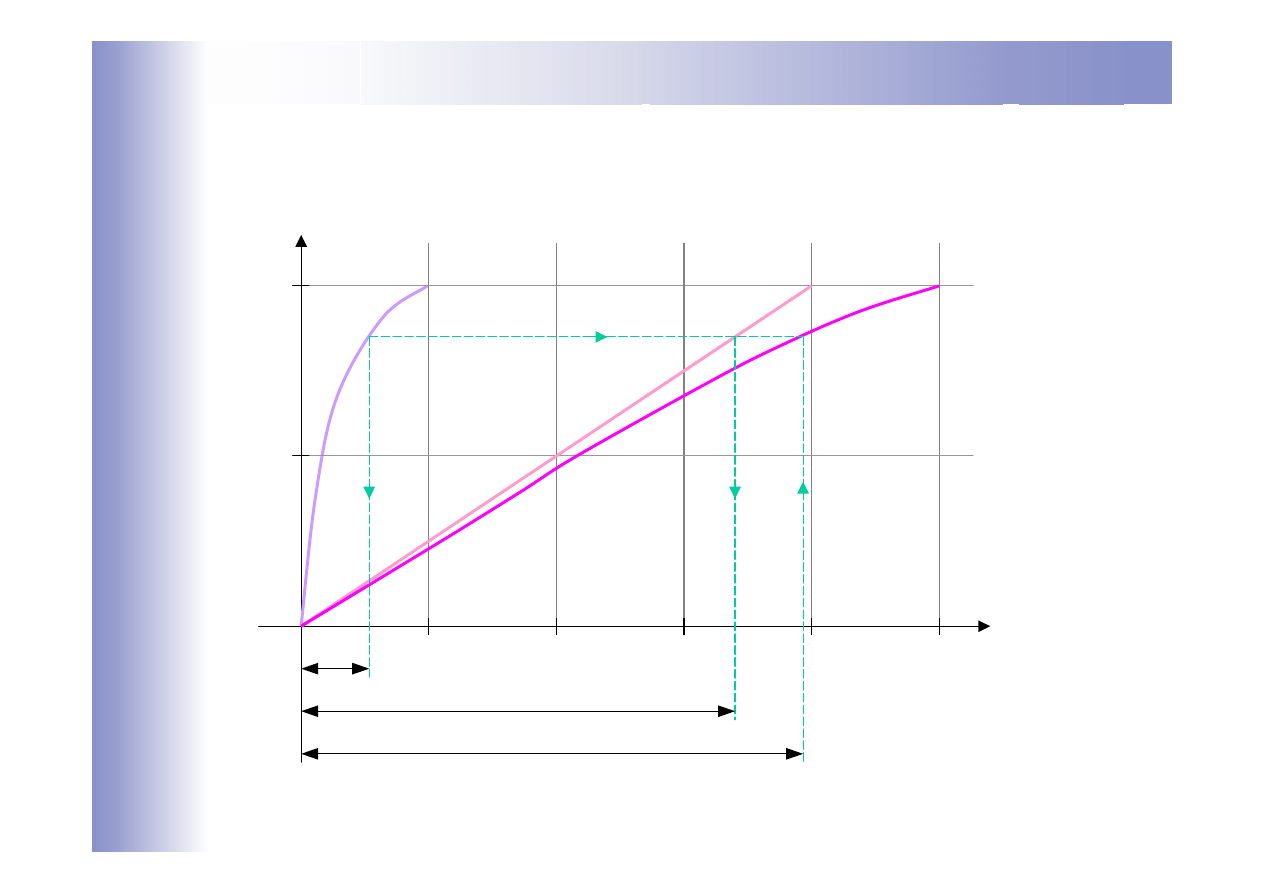
Linearyzacja charakterystyki statycznej
części G1 obiektu
wejście
y
p
0
0,5
1
1
2
3
4
5
u
2
B
A=u
2
+B
y
p
=f(u
2
)
y
p
=f(B)
y
p
=f(A)
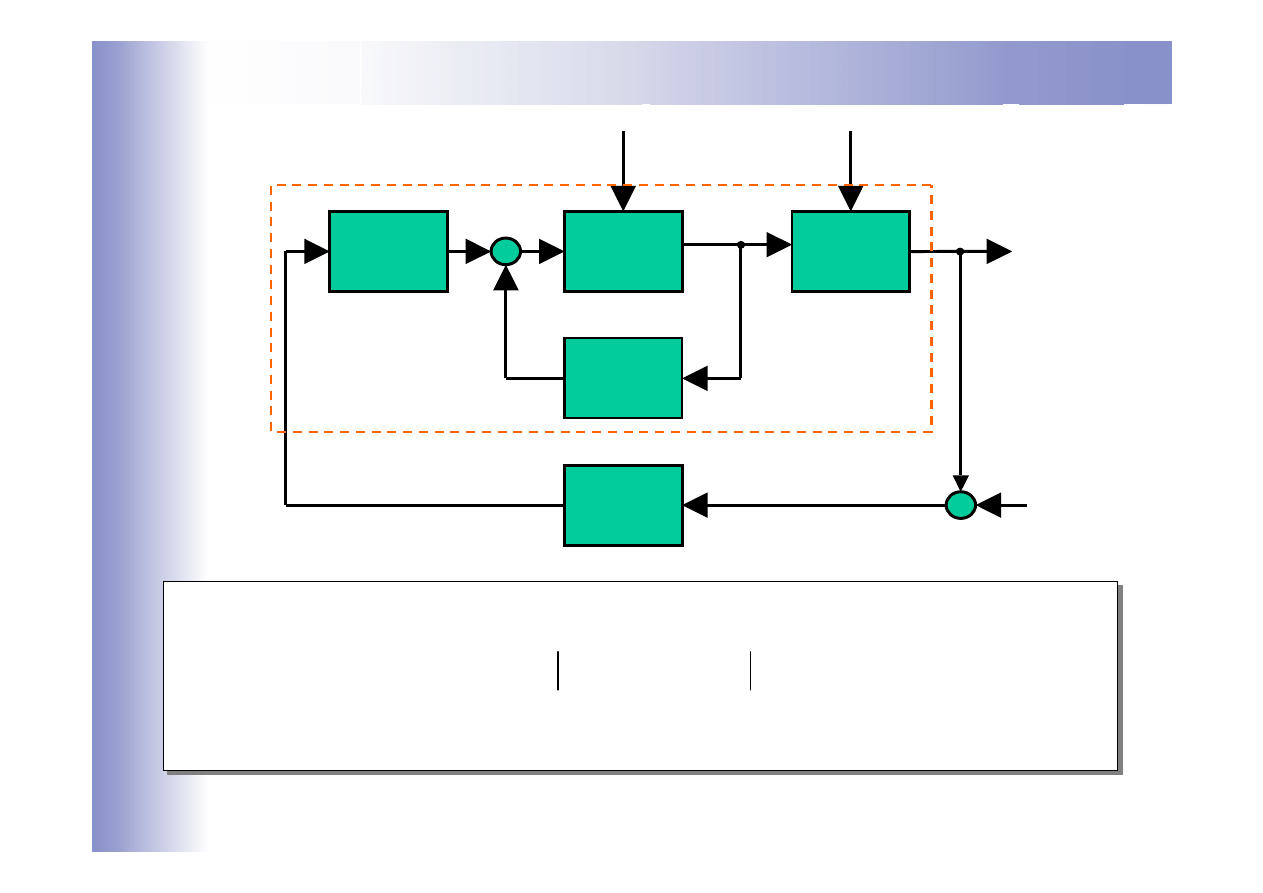
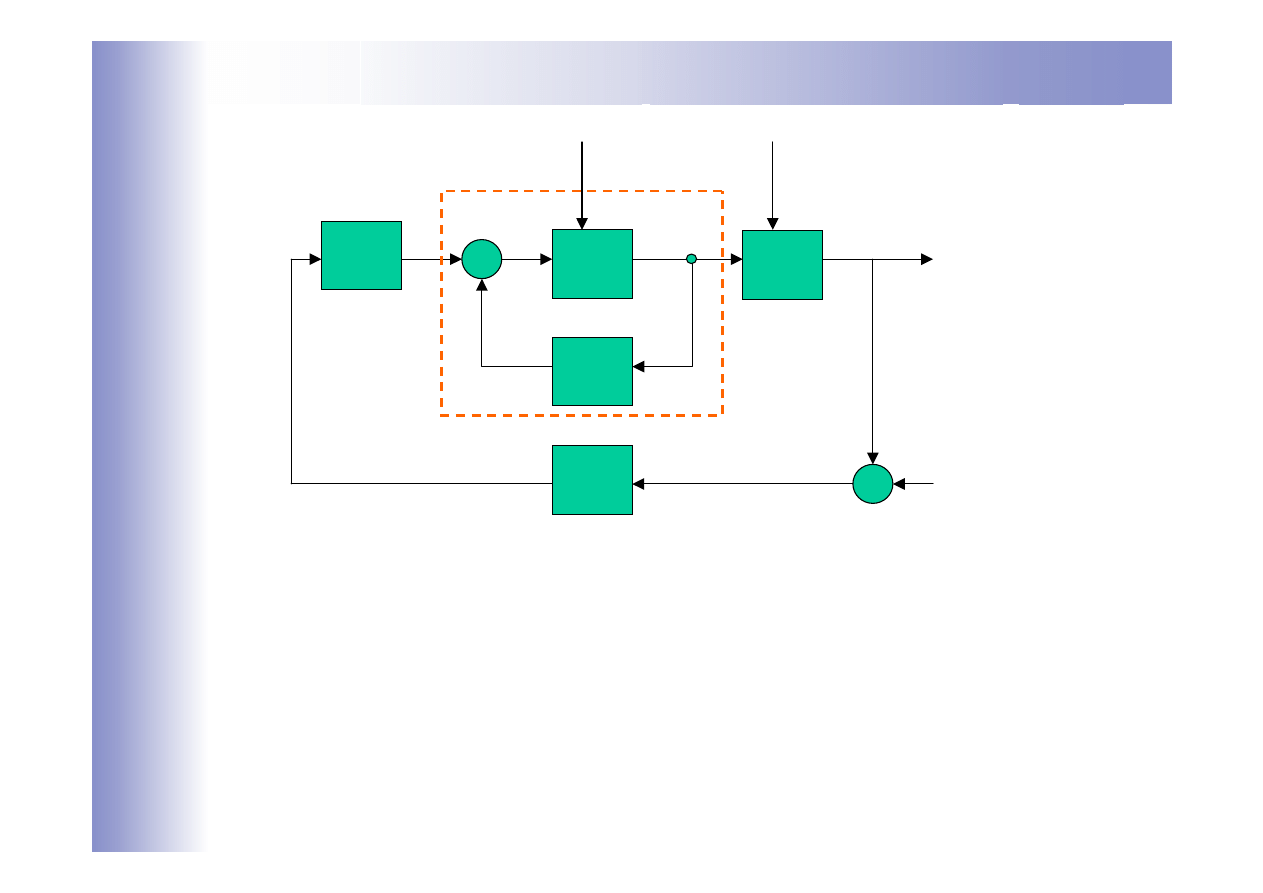
Kompensacja zakłóceń z
1
+
-
+
-
G
1
G
2
R
2
R
1
z
1
z
2
y
y
0
u
1
u
2
y
p
R
2
e
Zakłócenia z
1
kompensowane są
krotnie silniej niż w układzie jednoobwodowym z regulatorem R
1
.
[
]
)
(
)
(
1
2
1
ω
ω
j
R
j
G
+
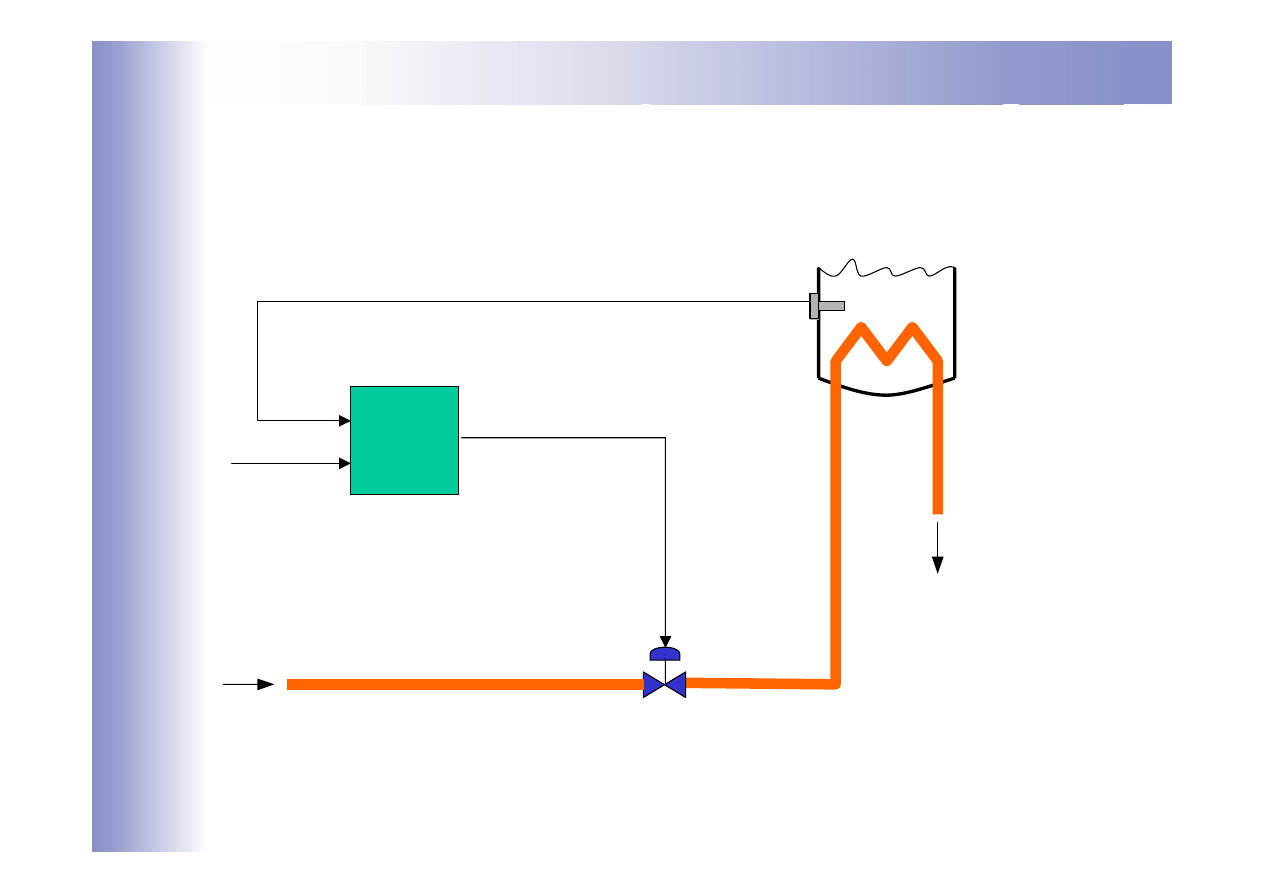
Układ regulacji temperatury
R
para
y
y
0
x
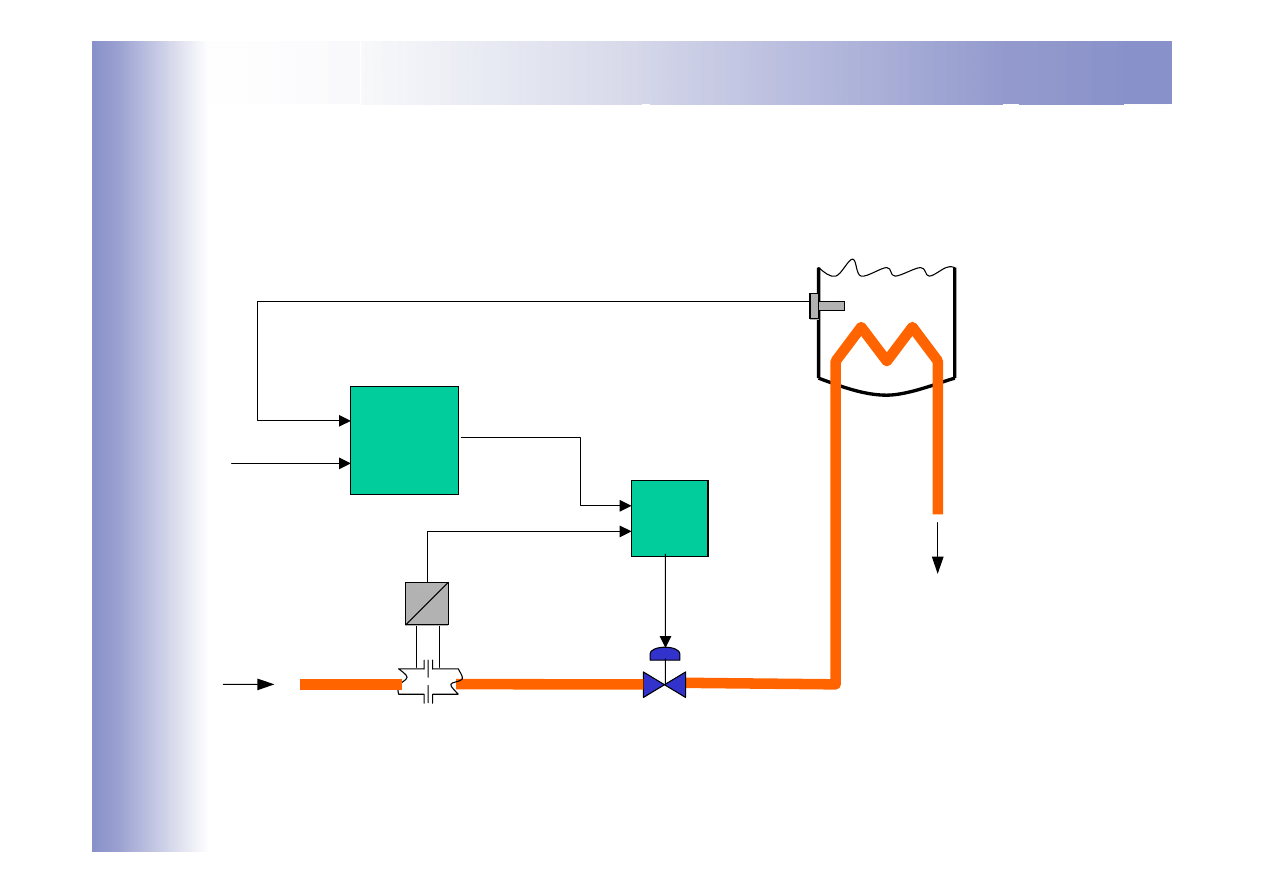
Kaskadowy układ regulacji temperatury
R
g
R
p
para
y
y
0
x
1
y
p
x
2

Dobór regulatorów i nastaw
Zazwyczaj:
– regulator główny typu PI lub PID
– regulator pomocniczy typu P lub PD
nastawy regulatora pomocniczego jak dla układu
jednoobwodowego (obwód pomocniczy),
nastawy regulatora głównego jak dla układu jednoobwodowego
(obiekt zmodyfikowany)
nastawy regulatora pomocniczego jak dla układu
jednoobwodowego (obwód pomocniczy),
nastawy regulatora głównego jak dla układu jednoobwodowego
(obiekt zmodyfikowany)
Zalety i ograniczenia
neutralizacja własności dynamicznych części G1 obiektu
silna kompensacja zakłóceń z1
linearyzacja charakterystyki statycznej części G1 obiektu
brak poprawy jakości regulacji względem zakłóceń z2
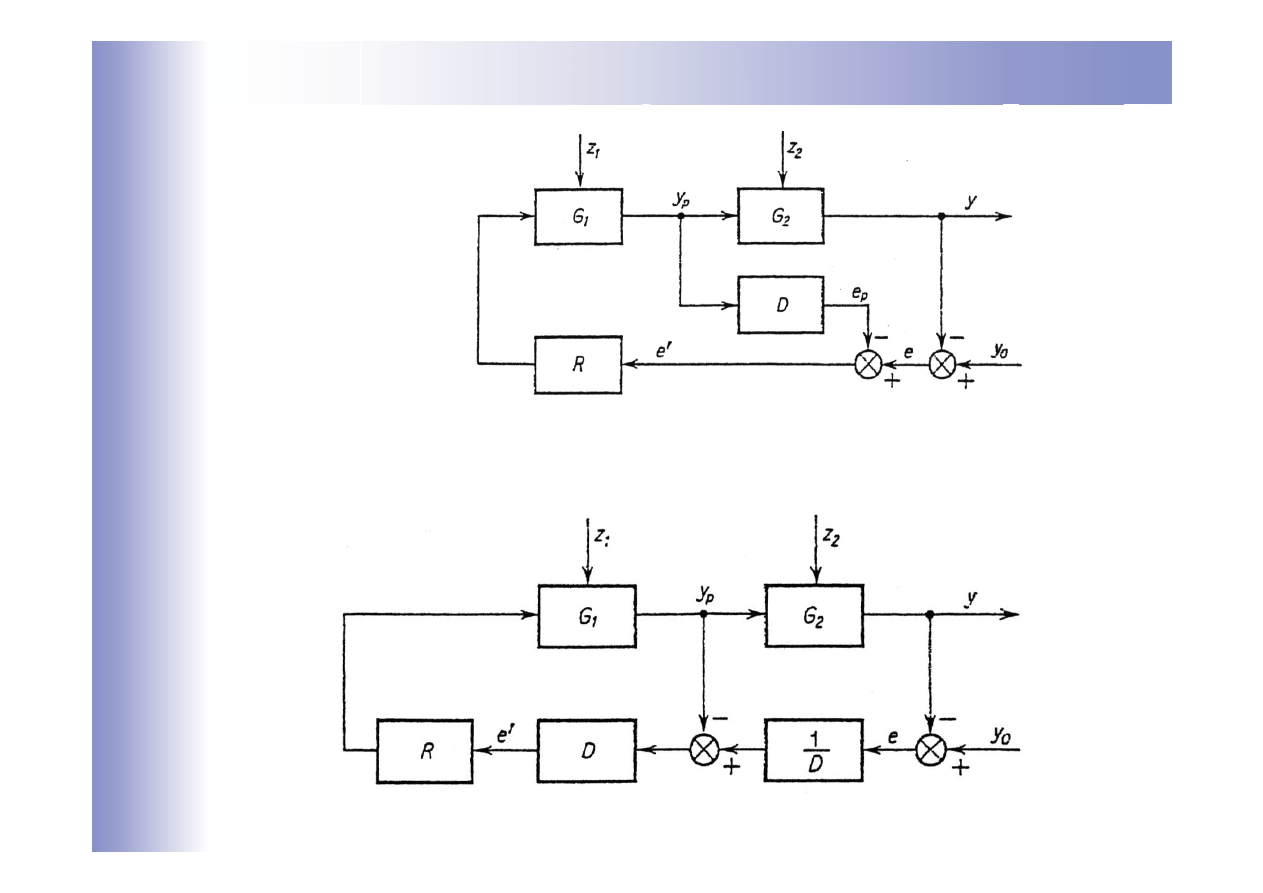
Układy z pomocniczą korekcją dynamiczną
Struktura pierwotna
Struktura przekształcona do równoważnego układu kaskadowego

Układy z pomocniczą korekcją dynamiczną
1
)
(
+
=
Ts
Ts
s
D
)
1
1
(
)
(
s
T
k
s
R
i
p
+
=
s
T
S
D
i
1
1
)
(
1
+
=
p
k
s
D
s
R
=
)
(
)
(
co odpowiada, dla T=T
i
, użyciu w układzie kaskadowym regulatora
głównego typu PI:
Najczęściej:
oraz regulatora pomocniczego typu P:
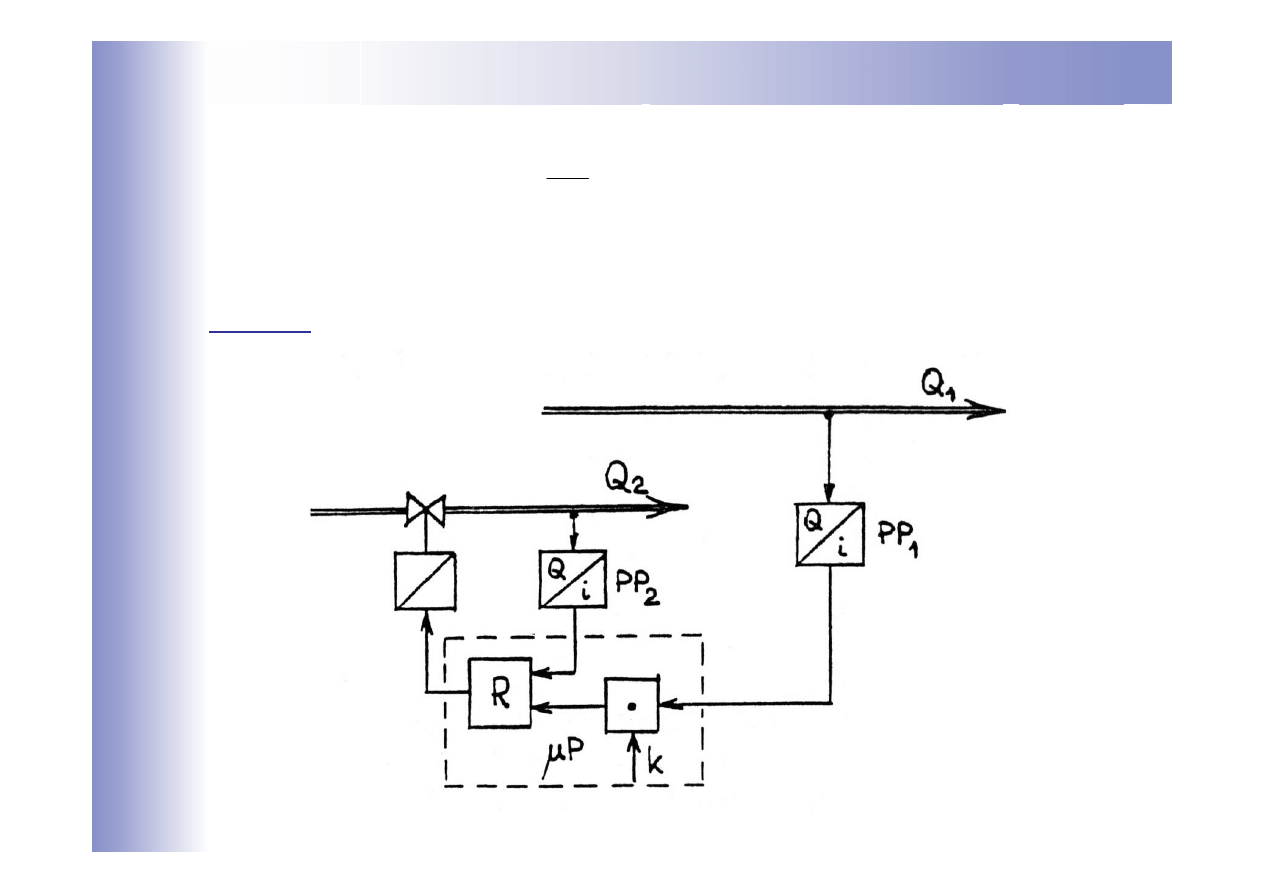
Regulacja stosunku
k
Q
Q =
1
2
Regulacja stosunku:
z możliwością oddziaływania jedynie na Q
2
.
(Uwaga: wpływ zakresów pomiarowych przetworników PP
1
i PP
2
)
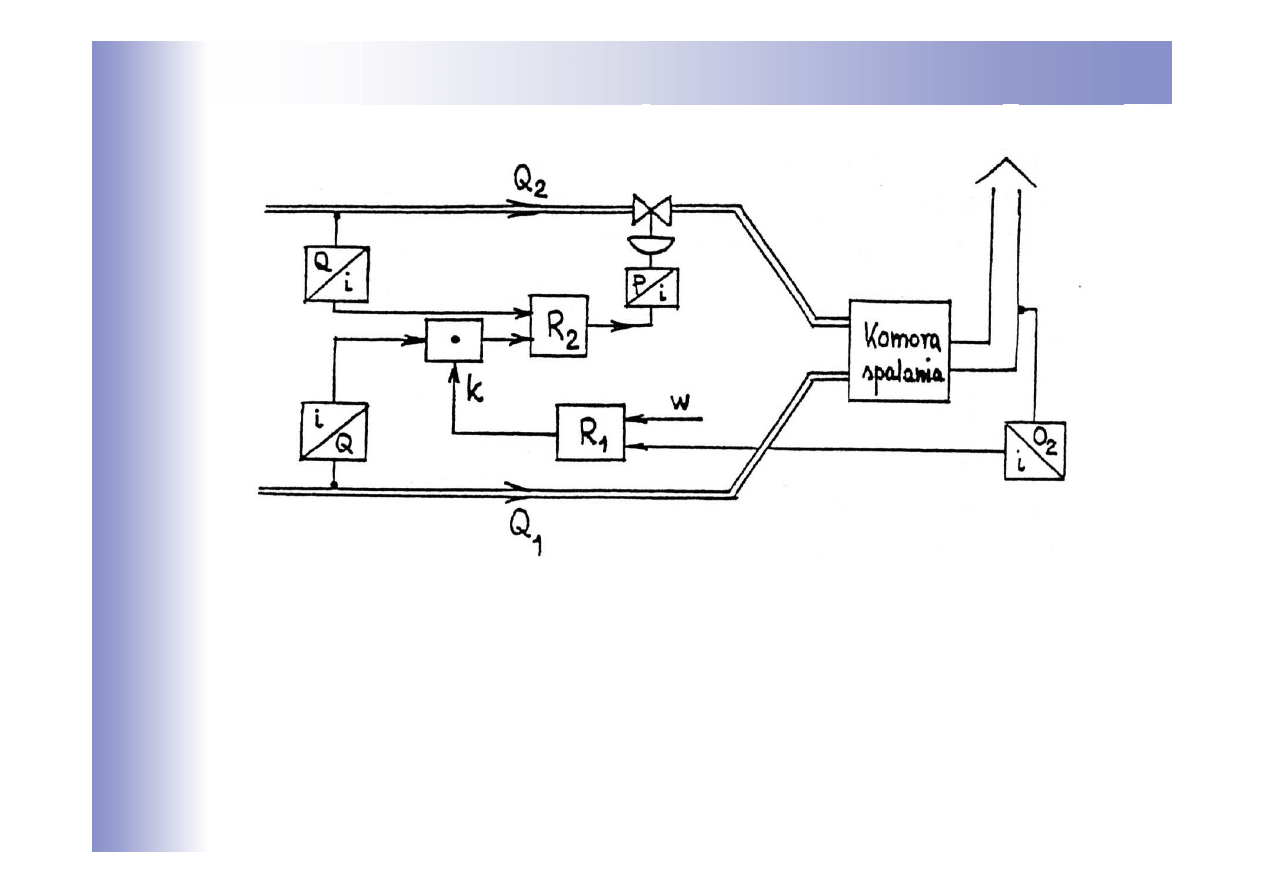
Kaskadowa regulacja stosunku
Przykład optymalizacji procesu spalania przez utrzymywanie stałej
zawartości O
2
w spalinach
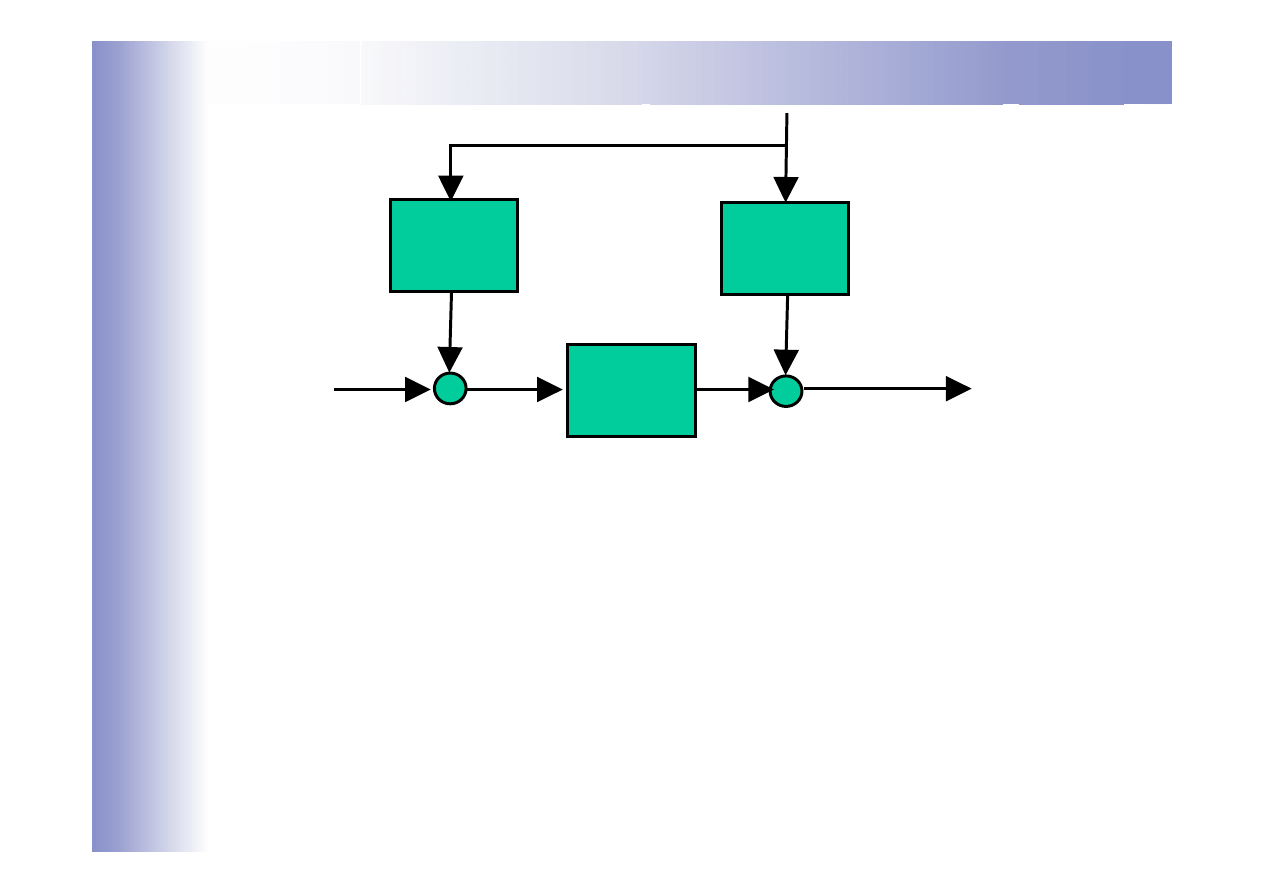
Zasada kompensacji zakłóceń
K
G
ob
+
+
z
y
G
z
u
+
+
Warunek realizacji:
możliwość pomiaru zakłócenia
znajomość własności dynamicznych obiektu G
ob
i toru zakłócenia G
z
Zasada kompensacji zakłóceń
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
s
z
s
G
s
K
s
z
s
G
s
u
s
G
s
y
ob
z
ob
+
+
=
0
)
(
)
(
)
(
=
+
s
G
s
K
s
G
ob
z
K
G
ob
+
+
z
y
G
z
u
+
+
)
(
)]
(
)
(
)
(
[
)
(
)
(
)
(
s
z
s
G
s
K
s
G
s
u
s
G
s
y
ob
z
ob
+
+
=
)
(
)
(
)
(
s
G
s
G
s
K
ob
z
−
=
Warunek absolutnej inwariantności: y(s)/z(s)=0
Wpływ zakłócenia jest całkowicie
skompensowany
Kompensacja a regulacja
błyskawiczne działanie
wolniejsze działanie
mała odporność na zmiany parametrów
obiektu
duża odporność na zmiany parametrów
obiektu
kompensuje wpływ tylko jednego
zakłócenia na wielkość sterowaną
zabezpiecza przed wpływem wszystkich
zakłóceń na wielkość regulowaną
teoretycznie jest możliwa całkowita
eliminacja wpływu zakłócenia na wyjście
obiektu
nie jest możliwa całkowita eliminacja
wpływu zakłócenia na wyjście obiektu
Układy kompensacji
Układy regulacji
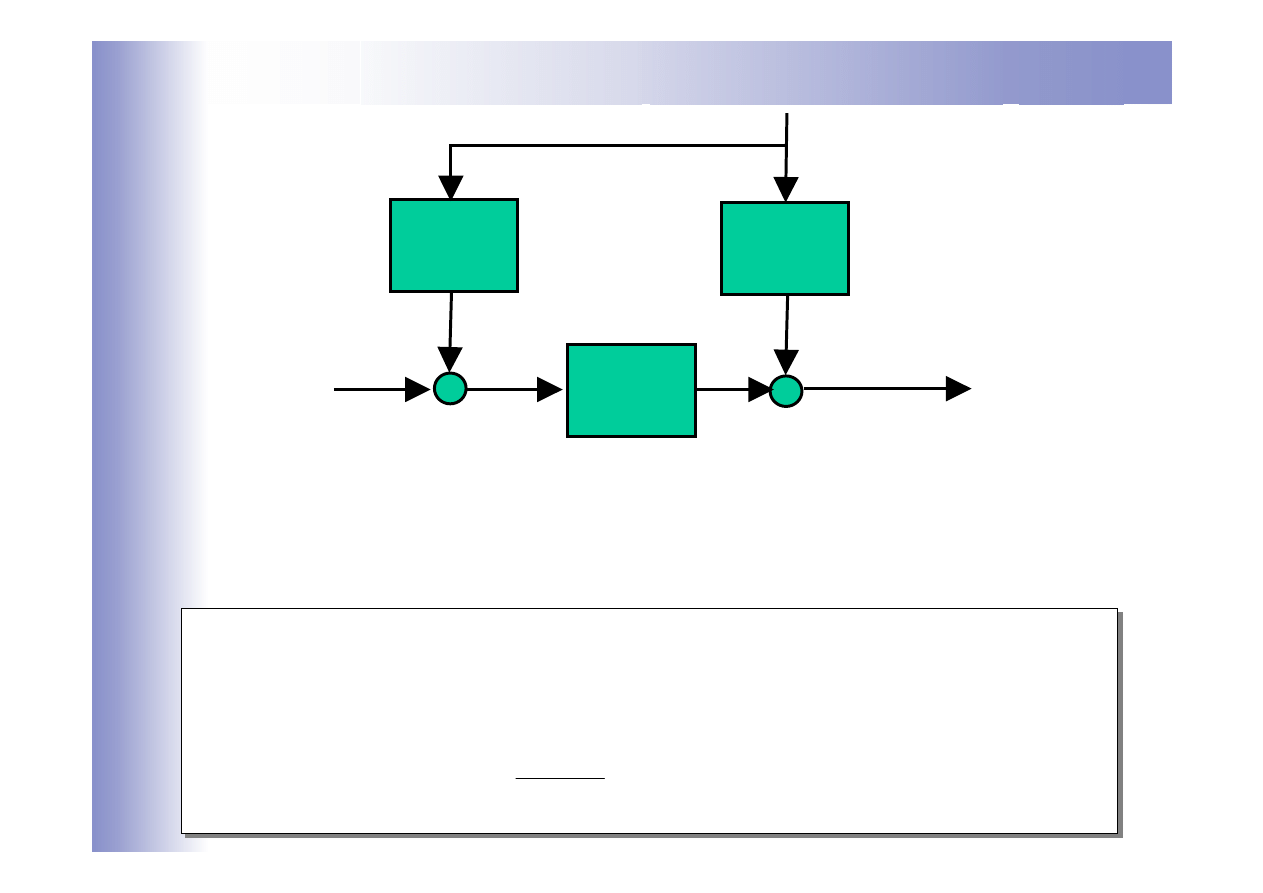
Układy zamknięto-otwarte
W układach tych wykorzystuje się bezpośredni pomiar zakłócenia
do wytworzenia oddziaływania kompensującego wpływ tego
zakłócenia na wyjście obiektu
)
(
)
(
1
)
(
1
ω
ω
ω
j
G
j
R
j
D
−
=
Struktura 1
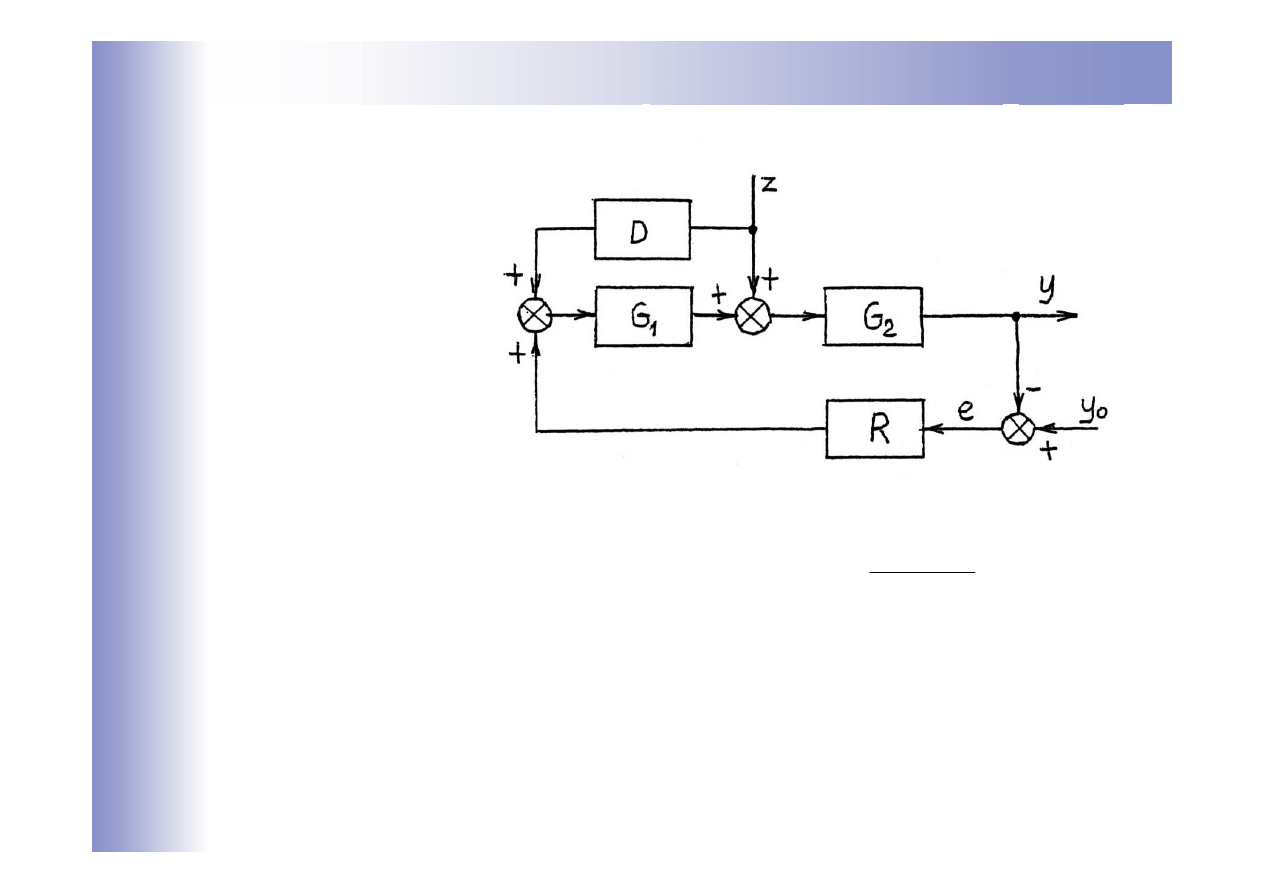
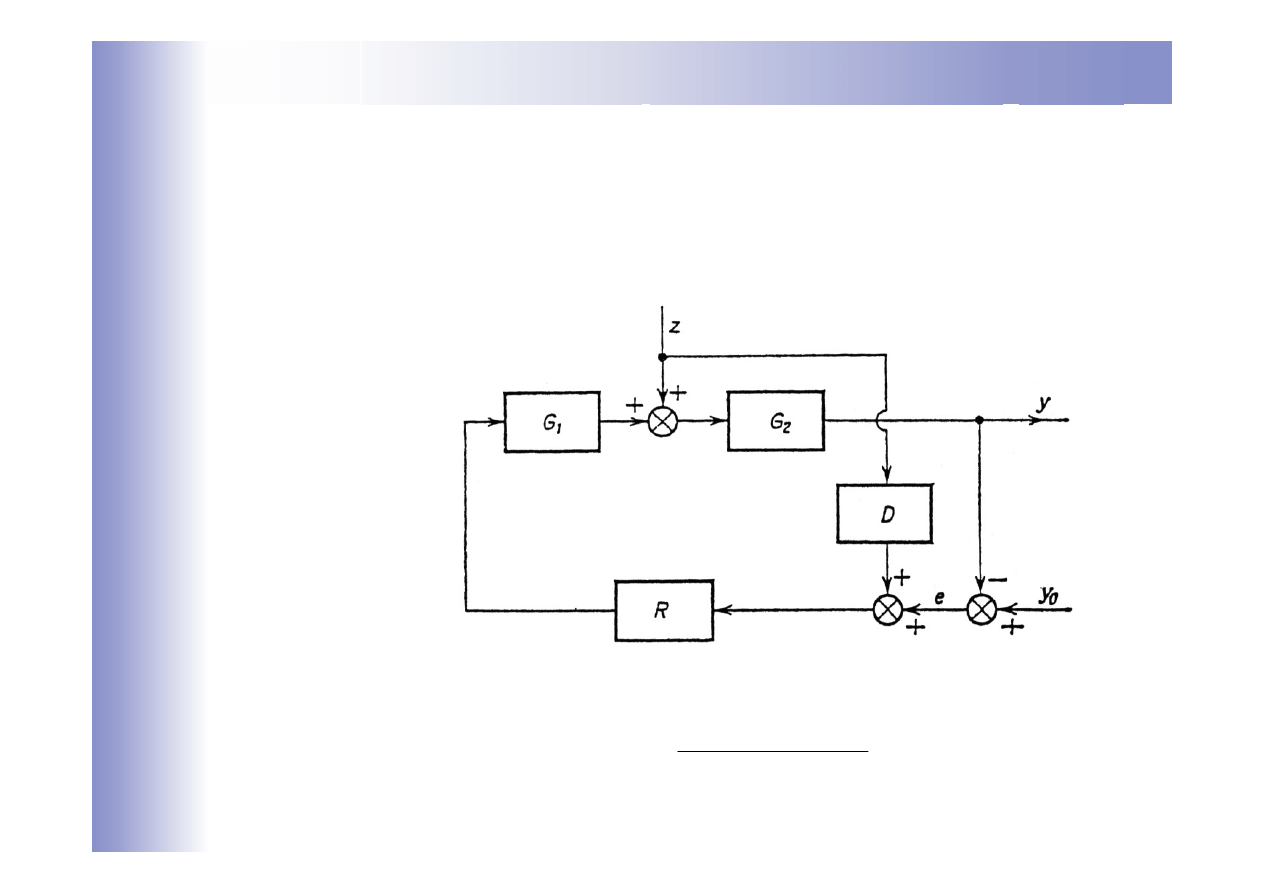
Układy zamknięto-otwarte
Struktura 2
)
(
1
)
(
1
ω
ω
j
G
j
D
−
=
Ograniczenia:
a)
zwykle zakłóceń jest wiele, część z nich może być trudna lub
niemożliwa do zmierzenia
b)
właściwości obiektu G
1
nie są stałe w czasie
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron