PRÓBNY EGZAMIN MATURALNY
Z FIZYKI I ASTRONOMII
Arkusz I
Poziom podstawowy
Czas pracy 120 minut
Instrukcja dla zdającego:
1. Proszę sprawdzić, czy arkusz zawiera 16 stron. Ewentualny
brak należy zgłosić przewodniczącemu zespołu
nadzorującego egzamin.
2. Na dwóch ostatnich stronach arkusza zamieszczona jest
karta wzorów i stałych fizycznych.
3. Proszę uważnie czytać wszystkie polecenia.
4. Rozwiązania i odpowiedzi należy zapisać czytelnie
w miejscu na to przeznaczonym przy każdym zadaniu.
5. W rozwiązaniach zadań rachunkowych trzeba przedstawić
tok rozumowania prowadzący do ostatecznego wyniku oraz
pamiętać o podaniu jednostek obliczanych wielkości.
6. W trakcie obliczeń można korzystać z kalkulatora.
7. Proszę pisać tylko w kolorze niebieskim lub czarnym, nie
pisać ołówkiem.
8. Nie wolno używać korektora.
9. Błędne zapisy trzeba wyraźnie przekreślić.
10. Brudnopis nie będzie oceniany.
11.
Obok każdego zadania podana jest maksymalna liczba
punktów, którą można uzyskać za jego poprawne
rozwiązanie.
Życzymy powodzenia!
ARKUSZ I
Poziom podstawowy
CZERWIEC
ROK 2004
Za rozwiązanie
wszystkich zadań
można otrzymać
łącznie 50 punktów
(wpisuje zdający przed rozpoczęciem pracy)
PESEL ZDAJĄCEGO
(wpisuje zdający
przed rozpoczęciem pracy)
KOD ZDAJĄCEGO
PRÓBNY EGZAMIN MATURALNY - CZERWIEC 2004
Fizyka – Arkusz I
strona 2 z 16
Wybrane odpowiedzi wpisz w kratki po prawej stronie pod zadaniem.
Zadanie 1. (1 pkt)
Samolot leciał najpierw 400 km na wschód, a następnie na północ. Przemieszczenie samolotu
na całej trasie wyniosło 500 km. Droga przebyta przez ten samolot jest równa
A) 500 km
B) 700 km
C) 800 km
D) 900 km
Zadanie 2. (1 pkt)
Aby ruszyć z miejsca ciężką szafę, należy ją pchnąć, działając siłą o wartości
200 N zwróconą poziomo. Gdy próbujemy przesunąć tę szafę, działając siłą o wartości 150 N
zwróconą poziomo, to siła tarcia ma wtedy wartość równą
A) 50 N
B) 150 N
C) 200 N
D) 350 N
Zadanie 3. (1 pkt)
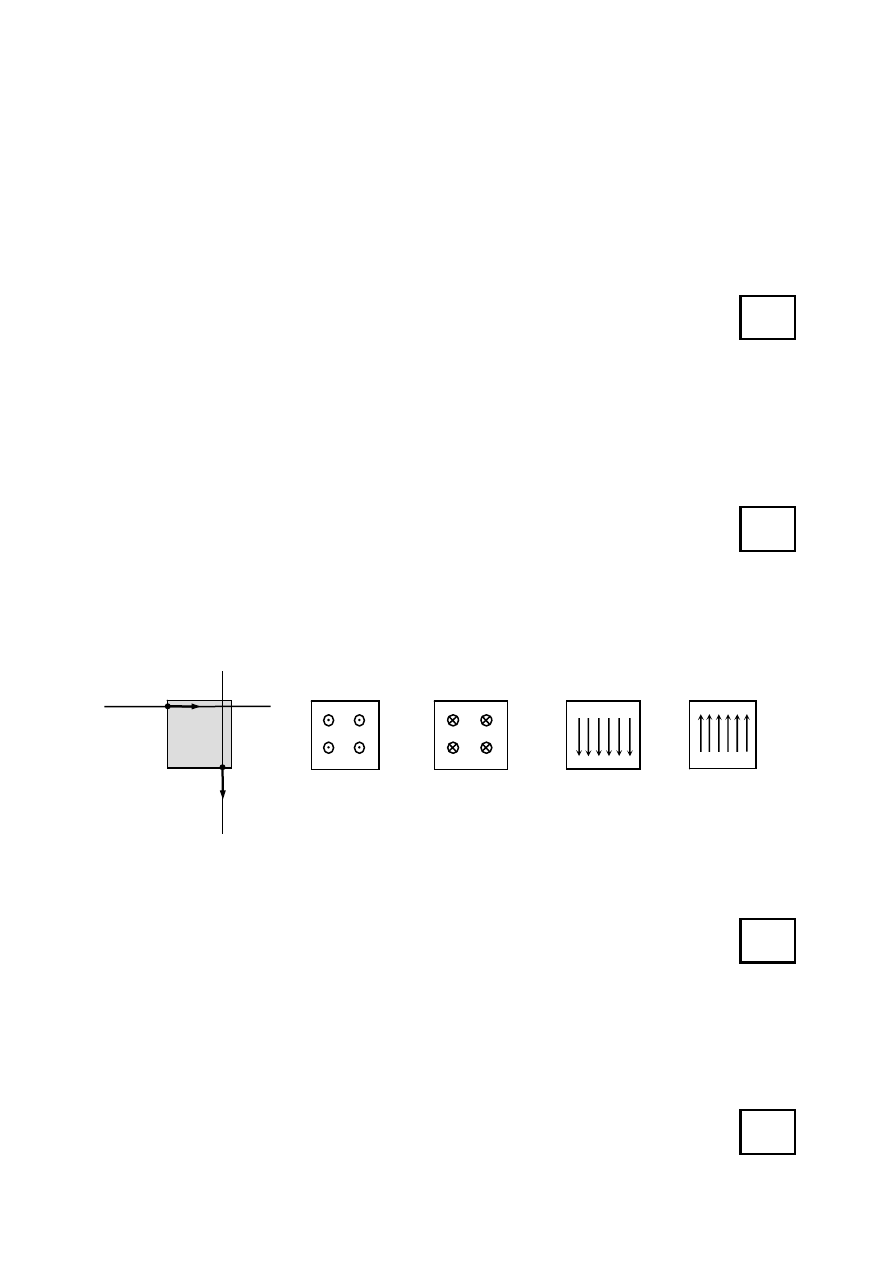
Dodatnio naładowana cząstka, poruszając się w próżni wzdłuż prostej m, wpada w obszar
zaznaczony na rysunku. Cząstka opuszcza ten obszar wzdłuż prostej n tak jak pokazano na
rysunku. Na podstawie powyższych informacji można stwierdzić, że w obszarze tym
wytworzono jednorodne pole, które schematycznie przedstawiono na rysunku
A)
1
B)
2
C)
3
D)
4
Zadanie 4. (1 pkt)
Temperatura chłodnicy idealnego silnika cieplnego stanowi 2/5 temperatury źródła ciepła.
Sprawność tego silnika jest równa
A)
20%
B) 40%
C) 60%
D)
80%
m
n
pole
magnetyczne
pole
elektryczne
pole
magnetyczne
pole
elektryczne
rys. 1
rys. 2
rys. 3
rys. 4
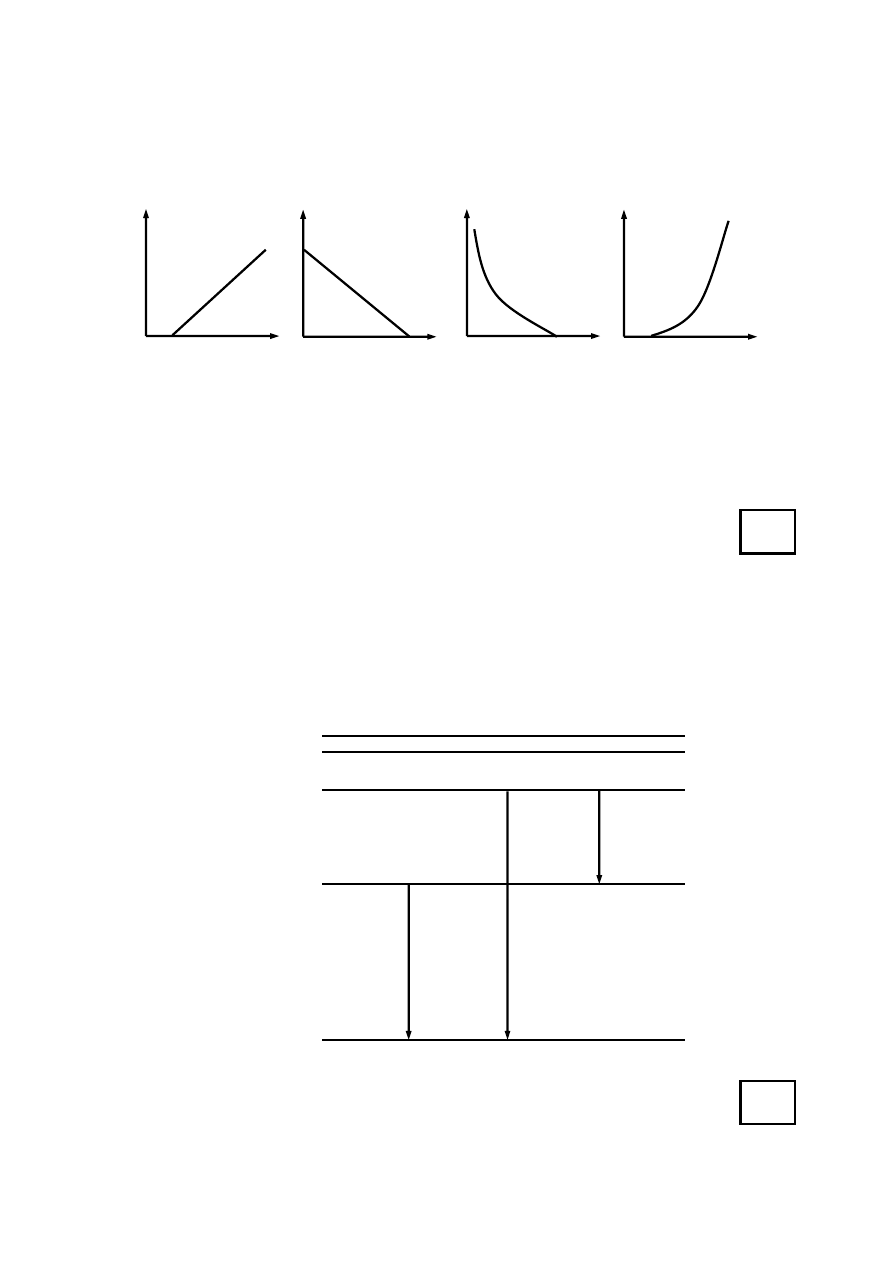
PRÓBNY EGZAMIN MATURALNY - CZERWIEC 2004
Fizyka – Arkusz I
strona 3 z 16
Zadanie 5. (1 pkt)
Zależność maksymalnej energii kinetycznej elektronów, wybijanych z katody fotokomórki,
od długości fali elektromagnetycznej, padającej na katodę, poprawnie przedstawia wykres
A) 1
B)
2
C)
3
D)
4
Zadanie 6. (1 pkt)
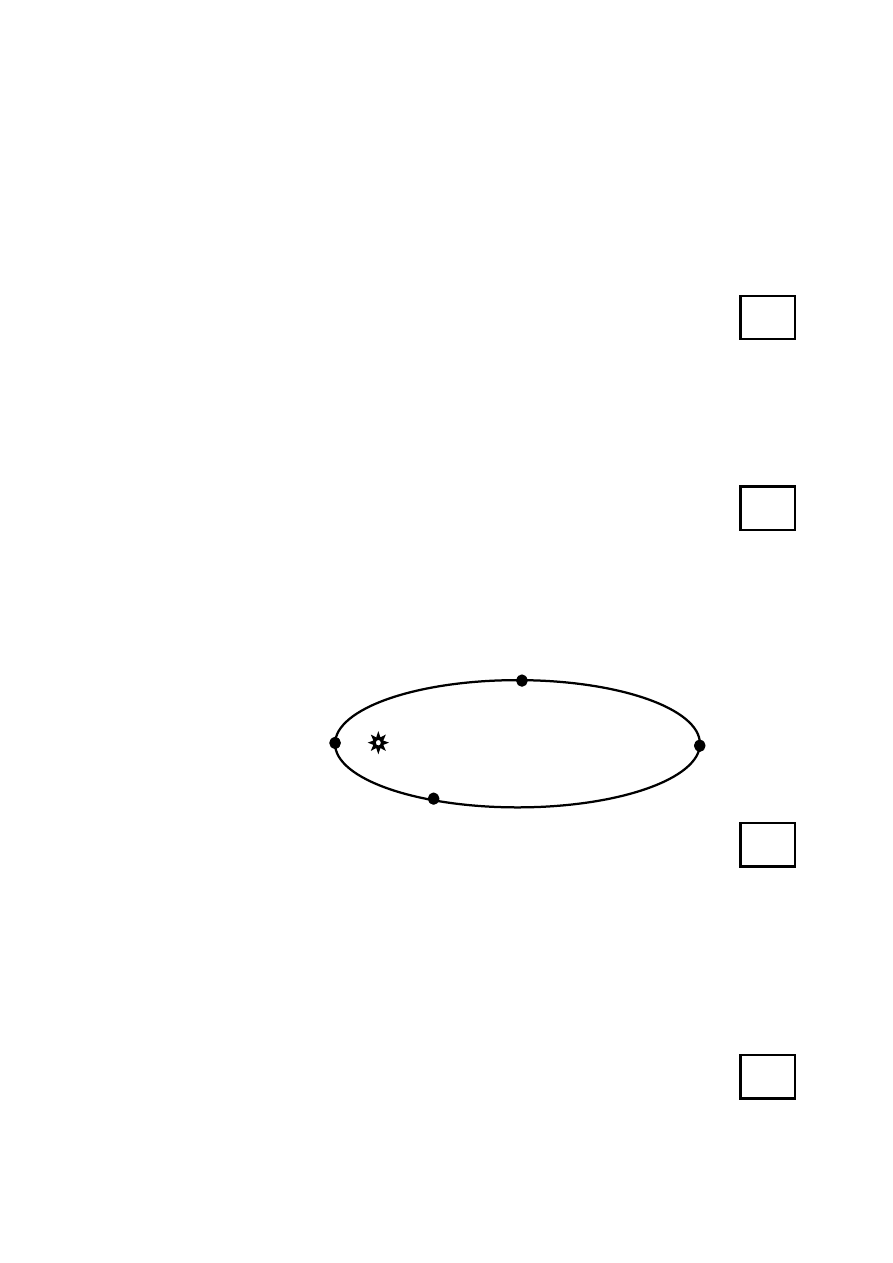
Według modelu Bohra atom wodoru pochłania lub emituje energię tylko podczas
przejść elektronu pomiędzy orbitami stacjonarnymi. Na rysunku poniżej przedstawiono
niektóre przejścia pomiędzy poziomami energetycznymi. Przejścia te oznaczono
liczbami 1, 2, 3. Odpowiada im odpowiada emisja fal o długościach
λ
1
,
λ
2
,
λ
3
. Wskaż
właściwe uszeregowanie długości fal.
A)
λ
1
<
λ
2
<
λ
3
B)
λ
2
<
λ
1
<
λ
3
C)
λ
1
<
λ
3
<
λ
2
D)
λ
3
<
λ
2
<
λ
1
3
1
2
n=5
n=4
n=3
n=2
n=1
n=1
E
λ
E
λ
λ
λ
E
λ
E
λ
λ
λ
wykres 1
wykres 2
wykres 3
wykres 4
PRÓBNY EGZAMIN MATURALNY - CZERWIEC 2004
Fizyka – Arkusz I
strona 4 z 16
Zadanie 7. (1 pkt)
Świecącą niewielką żarówkę umieszczono na głównej osi optycznej soczewki skupiającej,
w odległości 10 cm od środka soczewki. W tej sytuacji nie powstaje obraz żarówki. Jeżeli
żarówkę umieścimy w odległości 15 cm od soczewki, to otrzymany obraz żarówki będzie
A) rzeczywisty i pomniejszony.
B) pozorny i powiększony.
C) rzeczywisty i powiększony.
D) pozorny i pomniejszony.
Zadanie 8. (1 pkt)
Energia cieplna dociera ze Słońca na Księżyc dzięki
A) tylko konwekcji.
B) tylko promieniowaniu.
C) konwekcji i promieniowaniu.
D) przewodnictwu i promieniowaniu.
Zadanie 9. (1 pkt)
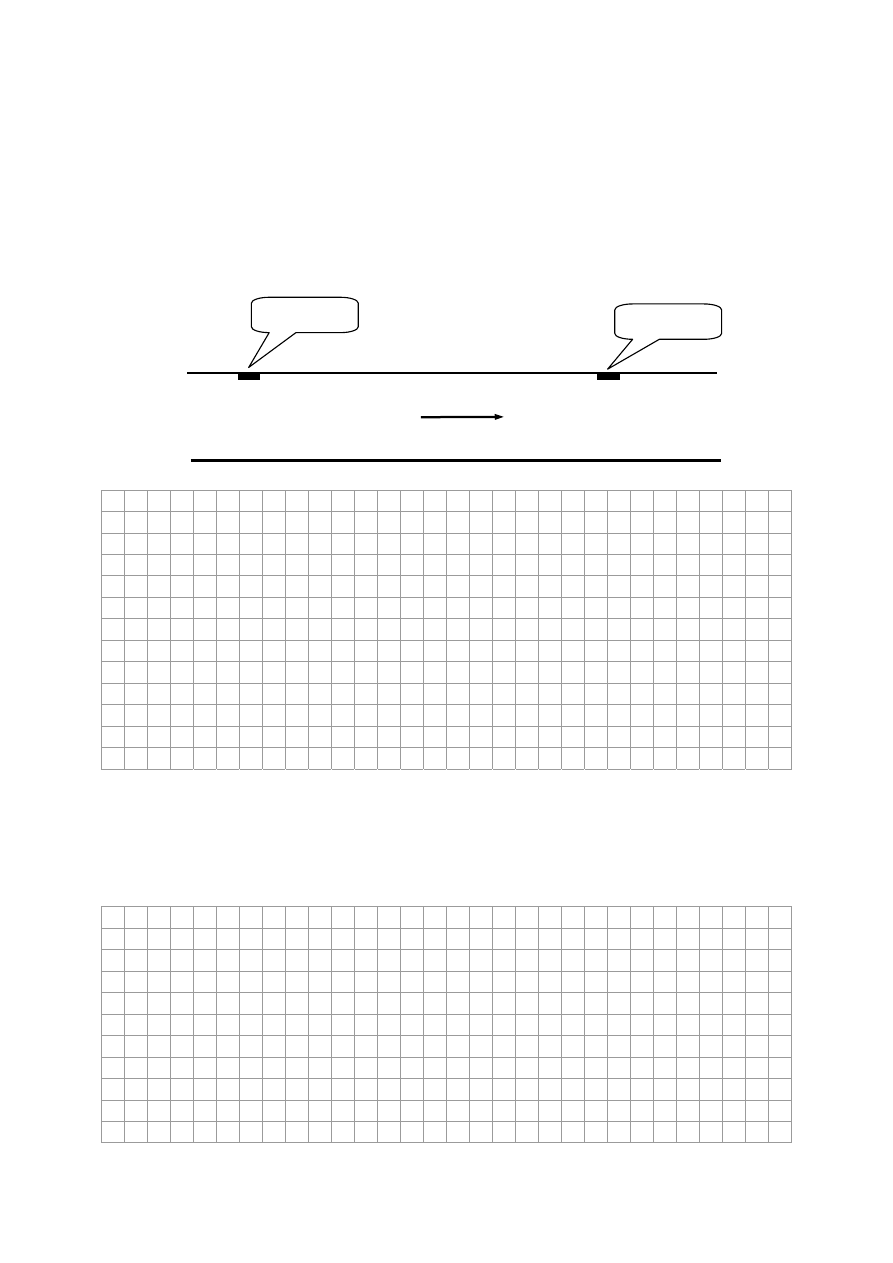
Planeta okrąża gwiazdę po orbicie eliptycznej. Wartość prędkości liniowej planety podczas jej
ruchu jest największa w punkcie oznaczonym numerem
A)
1
B)
2
C)
3
D)
4
Zadanie 10. (1 pkt)
Urządzeniem do odbioru fal elektromagnetycznych z odległych galaktyk jest
A)
laser.
B)
cyklotron.
C)
radioteleskop.
D)
mikroskop
elektronowy.
3
1
2
4
PRÓBNY EGZAMIN MATURALNY - CZERWIEC 2004
Fizyka – Arkusz I
strona 5 z 16
Zadania otwarte
Zadanie 11. Statek i tratwa (3 pkt)
Z przystani A wyruszają jednocześnie w dół rzeki statek i tratwa. Wartość prędkości statku
względem wody wynosi 5 m/s. Statek dopływa po 10 minutach do przystani B, gdzie zabiera
na pokład pasażerów, co trwa 20 minut. Gdy statek rusza z przystani B w stronę przystani A,
to tratwa dociera do przystani B. Oblicz wartość prędkości tratwy. W obliczeniach przyjmij
stałą wartość prędkości wody w rzece.
Zadanie 12. Łódka (2 pkt)
Chłopiec o masie 50 kg znajduje się w łódce, która spoczywa na powierzchni jeziora. Masa
łódki wynosi 50 kg. W pewnej chwili chłopiec wyrzuca poziomo z prędkością o wartości
4 m/s metalową kotwicę wzdłuż osi łódki. Masa kotwicy jest równa 5 kg. Oblicz wartość
prędkości łódki względem wody.
Przystań A
Przystań B
v
wody
PRÓBNY EGZAMIN MATURALNY - CZERWIEC 2004
Fizyka – Arkusz I
strona 6 z 16
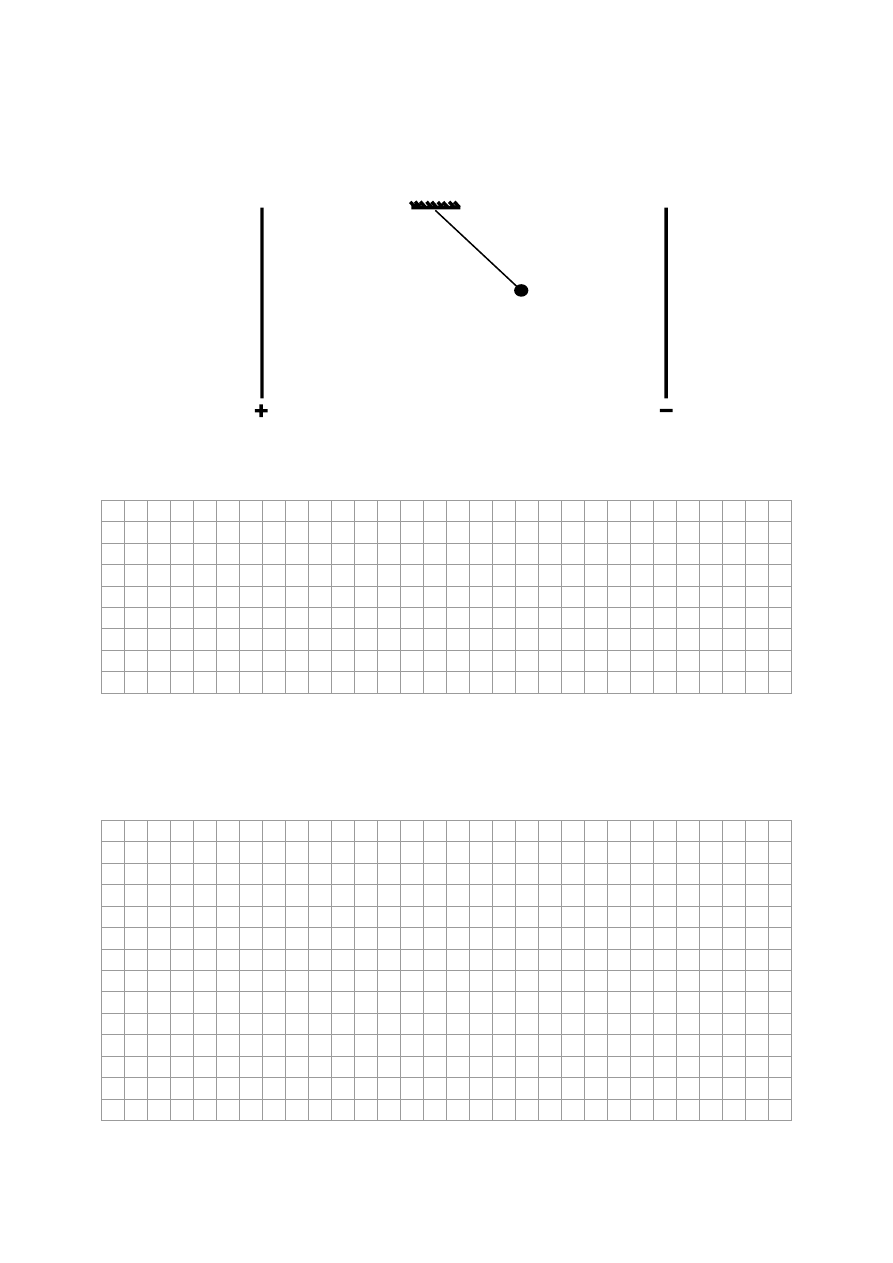
Zadanie 13. Piłeczka (3 pkt)
Pomiędzy pionowymi przewodzącymi płytami, naładowanymi tak jak na rysunku,
zawieszono na cienkiej, jedwabnej nici lekką, małą piłeczkę o masie 1 g naładowaną
dodatnim ładunkiem elektrycznym. Nić odchyliła się od pionu o kąt 45
o
.
a) Narysuj siły działające na piłeczkę. Zachowaj odpowiednie proporcje. (1 pkt)
b) Podaj wartość siły elektrostatycznej działającej na piłeczkę. Dokonaj niezbędnych
obliczeń, przyjmij wartość przyspieszenia ziemskiego równą 10 m/s
2
. (2 pkt)
Zadanie 14. Zbiornik z gazem (4 pkt)
Stalowy zbiornik o objętości 0,2 m
3
zawiera azot pod ciśnieniem 0,5 MPa i temperaturze 0
o
C.
Zbiornik zabezpieczony jest zaworem bezpieczeństwa otwierającym się wtedy, gdy ciśnienie
gazu osiągnie wartość 0,6 MPa. Masa molowa azotu jest równa 28 g/mol.
a) Oblicz masę azotu znajdującego się w zbiorniku. (2 pkt)
PRÓBNY EGZAMIN MATURALNY - CZERWIEC 2004
Fizyka – Arkusz I
strona 7 z 16
b) Zbiornik z gazem pozostawiono w nasłonecznionym miejscu. Oblicz, przy jakiej
temperaturze gazu nastąpi otwarcie zaworu bezpieczeństwa. Załóż, że objętość
zbiornika nie ulega zmianie. (2 pkt)
Zadanie 15. Ciężarki (2 pkt)
Uczniowie dysponowali dwoma różnymi ciężarkami i dwoma jednakowymi sprężynami oraz
dwoma nitkami. Znana była masa tylko jednego z ciężarków. Uczniowie zaproponowali trzy
nietypowe doświadczalne metody prowadzące do wyznaczenia masy drugiego ciężarka.
A. Zawiesić ciężarki na jednakowych sprężynach i zmierzyć wydłużenie sprężyn.
B. Zawiesić ciężarki na niciach o jednakowej długości i zmierzyć okresy drgań
takich wahadeł, które można traktować jak wahadła matematyczne.
C. Zawiesić ciężarki na jednakowych sprężynach i zmierzyć okresy drgań takich
wahadeł.
Wskaż, która z zaproponowanych metod nie nadaje się do wyznaczenia masy ciężarka. Swój
wybór krótko uzasadnij.
Zadanie 16. Dyskietka (2 pkt)
Podaj, jakie zjawisko magnetyczne wykorzystuje się podczas zapisu informacji na dyskietce
komputerowej. Nazwij własności magnetyczne materiału, który wykorzystano jako nośnik
informacji.
PRÓBNY EGZAMIN MATURALNY - CZERWIEC 2004
Fizyka – Arkusz I
strona 8 z 16
Zadanie 17. Laser (6 pkt)
Wiązka światła laserowego tworzy z powierzchnią wody kąt 60
o
.
Długość fali świetlnej,
wysyłanej przez laser, jest równa w powietrzu 633 nm, a bezwzględny współczynnik
załamania wody wynosi 4/3.
a) Oblicz długość fali świetlnej w wodzie. (3 pkt)
b) Wykaż, że w sytuacji opisanej w treści zadania następujące stwierdzenie jest fałszywe: Kąt
między promieniem odbitym od powierzchni wody i promieniem załamanym jest
mniejszy od 120
o
. Odpowiedź uzasadnij, odwołując się do odpowiednich praw. (2 pkt)
PRÓBNY EGZAMIN MATURALNY - CZERWIEC 2004
Fizyka – Arkusz I
strona 9 z 16
Zadanie 18. Samochód (2 pkt)
Gdy samochód porusza się po poziomej drodze ruchem jednostajnym prostoliniowym
z prędkością o wartości 54 km/h, konieczne jest działanie siły o wartości 1000 N.
Oblicz moc niezbędną do utrzymania stałej wartości prędkości samochodu.
Zadanie 19. Metalowa kulka (5 pkt)
Mała metalowa kulka o masie 0,1 kg spada swobodnie.
a) Zapisz formułę matematyczną (wzór) opisującą zależność energii kinetycznej kulki od
czasu jej spadania. (1 pkt)
b) Narysuj wykres ilustrujący zależność energii potencjalnej od czasu dla swobodnie
spadającej kulki. Załóż, że kulka ma masę 0,1 kg i spada z wysokości 45 m.
W obliczeniach przyjmij wartość przyspieszenia ziemskiego równą 10 m/s
2
.
Wykorzystaj tabelę zamieszczoną poniżej (dokonaj odpowiednich obliczeń). (4 pkt)
czas spadania
w sekundach
0 0,5 1 1,5 2 2,5 3
energia potencjalna
w dżulach
Obliczenia
PRÓBNY EGZAMIN MATURALNY - CZERWIEC 2004
Fizyka – Arkusz I
strona 10 z 16
Wykres
Zadanie 20. Atom wodoru (2 pkt)
W atomie wodoru nieoznaczoność położenia elektronu jest równa promieniowi jego orbity
w stanie podstawowym, czyli około 5,3·10
-11
m. Oblicz niepewność pomiaru wartości pędu
elektronu w tym stanie.
Zadanie 21. Izotop (4 pkt)
Czas połowicznego rozpadu izotopu
Po
210
84
wynosi około 140 dni.
a) Napisz równanie reakcji rozpadu tego izotopu wiedząc, że w jej wyniku powstaje izotop
ołowiu
Pb
206
82
. Podaj nazwę wyemitowanej cząstki. (2 pkt)
PRÓBNY EGZAMIN MATURALNY - CZERWIEC 2004
Fizyka – Arkusz I
strona 11 z 16
b) Oblicz, jaka część początkowej masy tego izotopu pozostanie po upływie 40 tygodni. (2 pkt)
Zadanie 22. Dwa satelity (4 pkt)
Po orbitach kołowych krążą wokół Ziemi dwa satelity. Minimalna odległość między
satelitami wynosi 6 R
z
(R
z
– promień Ziemi, R
z
≈ 6,37·10
6
m). Wartość prędkości liniowej
satelity znajdującego się dalej od Ziemi jest dwa razy mniejsza niż satelity znajdującego się
bliżej Ziemi. Oblicz długość promienia orbity satelity krążącego bliżej Ziemi. Załóż, że orbity
obu satelitów leżą w jednej płaszczyźnie.
PRÓBNY EGZAMIN MATURALNY - CZERWIEC 2004
Fizyka – Arkusz I
strona 12 z 16
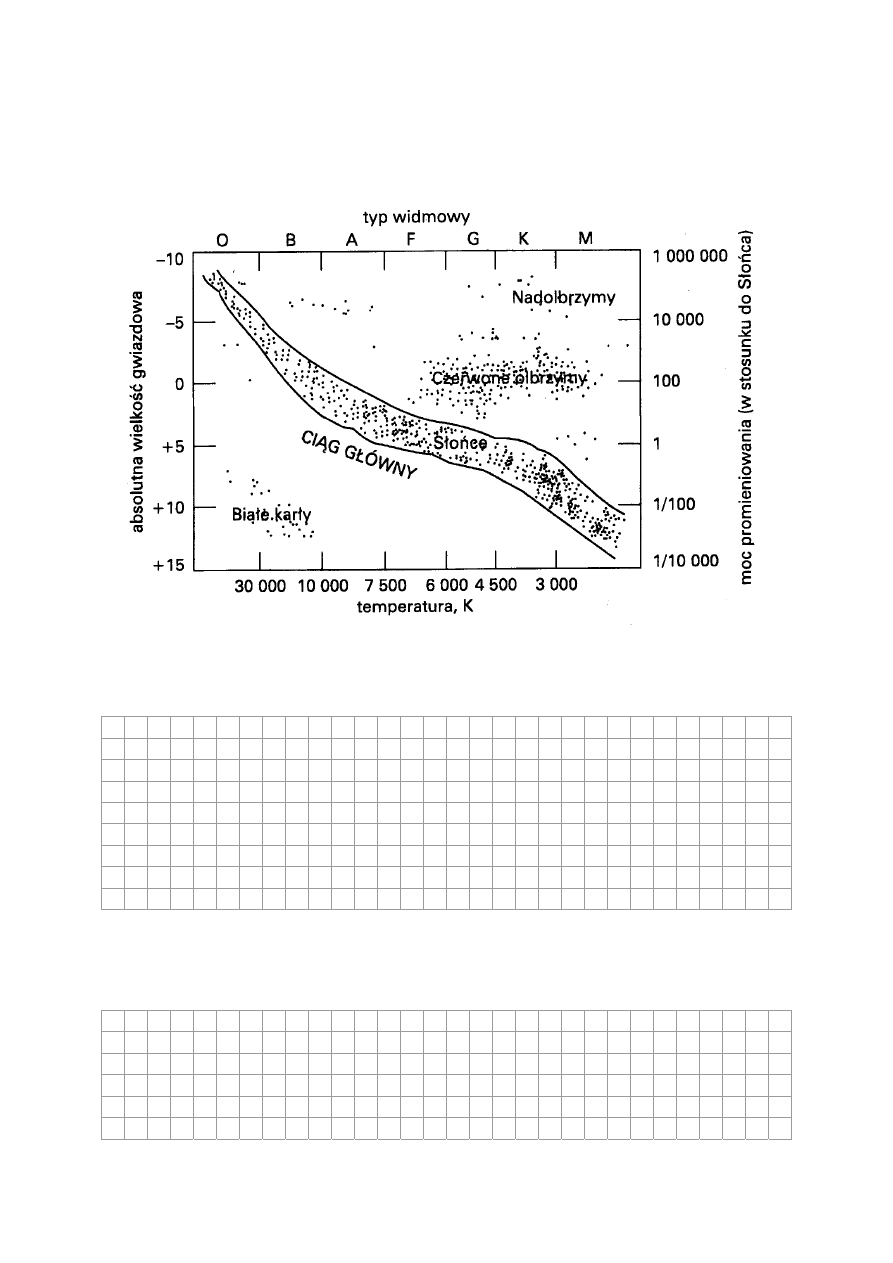
Zadanie 23. Diagram H – R (2 pkt)
Obserwacja gwiazd i badanie charakteryzujących je wielkości doprowadziły, na początku XX
wieku, do sporządzenia przez dwóch astronomów Ejnara Hertzsprunga i Henry’ego Norrisa
Russela tzw. diagramu Hertzsprunga i Russela nazywanego w skrócie diagramem H – R.
a) Podaj jak ze wzrostem temperatury gwiazd, leżących na ciągu głównym, zmienia się
ich moc promieniowania. (1pkt)
c) Astronomowie prowadząc obserwacje stwierdzili zależności między temperaturą,
jasnością gwiazd oraz ich typem widmowym (przedstawione na diagramie H – R).
Zależności te mogą zostać wykorzystane do rozwinięcia teorii opisującej ewolucję
gwiazd. Podaj nazwę takiej metody postępowania. (1pkt)
Diagram Hertzsprunga - Russela
PRÓBNY EGZAMIN MATURALNY - CZERWIEC 2004
Fizyka – Arkusz I
strona 13 z 16
Brudnopis
PRÓBNY EGZAMIN MATURALNY - CZERWIEC 2004
Fizyka – Arkusz I
strona 14 z 16
Brudnopis
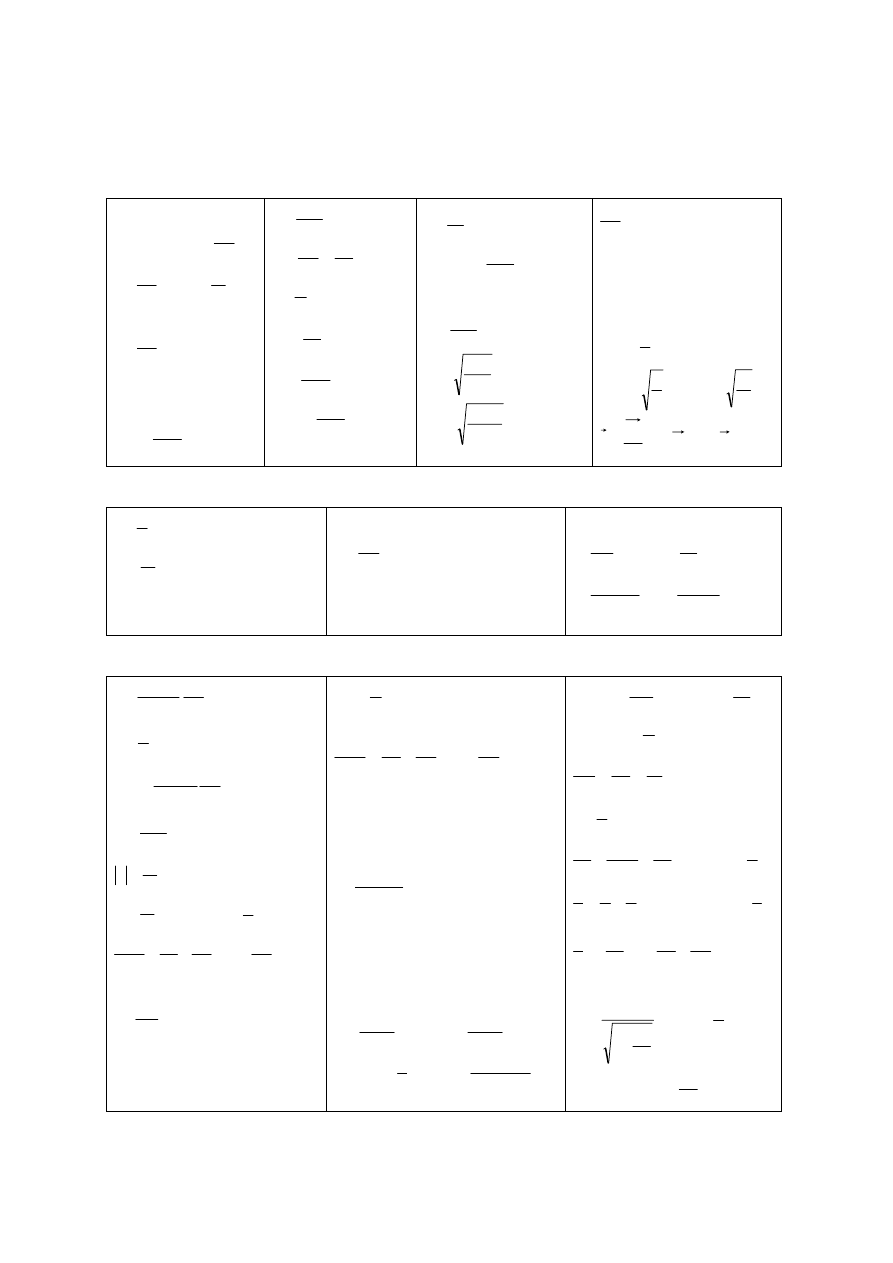
PRÓBNY EGZAMIN MATURALNY - CZERWIEC 2004
Fizyka – Arkusz I
strona 15 z 16
Karta wybranych wzorów i stałych fizycznych
Mechanika
at
v
)
t
(
v
0
+
=
2
at
t
v
s
)
t
(
s
2
0
0
+
+
=
t
v
a
∆
∆
=
r
r
m
F
a
r
r =
v
m
p
r
r =
t
p
F
∆
∆
=
r
r
N
T
F
F
µ
=
cos
Fs
W
=
∢
)
s
,
F
(
r
r
2
mv
E
2
kin
=
t
W
P
∆
∆
=
T
2
t
π
=
∆
ϕ
∆
=
ω
T
1
f
=
r
v
a
2
d
=
r
mv
F
2
d
=
2
r
Mm
G
F
g
=
m
F
g
r
r =
γ
r
Mm
G
E
pot
−
=
mgh
E
pot
=
∆
h << R
z
m
E
V
pot
=
Z
I
R
GM
v
=
Z
II
R
GM
2
v
=
.
const
R
T
3
2
=
kx
F
−
=
)
t
sin(
A
)
t
(
x
ϕ
+
ω
=
)
t
cos(
A
)
t
(
v
ϕ
+
ω
ω
=
)
t
sin(
A
)
t
(
a
2
ϕ
+
ω
ω
−
=
2
pot
kx
2
1
E
=
g
2
T
l
π
=
k
m
2
T
π
=
I
M
ε
=
ω
I
K
⋅
=
Termodynamika i własności materii
S
F
p
=
V
m
d
=
T
mc
Q
w
∆
=
∆
mL
Q
=
∆
mR
Q
=
∆
nRT
pV
=
ϰ
V
p
c
c
=
R
c
c
V
P
+
=
W
Q
U
+
=
∆
V
p
W
∆
=
Elektryczność, magnetyzm, fale, optyka i fizyka współczesna
2
r
0
r
Qq
4
1
F
ε
πε
=
q
F
E
r
r
=
r
Qq
4
1
E
r
0
pot
ε
πε
=
q
E
V
pot
=
d
U
E
=
U
Q
C
=
d
S
C
r
0
ε
ε
=
n
2
1
calk
C
1
C
1
C
1
C
1
+
+
+
=
L
n
2
1
calk
C
C
C
C
+
+
+
=
L
t
Q
I
∆
∆
=
IR
U
=
S
l
ρ
R
=
n
2
1
calk
R
R
R
R
+
+
+
=
L
n
2
1
calk
R
1
R
1
R
1
R
1
+
+
+
=
L
∑
=
=
n
1
k
k
calk
I
I
0
U
m
1
j
j
n
1
k
k
=
+
∑ε
∑
=
=
w
z
r
R
I
+
=
ε
IU
P
=
sin
qvB
F
=
∢
)
B
,
v
(
r
r
sin
B
F
Il
=
∢
)
B
,
(
r
r
l
cos
BS
=
Φ
∢
)
S
,
B
(
r
r
r
2
I
B
r
0
π
µ
µ
=
r
2
I
B
r
0
µ
µ
=
l
I
n
B
r
0
µ
µ
=
r
l
I
I
F
2
1
r
π
µ
µ
=
2
0
t
SEM
∆
∆Φ
−
=
ε
t
I
L
SEM
∆
∆
−
=
ε
l
S
2
r
0
n
L
µ
µ
=
2
1
1
2
1
2
I
I
n
n
U
U
=
=
f
v
=
λ
α
=
λ
sin
d
n
1
2
2
1
n
n
sin
sin
v
v
=
β
α
=
v
c
n
=
y
1
x
1
f
1
+
=
f
1
D
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
=
2
1
2
1
R
1
R
1
1
n
n
f
1
2
mc
E
=
hf
E
=
2
2
0
c
v
1
m
m
−
=
λ
h
p
=
π
≥
∆
⋅
∆
2
h
p
x
1
2
1
1
2
1
T
T
T
Q
Q
Q
Q
W
W
W
c
u
−
=
η
−
=
η
=
η
=
η
PRÓBNY EGZAMIN MATURALNY - CZERWIEC 2004
Fizyka – Arkusz I
strona 16 z 16
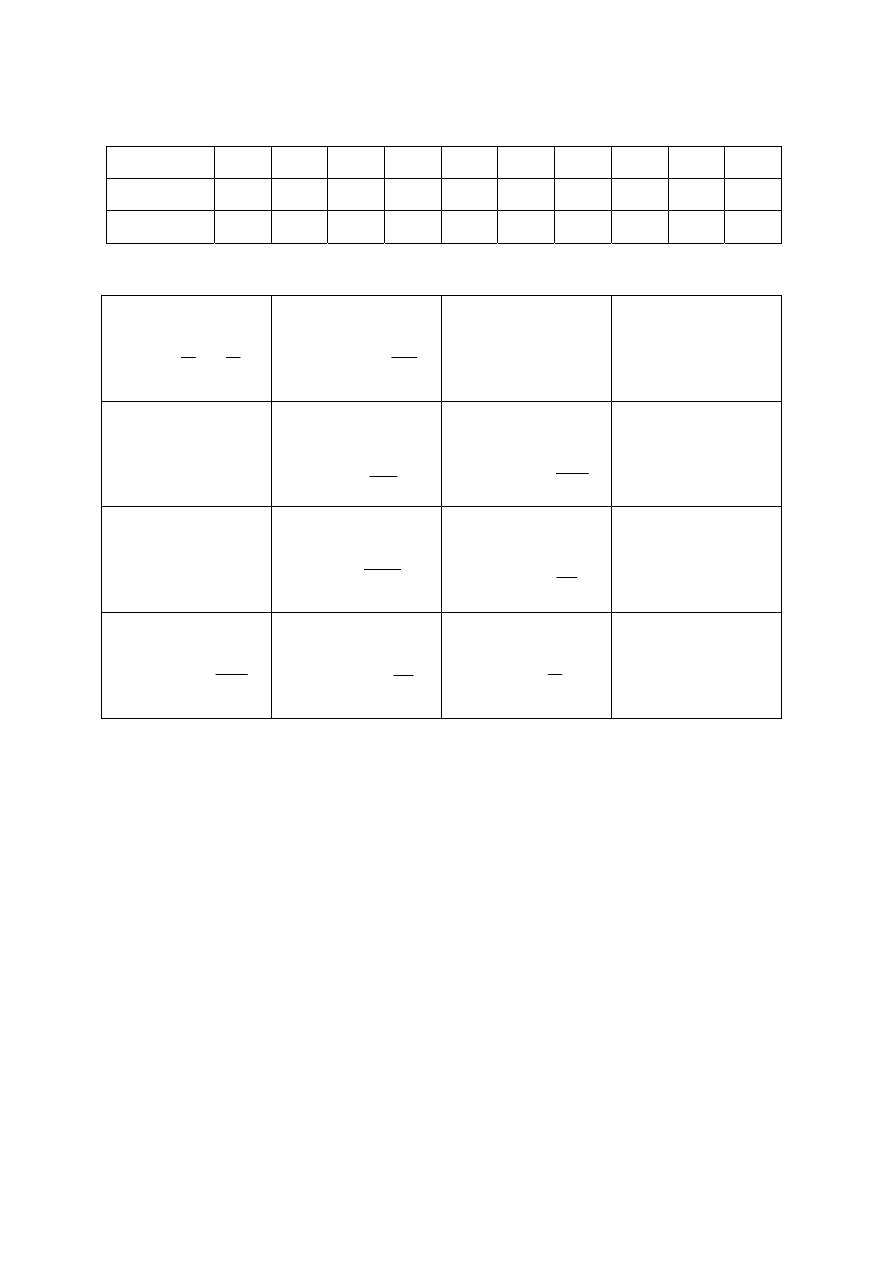
Przedrostki
Mnożnik
9
10
6
10
3
10
2
10
1
10
1
10
−
2
10
−
3
10
−
6
10
−
9
10
−
Przedrostek giga mega kilo hekto
deka decy centy
mili mikro nano
Oznaczenie G M k h da d c m µ n
Ważniejsze stałe fizyczne
Przyspieszenie ziemskie
2
2
s
m
10
s
m
81
,
9
g
≈
=
Liczba Avogadro
mol
1
10
02
,
6
N
23
A
⋅
=
Stała Plancka
Js
h
34
10
63
,
6
−
⋅
≈
Masa spoczynkowa
elektronu
kg
10
11
,
9
m
31
e
−
⋅
=
Masa Ziemi
kg
M
Z
24
10
98
,
5
⋅
=
Objętość 1 mola gazu
w warunkach normalnych
mol
dm
4
,
22
V
3
=
Przenikalność
dielektryczna próżni
2
2
12
0
Nm
C
10
85
,
8
−
⋅
=
ε
Masa spoczynkowa
protonu
kg
10
67
,
1
m
27
p
−
⋅
=
Średni promień Ziemi
km
6370
R
Z
=
Stała gazowa
molK
J
31
,
8
R
=
Przenikalność
magnetyczna próżni
2
7
0
A
N
10
4
−
⋅
π
=
µ
Masa spoczynkowa
neutronu
kg
10
68
,
1
m
27
p
−
⋅
=
Stała grawitacji
2
2
11
kg
Nm
10
67
,
6
G
−
⋅
=
Stała Boltzmanna
K
J
10
38
,
1
k
23
B
−
⋅
=
Prędkość światła w próżni
s
m
c
8
10
3
⋅
≈
Ładunek elektronu
C
10
6
,
1
e
19
−
⋅
=