
RURY GRUBOŚCIENNE
ZADANIE LAME

......................................

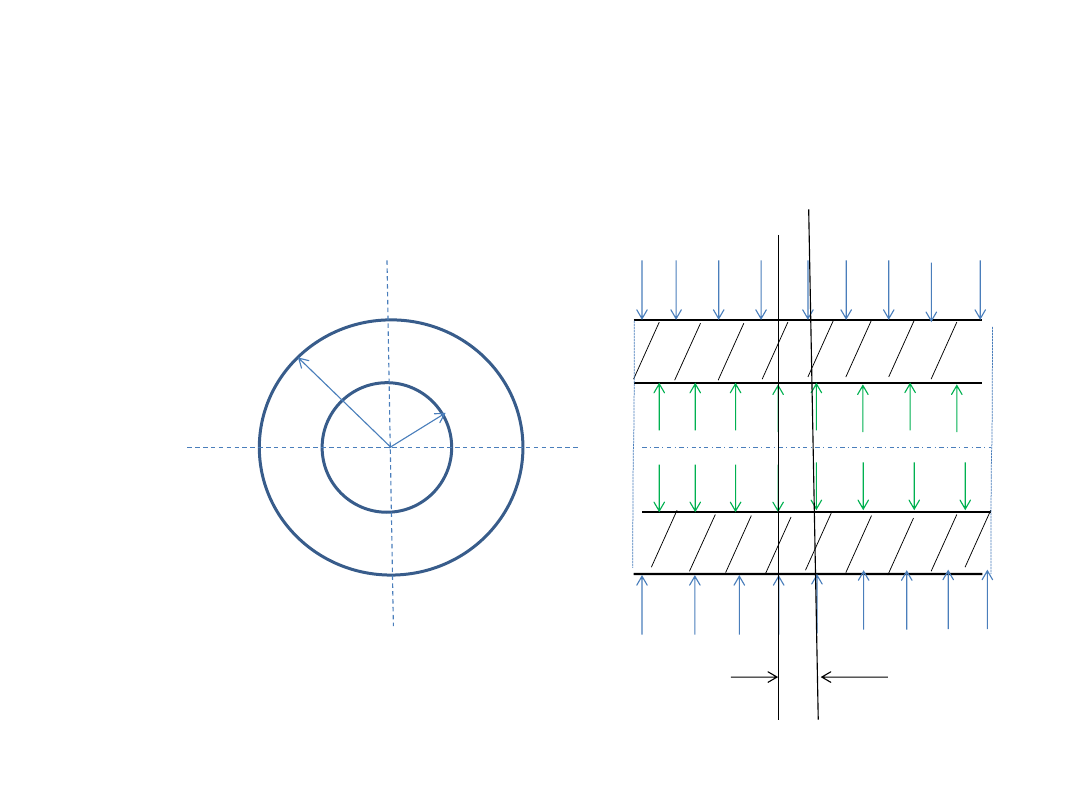
b
a
p
a
p
b
1
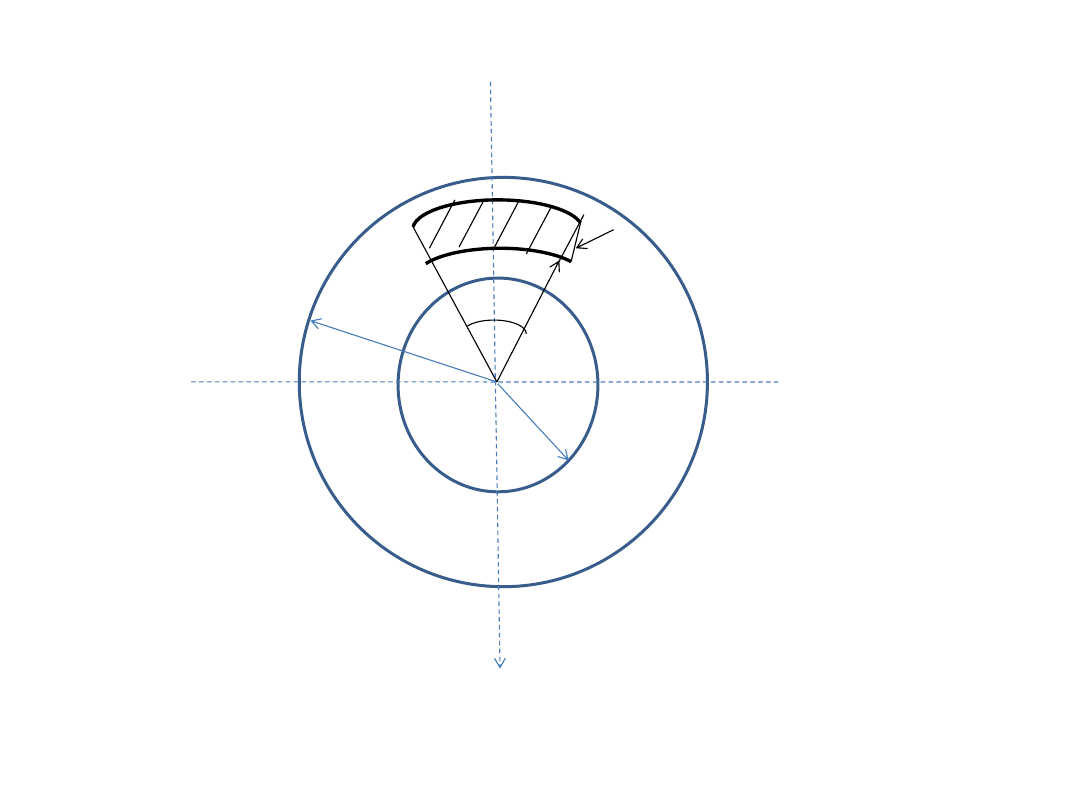
b
a
r
dr
dθ
a≤r≤b
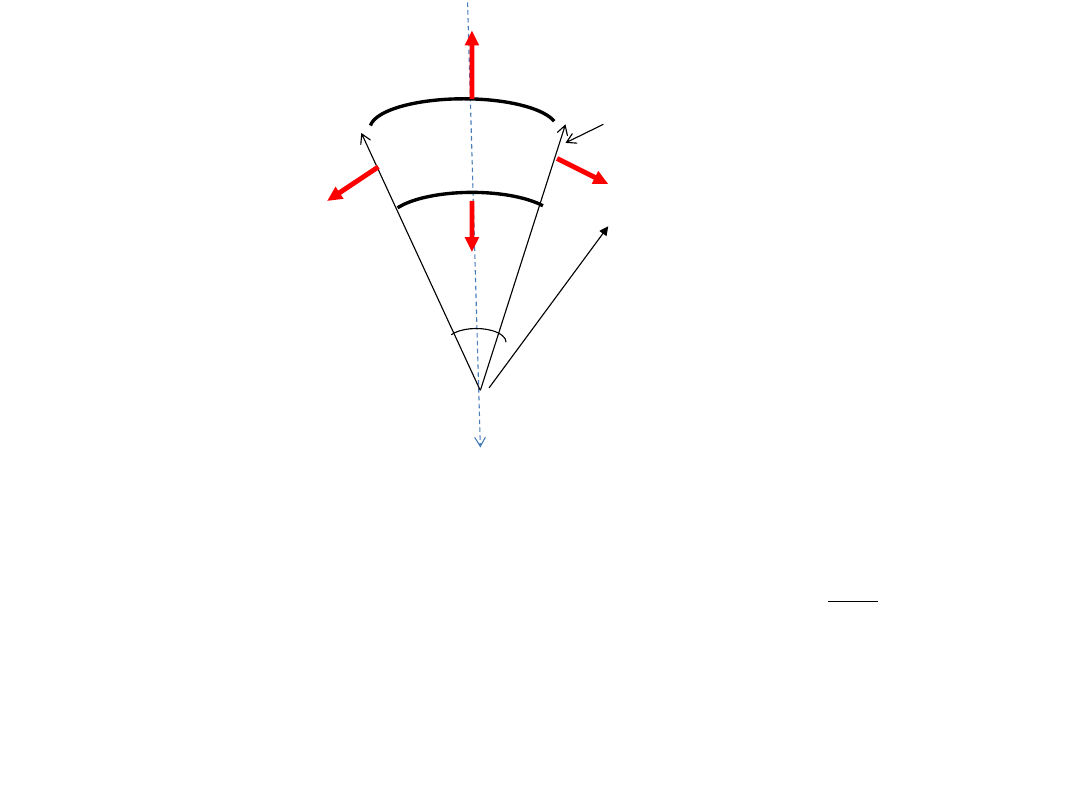
dr
dθ
a≤r≤b
r
s
t
s
t
s
r
+d
s
r
s
r
0
1
2
sin
2
1
1
dr
d
d
r
d
dr
r
d
t
r
r
r
s
s
s
s
Warunek równowagi – suma rzutów na kierunek promienia

0
0
2
2
dr
r
dr
r
d
dr
d
d
r
d
dr
r
d
t
r
r
r
t
r
r
r
s
s
s
s
s
s
s
s
0
dr
r
dr
d
dr
r
d
r
t
r
r
r
r
r
s
s
s
s
s
s
0
r
dr
d
t
r
r
s
s
s
1 równanie – 2 niewiadome!!!!
Po podzieleniu przez rdr
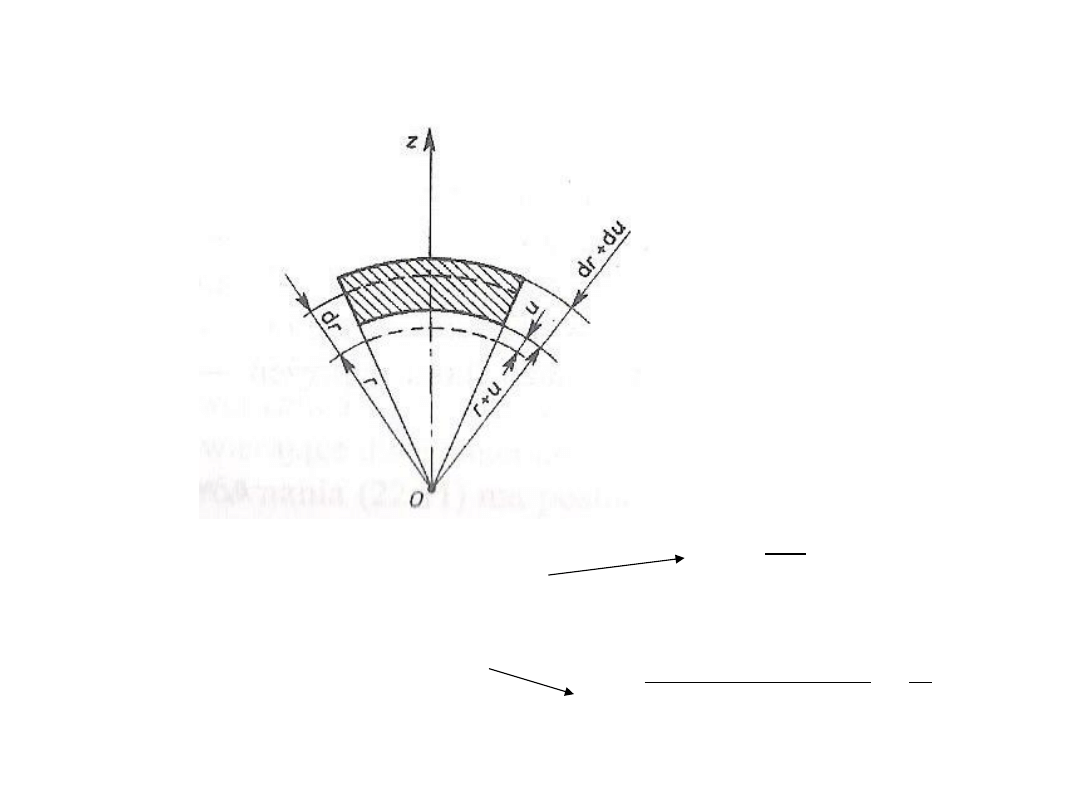
Zmiana długości promienia
- u(r)
r
u
rd
rd
d
u
r
t
)
(
Odkształcenie promieniowe
Odkształcenie obwodowe
dr
du
r

Prawo Hooke’a dla P.S.N
r
t
t
t
r
r
E
E
s
s
)
1
(
)
1
(
2
2
dr
du
r
u
E
r
u
dr
du
E
t
r
s
s
)
1
(
)
1
(
2
2
Po podstawieniu
2
2
2
2
1
1
r
u
r
dr
du
dr
u
d
E
dr
d
r
s
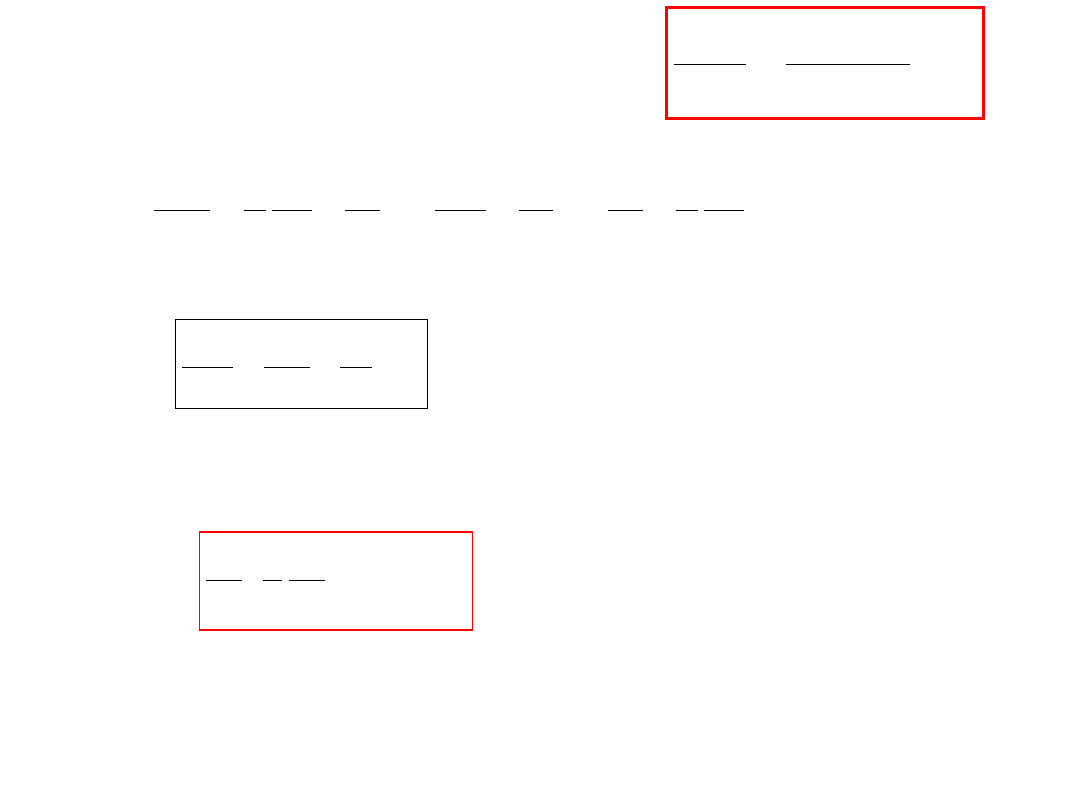
Po podstawieniu do równania równowagi
Po przekształceniu
0
2
2
2
2
2
dr
du
r
r
u
u
r
rdr
du
u
r
dr
du
r
dr
u
d
0
2
2
2
r
u
rdr
du
dr
u
d
0
1
r
u
dr
d
r
dr
d
0
r
dr
d
t
r
r
s
s
s
1 równanie – 1 niewiadoma!!!!

Zmiana promienia
r
1
C
r
C
2
1
)
r
(
u
2
1
;
p
)
b
r
(
;
p
)
a
r
(
b
r
a
r
s
s
Biorąc pod uwagę warunki brzegowe:
Otrzymujemy:
;
)
a
b
)(
1
(
b
a
)
p
p
(
E
1
C
;
)
a
b
)(
1
(
b
p
a
p
E
1
C
2
1
2
2
2
2
b
a
2
2
2
2
2
b
2
a
2
1
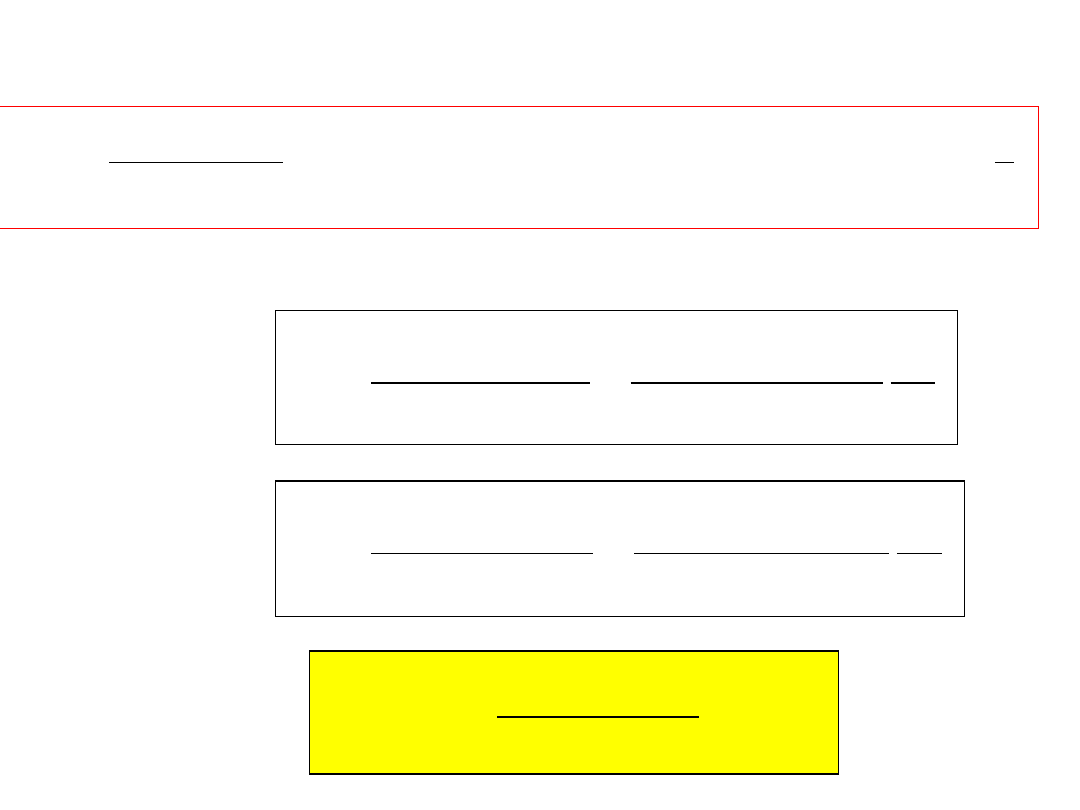
Zmiana promienia
r
1
b
a
)
p
p
)(
1
(
r
)
b
p
a
p
(
1
)
a
b
(
E
1
)
r
(
u
2
2
b
a
2
b
2
a
2
2
;
r
1
a
b
)
p
p
(
b
a
a
b
p
b
p
a
2
2
2
b
a
2
2
2
2
b
2
a
2
r
s
;
r
1
a
b
)
p
p
(
b
a
a
b
p
b
p
a
2
2
2
b
a
2
2
2
2
b
2
a
2
t
s
Naprężenia
.
const
a
b
p
b
p
a
2
2
2
b
2
a
2
t
r
s
s
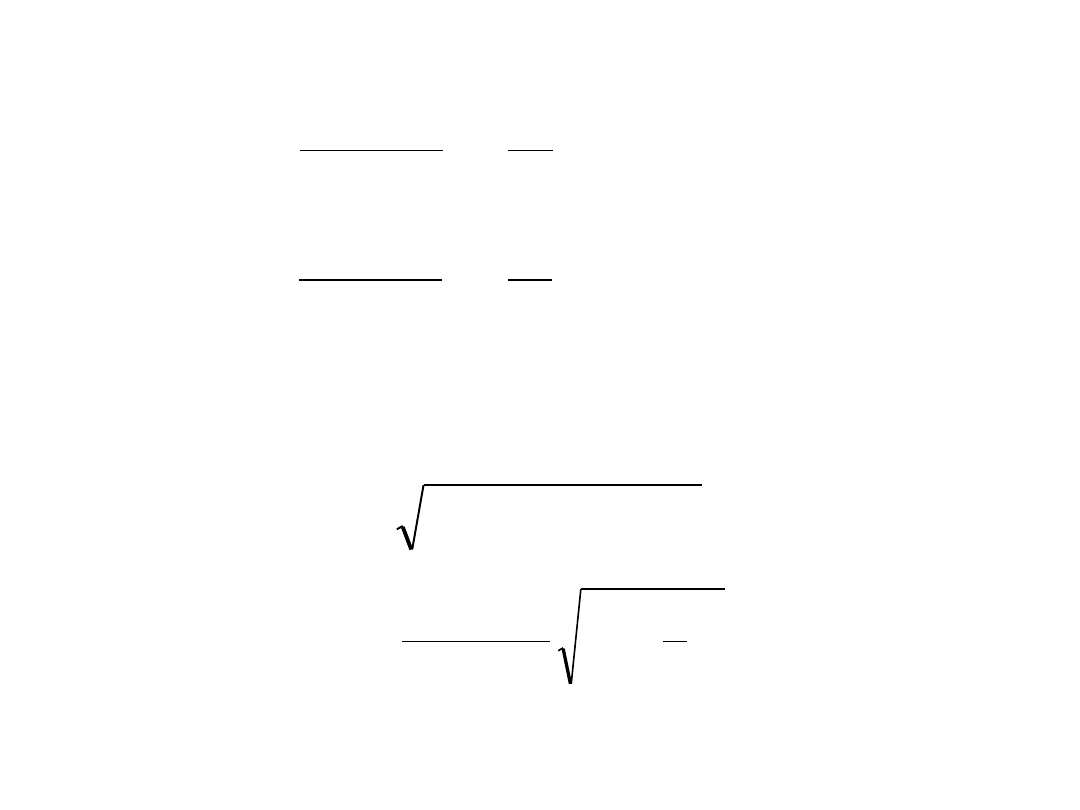
Ciśnienie zewnętrzne p
b
=0
);
r
b
1
(
)
a
b
(
p
a
);
r
b
1
(
)
a
b
(
p
a
2
2
2
2
a
2
t
2
2
2
2
a
2
r
s
s
;
)
r
b
(
3
1
)
a
b
(
p
a
4
2
2
a
2
red
s
Naprężenia zredukowane
2
2
t
t
r
r
red
s
s
s
s
s
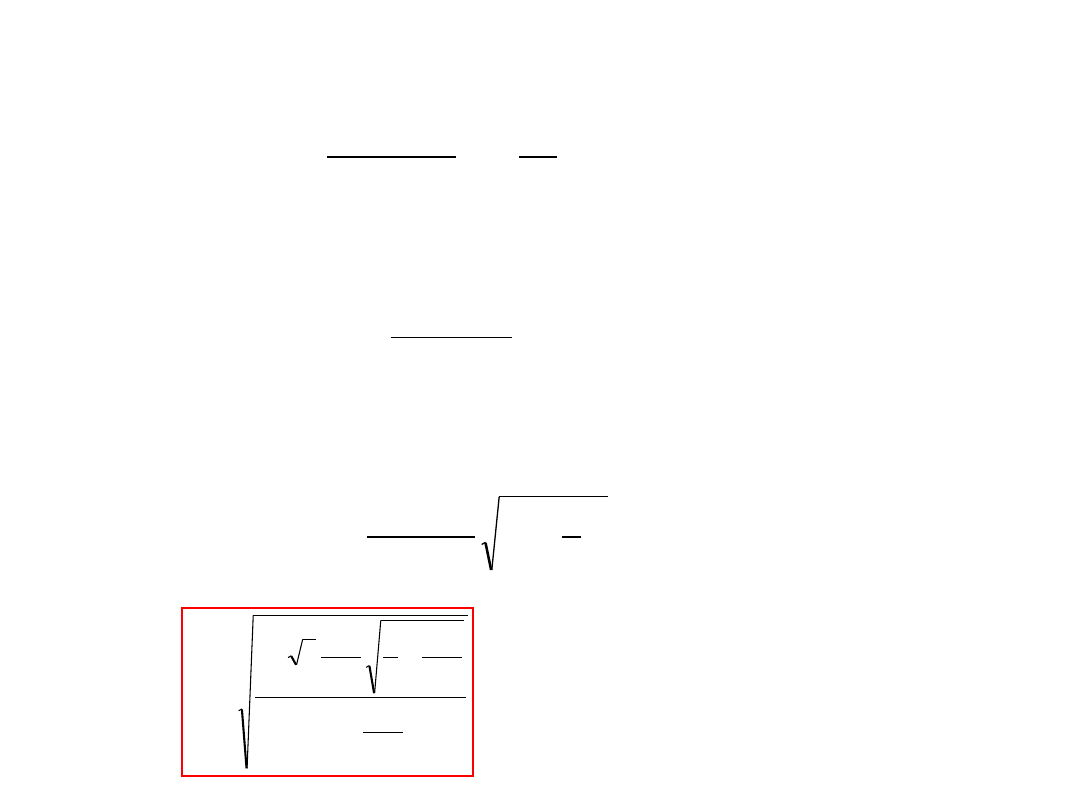
Dla r=a
max
2
2
2
2
2
)
1
(
)
(
t
a
t
a
r
a
b
a
b
p
a
p
s
s
s
dop
a
red
k
a
b
a
b
p
a
4
2
2
2
max
)
(
3
1
)
(
s
min
2
2
2
)
(
2
;
0
t
a
t
r
a
b
p
a
s
s
s
Naprężenia zredukowane – maksymalne r=a
Dla r=b
2
2
2
2
3
1
3
4
3
1
dop
a
dop
a
dop
a
k
p
k
p
k
p
a
b

Rura zamknięta dnami
Naprężenie osiowe
.
;
2
2
2
2
2
2
a
z
a
z
p
a
b
a
a
p
a
b
s
s
;
;
;
2
1
3
2
1
2
1
3
2
3
2
2
2
1
z
t
r
red
s
s
s
s
s
s
s
s
s
s
s
s
s
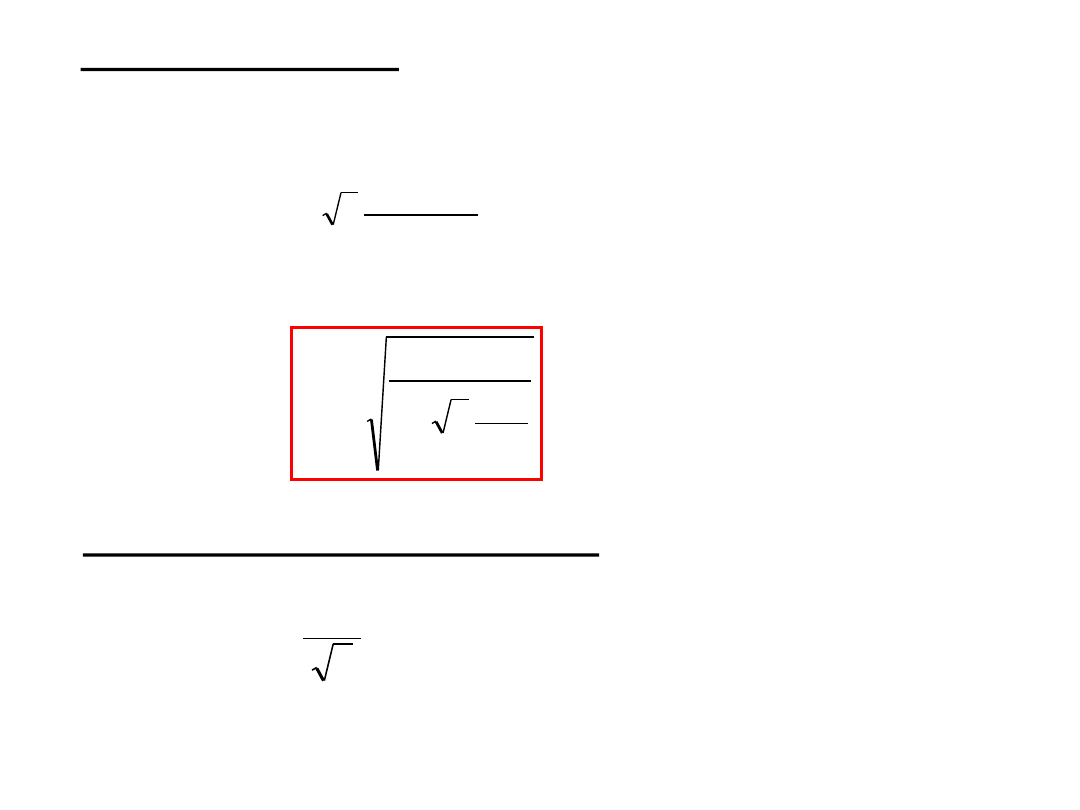
Naprężenia zredukowane
;
)
(
3
2
2
2
2
2
a
red
p
r
a
b
b
a
s
Naprężenia zredukowane – maksymalne r=a
dop
a
red
k
p
a
b
b
)
(
3
2
2
2
s
dop
a
k
p
a
b
3
1
1
Rura zamknięta dnami
3
dop
a
k
p
dla
Dla rury zamkniętej dnami i bez den
Zaprojektowanie rury jest niemożliwe!!!

Stan uplastycznienia rury grubościennej –
-
kryterium dopuszczalnej nośności
Hipoteza maksymalnego naprężenia stycznego
.
;
,
2
;
min
max
min
max
max
max
r
t
pl
s
s
s
s
s
s
.
)
(
2
2
2
max
a
b
b
p
a
r
a
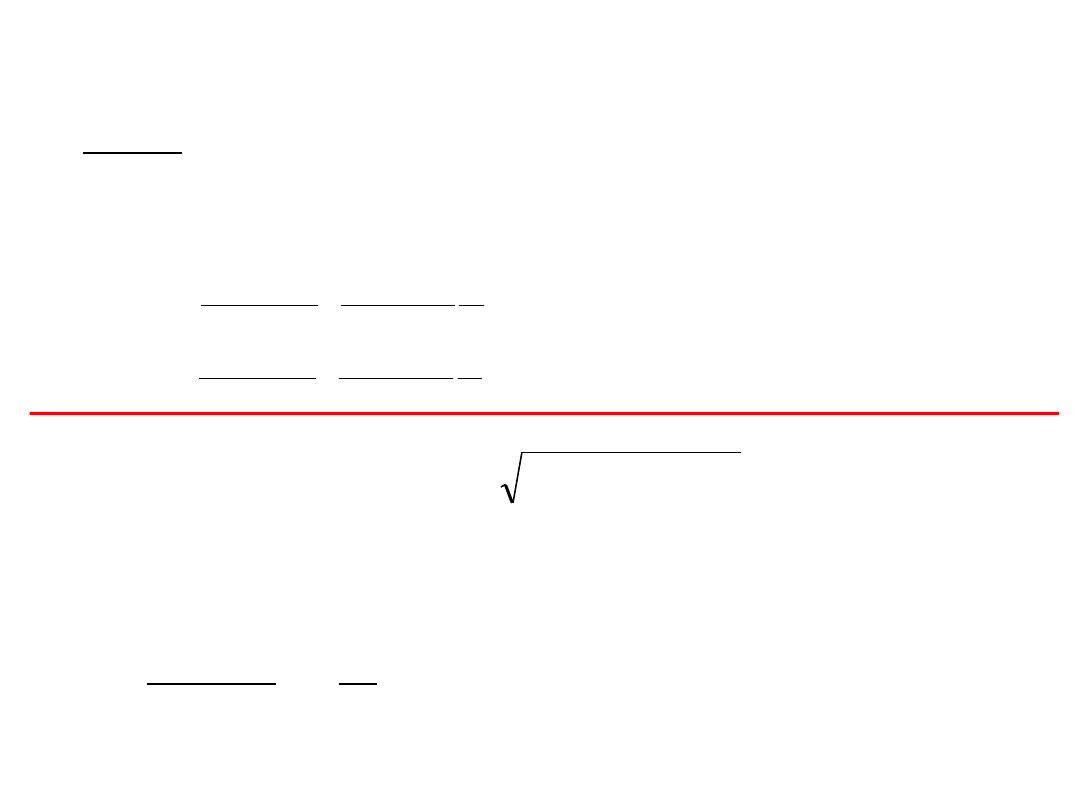
Uplastycznienie warstwy wewnętrznej
.
2
2
2
*
pl
a
b
a
b
p
Zadania przykładowe
Zadanie 1.
Obliczyć wartość maksymalnych naprężeń zredukowanych w rurze grubościennej obciążonej
ciśnieniem wewnętrznym p
a
=50 MPa. Stosunek promienia zewnętrznego b rury do promienia
wewnętrznego a wynosi 2. Wiedząc, że k
dop
=150 MPa oblicz maksymalne ciśnienie wewnętrzne
jakim może być obciążona rura.
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
)
(
)
(
)
(
)
(
r
b
a
b
p
p
a
a
b
p
b
p
a
r
b
a
b
p
p
a
a
b
p
b
p
a
b
a
b
a
t
b
a
b
a
r
s
s
2
2
t
t
r
r
red
s
s
s
s
s
max
2
2
2
2
2
)
1
(
)
(
t
a
t
a
r
a
b
a
b
p
a
p
s
s
s
Rozwiązanie
Dla r=a
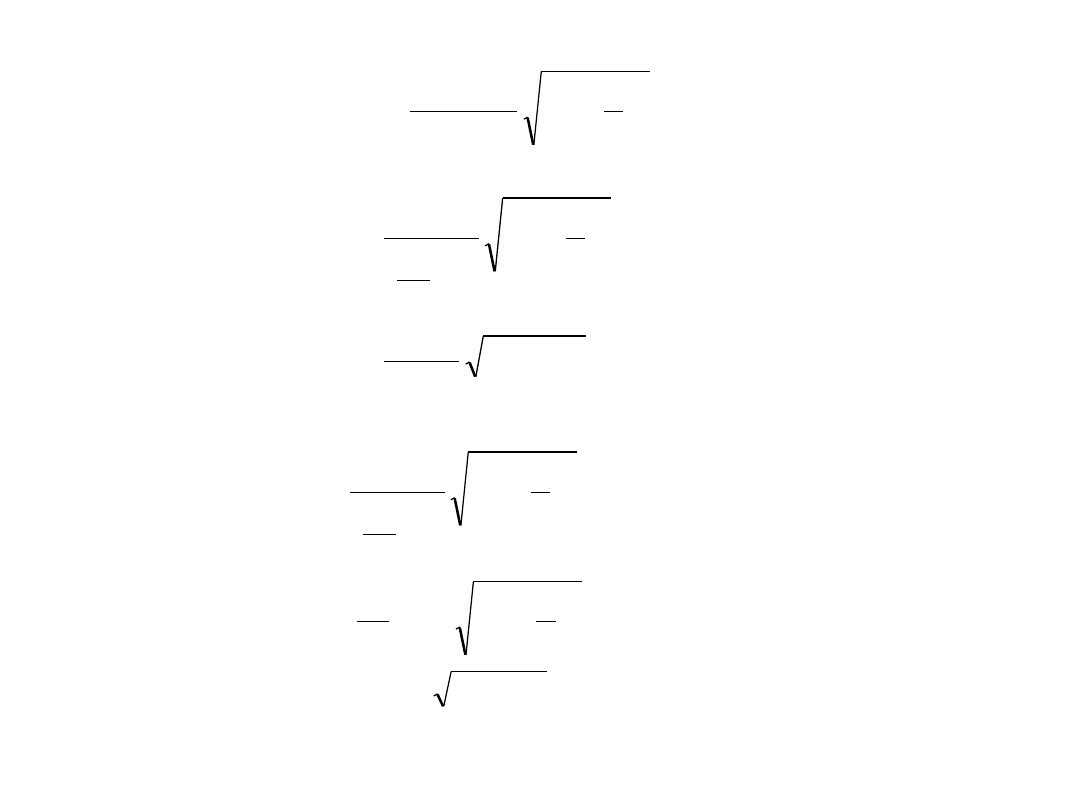
4
2
2
2
max
)
(
3
1
)
(
a
b
a
b
p
a
a
red
s
MPa
a
b
a
b
p
red
a
red
7
,
116
)
2
(
3
1
)
1
4
(
50
)
(
3
1
)
1
(
4
max
4
2
2
max
s
s
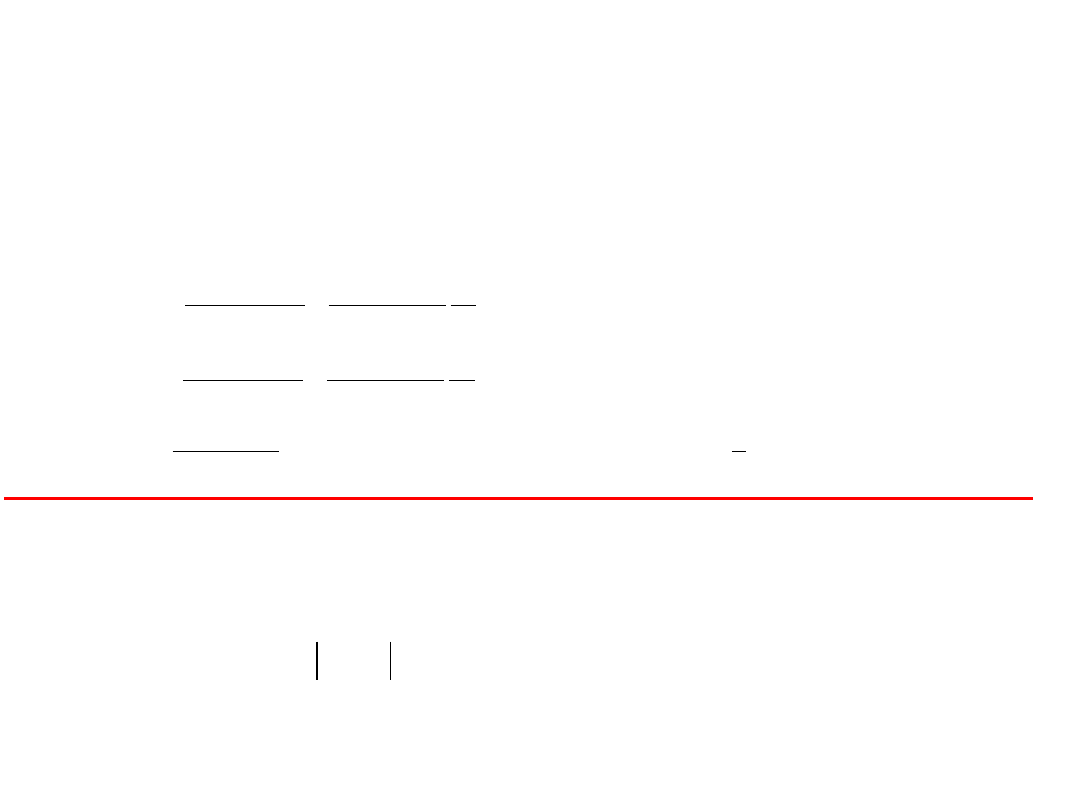
MPa
p
p
a
b
a
b
k
p
k
a
b
a
b
p
dop
a
dop
a
dop
a
red
2
,
64
2
3
1
/
)
1
4
(
150
)
(
3
1
/
)
1
(
)
(
3
1
)
1
(
4
4
2
2
4
2
2
max
s
Zadanie 2.
Obliczyć wartości naprężeń w rurze grubościennej osadzonej na wałku z wciskiem
promieniowym
. Stosunek promienia zewnętrznego b rury do promienia
wewnętrznego a wynosi 2, zaś
/a =0,001. Wałek i rura wykonane są z tego samego
materiału (dane: E, ν).
Dane: E=200 GPa, ν=0,3; k
dop
=180 MPa.
]
1
)
(
)
1
(
)
)(
1
[(
)
(
1
)
(
)
(
)
(
)
(
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
r
p
p
b
a
r
p
b
p
a
a
b
E
u
r
b
a
b
p
p
a
a
b
p
b
p
a
r
b
a
b
p
p
a
a
b
p
b
p
a
b
a
b
a
b
a
b
a
t
b
a
b
a
r
s
s
p
a
– wielkość statycznie niewyznaczalna
Warunek odkształcenia
);
(
a
r
u
a
a
a
rury
wał
rury
]
)
1
(
)
1
[(
)
(
]
1
)
1
(
)
1
[(
)
(
1
)
(
2
2
2
2
2
2
2
2
2
b
a
a
b
E
a
p
a
p
b
a
a
p
a
a
b
E
a
r
u
a
a
a
Zmiana promienia wałka:
E
ap
E
E
a
a
a
p
E
E
a
a
a
a
y
x
x
wał
a
y
x
y
x
x
wał
s
s
s
s
s
s
1
(
;
;
)
1
(
]
)
1
(
)
1
[(
)
(
2
2
2
2
E
a
p
b
a
a
b
E
a
p
a
a
Znaleźć wartość p
a
i sprawdzić czy nie zostały przekroczone naprężenia dopuszczalne
Wyszukiwarka
Podobne podstrony:
Medytacja na Lamę-cytaty mistrzów, ezoteryka, RÓŻNE TEKSTY BUDDYJSKIE
Plemiona Indian USA i Kanady, ♣Amerykanistyka
Trojan Lame Help Hand, DZIAŁ IT, Doc HACK
lame
Medytacja na Lamę
Erle Stanley Gardner [Mason 11] The Case of the Lame Canary (rtf)
Léame de Photoshop CS5
Léame de Adobe After Effects CS4
Léame de Captivate 6 0
Léame de Dreamweaver CS4
the lame shall enter first summary and analisisdocx
Léame
więcej podobnych podstron