Katedra Mechaniki Budowli 

Wykład 

Mechanika Budowli 1 [C16] 

Politechnika Gdańska 

2006 

Marek Krzysztof Jasina 

http://www.okno.pg.gda.pl – 

43 

– 

jasina@pg.gda.pl 

9. 

Wyznaczanie przemieszczeń z zasady prac wirtualnych 
dla odkształcalnych układów prętowych  
- obciążenia pozastatyczne 

9.1.  Przemieszczenia wywołane przemieszczeniem podpór 
W układach statycznie niewyznaczalnych przemieszczeniom podpór mogą 
towarzyszyć powstałe w ich wyniku wewnętrzne siły przekrojowe 

, 

∆

N

∆

M

, 

 

oraz siły 

 w więzach sprężystych (wewnętrznych lub zewnętrznych).  

∆

T

∆

S

Załóżmy,  że w układzie, co najmniej jedna podpora uległa przemieszczeniu, 
przy czym pewne dowolne przemieszczenie podpory oznaczymy przez 

. 

∆

r

Poszukiwane jest uogólnione przemieszczenie 

δ

i

 w miejscu 

, o określonym 

kierunku i zwrocie. Załóżmy, w tym miejscu, pewne jednostkowe obciążenie 
wirtualne 

( )

i

1

i

, które związane jest z przemieszczeniem 

δ

i

 związkiem pracy 

(tworzy parę sprzężoną).  
W wyniku działania wirtualnego obciążenia  1

i

 w więzach układu powstają 

reakcje 

ri

R

, siły w więzach 

i

S

, oraz wewnętrzne siły przekrojowe 

i

N

, 

i

M

, 

i

T

.  

Wykorzystując  2) postać zasady prac wirtualnych można zapisać następujące 
równanie pozwalające wyznaczyć poszukiwane przemieszczenie 

δ

∆

i

 

  1 δ

κ

∆

∆

∆

∆

∆

=

+

+

+

−

∑

∑

∫

∫

∫

i

i

i

i

i

i

ri

r

s

r

s

l

l

l

N N

M M

T T

S S

ds

ds

ds

R

EA

EI

GA

k

∆ . (9.1) 

Jako,  że w układach statycznie wyznaczalnych przemieszczenia podpór nie 
wywołują sił wewnętrznych i sił w więziach czyli siły przekrojowe 

, 

, 

 oraz 

, wzór (9.1) redukuje się do postaci  

0

∆

=

N

0

∆

=

M

0

∆

=

T

0

∆

=

S

 

δ

∆

= −

∆

∑

i

r

r

R

i

r

. (9.2) 

W przypadku układów kratowych, w których występują jedynie (stałe w prę-
tach) siły normalne zależność (9.1) przyjmuje postać 

(

)

δ

∆

∆

∆

=

+

−

∆

∑

∑

∑

ki

k

i

i

k

ri

r

k

s

r

k

s

N N

S S

l

R

EA

k

 

, (9.3) 

Katedra Mechaniki Budowli 

Wykład 

Mechanika Budowli 1 [C16] 

Politechnika Gdańska 

2006 

Marek Krzysztof Jasina 

http://www.okno.pg.gda.pl – 

44 

– 

jasina@pg.gda.pl 

a wzór dla układów statycznie wyznaczalnych pozostaje niezmieniony (zob. 
(9.2)). 

9.2.  Przemieszczenia wywołane zmianami temperatury

1

 

Zmiana temperatury (względem temperatury montażu) powoduje, w wyniku 
równomiernego działania temperatury - wzdłużne deformacje prętów (od-
kształcenia podłużne) oraz w wyniku nierównomiernego działania temperatu-
ry po wysokości przekroju prętów odkształcenia kątowe. 

 

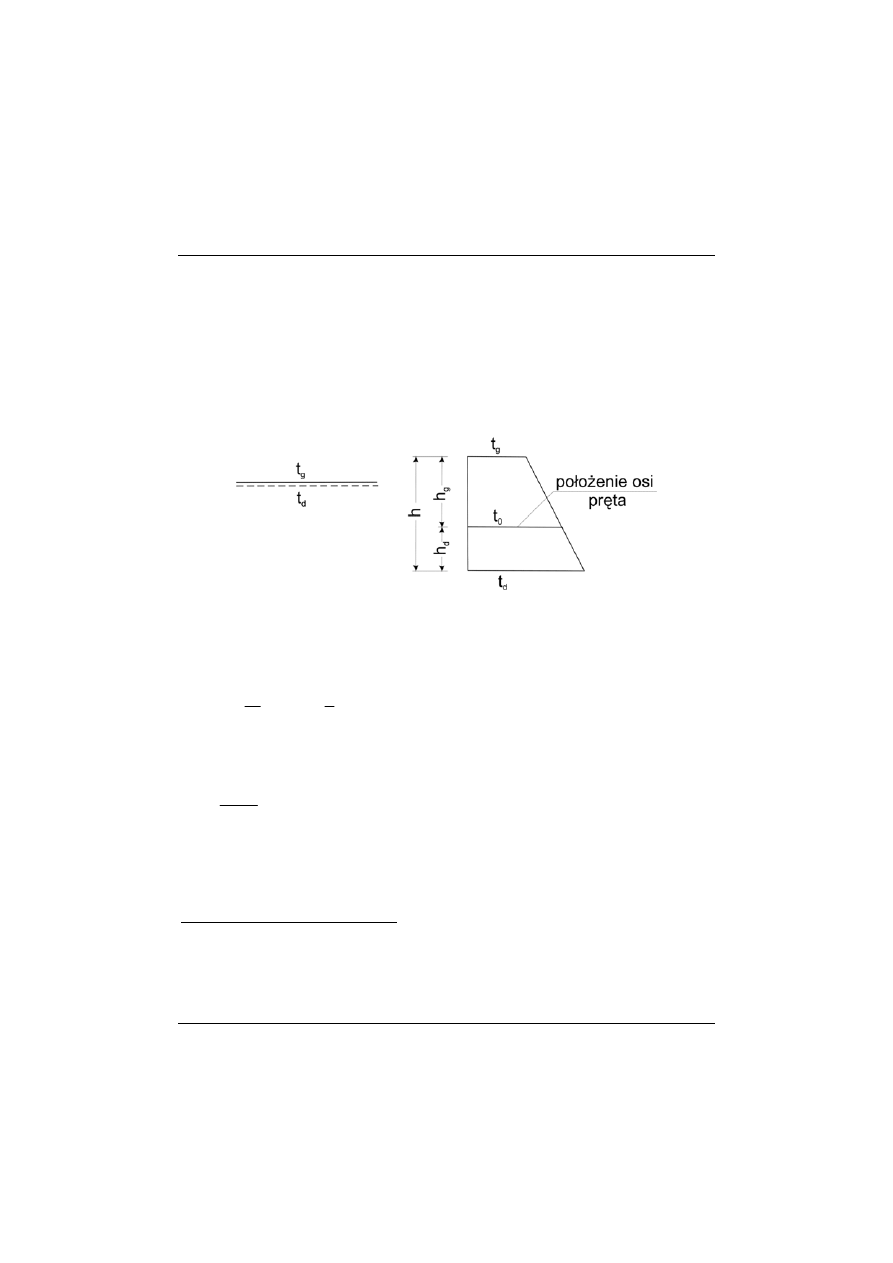
Rys. 9.1 

Temperatura w osi pręta (porównaj do równomiernego działania temperatury) 
wynosi  

 

0

1

(

)

(

= +

−

=

+

g

)

g

d

g

d

g

g

d

h

t

t

t

t

t h

t h

h

h

, (9.4) 

co w przypadku pręta symetrycznego względem poziomej osi przekroju po-
przecznego daje 

 

0

2

+

=

d

g

t

t

t

. (9.5) 

Deformacja (przemieszczenie płaskiego przekroju poprzecznego pręta) w wy-
niku nierównomiernego działania temperatury. Rozpatrzmy element pręta o 
długości 

. 

ds

                                                           

1

 Zmiana temperatury wywołuje w układach statycznie niewyznaczalnych do-

datkowe wewnętrzne siły przekrojowe 

, 

t

N

t

M

,   oraz siły   w więzach sprę-

żystych.  

t

T

t

S

Katedra Mechaniki Budowli 

Wykład 

Mechanika Budowli 1 [C16] 

Politechnika Gdańska 

2006 

Marek Krzysztof Jasina 

http://www.okno.pg.gda.pl – 

45 

– 

jasina@pg.gda.pl 

 

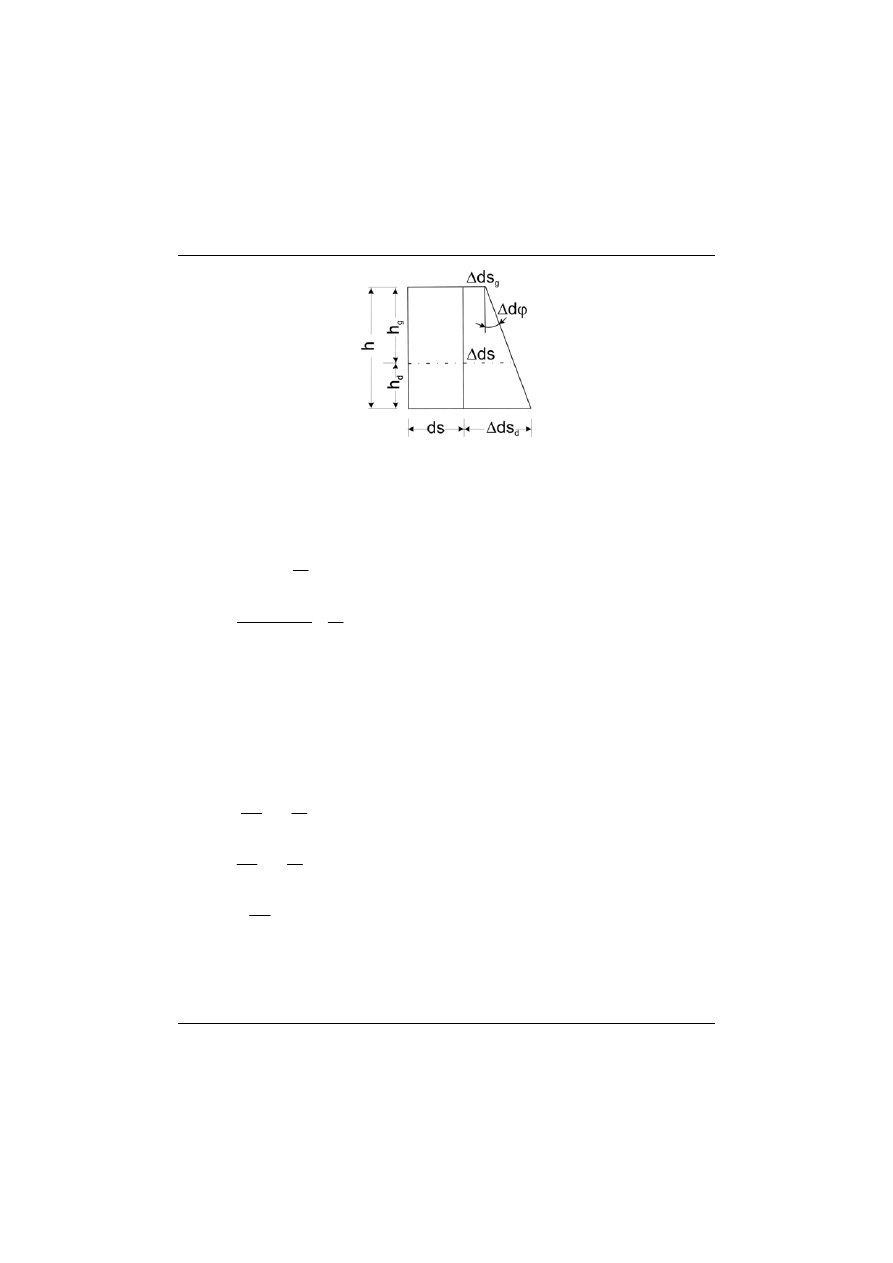
Rys. 9.2 

 

, (9.6) 

α

∆

=

g

t

g

ds

t ds

α

∆

=

d

t

d

ds

t ds

 

, (9.7) 

 

0

(

α

α

∆ =

=

+

t

t

d

g

g

ds

t ds

t h

t h

ds

h

)

d

, (9.8) 

 

(

)

α

ϕ

∆

−

∆

=

ds

d

∆

=

−

d

g

t

d

g

ds

t

t

ds

h

h

t

. (9.9) 

 
Zmiana temperatury wywołuje w układach statycznie niewyznaczalnych do-
datkowe wewnętrzne siły przekrojowe 

, 

t

N

M

,  T  oraz siły   w więzach sprę-

żystych.  

t

t

S

Można zatem zapisać, że w wyniku nierównomiernego działania temperatury 
wycinek pręta o długości 

 doznaje deformacji, które można zapisać odpo-

wiednio: 

ds

 

(

)

α

ϕ

∆

=

+

−

t

t

t

d

M

d

ds

t

t

EI

h

g

ds

, (9.10) 

 

(

α

∆

=

+

+

t

t

t

d

g

N

ds

ds

t h

t h

ds

)

g

d

h

, (9.11) 

EA

κ

∆

=

t

t

T

dh

ds

GA

. (9.12) 

 

 oznacza współczynnik rozszerzalności termicznej. 

W powyższych wzorach 

α

i

Katedra Mechaniki Budowli 

Wykład 

Mechanika Budowli 1 [C16] 

Politechnika Gdańska 

2006 

Marek Krzysztof Jasina 

http://www.okno.pg.gda.pl – 

46 

– 

jasina@pg.gda.pl 

Po uwzględnieniu zależności (9.10) - (9.12) można zapisać następujące równa-
nie pozwalające wyznaczyć poszukiwane przemieszczenie 

δ

it

 

 

0

1

(

)

δ

κ

α

α

=

+

+

+

+

+

−

∑

∫

∫

∫

∫

∫

i

t

i

t

i

t

i

t

i

it

s

s

l

l

l

t

i

t

i

d

g

l

l

N N

M M

T T

S S

ds

ds

ds

EA

EI

GA

k

N

t ds

M

t

t

ds

h

+

. (9.13) 

W przypadku układów statycznie wyznaczalnych zależność (9.13) redukuje się 
do postaci 

 

0

1

α

δ

α

=

+

−

∫

∫

t

i

it

i

t

i

d

g

l

l

N

t ds

M

t

t

ds

h

(

)

. (9.14) 

W przypadku układów kratowych, w których występują jedynie (stałe w prę-
tach) siły normalne zależności (9.13) i (9.14) redukują się do postaci 

 

0

(

)

δ =

+

+

∑

∑

∑

ki

kt

i

t

it

k

ki

t

k

k

k

s

k

k

s

N N

S S

l

N

EA

k

α t l , (9.15) 

0

δ

α

=

∑

it

ki

t

k

k

k

N

t l

. (9.16) 

 

9.3.  Przemieszczenia wywołane imperfekcjami  

(niedokładnościami) geometrycznymi 

Rzeczywiste konstrukcje zawierają różne niedokładności, w tym niedokładno-
ści (błędy) montażu. Najczęściej występują one w miejscu łączenia elementów. 
Tego typu niedokładności można określić mianem imperfekcji geometrycznych. 
Odchyłki od geometrii „idealnej”, czyli imperfekcje mogą mieć charakter ciągły 
(np. wygięcie pręta) lub dyskretny (np. błędy montażu na styku pretów). Po-
niższe rysunki prezentują pewne typowe błędy montażu.  
 
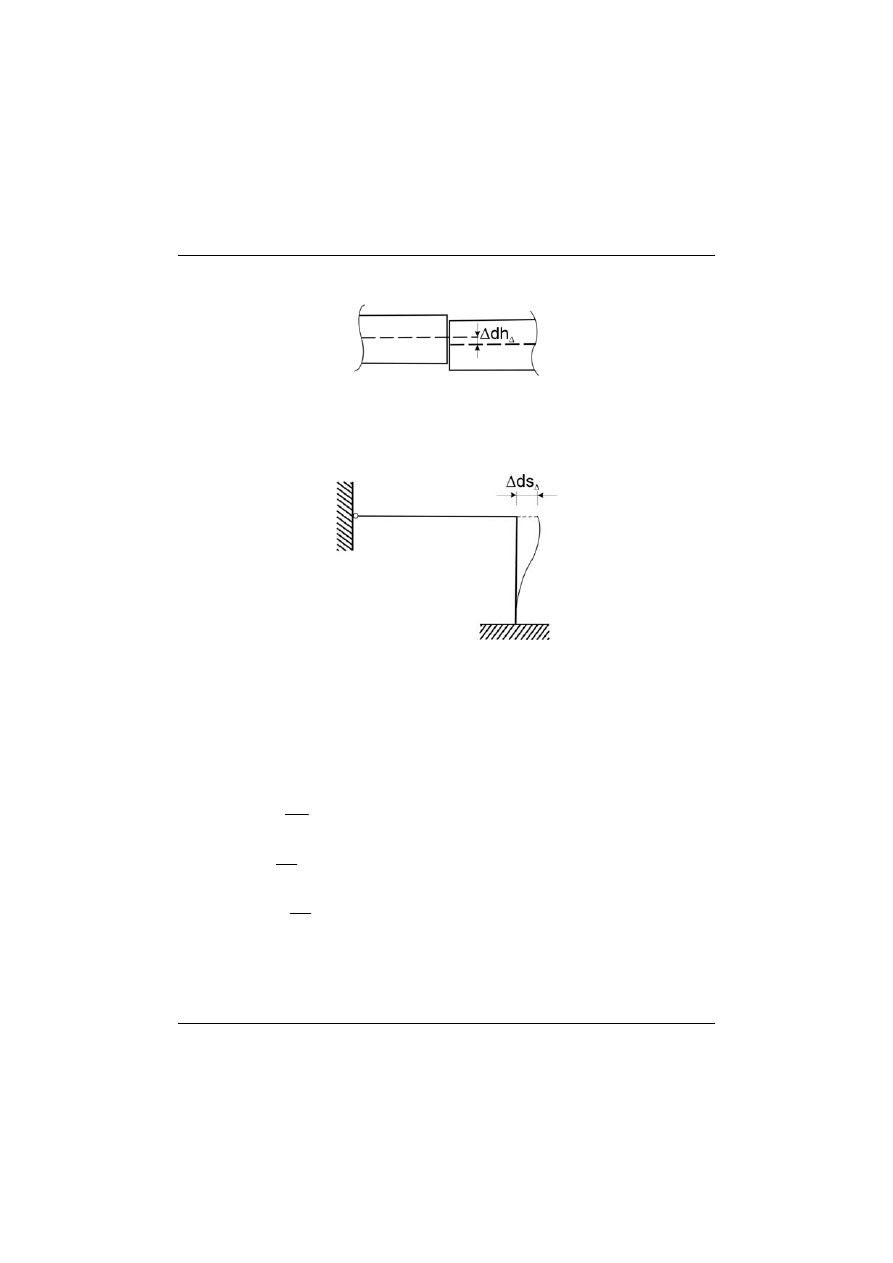
Łączenie elementów pod niewłaściwym kątem (rys. 9.3). 

 

Rys. 9.3 

Katedra Mechaniki Budowli 

Wykład 

Mechanika Budowli 1 [C16] 

Politechnika Gdańska 

2006 

Marek Krzysztof Jasina 

http://www.okno.pg.gda.pl – 

47 

– 

jasina@pg.gda.pl 

Łączenie elementów niewspółosiowo (rys. 9.4). 

 

Rys. 9.4 

Montaż elementów o nieprawidłowej (względem projektowanej) długości 
(rys. 9.5). 

 

Rys. 9.5 

Imperfekcje wywołują w układach statycznie niewyznaczalnych dodatkowe 
wewnętrzne siły przekrojowe 

∆

N

, 

∆

M

∆

T

∆

S

, 

 oraz siły 

 w więzach sprężystych 

(oznaczenia 

∆

 analogiczne jak w przypadku przemieszczeń podpór). 

Można zapisać, że w wyniku imperfekcji wycinek pręta o długości 

 doznaje 

deformacji, odpowiednio zapisanej poniżej. 

ds

 

ϕ

ϕ

∆

∆

∆

= ∆

+

M

d

d

EI

ds

, (9.17) 

 

∆

∆

∆ = ∆

+

N

ds

ds

ds

EA

, (9.18) 

κ

∆

∆

∆

= ∆

+

T

dh

dh

ds

GA

 

. (9.19) 

Po uwzględnieniu zależności (9.17) - (9.19) można zapisać następujące równa-
nie pozwalające wyznaczyć poszukiwane przemieszczenie 

δ

∆

i

 

Katedra Mechaniki Budowli 

Wykład 

Mechanika Budowli 1 [C16] 

Politechnika Gdańska 

2006 

Marek Krzysztof Jasina 

http://www.okno.pg.gda.pl – 

48 

– 

jasina@pg.gda.pl 

 

1

δ

κ

ϕ

∆

∆

∆

∆

∆

∆

∆

=

+

+

+

+

∆

+

∆

+

∆

∑

∫

∫

∫

∫

∫

∫

i

i

i

i

i

i

s

s

l

l

l

i

i

i

l

l

l

N N

M M

T T

S S

ds

ds

ds

EA

EI

GA

k

N ds

M

d

T dh

∆

+

. (9.20) 

W układach statycznie wyznaczalnych mamy 

0

∆

=

N

, 

0

∆

=

M

0

∆

=

T

0

∆

=

S

, 

 oraz 

. 

Ponieważ w układach błędy montażu występują na ogół tylko dyskretnie (w 
pewnych punktach) to w takich przypadkach odpowiednie całki we wzorze 
(9.20) można zapisać jako poniższe sumy. 

 

∆

∆

=

∆

∑

∫

l

N

d

i

mi

m

m

s

N

ds

, (9.21) 

 

ϕ

ϕ

∆

∆

=

∆

∑

∫

i

ni

n

l

n

M

d

M

d

, (9.22) 

 

∆

∆

=

∆

∑

∫

i

ki

k

l

T dh

T

dh

k

, (9.23) 

Co w przypadku układów statycznie wyznaczalnych pozwala zapisać wzór 
(9.20) w postaci 

 

δ

ϕ

∆

=

∆

+

∆

+

∆

∑

∑

∑

i

mi

m

ni

n

ki

m

n

k

N

ds

M

d

T

dh

k

. (9.24) 

W przypadku układów kratowych, w których występują jedynie (stałe w prę-
tach) siły normalne zależność (9.24) redukuje się do postaci 

 

(

)

δ

∆

∆

∆

=

+

+

∑

∑

∑

ki

k

i

i

k

k

s

k

k

s

N N

S S

l

EA

k

∆

ki

k

N

l

, (9.25)