1

Algorytmy

i struktury danych

Od problemu do jego
rozwiązania

Sformułowanie
problemu

Rozwiązanie problemu

Przykład: Dany
jest ciąg liczb.
Znaleźć
największą z nich.

Niech max ma
wartość równą
pierwszemu
elementowi ciągu.
Porównaj max z
kolejnymi
elementami ciągu i
jeśli spotkasz
wartość większą,
przyjmij ją jako
nową wartość max.

Algorytm

to metoda postępowania, która prowadzi do

rozwiązania jakiegoś problemu.

2

Algorytm



skończony, uporządkowany ciąg jasno

zdefiniowanych czynności, koniecznych do
wykonania dowolnego zadania

z określonej

klasy zadań.



Słowo "algorytm" pochodzi od nazwiska
Muhammeda Alchwarizmi - matematyka
perskiego z IX wieku.



Badaniem algorytmów zajmuje się algorytmika.



Algorytm może zostać zaimplementowany w
postaci programu komputerowego.

Oznaczmy przez:
We -

zestaw danych wejściowych

Wy -

zestaw danych wyjściowych

Algorytm jest rozumiany jako odwzorowanie O

, które

dla określonego zestawu We generuje zestaw Wy:
O: We → Wy,
gdzie liczności zbiorów We i Wy mogą być różne.

Algorytm

– definicja formalna

Dane

We

Algorytm

Wyniki

Wy

stan pamięci
przed
wykonaniem
algorytmu

stan
pamięci po
wykonaniu
algorytmu

3

Przykład algorytmu I



Algorytm wyznaczania pola kwadratu o boku a:



Jako dane wejściowe pobierz wartość długości
boku kwadratu a



Oblicz wartość pola P = a

2



Zwróć obliczoną wartość pola kwadratu P

Przykład algorytmu II



Algorytm Euklidesa wyznaczania NWD:



Dopóki x różne od y wykonuj:



Jeżeli x>y, to odejmij y od x i wynik podstaw na x;



W przeciwnym przypadku od y odejmij x i wynik
podstaw na y;



koniec dopóki



wynikiem jest y

Dane x =21, y =12.
(x,y) = (21,12)-> (9,12)-> (9,3)-> (6,3)-> (3,3)
Wynik 3

4

Cechy algorytmu



Ogólność



Rozwiązywanie określonej klasy zadań



Skończoność



Rozwiązanie zadania w skończonej liczbie kroków



Określoność



Jednoznaczność operacji



Efektywność



Czas wykonania, zapotrzebowanie na pamięć

Sposoby zapisu algorytmu



Język naturalny



Prostota, szeroki zasób słownictwa, mała precyzja



Schematy blokowe



Zapis sformalizowany, brak możliwości
przedstawienia skomplikowanych algorytmów



Języki formalne



Najczęściej używane w praktyce, ścisłość zapisu

5

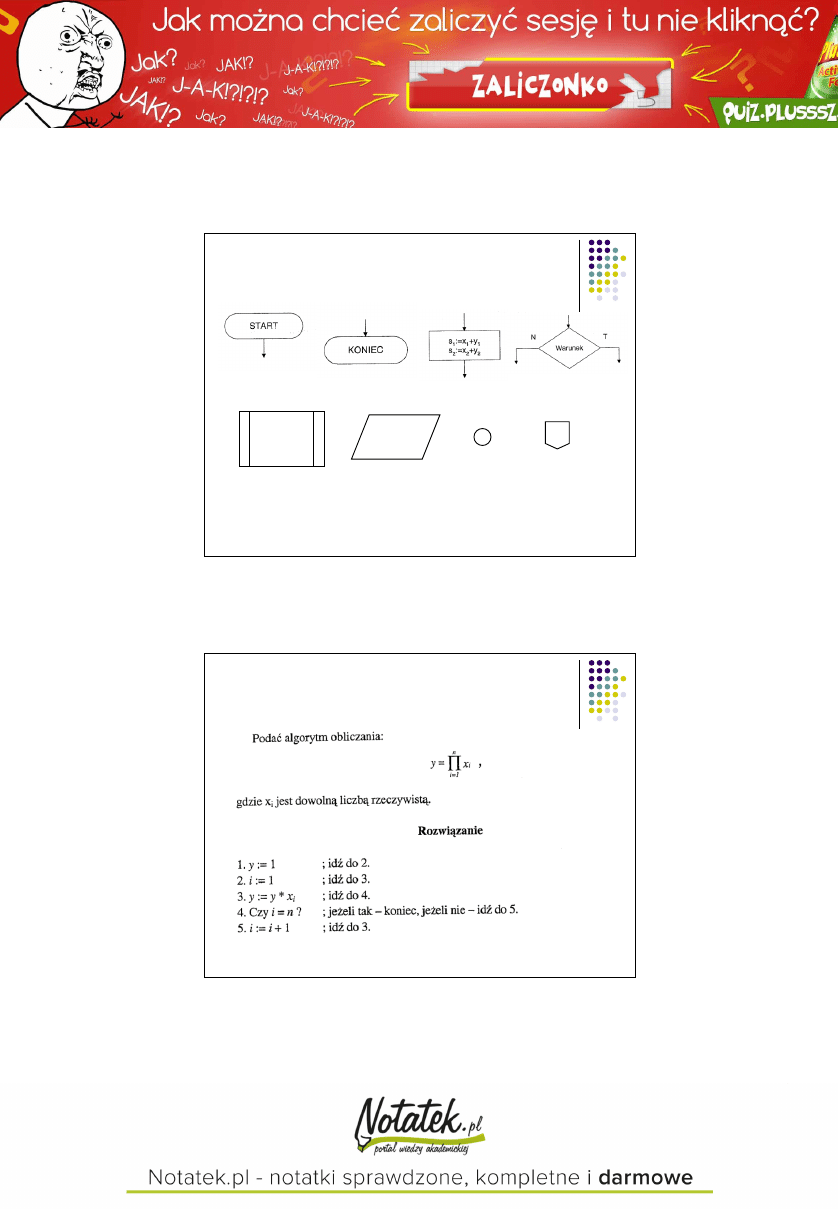
Schematy blokowe

Proces

uprzednio

zdefiniowany

Zapis/odczyt

danych

Łącznik

stronicowy

Łącznik

międzystronicowy

Algorytm wyznaczania
iloczynu

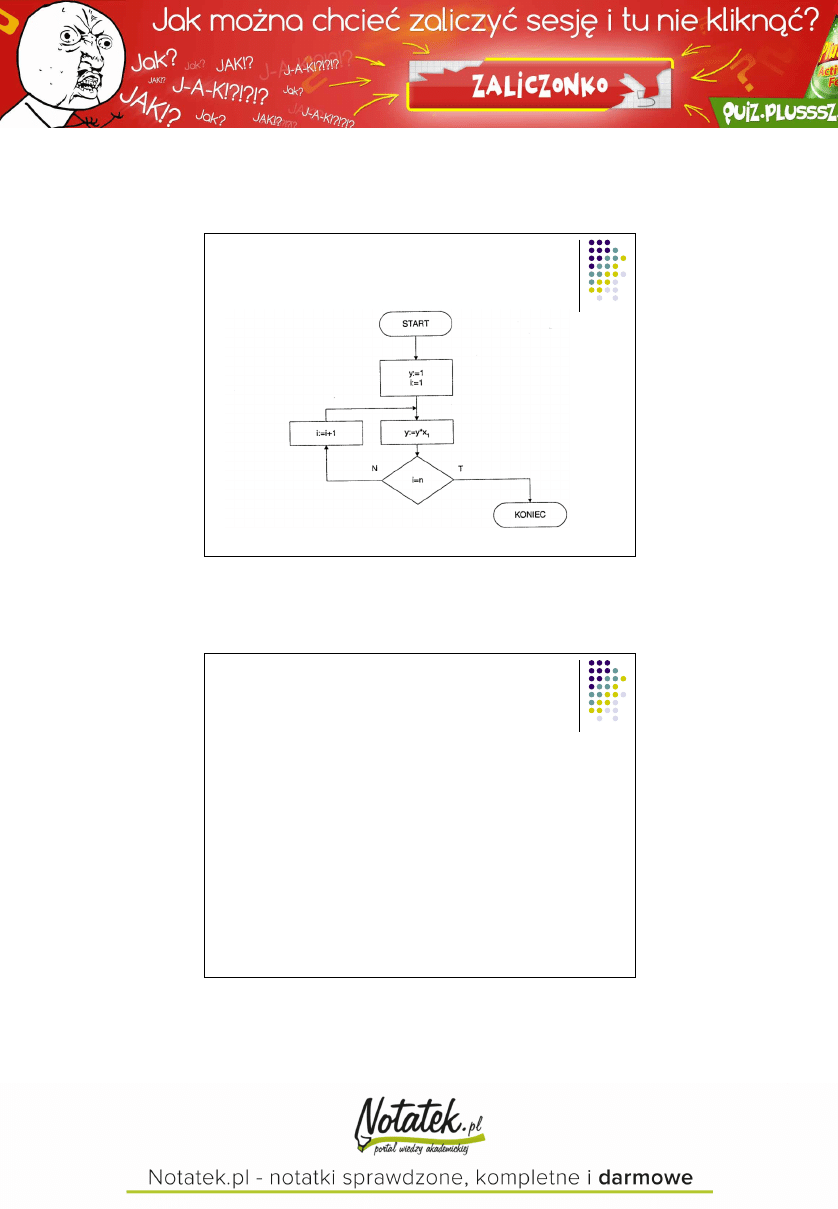
6

Algorytm wyznaczania
iloczynu

Algorytm wyznaczania
iloczynu



Język Pascal

y := 1;

for i := 1 to n do y := y * x [ i ];

7

Klasyfikacja algorytmów
(wybrane kategorie)



algorytmy proste

– rozgałęzione



algorytmy cykliczne

– mieszane



algorytmy równoległe – sekwencyjne



algorytmy numeryczne

– algorytmy

nienumeryczne



algorytmy rekurencyjne

– algorytmy

iteracyjne

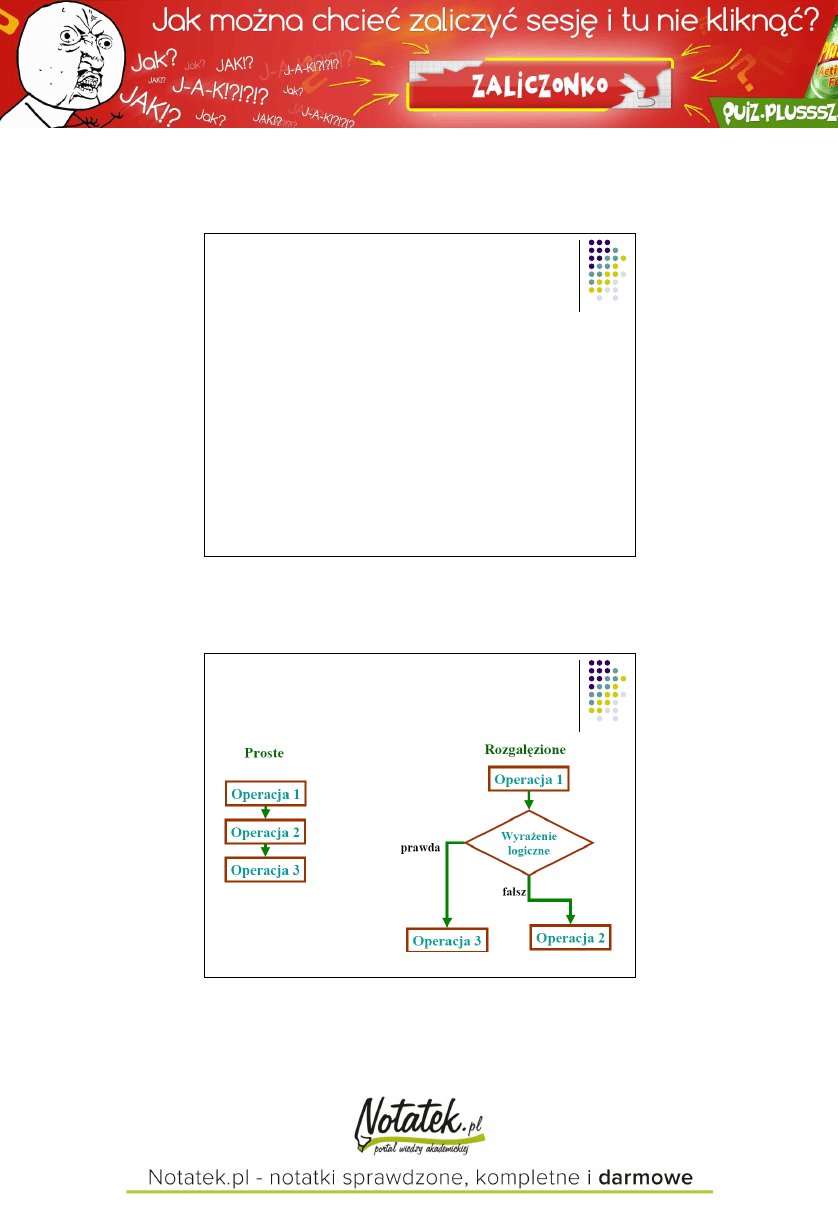
Algorytmy proste i
rozgałęzione

8

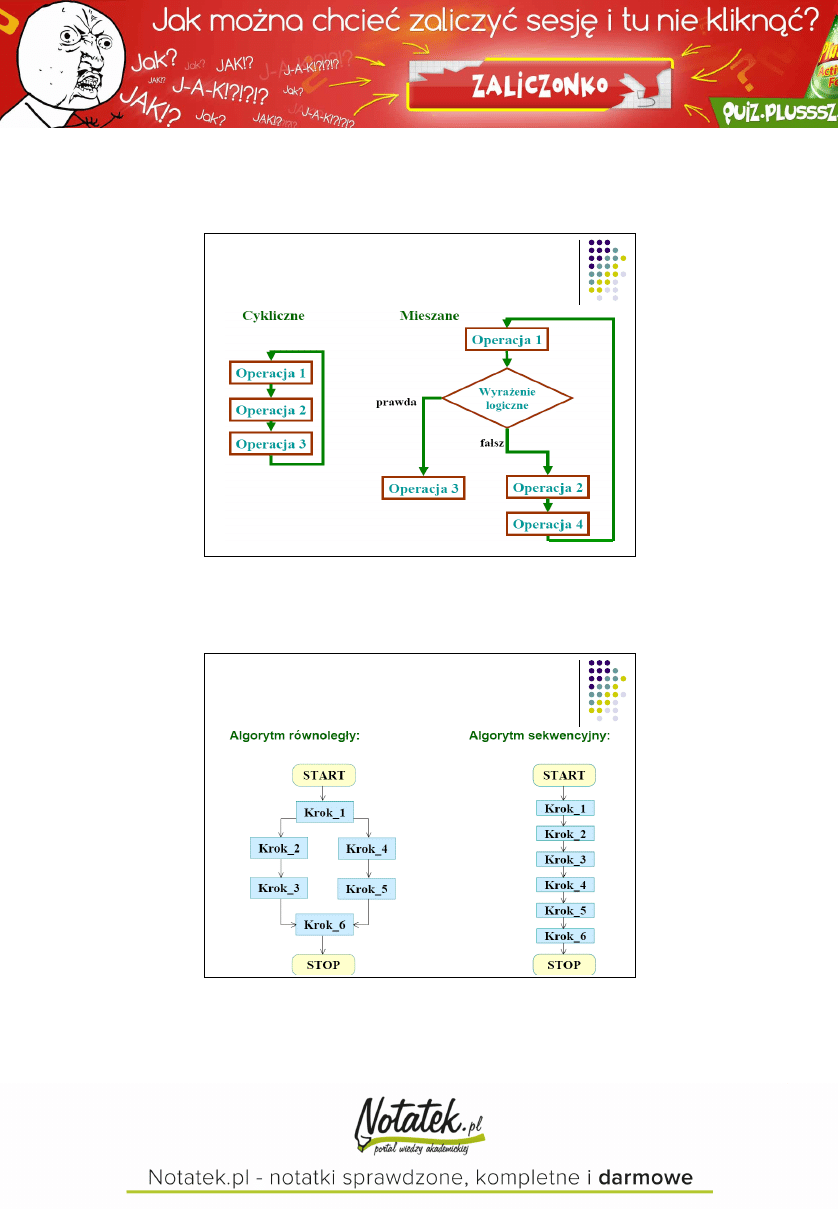
Algorytmy cykliczne i
mieszane

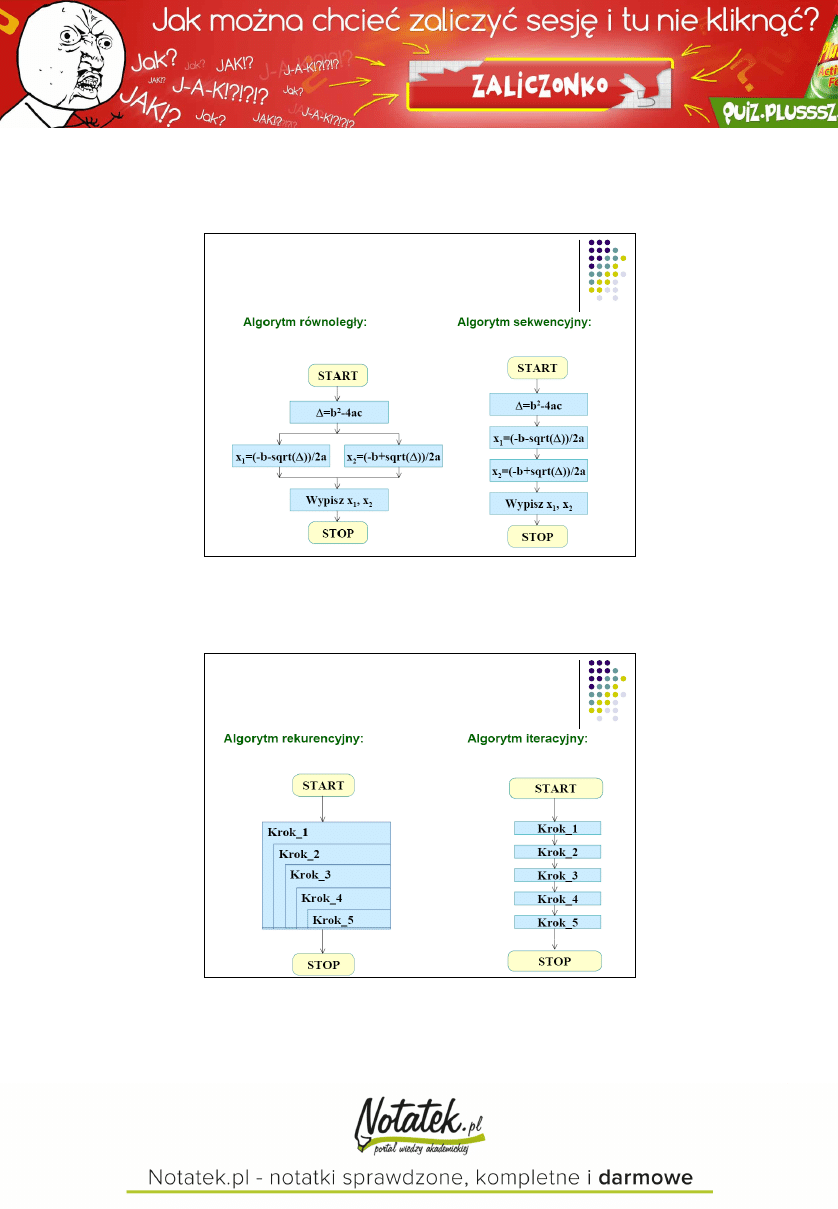
Algorytm równoległy i
sekwencyjny

9

Algorytm równoległy i
sekwencyjny

Algorytm rekurencyjny i
iteracyjny

10

Rekurencja



Rekurencja albo rekursja -

odwoływanie się

np. funkcji lub definicji do samej siebie.



Ważne jest, aby kolejne wywołania funkcji
rekurencyjnej były realizowane dla kolejnych
wartości parametrów formalnych w taki sposób,
aby nie doszło do zjawiska „nieskończonej pętli
rekurencyjnych wywołań funkcji”

Obraz rekurencyjny

11

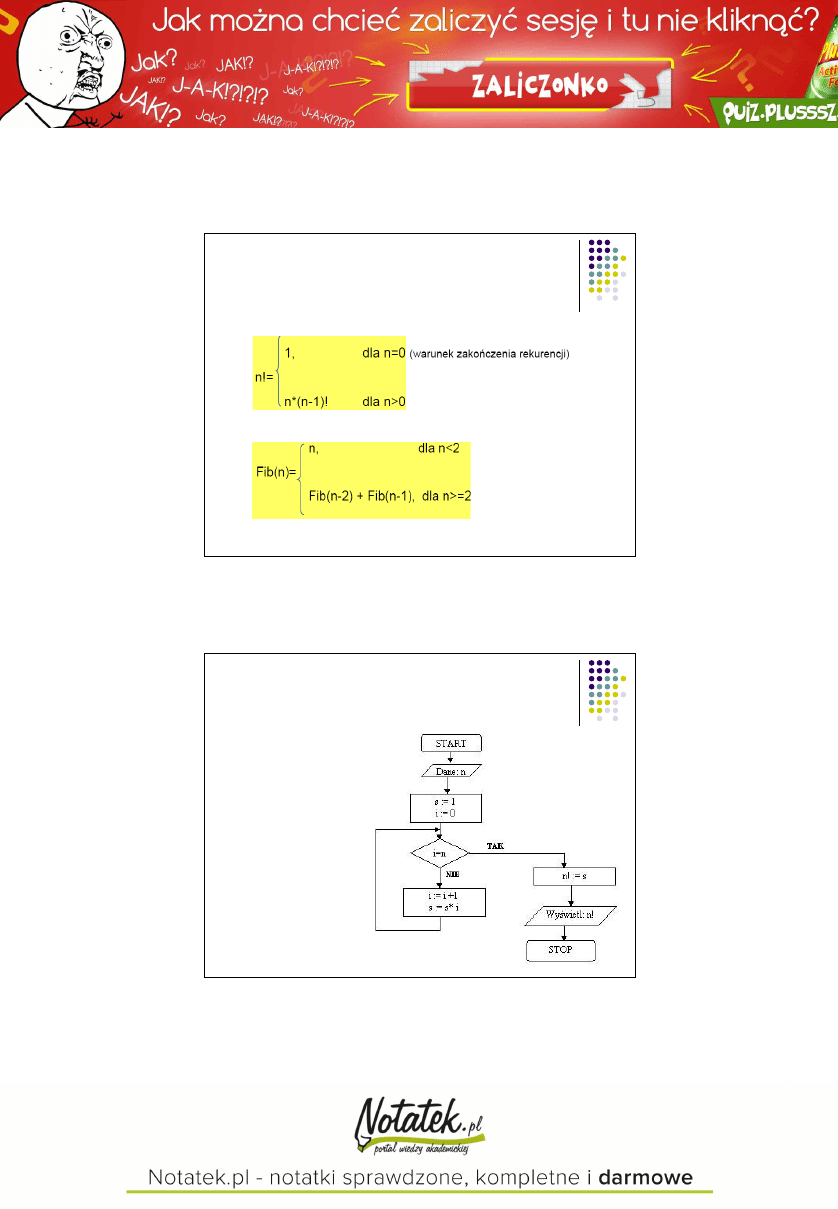
Przykłady funkcji
rekurencyjnych



Silnia



Ciąg Fibonacciego

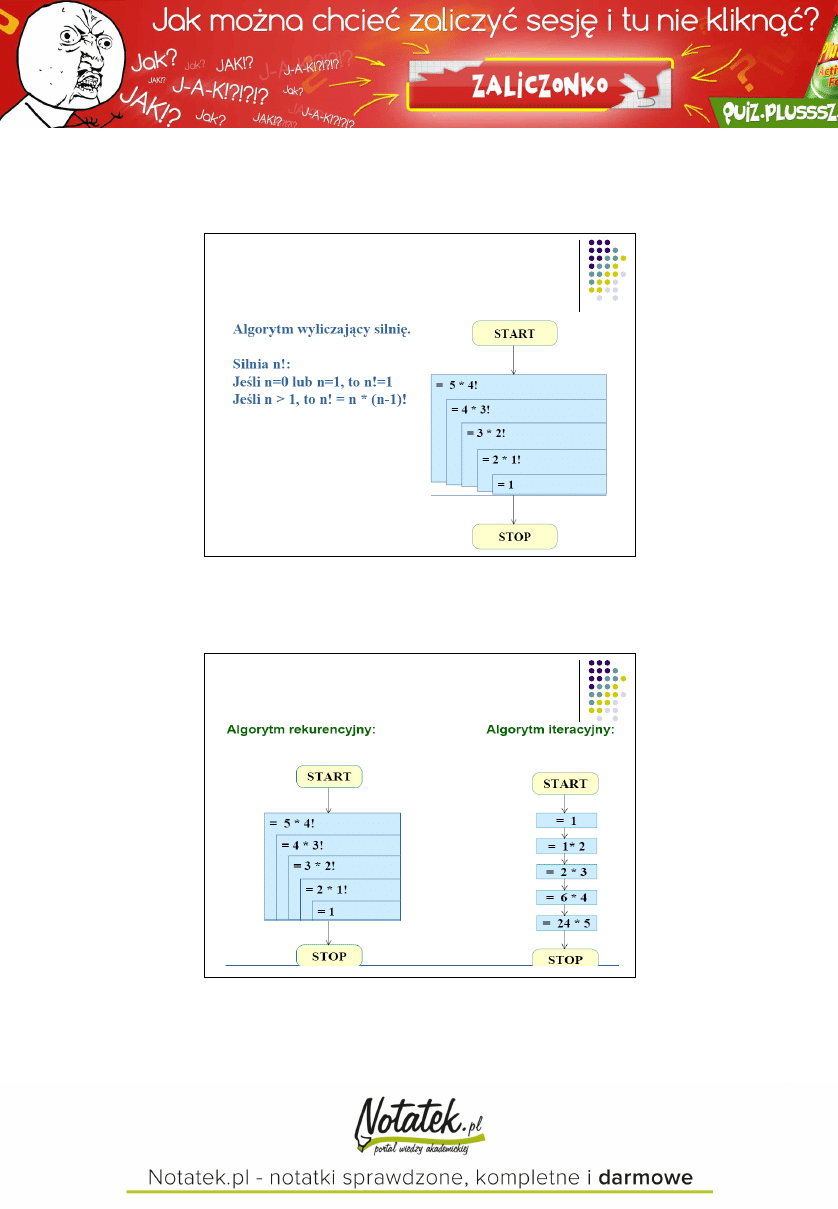
Silnia - Algorytm iteracyjny

Dane:
n - liczba rzeczywista
Szukane:
s = n! wartość silni liczby naturalnej.
Pomocnicze :
i - liczba naturalna (licznik).

START:
wczytaj liczbę n
s :=1
i := 0
jeśli i = n, to KONIEC
i := i +1;
s := s*i; WARUNEK;
KONIEC:
wyświetl liczbę s

12

Silnia - Algorytm rekurencyjny

5!

– porównanie algorytmów

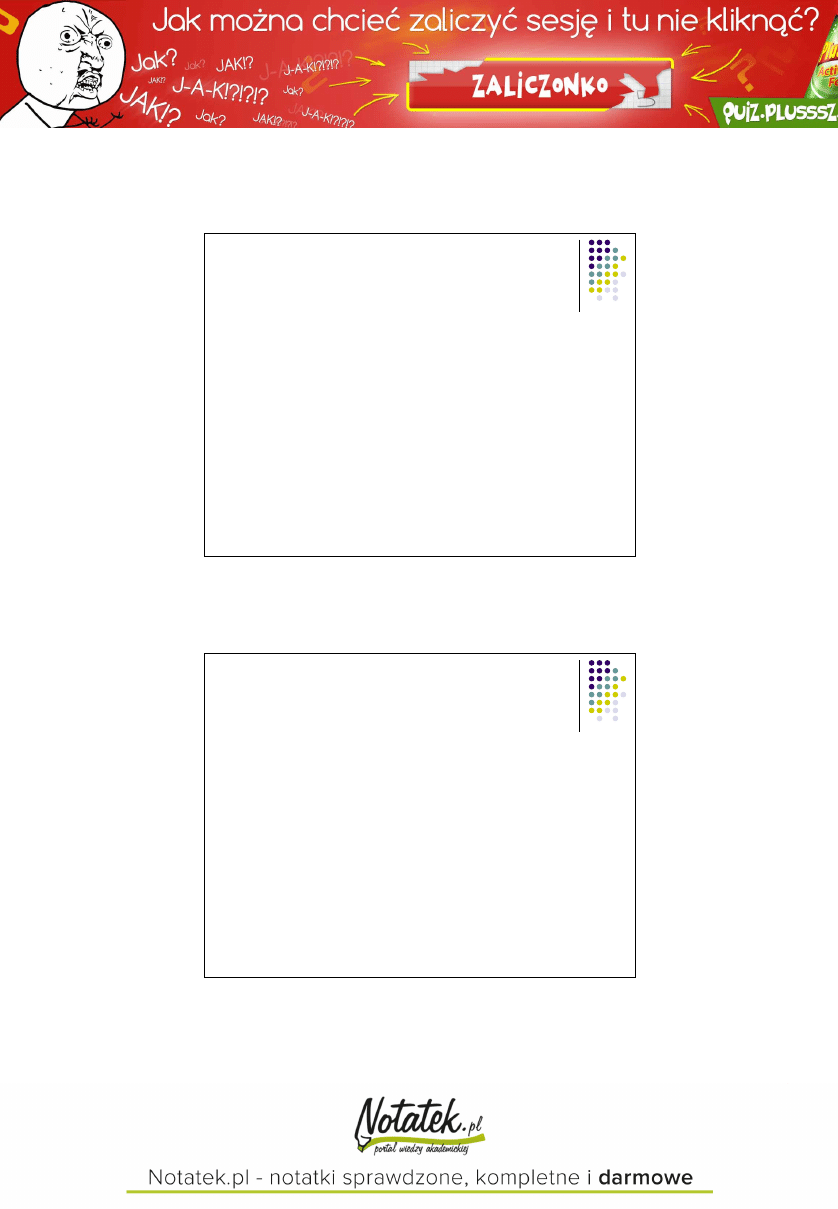
13

Algorytmy zachłanne



Wykonują działanie które wydaje się najlepsze w
danej chwili, nie

uwzględniając tego co może się

stać w przyszłości. Zaletą jest to że nie traci czasu

na rozważanie co może się stać później.



Decyzja lokalnie optymalna.



Jak wydać resztę przy minimalnej ilości monet?: użyj

zawsze najpierw monetę o największej dopuszczalnej

wartości.



Jak znaleźć globalne maximum? Rozpocznij od
pewnej liczby, kolejno

powiększaj ją o ustaloną

wielkość tak długo jak funkcja wzrasta. Gdy wartość

funkcji zaczyna się zmniejszać przerwij i cofnij się do
ostatniej pozycji.

Algorytmy „dziel i zwyciężaj”



Dzielimy problem na mniejsze części tej samej postaci co
pierwotny.



P

odproblemy dzielimy dalej na coraz mniejsze, używając tej

samej metody, aż rozmiar problemu stanie się tak mały, że

rozwiązanie będzie oczywiste lub będzie można użyć jakiejś
innej

efektywnej metody rozwiązania.



Rozwiązania wszystkich podproblemów muszą być

połączone w celu utworzenia rozwiązania całego problemu.



Metoda zazwyczaj implementowana z zastosowaniem
technik rekurencyjnych.



Jak znaleźć minimum ciągu liczb?: Dzielimy ciąg na dwie części,

znajdujemy minimum w każdej z nich, bierzemy minimum z obu

części jako minimum ciągu.



Jak sortować ciąg liczb?: Dzielimy na dwie części, każdą osobno

sortujemy a następnie łączymy dwa uporządkowane ciągi

(scalamy).

14

Upraszczanie algorytmów

1

1

15

15

18

18

3

33

x

1

x

2

y

1

y

2

s

1

s

2

przeniesienie

+

+

+

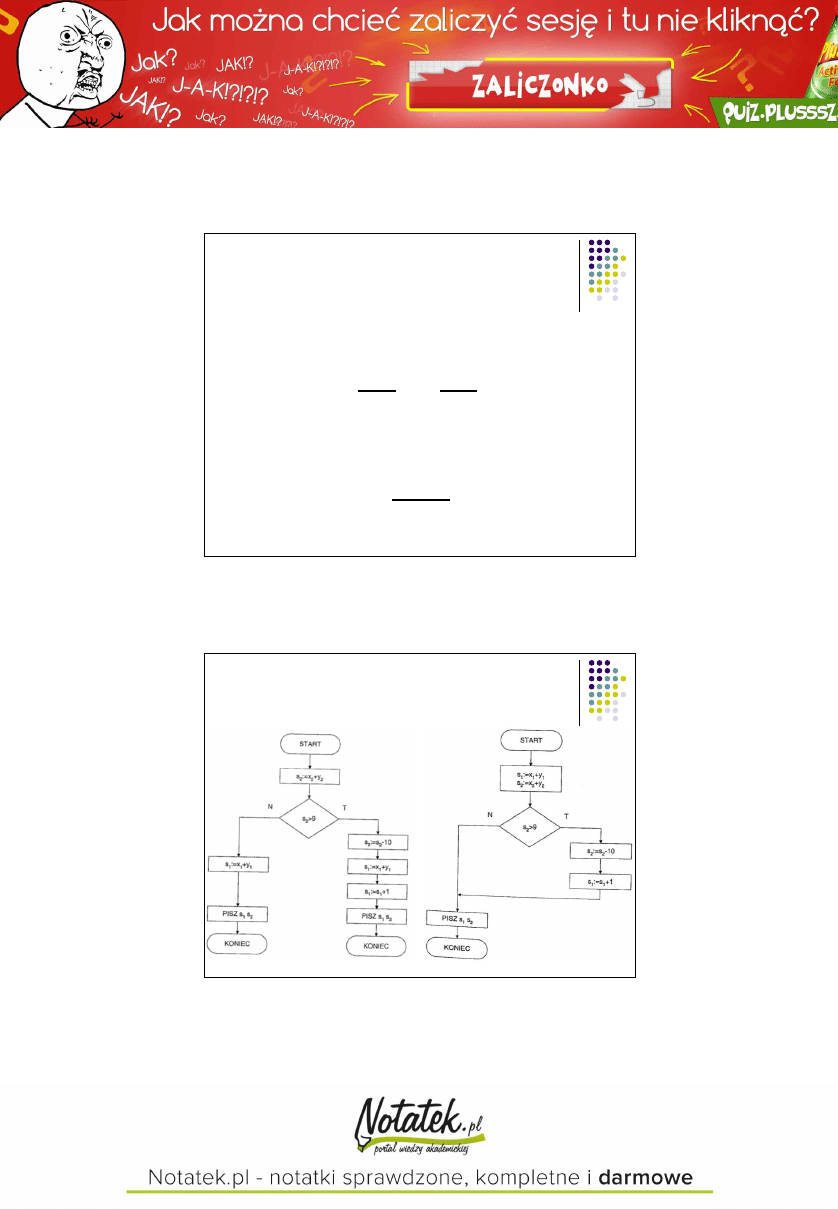
Algorytm dodawania
dwóch liczb
naturalnych

Upraszczanie algorytmów

15

Jak porównywać algorytmy?

• prostota

• czytelność

• długość kodu

• poprawność

• czas realizacji

• zajętość pamięci

Idealny algorytm to taki,
który ma prosty kod,
jest napisany w ogólnie
dostępnym języku
programowania, łatwo
go zrozumieć, liczy
szybko, nie wymaga
dużo miejsca w pamięci
i zawsze daje
poprawne wyniki.

Koszt algorytmu

Miary kosztu:

• Liczba instrukcji

• liczba operacji
arytmetycznych

• liczba wywołań
procedury

• Liczba
zmiennych

• ilość miejsca
potrzebna dla
danych

Ogólnie: wybór miary zależy od typu problemu, rodzaju
rozwiązania.

16

Efektywność algorytmów



Złożoność obliczeniowa



czas wykonania



Złożoność pamięciowa



Zapotrzebowanie na pamięć operacyjną



Zależy od



Rozmiaru danych wejściowych



Rodzaju danych wejściowych

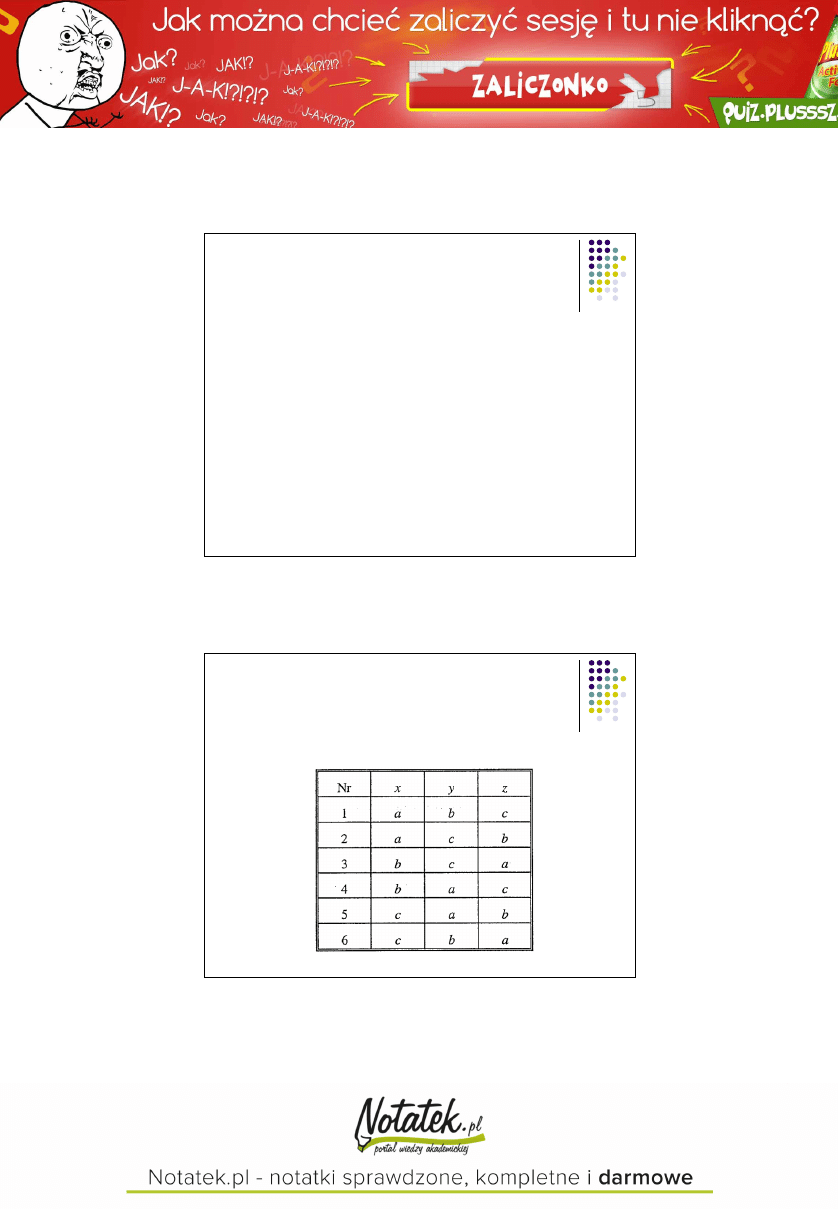
Efektywność algorytmów



Sortowanie

a < b < c

17

Sortowanie - algorytm 1

4,5,6

6

5

4

3

2

1

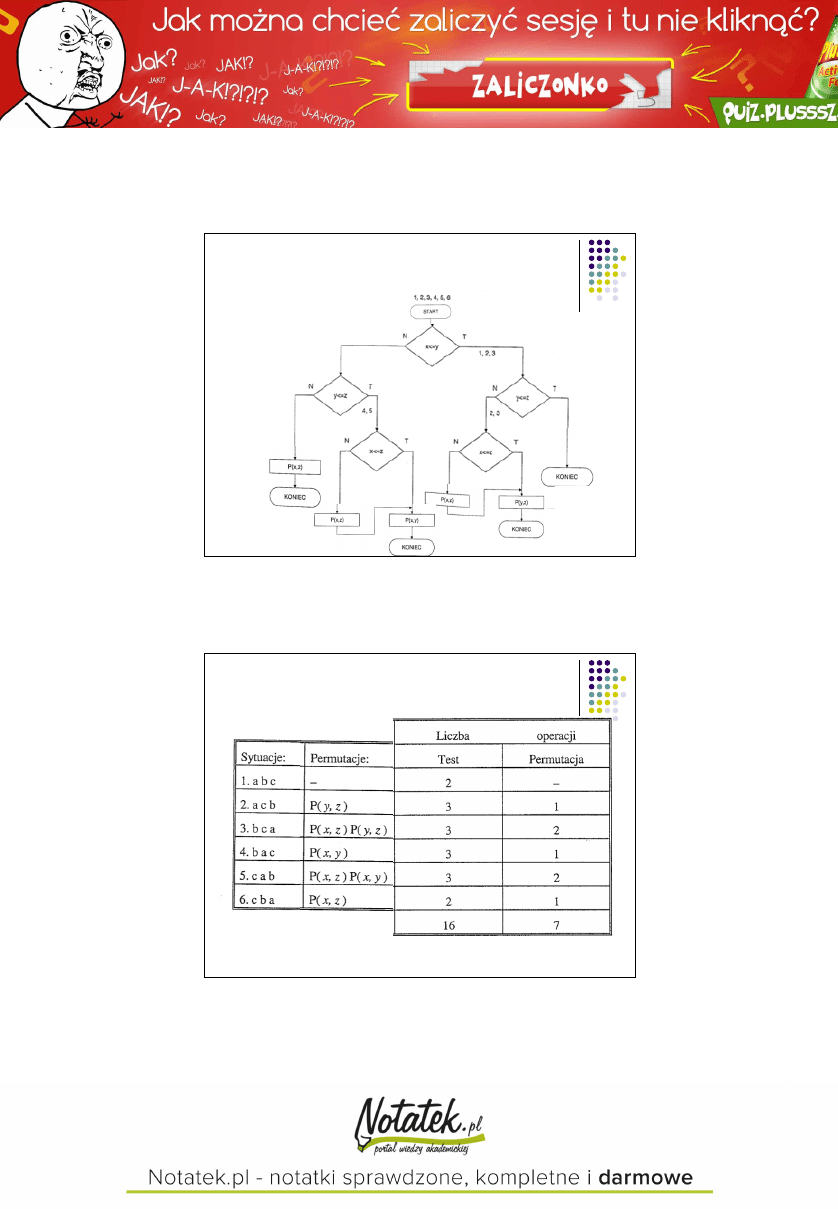
Sortowanie - algorytm 1

Razem:

Średnio:

2,7

1,2

18

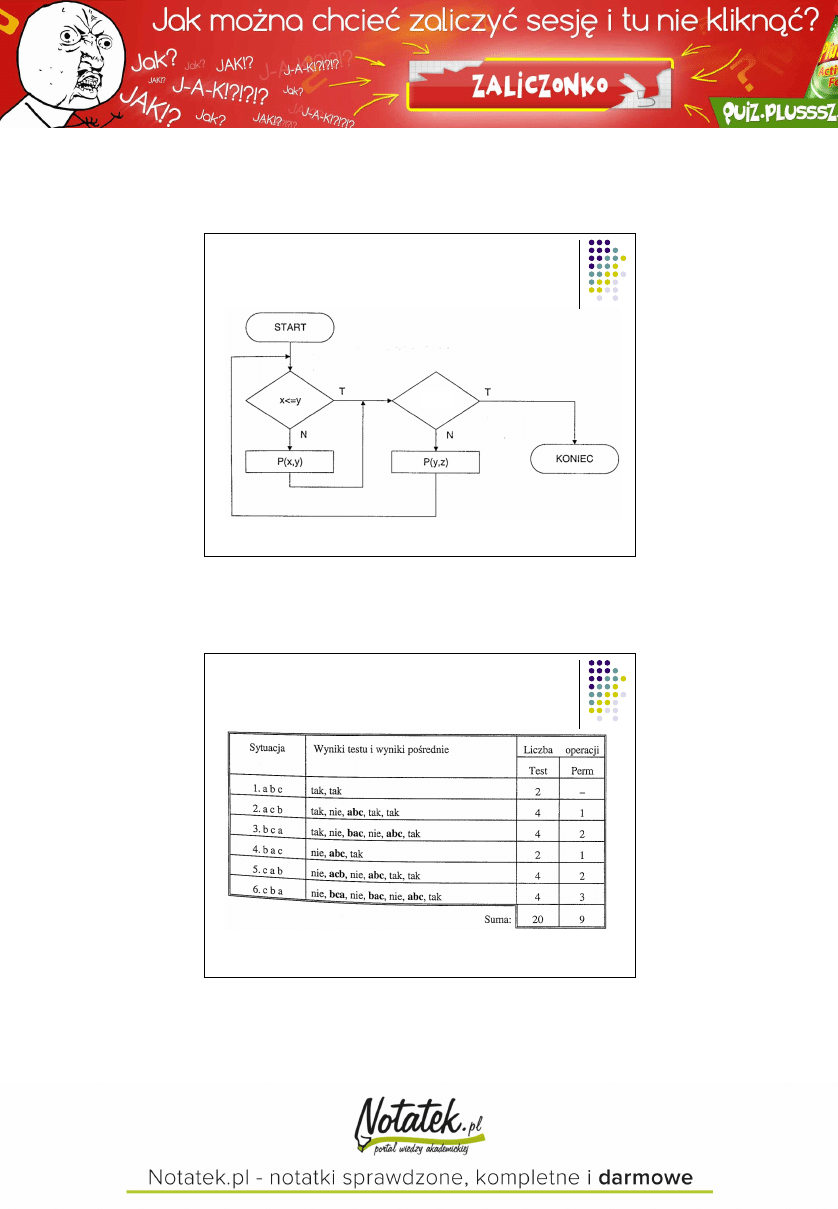
Sortowanie - algorytm 2

y<=z

Sortowanie - algorytm 2

Średnio: 3,3

1,5

19

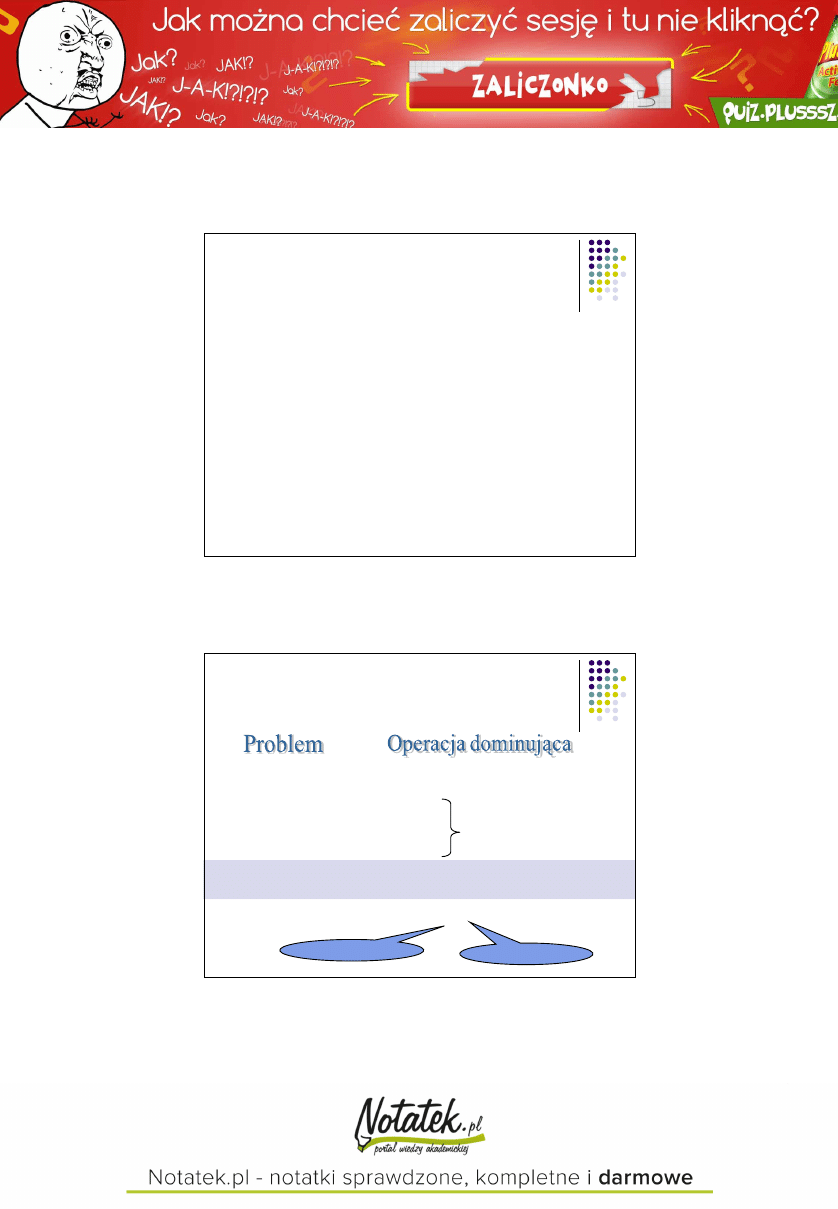
Porównanie efektywności



Algorytm 1:



Pamięć



5 operacji testu



5 operacji permutacji



Czas (średni)



2,7 t

testu

+ 1,2 t

permutacji



Algorytm 2:



Pamięć



2 operacje testu



2 operacje permutacji



Czas (średni)



3,3 t

testu

+ 1,5 t

permutacji

Operacje dominujące

Mnożenie macierzy

Wyszukiwanie elementu w tablicy

Sortowanie

Mając dany algorytm, konkretne środowisko i konkretne
dane możemy policzyć liczbę operacji dominujących.

Operacje + , *

porównywanie

Koszt algorytmu dla danych D

n

:

algorytm

dane

t(

α ,I)

20

Szacowanie złożoności
obliczeniowej



α - algorytm rozwiązujący decyzyjny problem Π ;



D

n

-

zbiór danych rozmiaru n dla rozważanego problemu;



t(α , I) - liczba operacji potrzebna do rozwiązania problemu Π
dla konkretnych danych I

∈D

n

przy pomocy algorytmu

α.



Pesymistyczna złożoność obliczeniowa:

W(

α ,

n) = max{t(

α ,

I): I



D

n

}



Średnia złożoność obliczeniowa:

W(

α ,

n) = Σ{p(I)·t(

α ,

I): I



D

n

}

Szacowanie złożoności
obliczeniowej



Mówimy, że algorytm α ma złożoność czasową:

wielomianową

wttw T(

α,n)=



(n

b

) b



N

wykładniczą

wttw T(

α,n) =



(a

n

) a



R+

liniową

wttw T(

α,n)=



(n)

kwadratową

wttw T(

α,n)=



(n

2

)

logarytmiczną

wttw T(

α,n)=



(lg n)

21

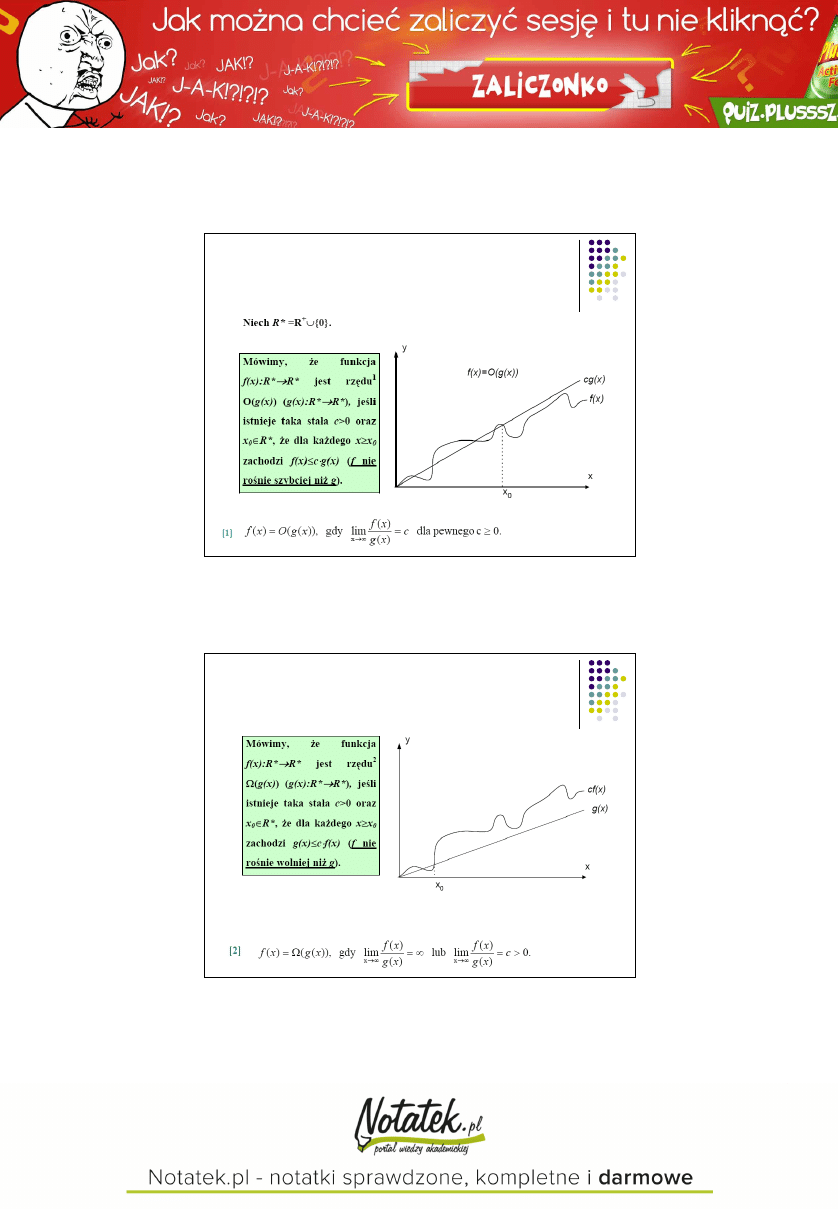
Rząd złożoności obliczeniowej

Rząd złożoności obliczeniowej

22

Rząd złożoności obliczeniowej

Struktury danych



Struktury są „pojemnikami na dane”, które gromadzą
dane

i układają je w odpowiedni sposób



Na strukturach danych operują algorytmy



Podstawowe struktury danych to:



rekord (struktura)



tablica



lista



stos



kolejka



drzewo (drzewo binarne)



graf

23

Rekord



W niektórych językach programowania nazywany

strukturą (ang. structure, struct, record)



Jest to obiekt programistyczny, grupujący dane

różnych typów



Posiada określone elementy (składowe), które mogą

być odczytywane i zmieniane



Odpowiednik rekordu w teorii relacyjnych baz danych
to krotka (wiersz tabeli)

Rekord -

przykład



Rekord typu pracownik

może zawierać np.:



Nazwisko

– element danych typu tekstowego



Imię - element danych typu tekstowego



Data urodzenia - rekord typu data



Data zatrudnienia - rekord typu data



Miejsce zamieszkania - rekord typu adres



stanowisko - dana typu tekstowego



Użyty tutaj rekord typu data może być definiowany jako:



Rok -

liczba całkowita lub tekst (4 cyfry)



Miesiąc - liczba całkowita lub tekst (2 cyfry)



Dzień - liczba całkowita lub tekst (2 cyfry)

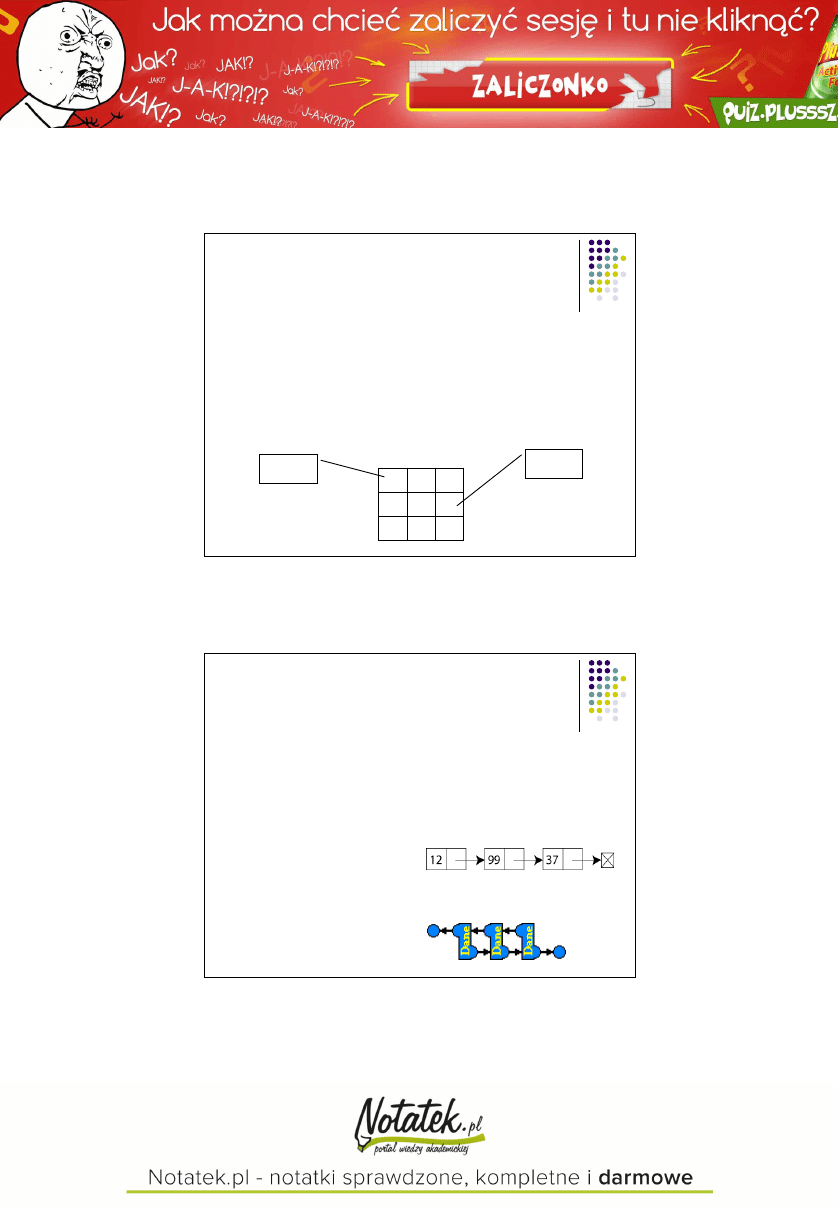
24

Tablica



Zbiór danych tego samego typu, w którym

poszczególne komórki adresowane są za

pomocą indeksów.



Rozmiar tablicy



jest albo ustalony z góry (tablice statyczne)



może się zmieniać w trakcie wykonywania programu
(tablice dynamiczne).



Odpowiednikiem tablicy dwuwymiarowej w
matematyce jest macierz.

4

3

7

3

8

4

6

9

7

Tab[1,2]

Tab[0,0]



Lista to liniowo uporządkowany zbiór
elementów, z których dowolny element można
usunąć oraz dodać w dowolnym miejscu.



Lista jednokierunkowa -

komórki zawierają

tylko wskaźniki do kolejnej komórki.



Lista dwukierunkowa -

komórki zawierają także

wskaźnik do poprzedniej komórki.

Lista

25

Szczególne przypadki listy



stos



pobrać, odczytać i wstawić element można
tylko na końcu listy



kolejka



pobrać i odczytać element można tylko na
początku listy, a dodać na końcu

Algorytm wyszukiwania



Lista nieuporządkowana



Szukana wartość: 6



5; 1; 7; 8; 2; 3; 4; 6; 0; 9



8 sprawdzeń,



Średnio potrzeba n/2 sprawdzeń (n=10)

26



Lista uporządkowana



Szukana wartość: 6



0; 1; 2; 3; 4; 5; 6; 7; 8; 9



4 sprawdzenia,



Średnio potrzeba ½ log

2

n sprawdzeń (n=10)

Algorytm wyszukiwania

1

2

3

4

1

2

3

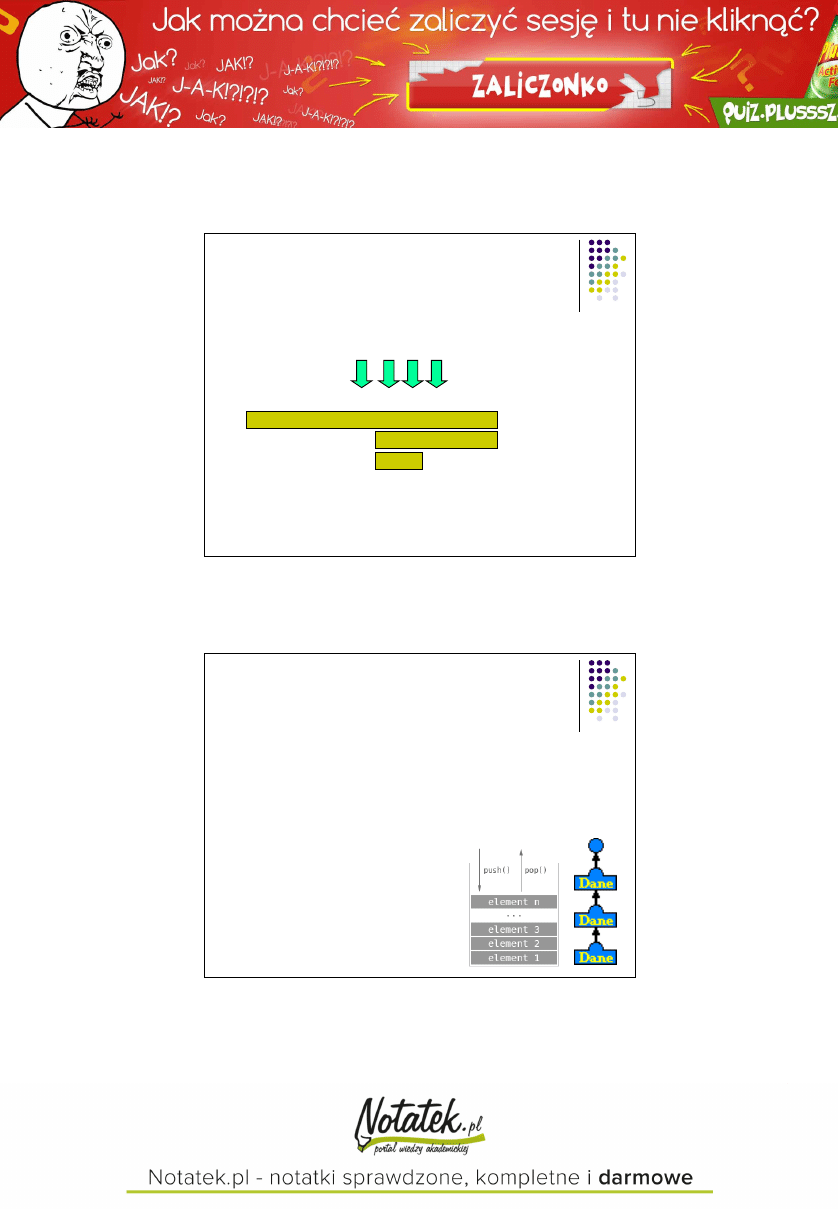
Stos



LIFO, Last In, First Out;

ostatni na wejściu,

pierwszy na wyjściu



Jedynie ostatni element stosu, zwany

wierzchołkiem, jest w danym momencie

dostępny.



W wierzchołku odbywa się dołączanie

nowych elementów, również jedynie

wierzchołek można usunąć.

27

Kolejka



FIFO (ang. First In, First Out) -

pierwszy na wejściu,

pierwszy na wyjściu



dołączać nowe dane można jedynie na koniec kolejki
a usuwać z początku

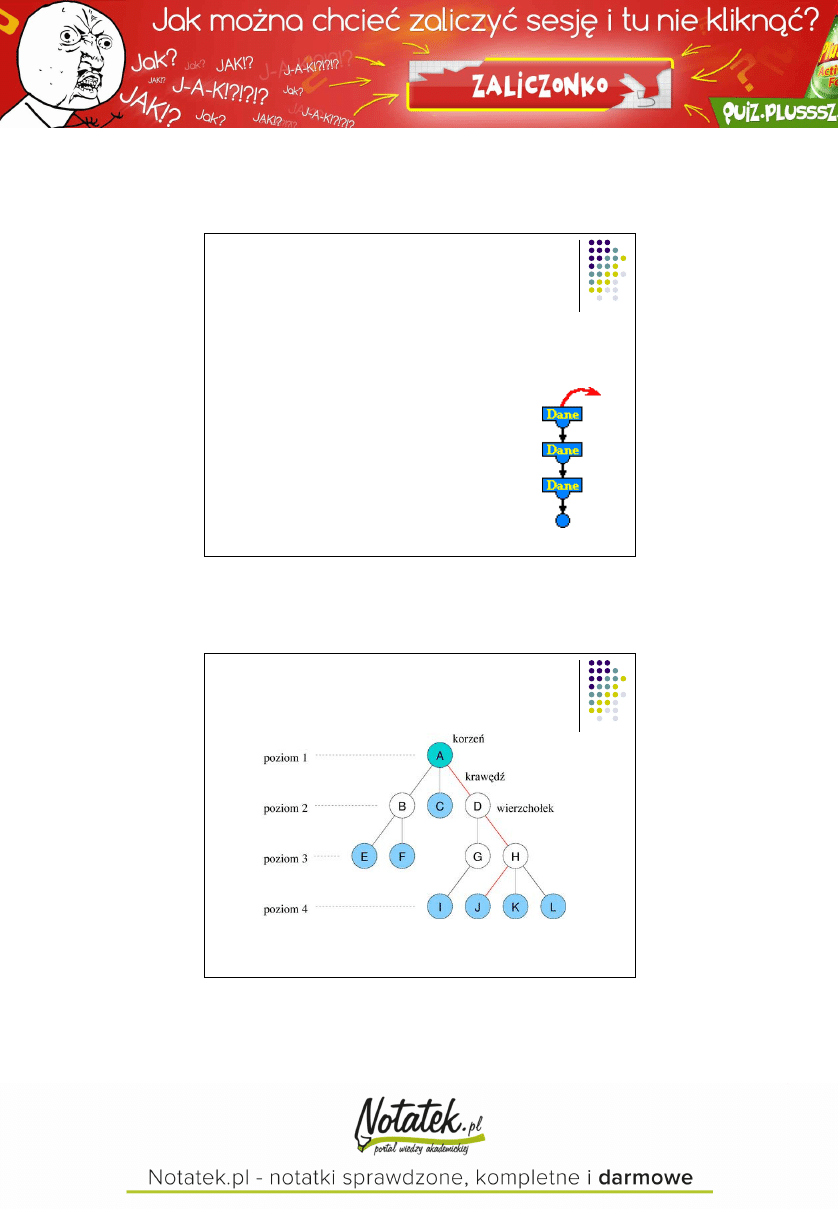
Drzewo

28

Drzewo



Przykład zastosowania: indeksy w bazach danych
(B-drzewo)

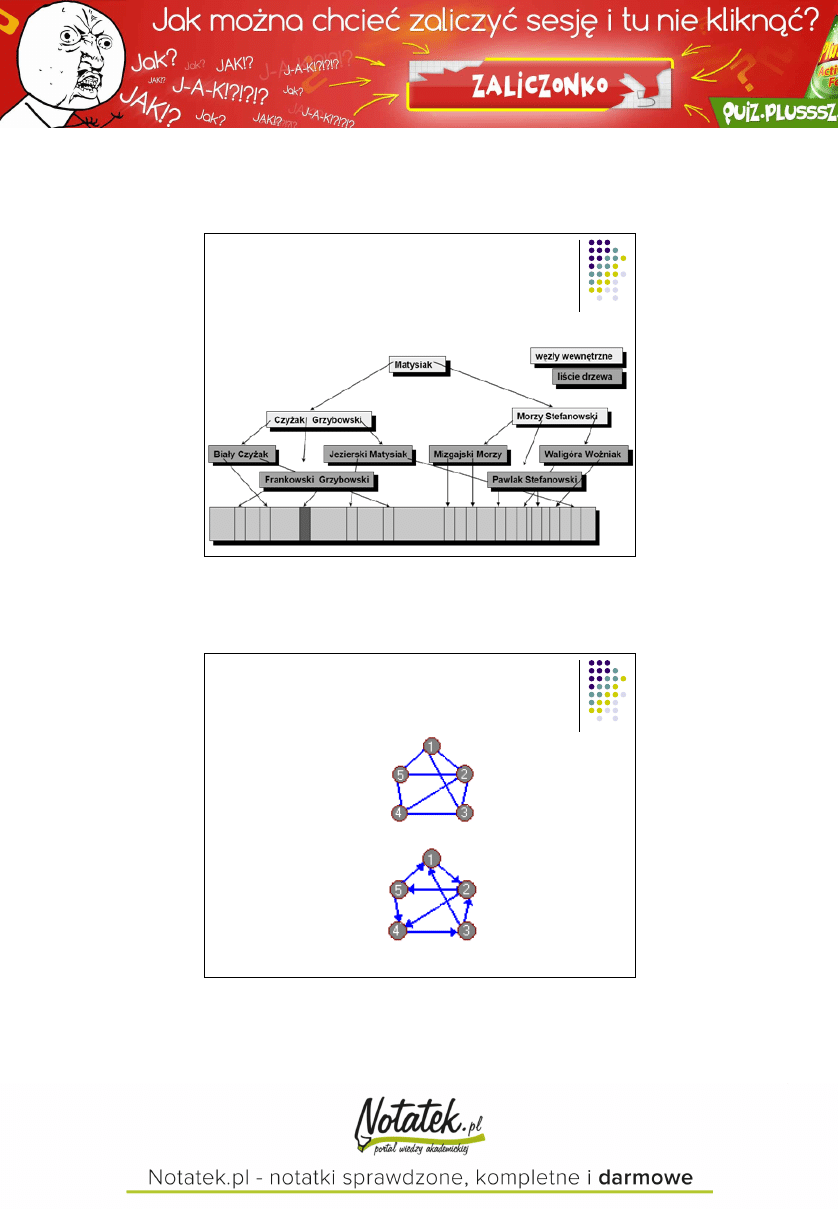
Graf



nieskierowany



skierowany

29

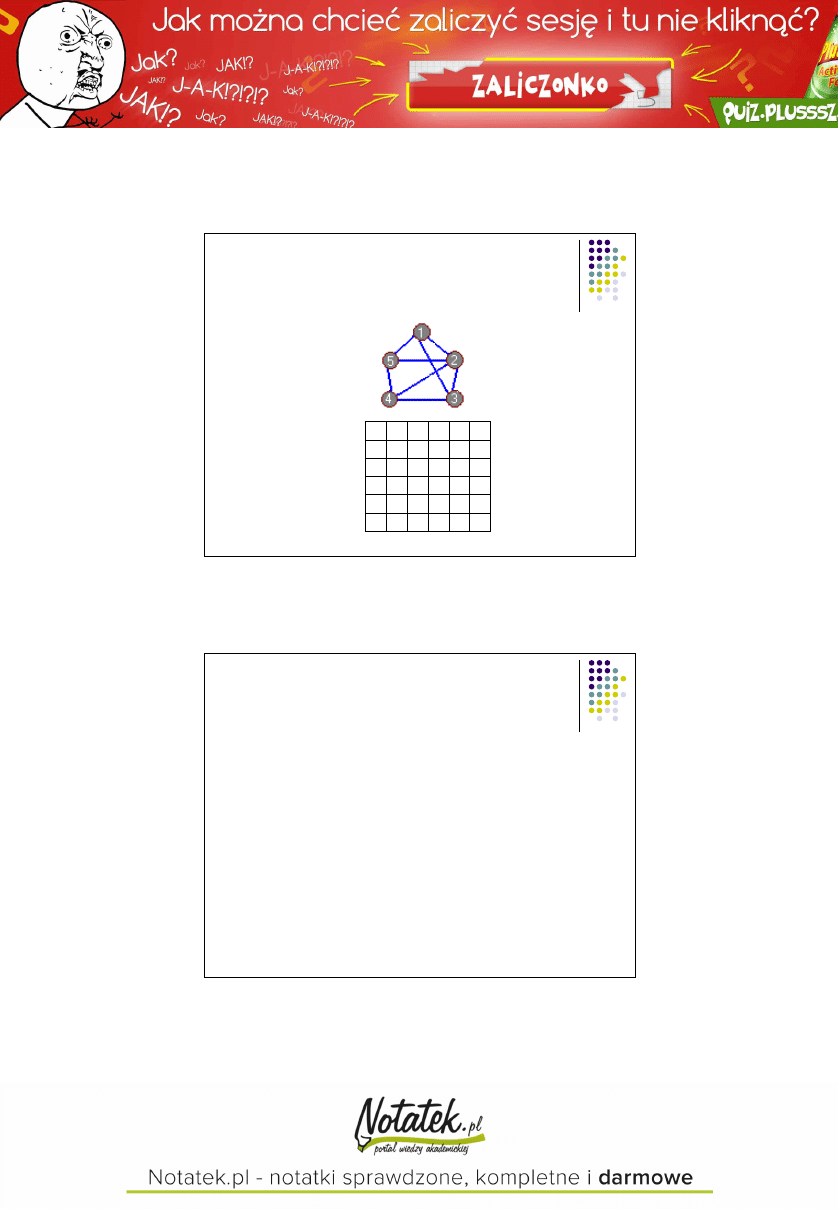
Macierz sąsiedztwa

1

2

3

4

5

1

0

1

1

0

1

2

1

0

1

1

1

3

1

1

0

1

0

4

0

1

1

0

1

5

1

1

0

1

0

Bibliografia



Algorytmy i struktury danych,
L. Banachowski, K. Diks, W. Rytter,
Wydawnictwa Naukowo - Techniczne, 2006.



Wprowadzenie do algorytmów,
Thomas H. Cormen, Charles E. Leiserson,
Ronald L. Rivest, Clifford Stein,
Wydawnictwa Naukowo - Techniczne, 2004.