Konwekcja

Konwekcja

Mechanizm konwekcji

T

Warstwa

Prandtla

Ściana

Obszar

burzliwy

T

w

x

x

Q

T

c

T

f

y

0

0

Obszar

przejściowy

dQ

w

x

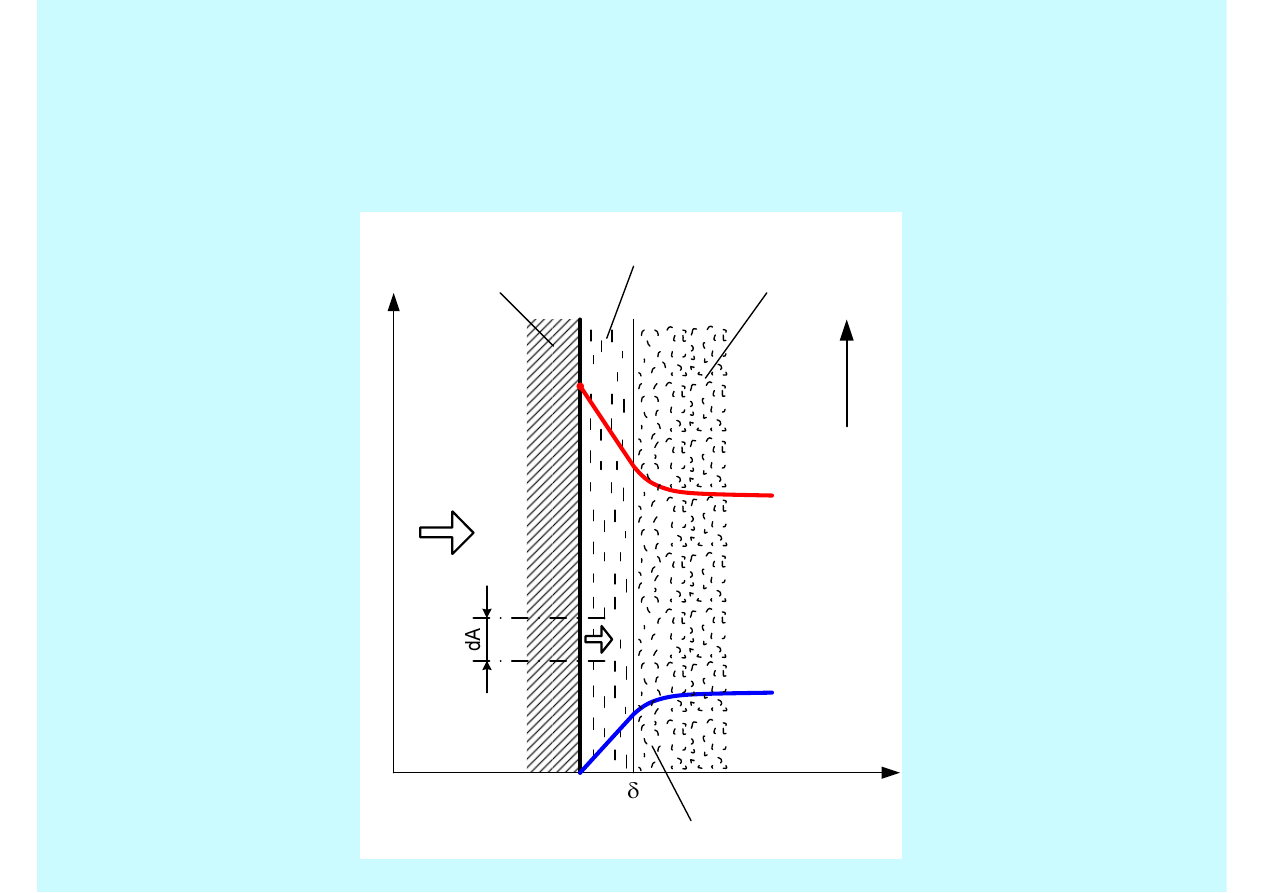
Procesowi konwekcji towarzyszy zjawisko przewodzenia
ciepła przy równoczesnym ruchu płynu względem ściany. W
dostatecznej odległości od ściany płyn porusza się w sposób
niezakłócony przez oddziaływanie ściany i jego temperatura
oraz prędkość w kierunku x jest wyrównana.

W sąsiedztwie ściany prędkość maleje aż do wartości

W sąsiedztwie ściany prędkość maleje aż do wartości
zerowej, przy czym przepływ w tym obszarze ma charakter
laminarny, a rozkład prędkości jest liniowy. Warstwę tę
określa się jako

warstwę przyścienną Prandtla

warstwę przyścienną Prandtla

. W warstwie

Prandtla wymiana ciepła zachodzi na drodze przewodzenia i
warstwa ta jest głównym źródłem oporu cieplnego gdyż
efektywność wymiany ciepła na drodze przewodzenia jest

efektywność wymiany ciepła na drodze przewodzenia jest
zdecydowanie mniejsza niż na drodze konwekcji.

Współczynnik przejmowania ciepła

Współczynnik przejmowania ciepła

zależy więc głównie od

grubości δ warstwy przyściennej. Grubość tej warstwy zależy
natomiast od prędkości płynu oraz jego właściwości
fizycznych.

Równanie wymiany ciepła

Podstawowymi problemami w nauce o wymianie ciepła są

problemy związane z określeniem wielkości strumienia ciepła,
rozkładu temperatury ośrodka oraz wartości współczynnika
przejmowania ciepła.

Rozważa się elementarną powierzchnię w warstwie Prandtla,

przez którą przepływa strumień ciepła.

Z prawa Fouriera wynika:

Z prawa Newtona wynika:

(

)

dA

T

T

Q

d

f

c

−

⋅

=

α

&

dA

y

T

Q

d

∂

∂

⋅

−

=

λ

&

Porównując prawe strony równań, otrzymuje się:

(

)

dA

T

T

Q

d

f

c

−

⋅

=

α

y

T

T

T

f

c

∂

∂

⋅

−

−

=

λ

α

Współczynnik wyrównywania temperatury – określa
właściwości fizyczne substancji:

Dla nieustalonych przypadków wymiany ciepła
współczynnik „a” określa prędkość zmiany temperatury.













⋅

=

s

m

c

a

p

2

ρ

λ

Lepkość

Pomiędzy poruszającymi się z różnymi prędkościami,
sąsiadującymi ze sobą warstwami płynu powstaje siła
tarcia wewnętrznego, która przeciwdziała ruchowi. Tę
siłę tarcia odniesioną do jednostki powierzchni nazywa się
naprężeniem stycznym. Naprężenie styczne jest

naprężeniem stycznym. Naprężenie styczne jest
proporcjonalnego do gradientu prędkości, a współczynnik
proporcjonalności nazywa się

współczynnikiem

współczynnikiem lepkości

lepkości

:









∂

∂

⋅

=

2

m

N

y

w

µ

τ

x

xy



 kg

- dynamiczny współczynnik lepkości,

- kinematyczny współczynnik lepkości,

µ









⋅

s

m

kg

ρ

µ

υ

=













s

m

2

Liczby p

Liczby podobieństw

odobieństwa

a hydrodynamiczne

hydrodynamicznego

go

Str = -

liczba Strouhala

– liczba równoczesności, stanowi

l

w

τ

⋅

kryterium równoczesności zjawisk nieustalonych.

Fr = -

liczba Frouda

– określa podobieństwo konwekcji

swobodnej wywołanej działaniem sił ciężkości na cząsteczki

l

2

w

g

l

⋅

swobodnej wywołanej działaniem sił ciężkości na cząsteczki

płynu o różnych gęstościach, spowodowanych ich różnymi

temperaturami.

Eu = -

liczba Eulera

– określa stosunek sił

wynikających z różnicy ciśnień do sił bezwładności.

Liczba ta jest kryterium podobieństwa przy przepływach o

2

w

p

⋅

ρ

∆

Liczba ta jest kryterium podobieństwa przy przepływach o

dużych gradientach ciśnień (dysze, dyfuzory, kanały

międzyłopatkowe turbin).

Re = -

liczba Reynoldsa

– określa stosunek sił

l

w

⋅

Re = -

liczba Reynoldsa

– określa stosunek sił

bezwładności do sił lepkości. Liczba ta stanowi kryterium

hydrodynamiczne przy konwekcji wymuszonej.

υ

W konwekcji swobodnej stosowana jest dodatkowo

liczba

Galileusza

:

Ga = Fr·Re

2

=

2

3

υ

l

g

⋅

która określa stosunek sił ciężkości do sił lepkości.

Często zamiast liczby Galileusza stosuje się

liczbę Grashofa

:

Gr = Ga·

·

∆

T =

·

·

∆

T

β

2

3

υ

l

g

⋅

β

– wsp. rozszerzalności objętościowej płynu,

∆

T – różnica temp. płynu,

β

W przypadku wystąpienia podobieństwa

hydrodynamicznego

hydrodynamicznego

liczby podobieństwa różnych zjawisk są takie same, np. liczby

Str, Re, Eu, Fr (Ga, Gr).

W pewnych przypadkach można jakąś liczbę podobieństwa

pominąć. Np. dla przepływu ustalonego pomija się liczbę

Strouhala, a dla konwekcji wymuszonej liczbę Frouda (Ga, Gr).

Liczby podobieństwa cieplnego

Liczby podobieństwa cieplnego

Fo = -

liczba Fouriera

- charakteryzuje nieustaloną

wymianę ciepła i określa kryterium jednoczesności.

2

l

a

τ

wymianę ciepła i określa kryterium jednoczesności.

Pe = -

liczba Pecleta

- określa podobieństwo pól

temperatur w przypadku konwekcji wymuszonej.

a

l

w

⋅

Dodatkowo można zdefiniować liczby:

Liczba Prandtla

:

Pr =

λ

µ

υ

p

c

a

Re

Pe

⋅

=

=

Liczba Prandtla określa podobieństwo właściwości

fizycznych substancji.

Nu = -

liczba Nusselta

- pozwala wyznaczyć

współczynnik przejmowania ciepła i charakteryzuje

λ

a

Re

λ

α

l

⋅

współczynnik przejmowania ciepła i charakteryzuje

podobieństwo warunków przyściennych dla przepływu
ciepła.

W ogólnym przypadku można zapisać:

Nu = f(Fo, Pe, Str, Re, Eu, Fr)

Dla konwekcji wymuszonej i ustalonego przepływu płynu i ciepła:

Dla konwekcji wymuszonej i ustalonego przepływu płynu i ciepła:

Nu = f(Pr, Re)

Dla konwekcji swobodnej i ustalonego przepływu płynu i ciepła:

Nu = f(Gr, Pr)

Nu = f(Gr, Pr)

Funkcje tego typu określane są na podstawie doświadczeń i mają
znaczenie wyników rozwiązań równań różniczkowych bez
całkowania.

Wzory, za pomocą których wyznacza się wartość liczby

Nusselta (a w konsekwencji współczynnik przejmowania

ciepła

α

) mają najczęściej postać iloczynu potęgowego:

- dla konwekcji wymuszonej,

- dla konwekcji swobodnej.

n

m

C

Nu

Pr

Re

1

⋅

⋅

=

p

k

Gr

C

Nu

⋅

⋅

=

Pr

2

Wartości stałych C

1

, C

2

i wykładników potęgowych k, m,

n, p wyznacza się doświadczalnie.

Konwekcja swobodna i wymuszona

Konwekcja swobodna i wymuszona

Konwekcja swobodna

Konwekcja swobodna

W konwekcji swobodnej ruch płynu spowodowany jest siłami

W konwekcji swobodnej ruch płynu spowodowany jest siłami

masowymi (najczęściej siłami ciężkości lub bezwładności).

Różnica temperatury ciała wymieniającego ciepło i temperatury

otaczającego go płynu powoduje różnicę gęstości płynu, która
jest przyczyną powstawania siły wyporu.

Ruch płynu w konwekcji swobodnej może być laminarny lub

Ruch płynu w konwekcji swobodnej może być laminarny lub

burzliwy.

Kryterium zmiany rodzaju ruchu jest krytyczna wartość liczby

Grashofa (Gr) lub Rayleigha: Ra = Gr·Pr.

Wymiana ciepła pomiędzy ścianą pionową i płynem

Wymiana ciepła pomiędzy ścianą pionową i płynem

(

)

25

0.

Pr

Gr

C

Nu

⋅

⋅

=

3

∆

β

T

L

g

Gr

⋅

⋅

⋅

=

L - wysokość ściany.

Wartości współczynnika C:

2

υ

∆

β

T

L

g

Gr

⋅

⋅

⋅

=

Pr

0.1

0.73

1

10

100

Pr

0.1

0.73

1

10

100

C

0.389

0.517

0.535

0.619

0.655

Wzór Michiejewa (zależność empiryczna):

(

)

n

Pr

Gr

C

Nu

⋅

⋅

=

Gr·Pr

C

n

Gr·Pr

C

n

≤≤≤≤

10

-3

0,5

0

10

-3

... 500

1,18

1/8

500 ... 2·10

7

0,54

1/4

2·10

7

... 10

13

0,135

1/3

Wymiarem charakterystycznym L w liczbie Grashofa i Nusselta

jest:

- wysokość ściany pionowej lub walca,
- średnica kuli lub walca poziomego,
- mniejszy z wymiarów ściany poziomej.

Układ zamknięty

Układ zamknięty -- szczeliny

szczeliny

Dla tych przypadków wprowadza się zastępczą wartość

współczynnika przewodzenia ciepła

λλλλ

e

.

(

)

λ

przy czym:

λ

- współczynnik przewodzenia ciepła płynu,

(

)

2

1

c

c

e

T

T

q

−

=

δ

λ

&

ε

λ

λ

=

e

λ

- współczynnik przewodzenia ciepła płynu,

ε

- współczynnik określający stopień intensyfikacji

przewodzenia ciepła w porównaniu z płynem nieruchomym.

Jeżeli prędkość płynu jest niewielka to płyn może być traktowany

jak nieruchomy.

Jeżeli: Ra = Gr ·Pr < (1 000...1 700) to

ε

= 1 .

Szczelina

pozioma

pozioma

:

(

)

n

Pr

Gr

C

⋅

⋅

=

ε

Wg Michiejewa, jeżeli:

Ra < 1 000

⇒

ε

= 1

⇒ C = 0,105; n = 0,3

⇒ C = 0,4; n = 0,2

10

6

6

3

10

10

10

10

<

<

≤

≤

Ra

Ra

Charakterystycznym wymiarem liniowym jest szerokość
szczeliny δ, a właściwości fizyczne wyznacza się dla średniej
temperatury płynu.

Szczelina

pionowa

pionowa

:

Wzory Jacoba, obowiązujące gdy

H/

δ

≥

3

.

- dla

5

4

10

2

10

2

⋅

<

<

⋅

Gr

- dla

9

/

1

4

/

1

)

/

(

18

.

0

H

Gr

δ

ε

⋅

⋅

=

9

/

1

3

/

1

)

/

(

065

.

0

H

Gr

δ

ε

⋅

⋅

=

6

5

10

11

10

2

⋅

<

<

⋅

Gr

gdzie: H – wysokość szczeliny,

δ

– szerokość szczeliny.

Konwekcja wymuszona

Konwekcja wymuszona

W procesie wymiany ciepła na drodze konwekcji wymuszonej
ruch płynu wywołany jest „sztucznie”, np. wentylatorem,
pompą, itp.

Przepływ płynu w przewodach

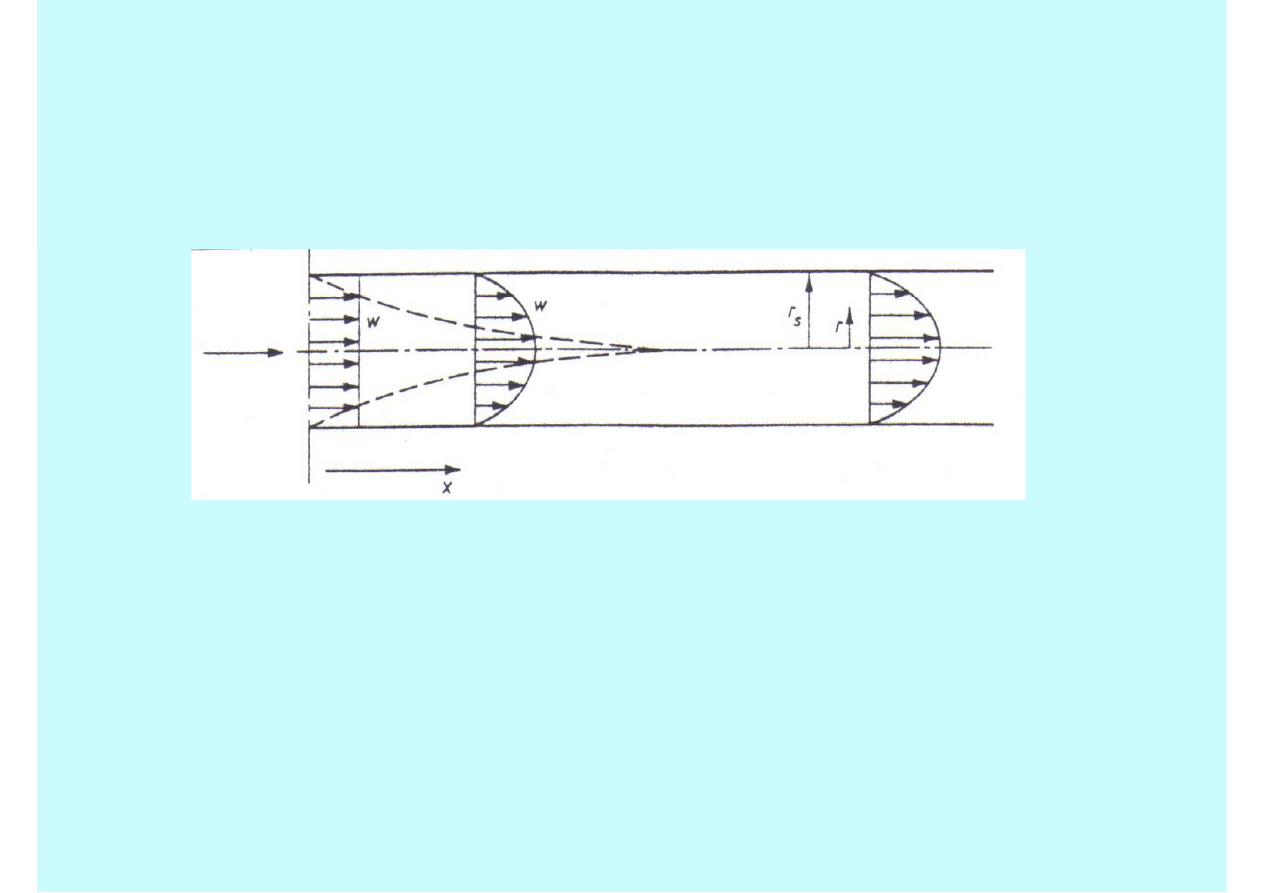
Podczas przepływu płynu w rurze następuje w jej początkowym

Podczas przepływu płynu w rurze następuje w jej początkowym

odcinku kształtowanie się profilu prędkości.

Na ściankach kanału powstaje warstwa przyścienna, której

grubość rośnie wzdłuż przepływu. Dla dostatecznie długiego
kanału warstwy te zbiegają się, a profil prędkości w rurze o
stałym przekroju ustala się.

Odcinek, na którym następuje wykształcenie się profilu

Odcinek, na którym następuje wykształcenie się profilu

prędkości określa się jako odcinek stabilizacji

hydrodynamicznej

hydrodynamicznej

.

Dla przepływu laminarnego długość tego odcinka wynosi:

20

Re

d

L

w

h

=

Przez analogię do odcinka stabilizacji hydrodynamicznej

wprowadza się pojęcie odcinka stabilizacji

termicznej

termicznej

oraz

termicznej warstwy przyściennej. W ogólności długość tych
odcinków może być różna.

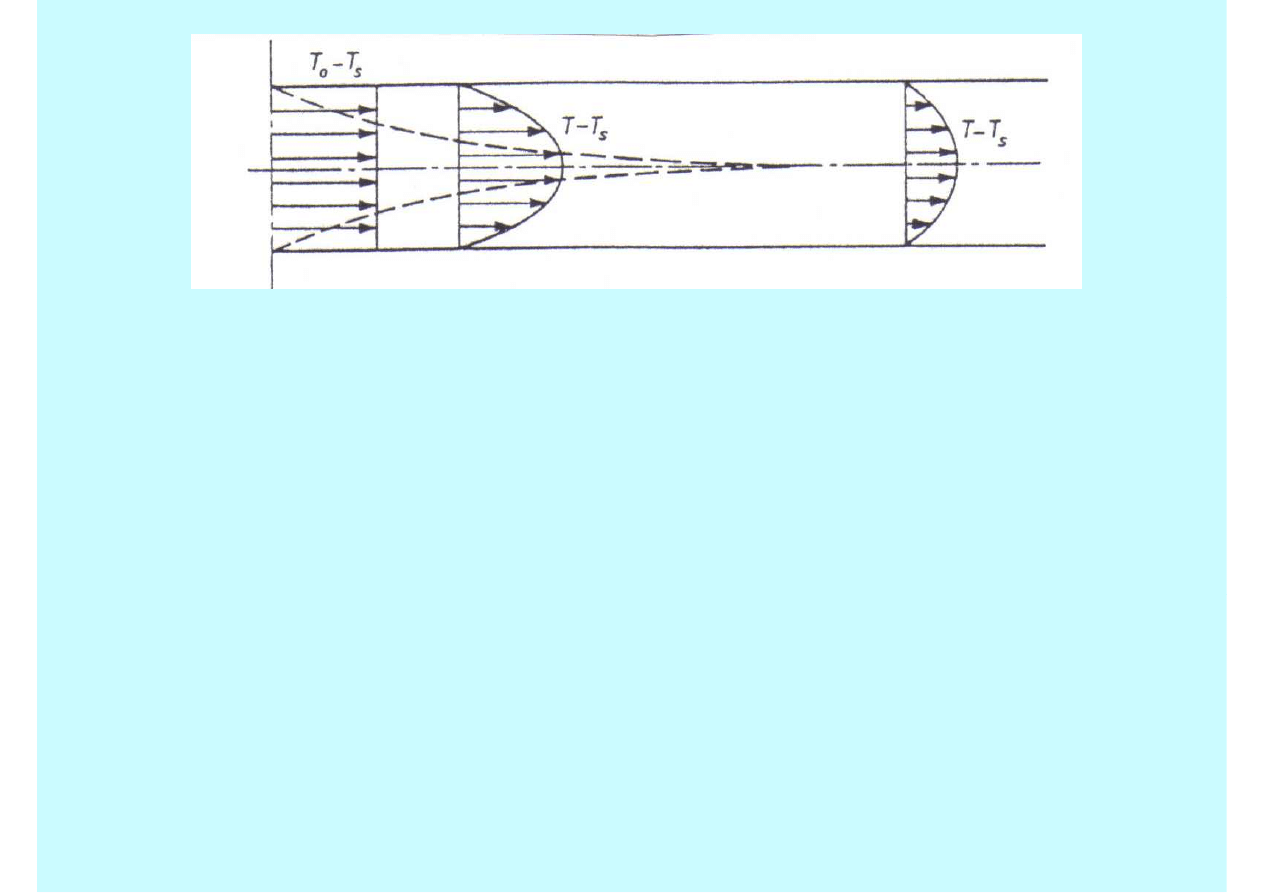
Wraz ze zmianą grubości termicznej warstwy przyściennej

zmienia się wartość współczynnika przejmowania ciepła
wzdłuż rury. Poza odcinkiem stabilizacji termicznej
wartość tego współczynnika jest praktycznie stała.

Warstwa przyścienna może mieć charakter laminarny na całej

długości przepływu albo początkowo ma charakter

długości przepływu albo początkowo ma charakter
laminarny i przy dostatecznie długim przepływie może
przekształcić się w postać burzliwą. Przy Re > 5 ·10

4

od samego wlotu do rury tworzy się burzliwa warstwa
przyścienna.

Przy przepływie burzliwym płynów o liczbie Pr

≅≅≅≅

1 długość

Przy przepływie burzliwym płynów o liczbie Pr

≅≅≅≅

1 długość

odcinka stabilizacji termicznej, na końcu którego osiągana jest

stała wartość miejscowego współczynnika przejmowania

ciepła, wynosi (10...15)·dw, natomiast średni współczynnik

przejmowania ciepła osiąga stałą wartość w odległości około

50·dw.

50·dw.

Współczynniki przejmowania ciepła

Współczynniki przejmowania ciepła

Przepływ

laminarny

laminarny

(Re < 2 300):

Wzór Hausena:

3

2

04

0

1

0668

0

66

3













+













+

=

L

d

Pe

,

L

d

Pe

,

,

Nu

w

w

α

w

d

Nu

⋅

=

ρ

w

d

w

Re

⋅

⋅

=

Pr

Re

Pe

⋅

=

Zakres stosowalności wzoru: Re < 2 300;

λ

w

Nu

=

µ

w

Re

=

Pr

Re

Pe

⋅

=

100

<

L

d

Pe

w

Przepływ

burzliwy

burzliwy

(Re > 10

4

):

Wzór Dittusa-Boeltera:

n

,

Pr

Re

,

Nu

⋅

⋅

=

8

0

023

0

n = 0,4 - dla ogrzewania płynu,

n = 0,3 - dla chłodzenia płynu.

Zakres stosowalności wzoru:

n

,

Pr

Re

,

Nu

⋅

⋅

=

8

0

023

0

>

L

Re > 10

4

; 0,7< Pr <160;

60

>

w

d

L