MATEMATYKA

KROK PO KROKU

Poradnik metodyczny

Klasa III gimnazjum

Kinga Gałązka

Edward Lesiak

Projekt okładki

Barbara Zawadzka

Opracowanie graficzne okładki

Iwona Zielak-Mamińska

Redaktor merytoryczny

Mariusz Bienias

Redaktor techniczny

Małgorzata Niedziałomska

Rysunki

Małgorzata Niedziałomska

Poradnik  jest  częścią  obudowy  programu  nauczania  matematyki  w  kla-
sach  I–III  gimnazjum  pod  tytułem  MATEMATYKA  KROK  PO  KROKU,
dopuszczonego do użytku szkolnego przez MEN.
Nr dopuszczenia: DKW-4014-91/99.
Został przygotowany do podręcznika MATEMATYKA KROK PO KROKU,
dopuszczonego do użytku szkolnego przez MEN.
Nr dopus

zczenia: 173/01.

Wydanie I

© Copyright by Wydawnictwo Edukacyjne

RES POLONA Sp. z o.o.

ISBN 83-7071-323-8

WYDAWCA:
Wydawnictwo Edukacyjne RES POLONA Sp. z o.o.
90-613 Łódź, ul. Gdańska 80, tel. (0-42) 636-36-34, fax 637-30-10
Internet: www.res-polona.com.pl; e-mail: info@res-polona.com.pl

Spis treści

Wstęp / 5

Komentarz do podręcznika / 7

Liczby rzeczywiste / 7
Przekształcenia geometryczne / 8
Doświadczenia losowe / 10
Wyrażenia algebraiczne / 10
Równania, nierówności, układy równań / 12
Związki miarowe w trójkącie / 13
Figury przestrzenne / 14

Odpowiedzi do zadań / 17

Odpowiedzi do zadań wyróżnionych w podręczniku

ramką z ,,!” / 17

Odpowiedzi do zadań w ćwiczeniach sprawdzających

oznaczonych  

/ 25

Ocenianie raz jeszcze / 37

Sprawdzian 1. Techniczne nowinki / 38
Sprawdzian 2. Do końca roku jeden krok / 42
Sprawdzian 3. Szaleństwo XX wieku / 46

Ścieżki edukacyjne w gimnazjum / 51

Ścieżka edukacyjna – co to takiego? / 51
Rodzaje i budowa ścieżek edukacyjnych/ 53
Modele realizacji ścieżek edukacyjnych/ 54
O realizacji każdej ze ścieżek na lekcjach matematyki
słów kilka / 57
Wykorzystanie treści ścieżek edukacyjnych/ 58

Scenariusze zajęć / 59

Kąty w okręgu / 59
Zaszyfrowana wiadomość / 65
Zbieranie danych statystycznych i ich interpretacja / 71

Metody aktywizujące w praktyce / 75

Która metoda jest lepsza? / 75
Przykłady metod aktywizujących/ 76

5

WSTĘP

A więc stało się. Jesteśmy w klasie trzeciej. Przed nami nowe zadania

związane z zakończeniem nauki w gimnazjum. Przypominamy, że porad-
nik jest częścią kompletu materiałów do nauczania matematyki w gimna-
zjum  MATEMATYKA KROK PO KROKU. Pozostałymi częściami skła-
dowymi tego kompletu są: program nauczania, podręcznik, zbiór zadań,
ćwiczenia sprawdzające oraz rozkład materiału.

Program nauczania.

 Opracowany został zgodnie z Podstawą progra-

mową kształcenia ogólnego dla sześcioletnich szkół podstawowych i gim-
nazjów

.  Zawiera:  założenia  ogólne,  szczegółowe  cele  kształcenia  mate-

matycznego, założenia szczegółowe programu, propozycje metod oceny
osiągnięć  uczniów,  ogólny  układ  materiału  w  gimnazjum,  orientacyjny
przydział  godzin  oraz  materiał  nauczania  z  podziałem  na  poszczególne
klasy.  W  programie  uwzględniono  tygodniowo  4  godziny  matematyki
i założono, że systematyczna realizacja programu nauczania jest możliwa
w ciągu 33 tygodni.

Podręcznik.

  Zawiera  wiele  różnych  elementów,  których  celem  jest

wzbudzenie  zainteresowania  uczniów.  Układ  podręcznika  Matematyka
krok po kroku

 umożliwia rytmiczną realizację programu oraz sprzyja sto-

sowaniu aktywnych metod nauczania.

Zbiór  zadań.

  Jest  uzupełnieniem  i  rozszerzeniem  zagadnień  zawar-

tych w podręczniku. Znajdują się w nim zadania o różnym stopniu trud-
ności, które umożliwiają utrwalenie zdobytych umiejętności i rozwijanie
zainteresowań  uczniów.  W  zbiorze  zawarte  są  zadania  z  treścią  łączącą
matematykę z innymi dziedzinami wiedzy oraz takie, które wskazują na
praktyczne zastosowania matematyki. Ustalając tematykę Impresji mate-
matycznych

,  można  bazować  na  znajdujących  się  w  zbiorze  zadaniach

otwartych.

6

Ćwiczenia  sprawdzające.

  Są  propozycją  krótkich  sprawdzianów,

które mogą być użyte do samodzielnych prac uczniów w klasie czy też
w domu. Sposoby ich wykorzystania zależą od inwencji nauczyciela.

Rozkład materiału.

 Został opracowany tak, że może być podstawą pla-

nowania pracy przez nauczyciela. W wielu placówkach dyrektorzy zezwo-
lili nauczycielom na bezpośrednie korzystanie z rozkładu bez konieczności
przepisywania  go.  Rozkład  materiału  zawiera  dokładny  plan  realizacji
zajęć z uwzględnieniem tematyki i celów określonych w sposób zopera-
cjonalizowany oraz oczekiwane efekty pracy z uczniem. W rozkładzie ma-
teriału jest zaplanowana bieżąca kontrola procesu nauczania–uczenia się
(kartkówki  Teraz  Ty,  prace  klasowe  Godzina  szczerości)  umożliwiająca
dokonanie ewaluacji procesu dydaktycznego. Proponowane Impresje ma-
tematyczne

 wskazują na miejsca, gdzie możliwe jest realizowanie ścieżek

międzyprzedmiotowych.

Na podstawie naszych doświadczeń możemy stwierdzić, że propono-

wana  koncepcja  realizacji  programu  nauczania  przedstawiona  w  cyklu
Matematyka  krok  po  kroku

  do  nauczania  matematyki  w  gimnazjum

sprawdziła się w klasie pierwszej i drugiej, dlatego też jest kontynuowana
w klasie trzeciej.

Nowością,  w  porównaniu  do  klas  poprzednich,  jest  wprowadzenie

w zbiorze zadań i ćwiczeniach sprawdzających zadań wyboru. Związane
jest to z koniecznością przygotowania uczniów do sprawdzianu po gimna-
zjum i zapewnienie im możliwości rozwiązywania większej liczby zadań
typu egzaminacyjnego.

Dziękujemy wszystkim, którzy wybrali nasze podręczniki do naucza-

nia  matematyki  i  życzymy  wielu  sukcesów  w  pracy  z  młodzieżą  oraz
w życiu osobistym.

Autorzy

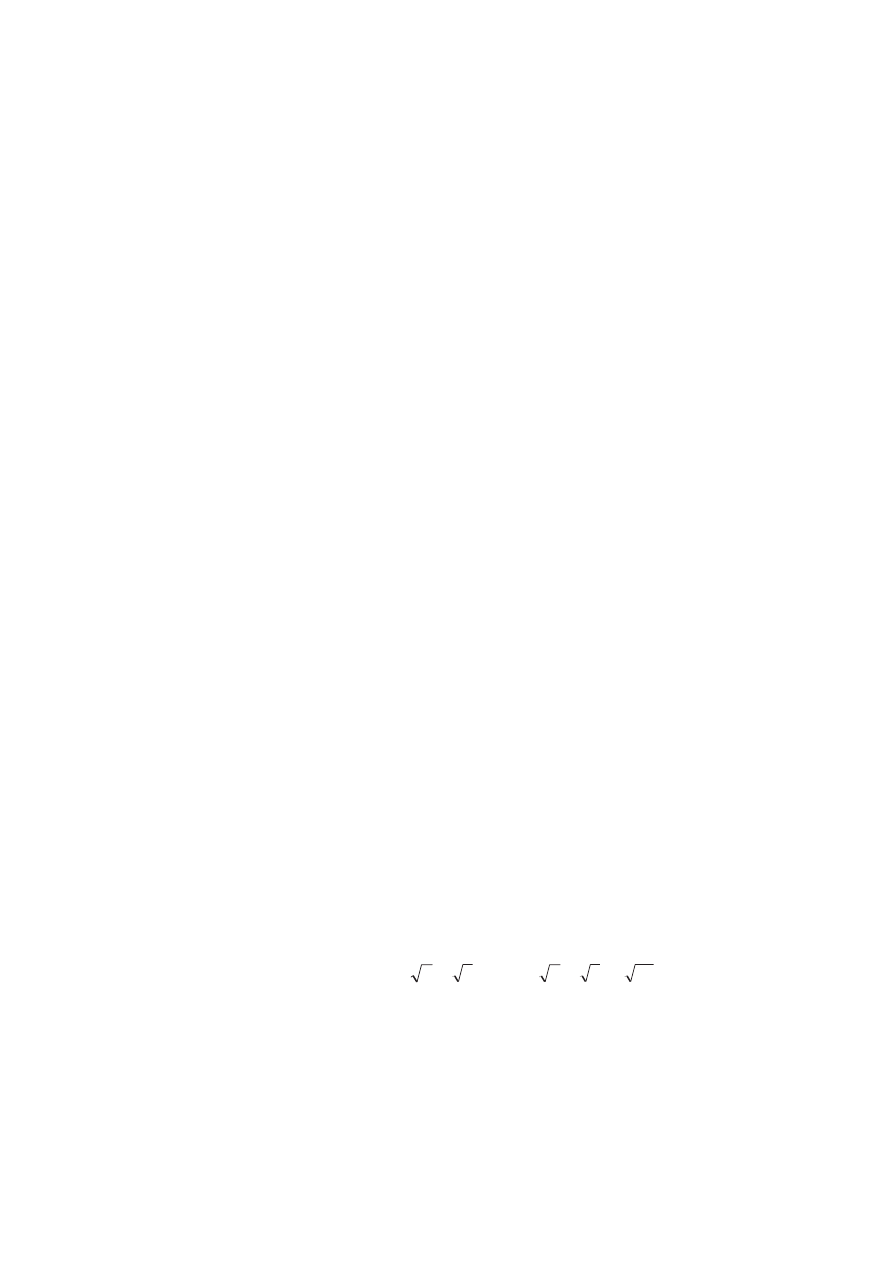
7

KOMENTARZ
DO PODRĘCZNIKA

Liczby rzeczywiste

W  rozdziale  Liczby  rzeczywiste  mówimy  o  podzbiorach  zbioru  liczb

rzeczywistych oraz własnościach działań w tych zbiorach. Pokazujemy, że
konieczne jest rozszerzanie zbiorów ze względu na wykonalność działań.

Mówiąc  o  liczbach  niewymiernych,  należy  pamiętać,  że  mnożenie

liczb niewymiernych nie jest działaniem w zbiorze liczb niewymiernych,
ponieważ o działaniu 

⊗

 mówimy, że jest wykonalne w zbiorze A, jeżeli

dla każdego a 

∈ 

A

 i każdego b 

∈ 

A

 wynik działania a 

⊗

 b 

∈ 

A

.

Weźmy liczby niewymierne 

2

 i 

8. Liczba 

2

 · 

8  =  16  = 4 nie

jest liczbą niewymierną, a więc mnożenie nie jest działaniem w zbiorze
liczb  niewymiernych,  co  nie  oznacza,  że  nie  możemy  mnożyć  liczb

W  podręczniku  dla  klasy  trzeciej  zachowaliśmy  wszystkie  elementy

występujące w podręcznikach dla klasy pierwszej i drugiej. Układ pod-
ręcznika  zsynchronizowany  jest  z  rozkładem  materiału,  zbiorem  zadań
i ćwiczeniami sprawdzającymi.

Ważną  funkcją  nauczania  jest  wyposażenie  uczniów  w  umiejętności

wynikające ze standardów egzaminacyjnych. Dlatego też zwracamy uwa-
gę  na  pokazanie  praktycznych  zastosowań  matematyki.  Znalazło  to  od-
zwierciedlenie  między  innymi  w  zakresie  proponowanego  do  realizacji
materiału  dotyczącego  związków  miarowych  w  trójkącie.  W  części  za-
sadniczej  podane  zostały  najważniejsze  zagadnienia  teoretyczne,  które
wykorzystane są później przy rozwiązywaniu zadań z zakresu obliczania
pól i objętości brył.

8

niewymiernych. Należy zwrócić w tym miejscu uwagę na fakt, że mnoże-
nie nie jest działaniem w zbiorze liczb niewymiernych, ale jest działaniem
w zbiorze liczb rzeczywistych.

W rozdziale tym staraliśmy się zebrać i przypomnieć również najważ-

niejsze wiadomości związane ze stosowaniem liczb rzeczywistych w róż-
nych sytuacjach.

Przekszta³cenia geometryczne

W klasie III wprowadzamy nowe przekształcenia płaszczyzny: jedno-

kładność i podobieństwo, które nie są przekształceniami izometrycznymi.
Uczniowie  nie  znają  pojęcia  wektora,  co  stwarza  pewne  niedogodności
przy  wprowadzaniu  jednokładności.  Dlatego  najpierw  wprowadzamy
twierdzenie Talesa i wnioski z niego wynikające oraz pokazujemy zasto-
sowania w różnych sytuacjach, w tym praktycznych, a następnie wprowa-
dzamy pojęcie jednokładności. Dysponując pojęciem jednokładności, ła-
twiejsze  byłoby  wprowadzenie  i  udowodnienie  twierdzenia  Talesa.  My
musimy postąpić odwrotnie.

W klasach o większych możliwościach matematycznych możemy, od-

wołując się do pojęcia wektora znanego uczniom z lekcji fizyki, pokazać
możliwość innego zdefiniowania jednokładności:

Punkt  A'  jest  obrazem  punktu  A  w  jedno-
kładności  o  środku  w  punkcie  S  i  skali  k
wtedy i tylko wtedy, gdy SA' = k · SA.

Przy  takiej  definicji  jednokładności  nie  musimy  oddzielnie  wprowa-

dzać określenia dla jednokładności o skali ujemnej i oddzielnie dla jedno-
kładności o skali dodatniej. W tym miejscu należy zauważyć, że w litera-
turze  możemy  spotkać  dwa  terminy:  jednokładność  prosta  i  jednokład-
ność odwrotna. Jednokładność prosta odnosi się do jednokładności o skali
dodatniej. Figura i jej obraz leżą wtedy po tej samej ,,stronie” punktu bę-
dącego środkiem jednokładności. Pojęcie jednokładność odwrotna odnosi
się do jednokładności o skali ujemnej. W tym przypadku figura i jej obraz
leżą po różnych „stronach” punktu będącego środkiem jednokładności.

W  przypadku  jednokładności  mówimy,  że  przekształcenie  to  nie  za-

chowuje  odległości  pomiędzy  punktami  i  ich  obrazami,  a  więc  nie  jest

→

→

A'

S

A

9

przekształceniem  izometrycznym.  Możemy  jednak  podkreślić  fakt,  że
jednokładność o skali k = 1 jest identycznością, a jednokładność o skali
k

= –1 jest symetrią środkową. Możemy w tym przypadku pokazać, jak

w zależności od pojęć, którymi dysponujemy, może się zmieniać sposób
definiowania nowych pojęć. Umożliwia to nam podkreślenie, jak ważne
staje się przestrzeganie przyjętych umów.

W oparciu o jednokładność definiujemy podobieństwo figur. Wymie-

niamy podstawowe własności figur podobnych. Możemy zatem przyjąć
wszystkie znane własności figur jednokładnych, poza równoległością od-
cinka i jego obrazu, jako własności figur podobnych. Nieco więcej czasu
przeznaczamy na podobieństwo trójkątów. Cechy podobieństwa formułu-
jemy  w  postaci  twierdzenia  prostego  i  twierdzenia  odwrotnego.  W  kla-
sach o większym stopniu zainteresowania matematyką cechy podobień-
stwa możemy podać w postaci równoważności:

Dwa trójkąty są podobne wtedy i tylko wtedy, gdy stosunek
długości odpowiednich boków trójkątów jest stały.

Dwa trójkąty  są  podobne  wtedy  i  tylko  wtedy,  gdy  miary
odpowiednich kątów są równe.

W literaturze możemy spotkać również cechę podobieństwa, którą po-

dajemy jako wniosek z cytowanych:

Dwa trójkąty są podobne wtedy i tylko wtedy, gdy stosunki
długości odpowiednich par boków są równe, a kąty zawarte
pomiędzy tymi bokami mają równe miary.

Zagadnienia związane z podobieństwem wykorzystujemy do interpre-

towania różnych informacji, które możemy odczytać zarówno z planu, jak
i z mapy. Tematyka ta umożliwia wykorzystanie wiadomości interdyscy-
plinarnych. Często w zadaniach występuje pojęcie skali. Zdarzają się sy-
tuacje, w których nadgorliwcy starają się zmuszać autorów do uściślania
zadań, twierdząc, że w takim przypadku nie wiadomo, czy zwiększa się
pole figury czy długości odcinków. Przypominamy, że skala odnosi się do
długości odcinków i tylko tak powinna być interpretowana w zadaniach.
Gdy  mówimy  o  powiększeniu  czy  pomniejszeniu  figury,  to  oczywiście
interpretujemy zadanie w ten sposób, że zmieniają się w określonym sto-
sunku długości odpowiednich odcinków. Oczywiście zmienia się również
pole figury, ale z własności figur podobnych wynika, że stosunek pól figur
podobnych jest równy kwadratowi skali podobieństwa.

10

Doœwiadczenia losowe

Zbieranie danych i ich interpretacja to ważne umiejętności, które zna-

lazły odzwierciedlenie w standardach egzaminacyjnych. W podręczniku
opieramy się na różnych przykładach, z którymi dosyć często się spotyka-
my. Umiejętność zdobywania informacji i wykorzystania ich występuje
w  podręczniku  we  wszystkich  rozdziałach.  W  rozdziale  Doświadczenia
losowe 

zajmujemy  się  zagadnieniami,  które  możemy  potraktować  jako

wstęp do zagadnień probabilistycznych.

W życiu codziennym bardzo często wykorzystywane jest pojęcie war-

tości  średniej.  Nie  zawsze  jednak  uśrednianie  wyników  wiąże  się  z  ich
właściwą interpretacją. Należy zwrócić uwagę na to, aby wnioski nie były
zbyt daleko idące.

Rozważmy oceny dwóch uczniów, którzy uzyskali je na koniec roku

szkolnego:
Adam – 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4,
Bartek – 4, 2, 5, 5, 3, 4, 2, 5, 5, 4, 4, 4, 5.
Zwróćmy uwagę, że zarówno Adam, jak i Bartek uzyskali taką samą oce-
nę średnią, czyli 4. Czy oznacza to, że obaj uczniowie uzyskują jednako-
we  wyniki  z  poszczególnych  przedmiotów?  Otóż  takiego  wniosku  nie
możemy wysunąć. Widzimy, że Bartek z pewnych przedmiotów uzyskuje
bardzo  dobre  wyniki,  a  z  innych,  w  których  nie  czuje  się  zbyt  mocny,
słabe.  Prawidłowa  interpretacja  danych  wymaga  wielu  różnorodnych,
związanych z nimi dodatkowych informacji.

Omawiając  częstość  względną  doświadczenia  losowego,  pojawia  się

pojęcie  częstości  teoretycznej,  które  jest  najbliższe  intuicyjnemu  rozu-
mieniu  prawdopodobieństwa.  Zagadnienia  te  nie  sprawiają  większych
trudności uczniom. Jednak nie rozwijamy zagadnień teoretycznych zwią-
zanych  z  prawdopodobieństwem.  Podstawowe  pojęcia,  które  zostały
wprowadzone,  umożliwiają  lepsze  zrozumienie  zagadnień  związanych
z doświadczeniami losowymi oraz ich interpretację.

Wyra¿enia algebraiczne

Umiejętność  przekształcania  wyrażeń  algebraicznych  jest  ważnym

aparatem  matematycznym  wykorzystywanym  w  innych  przedmiotach
matematyczno–przyrodniczych.  W  klasie  III  wprowadzamy  wyrażenia

11

wymierne.  Zagadnienia  występujące  w  tym  zakresie  umożliwiają  wy-
korzystanie,  w  oparciu  o  analogię,  umiejętności,  jakie  uczniowie  na-
byli  przy  wykonywaniu  działań  na  liczbach  wymiernych.  Możemy  tu
pokazać,  jak  uogólniamy  zagadnienia  wykorzystywane  przy  operacjach
liczbowych.

Ważną umiejętnością jest określanie dziedziny wyrażenia wymierne-

go.  Określanie  dziedziny  w  sposób  sformalizowany  może  sprawiać
uczniom trudności. Dlatego też proponujemy stosowanie, dość popular-
nego niegdyś, podawania zastrzeżeń, np. określenie dziedziny wyrażenia

x

y

x y

+

−

3

  w  formie  x 

≠

  y  jest  dla  uczniów  o  wiele  prostsze  niż  określenie

w postaci 

( )

{

}

D

x y x R y R x

y

=

, ;

∈ ∧ ∈ ∧ ≠

.

Wykonując  działania  na  wyrażeniach  wymiernych,  odwołujemy  się

do analogii z wykonywaniem działań na liczbach wymiernych. Staramy
się  jednak  wyrabiać  w  uczniach  nawyk  określania  dziedziny  wyrażeń,
na  których  operacje  te  są  wykonywane.  Istotne  jest  również  zwrócenie
uwagi  na  fakt,  że  nie  określając  dziedziny,  w  której  rozważamy  wyra-
żenia, nie możemy mówić o równości wyrażeń, np. nie określając dzie-

dziny, w której rozpatrujemy wyrażenia 

(

)

2

2

4

2

2

⋅

+

−

x

x

 i 

(

)

2

2

2

⋅

+

−

x

x

, nie może-

my uznać ich za równe. Wyrażenie 

(

)

2

2

4

2

2

⋅

+

−

x

x

 jest określone w zbiorze

R – {–2, 2}, a wyrażenie 

(

)

2

2

2

⋅

+

−

x

x

 w zbiorze R – {–2}. Jeżeli zbiorem,

w którym rozważamy te wyrażenia, jest zbiór R – {–2, 2}, to wówczas

możemy napisać, że 

(

)

2

2

4

2

2

⋅

+

−

x

x

 = 

(

)

2

2

2

⋅

+

−

x

x

.

W rozdziale tym pokazujemy również przykład funkcji danej wzorem

f

(x) = 

1

x

 określonej dla x 

≠

 0. Przypominamy przy okazji omawiania tej

funkcji sposoby odczytywania własności funkcji na podstawie jej wykresu.

12

Równania, nierównoœci, uk³ady równañ

W  części  tej  na  wstępie  przypominamy  najważniejsze  zagadnienia

związane z równaniami i nierównościami. Są one niezbędne w toku dal-
szych  rozważań,  gdy  zaczynamy  omawiać  równania  i  układy  równań
z dwiema niewiadomymi.

Mówiąc o równaniach liniowych z dwiema niewiadomymi, podajemy

ich interpretację geometryczną w układzie współrzędnych. Występuje tu
połączenie zagadnień związanych z funkcją liniową i równaniami. Umoż-
liwia to swobodne operowanie równaniami prostych. Istotne jest w tym
miejscu zwrócenie uwagi na fakt, że każdej funkcji liniowej odpowiada
określone równanie prostej. Fakt odwrotny nie jest prawdziwy, np. prostej
o równaniu x = 3, która jest równoległa do osi rzędnych, nie odpowiada
żadna funkcja liniowa.

Interpretacji  geometrycznej  układu  równań  liniowych  nie  łączymy

z metodami rozwiązywania układów równań, chociaż pokazujemy, że na
podstawie wykresów równań tworzących układ możemy określić liczbę
rozwiązań układu oraz odczytać jego rozwiązanie. Sposób taki w niektó-
rych sytuacjach daje zadowalające efekty, związany jest jednak z koniecz-
nością  bardzo  dokładnego  wykonywania  rysunków.  W  przypadku  gdy
rozwiązaniem  układu  nie  są  liczby  całkowite,  mogą  wystąpić  trudności
z  określeniem  jednostki  umożliwiającej  dokładne  odczytanie  rozwiąza-
nia.  Na  podstawie  interpretacji  geometrycznej  układu  równań,  możemy
mówić o przybliżonym rozwiązaniu układu.

Bardzo ważne jest, w świetle obowiązujących standardów egzamina-

cyjnych, umiejętne stosowanie równań, nierówności i układów równań do
rozwiązywania problemów z różnych dziedzin. Wykorzystując równania,
nierówności i układy równań do rozwiązywania zadań tekstowych, należy
zwrócić uwagę na konieczność sprawdzenia, czy otrzymane liczby speł-
niają warunki zadania. Rozpatrzmy zadanie:

Tomek  ma  w  swoim  zbiorze  znaczki  polskie  i  zagraniczne.  Razem
123 znaczki. Paweł ma tyle samo co Tomek znaczków zagranicznych
i  trzy  razy  więcej  znaczków  polskich.  W  sumie  ma  140  znaczków.
Ile polskich znaczków ma Tomek?
Oznaczając przez x liczbę znaczków polskich Tomka, a przez y liczbę

jego znaczków zagranicznych, otrzymujemy układ równań:

x y

x y

+ =

+ =







123

3

140

, którego rozwiązaniem jest para liczb x = 8,5 i y = 114,5.

13

Zwi¹zki miarowe w trójk¹cie

Własności trójkątów związane z wysokością, środkową i bokami trój-

kąta zostały omówione w klasach I i II. W klasie III zajmujemy się pew-
nymi  zależnościami,  jakie  można  określić  pomiędzy  bokami  trójkąta
i odpowiednimi dla tych boków kątami.

Posługujemy się pojęciami sin 

a, cos a, tg a oraz ctg a, gdzie a jest

miarą kąta ostrego. Stosujemy nazwy funkcji trygonometrycznych, cho-
ciaż zdajemy sobie sprawę z tego, że w przypadku określenia zależności
pomiędzy bokami i odpowiednimi kątami w trójkącie prostokątnym trud-
no  jest  mówić  o  funkcjach,  ponieważ  nie  rozpatrujemy  wielu  istotnych
zagadnień związanych z funkcjami. Nie zajmujemy się dziedziną funkcji,
nie określamy przedziałów monotoniczności, nie określamy zbioru warto-
ści  funkcji.  Zagadnienia  w  proponowanym  przez  nas  ujęciu  należy  po-
traktować jako wprowadzenie i rozszerzenie zakresu pojęciowego języka
matematyki.

Istotną sprawą jest jednak przybliżenie tych zagadnień tak, aby ucznio-

wie zrozumieli je. Może pomóc w uzyskaniu tego efektu rozpatrzenie na-
stępującej sytuacji.
Rysujemy trójkąt prostokątny.

Obliczamy stosunki długości boków: 

a

c

,

b

c

, 

a

b

, 

b

a

.  Wówczas 

a

c

  = 

4

5

, 

b

c

  = 

3

5

,

a

b

  = 

4

3

 i 

b

a

  = 

3

4

.  Po  obliczeniu  okreś-

lonych stosunków rysujemy trójkąt po-
dobny do trójkąta ABC w skali 2.
Ponownie  obliczamy  stosunki  długości  odpowiednich  boków.  Rów-

nież w tym przypadku otrzymujemy 

a

c

 = 

4

5

, 

b

c

 = 

3

5

, 

a

b

 = 

4

3

 i 

b

a

 = 

3

4

.

Powtarzamy  procedurę,  prosząc  uczniów,  aby  każdy  sam  określił  ska-
lę  podobieństwa,  w  jakiej  narysuje  trójkąt  podobny  do  trójkąta  ABC.

Jednak  otrzymane  liczby  nie  spełniają  warunków  zadania,  gdyż  nie  są
to liczby naturalne.

A

C

B

a 

= 4

b 

= 3

c = 5

14

Opisaną powyżej procedurę powtarzamy dla innego trójkąta prostokąt-

nego. Wskazane jest, aby długość przynajmniej jednego z boków wyraża-
ła  się  liczbą  niewymierną.  Po  obliczeniu  odpowiednich  ilorazów  okaże
się, że dla danego trójkąta ilorazy te znów są stałe. Możemy zatem sfor-
mułować następujący wniosek: Wartości obliczonych ilorazów nie zależą
od długości boków trójkąta, natomiast zależą od miary kąta

.

Przy obliczaniu wartości funkcji trygonometrycznych zalecamy stoso-

wanie kalkulatorów, gdyż wykorzystanie tablic funkcji trygonometrycz-
nych,  ze  względu  na  brak  znajomości  podstawowych  własności  tych
funkcji, jest utrudnione. Stosując w obliczeniach kalkulatory, wdrażamy
jednocześnie  uczniów  do  stosowania  rachunków  na  przybliżeniach,  co
odpowiada wymaganiom zawartym w standardach egzaminacyjnych.

W części tej omawiamy również podstawowe tożsamości trygonome-

tryczne, nie rozwijając zbytnio tych zagadnień.

Pokazujemy też zastosowania funkcji trygonometrycznych w pewnych

sytuacjach praktycznych. Przykłady stosowania funkcji trygonometrycz-
nych  do  wyznaczania  różnych  elementów  figur  znajdują  się  również
w ostatniej części podręcznika. Dlatego  w rozkładzie materiału uwzględ-
niliśmy  dla  części  poświęconej  funkcjom  trygonometrycznym  mniejszą
liczbę godzin na realizację niż przewidzieliśmy w programie nauczania,
wykorzystując wygospodarowane godziny w części, w której omawiamy
figury przestrzenne.

Figury przestrzenne

Wyobraźnia  przestrzenna  jest  bardzo  ważna  w  życiu  człowieka,  uła-

twia bowiem funkcjonowanie w otaczającej nas rzeczywistości. Dlatego
ogromnie  istotne  jest  bardzo  częste  odwoływanie  się  do  doświadczeń
uczniów  i  ich  obserwacji.  Równie  istotna  jest  umiejętność  dostrzegania
figur matematycznych w otaczającej nas przestrzeni.

Po obliczeniu ilorazów: 

a

c

, 

b

c

, 

a

b

, 

b

a

 okazuje się, że niezależnie od długo-

ści  boków  otrzymujemy  te  same  liczby.  Uczniowie  powinni  wyciągnąć
wniosek, że niezależnie od długości boków trójkąta prostokątnego przy
tych  samych  miarach  odpowiednich  kątów  określone  stosunki  długości
jego boków są niezmienne. Nie jesteśmy jednak w stanie odpowiedzieć na
pytanie: Czy stosunki zmienią się, jeżeli zmieni się miara kąta?

15

Omawianie zagadnień związanych z figurami przestrzennymi rozpo-

czynamy od rozpatrzenia wzajemnego położenia w przestrzeni prostych,
płaszczyzn  oraz  prostej  i  płaszczyzny.  Trudności,  na  jakie  napotykają
uczniowie przy realizacji zagadnień z geometrii przestrzennej, najczęściej
związane są z brakiem umiejętności przedstawiania figur przestrzennych
na płaszczyźnie. Dlatego też zdecydowaliśmy się na podanie podstawo-
wych  wiadomości  dotyczących  rzutu  równoległego.  Przy  realizacji  za-
gadnień  związanych  z  rzutem  równoległym  wskazane  byłoby  wsparcie
procesu  dydaktycznego  odpowiednimi  demonstracjami.  Możemy  bazo-
wać  na  cieniach  figur  i  pokazywać,  jak  zmieniają  się  rzuty  równoległe
figur w zależności od ustawienia względem rzutni, jak i kierunku rzutu.
Umożliwia  to  lepsze  zrozumienie  zagadnień  i  swobodniejsze  przedsta-
wianie figur przestrzennych na płaszczyźnie.

Omawiając wielościany, szczególną uwagę zwracamy na graniastosłupy

(w zasadzie zajmujemy się graniastosłupami prostymi) i ostrosłupy. W celu
rozwijania wyobraźni przestrzennej należy wykonywać z uczniami ćwicze-
nia polegające na projektowaniu różnych siatek graniastosłupów i ostro-
słupów, a następnie na wykonywaniu modeli tych brył. Przy rozwiązywa-
niu zadań na obliczanie pola powierzchni oraz objętości graniastosłupów
i ostrosłupów stosujemy funkcje trygonometryczne. W ten sposób prak-
tycznie utrwalamy umiejętności uczniów nabyte wcześniej.

Równie ważne są zagadnienia związane z bryłami obrotowymi. Oma-

wiamy  zagadnienia  związane  z  polem  powierzchni  i  objętością  walca,
stożka i kuli. W klasach o większym stopniu zainteresowania matematyką
możemy pozwolić sobie na zdefiniowanie pojęcia kuli i sfery:

Kulą o środku w punkcie S i promieniu R nazywamy zbiór

wszystkich punktów X przestrzeni, dla których 

XS

 

≤

  R.

Możemy  w  tym  przypadku  pokusić  się  również  o  zapis  symboliczny

K

(S, R) = {X : 

XS

 

≤

  R}.

W analogiczny sposób możemy określić sferę:

Sferą o środku w punkcie S i promieniu R nazywamy zbiór

wszystkich punktów X przestrzeni, dla których 

XS

 = R.

Możemy podać też zapis symboliczny S(S, R) = {X : 

XS

 

= 

R

}.

W  przypadku  brył  obrotowych  dobrymi  ćwiczeniami  rozwijającymi

wyobraźnię przestrzenną jest określanie lub szkicowanie figur na podsta-
wie ich przekroju osiowego.

16

17

s. 11.

Otrzymane róźnice są kolejnymi liczbami nieparzystymi.

s. 16.

Liczbę  taką  możemy  wskazać  w  zbiorze  liczb  całkowitych  ujemnych.
Jest nią –1.

s. 20.

Obliczenia takie możemy wykonać, korzystając z tarczy zegara. Na przy-
kład, jeżeli od godziny 4.00 upłynie 11 godzin, to będzie godzina 15.00.
Na tarczy zegara widnieje wówczas liczba 3; 9 + 5 = 2; 7 – 10 = 9.

s. 24.

Dla liczb będących wielokrotnościami liczby 5 reszta z dzielenia przez 5
jest równa 0. W pozostałych przypadkach reszta jest równa 1.

a) 8;

b) 80;

c) 800;

d) n – 

n

5

.

s. 29.

AA

AB

1

1

2

= ⋅

;

( )

AA

AB

2

2

1

2

=

⋅

;

( )

AA

AB

n

n

=

⋅

1

2

.

s. 34.

Konstrukcję odcinka wykonujemy w oparciu o twierdzenie Talesa.

ODPOWIEDZI DO ZADAŃ

Odpowiedzi do zadañ wyró¿nionych w podrêczniku
ramk¹ z ,,!”

Przygotowaliśmy odpowiedzi do zadań wyróżnionych w podręczniku ram-
ką z wykrzyknikiem. Zadania te są przeznaczone dla uczniów szczególnie
zainteresowanych matematyką i wymagają nietypowego rozwiązania.

18

s. 36.

Oś obrotu nóg deski do prasowania możemy traktować jako wierzchołek
kąta.  Stosunek  długości  odpowiednich  części  nóg  deski  do  prasowania
jest stały. Z twierdzenia Talesa wynika zatem, że odcinki łączące odpo-
wiednie końce nóg deski są równoległe.

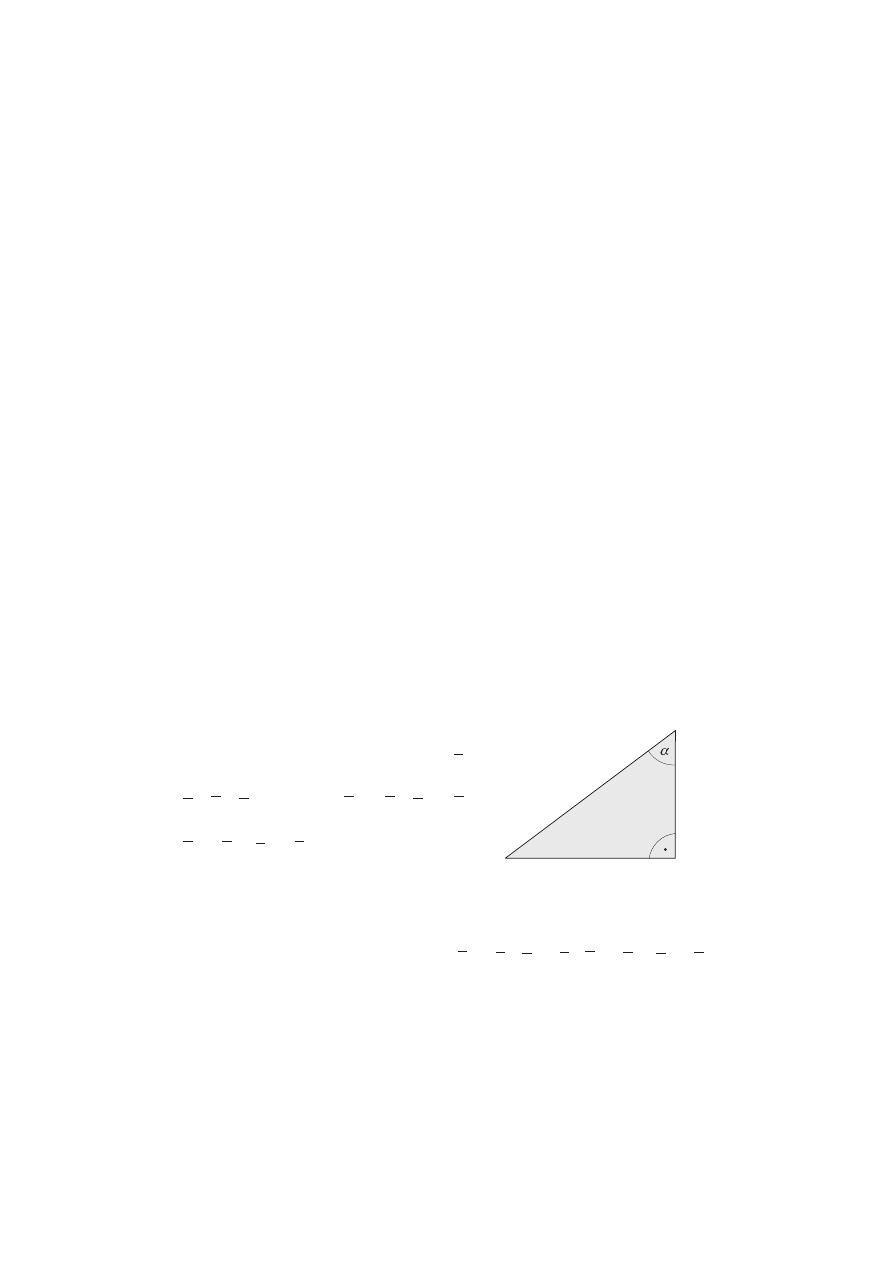
s. 41.

Przez wierzchołki trójkąta ABC prowadzimy półproste SA

→

, SB

→

 i SC

→

.

Punkty przecięcia prostej zawierającej odcinek A''C'' z półprostymi SA

→

i SC

→

 wyznaczają odpowiednio wierzchołki A' i C'  trójkąta A'B'C'. Sy-

metralna odcinka C'C'' jest poszukiwaną prostą.

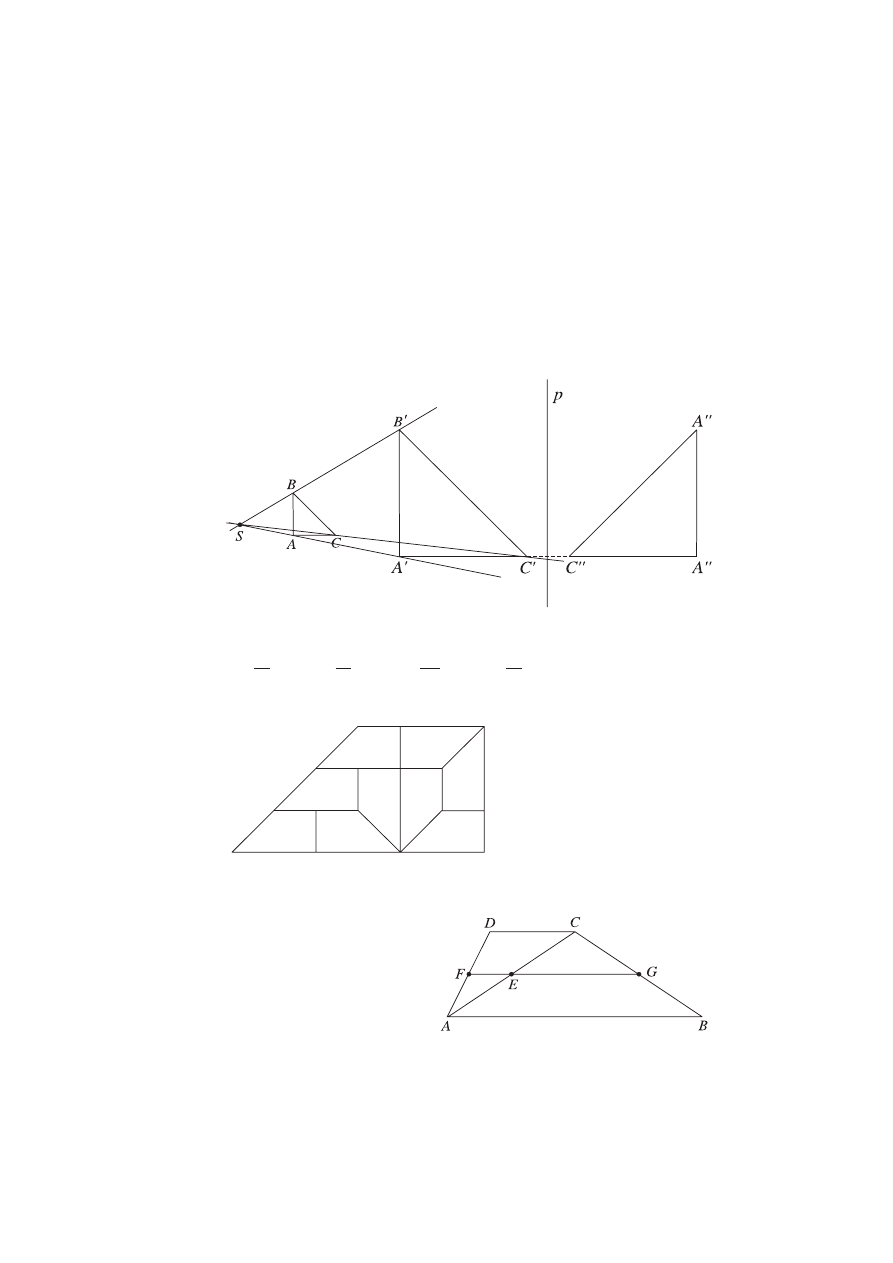
s. 46.

Pole otrzymanego sześciokąta jest równe:

a)

1

2

2

2









;

b)

1

2

3

2









;

c)

1

2

10

2









;

d)

1

2

2

n









pola sześciokąta ABCDEF.

s. 51.

s. 55.

Odległość  pomiędzy  tymi  miejscowościami  jest  równa  150  km.  Skala
otrzymanej przez Marka mapy jest równa 1 : 2 500 000.

s. 57.

W trapezie ABCD prowadzi-
my  przekątną  AC.  Przez
punkt  E  będący  środkiem
przekątnej  AC  prowadzimy
prostą równoległą do podstaw
trapezu,  która  ma  z  bokami

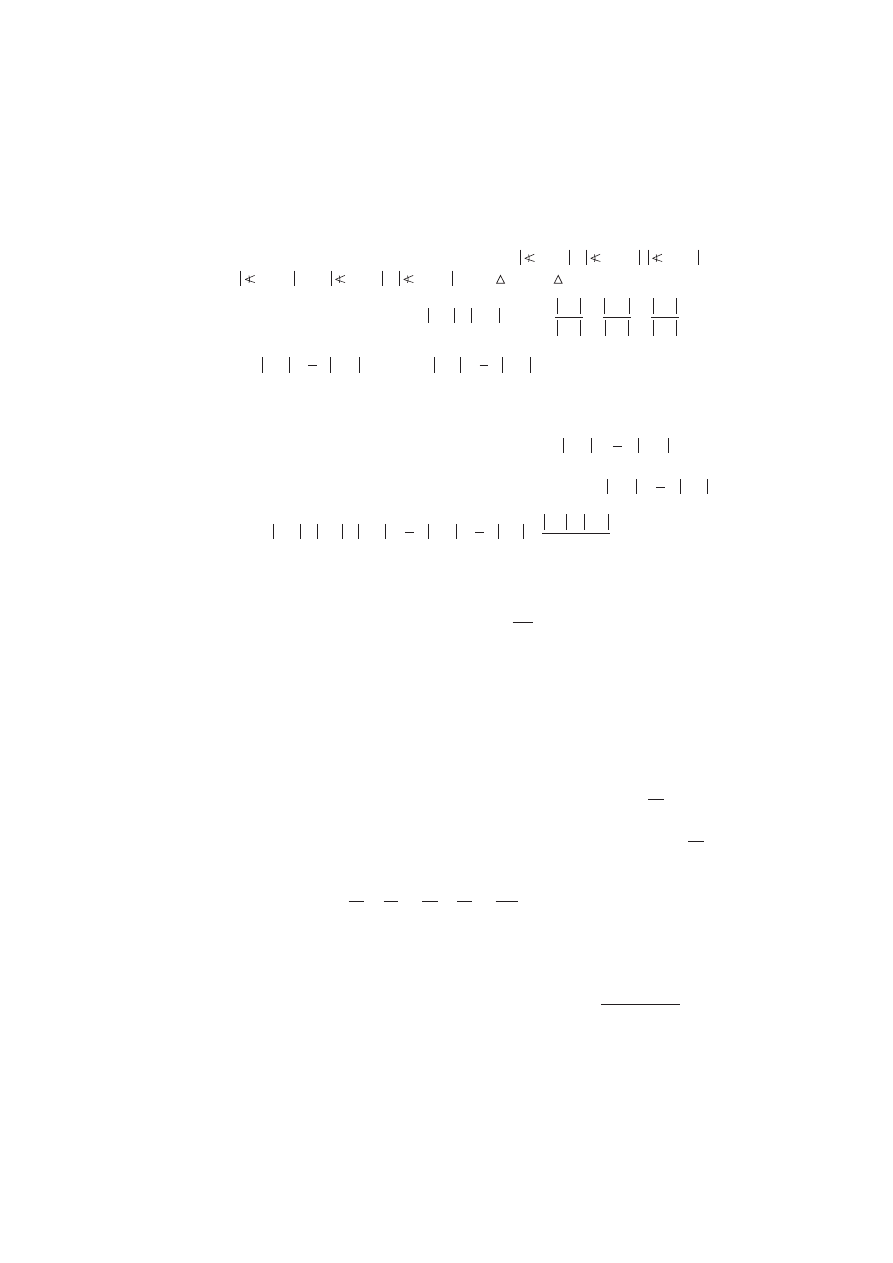
19

trapezu AD i BC punkty wspólne F i G. Należy wykazać, że punkty F i G
są środkami boków trapezu.
Rozważamy trójkąty AEF i ACD. Ponieważ   FAE  =   DAC ,   AFE  =
=   ADC  oraz   AEF  =   ACD , więc  AEF ~  ACD. Z podobieństwa

trójkątów oraz z założenia, że  AE  =  EC , mamy 

AD
AF

DC

FE

AC
AE

=

=

 = 2,

czyli  AF  = 

1

2

 ·  AD . Ponieważ  AF  = 

1

2

 ·  AD , więc punkt F jest środkiem

odcinka AD. Analogicznie, rozpatrując trójkąty ABC i EGC, wykazuje-
my, że punkt G jest środkiem odcinka BC.

Z podobieństwa trójkątów AEF i ACD wynika, że   FE  = 

1

2

 ·  DC , nato-

miast z podobieństwa trójkątów ABC i EGC, otrzymujemy  EG  = 

1

2

 ·  AB .

Zatem  FG  =  FE  +  EG  = 

1

2

 ·  DC  + 

1

2

 ·  AB  = 

AB

DC

+

2

. Wykazaliśmy

więc, że odcinek łączący środki ramion trapezu jest równoległy do pod-
staw i jego długość jest średnią arytmetyczną długości podstaw trapezu.

s. 62.

Średnia prędkość przejazdu wyniosła 22,5

km

h

.

Uwaga: patrz przykład na stronie 88 w podręczniku.

s. 68.

W rzucie jedną kostką możemy otrzymać 1, 2, 3, 4, 5 lub 6 oczek. Rzuca-
jąc druga kostką, do każdej z wyrzuconych liczby oczek możemy ,,dorzu-
cić” 1, 2, 3, 4, 5 lub 6 oczek. Tak więc w rzucie dwiema kostkami wszyst-
kich możliwych zdarzeń elementarnych jest 6 · 6 = 6

2

 = 36. Ogólnie, przy

rzucie n kostkami do gry wszystkich zdarzeń elementarnych jest 6

n

.

s. 71.

Prawdopodobieństwo,  że  odrzuconą  kartą  jest  as,  jest  równe 

4

52

,  nato-

miast prawdopodobieństwo, że odrzuconą kartą nie jest as, jest równe 

48

52

.

Tak więc prawdopodobieństwo wylosowania asa przy jednej odrzuconej

karcie jest równe 

4

52

 · 

3

51

 + 

48

52

 · 

4

51

 = 

51

663

.

s. 74.

Ewelina musi wyjąć 6 rękawiczek.

s. 79.

Z założenia a = b + c wynika, że a – b – c = b + c – b – c = 0, zatem nie

można wykonać dzielenia przez a – b – c, a tym samym 

(

)

a a b c

a b c

⋅

− −

− −

 ≠

 b.

20

s. 82.

Dla x 

≠

 –

1 

i x 

≠

 

1, 

mamy 

2

1
1

2

1

1

1

1

1

1

1

1

1

2

2

2

2

x

x

x

x

x

x

x

x

+
−

−

−

+

−

−

=

+

=

+

+

.

s. 86.

Wyrażenie rozpatrujemy dla x 

≠

 

0

. Wówczas:

1

1

x x

⋅

 = 1,  

1

1

1

x

x x

⋅

⋅

 = 

1

x

,  

1

1

1

1

x

x

x x

⋅

⋅

⋅

 = 1.

W zależności od liczby ,,pięter” ułamka otrzymujemy 1 lub 

1

x

.

s. 89.

Iloczyn ogniskowych obiektywu i okularu f

1

 · f

2

 musi spełniać warunek:

a) f

1

 · f

2 

 = 15;

b) f

1

 · f

2

 = 10;

c) f

1

 · f

2

 = 7,5.

W przypadku powiększenia 100 000 razy powinien być spełniony waru-
nek  f

1

 · f

2 

 = 0,015.

s. 93.

a) R = 

R R R

R R

R R

R R

1

2

3

1

2

2

3

1

3

⋅

⋅

⋅

+

⋅

+

⋅

;

b) R = 

R R R R

R R R

R R R

R R R

R R R

1

2

3

4

1

2

3

1

2

4

1

3

4

2

3

4

⋅

⋅

⋅

⋅

⋅

+

⋅

⋅

+

⋅

⋅

+

⋅

⋅

;

c) R = 

R R R

R R

R R

R R

R R

R R R

R R

R R

1

2

3

9

10

1

2

8

9

1

2

7

9

10

2

3

9

10

⋅

⋅

⋅ ⋅

⋅

⋅

⋅ ⋅

⋅

+

⋅

⋅ ⋅

⋅

⋅

+ +

⋅

⋅ ⋅

⋅

K

K

K

K

K

;

d) R = 

R R

R

R

R R

R

R

R R

R

R

n

n

n

n

n

n

1

2

-1

1

2

-2

-1

2

3

-1

⋅

⋅ ⋅

⋅

⋅

⋅ ⋅

⋅

+ +

⋅

⋅ ⋅

⋅

K

K

K

K

.

s. 98. x

3

 + x

2

 

≤

 –3x – 3

x

3

 + x

2 

+ 3x + 3 

≤

  0

x

2

(x + 1) + 3(x + 1) 

≤

 0

(x + 1) (x

2

 + 3) 

≤

 0 

⇔

 x + 1 

≤ 

0,

bo

x

2

 + 3 > 0

dla

x

 

∈

 R

x 

≤ 

–1.

s. 103.

Prosta o równaniu x = 3.

21

s. 112.

Układ równań  2

3

4

2

x y

x my

+ =

−

=







 ma jedno rozwiązanie, gdy m 

≠

 –2. Musi

być spełniony warunek –2m – 4 

≠ 

0.

s. 115.

Warunkiem  koniecznym,  aby  układ 

6

3

2

3

x my

x y

−

=

+ =







  był  układem  nie-

oznaczonym, jest, by był spełniony warunek 6 + 2m = 0, czyli m = –3.
Nie jest to jednak warunek wystarczający. Podstawiając m = –3, otrzy-

mujemy układ równań 

6

3

3

2

3

x

y

x y

+

=

+ =







, który jest równoważny układowi

2

1

2

3

x y

x y

+ =

+ =







,  a  ten  układ  jest  układem  równań  sprzecznych.  Oznacza

to, że nie istnieje taka liczba m, aby układ równań 

6

3

2

3

x my

x y

−

=

+ =







 miał

nieskończenie wiele rozwiązań.

s. 119.

Współczynniki kierunkowe prostych muszą być równe. Prostą o równa-
niu y + kx = 5 możemy zapisać y = –kx + 5, czyli k = –3.

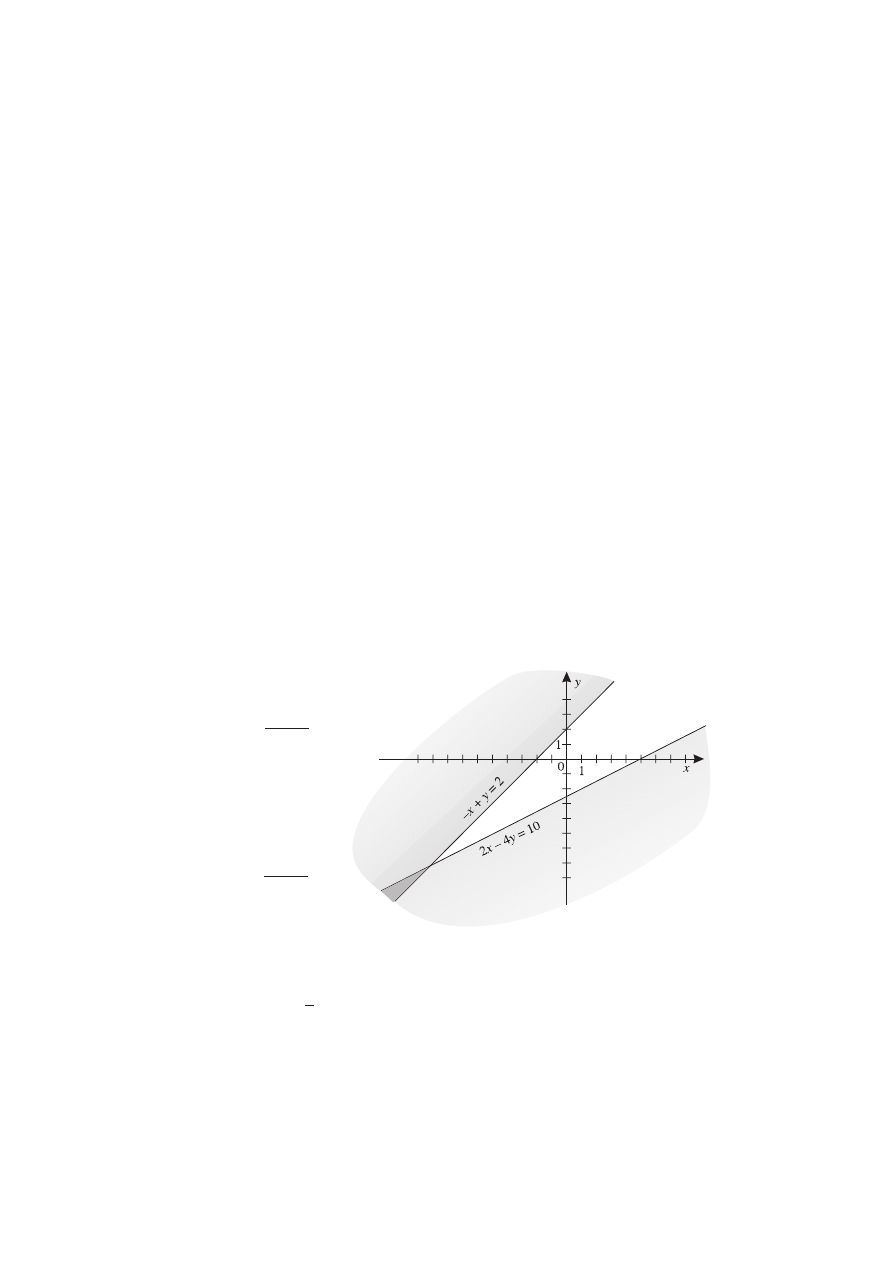
s. 123.

W układzie współrzędnych rysujemy proste odpowiadające równaniom

2x – 4y = 10 i –x + y = 2, czyli

4y = 2x – 10 i y = x + 2

y = 

2

10

4

x

−

.

Zaznaczamy
półpłaszczyz-
ny odpowia-
dające nie-
równościom

y

 < 

2

10

4

x

−

i y > x + 2.

Współrzędne  punktów,  należących  do  wspólnej  części  zaznaczonych
półpłaszczyzn, spełniają dany układ nierówności.

s. 129.

cos 30° 

≠

 

1

4

.

22

s. 136.

Z określenia funkcji sin 

α

, mamy sin 

a = 

a

c

 = cos 

b.

Ponieważ 

b = 90° – a, więc sin a = cos (90° – a).

W naszym przypadku sin 

a = cos (90° – a) = 

5

3

.

s. 143.

Z  zależności  tg 

a · ctg a = 1 wynika, że ctg a = 

4

3

. Aby  wyznaczyć

wartości sin 

a i cos a, budujemy układ równań:

sin

cos

3

4

sin

cos

1

2

2

a

a

a

a

=

+

=










,  skąd  

sin

cos

cos

cos

1

3

4

9

16

2

2

a

a

a

a

= ⋅

+

=








Rozpatrując drugie równanie układu, otrzymujemy

25

16

 · cos

2

a = 1

cos

2

a = 

16

25

cos 

a = 

4

5

(uwzględniamy wartość dodatnią ze względu na to, że 

a jest

kątem ostrym). Wykorzystując pierwsze równanie układu, otrzymujemy

sin 

a = 

3

4

 · 

4

5

sin 

a = 

3

5

.

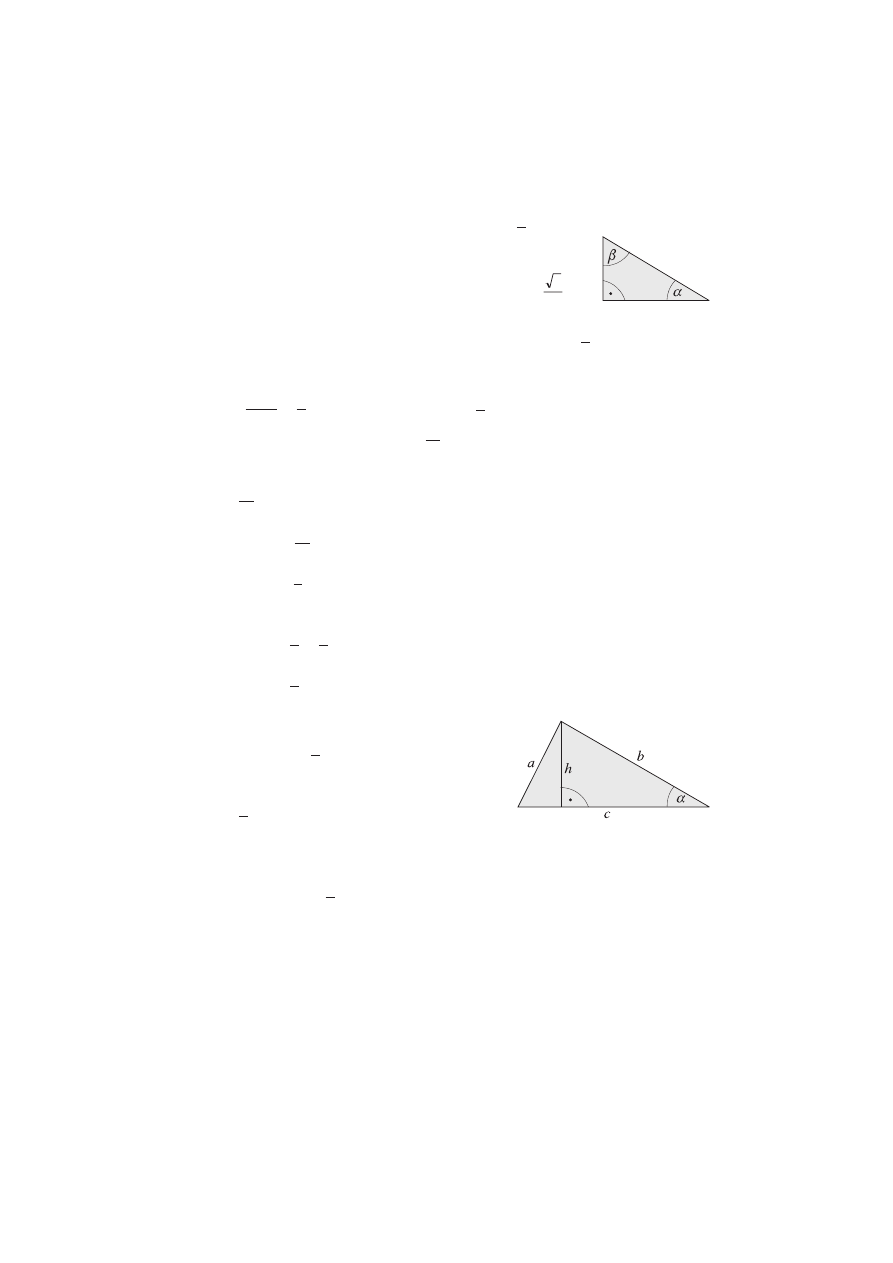
s. 145.

Pole trójkąta obliczamy, korzystając ze

wzoru P = 

1

2

 · c · h. Z określenia funk-

cji trygonometrycznych wynika, że

h

b

 = sin 

a

h

 = b · sin 

a.

Podstawiając do wzoru na pole trójkąta wyznaczoną wartość h, otrzy-

mujemy P = 

1

2

 · b · c · sin 

a.

s. 149.

Nie, gdyż punkty wspólne patyczków wyznaczają różne płaszczyzny.

s. 153.

Gdy człowiek zbliża się do latarni, długość jego cienia zmniejsza się,
natomiast gdy się oddala od latarni, długość cienia wydłuża się.

.

23

s. 158.

P P

1 2

2

2

20

4

416

4 26

=

+

=

=

.

s. 164.

Z wierzchołka graniastosłupa wychodzi n – 2 przekątnych, gdzie n jest
liczbą boków wielokąta znajdującego się w podstawie graniastosłupa.

s. 168.

Przekątne  ścian  bocznych  wraz  z  przekątna  podstawy  tworzą  trójkąt
równoboczny. 

a = 60°.

s. 173.

Sześcian

s. 178.

Ilość wylanej wody jest równa objętości zanurzonego ciała.

s. 182.

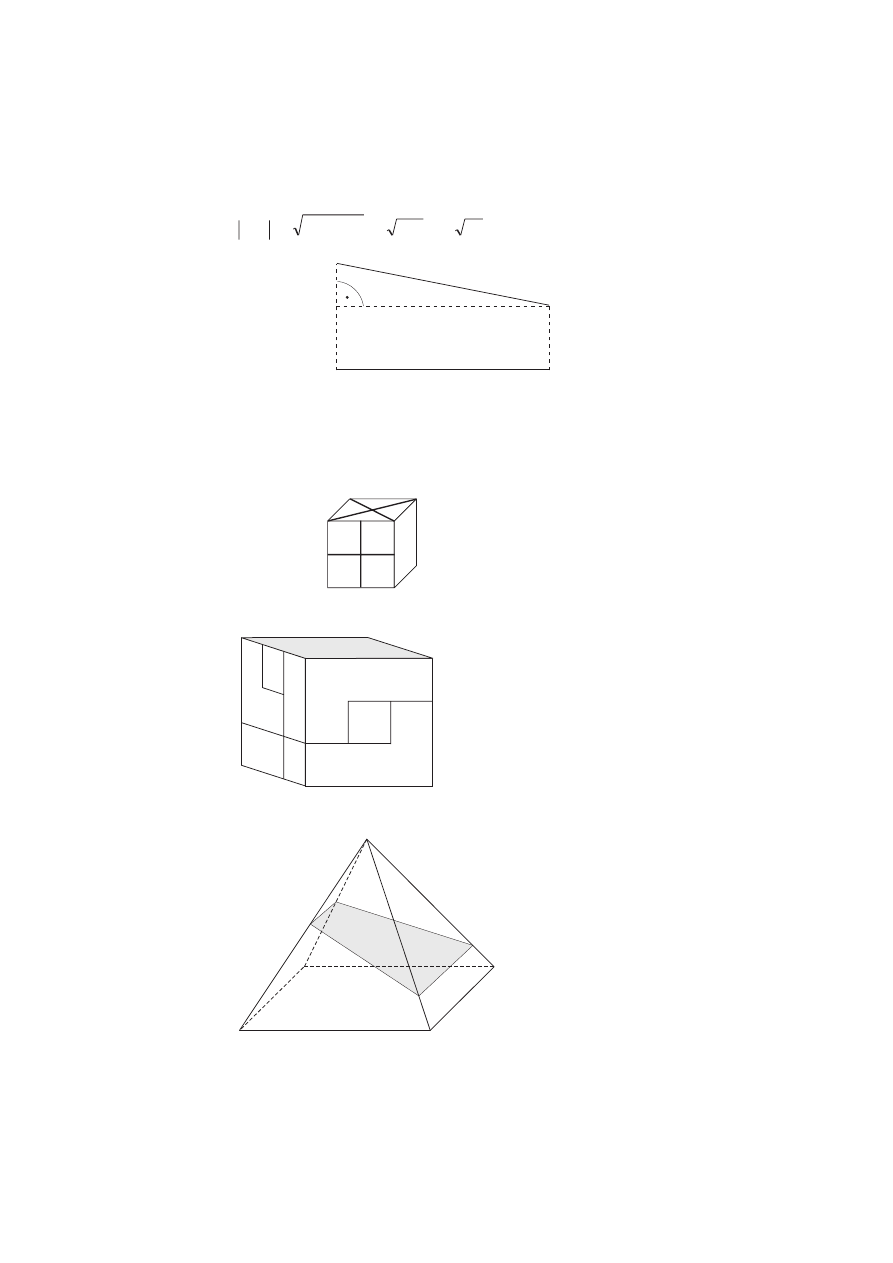
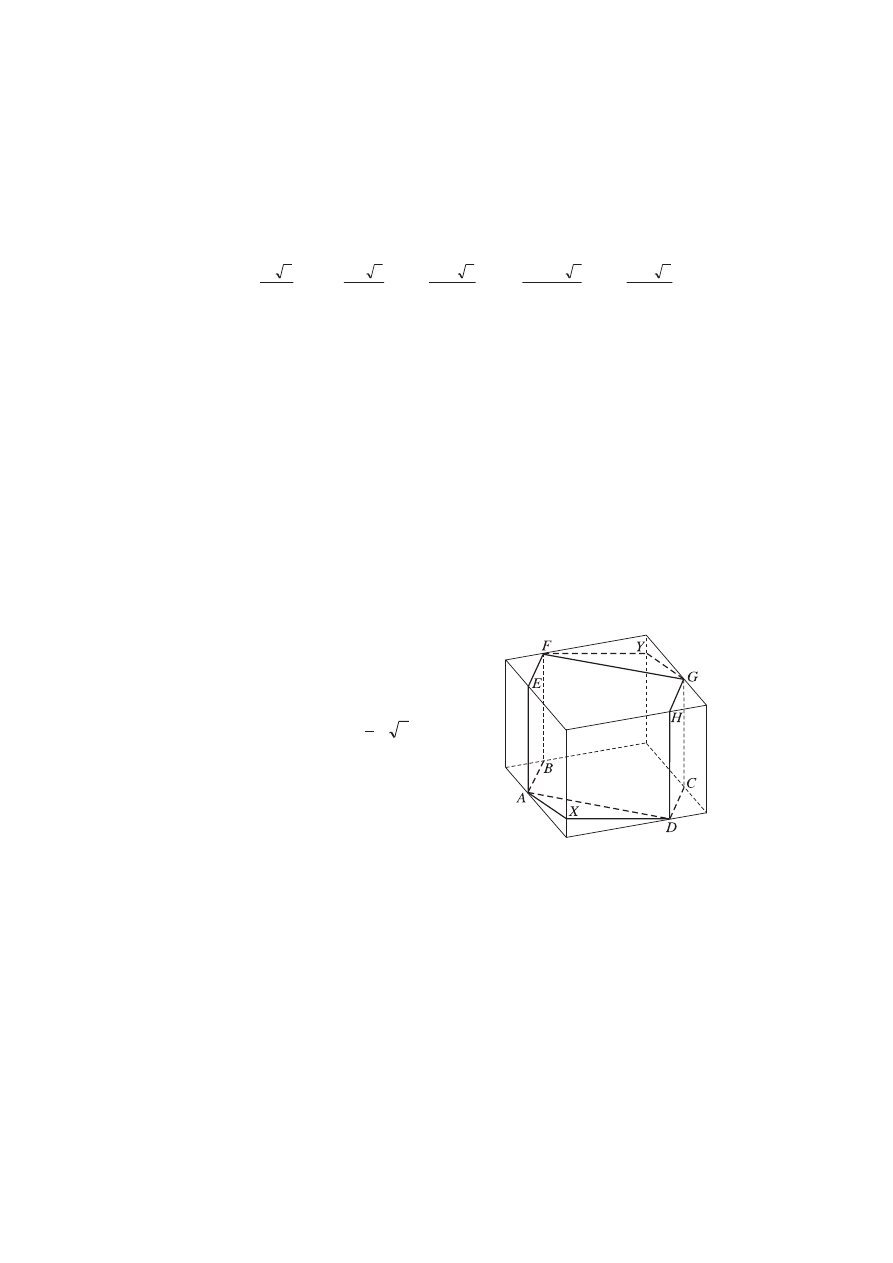
s. 188.

Zaznaczony przekrój jest trapezem.

4

6

20

P

1

6

20

P

2

P'

1

P'

2

24

s. 192.

Liczby zapisane na ścianach klocków są kolejnymi potęgami liczby zapi-
sanej na podstawie. Na podstawie trzeciego klocka zapisana jest liczba 2.

s. 195.

a)

a

3

2

12

;  b)

2

2

3

3

a

;  c) 

27

2

12

3

a

;  d) 

1000

2

12

3

a

;  e) 

n a

3 3

2

12

.

Objętość  czworościanu,  którego  krawędź  ma  długość  2a,  jest  8  razy
większa od objętości czworościanu, którego krawędź ma długość a.
Objętość  czworościanu,  którego  krawędź  ma  długość  3a,  jest  27  razy
większa od objętości czworościanu, którego krawędź ma długość a.
Objętość czworościanu, którego krawędź ma długość n · a, jest n

3

 razy

większa od objętości czworościanu, którego krawędź ma długość a.

s. 200.

Kolejne  bryły  mają  objętości  4a

3

,  7a

3

,  10a

3

,  13a

3

,  ...  Ich  pola  po-

wierzchni są odpowiednio równe 18a

2

, 30a

2

, 42a

2

, 54a

2

, ...

s. 204.

Przekrój bryły obrotowej mającej kształt doniczki i zawierający oś obro-
tu jest trapezem. Przekrój tej bryły płaszczyzną prostopadłą do osi obro-
tu jest kołem.

s. 210.

a) 8 razy; b) 27 razy; c) 64 razy; d) n

3

 razy;

e) a

3

 razy.

s. 215.

Nie, gdyż tworząca musiałaby mieć długość równą promieniowi.

s. 219.

Prostą prostopadłą do płaszczyzny wyznaczonej przez te punkty.

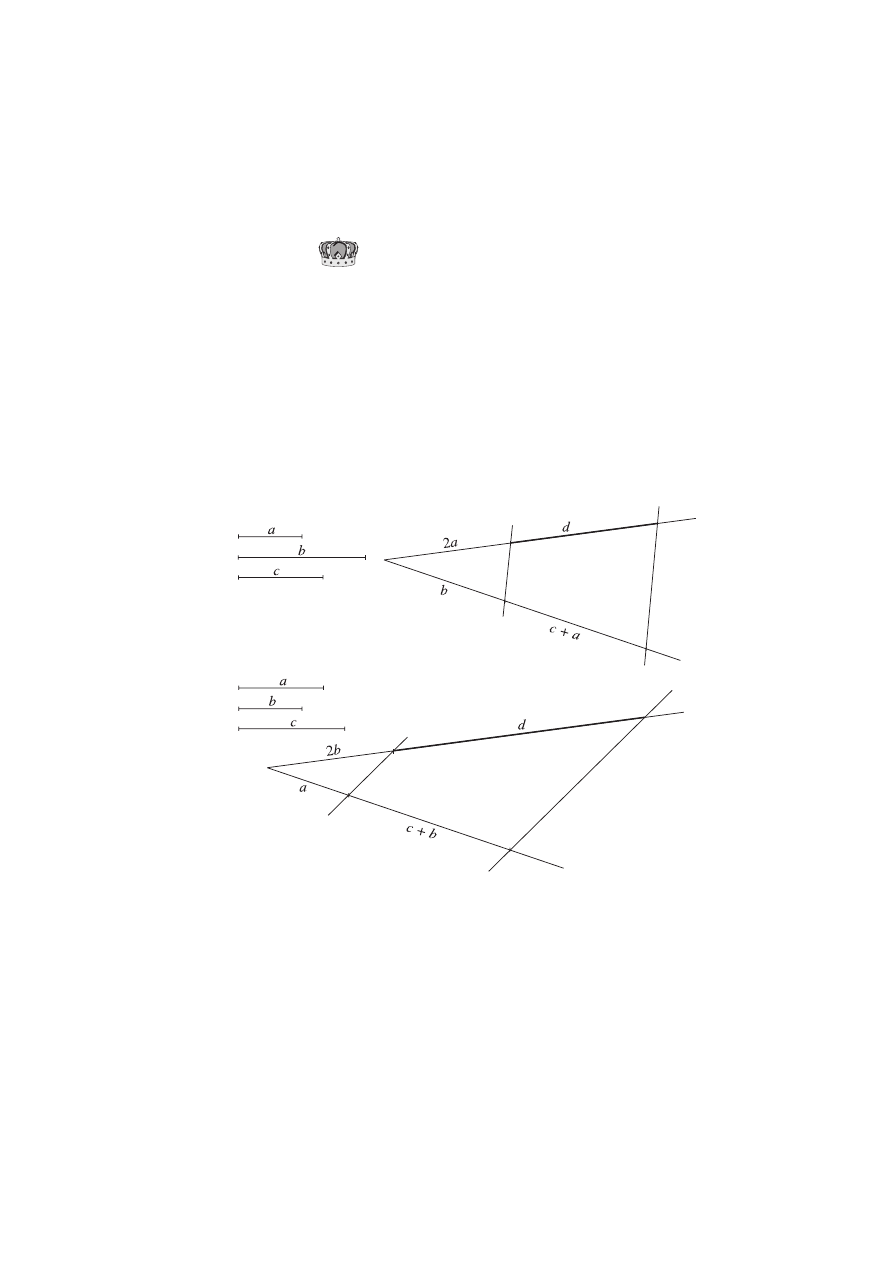
s. 223.

Oznaczmy  przez a  długość  krawędzi
danego  sześcianu.  Największy  kwa-
dratowy  otwór,  jaki  można  wyciąć
w danym sześcianie, ma bok, którego

długość jest równa 

4

3

a

2  

≈

 1,06 · a.

Tak więc przez dany sześcian można
przesunąć  sześcian,  którego  długość
krawędzi jest równa 1,06 · a, a więc
nieco większy od danego.

25

Odpowiedzi do zadañ w æwiczeniach sprawdzaj¹cych
oznaczonych 

s. 6.

Wypisujemy zbiór liczb dwucyfrowych, w których suma cyfr jest równa
13: {49, 58, 67, 76, 85, 94}, następnie skreślamy liczby parzyste. Pozo-
staje zbiór {49, 67, 85}. Z otrzymanego zbioru skreślamy liczby podziel-
ne przez 7. Pozostają liczby 67 i 85, które spełniają warunki zadania.

s. 8.

Wypisujemy zbiór liczb dwucyfrowych, w których suma cyfr jest równa
11: {29, 38, 47, 56, 65, 74, 83, 92}, następnie skreślamy liczby nieparzy-
ste.  Pozostaje  zbiór  {38,  56,  74,  92}.  Z  otrzymanego  zbioru  skreślamy
liczby podzielne przez 4. Pozostają liczby 38 i 74, które spełniają warunki
zadania.

s. 10.

s. 12.

s. 14.

Punkt A' = (x', y') jest obrazem punktu A = (x, y) w jednokładności o środ-
ku w punkcie (0, 0) i skali k wtedy i tylko wtedy, gdy x' = k · x i y' = k · y.
Muszą być zatem spełnione jednocześnie warunki 2 · (a + b + 1) = 2a + 4b
i 2 · (a + b) = a + b + 2. Rozwiązujemy układ równań

(

)

(

)

2

1

2

4

2

2

⋅

+ +

=

+

⋅

+

= + +







a b

a

b

a b

a b

26

2

2

2

2

4

2

2

2

a

b

a

b

a

b

a b

+

+ =

+

+

= + +







2

2

2

b

a b

=

+ =







b

a

=

=







1

1.

Para liczb a = 1 i b = 1 spełnia warunki zadania. Punktami, które są jed-
nokładne  w  skali  k = 2  względem  punktu  (0, 0)  są  punkty  A =  (3, 2)
i A' = (6, 4).

s. 16.

Punkt A' = (x', y') jest obrazem punktu A = (x, y) w jednokładności o środ-
ku w punkcie (0, 0) i skali k wtedy i tylko wtedy, gdy x' = k · x i y' = k · y.
Muszą być zatem spełnione jednocześnie warunki 2 · (a + b + 1) = 3a + 3b
i 2 · (2a – b) = a – 2b + 3. Rozwiązujemy układ równań

(

)

(

)

2

1

3

3

2 2

2

3

⋅

+ +

=

+

⋅

−

= −

+







a b

a

b

a b

a

b

2

2

2

3

3

4

2

2

3

a

b

a

b

a

b

a

b

+

+ =

+

−

= −

+







a b

a

+ =

=







2

3

3

a

b

=

=







1

1.

Para liczb a = 1 i b = 1 spełnia warunki zadania. Punktami, które są jed-
nokładne  w  skali  k = 2  względem  punktu  (0, 0)  są  punkty  A = (3, 1)
i A' = (6, 2).

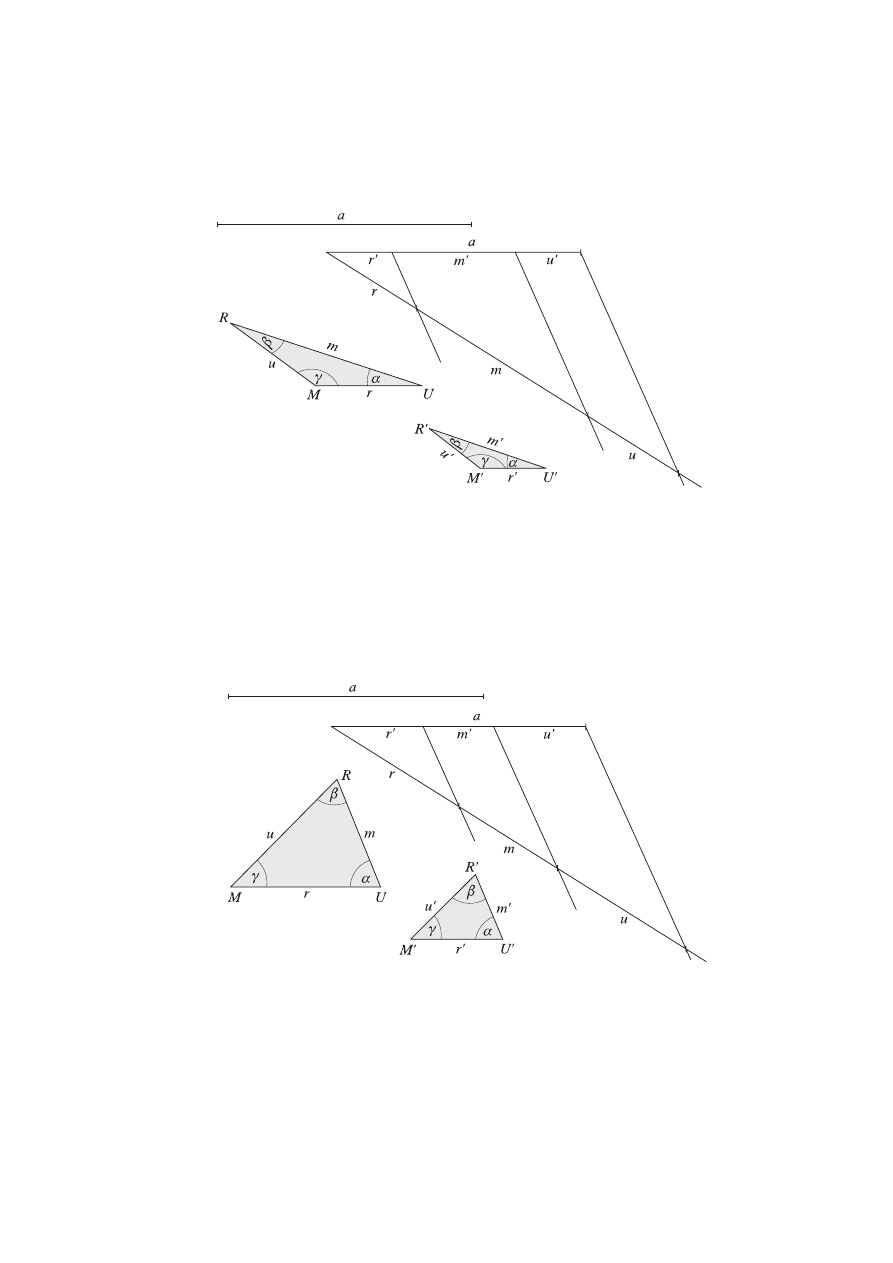
s. 18.

Korzystając z twierdzenia Talesa, dzielimy odcinek długości a na trzy czę-
ści, których długości są proporcjonalne do długości boków trójkąta MUR.
Na  prostej  k  odmierzamy  odcinek  M'U',  którego  długość  jest  równa  r'.
Konstruujemy kąt o wierzchołku U' taki, że jego miara jest równa 

a. Na

otrzymanym ramieniu kąta odkładamy odcinek U'R', którego długość jest
równa m'. Łączymy punkty R' i M'. Otrzymany trójkąt M'U'R' jest podob-
ny do trójkąta MUR. Poprawność konstrukcji wynika z cech podobień-
stwa trójkątów.

27

s. 20.

Korzystając z twierdzenia Talesa, dzielimy odcinek długości a na trzy czę-
ści, których długości są proporcjonalne do długości boków trójkąta MUR.
Na  prostej  k  odmierzamy  odcinek  M'U',  którego  długość  jest  równa  r'.
Konstruujemy kąt o wierzchołku U' taki, że jego miara jest równa 

a. Na

otrzymanym ramieniu kąta odkładamy odcinek U'R', którego długość jest
równa m'. Łączymy punkty R' i M'. Otrzymany trójkąt M'U'R' jest podob-
ny do trójkąta MUR. Poprawność konstrukcji wynika z cech podobień-
stwa trójkątów.

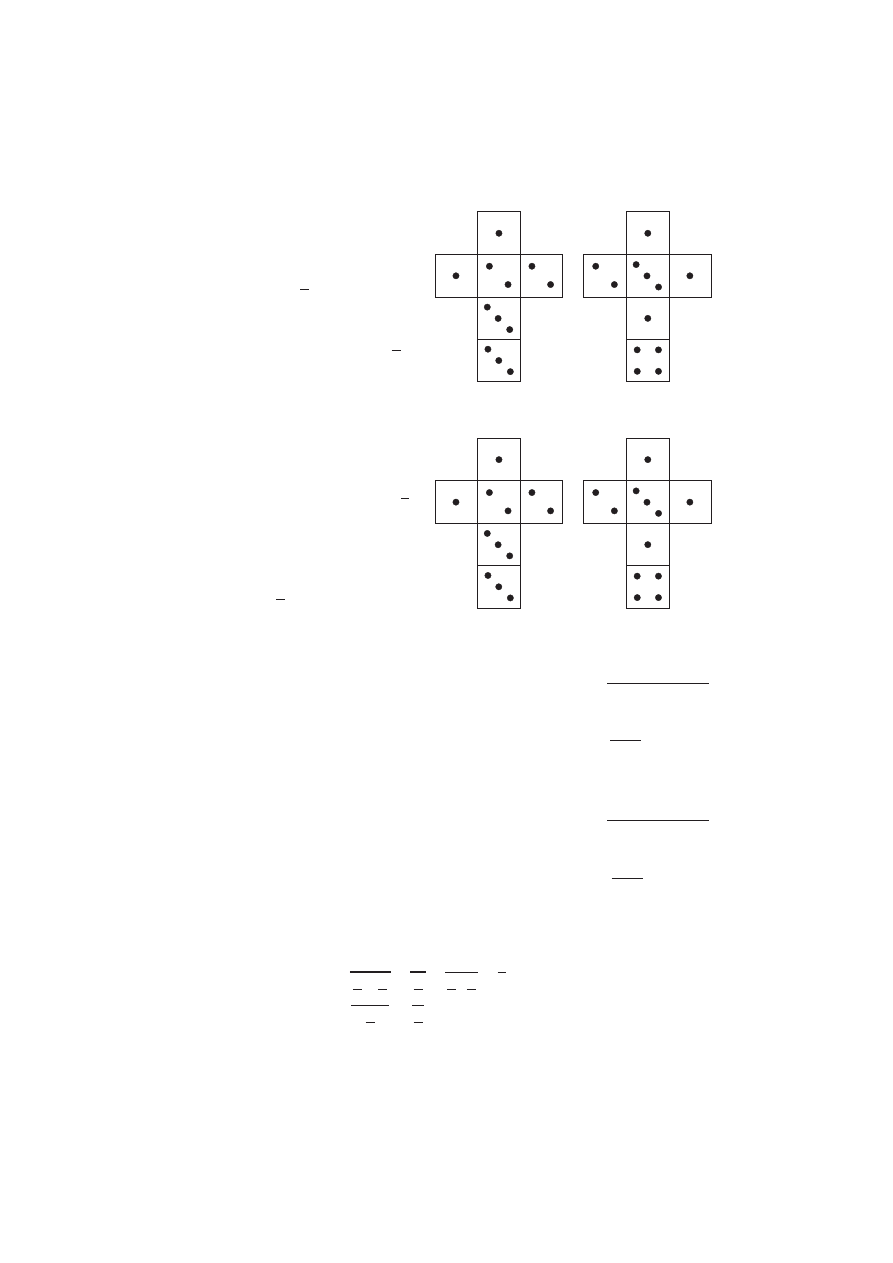
28

s. 22.

Gra  nie  jest  sprawiedliwa.
Prawdopodobieństwo  wyrzu-
cenia  jedynki  przez  Pawła

jest równe 

1

3

, a prawdopodo-

bieństwo wyrzucenia jedynki

przez Gawła jest równe 

1

2

.

Gra  jest  sprawiedliwa,  gdy
obaj  uczestnicy  mają  taką
samą szansę jej wygrania.

s. 24.

Prawdopodobieństwo  otrzy-
mania parzystej liczby oczek

przez  Pawła  jest  równe 

1

3

.

Prawdopodobieństwo  otrzy-
mania  przez  Gawła  niepa-
rzystej  liczby  oczek  jest

równe 

2

3

.

Gra nie jest sprawiedliwa.

s. 26.

Wyrażenia  te  nie  są  równe,  gdyż  dziedziną  wyrażenia 

(

)

(

)

(

)

(

)

x

x

x

x

2

2

16

5

25

4

−

⋅

+

−

⋅

−

jest zbiór R – {–5, 4, 5}, natomiast dziedziną wyrażenia 

x

x

+

−

4

5

 jest zbiór

R – {–5}.

s. 28.

Wyrażenia  te  nie  są  równe,  gdyż  dziedziną  wyrażenia 

(

)

(

)

(

)

(

)

x

x

x

x

2

2

16

5

25

4

−

⋅

−

−

⋅

+

jest zbiór R – {–5, –4, 5}, natomiast dziedziną wyrażenia 

x

x

−

+

4

5

 jest zbiór

R – {–5}.

s. 30.

Podane wyrażenie możemy rozważać, gdy x 

≠

 0. Zapisujemy wyrażenie

w prostszej postaci 

1

1

1

1

1

2

1

1

2

1

1

2

x

x

x

x

x

x

x

+

⋅

=

=

=

. Odwrotnością wyrażenia jest 2.

kostka Pawła

kostka Gawła

kostka Pawła

kostka Gawła

29

s. 32.

Podane wyrażenie możemy rozważać, gdy x 

≠

 0. Zapisujemy wyrażenie

w  prostszej  postaci 

1

1

1

1

1

1

2

1

1

2

2

x

x

x

x

x

x

x

+

⋅

=

=

=

.  Odwrotnością  wyrażenia

jest 

1

2

.

s. 34.

Oznaczmy przez k liczbę kominów. Wówczas spełnione muszą być wa-
runki  7 

≤

  k 

≤

  10  i  14 

≤

  3k 

≤

  24.  Przekształcając  ostatnią  nierówność,

otrzymujemy 4

2

3

 

≤

 k 

≤

 8. Oznacza to, że kominów może być 7 lub 8.

s. 36.

Oznaczmy przez k liczbę kominów. Wówczas spełnione muszą być wa-
runki 6 

≤

 k 

≤

 9 i 13 

≤

 3k 

≤

 21. Przekształcając ostatnią nierówność, otrzy-

mujemy 4

1

3

 

≤

 k 

≤

 7. Oznacza to, że kominów może być 5, 6 lub 7.

s. 38.

x y z

x y z
x y z

+ + =

− + =

+ − =








6

2
0

(1)
(2)
(3)

Z równania (2) i (3) otrzymujemy
2x = 2
x

 = 1.

Podstawiając do równania (1) i (2) x = 1, mamy 

x y

y z

+ + =

− + =







1 6

1

2 , skąd

2 + 2x = 8
2z = 6
z

 = 3.

Podstawiając do dowolnego równania wartości x = 1 i z = 3, otrzymujemy
y

 = 2. Rozwiązaniem są liczby: x = 1, y = 2 i z = 3.

s. 40.

x y z

z y x
z y x

+ + =

− + =

+ − =








6

2
0

(1)
(2)
(3)

Z równania (2) i (3) otrzymujemy
2z = 2
z

 = 1.

.

.

30

Podstawiając do równania (1) i (2) z = 1, mamy 

x y

y x

+ + =

− + =







1 6

1

2 , skąd

2x + 2 = 8
2x = 6
x

 = 3.

Podstawiając do dowolnego równania wartości x = 3 i z = 1, otrzymujemy
y

 = 2. Rozwiązaniem są liczby: x = 3, y = 2 i z = 1.

s. 42.

Odejmując  stronami  równania  układu 

ax

y

x

y

+

=

+

=







4

4

3

4

2

,  otrzymujemy

ax

 – 3x = 2, skąd x · (a – 3) = 2. Dla a = 3 otrzymujemy sprzeczność, gdyż

wówczas lewa strona równania przyjmuje wartość 0, a po prawej stronie
równania jest 3.

s. 44.

Układ  równań  jest  nieoznaczony,  jeżeli  odpowiednie  współczynniki  są
proporcjonalne. W tym przypadku a = 6.

s. 46.

Dla kąta ostrego 

a sin a 

≠

 0. Dzielimy obie strony równania przez sin 

a

i otrzymujemy  cos 

a = sin a, skąd a = 45°.

s. 48.

Dla kąta ostrego 

a cos a 

≠

 0. Dzielimy obie strony równania przez cos 

a

i otrzymujemy  sin 

a = cos a, skąd a = 45°.

s. 50.

x

x

⋅

°

− ⋅

°

tg 60

ctg 45

2

= 

(

)

3 0,5

3

⋅

−

x

(

)

x

x

x

⋅

°

− ⋅

°

=

⋅

−

tg60

ctg 45

2 3 0,5

3

x

x

x

⋅

°

− ⋅

°

=

−

tg60

ctg 45

3 6

x

x

x

⋅

°

− ⋅

°

−

= −

tg60

ctg 45

3

6

(

)

x

⋅

°

−

°

−

= −

tg60

ctg 45

3

6

(

)

x 3 1

3

6

− −

= −

– x

 = – 6

x

 = 6.

s. 52.

3 ctg 60

tg 45

2

x

x

⋅

°

− ⋅

°

= 

(

)

3 0,5

3

⋅

−

x

(

)

3 ctg60

tg 45

2 3 0,5

3

x

x

x

⋅

°

− ⋅

°

=

⋅

−

31

3 ctg60

tg 45

3 6

x

x

x

⋅

°

− ⋅

°

=

−

3 ctg60

tg 45

3

6

x

x

x

⋅

°

− ⋅

°

−

= −

(

)

x

⋅ ⋅

° −

° −

= −

3 ctg60

tg 45

3

6

x

⋅ ⋅

− −

= −











3

1

3

6

3

3

–x

 = –6

x

 = 6.

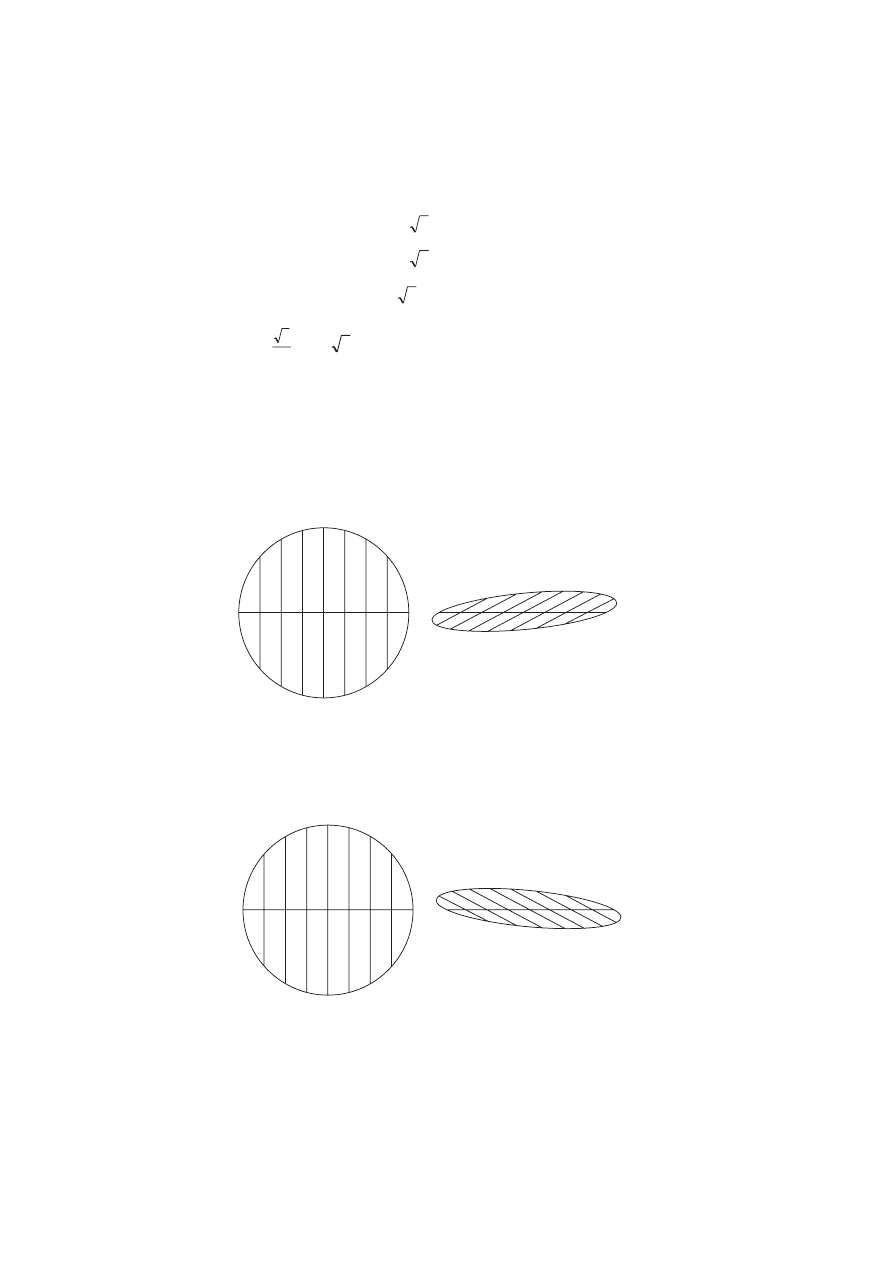
s. 54.

W każdej figurze możemy wskazać odcinek, który jest równoległy do rzutni.
Przyjmijmy,  że  odcinkiem  tym  jest  średnica  okręgu.  Rzuty  równoległe
cięciw rysujemy, korzystając w tym przypadku z własności: rzutami rów-
noległymi odcinków równoległych są odcinki równoległe, których długo-
ści ulegają skróceniu w tym samym stosunku

.

s. 56.

W każdej figurze możemy wskazać odcinek, który jest równoległy do rzutni.
Przyjmijmy,  że  odcinkiem  tym  jest  średnica  okręgu.  Rzuty  równoległe
cięciw rysujemy, korzystając w tym przypadku z własności: rzutami rów-
noległymi odcinków równoległych są odcinki równoległe, których długo-
ści ulegają skróceniu w tym samym stosunku

.

32

s. 58.

Na przykład

s. 60.

Na przykład

s. 62.

s. 64.

s. 66.

Niech a oznacza długość krawędzi sześcianu. Ze wzoru na długość prze-
kątnej sześcianu, mamy

a

a

3

4

− =

(

)

a

⋅

−

=

3 1

4

a

 = 

4

3 1

−

33

a

 = 

(

)

4

3 1

2

⋅

+

a

 = 

(

)

2

3 1

⋅

+

.

Korzystając ze wzoru na objętość sześcianu, otrzymujemy

V

 = 

(

)

[

]

2

3 1

3

⋅

+

.

Liczba 

(

)

8

3 1

3

⋅

+

 jest liczbą niewymierną, a więc nie jest liczbą całko-

witą.

s. 68.

Niech a oznacza długość krawędzi sześcianu. Ze wzoru na długość prze-
kątnej sześcianu, mamy

a

a

3

2

− =

(

)

a

⋅

−

=

3 1

2

a

 = 

2

3 1

−

a

 = 

(

)

2

3 1

2

⋅

+

a

 = 

(

)

3 1

+

.

Korzystając ze wzoru na objętość sześcianu, otrzymujemy V = 

(

)

3 1

3

+

.

Liczba 

(

)

3 1

3

+

 jest liczbą niewymierną, a więc nie jest liczbą całko-

witą.

s. 70.

Niech  a  oznacza  długość  krawędzi  czworościanu  foremnego.  Objętość

obliczymy, korzystając ze wzoru V = 

1

12

a

3

 · 

2

. Wyznaczamy długość

krawędzi czworościanu foremnego. Ściany czworościanu foremnego są

trójkątami równobocznymi. Wysokość jest zatem równa h

s

 = 

a

⋅

3

2

. Ko-

rzystając z twierdzenia Pitagorasa, otrzymujemy

144 + 

1

3

3

2

2

⋅

⋅











a

 = 

a

⋅











3

2

2

34

144 + 

a

2

12

 = 

3

4

2

a

3

4

2

a

 – 

a

2

12

 = 144

8

12

2

a

 = 144

a

 = 12

3 .

V

 = 

1

12

 · 

2

 · 

( )

12 3

3

V

 = 

1

12

 · 

2

 · 12

3

 · 3

3

V

 = 432

6 .

s. 72.

Niech  a  oznacza  długość  krawędzi  czworościanu  foremnego.  Objętość

obliczymy, korzystając ze wzoru V = 

1

12

a

3

 · 

2

. Wyznaczamy długość

krawędzi czworościanu foremnego. Ściany czworościanu foremnego są

trójkątami równobocznymi. Wysokość jest zatem równa h

s

 = 

a

⋅

3

2

. Ko-

rzystając z twierdzenia Pitagorasa, otrzymujemy

36 + 

1

3

3

2

2

⋅

⋅











a

 = 

a

⋅











3

2

2

36 + 

a

2

12

 = 

3

4

2

a

3

4

2

a

 – 

a

2

12

 = 36

8

12

2

a

 = 36

a

 = 3

6 .

V

 = 

1

12

 · 

2

 · 

( )

3 6

3

V

 = 

1

12

 · 

2

 · 3

3

 · 6

6

V

 = 

27 12

2

.

h

s

h

s

h

h

s

h

s

h

35

s. 74.

Z równości 

p · y

2

 · x = 

p · 

y

a









2

 · h wyliczamy wysokość h.

p · y

2

x

 = 

p · 

y

a

2
2

 · h

h = a

2

 · x

Aby objętość walca się nie zmieniła, jego wysokość należy zwiększyć a

2

razy.

s. 76.

Z równości 

p · y

2

 · x = 

p · (y · a)

2

 · h wyliczamy wysokość h.

p · y

2

 · x = 

p · y

2

 · a

2

 · h

h

 = 

x

a

2

Aby objętość walca się nie zmieniła, jego wysokość należy zmniejszyć a

2

razy.

s. 78.

Liczby wpisywane są według schematu
gdzie pole podstawy stożka P

p

,

wysokość stożka h, objętość V.

s. 80.

Liczby wpisywane są według schematu
gdzie pole podstawy stożka P

p

,

wysokość stożka h, objętość V.

P

p

h

V

P

p

h

V

,

,

36

s. 82.

Niech r oznacza promień kuli. Wówczas

4

p · r

2

 = 

4

3

p · r

3

4

3

p · r

3

 – 4

p · r

2

 = 0

4

p · r

2

 · 

(

)

1

3

1

r

−

 = 0

r

 = 0 lub 

1

3

r

 – 1 = 0

1

3

r

 = 1

r

 = 3.

Promień kuli jest równy 3.

s. 84.

Niech r oznacza promień pomarańczy. Wówczas

4

p · r

2

 = 

4

3

p · r

3

4

3

p · r

3

 – 4

p · r

2

 = 0

4

p · r

2

 · 

(

)

1

3

1

r

−

 = 0

r

 = 0 lub 

1

3

r

 – 1 = 0

1

3

r

 = 1

r

 = 3.

Promień pomarańczy jest równy 3.

37

OCENIANIE RAZ JESZCZE

Zbliżają się egzaminy po gimnazjum,

czas  pomyśleć  o  sprawdzianach  typu
egzaminacyjnego. Jeśli uczniowie praco-
wali  z  podręcznikami  i  zbiorami  zadań
z  serii  Matematyka  krok  po  kroku,  nie
będą  mieli  większych  problemów  ze
sprawdzianami. Wiele zadań układaliśmy
pod kątem standardów egzaminacyjnych.
Wystarczy  powtórzyć  i  utrwalić  przero-
biony materiał. Czas na powtórzenia wygospodarowujemy w ciągu całego
roku szkolnego, np. omawiając figury przestrzenne, przypominamy wiado-
mości na temat figur płaskich. Możemy dodatkowe godziny wygospodaro-
wać, rezygnując z części czasu przeznaczonego na impresje matematyczne.

W  ćwiczeniach  sprawdzających  oraz  zbiorze  zadań  wprowadziliśmy

zadania zamknięte. Układając prace klasowe, postarajcie się umieścić kil-
ka zadań tego typu. Mogą to być zadania klasyczne lub już nowego typu,
układane do konkretnego standardu.

Podajemy przykłady sprawdzianów, które można wykorzystać, podsu-

mowując  pewne  partie  materiału.  Każdy  ze  sprawdzianów  uczniowie
mogą  napisać  w  ciągu  45  minut.  Sprawdziany  zawierają  po  10  zadań
zamkniętych, punktowanych w skali od 0 –1 oraz po 4 zadania otwarte.
W  zadaniach  zamkniętych  należy  zaznaczyć  jedną  prawidłową  odpo-
wiedź,  do  zadań  otwartych  należy  podać  pełne  rozwiązanie.  Pierwszy
sprawdzian  można  przeprowadzić  po  zrealizowaniu  rozdziałów:  Liczby
rzeczywiste

, Przekształcenia geometryczne, Doświadczenia losowe. Dru-

gi sprawdzian jest podsumowaniem rozdziałów: Wyrażenia algebraiczne,
Równania,  nierówności,  układy  równań

,  Związki  miarowe  w  trójkącie

i  Figury  przestrzenne.  Trzeci  sprawdzian  jest  sprawdzianem  całorocz-
nym. Z każdego sprawdzianu można uzyskać maksymalnie 20 punktów.

38

SPRAWDZIAN 1

TECHNICZNE NOWINKI

Zadanie 1.

 (1 punkt)

Największym samolotem transportowym jest A 300-600 ST, zwany ,,Be-
luga”. Masa samego samolotu wynosi 87 ton, a po zatankowaniu paliwa
i zabraniu ładunku sięga 155 ton. Ile waży ładunek i paliwo, które może
zabrać ,,Beluga”?

A. 68 · 10

5

 kg

B. 6,8 · 10

4

 kg

C. 87 · 10

3

 kg

D. 0,68 · 10

3

 kg

Zadanie 2.

 (1 punkt)

Ostatnią,  18  grupę  układu  okresowego  pierwiastków  stano-
wią  gazy  szlachetne.  Dawniej  uważano,  że  nie  tworzą  one
żadnych  związków,  jednak  w  1962  roku  otrzymano  wiele
związków chemicznych niektórych gazów, np. fluorki kryp-
tonu  i  ksenonu.  Korzystając  z  rysunku,  odpowiedz,  które
z tych gazów to gazy szlachetne.

A. argon, krypton, ksenon i radon

B. hel i radon

C. neon i argon

D. hel i neon

Zadanie 3.

 (1 punkt)

Pewna japońska firma wyprodukowała przenośny telewizor wyposażony
w ekran o przekątnej 2,5 cala. Podaj długość tej przekątnej w centymetrach.

A. 6,35 cm

B. 8 cm

C. 6,25 cm

D. 4,9 cm

Zadanie 4.

 (1 punkt)

W 2000 roku rozpoczęto budowę nowoczesnego teleskopu. Budowę fi-
nansuje  kilka  państw,  w  tym  również  Polska.  Polska  jest  zobowiązana
pokryć 10% kosztów przedsięwzięcia, czyli ok. 2 mln dolarów. Ile dola-
rów będzie kosztowała budowa teleskopu?

A. 200 mln dolarów

B. 2000 mln dolarów

C. 20 mln dolarów

D. 10 mln dolarów

2

10

Neon

Hel

18

Argon

36

Krypton

54

Ksenon

86

Radon

1 cal 

=

 2,54 cm

39

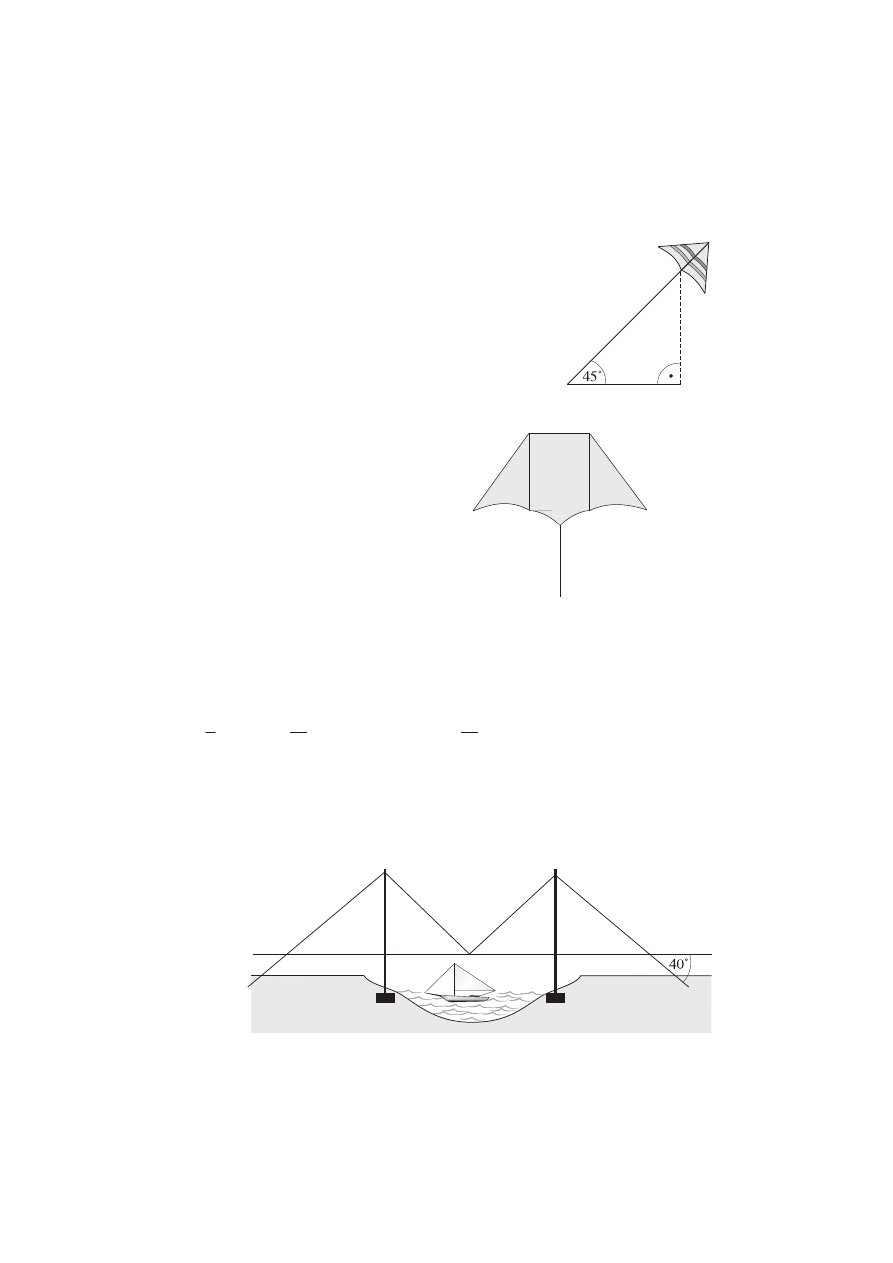
Zadanie 5.

 (1 punkt)

Jeśli chcesz robić zdjęcia lotnicze, możesz do tego
celu  wykorzystać  latawiec  typu  Delta.  Latawiec
ten może bez trudu wynieść w powietrze niewielki
aparat fotograficzny. Na jakiej wysokości znajduje
się latawiec przedstawiony na rysunku?

A. 102 m

B. 10 m

C. 200 m

D. 100 m

Zadanie 6.

 (1 punkt)

Na  rysunku  przedstawiony  jest  la-
tawiec  typu  Delta.  Latawiec  ma
kształt figury:

A. symetrycznej środkowo
B. symetrycznej osiowo
C. symetrycznej osiowo i środkowo
D. która nie ma osi symetrii

Zadanie 7.

 (1 punkt)

Podobno co 5 płyta CD znajdująca się na naszym rynku pochodzi z nagrań
pirackich. Dostałeś 10 płyt CD. Spośród otrzymanych płyt wybrałeś jed-
ną. Jakie jest prawdopodobieństwo, że jest to płyta piracka?

A. 

1

5

B. 

5

10

C. 1

D. 

1

10

Zadanie 8.

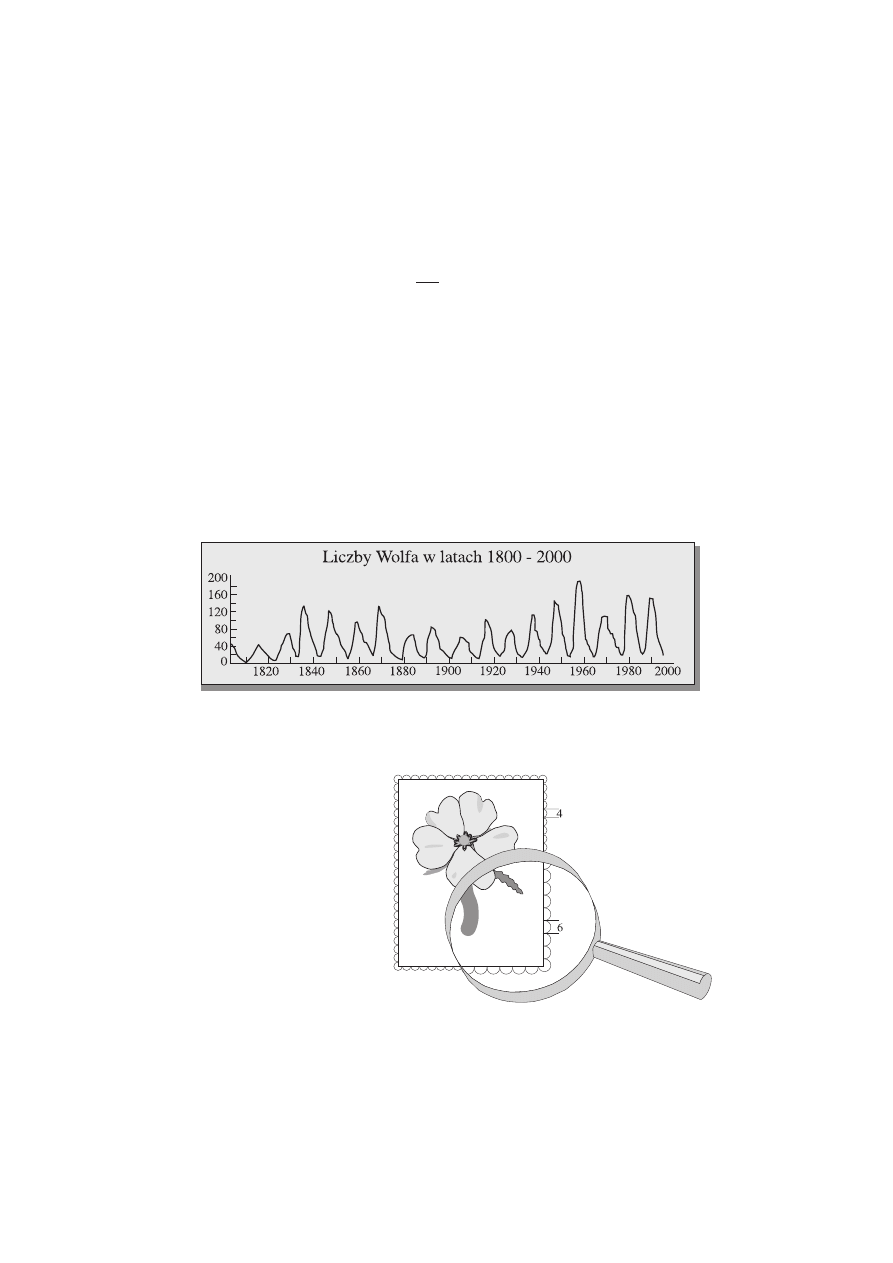
 (1 punkt)

Nowoczesne mosty to najczęściej mosty wiszące. Utrzymywane są przez
stalowe  liny  rozpięte  między  masztami  nośnymi  po  obu  stronach  rzeki.
Wskaż miarę kąta, jaki tworzy lina l z masztem w.

A. 40°

B. 90°

C. 60°

D. 50°

 

w

 

l

100 m

40

Zadanie 9.

 (1 punkt)

Sztuczny satelita, aby utrzymać się na orbicie wokółziemskiej, musi poru-

szać się z prędkością ok. 28 800

km

h

. Wskaż, ile kilometrów pokona sate-

lita w ciągu sekundy.

A. 6 km

B. 4 km

C. 8 km

D. 12 km

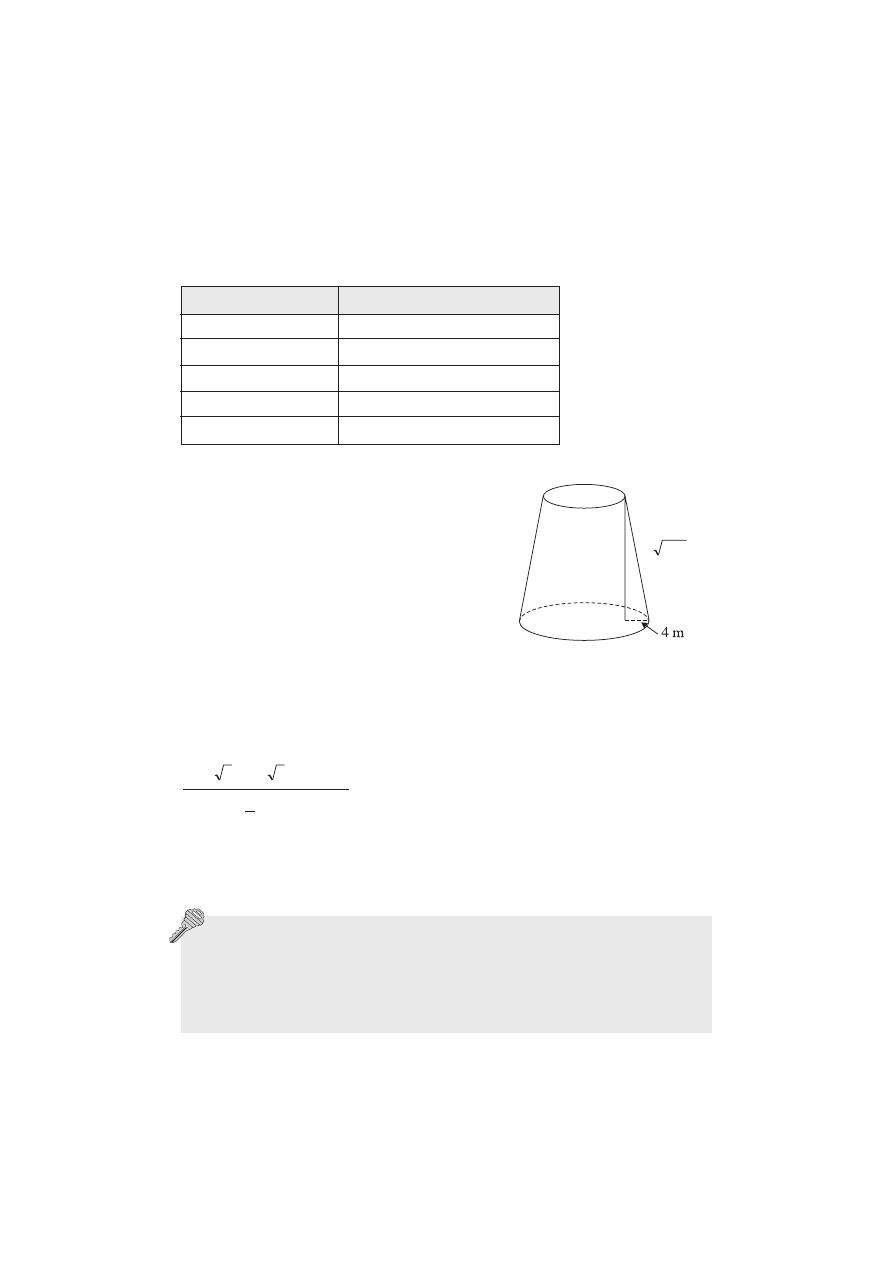
Zadanie 10.

 (1 punkt)

Badania poziomu aktywności Słońca prowadzi się dziś w specjalnych ob-
serwatoriach  heliofizycznych  oraz  w  przestrzeni  kosmicznej.  Dawniej
pomiary te polegały na zliczaniu plam słonecznych, a parametr określają-
cy stopień zaplamienia tarczy słonecznej nazywamy dziś liczbą Wolfa. Na
podstawie rysunku określ, w którym roku poziom aktywności słonecznej
był największy.

A. 1810 r.

B. 1980 r.

C. 1960 r.

D. 1900 r.

Zadanie 11.

 (2 punkty)

Współczesna  astronomia
nie  może  się  obyć  bez
teleskopów  przybliżają-
cych  obrazy  odległych
obiektów. Nam natomiast
nadal wystarcza tradycyj-
na lupa. Ile razy większy
wydaje  się  patrzącemu
przedmiot  przedstawiony
na rysunku?

41

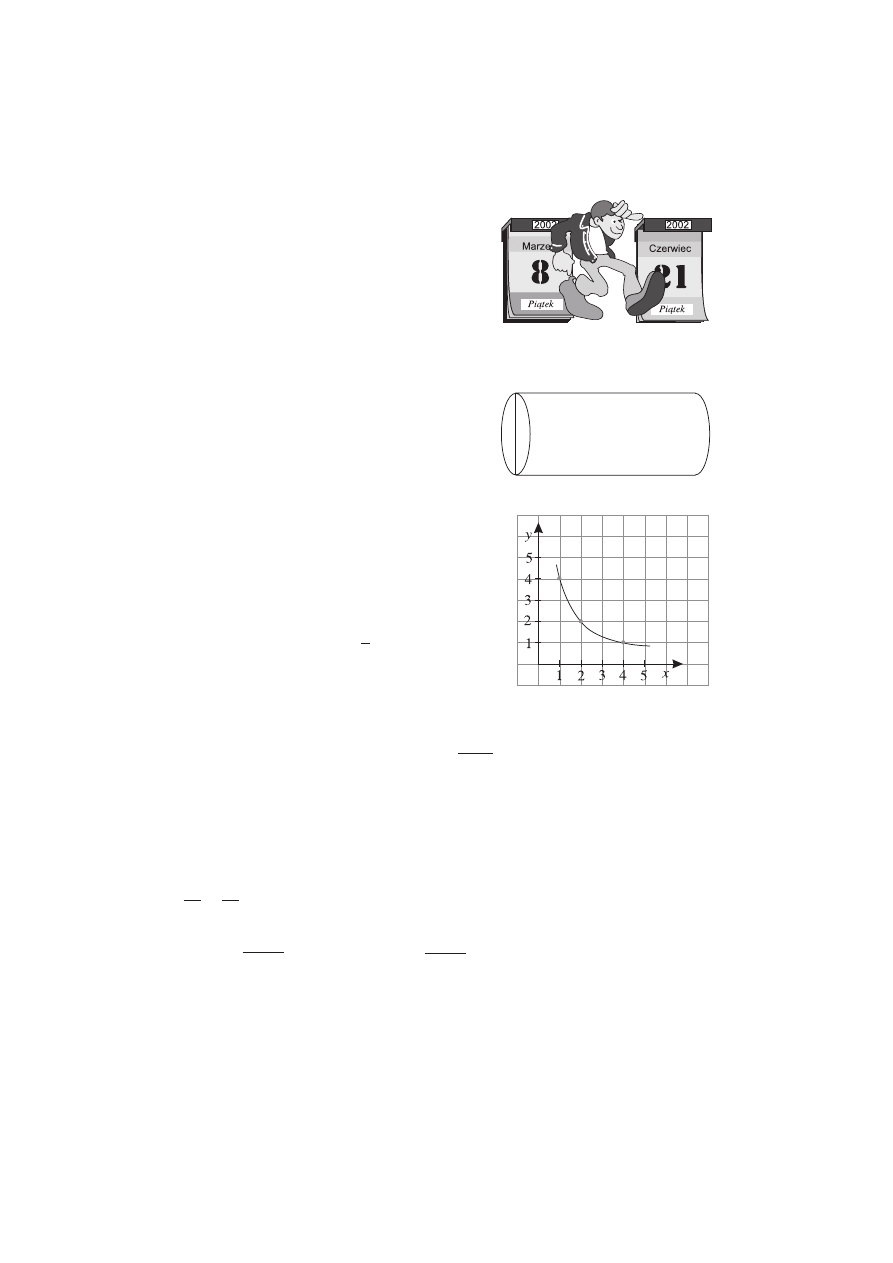
Zadanie 12.

 (3 punkty)

W tabeli podany jest procent użytkowników Internetu w wybranych re-
gionach świata. Przedstaw te dane na diagramie słupkowym.

Zadanie 13.

 (2 punkty)

Na  świecie  pracują  obecnie  434  jądrowe
bloki energetyczne. W Polsce jednak nadal
dominuje  energetyka  cieplna  bazująca  na
węglu kamiennym i brunatnym. Oblicz, jaką
wysokość ma chłodnia kominowa przedsta-
wiona na rysunku.

2 629 m

Zadanie 14.

 (3 punkty)

Jedną z największych imprez w 2000 r. była wystawa światowa w Hano-
werze.  Na  wystawie  tej  zaprezentowano  najnowsze  osiągnięcia  nauki
i techniki. Oblicz wartość wyrażenia

(

)(

)

( )

2

3 2

3

4 : 4

1

2

: 2

3

2

1

1,5 100,

+

−

+

−

+

⋅

a dowiesz się, ile państw miało swoje pawilony na tej wystawie.

Klucz do odpowiedzi

Zadanie 1. B; zadanie 2. D; zadanie 3. A; zadanie 4. C; zadanie 5. D;
zadanie 6. B; zadanie 7. A; zadanie 8. D; zadanie 9. C; zadanie 10. C;
zadanie 11. 1,5 raza; zadanie 13. 50 m; zadanie 14. 155.

Obszar

USA

Europa Wschodnia

Ameryka Łacińska

Azja Wschodnia

Kraje arabskie

Użytkownicy Internetu w %

54

4

3

2

1

42

SPRAWDZIAN 2

DO KOÑCA ROKU JEDEN KROK

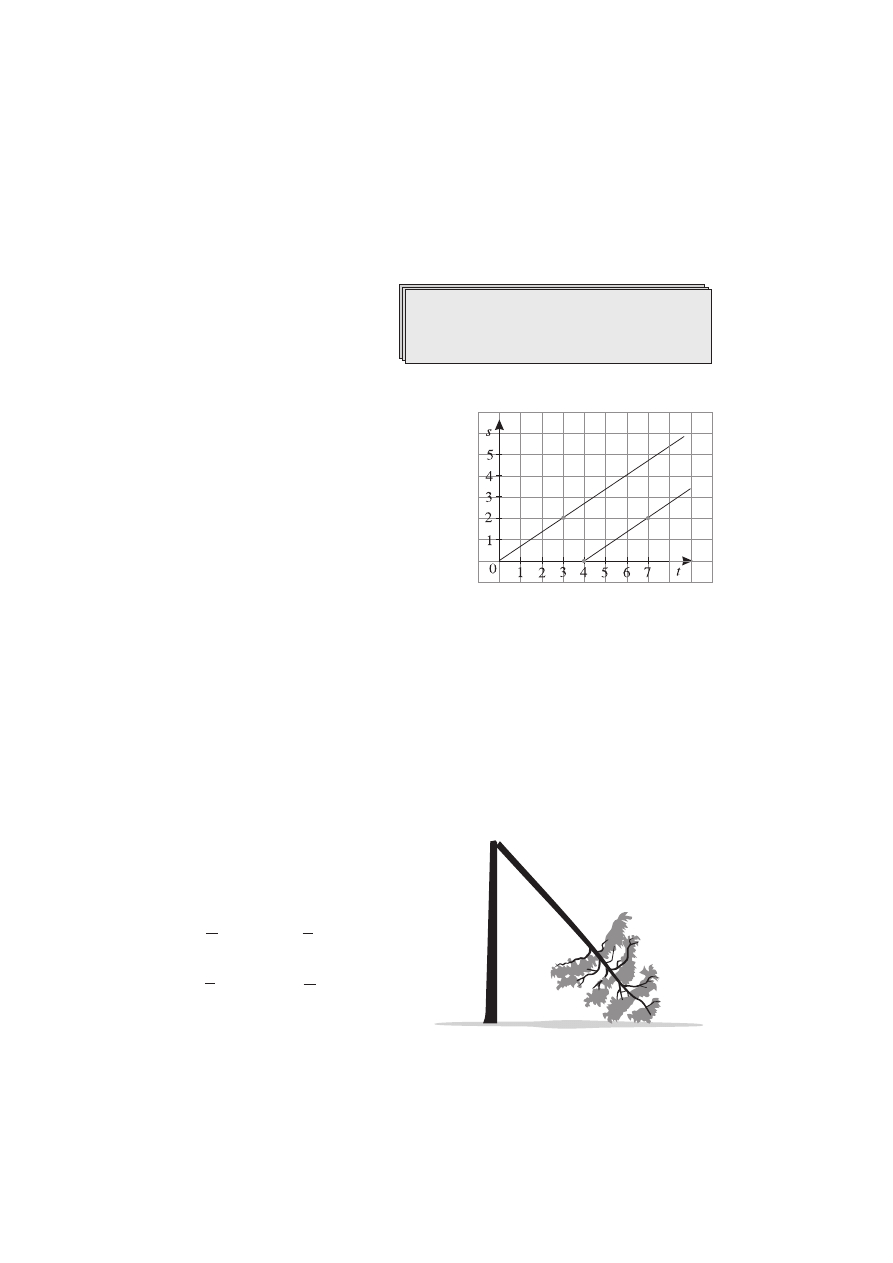
Zadanie 1.

 (1 punkt)

Podaj,  ile  m

3

  ziemi  usunięto  podczas

budowy tunelu, którego schemat przed-
stawia rysunek. Przyjmij, że 

p » 3.

A. 300 000

B. 30 000

C. 1 200 000

D. 400

Zadanie 2.

 (1 punkt)

Wykres przedstawia krzywą toru lotu pew-
nego  wróbla.  Zaznacz  wyrażenie,  którym
można opisać tę krzywą, dla x > 0.

A. y = 4x – 4

B. y = 4x

C. y = x + 4

D. y = 

4

x

Zadanie 3.

 (1 punkt)

Podaj, w jakim przypadku wyrażenie 

x

x

+

−

4

2

 ma sens liczbowy.

A. x 

≠

 – 4

B. x = 2

C. x 

≠

 2

D. x 

≠

 0

Zadanie 4.

 (1 punkt)

Zależność ciśnienia gazu od jego objętości przy stałej masie określa wzór

p

p

V

V

1
2

1
2

=

. Wyznacz z tego wzoru V

1

.

A. V

1

 = 

p

p V

2

1

2

⋅

B. V

1

 = 

p V

p

1

2

2

⋅

C. V

1

 = p

2

 · V

2

 · p

1

D. V

1

 = p

2

 + p

1 

· V

2

20 m

1 km

43

Zadanie 5.

 (1 punkt)

Wskaż wyrażenie, które określa, jaką kwotę (w zł) będziesz mógł wypła-
cić po roku oszczędzania w ,,Banku Wspaniałym”.

A. 115%x

B. x

 

·

 

15%x

C. 15%x

D. 85%x

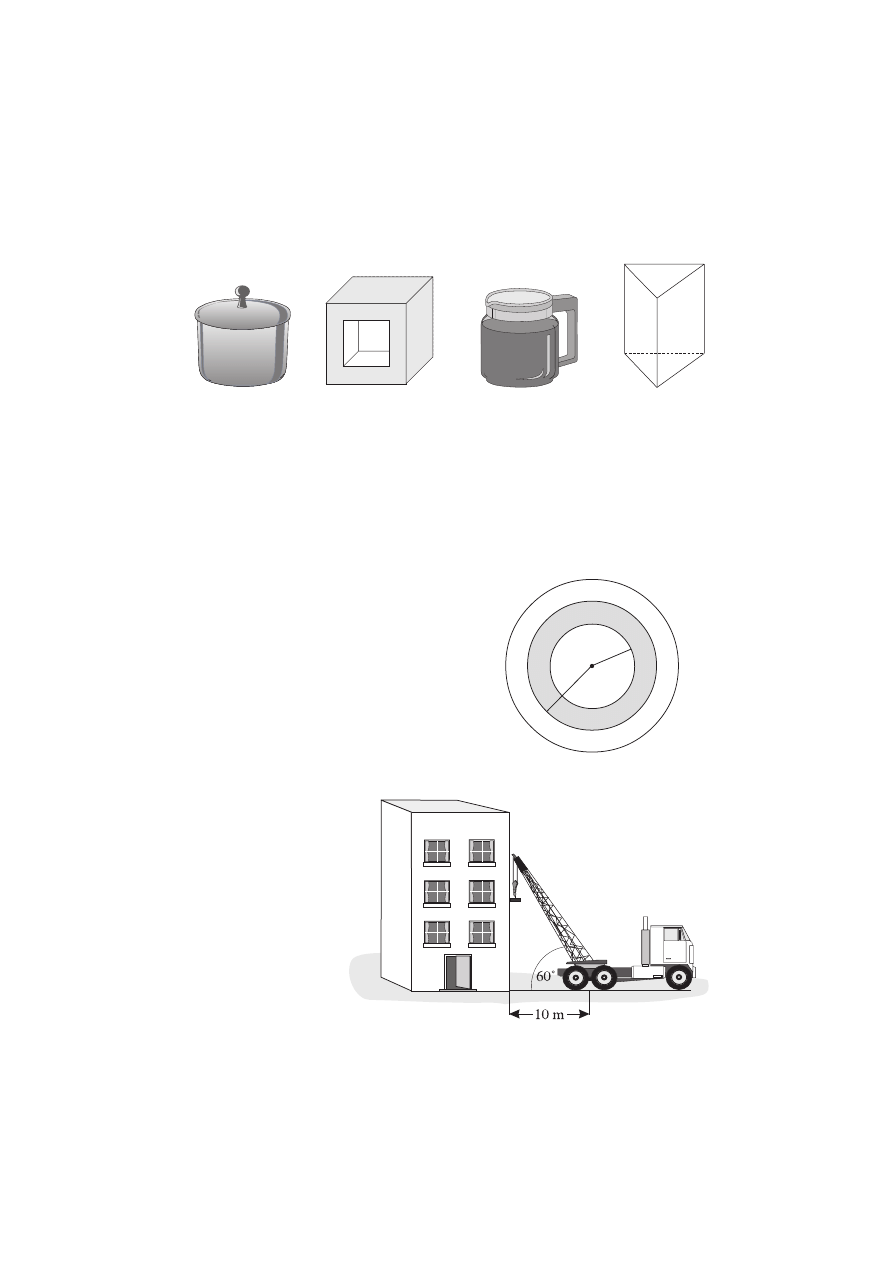
Zadanie 6.

 (1 punkt)

Z  tej  samej  stacji  o  różnych  porach
wyruszają  dwa  pociągi.  Wykresy  ich
ruchu przedstawiono na rysunku. Któ-
ry z pociągów poruszał się z większą
prędkością?

A. P

1

B. P

2

C. nie można tego sprawdzić

D. pociągi poruszają się z tą samą prędkością

Zadanie 7.

 (1 punkt)

Suma  cyfr  liczby  dwucyfrowej  jest  równa  10.  Różnica  cyfry  dziesiątek
i cyfry jedności jest równa 2. Zaznacz układ równań, który da ci możliwość
wyznaczenia cyfry jedności x danej liczby i cyfry dziesiątek y tej liczby.

A. 

x y

x y

+ =

− =







10

2

 B. 

x y

x y

− =

+ +







10

2

 C. 

x y

y x

+ =

− =







10

2

 D. 

10

10

2

x y

y x

+ =

− =







Zadanie 8.

 (1 punkt)

Sinus kąta, jaki tworzy złamany
pień  drzewa  z  poziomem,  jest
równy:

A. 

w

d

B. 

h

d

C. 

d

h

D. 

h

w

d

h

w

P

1

P

2

Wp³acam do „Banku Wspania³ego” x z³.

Oprocentowanie  w  tym  banku  w  skali

rocznej wynosi 15%.

44

Zadanie 9.

 (1 punkt)

Wskaż rysunek, na którym przedstawiony jest graniastosłup.

Zadanie 10.

 (1 punkt)

Świeca  w  kształcie  ostrosłupa  ma  taką  samą  wysokość  i  podstawę  jak
świeca w kształcie graniastosłupa. Ile razy więcej wosku zużyto na wyko-
nanie świecy w kształcie graniastosłupa?

A. 3

B. 9

C. 13

D. 27

Zadanie 11.

 (2 punkty)

Na  rysunku  przedstawiono  słoje  przyro-
stu rocznego drzewa. Oblicz pole zazna-
czonej figury.

Zadanie 12.

 (2 punkty)

Oblicz,  na  jaką  wy-
sokość  sięga  ramię
dźwigu przedstawio-
nego na rysunku.

A.

B.C.

D.

2 cm

3 cm

45

Zadanie 13.

 (3 punkty)

Ile skóry potrzeba na wykonanie piłki o średnicy 20 cm? Na szwy i odpa-
dy dolicz 10% powierzchni. Przyjmij, że 

p » 3.

Zadanie 14.

 (3 punkty)

Rozwiąż równanie (x – 4)

2

 – (x – 1) (x + 1) = 1.

Klucz do odpowiedzi

Zadanie 1. A; zadanie 2. D; zadanie 3. C; zadanie 4. B; zadanie 5. A;
zadanie 6. D; zadanie 7. C; zadanie 8. B; zadanie 9. D; zadanie 10. A;

zadanie 11. 

5p cm

2

; zadanie 12. 10

3 m; zadanie 13. 1320 cm

2

;

zadanie 14. x = 2.

46

SPRAWDZIAN 3

SZALEÑSTWO XX WIEKU

Jednym z najlepiej znanych wyna-

lazków lat siedemdziesiątych XX wie-
ku  jest  telefonia  komórkowa.  Ciągle
toczą się spory o to, czy używanie tele-
fonów  komórkowych  jest  szkodliwe
dla  zdrowia.  Telefony  te  emitują  pro-
mieniowanie elektromagnetyczne o częstotliwości od 800 do 2000 MHz.
Jeśli  ktoś  trzyma  telefon  przy  uchu  przez  kilka  minut,  fale  emitowane
przez aparat mogą podnieść temperaturę tkanki mózgowej o 0,1°C.

Zadanie 1.

 (1 punkt)

Pani Adela posiada telefon komórkowy w sieci ,,Plum-Plum”. Jaka jest
częstotliwość promieniowania emitowanego przez ten telefon?

A. 300 MHz

B. 3000 MHz

C. 600 MHz

D. 1400 MHz

Zadanie 2.

 (1 punkt)

W którym roku zaczęła działać pierwsza sieć telefonii komórkowej?

A. 1872 r.

B. 1990 r.

C. 1979 r.

D. 2000 r.

Zadanie 3.

 (1 punkt)

Pan Arnold  rozmawiał  przez  telefon  komórkowy  8  minut.  O  ile  stopni
wzrosła temperatura jego tkanki mózgowej?

A. 0,1°C

B. 0,8°C

C. 8°C

D. 8,1°C

Zadanie 4.

 (1 punkt)

W  pewnym  miasteczku  co  roku  przeprowadzano  sondaż  w  grupie  50
osób, pytając, kto ma telefon komórkowy. Wyniki sondażu pokazano na
diagramie. Jaki procent osób objętych sondażem w 1998 r. posiadało tele-
fon komórkowy?

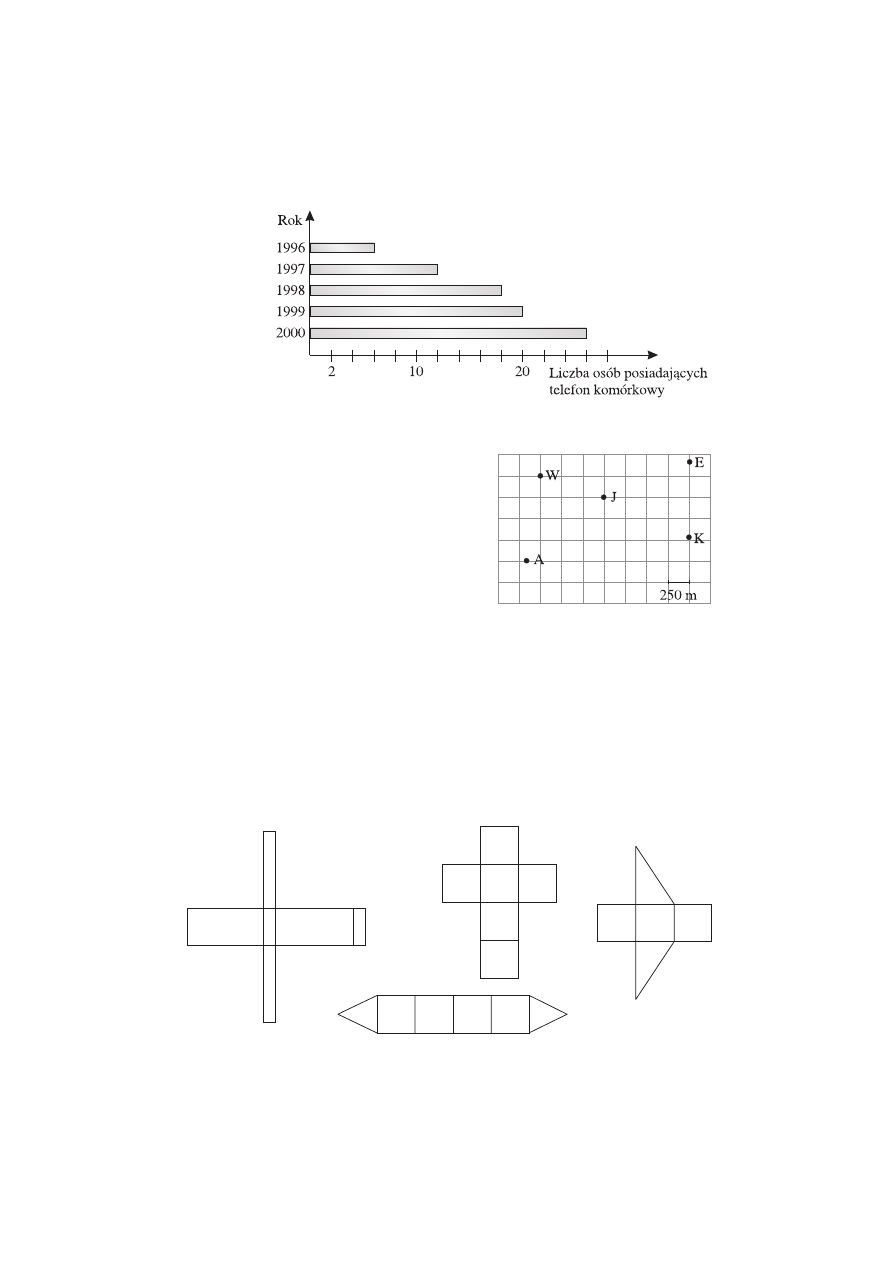
47

A. 9%

B. 20%

C. 12%

D. 36%

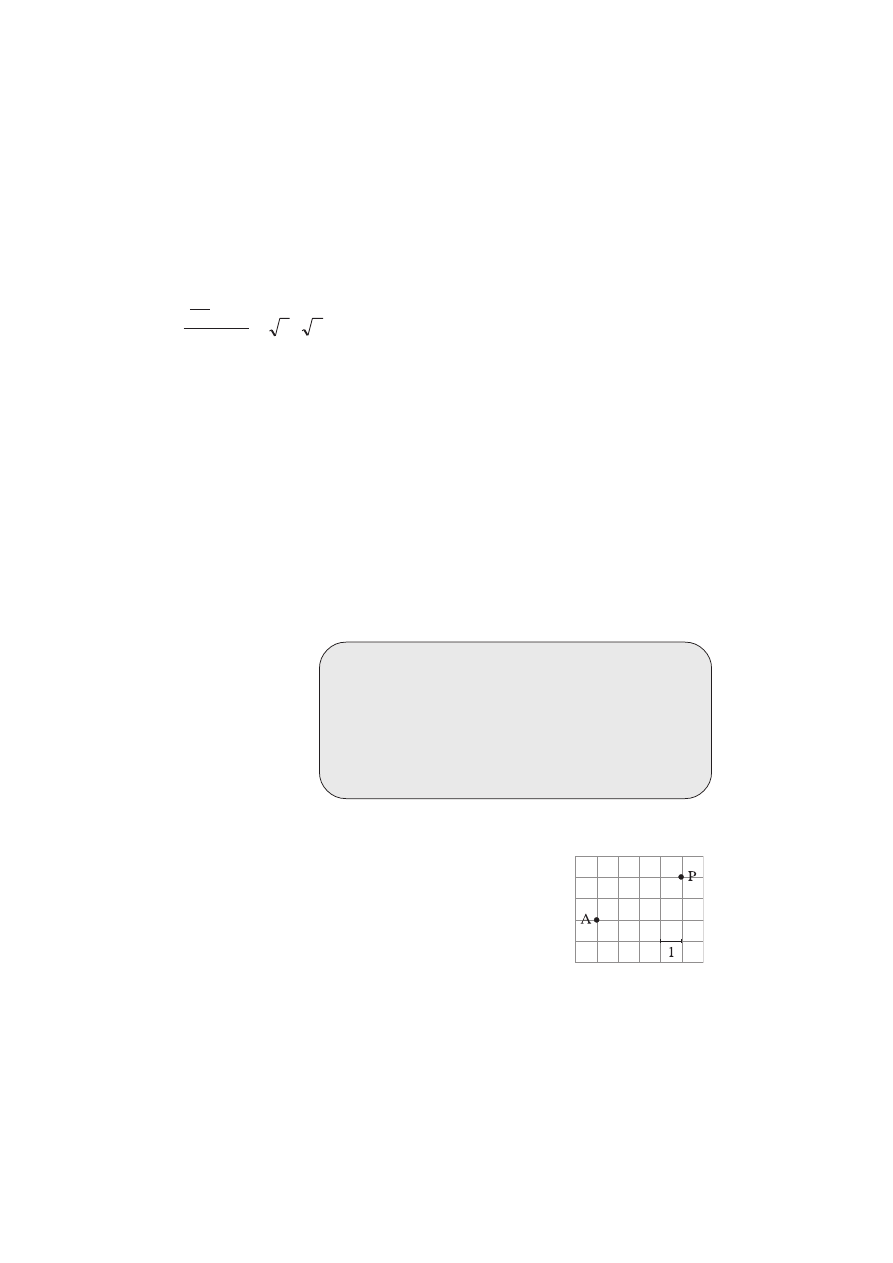
Zadanie 5.

 (1 punkt)

Pierwsze telefony komórkowe miały za-
sięg  do  1  km.  Który  z  chłopców  mógł
porozmawiać z Julkiem (J) przez jeden
z pierwszych telefonów komórkowych?

A. Edek (E)

B. Alek (A)

C. Włodek (W)

D. Karol (K)

Zadanie 6.

 (1 punkt)

Aparat komórkowy Franciszka jest w kształcie prostopadłościanu o wy-
miarach 15 cm, 8 cm i 2 cm. Oblicz objętość tego prostopadłościanu.

A. 120 cm

3

B. 2400 cm

3

C. 240 cm

3

D. 16 cm

3

Zadanie 7.

 (1 punkt)

Gdyby  Franciszek  chciał  uszyć  pokrowiec  na  swój  telefon,  to  z  której
z narysowanych siatek mógłby skorzystać?

A.

B.

C.

D.

48

Zadanie 8.

 (1 punkt)

W  niektórych  przypadkach  aparat  telefonu  komórkowego  może  służyć
jako  kalkulator.  Korzystając  z  kalkulatora,  podaj  wartość  wyrażenia

( )

−

⋅

⋅

−

⋅

1

3

3

0,1 30

2

3

8

2.

A. 3

B. – 4

C. –3

D. 0

Zadanie 9.

 (1 punkt)

Za 3 telefony komórkowe i 2 czekolady trzeba zapłacić 124 zł. Za 1 tele-
fon i 3 czekolady trzeba zapłacić 46 zł. Ile kosztuje telefon komórkowy?

A. 24 zł

B. 120 zł

C. 40 zł

D. 2 zł

Zadanie 10.

 (1 punkt)

Tadeusz  ma  telefon  komórkowy  pracujący  w  sieci  ,,Ble-Ble”.  Wczoraj
o godz. 14.00 zadzwonił do mamy i rozmawiał z nią 6 minut. Dzisiaj wy-
słał bratu wiadomość składającą się z 184 znaków. Ile zapłaci za rozmowę
i wysłaną wiadomość?

A. 10,20 zł

B. 10,70 zł

C. 8,80 zł

D. 11,20 zł

Zadanie 11.

 (2 punkty)

Oblicz w jakiej odległości od abonenta A znajduje
się  stacja  bazowa  P  sieci  telefonii  komórkowej
,,Ble-Ble”.

Lubisz rozmawiać?

Lubisz rozmawiać?

Lubisz rozmawiać?

Lubisz rozmawiać?

Lubisz rozmawiać?

Zrób to taniej w sieci „Ble−Ble”

Zrób to taniej w sieci „Ble−Ble”

Zrób to taniej w sieci „Ble−Ble”

Zrób to taniej w sieci „Ble−Ble”

Zrób to taniej w sieci „Ble−Ble”

Usługa

Usługa

Usługa

Usługa

Usługa

Cena

Cena

Cena

Cena

Cena

wysłanie SMS−a (do 160 znaków) .......... 0,50 zł
minuta rozmowy (godz. 8.00 − 16.00) ...... 1,70 zł
minuta rozmowy (godz. 16.00 − 8.00) ...... 1,30 zł

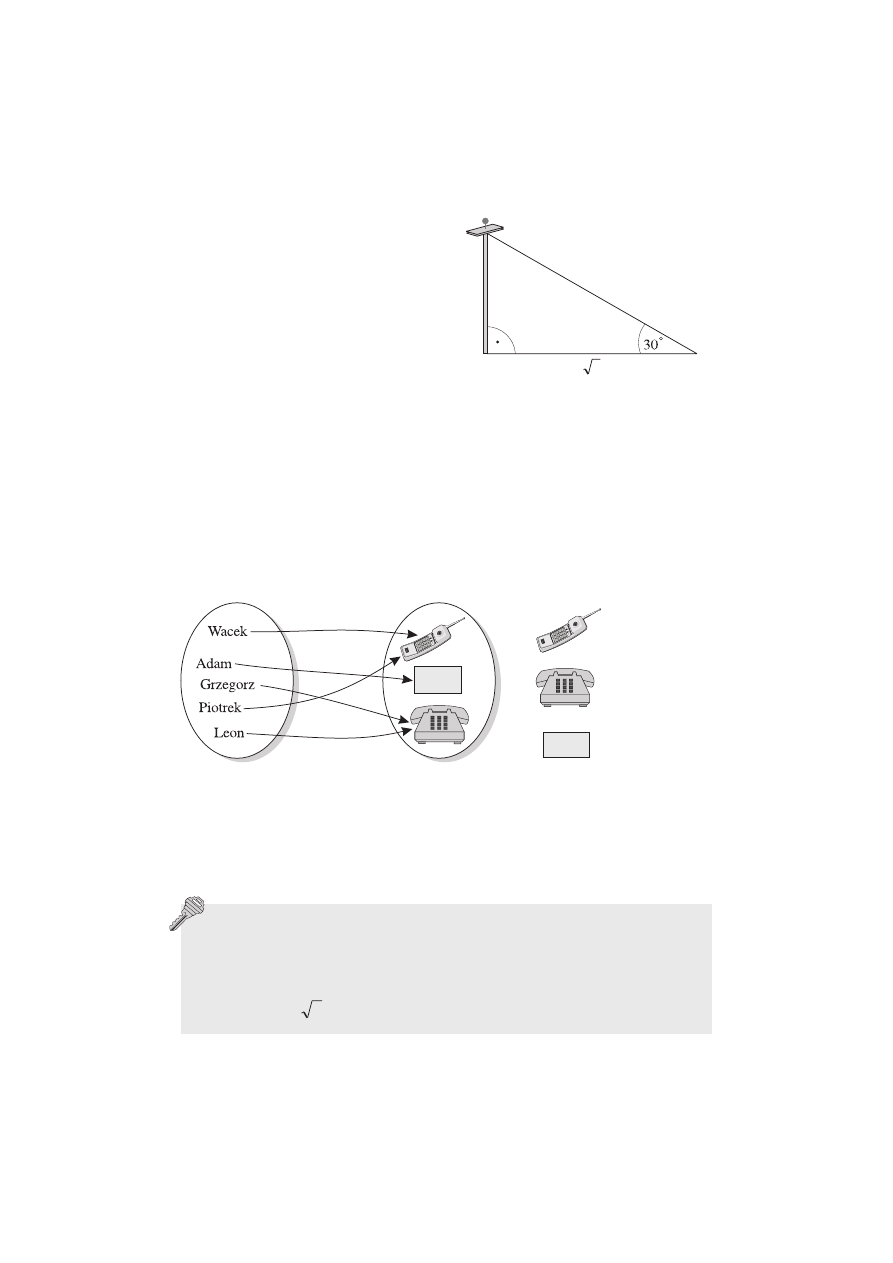
49

Zadanie 12.

 (3 punkty)

Oblicz, na jakiej wysokości umiesz-
czono przekaźnik sieci ,,Ble-Ble”.

Zadanie 13.

 (2 punkty)

Wiemy, że jedna ze stacji bazowych (nadawczo-odbiorczych) sieci ,,Ble-Ble”
obsługuje  abonentów  telefonii  komórkowej  na  obszarze  o  powierzchni
48 km

2

. Przyjmując, że obszar ten jest kołem, oblicz jego promień. Przyj-

mij 

p » 3.

Zadanie 14.

 (3 punkty)

Bogdan przeprowadził ankietę w grupie pięciu kolegów. Wyniki przedsta-
wił w następujący sposób:

a) Jak myślisz, o co pytał Bogdan w ankiecie?
b) Graf narysowany przez Bogdana przedstawia pewną funkcję. Wymień

elementy dziedziny tej funkcji.

c) Ile elementów należy do zbioru wartości tej funkcji?

telefon
komórkowy

telefon
stacjonarny

brak telefonu

10 3 m

Klucz do odpowiedzi

Zadanie 1. D; zadanie 2. C; zadanie 3. A; zadanie 4. D; zadanie 5. C;
zadanie 6. C; zadanie 7. A; zadanie 8. C; zadanie 9. C; zadanie 10. D;

zadanie 11. 2

5 ; zadanie 12. 10 m; zadanie 13. 4 km.

50

51

Œcie¿ki  edukacyjne – co to takiego?

Od kilku lat borykamy się z problemem ścieżek edukacyjnych. Refor-

ma edukacji spowodowała bowiem, że musimy poszukiwać nowych roz-
wiązań dydaktycznych. Wielu nauczycieli opracowało system wplatania
treści ścieżek do lekcji. Ale nauczyciele rozpoczynający pracę zapewne
nie bardzo orientują się w tym zagadnieniu. A więc najpierw o tym, co to
są ścieżki edukacyjne.

Aby  dobrze  funkcjonować  w  otaczającej  nas  rzeczywistości,  należy

posiadać wiedzę i umiejętności z wielu dziedzin. I to umiejętności zinte-
growane,  umożliwiające  szybką  analizę  zachodzących  zjawisk,  a  co  za
tym idzie – błyskawiczne podejmowanie decyzji. Dobrym porównaniem
jest tu jazda samochodem – dojeżdżając do skrzyżowania nie tylko spo-
glądamy na znaki drogowe, ale analizujemy również panującą na nim sy-
tuację i w zależności od oceny dostosowujemy do niej nasze postępowanie.

W  nauczaniu  przedmiotowym  często  mamy  do  czynienia  z  wiedzą

czysto  teoretyczną  i  poszufladkowaną,  stosowaną  tylko  w  sytuacjach
specyficznych dla danej edukacji, nie próbującą wyjaśnić zjawisk z inne-
go  punktu  widzenia.  W  wielu  jeszcze  wypadkach,  niestety,  niespójną.
Chcemy  przyzwyczajać  ucznia  do  kompleksowego  spojrzenia  na  świat,
staramy  się  pokazywać  praktyczne  wykorzystanie  wiedzy  i  umiejętno-
ści  w  konkretnych  sytuacjach.  Pociąga  to  jednak  za  sobą  konieczność
łączenia wiedzy z kilku dziedzin nauki. Pomysłem na taką integrację są
ścieżki  edukacyjne.  Podają  one  konkretne  treści,  wokół  których  można
budować zajęcia z danej edukacji lub zajęcia wykorzystujące umiejętno-
ści z kilku edukacji.

ŚCIEŻKI EDUKACYJNE
W GIMNAZJUM

52

Treści ścieżek zawierają hasła, któ-

re  zwykle  były  realizowane  w  szko-
łach  na  poszczególnych  przedmio-
tach. Na przykład za edukację związa-
ną  ze  zdrowiem  byli  odpowiedzialni
nauczyciele biologii, za edukację czy-
telniczą – poloniści. Teraz każdy z na-
uczycieli, planując pracę uczniów, po-
winien brać pod uwagę treści ścieżek
i realizować je na swoim przedmiocie
w  mniejszym  lub  większym  stopniu,
w zależności od potrzeb i możliwości.

Dobrze zaplanowana w szkole realizacja ścieżek umożliwia ujednolicenie
tych samych pojęć występujących w różnych podręcznikach. Zmusza na-
uczycieli  do  współpracy,  czego  efektem  powinno  być  odciążenie  mło-
dzieży od uczenia się tych samych pojęć dla potrzeb kilku przedmiotów
i wykorzystanie posiadanych umiejętności niezależnie od edukacji.

Realizacja zagadnień związanych z daną ścieżką lub z kilkoma ścież-

kami  edukacyjnymi  daje  możliwość  prowadzenia  przez  uczniów  prac
badawczych,  prezentacji  swoich  zainteresowań,  odejścia  od  szablono-
wego  sposobu  uczenia,  poprzez  wprowadzenie  aktywizujących  metod
nauczania.

Każda ze ścieżek edukacyjnych przeznaczonych do realizacji w gim-

nazjum zawiera kilka haseł, z którymi powinien się zapoznać gimnazja-
lista.  Jeśli  przynajmniej  część  z  nich  zostanie  zrealizowana,  absolwent
gimnazjum potrafi zadbać o swoje zdrowie, dostrzegać zagrożenia środo-
wiska  przyrodniczego  występujące  w  miejscu  zamieszkania,  określić
wkład Polski w rozwój kultury europejskiej, odczuwać przynależność do
regionu,  z  którego  pochodzi,  przygotować  się  do  prawidłowego  współ-
działania  w  różnych  sytuacjach.  Będzie  przygotowany  do  korzystania
z różnych źródeł informacji. Umiejętności, wynikające z realizacji ście-
żek edukacyjnych, dają więc możliwość młodemu człowiekowi dobrego
funkcjonowania w nowoczesnym europejskim kraju.

53

Rodzaje i budowa  œcie¿ek edukacyjnych

Do realizacji w gimnazjum wytyczono treści siedmiu ścieżek eduka-

cyjnych:  edukacji  ekologicznej,  europejskiej,  regionalnej,  filozoficznej,
prozdrowotnej, czytelniczej i medialnej oraz obrony cywilnej.

Każda  ścieżka  edukacyjna  zawiera:  cele  edukacyjne,  zadania  szkoły,

treści oraz osiągnięcia.

W celach edukacyjnych zawarte są ogólne zamierzenia towarzyszące

utworzeniu danej ścieżki. Cele te realizowane są w ciągu całego trzeciego
etapu edukacji. Niektóre z nich to pogłębienie i rozszerzenie celów reali-
zowanych w szkole podstawowej, np. rozwijanie wiedzy o kulturze włas-
nego regionu i jej związkach z kulturą narodową.

W zadaniach szkoły wskazano, w jaki sposób szkoła powinna pomóc

uczniowi w realizacji celów ścieżki, np. wprowadzenie w świat tradycji
regionu i należących do niej wartości.

Treści ścieżki to konkretne tematy, które mogą posłużyć w całości lub

częściowo  jako  inspiracje  do  zajęć  z  uczniami,  np.    rola  regionu  i  jego
związki z innymi regionami Polski.

W osiągnięciach zapisano, zdobycie jakich umiejętności powinno być

wynikiem  realizacji  danej  ścieżki,  np.  prezentowanie  własnego  regionu
i jego walorów oraz cech wyróżniających.

54

 Modele realizacji œcie¿ek edukacyjnych

Sensowna  realizacja  treści

ścieżek 

edukacyjnych 

może

sprawić 

wielu 

nauczycielom

duże trudności. Niektórzy starają
się ominąć ten problem, tworząc
osobne  przedmioty,  na  których
uczniowie  zdobywają  potrzebne
umiejętności.  Wiadomości  po-
trzebne  do  osiągnięcia  celów
ścieżki  obrona  cywilna  zwykle
realizowane są w czasie oddziel-

nych godzin lekcyjnych, gdyż prowadzenie takich zajęć wymaga facho-
wego  przygotowania.  Natomiast  próba  tworzenia  oddzielnych  edukacji
do realizacji innych ścieżek może doprowadzić do tego, że nagle uczeń
będzie miał o 7 przedmiotów więcej, a przecież nie to było celem autorów
Podstawy programowej

.

Ścieżki  edukacyjne  powinny  być  realizowane  na  wszystkich  eduka-

cjach i najlepiej, aby model ich wykorzystania opracowywany był wspól-
nie przez nauczycieli uczących w danej klasie. W takim przypadku wy-
chowawca może być koordynatorem wspólnych działań. Zapewni to cią-
głość realizacji zagadnień, zapobiegnie powielaniu treści. Kompleksowe
planowanie bloków tematycznych umożliwi szybsze realizowanie celów
oraz tworzenie atrakcyjniejszych zajęć dla uczniów. Zajęcia takie mogą
być jednodniowe, kilkudniowe lub nawet dłuższe (realizowane w czasie
trwania ,,zielonej szkoły”). Uczeń  przekona się o możliwości praktyczne-
go wykorzystania wiedzy i umiejętności zdobytych w szkole. Będzie rów-
nież twórcą i pomysłodawcą stawiającym zadania i rozwiązującym ćwi-
czenia.  Najprościej  planować  tematy  lekcji  z  wykorzystaniem  ścieżek
edukacyjnych  na  początku  roku  szkolnego.  Wtedy  wychowawca  może
zaprosić wszystkich nauczycieli uczących w jego klasie na wspólne spot-
kanie i przedstawić propozycję – tytuły bloków tematycznych, pomysły
na sposób realizacji danych zagadnień, posiadane materiały – do wyko-
rzystania  w  ciągu  danego  roku  szkolnego.  Treści  powinny  być  zgodne
z zagadnieniami wynikającymi z programu szkoły, planami zespołów sa-
mokształceniowych. Nie powinno być ich również zbyt dużo, aby spokoj-
nie można było je zrealizować.

55

W czasie wspólnej dyskusji, dzielenia się pomysłami i doświadczenia-

mi  na  pewno  zostanie  wypracowana  tematyka,  którą  warto  uwzględnić
w danej klasie. W ten sposób na każdym przedmiocie nauczania zostaną
zrealizowane wyznaczone treści. Wychowawca będzie mógł więc zadbać
o  to,  aby  jak  najwięcej  celów  osiągnął  uczeń  w  czasie  trzech  lat  nauki
w  gimnazjum.  Będzie  jednocześnie  miał  rozeznanie,  jakie  treści  były
w jego klasie realizowane i w jakim zakresie.

Poradnik wychowawcy

Planując spotkanie dotyczące ścieżek edukacyjnych z osobami

uczącymi w twojej klasie, pamiętaj o tym, aby:

•

przygotować argumenty, które przekonają sceptyków, że warto

działać wspólnie,

•

przygotować  propozycje  tematów  do  wykorzystania  i  form  ich

realizacji,

•

pokazać gotowe materiały do wykorzystania na wszystkich lek-

cjach,

•

przypomnieć,  że  obowiązek  realizacji  ścieżek  spoczywa  na

wszystkich nauczycielach, a więc i na nauczycielach, np. wycho-
wania fizycznego, chemii i matematyki,

•

pokazać  nauczycielom  przykłady  prac  projektowych  stworzo-

nych przez uczniów w czasie realizacji bloków tematycznych.

Jeśli nauczyciele, mimo twoich argumentów, będą mieli nadal

obawy typu: nie zdążę zrealizować programu, mam tak mało go-
dzin, zaproponuj, aby tematykę związaną z daną ścieżką zrealizo-
wać, np. w czasie walentynek, dnia wiosny itp.

Planując bloki tematyczne, można postąpić na dwa sposoby: albo do-

pasować temat do treści danej ścieżki, albo wybrać zagadnienie i oriento-
wać się, treści jakich ścieżek można wykorzystać. Na przykład budujemy
zajęcia do ścieżki edukacja regionalna. Proponujemy temat Sztuka ludo-
wa naszego regionu

. Załóżmy, że w naszym regionie twórcy ludowi zaj-

mują się garncarstwem. Wtedy:
– w  ramach  lekcji  języka  polskiego  uczniowie  przeprowadzą  wywiad

z twórcami ludowymi działającymi w naszym regionie,

56

– na lekcji informatyki uczniowie opracują graficznie zebrane wiadomości,
– na matematyce przy okazji omawiania zagadnień związanych z syme-

trią poznają wyroby twórców ludowych,

– na chemii omówią procesy zachodzące w czasie wypalania gliny,
– na geografii zastanowią się, jakie czynniki umożliwiły tworzenie na na-

szym terenie wyrobów glinianych,

– na lekcji historii dowiedzą się, od jak dawna prowadzi się wyrób glinia-

nych naczyń,

– na plastyce uczniowie sami spróbują uformować, a następnie wypalić

gliniane naczynie,

– na godzinę wychowawczą uczniowie przyniosą gliniane naczynia uży-

wane w ich domach i opowiedzą, do czego służą,

– na  lekcji  wychowania  fizycznego  można  zorganizować  wycieczkę  do

miejsc, w których wydobywa się glinę,

– na  lekcji  biologii  można  porozmawiać,  dlaczego  doniczki  gliniane  są

lepsze od plastikowych,

– na  lekcji  fizyki  uczniowie  mogą  omówić  fizyczne  właściwości  gliny

i możliwości jej wykorzystania.

Wyobraźmy sobie teraz, że nasi ucznio-

wie postanowili się zająć tematyką związa-
ną z wodą. Zagadnienia oscylujące wokół
problemu  woda  można  tak  zaplanować,
aby  wykorzystać  treści  różnych  ścieżek
edukacyjnych. Na przykład na zajęcia z ję-
zyka polskiego uczniowie poszukają wier-
szy  związanych  z  wodą  (edukacja  czytel-
nicza  i  medialna),  na  lekcji  biologii  za-
stanowią  się  nad  znaczeniem  wody  dla

organizmu ludzkiego (edukacja prozdrowotna), na geografii poznają cieki
oraz  naturalne  i  sztuczne  zbiorniki  wodne  najbliższej  okolicy  (edukacja
regionalna)  oraz  omówią  przyczyny  zanieczyszczenia  wody  (edukacja
ekologiczna), na godzinie wychowawczej przeanalizują słynny aforyzm:
Wszystko płynie

 (edukacja filozoficzna).

Jak  widać  z  powyższych  przykładów,  wykorzystanie  treści  ścieżek

edukacyjnych może się odbywać w trakcie realizacji programów naucza-
nia z poszczególnych przedmiotów. Problemem może być jedynie zdoby-
cie potrzebnych materiałów, których jest, niestety, jeszcze bardzo mało.

57

O realizacji ka¿dej ze œcie¿ek na lekcjach matematyki

s³ów kilka

Jedną z najważniejszych ścieżek edukacyjnych jest edukacja czytel-

nicza  i  medialna

.  Treści  tej  ścieżki  są  realizowane  w  mniejszym  bądź

większym zakresie w czasie niemal każdej lekcji, ponieważ uczeń komu-
nikuje się w różny sposób: czyta krótkie teksty (np. polecenia do zadań),
wyszukuje  potrzebne  informacje  z  różnych  źródeł.  Lekcje  matematyki
można tak zaplanować, aby wykorzystać również inne treści ścieżki. Pro-
simy uczniów o odszukanie w bibliotece szkolnej bądź w Internecie infor-
macji np. o Talesie. Sporządzenie odpowiedniej notatki i zamieszczenie
bibliografii powoduje, że dzieci uczą się sporządzania opisów bibliogra-
ficznych i bibliografii załącznikowej do własnych opracowań

, a to jest jed-

no z osiągnięć, które chcemy uzyskać, realizując tematykę ścieżki eduka-
cji czytelniczej i medialnej. Gdy uczniowie poznają nowe symbole mate-
matyczne, uczą się je stosować i rozpoznawać w tekstach, to nic innego
jak temat z cyklu Pojęcia komunikacji medialnej: znak, symbol, kod, ję-
zyk, denotacja, konotacja

.

Zagadnienia  związane  z  edukacją  ekologiczną  omawiamy  np.  przy

okazji tematyki dotyczącej potęg. Podajemy ilości ścieków powstających
w wyniku działalności człowieka w ciągu doby (zapisujemy dane w po-
staci  notacji  wykładniczej),  analizujemy  przyczyny  powstawania  tak
dużej ilości ścieków, zastanawiamy się nad sposobami ich zmniejszenia.

Denotacja – zakres nazwy, zbiór
wszystkich desygnatów nazwy.

Słownik języka polskiego PWN, 1992 r.

Konotacja  –  cechy  współoznaczane  łącznie
przez daną nazwę; zespół cech, których posiada-
nie  sprawia,  że  odpowiednie  przedmioty  należą
do tej samej klasy, są desygnatami danej nazwy.

Słownik języka polskiego PWN, 1992 r.

58

Lekcje  poświęcone  gromadzeniu  i  interpretowaniu  danych,  to  dobry
moment do porównywania np. emisji gazów w ciągu kilku ostatnich lat.
Realizujemy w ten sposób treść Przyczyny i skutki niepożądanych zmian
w litosferze, hydrosferze, atmosferze oraz biosferze

.

Wątki dotyczące edukacji

europejskiej

 wykorzystamy,

prosząc  uczniów  o  określe-
nie relacji pomiędzy waluta-
mi kilku państw europejskich
(tematy  dotyczące  przybli-
żeń).  Ćwicząc  umiejętność
wykonywania działań na licz-
bach rzeczywistych, możemy
wspólnie  z  uczniami  zapla-
nować  całodniowy  jadłospis

uwzględniający  ograniczenia  cenowe  kupowanych  produktów,  ich  war-
tość odżywczą i kaloryczną, nawiązując w ten sposób do treści Żywność
i żywienie

 ścieżki edukacja prozdrowotna.

Z edukacją filozoficzną na lekcjach matematyki nie mamy najmniej-

szego  problemu,  ponieważ  prawie  każdy  sławny  matematyk  był  filozo-
fem. Zatem rozwinięcie treści Filozofia a nauki szczegółowe jest dla nas
aktualne nie tylko przy okazji omawiania twierdzenia Pitagorasa.

Przekształcenia geometryczne (np. symetria osiowa i środkowa) umo-

żliwiają nam poznanie głównych zabytków architektury w regionie, a to
nic innego jak problematyka związana ze ścieżką edukacja regionalna.

Wykorzystanie treœci œcie¿ek edukacyjnych

W tym rozdziale podajemy przykłady scenariuszy lekcji matematyki,

wykorzystujących treści ścieżki edukacja czytelnicza i medialna. W opi-
sie  celów  zajęć  znajdą  się  więc  oprócz  celów  typowo  matematycznych
również cele wynikające z realizacji zagadnień związanych z daną ścież-
ką edukacyjną. Proponowane zajęcia można zaplanować wraz z nauczy-
cielami innych edukacji jako cykl jednodniowy lub kilkudniowy.

Lekcję Kąty w okręgu umieszczamy w cyklu lekcji powtórzeniowych.

Może zatem ona się odbyć pod koniec roku szkolnego lub w momencie,
w którym nauczyciel przystąpi do powtarzania wiadomości z geometrii.

59

Program MATEMATYKA
KROK PO KROKU
DKW-4014-91/99

Temat  przewidziany  do  realizacji
jako powtórzeniowy

SCENARIUSZ ZAJĘĆ
DLA KLASY III GIMNAZJUM
MATEMATYKA

KĄTY W OKRĘGU

60

Czas:

 45 minut.

Cele.

W czasie zajęć uczeń:

❐

przypomni sobie i będzie doskonalił umiejętności związane z kąta-
mi w okręgu,

❐

pozna własności dotyczące kąta dopisanego do okręgu,

❐

będzie posługiwał się analogiami, stawiał hipotezy i je weryfikował,

❐

przeprowadzi prosty dowód matematyczny,

❐

zapozna się z możliwościami praktycznego wykorzystania wiedzy
matematycznej,

❐

będzie sprawnie i szybko czytał, wybierając i zapisując informacje,

❐

posłuży się słowem, gestem i ruchem jako formą wypowiedzi.

Sposoby pracy:

❐

praca w grupach,

❐

inscenizacja,

❐

samoocena,

❐

refleksja.

Materiały do zajęć:

❐

Instrukcje do pracy grupy

 – kroki 1–3,

❐

Projektujemy widownię

 – krok 4,

❐

magnetofon, kasety magnetofonowe,

❐

tekst sceny balkonowej – fragment dramatu W. Szekspira Romeo
i Julia

,

❐

Arkusz refleksji

,

❐

cyrkle, linijki.

Uwagi:

❐

Na kilka dni przed lekcją wyznaczamy dwie osoby, które odegrają
role Romea i Julii. Wręczamy im tekst – fragment sceny balkonowej.
Prosimy,  aby  przygotowali  na  lekcję  inscenizację  tej  sceny.  Jeśli
nauka  tekstu  będzie  sprawiała  dzieciom  kłopot,  mogą  korzystać
w  czasie  przedstawienia  z  kartki.  Dobrze  jednak  by  było,  gdyby
uczniowie przygotowali odpowiednie stroje i dekoracje. Jeśli ode-
granie przez uczniów sceny balkonowej wydaje nam się z różnych
względów niewłaściwe, możemy poprosić uczniów o przygotowa-
nie inscenizacji fragmentu książki, którą aktualnie omawiają na lek-
cjach języka polskiego. Warto wtedy na lekcję zaprosić nauczycie-
la języka polskiego lub nawet część lekcji przeznaczoną na przed-
stawienie przygotować z nim wspólnie. Należy również zapewnić

61

inscenizacji  odpowiednią  oprawę  plastyczną.  Aktorów  prosimy
o dyskrecję, przedstawienie ma być dla innych niespodzianką.

❐

Zajęcia  powinny  się  odbywać  w  sali,  z  której  usuniemy  zbędne
ławki, co pomoże uczniom w drugiej części lekcji szybko przygo-
tować  ,,widownię”.  Uczniowie  będą  pracować  w  grupach,  zatem
stolików zostawiamy tylko tyle, ile ma być grup.

❐

Prosimy,  aby  uczniowie  na  lekcję  przynieśli  cyrkle  i  linijki.  Dla
zapominalskich możemy przygotować na stoliku nauczyciela kilka
cyrkli i linijek.

❐

W klasie słabszej możemy zrezygnować z prób udowodnienia od-
krytego przez uczniów twierdzenia. Możemy też nie wprowadzać
pojęcia kąt dopisany do okręgu, ograniczając się tylko do stwier-
dzenia, że na lekcji powtarzamy i utrwalamy zdobyte wiadomości
o kątach środkowych i wpisanych w okrąg.

Przebieg zajęć:

1.Dzielimy  uczniów  na  grupy;  każda  z  grup  zajmuje  miejsce  przy

osobnym stoliku.

2.Prosimy uczniów, aby przypomnieli wiadomości zdobyte w klasie I

i II dotyczące kątów w okręgu. Uczniowie podają twierdzenia doty-
czące kątów wpisanych w okrąg i opisanych na okręgu.

3.Rozdajemy uczniom Instrukcję do pracy grupy – krok 1–3. Ucznio-

wie pracują nad zadaniami.

4.Omawiamy otrzymane wyniki, jedna z grup przedstawia szczegóło-

we  rozwiązania.  Uczniowie  powinni  sformułować  i  ewentualnie
uzasadnić następujące twierdzenia:
Kąt wpisany i dopisany oparte na tym samym łuku mają równe miary.
Kąt dopisany ma miarę dwa razy mniejszą niż kąt środkowy oparty
na tym samym łuku.

5.Teraz  przystępujemy  do  zastosowań  zdobytych  wiadomości  –

uczniowie wspólnie projektują widownię – krok 4.

6.Uczniowie siadają na krzesłach ustawionych na widowni. Informu-

jemy  młodzież,  że  skoro  mamy  scenę  i  widownię,  to  powinno  się
odbyć przedstawienie. Zapowiadamy tytuł sztuki i wybrani wcześ-
niej uczniowie przedstawiają fragmenty sceny balkonowej.

7.Rozmawiamy z uczniami o ważnych, ich zdaniem, momentach w cza-

sie lekcji, o tym, czego się nauczyli. Uczniowie dokonują samooceny.

8.Uczniowie wypełniają Arkusze refleksji. Omówimy je na początku

następnych zajęć.

62

INSTRUKCJA DO PRACY GRUPY

W  czasie  zajęć  będziecie  wykorzystywać  poznane  twierdzenia  doty-

czące kątów w okręgu, poznacie też nowe twierdzenia, analogiczne do już
wam znanych.

Wykonujcie wszystkie polecenia po kolei.

KROK 1
Kroczek 1
Narysujcie okrąg i zaznaczcie w nim cięciwę nie będącą średnicą.

Kroczek 2
Przez jeden z końców cięciwy poprowadźcie styczną do okręgu.

Kroczek 3
Zaznaczcie kąty wypukłe, jakie styczna do okręgu tworzy z cięciwą.
Każdy z tych kątów nazywamy kątem dopisanym do okręgu.

Kątem dopisanym do okręgu nazywamy kąt o jednym ramieniu zawie-
rającym cięciwę i drugim stycznym do okręgu w jednym końcu cięciwy.

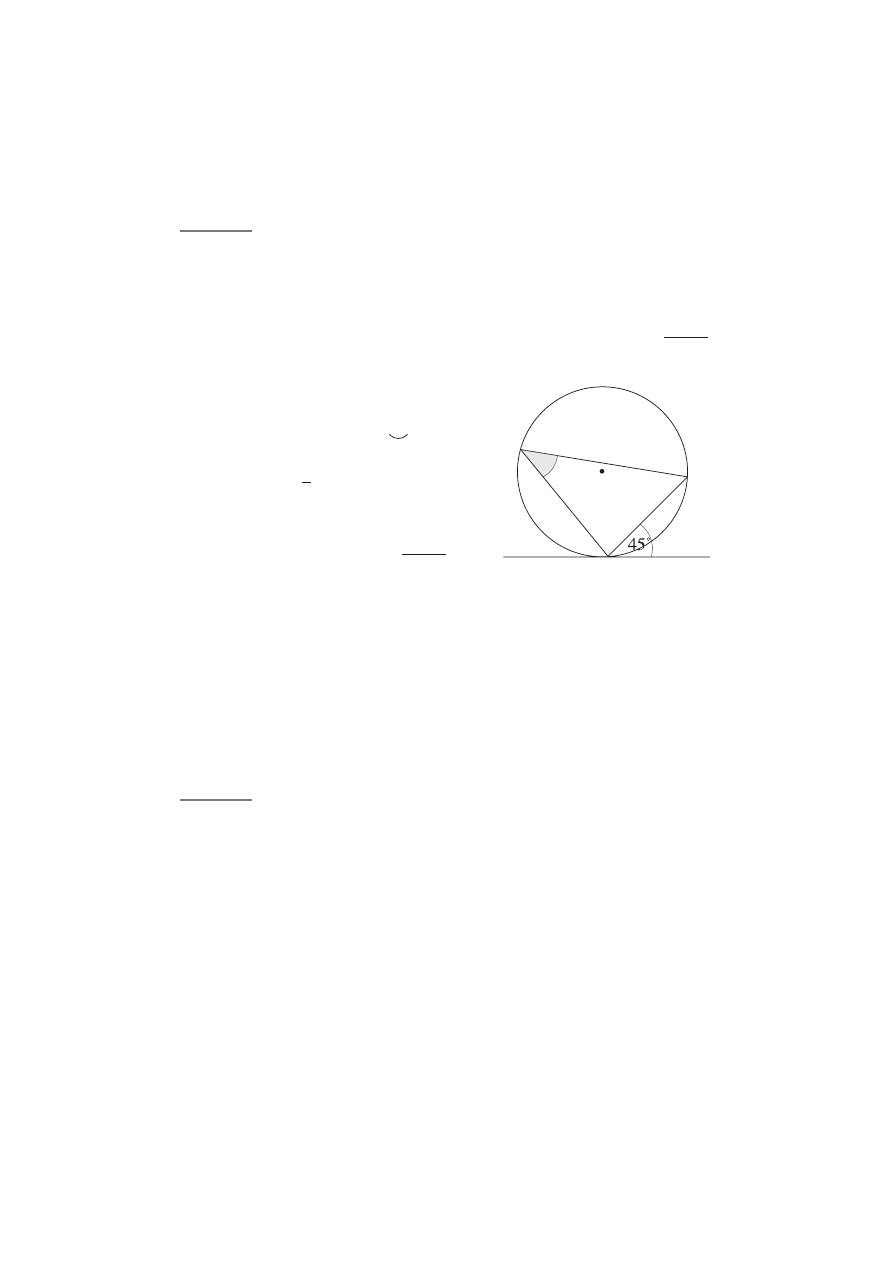
63

KROK 2
Kroczek 1
Uzupełnijcie zdanie, korzystając z rysunku.

Kąt dopisany do okręgu tworzy ze średnicą kąt prosty.
Kąt wpisany oparty na tym samym łuku co kąt dopisany ma miarę 

.

Kroczek 2
Uzupełnijcie zdanie, korzystając z rysunku.

Kąt wpisany oparty na łuku AB ma mia-

rę 45° i stanowi 

1

4

 długości okręgu.

Kąt dopisany do tego okręgu, oparty

na tym samym łuku ma miarę 

.

Kroczek 3
Spróbujcie uogólnić własność zaobserwowaną w kroczkach 1 i 2. Uzasad-
nijcie tę własność.

KROK 3
Sformułujcie  twierdzenie  dotyczące  kąta  dopisanego  do  okręgu  i  odpo-
wiadającego mu kąta środkowego opartego na tym samym łuku.

A

B

C

64

PROJEKTUJEMY WIDOWNIÊ

KROK 4
Kroczek 1
Przyjmuje  się,  że  najlepszy  kąt,
pod którym widać scenę, ma mia-
rę 53°. Zaprojektujcie widownię,
wykorzystując własności kąta do-
pisanego,  tak  aby  z  każdego  jej
miejsca można było obserwować
scenę pod kątem 53°.

Kroczek 2
A  teraz  wyobraźcie  sobie,  że  wasza  klasa  to  sala  teatralna.  Wyznaczcie
scenę i ustawcie tak krzesła, aby każdy z siedzących widział scenę pod
kątem najlepszego widzenia.

ARKUSZ REFLEKSJI

Napisz o swoich odczuciach w czasie lekcji. Czy zdarzyło się coś ważne-
go dla ciebie, czy podobały ci się zajęcia? A może masz jakieś uwagi?

Scena

65

Program MATEMATYKA
KROK PO KROKU
DKW-4014-91/99

Dział

Równania, nierówności,
układy równań

Numer i temat zajęć

71. Praktyczne wykorzystanie
układów równań

SCENARIUSZ ZAJĘĆ
DLA KLASY III GIMNAZJUM
MATEMATYKA

ZASZYFROWANA WIADOMOŚĆ

66

Czas:

 45 minut.

Cele.

W czasie zajęć uczeń:

❐

będzie doskonalił umiejętność rozwiązywania układów równań,

❐

będzie rozpoznawał i nazywał rodzaje układów równań,

❐

wykorzysta  graficzną  interpretację  układu  równań  do  określania
liczby jego rozwiązań i znalezienia tych rozwiązań,

❐

będzie  analizował  komunikaty  informacyjne,  odczytywał  znaki
i symbole w nich zawarte,

❐

będzie projektował komunikat medialny.

Sposoby pracy:

❐

praca w grupach,

❐

wspólna rozmowa.

Materiały do zajęć:

❐

karta Zadanie dla grupy,

❐

arkusz Zadania do rozwiązania,

❐

tekst Pilna wiadomość.

Uwagi:

❐

Zadania  dla  grup  są  tak  dobrane,  aby  ich  rozwiązanie  nie  zajęło
więcej niż 15 minut. Niektóre z zadań można rozwiązać w pamięci,
niektórych można wcale nie rozwiązywać (zad. 6).

❐

Zajęcia można przeprowadzić jako podsumowujące rozważania na
temat układów równań.

Przebieg zajęć:

1.Informujemy uczniów, że otrzymaliśmy pilną zaszyfrowaną wiado-

mość. Prosimy uczniów o pomoc w jej rozszyfrowaniu.

2.Dzielimy młodzież na grupy i wręczamy liderom grup Zadania dla

grupy

, Zadania do rozwiązania i tekst Pilna wiadomość.

3.Uczniowie rozwiązują zadania, rozszyfrowują wiadomość.
4.Następuje prezentacja prac grup. Pytamy uczniów:

– rozwiązanie którego zadania sprawiło kłopot i dlaczego,
– czy lekcja pomogła w usystematyzowaniu wiadomości o układach

równań,

– jakie umiejętności wykorzystali w czasie pracy,

67

– czy  rozwiązali  wszystkie  zadania,  czy  odgadli  znaczenie  niektó-

rych liczb,

– którego z zdań nie potrzeba było rozwiązywać, a tylko wystarczy-

ło uważnie je przeczytać,

– czy analiza komunikatu informacyjnego sprawiła kłopot i czy były

problemy z zamianą znaków na litery.

5.Oceniamy pracę uczniów. W ramach pracy domowej polecamy, aby

uczniowie ułożyli komunikat, który mógłby być zamieszczony w pra-
sie bądź podany w radiu lub telewizji. Komunikat ma zawierać za-
szyfrowaną wiadomość i być napisany z użyciem specyficznego ro-
dzaju języka używanego przez media. Odszyfrować wiadomość bę-
dzie mogła tylko osoba posiadająca klucz do użytego w informacji
kodu.  Klucz  należy  również  podać.  Może  on  być  skonstruowany
podobnie  jak  ten  z  lekcji.  Można  przy  tym  wykorzystać  zadania
z podręcznika lub zbioru zadań.

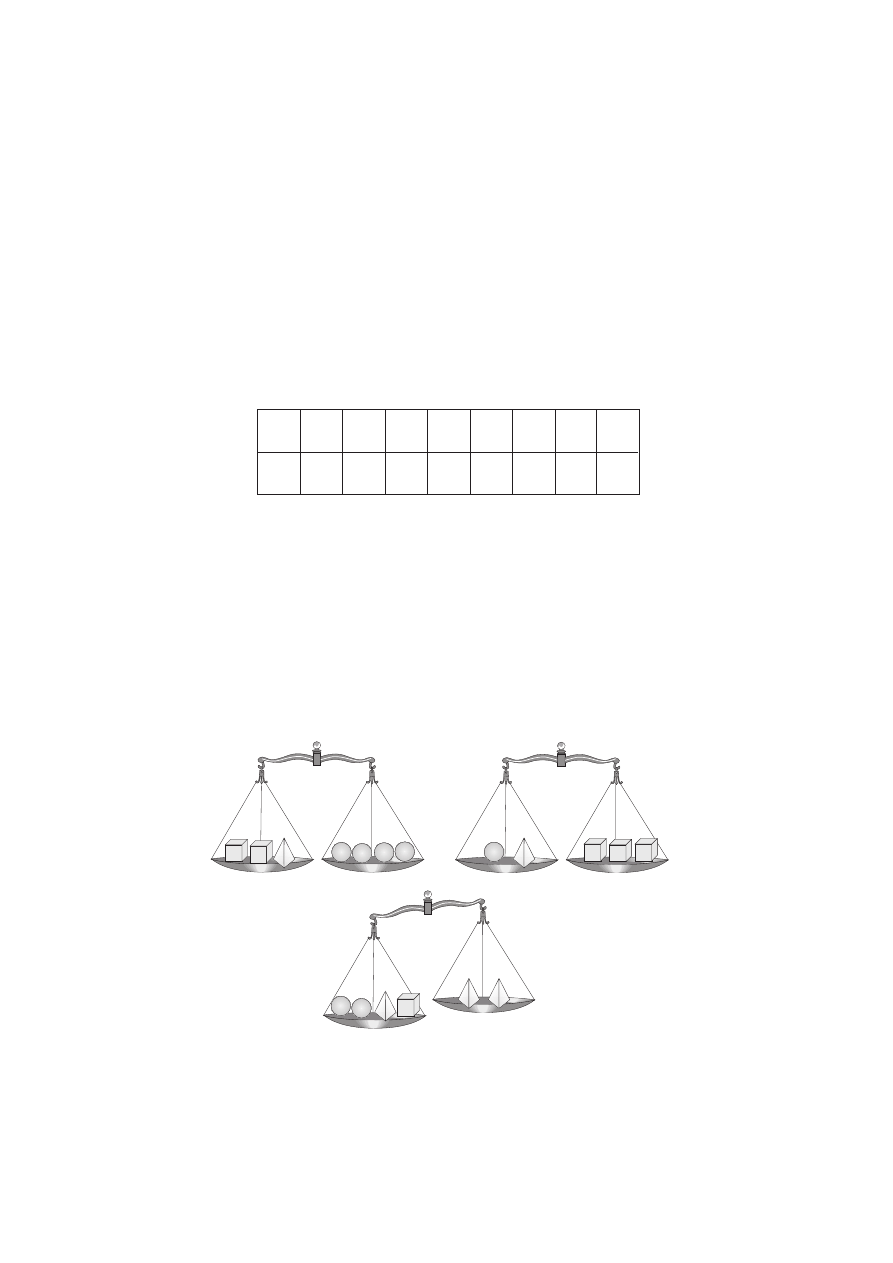
68

ZADANIE DLA GRUPY

Zadaniem grupy jest rozszyfrowanie wiadomości, tzn. podanie miejsca,
dnia i godziny spotkania oraz imienia nadawcy.
Kluczem do rozwiązania jest hasło składające się z dziewięciu liter. Lite-
ry  te  znajdziecie,  rozwiązując  zadania  zapisane  na  arkuszu  Zadania  do
rozwiązania

.  Każdą  ze  znalezionych  liter  wpiszcie  do  tabeli  pod  liczbą

odpowiadającą numerowi zadania. Odczytajcie hasło i rozszyfrujcie wia-
domość.

1

2

3

4

5

6

7

8

9

ZADANIA DO ROZWI¥ZANIA

Zadanie 1.

Przystojny Fred i Mały Alan podzielą wydobyte złoto równo pomiędzy sie-
bie. Mały Alan weźmie złoto znajdujące się na prawej szalce wagi (rysu-
nek 3), a Fred na lewej. Ile sześciennych sztabek złota powinni jeszcze
położyć na prawej szalce, aby podział był sprawiedliwy? Znalezioną licz-
bę wyraźcie słowami i do tabeli wpiszcie pierwszą literę wyrazu.

Rys. 1

Rys. 2

Rys. 3

69

Zadanie 2.

Urszula twierdzi, że jeżeli w kratkę wpisze liczbę 6, to układ równań

x

y =

y

x

+

=

+







4

3

3 4

5

będzie miał dokładnie jedno rozwiązanie. Natomiast Paulina jest przeko-
nana, że taki układ nie będzie miał rozwiązania. Wpiszcie do tabeli pierw-
szą literę imienia dziewczynki, która ma słuszność.

Zadanie 3.

Żona i mąż w ubiegłym roku ważyli łącznie 130 kg. W ciągu roku żona
utyła 6 kg, a mąż schudł 6 kg. Teraz mąż waży tylko 10 kg więcej od żony.
Czyja waga, męża czy żony, wyraża się liczbą podzielna przez 6? Wpisz-
cie pierwszą literę wyrazu żona lub pierwszą literę wyrazu mąż do tabeli.

Zadanie 4.

Mucha porusza się po prostej o równaniu y = –x – 2, a pająk po prostej
o równaniu y = x – 6. Podajcie pierwszą współrzędną punktu, w którym
pająk  i  mucha  mogą  się  spotkać.  Zapiszcie  otrzymaną  liczbę  słownie
i wpiszcie do tabeli jej drugą literę.

Zadanie 5.

Dodajcie stronami układ równań

x

y

x

y

−

=

+

=







3

6

3

4.

Po prawej stronie otrzymanego równania uzyskaliście pewną liczbę. Wy-
raźcie  słowami  tę  liczbę  i  wpiszcie  do  tabeli  trzecią  literę  otrzymanego
wyrazu.

Zadanie 6.

Za sokoła i konia pewien sułtan zapłacił 400 dukatów. Po jakimś czasie
zwierzęta znudziły mu się, więc sprzedał je za łączną kwotę 330 dukatów.
Przy czym sokoła sprzedał o 10% taniej niż kupił, a konia sprzedał za 80%
początkowej ceny. Które zwierzę kupił sułtan za 300 dukatów: konia czy
sokoła? Wpiszcie do tabeli drugą literę nazwy zwierzęcia.

70

Zadanie 7.

Narciarz jadący po stoku góry  zakreślił
ślad taki, jak na rysunku. Jakiego układu
równań jest to wykres? Wpiszcie do ta-
beli pierwszą literę nazwy tego układu.

Zadanie 8.

Benedykt zapisał następujące równanie x – 4y = 6, a Grzegorz pomnożył
obie strony tego równania przez 3. Zygmunt z obu tych równań utworzył
układ. Jaki to rodzaj układu? Wpisz do tabeli pierwszą literę nazwy tego
układu.

Zadanie 9.

Czy to prawda, że bilet ulgowy kosztuje 5 zł? Wpisz do tabeli drugą literę
odpowiedniego wyrazu: tak lub nie.

PILNA WIADOMOή

Musimy się koniecznie spotkać. Czekam UI  marca o godzinie JN
w kawiarni 864589.
                                        198

71

Program MATEMATYKA
KROK PO KROKU
DKW-4014-91/99

Dział

Doświadczenia losowe

Numer i temat zajęć

33.– 34. Zbieranie danych
statystycznych i ich interpretacja

SCENARIUSZ ZAJĘĆ
DLA KLASY III GIMNAZJUM
MATEMATYKA

ZBIERANIE
DANYCH STATYSTYCZNYCH
I ICH INTERPRETACJA

72

Czas:

 45 minut.

Cele.

W czasie zajęć uczeń:

❐

będzie odczytywał i interpretował dane przedstawione graficznie,

❐

będzie przedstawiał dane liczbowe w postaci diagramu i tabeli,

❐

będzie doskonalił umiejętność współpracy z partnerem,

❐

będzie posługiwał się przybliżeniami,

❐

zdobędzie wiadomości dotyczące wybranych województw w Polsce.

Sposoby pracy:

❐

praca w parach,

❐

prezentacja.

Materiały do zajęć:

❐

karta pracy Kilka słów o kilku województwach,

❐

mapa administracyjna Polski.

Uwagi:

❐

Mapę  z  podziałem  administracyjnym  kraju  wieszamy  na  stojaku
w klasie.

Przebieg zajęć:

1.Informujemy uczniów, że na lekcji będą pracować w parach. Efekty

pracy każdej pary zostaną ocenione przez nauczyciela. Uczniowie
pracujący wspólnie otrzymają takie same oceny.

2.Rozdajemy każdej z par kartę pracy Kilka słów o kilku wojewódz-

twach

.

3.Uczniowie pracują 25 minut nad zadaniem. Po upływie tego czasu

wyznaczeni przez nas uczniowie prezentują efekty pracy.

4.Ich wystąpienie oceniają uczniowie wspólnie z nami.
5.Od pozostałych par zbieramy karty pracy, które ocenimy w domu.
6.W czasie dyskusji podsumowującej lekcję wspólnie zastanawiamy się:

– czy graficzna prezentacja danych ułatwia ich interpretację,
– w jaki sposób i gdzie można szybko znaleźć potrzebne dane licz-

bowe o którymś z województw,

– czy posiadamy jeszcze jakieś inne niż te, które były zaprezentowa-

ne na lekcji, wiadomości o województwach.

7.W ramach pracy domowej prosimy zebrać dane o dowolnym woje-

wództwie (ale innym niż omówione na lekcji) oraz zaprezentowanie
ich w postaci graficznej.

73

KARTA PRACY
KILKA S£ÓW O KILKU WOJEWÓDZTWACH

LUBELSKIE
Powierzchnia – 25 115 km

2

Liczba ludności – 2242 tys.
Liczba powiatów – 20
Liczba gmin – 213

MAZOWIECKIE
Powierzchnia – 35 715 km

2

Liczba ludności – 5065 tys.
Liczba powiatów – 38
Liczba gmin – 325

ŚLĄSKIE
Powierzchnia – 12 309 km

2

Liczba ludności – 4894 tys.
Liczba powiatów – 17
Liczba gmin – 166

PODKARPACKIE
Powierzchnia – 17 890 km

2

Liczba ludności – 2117 tys.
Liczba powiatów – 20
Liczba gmin – 160

KUJAWSKO-POMORSKIE
Powierzchnia – 17 970 km

2

Liczba ludności – 2098 tys.
Liczba powiatów – 19
Liczba gmin – 144

Rzeszów

Lublin

Bydgoszcz

Warszawa

Katowice

74

Korzystając z przedstawionych na karcie pracy informacji, rozwiąż po-

niższe zadania.

1.Sporządź  diagram  przedstawiający  gęstość  zaludnienia  w  wybra-

nych województwach.

2.  Posługując  się  mapą,  znajdź  stolicę  każdego  z  wybranych  woje-

wództw.

3.Ile  razy  powierzchnia  województwa  podkarpackiego  jest  mniejsza

od powierzchni województwa mazowieckiego?

4.Oblicz średnią liczbę powiatów w województwach.
5. Opisz herb stolicy wybranego województwa.
6. Odszukaj na mapie województwo lubuskie i powiedz, z jakimi woje-

wództwami graniczy. Które z tych województw ma największą po-
wierzchnię?

7.Narysuj tabelę i wypełnij ją danymi przedstawiającymi liczbę gmin

w poszczególnych województwach.

Warszawa

Gdańsk

Olsztyn

Białystok

Lublin

Rzeszów

Kraków

Katowice

Opole

Wrocław

Szczecin

Poznań

Bydgoszcz

Łódź

Kielce

WARMIŃSKO-
-MAZURSKIE

PODLASKIE

LUBELSKIE

PODKARPACKIE

MAŁOPOLSKIE

ŚLĄSKIE

OPOLSKIE

DOLNOŚLĄSKIE

LUBUSKIE

ZACHODNIO-
POMORSKIE

POMORSKIE

KUJAWSKO-
-POMORSKIE

WIELKOPOLSKIE

MAZOWIECKIE

ŁÓDZKIE

ŚWIĘTO-
KRZYSKIE

Zielona Góra

75

Która metoda jest lepsza?

Planując  lekcję,  która  będzie  atrakcyjna  dla

ucznia,  musimy  brać  pod  uwagę  możliwości
dzieci, wymagania programowe i bazę material-
ną szkoły, tzn. dostępność pomocy naukowych,
możliwości lokalowe, dostęp do nowoczesnych
źródeł informacji. Niestety, nie wszystkie lekcje
udaje nam się przeprowadzić w sposób pasjonu-
jący i mobilizujący ucznia. Aby zdobyć umiejętności matematyczne, trze-
ba wykonać wiele ćwiczeń i szablonowych zadań, co nie zawsze jest cie-
kawe i porywające. Postarajmy się więc, aby przynajmniej raz w tygodniu
przygotować materiały na takie zajęcia, które zmuszą naszych uczniów do
samodzielnej  pracy,  wymagającej  zaangażowania  wszystkich  uczniów.
Mogą nam w tym pomóc, np. propozycje scenariuszy zajęć umieszczone
w naszych poradnikach metodycznych dla nauczyciela lub inne materiały
dostarczające  gotowych  pomysłów  na  konkretne  lekcje.  Jeśli  pokusimy
się o samodzielne opracowanie scenariusza zajęć, możemy oprzeć się na
jednej z aktywizujących metod nauczania, przedstawionych poniżej.

METODY AKTYWIZUJĄCE
W PRAKTYCE

Metoda – świadome i konsekwentnie
stosowany sposób postępowania dla
osiągnięcia określonego celu; zespół
celowych czynności i środków.

Słownik języka polskiego PWN, 1992 r.

76

Metoda  nauczania  decyduje  w  znacznym  stopniu  o  ilości  i  jakości

przyswajanej wiedzy. Właściwy jej wybór jest więc bardzo ważny i wy-
maga dużej wprawy. Istnieje wiele klasyfikacji metod nauczania. Dla na-
uczyciela nie ważna jest jednak nazwa danej metody, ale efekty, jakie ona
przynosi. Jeśli chcemy, aby w naszej pracy dominował model uczenia się,
a nie nauczania, spróbujmy przyjrzeć się metodom aktywnym. Metody te
mogą  być  stosowane  począwszy  od  nauczania  zintegrowanego  do  klas
maturalnych. Stosowanie tych metod pomaga w samodzielnym zdobywa-
niu przez ucznia wiedzy i umiejętności. Nauczyciel jest tylko organizato-
rem  i  doradcą.  Stosowanie  aktywnych  metod  pozwala  na  zwiększenie
skuteczności  uczenia  się,  integracji  i  korelacji  umiejętności,  rozwoju
twórczego myślenia i kreatywności ucznia, lepszej motywacji ucznia do
pracy. Umożliwia również rozwój umiejętności współpracy w grupie, ko-
munikowania się, planowania i organizowania własnej pracy. Uczeń bie-
rze większą odpowiedzialność za efekty swojej pracy, jest w większym
stopniu zainteresowany jej wynikami, potrafi prezentować swoje dokona-
nia i przeprowadzić samoocenę.

Stosowanie 

metod  aktywizujących,

to  nauczanie  polegające  na  wzajem-
nym oddziaływaniu nauczyciela i ucznia
w celu spowodowania zmian w sposo-
bie działania i uczenia.

Stosowanie 

metod aktywnych,

to  uczenie  się  prowadzące  do
trwałych zmian w działaniu i my-
śleniu,  do  zdobywania  nowych
doświadczeń.

Przyk³ady metod aktywizuj¹cych

Burza  mózgów.

  Metoda  ta  będzie

przydatna w momencie, gdy uczniowie
wspólnie będą rozwiązywać jakiś pro-
blem.  W  pierwszej  fazie  pozwalamy
uczniom podawać różne, nawet najbar-
dziej niewiarygodne rozwiązania dane-
go problemu. Dopiero następnie ocenia-
my  i  analizujemy  zgłoszone  pomysły

i wreszcie wybrane rozwiązania stosujemy w praktyce. Metodę możemy
stosować, pracując z całą klasą lub gdy uczniowie pracują w grupach (wte-
dy lider każdego z zespołów zbiera pomysły uczestników swojej grupy).

77

Ważne jest przy tym, aby:

•

pomysł  każdego  z  uczniów  (nawet  ten  najbardziej  niewiarygodny)
był brany pod uwagę,

•

nie krytykować i nie wyśmiewać pomysłów innych,

•

zgłaszać pomysł w czasie wyznaczonym przez nauczyciela i na jego
znak,

•

każdy pomysł został zapisany.

W praktyce możemy tę metodę zastosować, np. wprowadzając doda-

wanie dwóch wyrażeń wymiernych.

Etapy lekcji mogą wyglądać następująco.

Krok 1

Przedstawiamy problem, który
chcemy wspólnie rozwiązać.

Dziś zastanawiamy się, w jaki sposób
dodać dwa wyrażenia wymierne.

Krok 2

Zapisujemy  problem  na  tabli-
cy lub na kartonie.

5

5
1

5

1

2

x

x

x

x

+

−

−

−

+

Krok 3

Określamy zasady pracy.

W ciągu najbliższych 10 minut może-
cie  podawać  nawet  najbardziej  zwa-
riowane pomysły na rozwiązanie tego
problemu. Każdy z pomysłów zapiszę
na tablicy.

Krok 4

Uczniowie zgłaszają pomysły,
nauczyciel  zapisuje  te  pomy-
sły na tablicy.

•

skrócić wyrażenie

•

rozłożyć na czynniki

•

pomnożyć oba wyrażenia przez 2

•

rozłożyć  mianownik  pierwszego
wyrażenia na czynniki

•

sprowadzić  do  wspólnego  mianow-
nika

•

dodać liczniki

78

Krok 5

Następuje  wybór  najbardziej
przydatnego  i  możliwego  do
zrealizowania pomysłu.

Przedyskutujcie teraz w parach przed-
stawione pomysły i wybierzcie najlep-
szy z nich.
Uczniowie dzielą się swoimi przemy-
śleniami  i  wspólnie  orzekają,  że  naj-
prościej  będzie  postąpić  podobnie  jak
przy dodawaniu ułamków, a więc spro-
wadzić wyrażenia do wspólnego mia-
nownika i dodać liczniki.

Krok 6

Stosowanie  wybranego  roz-
wiązania w praktyce.

5 5

1

5

1

2

x

x

x

x

+

−

−

−

+

=

 

(

) (

)(

)

(

)(

)

5

5

5

1

1

1

x

x

x

x

x

+

+

−

+

−

+

=

(

)(

)

=

=

+ +

+ −

−

−

+

5

5

5

5

1

1

2

x

x

x

x

x

x

(

)(

)

=

=

+

−

+

x

x

x

x

2

1

1

 

(

)

(

)(

)

x x

x

x

x

x

+

−

+

=

−

1

1

1

1

Metoda aktywnego opisu.

 Metoda aktywnego

opisu, to metoda polegająca na lepszym zapamię-
tywaniu  cech  i  własności  przedmiotów,  zjawisk,
osób, liczb, figur itp. za pomocą wizualizacji pro-
blemu, analogii i systemu skojarzeń. Można stoso-
wać ją, pracując z całą klasą bądź w grupach.

Metodę  aktywnego  opisu  można  wykorzystać,

omawiając np. budowę stożka.

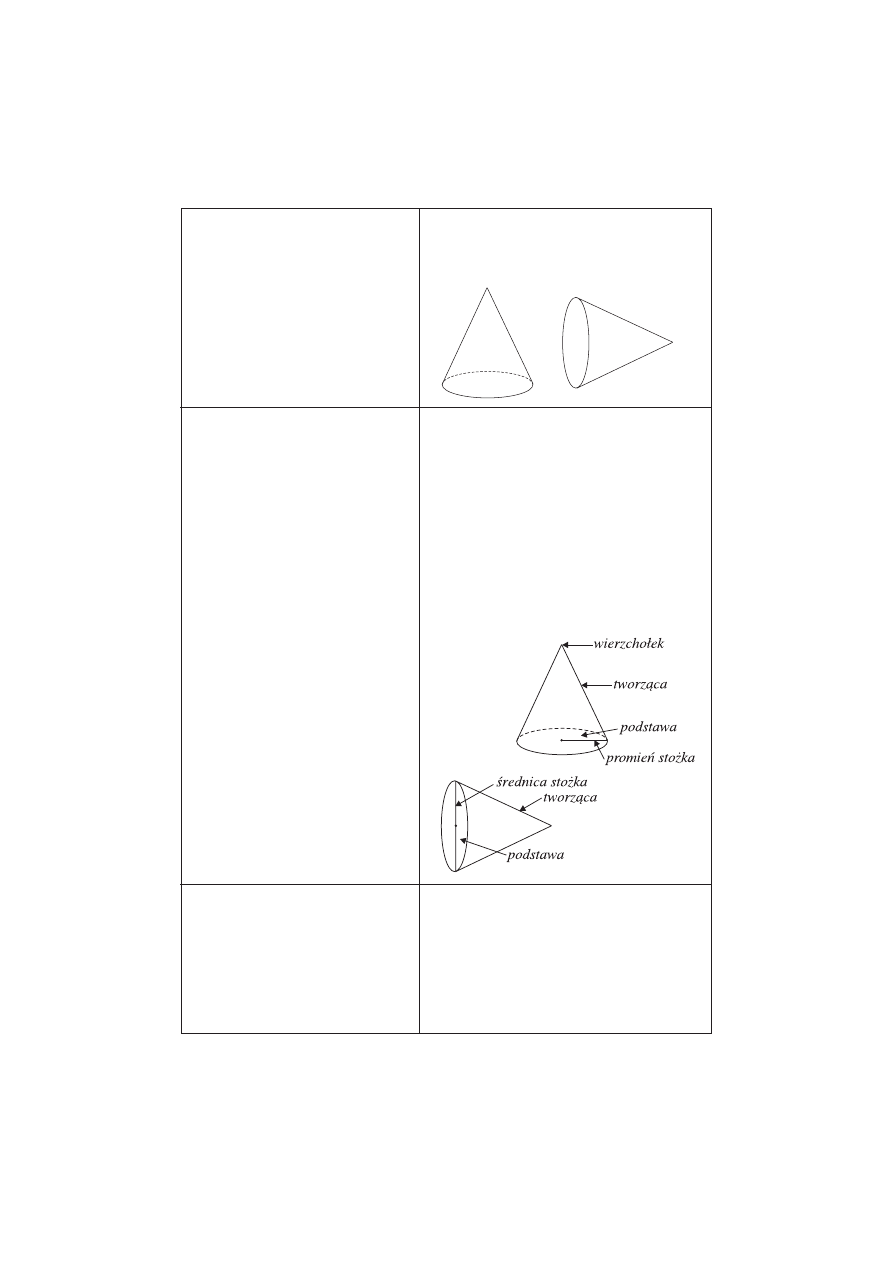
79

Krok 1

Polecamy,  aby  kilku  uczniów
narysowało  na  tablicy  figury,
o których mówimy na lekcji.

Proszę, abyście narysowali na tablicy
dwa różne stożki.

Krok 2

Na  zasadzie  analogii  i  skoja-
rzeń z budową znanych figur,
uczniowie  określają  elementy
narysowanych na tablicy figur
i zaznaczają je na rysunku.

Budowa  stożka  przypomina  budowę
walca, ale również budowę ostrosłupa.
Posługując  się  analogią,  spróbujmy
wyodrębnić elementy figur narysowa-
nych  na  tablicy.  Proszę,  aby  osoby,
które  mają  pomysły,  jak  mogą  nazy-
wać się elementy stożka, podchodziły
do  tablicy  i  wskazywały  te  elementy
oraz zapisywały ich nazwy.

Krok 3

Wspólna rozmowa o tym, czy
dokonany  opis  jest  właściwy.
Naniesienie ewentualnych po-
prawek i uzupełnień.

Wszyscy uczniowie dobrze zaznaczy-
li  elementy  stożków.  Na  jednym  ry-
sunku brak tylko zaznaczonego wierz-
chołka.  Proszę,  aby  Adam  wskazał,
gdzie ten wierzchołek się znajduje.

80

Pytania  do  ekspertów.

  Metoda  ta  po-

zwala na wykorzystanie różnych technik in-
formacyjnych  oraz  umiejętne  przekazanie
zdobytych  informacji.  Wykorzystujemy  ją
w  celu  wyćwiczenia  umiejętności  uczenia
się od innych. Grupę ekspertów wybieramy
na kilka dni przed planowaną lekcją. Prze-
kazujemy  im  problem,  nad  którym  muszą
pracować w domu. Możemy dołączyć pyta-
nia  pomocnicze.  Eksperci  mają  za  zadanie

zebrać materiał na zadany temat, wykorzystując różne źródła informacji.
Każdy z ekspertów musi być tak przygotowany, aby odpowiedzieć na py-
tania, które zadadzą mu koledzy w czasie lekcji. Powinien również zgro-
madzić  takie  wiadomości,  aby  zaciekawić  kolegów  danym  problemem.
Zadaniem eksperta będzie przekazanie zdobytej wiedzy kolegom.

Lekcję z wykorzystaniem metody pytań do ekspertów możemy prowa-

dzić, np. wprowadzając pojęcie tangensa kąta ostrego w trójkącie prosto-
kątnym.

Poznaliście już jedną z funkcji  trygonometrycz-
nych  –  funkcję  sinus.  Oprócz  tej  funkcji  znamy
również inne funkcje trygonometryczne, np. funk-
cję  cosinus,  którą  poznacie  na  następnej  lekcji.
Chcemy, abyście spróbowali samodzielnie zdobyć
informacje na temat jeszcze innej funkcji – funkcji
tangens.  Postarajcie  się  wykorzystać  w  tym  celu
różne źródła informacji. Zdobyta wiedza musi być
jednak na tyle rzetelna i solidna, abyście wystąpili
w  charakterze  ekspertów,  których  zadaniem  bę-
dzie przekazanie swojej wiedzy kolegom. Jest was
pięcioro. W czasie lekcji każdy zostanie przydzie-
lony do innej grupy, a więc każdy musi dyspono-
wać pełną wiedzą na dany temat. Waszym zada-
niem  będzie  również  zainteresowanie  innych
funkcją tangens, a więc przygotujcie ciekawostki
na jej temat, przykłady wykorzystania w praktyce.

Krok 1

Wybieramy grupę
ekspertów i przed-
stawiamy temat,
nad którym grupa
ta ma pracować.
Określamy czas
wykonania pracy.

81

Aby ułatwić zadanie, przedstawiam listę pytań, na
które musicie znać odpowiedź. Nie ograniczajcie
się  jednak  tylko  do  odpowiedzi  na  dane  pytania.
Wzbogaćcie  swoje  wystąpienia,  możecie  nawet
przygotować materiały w formie graficznej.
Nauczyciel  przekazuje  ekspertom  listę  pytań,  na
której mogą się znaleźć następujące problemy:
– co nazywamy tangensem kąta ostrego w trójką-

cie prostokątnym,

– jak obliczyć tangens 60°,
– jak  obliczyć  długość  drugiej  przyprostokątnej

trójkąta prostokątnego, w którym dany jest tan-
gens jednego z kątów ostrych i przyprostokątna
leżąca naprzeciw tego kąta.

Krok 2

Przekazujemy
ekspertom pytania
pomocnicze.

Przedstawiam ekspertów, którzy wiedzą wszystko
o funkcji tangens. Zadaniem każdej grupy będzie
dowiedzieć  się  jak  najwięcej  o  tej  funkcji,  gdyż
w  drugiej  części  lekcji  będziecie  już  bez  pomocy
eksperta musieli rozwiązać kilka zadań na ocenę.

Krok 3

W oznaczonym
dniu dzielimy kla-
sę na grupy. Do
każdej grupy przy-
dzielamy eksperta,
którego zadaniem
będzie zapoznanie
uczniów z tema-
tem podanym na
początku zajęć.

Ekspert odpowiada na pytania, przedstawia cieka-
wostki i zastosowania funkcji tangens.

Krok 4

Ekspert przekazuje
swoją wiedzę gru-
pie, która jest pod
jego opieką.

82

Każda z grup rozwiązuje zadania. Eksperci przy-
glądają się pracy swoich grup. Ale nie wolno im
podpowiadać. Ich celem jest zaobserwowanie, ja-
kie umiejętności udało się im przekazać, a na jakie
zwrócili  zbyt  małą  uwagę.  Można  wykorzystać
zadania z podręcznika lub zbioru zadań.

Krok 5

Uczniowie rozwią-
zują zadania.

Ekspert otrzymuje taką ocenę, jak grupa, z którą
pracował.  Każda  z  grup  wypowiada  się  również
na temat umiejętności eksperta.

Krok 6

Następuje przed-
stawienie prawi-
dłowych wyników
i ocena pracy
uczniów.

Odgrywanie  ról.

  Korzystając  z  tej

metody  uczniowie  na  lekcjach  mate-
matyki  mogą  odgrywać  role,  wcielając
się  w  postacie  z  przeszłości,  poznając
wcześniej  realia  danej  epoki  oraz  spoj-
rzenie ówczesnych ludzi na świat. Mło-
dzież  może  oczywiście  odgrywać  role
również  współczesne,  a  nawet  z  przy-
szłości.  Konwencja  przez  nas  przyjmo-
wana  zależna  jest  od  potrzeb  i  możli-
wości uczniów.

Metodę  tę  możemy  w  klasie  III  zastosować  przy  okazji  omawiania

twierdzenia Talesa. Prosimy jednego z uczniów, aby odegrał rolę Talesa.
Innego z uczniów wyznaczmy do roli współczesnego Talesowi uczonego
– sceptycznie nastawionego do osiągnięć Talesa. Jeszcze inny uczeń bę-
dzie uczonym dwudziestopierwszowiecznym, który przedstawi zastoso-
wania najważniejszych twierdzeń firmowanych nazwiskiem Talesa. Każ-
dy z uczniów powinien się w domu zapoznać z historią życia i dokonania-
mi  wielkiego  uczonego.  Młodzież  ma  za  zadanie  przygotować  w  domu
kilka scen, tak skonstruowanych, aby oglądający je uczniowie jak najwię-
cej  dowiedzieli  się  o  życiu  i  osiągnięciach  matematycznych  Talesa.
Uczniowie mogą się przebrać w stroje z epoki, w której żył i tworzył Tales.

83

Można też wprowadzić narratora, który będzie informował widzów, gdzie
i kiedy dzieją się poszczególne sceny oraz kim są występujące postacie.

Jeśli uważamy, że nasza klasa nie poradzi sobie z tym zadaniem, może-

my  sami  przygotować  odpowiedni  scenariusz  i  tylko  poprosić  uczniów
o odegranie ról.

Film.

 W metodzie tej do opisu sy-

tuacji wykorzystuje się klatki filmo-
we,  które  odpowiednio  poukładane
utworzą rozwiązanie problemu. Dzię-
ki filmowi ważne informacje można
przekazywać  w  formie  wizualnej,
zaangażować  do  pracy  wszystkich
uczniów,  spowodować,  aby  ucznio-
wie  uporządkowali  swoją  wiedzę
i wykorzystali ją do poznania nowego obszaru matematyki. Do tworzenia
filmu  można  wykorzystać  fotografie  lub  ,,klatki”  zawierające  rysunki
wykonane  przez  nauczyciela.  Pracujący  tą  metodą  uczniowie  nabywają
umiejętności skutecznego porozumiewania się, koncentracji, wyszukiwa-
nia informacji oraz kojarzenia faktów. Metodę filmu możemy wykorzy-
stać omawiając, np. zagadnienia związane z dzieleniem wyrażeń wymier-
nych. Uczniowie mogą pracować w parach, w grupach bądź indywidualnie.

Krok 1

Wręczamy uczniom koperty, informując ich, że zawierają one klatki fil-
mowe. Zadaniem uczniów jest takie ułożenie klatek filmowych, aby po-
wstał film, obrazujący, w jaki sposób podzieliliśmy dwa wyrażenia wy-
mierne.  Niewykorzystane  klatki  filmowe  mogą  posłużyć  uczniom  do
stworzenia własnych obrazów. Mogą również zaopatrzyć film w napisy,
które zastąpią ścieżkę dźwiękową.
Uwaga!

 W klasie zdolniejszej, każda grupa może otrzymać inne obrazki,

tzn. obrazki pokazujące sposób dzielenia innych wyrażeń.

Krok 2

Uczniowie pracują nad zadaniem, układają obrazki w odpowiedniej kolej-
ności.

84

Krok 3

Następuje  prezentacja  wykonanych  filmów.  Uczniowie  oceniają  prace
oraz wybierają filmy, na których najlepiej zaprezentowano dzielenie da-
nego  wyrażenia.  Staramy  się  teraz  uogólnić  problem  i  porozmawiać
o tym, w jaki sposób podzielić dwa dowolne wyrażenia wymierne.

Krok 4

Każda z grup tworzy swój film, a następnie miesza wykonane kadry fil-
mowe.  Następnie  wręcza  je  sąsiedniej  grupie,  która  musi  ułożyć  kadry
w odpowiedniej kolejności.

6

2

3

6

2

9

2

3

:

x

x

x

x

x

x

+

+

+

−

6

2

3

9

6

2

2

3

x

x

x

x

x

x

+

+

−

+

⋅

(

) (

)(

)

(

)

2 3

1

3

3

3

2 3

1

x x

x

x x

x

x

+

+

−

+

+

⋅

(

)

x x x

1

3

1

⋅

−

(

)

(

)

(

)

2 3

1

3

9

2 3

1

2

x x

x

x x

x

+

+

−
+

⋅

(

) (

)(

)

(

)

2 3

1

3

3

3

2 3

1

x x

x

x x

x

x

+

+

−

+

+

⋅

(

)

x x

2

3

1

−

x

3

 – 3x

85

Matematyczne  domino  może  być  wykorzystane
w  czasie  lekcji  powtórzeniowych.  Proponujemy
grę opartą na wiadomościach z geometrii.
Gra  ta  może  być  także  inspiracją  do  stworzenia
podobnej gry wykorzystującej wiedzę z różnych
działów matematyki. Domino może być przepro-
wadzone w oparciu o różne zasady, np. ułożenie
najdłuższego  łańcucha  w  określonym  czasie  lub
ułożenie w najkrótszym czasie łańcucha złożone-
go ze wszystkich części domina.
Gra polega na skojarzeniu odpowiednich elemen-
tów  domina.  Wolne  pola  można  wykorzystać,
uzupełniając je odpowiednimi rysunkami lub też
pozostawić je puste tak jak to jest w tradycyjnym
dominie.

Matematyczne domino

V 

=

1
3

P

p

·h

a
2

a

V

 = 
P

p

 · 

h

3

2

sin 60°

3

13

tg 

a

 = 1,5

P

 = 4

pr

2

P

 =

 

d

2

2

ctg 45°

tg 45°

2

86

V

 = 

1

3

P

p

 · h

V

 = P

p

 · h

3

2

sin 60°

a

a

2

87

3

13

tg 

a = 1,5

P

 = 4
p

r

2

P

 = 

d

2

2

ctg 45°

tg 45°

2