Budowle i urządzenia hydrotechniczne

mgr inż. Dominik Sołtys

Przyjęcie ilości przęseł jazu oraz obliczenie szerokości światła jazu

B= B

RZ

⋅

0,7−1,0 , b=



B−a⋅n

n

B

RZ

– szerokość rzeki przed spiętrzeniem

B - szerokość jazu
b – szerokość jednego przęsła
n – ilość przęseł jazu
a – szerokość filarów jazu

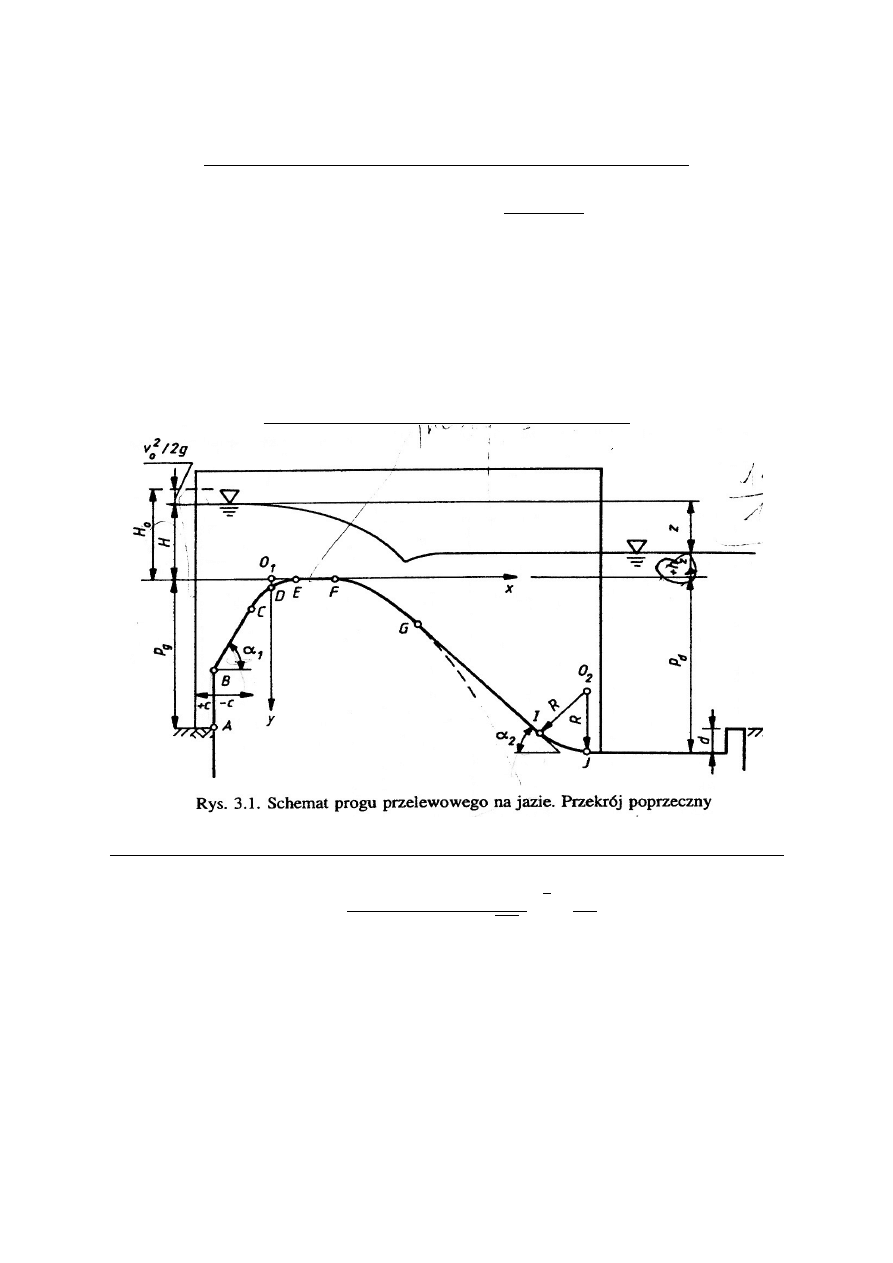
Schemat przekroju jazu o kształtach praktycznych:

Obliczenie grubości warstwy wody przelewającej się przez próg dla przepływu miarodajnego

H

0

=



Q

m



n⋅b⋅m⋅

k



z

⋅⋅



2g





2
3





v

0

2

2g

Q

m

- przepływ miarodajny

n – ilość przęseł jazu
b – szerokość jednego przęsła jazu
m – współczynnik wydatku przelewu

σ

k

– współczynnik kształtu progu

σ

z

– współczynnik zatopienia przelewu

ε

- współczynnik kontrakcji bocznej i czołowej

I – przybliżenie

Do wstępnych obliczeń przyjmujemy początkowe wartości współczynników:

m – 0,38

σ

k

– 1

σ

z

– 1

ε

- 1

Po obliczeniu wartości H

0

możemy przystąpić do kolejnego przybliżenia

Jeżeli v

0



1 m/s to wartość tą pomijamy (v

0

=Q/A

d

)

Q – przepływ
A

d

– światło doliny po spiętrzeniu

II – przybliżenie

Współczynniki przyjmujemy w następujący sposób:

1. “m”

Dokonujemy sprawdzenia czy wstawka prosta będzie miał istotny wpływ na wydatek
przelewu.

∣

EF∣= L

Jeżeli L<0,6 H to współczynnik “m” obliczamy jak dla przelewu bez wstawki prostej.
Współczynnik przyjmujemy z tabeli 3.5 i zależny będzie on od stosunku wysokości progu
“p

g

” do grubości warstwy wody przelewającej się przez próg “H”.

p

g

= H

NPP –

H

0

Tabele 3.5 należy odczytywać w następujący sposób: w lewej kolumnie podano wartości
całkowite stosunku H/p

g

a w pierwszym wierszu podano wartości dziesiętne

W przypadku, gdy L

≥

0,6 H postępujemy następująco:

Wartość współczynnika “m” przyjmujemy z tabeli 3.6 i zależny on będzie od stosunku
długości wstawki prostej “L” do grubości warstwy wody przelewającej się przez próg “H”.

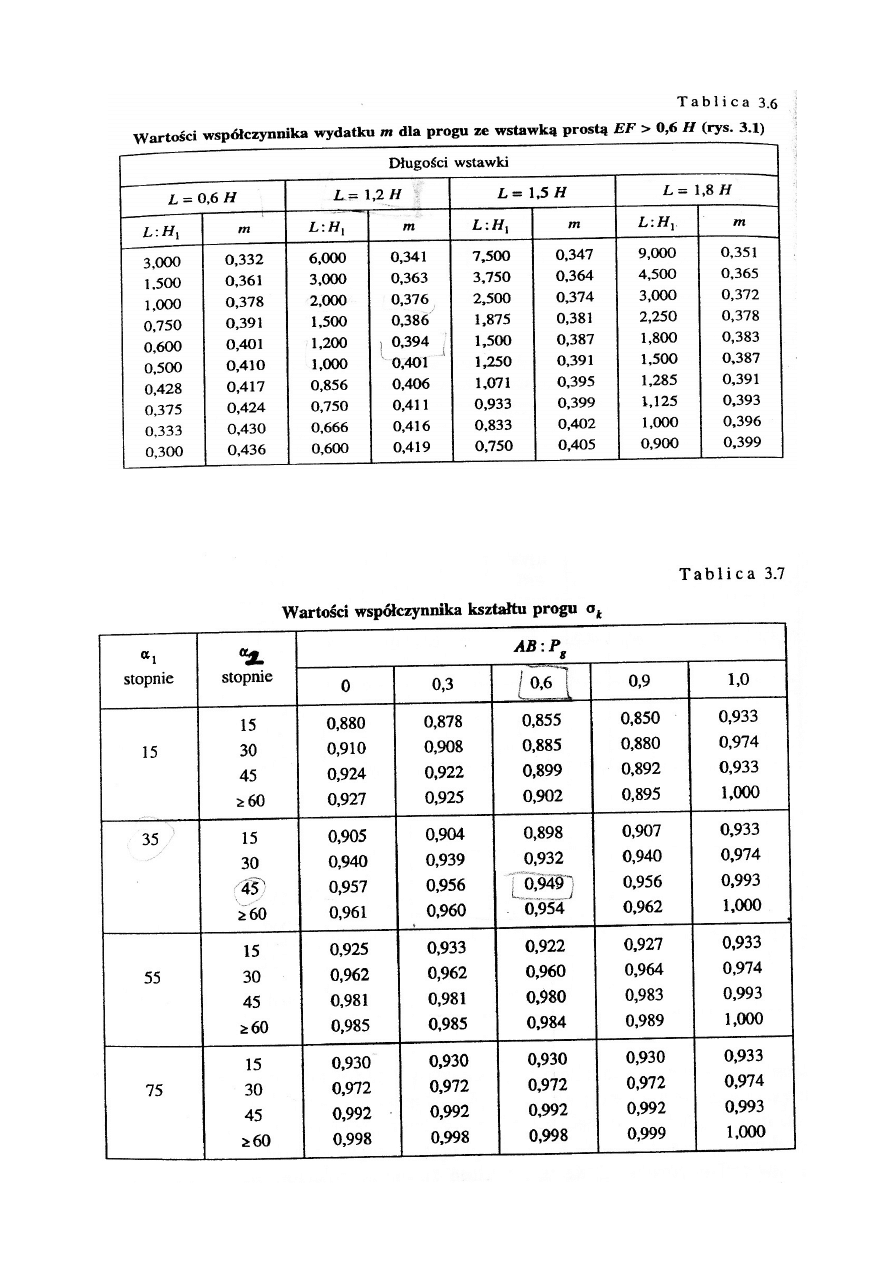
2. σ

k

” – współczynnik kształtu progu

Przyjmujemy z tabeli 3.7 na podstawie stosunku odcinka “AB” do wysokości progu “p

g

”

3.

σ

z

” – współczynnik zatopienia przelewu

zmniejszenie wydatku przelewu ze względu na jego zatopienie zachodzi wówczas gdy
spełnione są dwa warunki:

h

z

>0 oraz

z

p

d

≤



z

p

d



kr

do obliczenia wartości “p

d

“ należy przyjąć głębokość niecki wypadowej “d” równa 2 m

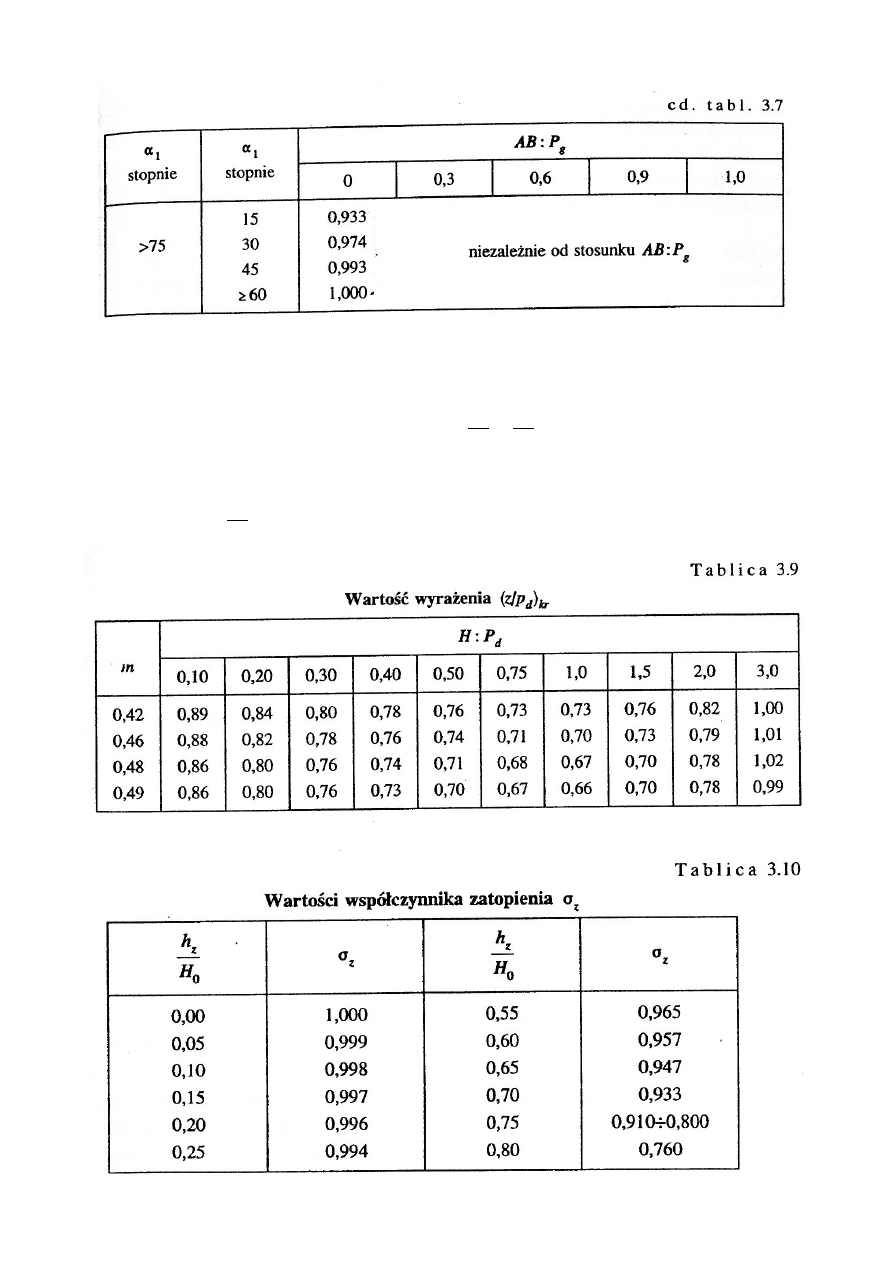
Wartość



z

p

d



kr

przyjmujemy z tabeli 3.9 w zależności od stosunku “H” do “p

d

”

Jeżeli spełnione są oba powyższe warunki to przyjmujemy wartość

σ

z

” z tabeli 3.10.

W przeciwnym przypadku wartość tego współczynnika równa jest 1

4.

ε

- współczynnik kontrakcji bocznej i czołowej

Jeżeli B

rz

>B oraz

h

z

H

0

≤

0,90 to :

=

1−



0,2



p



n−1

f



n



H

0

b

Jeżeli H

0

>b to za należy przyjąć stosunek tych wartości równy 1

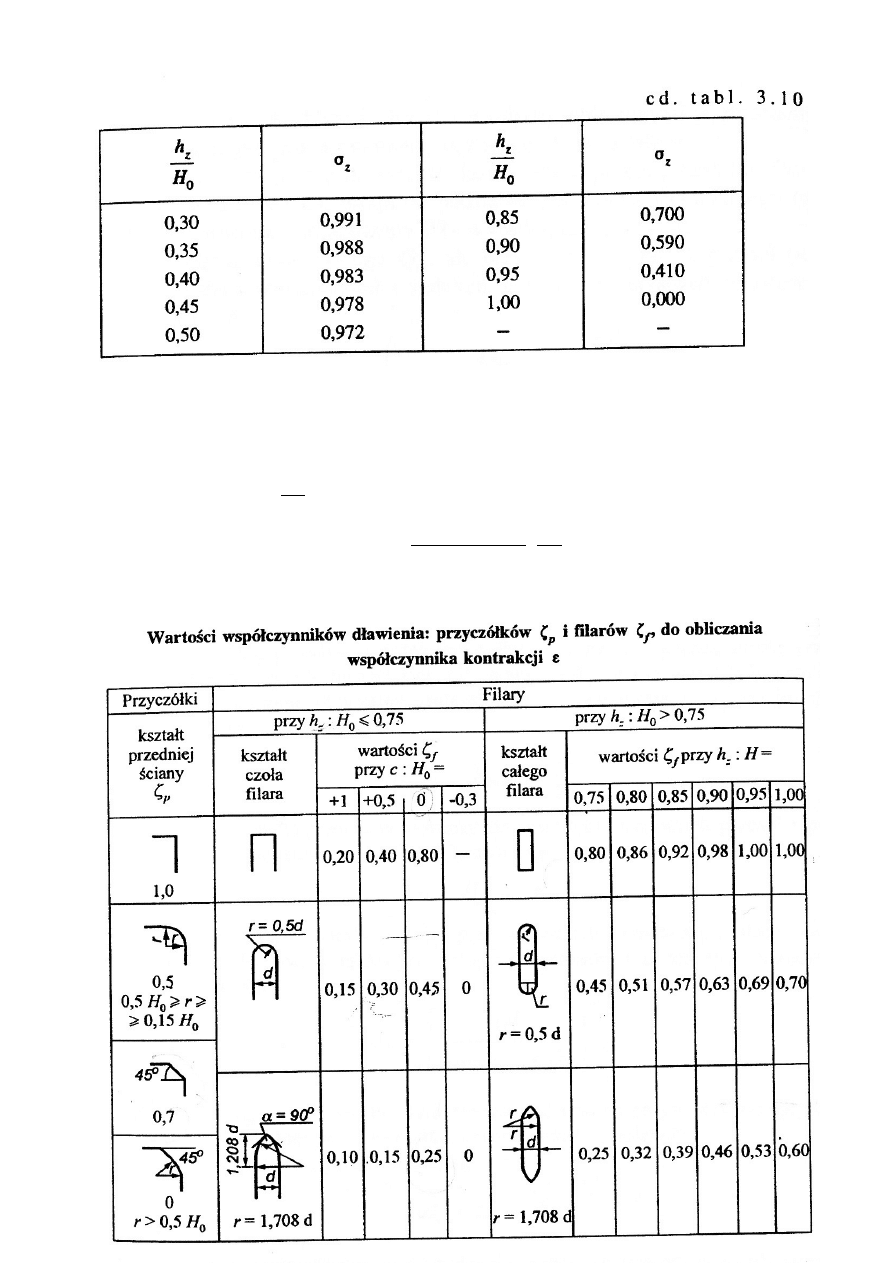
Gdzie ”

ζ

p

” oraz ”

ζ

f

” przyjmujemy z tabeli 3.11:

W przeciwnym przypadku

ε

obliczamy ze wzoru

:

=

1−0,2 

f

H

0

b

Kolejne iteracje wykonujemy do momentu gdy spełniony zostanie warunek że:

∆

H = H

i

- H

i+1

=

±

5 cm

Obliczenie grubości warstwy wody przelewającej się przez próg dla przepływu miarodajnego

Po obliczeniach grubości warstwy wody przelewającej się przez próg dla przepływu miarodajnego
należy przeprowadzić tą sama metoda obliczenia dla:

1. Przypadku remontowego:

H

0

=



Q

m



n−1⋅b⋅m⋅

k



z

⋅⋅



2g





2
3





v

0

2

2g

Q

m

- przepływ miarodajny

n – ilość przęseł jazu
b – szerokość jednego przęsła jazu
m – współczynnik wydatku przelewu

σ

k

– współczynnik kształtu progu

σ

z

– współczynnik zatopienia przelewu

2. Przepływu kontrolnego:

H

0

=



Q

k



n⋅b⋅m⋅

k



z

⋅⋅



2g





2
3





v

0

2

2g

Q

k

- przepływ kontrolny

n – ilość przęseł jazu
b – szerokość jednego przęsła jazu
m – współczynnik wydatku przelewu

σ

k

– współczynnik kształtu progu

σ

z

– współczynnik zatopienia przelewu

Następnie należy przyjąć wysokość korony i rzędne innych urządzeń zapory wg. rozporządzenia
omawianego na pierwszych zajęciach.

Powyższe materiały stanowią jedynie uzupełnienie prowadzonych zajęć i

stanowią integralną część z rysunkami oraz tematami omawianymi i

tworzonymi na ćwiczeniach.